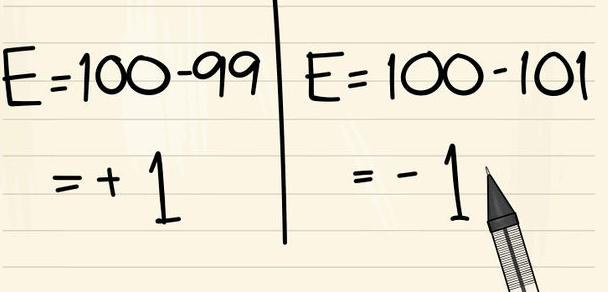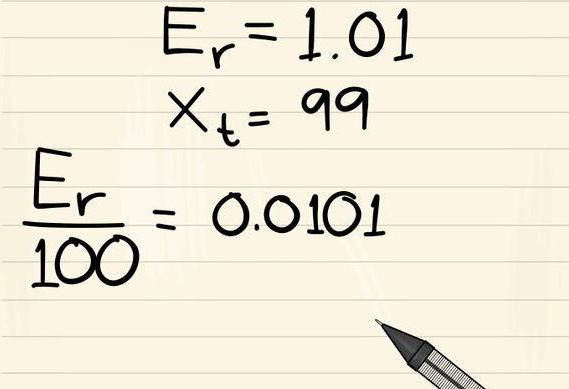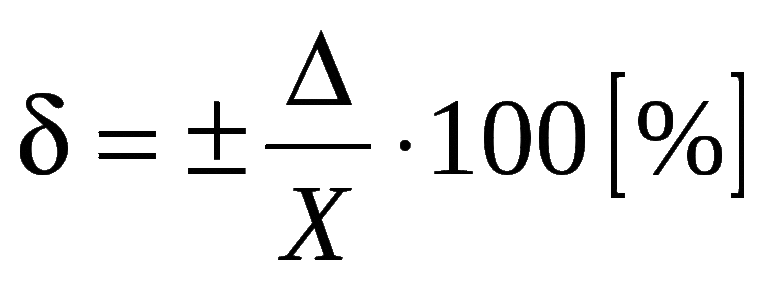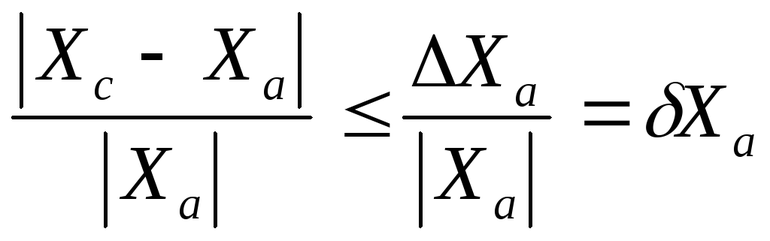|
Известны данные за отчетный период и данные за аналогичный период предыдущего года. Абсолютное отклонение это разница между отчетным и базовым периодом. Допустим, в прошлом году у нас было 3 яблока, а в этом 4. Абсолютное отклонение 4-3=1 яблоко Относительное отклонение — это соотношение отчетного к базовому периоду (обычно в процентах выражается, т.е. нужно еще на 100 умножить). Относительное отклонение (4/3)*100=133,3% (т.е. колическтво яблок увеличилось на 33,3 %=133,3%-100%) система выбрала этот ответ лучшим Koriandr 17 4 года назад Абсолютным отклонением считается разница, которая имеется между отчетным и базовым периодом. Относительное отклонение — это соотношение отчетного к базовому периоду. Отчетный период — это определенный период в деятельности, по результатам которого составляются основные документы финансовой отчетности(например — отчет о прибылях и убытках ). Базовый период — период времени, с которым производится сравнение проектируемых или отчетных показателей(ВВП, прибыли и др.) какого-либо другого, обычно более позднего периода. Относительное отклонение — текущий период «a», базовый период «b». Aо = a-b. Относительное отклонение высчитывается в процентах 0о = a/b х 100% Вот так это решается и сложного ничего нет. А555АА 7 лет назад Для этого сначала вспомним что такое абсолютное отклонение и относительное отклонение. Абсолютное отклонение (Ао): это разница между отчетным периодом ( это цифры текущего отчетного года обозначим О) и базовым периодом( это цифры прошлого года обозначим буквой Б) И так: Ао = О — Б Относительное отклонение (выражается в процентах и обозначим Оо) и определяется делением отчетного периода на базовый и умножением на сто для перевода в проценты. И так это будет будет выглядеть вот так: Оо = (О/Б)*100 Примет: прошлом году выращено 50 тонн картошки, а в этом году 60 тонн картошки. Абсолютное отклонение будет равняться 10 тоннам. 60-50=10 Относительное отклонение будет составлять 20 процентов. (60/50)*100=20% Peresvetik 8 лет назад Главной чертой такой, как показатель любого отклонения- будет тот факт, который позволит отклониться от определенного различия абсолютной величины. Это этот факт даст возможность сравнить всевозможные явления те, где абсолютное значение по своей сути является не сопоставимым. Данное отклонение является разностью между какими то величинами, и оно может быть как положительным,так и отрицательным. Любое относительное отклонение может быть рассчитано по отношению к другой величине. И оно будет выражаться либо в процентном исчислении, либо в долевом. Такой индекс исчисления повышает уровень для анализа,который проводится и позволит точно оценить все изменения. Абсолютное отклонение это простое арифметическое действие с использованием знака (-) минус. К примеру; Вчера я выпил две бутылки лимонада, а сегодня три бутылки, абсолютное отклонение будет 3-2=1 равно 1 бутылка. Относительное отклонение выражается исключительно в процентах и определяется отношение отчетных цифр к базовым умножением на 100, в нашем случае это выглядит так; 3/2*100=150 то есть относительное отклонение составляет 50 процентов. Абсолютное отклонение равно: рентабельность по факту минус рентабельность по плану. Это отклонение может быть как положительным, так и отрицательным. Относительное отклонение равно: абсолютное отклонение разделить на рентабельность по плану и умножить на 100%, тоже может быть как положительным, так и отрицательным. Ниннелль 9 лет назад Абсолютное отклонение рассчитывается как разница между текущим (отчетным периодом) и аналогичным периодом прошлого года (АППГ), либо просто другим прошедшим периодом, который нужен нам для сравнения рентабельности предприятия. То есть из значения текущего периода мы отнимаем значение базового периода, полученная разница и будет являться абсолютным отклонением. А относительное отклонение — соотношение тех же показателей друг к другу, только выраженное в процентах. Показатели текущего периода надо разделить на показатели базового периода и умножить на 100. Так мы получаем в процентах относительное отклонение. Ky3HEts 5 лет назад Абсолютное отклонение — это величина между двумя периодами, измеряется оно в единицах. Например: В позапрошлом месяце Вы заработали на БВ 10- кредитов, а в прошлом — 200 кредитов. Абсолютная отклонение будет высчитываться по схеме 200-100 = 100 кредитов. Относительное отклонение — это соотношение между периодами, которое измеряется в процентах и формула с тем же данными выглядела бы следующим образом: 200/100 = 2*100% = 200%-100% (Процент кредитов за предыдущий месяц) = 100%. Ровно на 100% увеличилась Ваша прибыль за прошлый месяц. Kobayashi 3 месяца назад Абсолютные и относительные отклонения — это два важных показателя, используемых для количественной оценки того, насколько конкретное значение отличается от контрольного значения. Эти показатели обычно используются в таких областях, как статистика, финансы, инженерное дело и многие другие, чтобы понять изменчивость набора данных и принимать решения на основе результатов. Абсолютное отклонение: Абсолютное отклонение, также известное как абсолютная разница, — это разница между значением и эталонным значением. Он выражается как величина разницы между двумя значениями и вычисляется как: Абсолютное отклонение = |значение — исходное значение| Например, если значение равно 75, а исходное значение равно 100, то абсолютное отклонение равно |75-100| = 25. Абсолютное отклонение измеряет разницу между значением и эталонным значением в абсолютных величинах и не зависит от размера значения или эталонного значения. Относительное отклонение: Относительное отклонение, также известное как процентное отклонение, представляет собой абсолютное отклонение, выраженное в процентах от контрольного значения. Он рассчитывается как: Относительное отклонение = (Абсолютное отклонение / исходное значение) х 100% Например, если значение равно 75, а исходное значение равно 100, то абсолютное отклонение равно 25, а относительное отклонение равно (25/100) х 100% = 25%. Относительное отклонение измеряет процентную разницу между значением и эталонным значением, и оно обеспечивает более осмысленное представление отклонения, особенно при сравнении значений разных размеров. Использование абсолютного и относительного отклонения: Абсолютные и относительные отклонения используются в различных приложениях, таких как контроль качества, финансовый анализ и инженерное проектирование. При контроле качества абсолютное отклонение используется для определения точности измерения или продукта, в то время как относительное отклонение используется для определения изменчивости измерения или продукта по отношению к контрольному значению. В финансовом анализе абсолютное отклонение используется для определения разницы между фактическими и ожидаемыми значениями, в то время как относительное отклонение используется для определения процентной разницы между фактическими и ожидаемыми значениями. В инженерном проектировании абсолютное отклонение используется для определения разницы между желаемыми и фактическими значениями расчетного параметра, в то время как относительное отклонение используется для определения процентной разницы между желаемыми и фактическими значениями расчетного параметра. Вывод: В заключение, абсолютное и относительное отклонение — это два важных показателя, используемых для количественной оценки отклонения между значением и эталонным значением. Абсолютное отклонение измеряет отклонение в абсолютном выражении, в то время как относительное отклонение измеряет отклонение в процентах от контрольного значения. Эти показатели широко используются в различных приложениях для принятия обоснованных решений на основе отклонения между значениями и контрольными значениями. Kin963 8 лет назад Можно показать на примере. Примем за условие, что:
Для того, чтобы узнать относительное отклонение между этими периодами, надо ((9/6) *100)-100=50%, то есть относительное отклонение за эти два периода 50%. Для расчета абсолютного отклонения между этими периодами нужно 9-6=3, то есть абсолютное отклонение 3 у.е. НеЯэто 4 года назад Есть фактическая (индекс 1) и базовая (инд 0) величина показателей. Вот разность между ними и будет абсолютное отклонение. Относительное — это соотношение между инд 0 и 1, умноженное на 100. В поликлинику обратились за прошлый год 2000 первичных, за отчетный — 2135, абс откл = 135 2 135/2000х100 = 106,75 — 100 = 6,75 — относ откл В отчетном периоде первичных обращений увеличилось на 6,75 процентов. Андрей1961 6 лет назад Отклонение абсолютное выражено разницей между двумя периодами отчетным и периодом базовым. К примеру в прошлом месяце ваш уровень зарплаты составлял 20 тыс. рублей, в следующем месяце уже 21 тыс. рублей. Абсолютное отклонение выразится разницей месяцев и будет равна 1 тыс. рублей. А вот относительная-это уже соотношение 21/20х100=105, обычная единица измерения в данном случае-% розовый фламинго 9 лет назад Абсолютное отклонение всегда выражено в точной математической цифре, дающую точную информацию о некоем промежутке времени между точкой отсета начала события до точки отсета конца события. Относительное отклонение никогда не выражено в точных цифрах. Информация в данном случае выдана в процентом показателе дающем косвенную информацию не точную, а приблизительную. biggold 9 лет назад Если вычесть из фактической рентабельности плановую, то мы получим Абсолютное отклонение Очевидно что этот показатель может быть положительным если предприятие успешное, и наоборот. Если абсолютное отклонение разделить на плановую рентабельность, а затем умножить на сотню, то мы получим относительное отклонение выраженное в процентах. nikumarina2011 9 лет назад Разница между текущим периодом и прошлогодним и будет считаться абсолютным отклонением. Эти цифры просто вычитаются. А результат может быть как положительным, так и отрицательным. А относительное отклонение соответственно выражается в процентном отношении этих показателей по отношению друг к другу, является всегда положительным. Анна Сергеевна Саченко 7 лет назад Для определения обсолютного отклонения нужно, от полученного показателя отнять базовый. Следовательно отчетный минус аналогичный.В модуле! Относительное отклонение исчисляется отношением обсолютного отклонения к базовой(аналогичной) величине и умножено на 100%. ворчунов 9 лет назад Абсолютное отклонение — это разность между величинами, может быть положительной и отрицательной. Относительное отклонение — это отношение между величинами и соответственно его выражают в процентах и отрицательным оно быть не может. mister 4 года назад Абсолютное отклонение — это разница в количестве, выражается в абсолютной величине. А вот чтобы получить относительное отклонение, нужно разделить эту разницу на то количество, которое было, и умножить на 100 процентов. Alen4uk 9 лет назад Абсолютное значение представляет собой разницу между начальным результатом и достигнутым. Если даны 2 показателя, между которыми необходимо найти абсолютное отклонение, нужно вычесть из большего меньшее. Например, в одном магазине товар стоит 50 руб, в другом — 55 руб. 55-50=5 . Это есть абсолютное отклонение цены. Абсолютное отклонение 2 параметров во времени. Например, Доход фирмы в январе -5000 руб, в феврале — 4000 руб. Абсолютное отклонение = 4000 — 5000 = (-1000). Берем модуль числа . Понятно, что прибыль предприятия уменьшилась. Относительные показатели представляют собой отношение одной абсолютной величины к другой. Расчет относительного отклонения производится для оценки деятельности предприятия. Валерий Валерьевич 4 года назад Абсолютное отклонение — это как правило разница между начальным этапом и достигнутым. Например, если вам известна стоимость услуги в двух парикмахерских.Допустим это 300 и 350 рублей за стрижку, рассчитаем разницу: 350-300=50 (рублей) – это абсолютное отклонение цены. Относительное отклонение — это соотношение тех же услуг только в процентном выражении. Т. е. (350/300)*100 Получим результат выраженный в процентах.Такой принцип расчетов позволяет более правильно анализировать и оценить все изменения. Если в этом разобраться то ничего сложного тут нет. Cranium 5 лет назад относительное отклонение рассчитывают по отношению к другим данным(общему показателю или параметру) и оно выражается в процентах- т.е. одну величину делим на другую и еще*100%, носит дополнительную информативность и позволяет более точно оценить изменение контольной величины. А абсолютное отклонение — это разница(путем вычетания) между величинами- отчетным и базовым периодом. например, в прошлом году мы получили на урожай 50 огурцов, а в этом — 56. Абсолютное отклонение — 56-50=6; относительное — (56/50)*100=112%. Скрепка 9 лет назад Абсолютное отклонение — разница между данными за отчетный период и данными за аналогичный период предыдущего года. Поскольку Вы не приводите самих данных, то будем оперировать именно этим термином. Данные (текущий период) — Данные (прошлый период) Относительное отклонение — это отношение данных текущего периода к данным предыдущего, выраженное в процентах. (Данные (текущий период) / Данные (предудыщий период))*100%-100 jarptica 9 лет назад Абсолютное отклонение выражается, как правило, в каких-то единицах, в абсолютном выражении (рублях, килограммах, метрах, штуках и прочим). То есть берем одну цифру и вычитаем из такой же цифры предыдущего периода. Получаем абсолютное отклонение. А относительное считается в процентах. То есть берем цифру текущего года и делим ее на цифру предыдущего года, получается выражение в процентах. Знаете ответ? |
Под абсолютными
величинами
в статистике понимают показатели,
которые характеризуют размеры изучаемых
явлений и процессов. Например, объем
товарной продукции предприятия,
численность промышленно-производственного
персонала, размер прибыли и др.
Абсолютные величины
в статистике являются исходной базой
статистического анализа. Они выражаются
в натуральных, условно-натуральных,
стоимостных и трудовых единицах.
Натуральные
показатели имеют
наименование, даны в натуральных единицах
измерения (тонны, килограммы, метры,
литры, штуки и т.д.) Условно-натуральные
показатели
используются в тех случаях, когда какой
либо продукт имеет несколько разновидностей,
и общий объем можно определить только
исходя из общего для всех разновидностей
потребительского свойства. Перевод в
условные единицы измерения осуществляется
на основе специальных коэффициентов,
рассчитываемых как отношение
потребительских свойств отдельных
разновидностей продукта к их эталонному
значению.
Стоимостные
показатели дают
денежную оценку социально- экономическим
явлениям и процессам.
К трудовым
единицам измерения
относятся показатели, характеризующие
общие затраты труда, трудоемкость. Они
измеряются в человеко-днях, человеко-часах
и т.д.
Различают
индивидуальные и сводные (суммарные)
абсолютные показатели.
Индивидуальные
показатели получают непосредственно
в процессе статистического наблюдения
как результат замера, взвешивания,
подсчета и т. д. изучаемого количественного
признака.
Сводные (суммарные)
показатели характеризуют объем признака
или объем совокупности либо всего
объекта, либо его части. Их определяют
в результате сводки и группировки
индивидуальных значений.
Относительные
величины представляют собой результат
сравнения (деления) двух показателей.
В зависимости от
того, к какому числу единиц приравнена
база сравнения, относительные величины
могут выражаться в форме:
-
коэффициента,
если основание принято за 1; -
процента (%), если
основание принято за 100; -
промилле (0/00),
если основание принято за 1000; -
продецимилле
(0/000),
если основание принято за 10000.
Следует иметь в
виду, что большинство относительных
величин являются неименованными числами,
за исключением тех, которые получаются
в результате сравнения разноименных
показателей и внешне напоминают средние
величины (например, плотность населения).
В отличие от
абсолютных величин, относительные
показатели являются величинами
производственными и рассчитываются на
основе абсолютных величин.
В статистическом
анализе рассчитывают следующие виды
относительных
величин: динамики, выполнения плана,
планового задания, структуры, координации,
интенсивности, сравнения.
Относительный
показатель динамики(ОПД) – показатели,
характеризующие соотношение одноименных
величин во времени. Они рассчитываются
по формуле:
Частное от деления
числителя на знаменатель дроби называют
коэффициентом
динамики.
Коэффициент динамики, выраженный в
процентах, называют темпом
роста. Не
следует путать отчетный и базисный
периоды. Отчетный
период –
всегда текущий, базисный—
период, предшествующий отчетному.
Приведем пример
расчета относительных величин динамики
(табл. 8).
Таблица 8
Расчет относительных
величин динамики
по данным выпуска
товарной продукции
в организации
|
Месяц |
Товарная продукция, млн. |
Относительная |
|||
|
С |
С переменной сравнения |
||||
|
коэффициент |
% |
коэффициент |
% |
||
|
Январь |
1390,7 |
1,000 |
100,0 |
— |
— |
|
Февраль |
1426,9 |
1,026 |
102,6 |
1,026 |
102,6 |
|
Март |
1492,6 |
1,073 |
107,3 |
1,046 |
104,6 |
|
Апрель |
1547,5 |
1,113 |
111,3 |
1,037 |
103,7 |
Вычислим относительные
величины динамики с постоянной базой
сравнения, приняв за базу
январь:1426,9/1390,7=1,026*100=102,6%;
1492,6/1390,7=1,073*100=107,3% и т.д. Такие величины
с постоянной базой сравнения называют
базисными
темпами роста.
Здесь каждый последующий уровень
сравнивается с одним постоянным
закрепленным уровнем.
Вычислим относительные
величины динамики с переменной
базой сравнения, используя
соотношения каждого последующего месяца
к предыдущему:
1426,9/1390,7=1,026*100=102,6%;1492,6/1426,9=1,046*100=104,6% и т.д.
Эти полученные относительные показатели
с переменной базой сравнения называют
цепными
темпами роста.
Между базисными
и цепными темпами роста существует
взаимосвязь: произведение цепных темпов
роста равно базисному темпу последнего
периода.
Относительный
показатель выполнения плана (ОПВП) —
показатели,
характеризующие степень выполнения
планового задания. Они рассчитываются
по формуле:
Рассмотрим расчет
показателей выполнения плана по данным
табл. 8.
За I
квартал ОПВП .=(24,15/22,28)*100%=108,4%;
За II
квартал ОПВП .=(23,62/21,35)*100%=110,6%.
Аналогичные расчеты
произведем за остальные периоды. По
расчетам можно сделать следующие выводы:
более высокий процент выполнения плана
по выпуску продукции приходится на II
квартал (110,6%). Меньше всего перевыполнен
план был в III
квартале – на 4,3%.
Относительный
показатель планового задания (ОППЗ) –
показатели, характеризующие степень
установления планового задания на
отчетный период. Они рассчитываются
по формуле:
Рассмотрим расчет
относительных показателей планового
задания по данным табл. 9.
Таблица 9
Расчет относительных
величин выполнения плана и планового
задания по данным выпуска продукции
бригадой в организации
|
Квартал |
Выпуск |
Выполнение |
Выполнение |
||
|
Базисный |
Отчетный |
||||
|
план |
факт |
||||
|
I |
22.25 |
22,28 |
24,15 |
108,4 |
100,1 |
|
II |
21.30 |
21,35 |
23,62 |
110,6 |
100,2 |
|
III |
22.3 |
22,94 |
23,93 |
104,3 |
102,9 |
|
IV |
22.20 |
22,29 |
24,08 |
108,0 |
100,4 |
За I
квартал
ОППЗ = (22,28/22,25)*100=100,1 %.
Аналогичные расчеты
производим за остальные периоды. По
расчетам можно сделать следующие выводы:
самый высокий процент установления
планового задания приходится на III
квартал (102,9%).
Относительные
величины динамики планового задания
и выполнения плана находиться в
определенной зависимости, а именно:
произведение относительных величин
выполнения плана и планового задания
равно относительной величине динамики.
Между указанными
показателями существует связь вида:
ОПД = ОПВП
ОППЗ.
Относительный
показатель структуры (ОПС) —
показатели, характеризующие долю
составных частей целевого в общем итоге.
Если задать условие, что:
n
X1+X2+X3+…Xn=∑X
1
то, приняв итоговую
величину за 100%, можно рассчитать по
отношению к этой величине в процентном
соотношении каждую составляющую. При
этом сумма
рассчитанных относительных величин
структуры должна составлять 100% или
1.
Относительный
показатель координации (ОПК) — показатели,
характеризующие соотношение друг к
другу составных частей целого.
При вычислении
относительных величин координации за
базу, сравнения принимается какая –
либо одна часть изучаемой совокупности,
а остальные соотносятся с ней.
Относительные
величины координации могут быть выражены
не только в коэффициентах, но и в
процентном соотношении, и тех же
именованных единицах, в которых выражен
признак.
В качестве базы
сравнения целесообразно выбирать ту,
которая имеет наибольший удельный вес
или является приоритетной (например,
число мужчин на 1000 женщин).
Относительный
показатель интенсивности (ОПИ) –
показатели,
характеризующие соотношение одного
экономического явления в расчете на
единицу другого
При вычислении
относительных величин интенсивности
необходимо помнить, что они, в отличие
от величин динамики, выполнения плана
и структуры являются величинами
именованными.
К относительным
величинам интенсивности можно отнести
показатели выработки, фондоотдачи,
число родившихся или умерших на 1000
человек населения, производство продукции
на душу населения.
Относительный
показатель сравнения (ОПСр)
— показатели,
характеризующие сравнительные размеры
одноименных явлений за один и тот же
период времени, но по разным объектам.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В экономической науке статистические дисциплины находятся на приоритетных позициях. Это обусловлено различными причинами. В первую очередь в рамках общеэкономических специальностей статистические исследования выступают в качестве основы разработки и совершенствования аналитических методов. Кроме этого, они являются самостоятельным направлением, имеющим собственный предмет.
Абсолютные и относительные величины
Эти понятия выступают как ключевые элементы в статистической науке. Они используются для определения количественных характеристик, динамики их изменения. Абсолютные и относительные величины отражают разные характеристики, но без одних не могут существовать другие. Первые выражают количественные размеры того или иного явления безотносительно к другим. По ним нельзя оценить происходящие изменения и отклонения. Они выражают объем и уровень процесса или явления. Абсолютные величина являются всегда именованными числами. Они имеют размерность или единицу измерения. Они могут быть натуральными, трудовыми, денежными и проч. К примеру, нормо-часы, шт., тыс. руб. и так далее. Средние и относительные величины, наоборот, выражают соотношение нескольких точных размеров. Оно может устанавливаться для нескольких явлений или для одного, но взятого в другом объеме и в иной период. Эти элементы выступают как частное от статистических чисел, которое характеризует количественное их соотношение. Чтобы определить относительные величины, нужно один размер разделить на другой, принятый в качестве базового. Последними могут быть плановые данные, фактические сведения предыдущих лет или другого предприятия и так далее. Относительная величина сравнения может выражаться в процентах (при базе, принятой за 100) или коэффициентах (если база единица).
Классификация статистических чисел
Абсолютные величины представлены в двух типах:
- Индивидуальные. Они характеризуют размер признака у конкретных единиц. Например, это может быть величина зарплаты сотрудника, вклада в банке и так далее. Эти размеры находят непосредственно в ходе статистического наблюдения. Они фиксируются в первичной учетной документации.
- Суммарные. Величины этого типа отражают итоговый показатель признака по совокупности объектов. Эти размеры выступают в качестве суммы количества единиц (численности совокупности) или объема варьирующей характеристики.
Единицы измерения
Натуральные абсолютные величины могут быть простыми. Это, например, тонны, литры, рубли, штуки, километры. Они могут быть и сложными, характеризовать комбинацию нескольких величин. К примеру, в статистике используются тонно-километры для установления грузооборота железнодорожного транспорта, киловатт-часы — для оценки производства электроэнергии и проч. В исследованиях применяются и условно-натуральные единицы. К примеру, тракторный парк может пересчитываться в эталонные машины. Стоимостные единицы применяют для характеристики разнородного товара в денежном выражении. Эта форма, в частности, используется при оценке дохода населения, валового выпуска продукции. Используя стоимостные единицы, статисты принимают во внимание динамику цен во времени, а недостаток преодолевают за счет «сопоставимых» или «неизменных» цен по одному и тому же периоду. Трудовыми величинами учитывают общие затраты работы, трудоемкость тех или иных операций, составляющих технологический цикл. Они выражаются в человеко-днях, человеко-часах и проч.
Относительные величины
Основным условием их расчета выступает сопоставимость единиц и наличие реальной связи между исследуемыми явлениями. Та величина, с которой осуществляется сравнение (знаменатель в дроби), выступает, как правило, в качестве базы или основания соотношения. В зависимости от ее выбора, результат может выражаться в различных долях единицы. Это могут быть десятые, сотые (проценты), тысячные (10-я часть % — промилле), десятитысячные (сотая доля % — продецимилле). Сопоставляемые единицы могут являться как одно-, так и разноименными. Во втором случае их наименования формируются от используемых единиц (ц/га, руб./чел. и т. д.).
Виды относительных величин
В статистике используется несколько типов этих единиц. Так, существует относительная величина:
- Структуры.
- Планового задания.
- Интенсивности.
- Динамики.
- Координации.
- Сравнения.
- Степени экономического развития.
Относительная величина задания выражает отношение запланированного на предстоящий срок к фактически сложившемуся на текущий период. Аналогично рассчитывается единица плана. Относительная величина структуры — это характеристика доли конкретных частей исследуемой совокупности в ее общем объеме. Их расчет осуществляется посредством деления численности в отдельных частях на общее их количество (или объем). Выражаются эти единицы в процентах или простом кратном отношении. К примеру, так рассчитывается удельный вес городского населения.
Динамика
Относительная величина отражает в этом случае отношение уровня объекта в конкретный период к его статусу в прошедшее время. Другими словами, характеризуется изменение явления в течение какого-либо срока. Относительная величина, характеризующая динамику, именуется темпом роста. Выбор базы при расчете осуществляется в зависимости от цели исследования.
Интенсивность
Относительная величина может отражать степень развития какого-либо явления в конкретной среде. В этом случае говорят об интенсивности. Их вычисление производится сравнением разноименных величин, которые находятся в связи друг с другом. Они устанавливаются, как правило, в расчете на 1000, 100 и так далее единиц исследуемой совокупности. Например, на 100 га земли, на тысячу человек и проч. Эти показатели относительных величин — именованные числа. Например, так рассчитывается плотность населения. Она выражается средним числом граждан на 1 кв. км территории. В качестве подтипа таких единиц выступают характеристики степени экономического развития. К ним, например, относят такие виды относительных величин, как уровень ВНП, ВВП, ВИД и проч. на душу населения. Эти характеристики играют важную роль при анализе экономической ситуации в стране.
Координация
Значение относительных величин может характеризовать пропорциональность отдельных элементов целого друг к другу. Расчет осуществляется путем деления одной части на другую. Относительные величины в этом случае выступают как подтип единиц интенсивности. Разница заключается в том, что они отражают уровень распространения разнородных частей одной совокупности. Базой может выступать тот или иной признак, в зависимости от поставленной цели. В этой связи для одного и того же целого можно вычислить несколько относительных величин координации.
Сопоставление
Относительные величины сравнения — это единицы, которые представляют собой частные от деления одноименных статистических признаков, выступающих характеристиками для разных объектов, но относящихся к одному моменту или периоду. К примеру, вычисляется соотношение уровня себестоимости конкретного типа продукции, произведенной двумя предприятиями, производительность труда для разных отраслей и так далее.
Экономическая оценка
В этом исследовании активно используются абсолютные и относительные единицы. Первые применяются для установления соотношения запасов и расходов с источниками финансирования и оценки предприятия по уровню денежной устойчивости. Относительные показатели отражают структуру фондов с состоянием основных и оборотных средств. При экономической оценке используется горизонтальный анализ. В качестве наиболее обобщающей абсолютной величины, характеризующей финансовую устойчивость фирмы, выступает недостаток или излишек источников финансирования затрат и запасов. Расчет производится путем вычитания. Результатом является разница размера источников (за минусом внеоборотных активов), средствами которых формируются запасы, и их количеством. Ключевыми элементами в этом служат следующие статистические единицы:
- Собственные оборотные активы.
- Общий показатель плановых источников.
- Долгосрочные заемные и собственные средства.
Детерминированное факторное исследование
Этот анализ представляет собой определенную методику изучения воздействия факторов, взаимодействие которых с результатами обладает функциональным характером. Это исследование проводится созданием и оценкой детерминированных моделей. В этом анализе достаточно широко применяются относительные показатели. В большинстве случаев в факторном анализе используются мультипликативные модели. К примеру, прибыль можно выразить произведением количества товаров на стоимость единицы. Часть анализа в этом случае ведется 2 способами:
- Метод абсолютных разниц предполагает цепную подстановку. Изменение результата за счет фактора вычисляется как произведение отклонения изучаемого признака на базу другого по выбранной последовательности.
- Метод относительных разниц используется при измерении воздействия факторов на прирост результата. Он применяется тогда, когда в исходных данных присутствуют ранее вычисленные отклонения в процентах.
Динамические ряды
Они представляют собой изменение числовых показателей общественных явлений в течение времени. В качестве одного из важнейших направлений в этом анализе выступает исследование особенностей развития событий за конкретные периоды. Среди них:
- Темпы роста. Это относительный показатель, который рассчитывается делением двух уровней в одном ряде друг на друга. Они могут вычисляться как цепные или как базисные. В первом случае производится сопоставление каждого уровня ряда с предшествующим. Во втором случае выбирается база. Все уровни в ряду сопоставляются с одним, выступающим как основание. Темпы роста выражаются в коэффициентах или процентах.
- Абсолютный прирост. Он представляет собой разницу между двумя уровнями динамического ряда. В зависимости от метода выбора основания он бывает базисным и цепным. Этот показатель обладает той же размерностью, что и уровни ряда.
- Темпы прироста. Этот относительный показатель отражает количество процентов, на которое один уровень динамического ряда больше/меньше другого, который принят за базу.
Заключение
Несомненно, относительные величины обладают высокой научной ценностью. Однако на практике их нельзя использовать обособленно. Они всегда находятся во взаимосвязи с абсолютными показателями, выражая соотношения последних. Если это не учитывать, то невозможно точно охарактеризовать исследуемые явления. Используя относительные величины, нужно показать, какие конкретно абсолютные единицы скрыты за ними. Иначе можно сделать неверные выводы. Только комплексное использование относительных и абсолютных величин может выступать в качестве важнейшего средства информации и анализа при изучении разнообразных явлений, происходящих в социально-экономической жизни. В целом переход к вычислению отклонений позволяет сопоставлять хозяйственный потенциал и результат деятельности предприятий, которые значительно отличаются по объему используемых ресурсов или иным характеристикам. Относительные величины, кроме того, могут сгладить некоторые процессы (форс-мажор, инфляцию и прочие), которые могут исказить абсолютные единицы в финансовой отчетности.
Абсолютное
отклонение
– это разность между фактической и
базовой величиной показателя. Абсолютные
отклонения могут быть рассчитаны для
любых количественных и качественных
показателей (объема продукции,
количественных и качественных показателей,
характеризующих использование ресурсов,
величины активов, прибыли, финансовых
коэффициентов и т. п.). Например,
ΔN
= N 1
– N 0 ;
ΔR
= R 1
– R 0 ;
ΔD
= D 1
– D 0 ,
Базовые
значения показателей в анализе принято
обозначать индексом 0, фактические –
1, отклонения (изменения) – символом Δ.
Относительное
отклонение
позволяет
измерить прирост ресурса с учетом темпов
роста продукции, выпущенной с использованием
данного ресурса. Относительные отклонения
вычисляются только для количественных
показателей, характеризующих величину
потребленных ресурсов (затрат ресурсов).
Чтобы
найти относительное отклонение, нужно
из фактической величины ресурса вычесть
его базовую величину, скорректированную
на коэффициент
изменения объема продукции
.
ΔR’
= R 1
– R 0
× k N ;
k N
= N 1
/ N 0 .
Величина
R 0
× k N
показывает, сколько ресурсов было бы
необходимо для производства фактического
объема продукции, если бы не изменялись
качественные характеристики использования
ресурсов.
Отрицательное
относительное отклонение называется
относительной
экономией ресурса
,
положительное – относительным
перерасходом
.
Если
представить фактическую величину
ресурса через его базовую величину и
темп роста, формулу исчисления
относительного отклонения можно
преобразовать следующим образом:
ΔR’
= R 1
– R 0
× k N
= R 0
× k R
– R 0
× k N
= R 0
× (k R
– k N).
Такое
представление демонстрирует, что
относительное отклонение возникает за
счет разницы темпов роста ресурса и
продукции. Если темп роста продукции
опережает темп роста ресурса, возникает
относительная экономия, что свидетельствует
о достаточно эффективном использовании
ресурса. Если же темп роста ресурса
превышает темп роста продукции, ресурс
используется неэффективно, о чем
свидетельствует относительный перерасход.
Если
же темпы роста ресурса и продукции
совпадают, относительное отклонение
равно нулю. Это означает, что прирост
продукции получен экстенсивным путем,
т. е. только за счет привлечения
дополнительных ресурсов. При этом
качественные показатели использования
ресурса не изменяются.
На
основании данных таблицы 3.1 оценим
эффективность использования трудовых
ресурсов.
Таблица
3.1
Исходные
данные для оценки эффективности
использования трудовых ресурсов
Относительное
отклонение может быть вычислено только
для показателя, характеризующего
численность работающих.
ΔR’
= R 1
– R 0
×∙k N
= 96 – 90 ×∙1,111 = 96 – 100 = -4.
Данные
таблицы 3.1, а также расчет относительного
отклонения позволяют сделать вывод,
что трудовые ресурсы использовались
достаточно эффективно. Об этом
свидетельствует опережающий темп роста
объема продукции по сравнению с темпом
роста численности работающих, что и
привело к относительной экономии данного
вида ресурса, а также к росту выработки
продукции на одного работающего.
Таблица 1.1
|
Показатели |
Предш. год |
Отчет. год |
Выполнение плана, % |
Отклонение от плана |
Абс. прир. за год |
Темп роста, % |
Темп прироста,% |
||
|
Объем ТП в сопостав. ценах, млн. руб. |
Выполнение плана в %
=72166 / 68952 *100 % = 104,66 %
Т.о. можно сделать вывод, что план перевыполнен на 4,66 %
Абсолютное отклонение
= Отчетный год факт – Отчетный год план
Абсолютное отклонение
= 72166 – 68952 = 3214 млн. руб.
Т.о. можно сделать вывод о том, что план по производству товарной продукции перевыполнен на 3214 млн. руб.
Относительное отклонение
= Выполнение плана % — 100
Относительное отклонение
= 104,66 – 100 = 4,66 %
Полученное отклонение говорит о том, что план перевыполнен на 4,66 % .
Абсолютный прирост за год
= Отчетный год факт – предшествующий год
Абсолютный прирост за год
= 72166 –67485 = 4681 млн. руб.
Т.о. по сравнению с предыдущим годом произошло увеличение объема выпуска продукции на 4681 млн. руб.
Темп роста %
= Отчетный год фактически / предшествующий год * 100 %
Темп роста %
= 72166 / 67485 * 100 % = 106,94%
В отчетном году по сравнению с предыдущим годом производство продукции в % соотношении составило 106,9 %. Чтобы определить на сколько % увеличился объем выпуска товарной продукции в отчетном году по сравнению с предыдущим годом рассчитаем:
Темп прироста %
= Темп роста % — 100 %
Темп роста %
= 106,94% – 100 % = 6,94%
В предыдущим годом объем выпуска продукции увеличился до 72166 млн.руб., причем произошло перевыполнение плана на 4,66 %, что в абсолютном выражении составляет 3214 млн. руб. Плановое увеличение объема продукции составило 1467 млн. руб (1), а фактически было произведено продукции на сумму 5442 млн. руб., таким образом темп прироста по плану составил 2,2% (2), а фактически составил 6,94%
1: 68952-67485=1467
2: (68952-67485)/67485*100%=2,2%
Причиной перевыполнения плана может служить изменение конъюнктуры рынка, повышение спроса на отдельные виды продукции, улучшение организационной структуры предприятия.
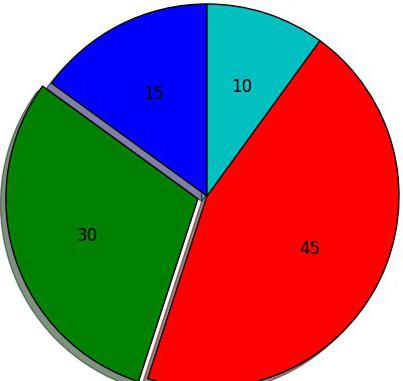
2. АНАЛИЗ ВЫПОЛНЕНИЯ ПЛАНА ПО АССОРТИМЕНТУ
Определим процент выполнения плана по ассортименту, а полученные расчеты сведем в аналитическую таблицу 2.1.
Таблица 2.1
|
Наименование изделий |
Выпуск изделий, шт. |
Сопоставимая цена, т.р. |
Выпускв изделий в стоимост. выр., т.р. |
Выполнение плана, % |
Условный выпуск,руб. |
||
|
Муз. центр |
|||||||
|
Телевизор |
|||||||
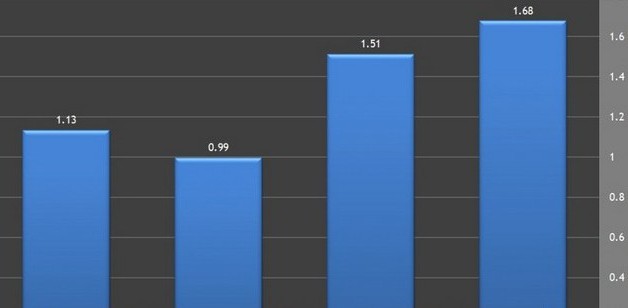
Определение процента выполнения плана по ассортименту
.
Выполнение плана в %
= Выпуск изделий факт / Выпуск изделий план *100 %
Выполнение плана в %:
50400 / 45360 *100 % = 111,11 % (план перевыполнен на 11,11 %)
41600 / 46800 *100 % = 88,89 % (план недовыполнен на 11,11 %)
16500 / 14400 *100 % = 114,58 % (план перевыполнен на 14,58 %)
Коэффициент выполнения плана по муз. центрам составил 111,11%, по пылесосам 88,89 % ,а телевизорам 114,58%.
Условный выпуск (принимается в расчет выполнение плана по ассортименту).
Если факт ниже плана – выбираем факт.
Если факт выше плана – выбираем план.
Условный выпуск / Выпуск изделий в стоимостном выражении по плану *100 %
Коэффициент выполнения плана по ассортименту
= 101360/ 106560 *100 % =
По пылесосам произошло недовыполнение плана на 11,11%, но несмотря на это, муз. центров произведено на 11,11% больше запланированного, а телевизоров перевыполнено на 14,58%. В целом же наблюдается недовыполнение плана по ассортименту на 4,9%.
Проведем графическое моделирование: построим столбиковые диаграммы в ассортиментном составе.
Для эффективного анализа данных и для нахождения проблемных участков в производстве необходимо находить отклонения в показателях. Отклонения бывают нескольких видов и отличаются как единицами измерения, так и способом получения, среди них можно выделить:
- Стандартное отклонение;
- Абсолютное отклонение;
- Относительное отклонение;
- Селективное отклонение;
- Кумулятивное отклонение;
- Отклонение во временном разрезе.
Как определить динамику изменения значений при отклонении
Нередко для того, чтобы понять насколько плавно изменяется тот или иной показатель на нескольких отрезках времени, простого среднего значения, сравниваемого с наименьшим или наибольшим числом из ряда – недостаточно. В таких случаях для более глубоко анализа применяется нахождение стандартного отклонения, показывающего более четко динамику изменения значений.
Даны показатели затрат на средства уборки для двух заведений: 10, 21, 49, 15, 59 и 31, 29, 34, 27, 32, где средним значением будет 30,8 и 30,6. Показатели в среднем приблизительно одинаковы, однако даже визуально видно, что значения в одном заведении изменяются не равномерно, что их контроль производится от случая к случаю. Но для более полного представления необходимо найти стандартное отклонение. Оно будет равно: 19,51 и 2,4. При среднем значении в первом заведении 30,8 показатели отклоняются от него более чем существенно – 21,8, соответственно у вас есть подтверждение небрежного отношения к работе.
Рассчитывается оно следующим образом:
- Необходимо рассчитать среднее значение для проверяемого ряда данных. (10+21+49+15+59)/5=30,8
- Найти разницу между каждым показателем и средним значением. 10-30,8=-20,8; 21-30,8=9,8; 49-30,8=18,2; 15-30,8=15,8; 59-30,8=28,2
- Возвести каждое значение разницы в квадрат. -20,82=432,64; 9,82=96,04; 18,22=331,24; 15,82=249,64; 28,22=795,24.
- Сложить полученные результаты. 432,64+96,04+331,24+249,64+795,24=1904,8
- Полученный результат делиться на количество значений в ряду. 1904,8/5=380,96
- Корень из полученного числа и будет средним отклонением √380,96=19,51
Обязательный минимум
Под понятием абсолютного отклонения принято подразумевать отличия одного показателя от другого в числовом значении. Например, разница выручки за два дня: 15-13=2, где 2 – абсолютное отклонение. Этот способ подходит для нахождения отклонения между фактическим и планируемым результатом.
Для правильного выбора уменьшаемого и вычитаемого, необходимо четко понимать, для чего находится отклонения, например в случае с прибылью, планируемая будет уменьшаемым, а фактическая – вычитаемым. Использование абсолютного отклонения редко помогает при глубоком анализе ситуации.
Процент воспринимается лучше
Относительным отклонением считают процентное отношение одного показателя к другому. Чаще всего его рассчитывают для понимания того, как тот или иной компонент относится к целому значению ли параметру, а также для нахождения отношения между планируемым показателем и фактическим. Это помогает найти отношение затрат на транспортировку к сумме всех затрат, или объясняет, как в процентах относится полученная выручка к планируемой.
Применение относительного отклонения позволяет повысить уровень наглядности проводимого анализа, что в свою очередь дает возможность более точно вычленить и оценить произошедшие в системе изменения.
Для примера можно найти абсолютное отклонение для полученной выручки относительно планируемой: при соответствующих значениях 1600 и 2000, оно составит 2000-1600=400. Это визуально воспринимается не так серьезно, как процентное отношение (2000-1600)/1600*100%=25%. Отклонение в 25% воспринимается более серьезно.
Как это поможет в сезонной работе
Селективное отклонение призвано помочь сравнить исследуемые данные за определенные промежутки времени. Данным отрезком времени могут быть кварталы, месяцы, не редко это сравнения дней. И для большей информативности необходимо сравнивать временные отрезки не в пределах одного года, а с такими же за прошлые года. Это более точно покажет общую тенденцию изменений величин на протяжении нескольких лет и поможет четче выявить влияющие на них факторы.
Наибольшую актуальность применение селективного отклонения находит в фирмах, доход которых неравномерно распределен на протяжении года. То есть поставщики сезонных продуктов или услуг.
Как выявить тренд отклонения
Сумма, исчисляемая нарастающим итогом, называется кумулятивным отклонением. Благодаря ему производится оценка параметра, его рост или падение за заданный промежуток времени, чаще всего месяц. А также позволяет спланировать конечный результат изменений за период. Благодаря этому можно игнорировать случайные, несистематические изменения параметра, не влияющие на долгосрочную перспективу (весь период) и давать более четкую тенденцию движения параметра. Она чаще всего показывается в виде прямой на графике, последовательно отмечающем все показатели параметра, и соединяющей начальную и конечную точки ломаной линии. Ее направление вниз или вверх и будет тенденцией.
Отклонение во временном разрезе
Зачастую с его помощью происходит сравнение фактического и планируемого показателя. Является крайне важным в случае негативного отклонения планового значения от фактического. Позволяет использовать в анализе реальный результат вместо планируемого или желаемого показателей.
2. Абсолютное и относительное отклонение от плана.
Расчёт влияния факторов на изменение переменной части фонда оплаты труда проводят по формулам:
1) влияние объёма производства продукции:
2) влияние изменения структуры произведённой продукции:
3) влияние изменения удельной трудоёмкости продукции:
4) влияние изменения оплаты труда:
1.1.4 Факторная модель постоянной части ФЗП
Факторная модель постоянной части фонда оплаты труда представлена на рис.2.
Рис. 2. Детерминированная факторная система фонда заработной платы рабочих-повременщиков
Согласно этой схеме модель будет иметь следующий вид:
Фонд повременной заработной платы;
Среднесписочная численность работников;
Количество отработанных дней одним рабочим в среднем за год;
Средняя продолжительность смены.
Расчет влияния факторов по данной модели можно произвести способом абсолютных разниц:
Аналогично можно представить факторную модель для фонда заработной платы служащих.
В процессе анализа необходимо также установить эффективность использования фонда заработной платы.
1.1.5 Анализ соотношения производительности и оплаты труда
Для расширенного воспроизводства получения необходимой прибыли и рентабельности необходимо, чтобы темпы роста производительности труда опережали темп роста его оплаты. Если этот принцип не соблюдается, то происходит перерасход фонда зарплаты, повышение себестоимости продукции и, соответственно, уменьшение суммы прибыли.
Изменение среднего заработка работающих за период характеризуется его индексом:
Индекс изменения заработной платы;
Средняя заработная плата за отчетный период;
Средняя заработная плата за базисный период.
Изменение среднегодовой выработки определяется аналогично на основе индекса производительности труда:
, где
Средняя производительность труда за отчетный период;
Средняя производительность труда за базисный период.
Темп роста производительности труда должен опережать темп роста средней заработной платы. Для этого рассчитывают коэффициент опережения и анализируют его в динамике:
Коэффициент опережения роста производительности труда над ростом средней заработной платы;
Индекс изменения производительности труда;
Затем производят подсчёт суммы экономии (перерасхода) фонда заработной платы в связи с изменением соотношений между темпами роста производительности труда и его оплаты:

Индекс изменения производительности труда;
Индекс изменения заработной платы.
1.2 Анализ показателей рентабельности предприятия 1.2.1 Рентабельность: понятие и виды
Рентабельность – это относительный показатель, определяющий уровень доходности бизнеса. Показатели рентабельности характеризуют эффективность как работы предприятия в целом, так и доходность различных направлений его деятельности. Они более полно, чем прибыль, характеризуют окончательные результаты хозяйствования, так как их величина показывает соотношение эффекта с наличными или использованными ресурсами.
Все существующие показатели рентабельности можно объединить в следующие группы, которые характеризуют
1) доходность капитала и его частей;
2) прибыльность продаж;
3) рентабельность (окупаемость) издержек производства и инвестиционных проектов.
Эти показатели могут рассчитываться на основе балансовой прибыли, прибыли от реализации продукции и чистой прибыли.
К первой группе относятся такие показатели, как общая рентабельность активов, чистая рентабельность оборотных активов, а также рентабельность собственного капитала. Одним из ключевых показателей эффективности деятельности предприятия является общая рентабельность активов. Она представляет собой отношение балансовой прибыли к стоимости имущества, т.е. хозяйственных средств (активам), находящимся в распоряжении предприятия и рассчитывается по следующей формуле:
Общая рентабельность активов;
Балансовая прибыль;
Средняя величина активов предприятия за анализируемый период (без учета убытков).
Чистая рентабельность оборотных активов показывает, какую чистую прибыль получает предприятие с каждого рубля, вложенного в активы:
Чистая рентабельность оборотных активов;
Чистая прибыль предприятия;
Среднее значение величины оборотных активов (второй раздел актива баланса).
Рентабельность активов сравнивается со средней процентной ставкой по заемным средствам, т.е. с альтернативной стоимостью. Если прибыль, получаемая на один рубль активов, меньше процентной ставки по заемным средствам, то можно сделать вывод о недостаточно эффективном управлении активами, так как денежные средства, вложенные в активы, принесли бы больший доход, будучи размещенными на депозитных счетах в банке.
Рентабельность собственного капитала показывает то, какую прибыль получает предприятие с каждого рубля собственных средств:
, где
Рентабельность собственного капитала;
Чистая прибыль предприятия;
Величина собственного капитала предприятия соответственно в начале и конце отчетного периода.
Ко второй группе можно отнести такой показатель, как рентабельность продаж, который рассчитывается делением прибыли от реализации продукции, работ и услуг до выплаты процентов и налогов на сумму полученной выручки:
Рентабельность оборота;
Прибыль от реализации продукции, работ и услуг до выплаты процентов и налогов;
Сумма выручки от реализации продукции, работ и услуг.
Данный показатель характеризует эффективность предпринимательской деятельности: сколько прибыли имеет предприятие с рубля продаж. Он рассчитывается в целом по предприятию и отдельным видам продукции.
И наконец, третья группа включает в себя рентабельность продукции (окупаемость издержек). Он исчисляется путем отношения прибыли от реализации до выплаты процентов и налогов к сумме затрат по реализованной продукции:
Рентабельность продукции;
Прибыль от реализации продукции до выплаты процентов и налогов;
Этот показатель показывает, сколько предприятие имеет прибыли с каждого рубля, затраченного на производство и реализацию продукции. Может рассчитываться как по отдельным видам продукции, так и в целом по предприятию. При определении его уровня в целом по предприятию целесообразно учитывать не только реализационные, но и внереализационные доходы и расходы, относящиеся к основной деятельности.
Аналогичным образом определяется и доходность инвестиционных проектов:
Рентабельность инвестиционных проектов;
Полученная или ожидаемая сумма прибыли от инвестиционной деятельности;
Сумма инвестиционных затрат.
1.2.2 Факторный анализ рентабельности продукции
В данном разделе будет подробно рассмотрен именно факторный анализ рентабельности продукции, так как подобный анализ других видов рентабельности производится аналогичным образом.
Итак, уровень рентабельности продукции (коэффициент окупаемости затрат), исчисленный в целом по предприятию, зависит от четырех основных факторов первого порядка: изменения объема реализации продукции , структуры реализованной продукции , ее себестоимости и средних цен реализации .
Расчет влияния факторов первого уровня на изменение рентабельности в целом по предприятию можно выполнить способом цепной подстановки:
1. по плану:
;
2. по плану, пересчитанному на фактический объем реализации продукции:
;
3. фактически при фактической структуре реализации продукции и плановой величине средней цены реализации и себестоимости реализованной продукции:
;
4. фактически при фактических структуре реализации продукции, величине средней цены реализации и плановой себестоимости реализованной продукции:
;
5. по факту:
.
Изменение рентабельности продукции общее:
В том числе за счет:
1. влияние объёма реализованной продукции:
;
2. влияние изменения структуры реализованной продукции:
;
3. влияние изменения среднего уровня цен реализации:
;
4. влияние изменения уровня себестоимости продукции:
.
После этого необходимо выполнить факторный анализ рентабельности по каждому виду продукции. Уровень рентабельности отдельных видов продукции зависит от изменения среднереализационных цен и себестоимости единицы продукции:
Расчет влияния выше перечисленных факторов на изменение рентабельности по определенному виду продукции также проводится способом цепной подстановки:
1. по плану:
2. по плану, пересчитанному на фактические среднереализационные цены:
;
3. по факту:
Общее изменение рентабельности продукции по определенному виду продукции:
В том числе за счет изменения:
1. среднего уровня отпускных цен
;
2. уровня себестоимости продукции:
.
Необходимо также более детально изучить причины изменения среднего уровня цен и способом пропорционального деления рассчитать их влияние на уровень рентабельности. Далее нужно установить, за счет каких факторов изменилась себестоимость единицы продукции, и аналогичным образом определить их влияние на уровень рентабельности.
Такие расчеты проводятся по каждому виду продукции (услуг), что позволяет точнее оценить работу хозяйствующего субъекта и полнее выявить внутрихозяйственные резервы роста рентабельности на анализируемом предприятии.
2 Практическая часть
Таблица 1
Для того чтобы проанализировать соотношение темпов роста производительности труда и средней заработной платы, необходимо определить:
1. плановую и фактическую величину производительности труда;
2. плановую и фактическую величину средней заработной платы;
3. темпы роста производительности труда и средней заработной платы.
Производительность труда;
Объем производства продукции;
Таким образом, из-за более быстрого темпа роста объема производства продукции по сравнению с темпом роста среднесписочной численности работников (см. табл.2) фактическая производительность труда увеличилась на 1,5 тыс. руб./чел. Среди других возможных факторов, повлиявших на уровень производительности труда можно выделить такие, как ликвидация потерь рабочего времени, увеличение норм выработки, повышение удельного веса покупных полуфабрикатов, повышение мощности оборудования, внедрение прогрессивных технологий, механизация и автоматизация производственных процессов.
Средняя заработная плата;
Среднесписочная численность работников.
Используя исходные данные получим:
Итак, фактическая средняя заработная плата составила 3042 тыс. рублей, что на 30 000 рублей больше плановой величины. Росту данного показателя способствовали такие факторы, как увеличение количества отработанных дней каждым рабочим, средней продолжительности рабочего дня, а также среднечасовой заработной платы.
, где
Плановая величина производительности труда;
Фактическая величина производительности труда.
, где
Темп роста средней заработной платы;
Плановая величина средней заработной платы;
Фактическая величина средней заработной платы.
Используя выше приведенную формулу получим:
Таким образом, приведенные расчеты свидетельствуют о том, что на анализируемом предприятии темпы роста производительности труда опережают темпы роста труда. Коэффициент опережения составляет 1,064.
Опережение темпов роста производительности труда над темпами роста средней заработной платы, несомненно, является положительным моментом в работе данного предприятия, так как несоблюдение этого принципа влечет за собой перерасход фонда заработной платы, повышение себестоимости и соответственно уменьшение суммы полученной прибыли.
В связи с изменением соотношений между темпами роста производительности труда и его оплаты можно определить сумму экономии (перерасхода) фонда заработной платы. Для этого необходимо использовать следующую формулу:

Сумма экономии (-Э) или перерасхода (+Э) фонда заработной платы;
Фактическая величина фонда заработной платы;
Темп роста производительности труда;
Темп роста средней заработной платы.
Итак, более высокие темпы роста производительности труда по сравнению с темпами роста оплаты труда способствовали экономии фонда заработной платы в размере 37 378 руб.
Сведем все исходные и полученные данные в ниже приведенную таблицу (табл.2).
Таблица 2
| Показатели | План | Факт | Отклонение | Темп роста, % | ||
|
Абсолютное |
Относительное, |
|||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1. | Объем производства продукции, тыс. руб. | 3740,0 | 4150,0 | +410 | +10,96 | 110,96 |
| 2. | Среднесписочная численность работников, чел. | 186 | 192 | +6 | +3,23 | 103,23 |
| 3. | Фонд заработной платы, тыс. руб. | 560,2 | 584,4 | +24,2 | +4,32 | 104,32 |
| 4. | Производительность труда, тыс. руб./чел. | 20,1 | 21,6 | +1,5 | +7,46 | 107,46 |
| 5. | Среднегодовая заработная плата работников, тыс. руб. | 3012 | 3042 | +30 | +1 | 101 |
2.2 Задача
Определить влияние факторов на рентабельность продукции способом цепных подстановок по следующим исходным данным:
Таблица 3
Из таблицы исходных данных видно, что и прибыль от реализации продукции и себестоимость реализованной продукции возросли по сравнению с плановыми показателями – на 69 800 рублей и 150 000 рублей соответственно. Рост величины прибыли от реализации продукции в целом по предприятию может быть обусловлен такими причинами, как увеличение объема реализации продукции, увеличение удельного веса более доходных видов продукции в общем объеме продаж, повышение уровня среднереализационных цен. Увеличение показателя себестоимости реализованной продукции может быть связан, во-первых, с увеличением выпуска продукции, во-вторых, с изменением структуры производства (например, увеличение удельного веса более трудоемкой продукции в общем объеме производства), в-третьих, с повышением уровня переменных затрат (повышение цен на используемое в производстве сырье, материалы, на электроэнергию, топливо и т.д.) и, наконец, из-за увеличения суммы постоянных расходов (повышение в отчетном периоде заработной платы административно-управленческому персоналу, увеличение его численности, увеличение общехозяйственных расходов).
Для дальнейшего анализа рентабельности важно рассчитать такой показатель, как темп роста прибыли и себестоимости:
Итак, согласно приведенным выше расчетам темп роста прибыли на предприятии выше темпа роста себестоимости.
1. Прежде чем определить влияние факторов на рентабельность продукции необходимо рассчитать плановую и фактическую величину данного показателя, который определяется по следующей формуле:
, где
Рентабельность продукции, или коэффициент окупаемости затрат;
Прибыль от реализации до выплаты налогов и процентов;
Сумма затрат по реализованной продукции.
Применительно к нашим данным получим:
Таким образом, с каждого рубля, затраченного на производство и реализацию продукции, анализируемое нами предприятие по плану должно было иметь прибыль в размере 42,91 копеек.
Таким образом, фактически с каждого, затраченного на производство и реализацию продукции, предприятие получило прибыль в размере 43,37 копеек.
По сравнению с планом рентабельность увеличилась на 0,46%, что является положительным моментом для предприятия. Увеличение данного показателя произошло за счет более быстрого темпа роста прибыли от реализации продукции по сравнению с темпами роста суммы затрат реализованной продукции.
Вообще положительное значение показателя рентабельности продукции свидетельствует об эффективности основной деятельности предприятия и о необходимости сохранения производства данного вида (видов) продукции.
2. Определим влияние факторов на рентабельность продукции способом цепных подстановок.
Уровень рентабельности продукции (коэффициент окупаемости затрат), исчисленный в целом по предприятию, зависит от двух факторов: изменения уровня прибыли от реализации продукции и изменения уровня себестоимости реализованной продукции.
Факторная модель этого показателя имеет следующий вид:
1. по плану:
2. по плану, пересчитанному на фактическую величину прибыли:
3. по факту:
Изменение рентабельности общее:
В том числе за счет:
Полученные результаты свидетельствуют о том, что за счет увеличения прибыли на 69 800 рублей уровень рентабельности продукции увеличился на 6,65%. Рост же суммы затрат по реализованной продукции на 150 000 рублей вызвал снижение уровня рентабельности продукции на 6,19%.
Заключение
Итак, можно утверждать, что анализ хозяйственной деятельности является базой для принятия управленческих решений в бизнесе. С помощью него изучаются тенденции развития, глубоко и системно исследуются факторы изменения результатов деятельности, устанавливаются причинно-следственные взаимосвязи и взаимозависимости по формированию экономических показателей и факторов, обосновываются бизнес-планы, выявляются резервы повышения эффективности производства, оцениваются результаты деятельности предприятия и их чувствительность к управленческим воздействиям, вырабатывается экономическая стратегия развития хозяйствующего субъекта.
В современных рыночных условиях овладение методикой экономического анализа менеджерами всех уровней является составной частью их профессиональной подготовки, так как, зная технику и технологию анализа, они смогут легко адаптировать предприятие к внешним изменениям и найти правильные ответы и решения.
Список использованной литературы
1. Бердникова Т.Б. Анализ и диагностика финансово-хозяйственной деятельности предприятия: учебное пособие. – М.: Инфра-М, 2007.
2. Грищенко О.В. Анализ и диагностика финансово-хозяйственной деятельности предприятия: учебное пособие. – Таганрог: изд-во ТРТУ, 2000.
3. Пивоваров К.В. Финансово-экономический анализ хозяйственной деятельности коммерче6ской организации. – М.: Дашко и Ко, 2003.
4. Пястолов С.М. Анализ финансово-хозяйственной деятельности предприятия: учебник. – М.: Академия, 2004.
5. Савицкая Г.В. .Анализ хозяйственной деятельности предприятия: учебник.– М.: Инфра-М, 2008.
Счетам Бухгалтерский баланс и другие отчетные формы Рис. 2. Схема журнально-ордерной формы учета АОЗТ «Колпнянское» 3. Организация учета оплаты труда на предприятии 3.1. Состояние учета оплаты труда на предприятии Для учета затрат труда, выполненных работ и начисления заработной платы на АОЗТ «Колпнянское» используется несколько форм первичных…
О финансовых результатах»), данные оперативного учета. Анализ прибыли и рентабельности осуществляется в определенной последовательности. Основные этапы анализа приведены на рис. 8.7. Первый этап – анализ формирования прибыли и рентабельности на предприятиях торговли и общественного питания. Он включает три стадии. На первой стадии рассматривается динамика суммы и уровня показателей прибыли и…
Тех производственных фондов, с которых взимается плата за фонды. Применяется также показатель уровня рентабельности к текущим затратам – отношение прибыли к себестоимости товарной или реализованной продукции. Каждое предприятие самостоятельно осуществляет свою производственную и хозяйственную деятельность на принципах самоокупаемости и прибыльности. Предприятие имеет определенные расходы по…
Классификация отклонений. Расчет отклонений
К числу важнейших задач оперативного контроллинга относятся: контроль над исполнением бюджета предприятия, установление отклонений, анализ причин, вызвавших отклонения, выработка корректирующих мероприятий.
В результате бюджетирования устанавливаются плановые значения контролируемых величин, в качестве которых могут выступать количественные параметры деятельности предприятия, выраженные в натуральных и стоимостных показателях, а также качество, сроки и т.д. Объем контролируемых величин с целью выявления отклонений и анализа их причин устанавливается экономической целесообразностью, определяемой через соотношение выгоды, получаемой от устранения причин отклонения, и затрат на их выявление. Возможен частичный контроль наиболее значимых величин.
Фактические значения контролируемых величин выявляются на основе данных стратегического, финансового и управленческого учета на предприятии.
Обязательное условие сопоставления плановых и фактических величин — их содержательная однородность, которая, в принципе, должна быть обеспечена на стадии планирования. Кроме того, все плановые единицы предприятия — цехи, отделы и т.д. — должны работать в единой информационной базе данных, признаваемой всеми участниками процесса контроля и анализа, чтобы избежать конфликтов, вызванных неоднозначными пониманием терминов.
Отклонения плановых и фактических величин могут возникать по всем параметрам, определенным в бюджете:
— стоимостные параметры
— затраты, доходы с оборота, маржинальная прибыль, поступления, выплаты, дебиторские и кредиторские задолженности, капитал и т.п.;
— параметры организационной структуры
— места возникновения затрат, продуктовые и региональные дивизионы, закупочные, производственные, сбытовые, проектные подразделения и т.д.;
— временные параметры
— дни, недели, месяцы, кварталы, годы.
Различают следующие виды отклонений:
Абсолютные отклонения.
Разница, получаемая путем вычитания одной величины из другой, является выражением сложившегося положения вещей между плановыми и фактическими параметрами. Определенную проблему вызывает знак абсолютного отклонения. Принято, что если отклонение позитивно влияет на прибыль предприятия, то его исчисляют со знак “плюс”. Относительно формальной математики такой подход считается некорректным, поэтому иногда возникает непонимание между специалистами. В связи с этим в практике исчисления абсолютных отклонений иногда используют не экономический, а математический подход: рост фактического оборота по сравнению с плановым обозначают знаком “плюс”, а уменьшение фактических издержек по сравнению с плановыми — знаком “минус”.
Относительные отклонения.
Отклонения рассчитываются по отношению к другим величинам и выражаются в процентах. Чаще всего относительное отклонение исчисляется по отношению к более общему показателю или параметру. Например, относительное отклонение затрат на материалы можно выразить в отношении к суммарным затратам или в процентах к обороту. Применение относительных отклонений повышает уровень информативности проводимого анализа и позволяет более отчетливо оценить изменения. Так, например, величина абсолютного отклонения оборота, равная 10-8=2, воспринимается не так остро, как величина отклонения в процентах: (10-8)/8*100%=25%.
Селективные отклонения.
Этот метод расчета отклонений предполагает сравнение контролируемых величин во временном разрезе: квартал, месяц и даже иногда год. Сравнение контролируемых величин за определенный месяц текущего года с тем же месяцем предыдущего года может быть гораздо информативнее сравнения с предыдущим месяцем рассматриваемого планового периода. Использование селективных отклонений для анализа причин особенно актуально для предприятий, занимающихся сезонным бизнесом.
Кумулятивное отклонение.
Суммы, исчисленные нарастающим итогом (кумулятивные суммы), и их отклонения позволяют оценить степень достижения за прошедшие периоды (месяцы) и возможную разницу к концу планового периода (года). Возникающие в отдельных периодах случайные колебания параметров деятельности предприятия могут привести к значительным отклонениям на коротком отрезке времени. Кумуляция позволяет компенсировать случайные отклонения (и более точно выявить тренд).
Отклонения во временном разрезе.
Для контроллинга типичным является сравнение план-факт
. Отклонения определяются на основании сравнения бюджетных и фактически реализованных значений контролируемых параметров. Для аналитических целей может представлять интерес сравнение фактически реализованных значений планового периода с фактами соответствующего предыдущего периода (предыдущего месяца, года). Такой подход к исчислению отклонений особенно важен при негативных отклонениях плановых величин от фактических.
Оба подхода к сравнению: план-факт и факт-факт
опираются на статистику прошлого и позволяют уменьшить отклонения в будущем. На основе результатов анализа отклонений может быть составлен другой прогноз или ожидание результатов на конец планового периода. Сравнение планового результата на конец года с прогнозным или ожидаемым с учетом происходящих изменений во внешней среде или внутри предприятия позволяет получить отклонение типа план — желаемый результат
, что дает возможность более глубоко исследовать причины, влияющие на развитие бизнеса в будущем. При этом подходе сравниваются планы, разработанные в начале периода, и потребности современного момента. Простая экстраполяция прошлого на будущее, результаты которой часто используются при традиционном подходе к планированию, может привести к существенным ошибкам. В современных условиях будущее следует просматривать не через призму статистических экстраполяционных прогнозов, а путем изучения текущих отклонений и анализа причин их возникновения.
Загрузить PDF
Загрузить PDF
Абсолютная ошибка – это разность между измеренным значением и фактическим значением.[1]
Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.[2]
Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.
-
1
Запишите формулу для вычисления абсолютной ошибки. Формула:
, где
– абсолютная ошибка (разность между измеренным и фактическим значениями),
– измеренное значение,
– фактическое значение.[3]
-
2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
-
3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
-
4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[4]
Так вы вычислите абсолютную ошибку.- В нашем примере:
, то есть абсолютная ошибка измерения равна 1 м.
Реклама
- В нашем примере:
-
1
Запишите формулу для вычисления относительной ошибки. Формула:
, где
– относительная ошибка (отношение абсолютной ошибки к фактическому значению),
– измеренное значение,
– фактическое значение.[5]
-
2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
-
3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо
.
- Например, если фактическое значение равно 105 м, формула запишется так:
.
- Например, если фактическое значение равно 105 м, формула запишется так:
-
4
Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
-
5
Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете
, то есть измеренное значение.
-
6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[6]
Так вы вычислите абсолютную ошибку.- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
. Таким образом, абсолютная ошибка равна 2,1 м.
Реклама
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
-
1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
-
2
-
3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.[9]
Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[10]
Так вы вычислите абсолютную ошибку.- Например, если измеренная длина поля равна
м, то есть абсолютная ошибка равна 0,5 м.
Реклама
- Например, если измеренная длина поля равна
Советы
- Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.
Реклама
Об этой статье
Эту страницу просматривали 24 549 раз.
Была ли эта статья полезной?
Абсолютная погрешность
- Причины возникновения погрешности измерения
- Систематическая и случайная погрешности
- Определение абсолютной погрешности
- Алгоритм оценки абсолютной погрешности в серии прямых измерений
- Значащие цифры и правила округления результатов измерений
- Примеры
Причины возникновения погрешности измерения
Погрешность измерения – это отклонение измеренного значения величины от её истинного (действительного) значения.
Обычно «истинное» значение неизвестно, и можно только оценить погрешность, приняв в качестве «истинного» среднее значение, полученное в серии измерений. Таким образом, процесс оценки проводится статистическими методами.
Виды погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Теоретическая погрешность
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Систематическая и случайная погрешности
Систематической погрешностью называют погрешность, которая остаётся постоянной или изменяется закономерно во времени при повторных измерениях одной и той же величины.
Систематическая погрешность всегда имеет знак «+» или «-», т.е. говорят о систематическом завышении или занижении результатов измерений.
Систематическую погрешность можно легко определить, если известно эталонное (табличное) значение измеряемой величины. Для других случаев разработаны эффективные статистические методы выявления систематических погрешностей. Причиной систематической погрешности может быть неправильная настройка приборов или неправильная оценка параметров (завышенная или заниженная) в расчётных формулах.
Случайной погрешностью называют погрешность, которая не имеет постоянного значения при повторных измерениях одной и той же величины.
Случайные погрешности неизбежны и всегда присутствуют при измерениях.
Определение абсолютной погрешности
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:
$$ Delta x = |x_{изм}-x_{ист} | $$
Например:
При пяти взвешиваниях гири с маркировкой 100 г были получены различные значения массы. Если принять маркировку за истинное значение, то получаем следующие значения абсолютной погрешности:
$m_i,г$
98,4
99,2
98,1
100,3
98,5
$Delta m_i, г$
1,6
0,8
1,9
0,3
1,5
Граница абсолютной погрешности – это величина h: $ |x-x_{ист}| le h $
Для оценки границы абсолютной погрешности на практике используются статистические методы.
Алгоритм оценки абсолютной погрешности в серии прямых измерений
Шаг 1. Проводим серию из N измерений, в каждом из которых получаем значение измеряемой величины $x_i, i = overline{1, N}$.
Шаг 2. Находим оценку истинного значения x как среднее арифметическое данной серии измерений:
$$ a = x_{cp} = frac{x_1+x_2+ cdots +x_N}{N} = frac{1}{N} sum_{i = 1}^N x_i $$
Шаг 3. Рассчитываем абсолютные погрешности для каждого измерения:
$$ Delta x_i = |x_i-a| $$
Шаг 4. Находим среднее арифметическое абсолютных погрешностей:
$$ Delta x_{cp} = frac{Delta x_1+ Delta x_2+ cdots + Delta x_N}{N} = frac{1}{N} sum_{i = 1}^N Delta x_i $$
Шаг 5. Определяем инструментальную погрешность при измерении как цену деления прибора (инструмента) d.
Шаг 6. Проводим оценку границы абсолютной погрешности серии измерений, выбирая большую из двух величин:
$$ h = max {d; Delta x_{cp} } $$
Шаг 7. Округляем и записываем результаты измерений в виде:
$$ a-h le x le a+h или x = a pm h $$
Значащие цифры и правила округления результатов измерений
Значащими цифрами – называют все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Например:
0,00501 — три значащие цифры 5,0 и 1.
5,01 — три значащие цифры.
5,0100 – пять значащих цифр; такая запись означает, что величина измерена с точностью 0,0001.
Внимание!
Правила округления.
Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу (округление по избытку, “ceiling”).
Округлять результаты измерений и вычислений нужно так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.
Например: если при расчетах по результатам серии измерений получена оценка истинного значения a=1,725, а оценка абсолютной погрешности h = 0,11, то результат записывается так:
$$ a approx 1,7; h approx ↑0,2; 1,5 le x le 1,9 или x = 1,7 pm 0,2 $$
Примеры
Пример 1. При измерении температура воды оказалась в пределах от 11,55 ℃ до 11,63 ℃. Какова абсолютная погрешность этих измерений?
По условию $11,55 le t le 11,63$. Получаем систему уравнений:
$$ {left{ begin{array}{c} a-h = 11,55 a+h = 11,63 end{array} right.} Rightarrow {left{ begin{array}{c} 2a = 11,55+11,63 = 23,18 2h = 11,63-11,55 = 0,08 end{array} right.} Rightarrow {left{ begin{array}{c} a = 11,59 h = 0,04end{array} right.} $$
$$ t = 11,59 pm 0,04 ℃ $$
Ответ: 0,04 ℃
Пример 2. По результатам измерений найдите границы измеряемой величины. Инструментальная погрешность d = 0,1.
$x_i$
15,3
16,4
15,3
15,8
15,7
16,2
15,9
Находим среднее арифметическое:
$$ a = x_{ср} = frac{15,3+16,4+ cdots +15,9}{7} = 15,8 $$
Находим абсолютные погрешности:
$$ Delta x_i = |x_i-a| $$
$ Delta x_i$
0,5
0,6
0,5
0
0,1
0,4
0,1
Находим среднее арифметическое:
$$ Delta x_{ср} = frac{0,5+0,6+ cdots + 0,1}{7} approx 0,31 gt d $$
Выбираем большую величину:
$$ h = max {d; Delta x_{ср} } = max {0,1; 0,31} = 0,31 $$
Округляем по правилам округления по избытку: $h approx ↑0,4$.
Получаем: x = 15, $8 pm 0,4$
Границы: $15,4 le x le 16,2$
Ответ: $15,4 le x le 16,2$
Пример 3*. В первой серии экспериментов было получено значение $x = a pm 0,3$. Во второй серии экспериментов было получено более точное значение $x = 5,631 pm 0,001$. Найдите оценку средней a согласно полученным значениям x.
Более точное значение определяет более узкий интервал для x. По условию:
$$ {left{ begin{array}{c} a-0,3 le x le a+0,3 5,630 le x le 5,632 end{array} right.} Rightarrow a-0,3 le 5,630 le x le 5,632 le a+0,3 Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} a-0,3 le 5,630 5,632 le a+0,3 end{array} right.} Rightarrow {left{ begin{array}{c} a le 5,930 5,332 le a end{array} right.} Rightarrow 5,332 le a le 5,930 $$
Т.к. a получено в серии экспериментов с погрешностью h=0,3, следует округлить полученные границы до десятых:
$$ 5,3 le a le 5,9 $$
Ответ: $ 5,3 le a le 5,9 $
Абсолютная и относительная погрешности (ошибки).
Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x1,
x2,
x3,
…, xn
Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:
Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.
Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:
(13)
Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.
Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):
(14)
Отношения
называются относительными погрешностями
(ошибками) отдельных измерений.
Отношение средней
абсолютной погрешности результата
к среднему арифметическому значению
измеряемой величины называют относительной
ошибкой результата и выражают в процентах:
Относительная
ошибка характеризует точность измерения.
Законы распределения случайных величин.
Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.
Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.
Непрерывная
случайная величина принимает любые
значения в данном интервале.
Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.
Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.
Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.
Два события,
одновременное появление которых
невозможно, называются несовместными.
Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:
называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:
При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:
Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.
Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений хi
на вероятность этих значений рi:
Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:
,
где mi
— число дискретных случайных величин,
имеющих значение хi.
Для непрерывной
случайной величины математическим
ожиданием служит интеграл:
,
где р(х) — плотность
вероятности.
Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:
(15)
(16)
Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:
(17)
Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».
Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:
а) ряд распределения
(для дискретных величин);
б) функция
распределения;
в) кривая распределения
(для непрерывных величин).
Существует
относительно много законов распределения
случайных величин.
Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина
распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:
(18),
где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);
—
среднее квадратичное отклонение;
—
основание натурального логарифма
(неперово число);
f
(x)
– плотность вероятности (функция
распределения вероятностей).
Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).
Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:
(19)
Таким образом,
максимальное значение функции fmax(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом 2>1.
(При увеличении
кривая распределения становится более
пологой, а при уменьшении
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и 3
= 2.
Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал
теоретически была определена в 1860 году
английским физиком Максвеллом
. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т1
< Т2).
Закон распределения Максвелла определяется
формулой:
(20),
где mо
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.
Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:
(21)
Где n(h)
– концентрация молекул газа на высоте
h,
n0
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.
Распределение
Больцмана.
Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному
статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).
n
-
h
Гистограмма
распределения Больцмана.
Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов xi
одинаковой ширины. Для каждого интервала
подсчитывают число mi
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины
для каждого интервала xi
и среднее значение случайной величины
<xi
> в каждом интервале.
Затем по оси абсцисс
откладывают интервалы xi,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой
– плотностью относительной частоты
).
Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).
Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:
(22)
Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:
(23)
Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.
Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.
Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.
Доверительной
вероятностью
(надежностью)
результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.
Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t,n<>,
<x>
+ t,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .
Коэффициент t,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).
Значении коэффициента
Стьюдента t,n
зависит от доверительной вероятности
и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.
Таблица 1
|
n |
|
||||||
|
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
4 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
В таблице 1 в верхней
строке заданы значения доверительной
вероятности
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.
Окончательный
результат измерений записывается в
виде:
(25)
Где
– полуширина доверительного интервала.
Результат серии
измерений оценивается относительной
погрешностью:
(26)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статья обновлена 10.07.2022
Что такое погрешность измерения
Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.
- Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
- Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.
Математическая погрешность: формула для каждого типа
Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?
Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.
Формулы погрешностей вычисляются следующим образом.
Абсолютная погрешность измерений: формула
Формула дает разницу между измеренным и реальным значением.
Относительная погрешность: формула
Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.
Приведенная погрешность: формула
Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.
Классификация оценочной погрешности
Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.
Что такое случайная погрешность
Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.
Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.
Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.
Что такое систематическая погрешность
Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.
В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.
Погрешность выборки
Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.
Погрешность структуры
Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.
Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.
Погрешность аудитории
Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.
Погрешность отбора
Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.
Как минимизировать погрешность выборки
- Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам. - Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию. - Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.
Погрешность измерения
Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.
К погрешностям измерения приводят следующие виды ошибок.
Ошибка цели
Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.
Предвзятость ответов
Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.
Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.
Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.
Предвзятость интервьюера
Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.
Ошибка обработки
Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.
Ошибка ввода
Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.
Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.
Как минимизировать погрешность измерения
- Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью. - Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка. - Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования. - Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.
Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.
ВИДЕО УРОК
Абсолютная погрешность.
Разность между истинным значением измеряемой величины
и её приближённым значением называется абсолютной погрешностью.
Для подсчёта
абсолютной погрешности необходимо из большего числа вычесть меньшее число.
Существует формула
абсолютной погрешности. Обозначим точное число буквой А, а буквой а –
приближение к точному числу. Приближённое число – это число, которое
незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда
формула будет выглядеть следующим образом:
∆а = А – а.
ПРИМЕР:
В школе учится 374 ученика. Если округлить это число до 400,
то абсолютная погрешность измерения равна:
400 – 374 = 26.
ПРИМЕР:
На предприятии 1284 рабочих и
служащих. При округлении этого числа до 1300 абсолютная
погрешность составляет
1300 – 1284 = 16.
При округлении до 1280 абсолютная
погрешность составляет
1284 – 1280 = 4.
Редко когда можно
точно знать значение измеряемой величины, чтобы рассчитать абсолютную
погрешность. Но при выполнении различных измерений мы обычно представляем себе
границы абсолютной погрешности и всегда можем сказать, какого определённого
числа она не превосходит.
ПРИМЕР:
Торговые весы могут дать абсолютную погрешность, не
превышающую 5 г, а аптекарские – не превышающую одной сотой грамма.
Записывают
абсолютную погрешность числа, используя знак
±.
ПРИМЕР:
Длина рулона обоев составляет.
30 м ± 3
см.
Границу абсолютной
погрешности называют предельной абсолютной погрешностью.
Но абсолютная
погрешность не даёт нам представление о качестве измерения, то есть о том,
насколько тщательно это измерение выполнено. Чтобы понять эту мысль, достаточно
разобраться в таком примере.
ПРИМЕР:
Допустим, что при измерении коридора длиной в 20
м мы допустили абсолютную погрешность
всего только в 1 см. Теперь представим себе, что, измеряя корешок книги,
имеющий 18
см длины, мы тоже допустили абсолютную
погрешность в 1 см. Тогда понятно, что первое измерение нужно признать
превосходным, но зато второе – совершенно неудовлетворительным. Это значит, что
на 20
м ошибка в 1
см вполне допустима и неизбежна, но
на 18
см такая ошибка является очень грубой.
Отсюда ясно, что для оценки качества измерения
существенна не сама абсолютная погрешность, а та доля, какую она составляет от
измеряемой величины. При измерении коридора длиной в 20 м погрешность в 1 см
составляет
долю
измеряемой величины, а при измерении корешка книги погрешность в 1 см составляет
долю
измеряемой величины.
Делаем вывод, что измеряя корешок книги, имеющий 18
см длины и допустив погрешность в 1
см, можно считать измерение с большой ошибкой. Но если погрешность в 1
см была допущена при измерении коридора
длиной в 20
м, то это измерение можно считать максимально точным.
Если ошибка,
возникающая при измерении линейкой или каким либо другим измерительным
инструментом, значительно меньше, чем деления шкалы этой линейки, то в качестве
абсолютной погрешности измерения обычно берут половину деления. Если деления на
линейке нанесены достаточно точно, то ошибка при измерении близка к нулю.
Тогда
значение измеряемой длины предмета будет значение ближайшей метки линейки.
Поэтому, если измерение выполнено аккуратно, то истинная длина предмета может
отличаться от измеренной длины не более чем на половину деления шкалы, то есть 0,5 мм.
ПРИМЕР:
Для измерения длины болта использованы метровая линейка с
делениями 0,5 см и линейка с
делениями 1 мм. В обоих случаях получен результат 3,5
см. Ясно, что в первом случае отклонение найденной длины 3,5
см от истинной, не
должно по модулю превышать 0,5 см, во втором случае
0,1 см.
Если этот же результат получится при измерении
штангенциркулем, то
p(l; 3,5) = |l – 3,5 ≤ 0,01|.
Данный пример показывает зависимость абсолютной
погрешности и границ, в которых находится точный результат, от точности
измерительных приборов. В одном случае ∆l = 0,5 и, следовательно,
3
≤ l ≤ 4,
в другом – ∆l = 0,1 и
3,4
≤ l ≤ 3,6.
ПРИМЕР:
Длина листа бумаги формата А4 равна (29,7 ± 0,1)
см. А расстояние от Санкт-Петербурга до Москвы равно (650 ± 1) км. Абсолютная погрешность в первом случае
не превосходит одного миллиметра, а во втором – одного километра. Необходимо
сравнить точность этих измерений.
РЕШЕНИЕ:
Если вы думаете, что длина листа измерена точнее потому,
что величина абсолютной погрешности не
превышает 1 мм, то вы ошибаетесь.
Напрямую сравнить эти величины нельзя. Проведём некоторые рассуждения.
При измерении длины листа абсолютная погрешность не
превышает 0,1 см на 29,7 см, то есть в процентном отношении это составляет
0,1
: 29,7 ∙ 100% ≈ 0,33%
измеряемой величины.
Когда мы измеряем расстояние от Санкт-Петербурга до
Москвы, то абсолютная погрешность не превышает
1 км
на 650 км, что в процентном соотношении составляет
1
: 650 ∙ 100% ≈ 0,15%
измеряемой величины.
Видим, что расстояние между городами измерено точнее, чем
длинна листа формата А4.
Истинное значение
измеряемой величины известно бывает лишь в очень редких случаях, а поэтому и
действительная величина абсолютной погрешности почти никогда не может быть вычислена.
На практике абсолютной погрешности недостаточно для точной оценки измерения.
Поэтому на практике более важное значение имеет определение относительной
погрешности измерения.
Относительная погрешность.
Абсолютная
погрешность, как мы убедились, не даёт возможности судить о качестве измерения.
Поэтому для оценки качества приближения вводится новое понятие – относительная
погрешность. Относительная погрешность позволяет судить о качестве измерения.
Относительная погрешность –
это частное от деления абсолютной погрешности на модуль приближённого значения
измеряемой величины, выраженная в долях или процентах.
Относительная
погрешность величина всегда положительная. Это следует из того, что абсолютная погрешность
всегда положительная величина, и мы делим её на модуль приближённого значения
измеряемой величины, а модуль тоже всегда положителен.
ПРИМЕР:
Округлим дробь 14,7 до целых и найдём относительную погрешность приближённого
значения:
14,7 ≈ 15,
Для вычисления
относительной погрешности, кроме приближённого значения, нужно знать ещё и
абсолютную погрешность. Обычно абсолютная погрешность неизвестна, поэтому
вычислить относительную погрешность нельзя. В таких случаях ограничиваются
оценкой относительной погрешности.
ПРИМЕР:
При измерении в (сантиметрах) толщины
b
стекла и длины l книжной полки
получили следующие результаты:
b ≈ 0,4 с
точностью до 0,1,
l ≈ 100 с
точностью до 0,1.
Абсолютная погрешность каждого из этих измерений не
превосходит 0,1. Однако 0,1 составляет
существенную часть числа 0,4 и
ничтожную часть числа 100. Это показывает, что качество второго
измерения намного выше, чем первого.
В результате измерения нашли,
что b ≈ 0,4 с точностью до 0,1, то
есть абсолютная погрешность измерения не превосходит 0,1.
Значит, отношение абсолютной погрешности к приближённому значению меньше или равно
то есть относительная погрешность приближения не превосходит 25%.
Аналогично найдём, что
относительная погрешность приближения, полученного при измерении длины полки,
не превосходит
Говорят, что в первом случае измерение выполнено с
относительной точностью до 25%,
а во втором – с относительной точностью до 0,1%.
ПРИМЕР:
Если взять абсолютную погрешность в 1
см, при измерении длины отрезков 10
см и 10
м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для
отрезка длиной в 10 см погрешность
в 1
см очень велика, это ошибка в 10%. А для десятиметрового отрезка 1 см не имеет значения, эта ошибка всего в 0,1%.
Чем меньше относительная погрешность
измерения, тем оно точнее.
Различают
систематические и случайные погрешности.
Систематической погрешностью называют ту погрешность, которая остаётся неизменной при
повторных измерениях.
Случайной погрешностью называют ту погрешность, которая возникает в результате
воздействия на процесс измерения внешних факторов и может изменять своё
значение.
В большинстве
случаев невозможно узнать точное значение приближённого числа, а значит, и
точную величину погрешности. Однако почти всегда можно установить, что
погрешность (абсолютная или относительная) не превосходит некоторого числа.
ПРИМЕР:
Продавец взвешивает арбуз на чашечных весах. В наборе
наименьшая гиря – 50
г. Взвешивание показало 3600 г. Это число – приближённое. Точный вес арбуза
неизвестен. Но абсолютная погрешность не превышает 50
г. Относительная погрешность не превосходит
50/3600 ≈
1,4%.
Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной
погрешностью.
Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей), называется предельной относительной
погрешностью.
В предыдущем примере
за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность 1,4%.
Величина предельной
погрешности не является вполне определённой. Так в предыдущем примере можно
принять за предельную абсолютную погрешность
100 г, 150 г и вообще всякое
число, большее чем 50 г.
На практике берётся по возможности меньшее значение предельной погрешности. В
тех случаях, когда известна точная величина погрешности, эта величина служит
одновременно предельной погрешностью. Для каждого приближённого числа должна
быть известна его предельная погрешность (абсолютная или относительная). Когда
она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено
приближённое число 4,78 без указания предельной погрешности, то подразумевается,
что предельная абсолютная погрешность составляет 0,005. В следствии этого соглашения всегда можно обойтись без указания
предельной погрешности числа.
Предельная
абсолютная погрешность обозначается греческой буквой ∆ (<<дельта>>),
предельная относительная погрешность – греческой буквой δ
(<<дельта малая>>). Если приближённое число обозначить буквой а,
Правила округления.
На практике
относительную погрешность округляют до двух значащих цифр, выполняя округление
с избытком, то есть, всегда увеличивая последнюю значащую цифру на единицу.
ПРИМЕР:
Для х = 1,7 ± 0,2 относительная погрешность измерений равна:
ПРИМЕР:
Длина карандаша измерена линейкой с миллиметровым
делением. Измерение показало 17,9 см. Какова предельная относительная погрешность этого
измерения ?
РЕШЕНИЕ:
Здесь а =
17,9 см. Можно принять ∆ = 0,1 см, так как с точностью
до 1 мм
измерить карандаш нетрудно, а значительно уменьшить предельную
погрешность не удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но
у самого карандаша рёбра могут отличаться на большую величину). Относительная погрешность равна
Округляя, находим
ПРИМЕР:
Цилиндрический поршень имеет около 35
мм в диаметре. С какой точностью нужно
его измерить микрометром, чтобы предельная относительная погрешность составляла 0,05% ?
РЕШЕНИЕ:
По условию, предельная относительная
погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная абсолютная
погрешность равна
или, усиливая, 0,02
мм.
Можно воспользоваться
формулой
Подставляя в формулу
а = 35,
𝛿 = 0,0005,
имеем
Значит,
∆
= 35 × 0,0005 = 0,0175 мм.
Действия над приближёнными числами.
Сложение и вычитание приближённых чисел.
Абсолютная погрешность суммы двух величин равна сумме
абсолютных погрешностей отдельных слагаемых.
ПРИМЕР:
Складываются приближённые числа
265 и 32.
РЕШЕНИЕ:
Пусть предельная погрешность первого есть 5,
а второго 1. Тогда предельная погрешность суммы равна
5
+ 1 = 6.
Так, если истинное значение первого есть 270,
а второго 33, то приближённая сумма
265
+ 32 = 297
на 6 меньше истинной
270
+ 33 = 303.
ПРИМЕР:
Найти сумму приближённых чисел:
0,0909
+ 0,0833 + 0,0769 + 0,0714 + 0,0667
+ 0,0625 + 0,0588 + 0,0556 + 0,0526.
РЕШЕНИЕ:
Сложение даёт следующий результат – 0,6187.
Предельная погрешность каждого слагаемого
0,00005.
Предельная погрешность суммы:
0,00005
∙ 9 = 0,00045.
Значит, в последнем (четвёртом) знаке суммы возможна ошибка до 5
единиц. Поэтому округляем сумму до третьего знака, то есть до тысячных.
Получаем 0,619,
здесь все знаки верные.
При значительном
числе слагаемых обычно происходит взаимная компенсация погрешностей, поэтому
истинная погрешность суммы лишь в исключительных случаях совпадает с предельной
погрешностью или близка к ней. Насколько редки эти случаи, видно из предыдущего
примера, где 9 слагаемых. Истинная величина каждого из них может
отличаться в пятом знаке от взятого приближённого значения на 1, 2, 3, 4 или даже на 5 единиц в ту и в другую сторону.
Например, первое
слагаемое может быть больше своего истинного значения на 4 единицы пятого знака, второе – на две, третье – меньше
истинного на одну единицу и так далее.
Расчёт показывает,
что число всех возможных случаев распределения погрешностей составляет около
одного миллиарда. Между тем лишь в двух случаях погрешность суммы может
достигнуть предельной погрешности 0,00045,
это произойдёт:
– когда истинная величина каждого слагаемого больше
приближённой величины на 0,00005;
– когда истинная величина каждого слагаемого меньше
приближённой величины на 0,00005.
Значит, случаи,
когда погрешность суммы совпадает с предельной, составляют только 0,0000002% всех возможных случаев.
Дальнейший расчёт
показывает, что случаи, когда погрешность суммы девяти слагаемых может
превысить три единицы последнего знака, тоже очень редки. Они составляют
лишь 0,07%
из числа всех
возможных. Две единицы последнего знака погрешность может превысить 2% всех возможных случаев, а одну единицу –
примерно в 25%.
В остальных 75% случаев погрешность девяти слагаемых не
превышает одной единицы последнего знака.
ПРИМЕР:
Найти сумму точных чисел:
0,0909
+ 0,0833 + 0,0769 + 0,0714 + 0,0667
+ 0,0625 + 0,0588 + 0,0556 + 0,0526.
РЕШЕНИЕ:
Сложение даёт следующий результат – 0,6187.
Округлим их до тысячных и сложим:
0,091
+ 0,083 + 0,077 + 0,071 + 0,067
+ 0,062 + 0,059 + 0,056 + 0,053 = 0,619.
Предельная погрешность суммы:
0,0005
∙ 9 = 0,0045.
Приближённая сумма отличается от истинной на 0,0003,
то есть на треть единицы последнего знака приближённых чисел. Все три знака
приближённой суммы верны, хотя теоретически последняя цифра могла быть грубо
неверной.
Произведём в наших слагаемых округление до сотых. Теперь
предельная погрешность суммы будет:
0,005
∙ 9 = 0,045.
Между тем получим:
0,09
+ 0,08 + 0,08 + 0,07 + 0,07
+ 0,06 + 0,06 + 0,06 + 0,05 = 0,62.
Истинная погрешность составляет только 0,0013.
Предельная абсолютная погрешность разности двух величин
равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.
ПРИМЕР:
Пусть предельная погрешность приближённого
уменьшаемого 85 равна 2,
а предельная погрешность вычитаемого 32 равна 3.
Предельная погрешность разности
85
– 32 = 53
есть
2
+ 3 = 5.
В самом деле, истинное значение уменьшаемого и
вычитаемого могут равняться
85
+ 2 = 87 и
32
– 3 = 29.
Тогда истинная разность есть
87
– 29 = 58.
Она на 5 отличается от
приближённой разности 53.
Относительная погрешность суммы и разности.
Предельную
относительную погрешность суммы и разности легко найти, вычислив сначала
предельную абсолютную погрешность.
Предельная
относительная погрешность суммы (но не разности!) лежит между наименьшей и
наибольшей из относительных погрешностей слагаемых. Если все слагаемые имеют
одну и ту же (или примерно одну и ту же) предельную относительную погрешность,
то и сумма имеет ту же (или примерно ту же) предельную относительную
погрешность. Другими словами, в этом случае точность суммы (в процентном
выражении) не уступает точности слагаемых. При значительном же числе слагаемых
сумма, как правило, гораздо точнее слагаемых.
ПРИМЕР:
Найти предельную абсолютную и предельную относительную
погрешность суммы чисел:
24,4
+ 25,2 + 24,7.
РЕШЕНИЕ:
В каждом слагаемом суммы
24,4
+ 25,2 + 24,7 = 74,3
предельная относительная погрешность примерно одна и та
же, а именно:
0,05
: 25 = 0,2%.
Такова же она и для суммы.
Здесь предельная абсолютная погрешность равна 0,15,
а относительная
0,15
: 74,3 ≈ 0,15 : 75 = 0,2%.
В противоположность
сумме разность приближённых чисел может быть менее точной, чем уменьшаемое и
вычитаемое. <<Потеря точности>> особенно велика в том случае, когда
уменьшаемое и вычитаемое мало отличаются друг от друга.
Относительные погрешности при сложении и вычитании
складывать нельзя.
Умножение и деление приближённых чисел.
При делении и умножении чисел требуется сложить
относительные погрешности.
ПРИМЕР:
Пусть перемножаются приближённые числа 50 и 20, и пусть предельная относительная погрешность первого
сомножителя есть 0,4%, а второго
0,5%.
Тогда предельная относительная погрешность произведения
50
× 20 = 1000
приближённо равна 0,9%.
В самом деле предельная абсолютная погрешность первого сомножителя есть
50
× 0,004 = 0,2,
а второго
20
× 0,005 = 0,1.
Поэтому истинная величина произведения не больше чем
(50
+ 0,2)(20 + 0,1) = 1009,02,
и не меньше, чем
(50
– 0,2)(20 – 0,1) = 991,022.
Если истинная величина произведения есть 1009,2,
то погрешность произведения равна
1009,2
– 1000 = 9,02,
а если 991,02, то погрешность произведения равна
1000
– 991,02 = 8,98.
Рассмотренные два случая – самые неблагоприятные. Значит,
предельная абсолютная погрешность произведения есть 9,02.
Предельная относительная погрешность равна
9,02
: 1000 = 0,902%,
то есть приближённо 0,9%.
Задания к уроку 16
- Задание 1
- Задание 2
- Задание 3
- Урок 1. Числовые неравенства
- Урок 2. Свойства числовых неравенств
- Урок 3. Сложение и умножение числовых неравенств
- Урок 4. Числовые промежутки
- Урок 5. Линейные неравенства
- Урок 6. Системы линейных неравенств
- Урок 7. Нелинейные неравенства
- Урок 8. Системы нелинейных неравенств
- Урок 9. Дробно-рациональные неравенства
- Урок 10. Решение неравенств с помощью графиков
- Урок 11. Неравенства с модулем
- Урок 12. Иррациональные неравенства
- Урок 13. Неравенства с двумя переменными
- Урок 14. Системы неравенств с двумя переменными
- Урок 15. Приближённые вычисления
Абсолютная и относительная погрешность

4.2
Средняя оценка: 4.2
Всего получено оценок: 2108.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2108.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2108.
А какая ваша оценка?
Вычисление погрешностей измерений
Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.
Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.
Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δиx + Δоx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Абсолютная инструментальная погрешность Δиx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.
Таблица 1
| Средства измерений | Диапазон измерений | Абсолютная инструментальная погрешность |
| Линейки: металлические деревянные пластмассовые |
150, 300, 500 мм 400, 500, 750 мм 200, 250, 300 мм |
0,1 мм 0,5 мм 1 мм |
| Лента измерительная | 150 см | 0,5 см |
| Мензурки 2-го класса | 100, 200, 250 см3 | 5 см3 |
| Амперметр школьный | 2 А | 0,05 А |
| Миллиамперметр | от 0 до Imax | 4 % максимального предела измерений Imax |
| Вольтметр школьный | 6 В | 0,15 В |
| Термометр лабораторный | 100 °С | 1 °С |
| Барометр-анероид | 720–780 мм рт. ст. | 3 мм рт. ст. |
| Штангенциркули с ценой деления 0,1; 0,05 мм | 155, 250, 350 мм | 0,1; 0,05 мм в соответствии с ценой деления нониуса |
| Микрометры с ценой деления 0,01 мм | 0–25, 25–50, 50–75 мм | 0,004 мм |
Абсолютная погрешность отсчёта Δоx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.
Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:
Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:
Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.
Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.
Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.
Таблица 2
| Вид функции y | Абсолютная погрешность Δy | Относительная погрешность |
| x1 + x2 | Δx1 + Δx2 | |
| x1 − x2 | Δx1 + Δx2 | |
| Cx | CΔx | |
| x1x2 | |x1| Δx2 + |x2| Δx1 | |
| xn | |n||x|n−1Δx | |
| lnx | ||
| sinx | |cosx| Δx | |
| cosx | |sinx| Δx | |tgx| Δx |
| tgx |
Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.
Download Article
Download Article
Absolute error is the difference between the measured value and the actual value.[1]
It is one way to consider error when measuring the accuracy of values. If you know the actual and measured values, calculating the absolute error is a simple matter of subtraction. Sometimes, however, you may be missing the actual value, in which case you should use the maximum possible error as the absolute error.[2]
If you know the actual value and the relative error, you can work backwards to find the absolute error.
-
1
Set up the formula for calculating the absolute error. The formula is
, where
equals the absolute error (the difference, or change, in the measured and actual value),
equals the measured value, and
equals the actual value.[3]
-
2
Plug the actual value into the formula. The actual value should be given to you. If not, use a standardly accepted value. Substitute this value for
.[4]
- For example, you might be measuring the length of a football field. You know that the actual, or accepted length of a professional American football field is 360 feet (including both end zones). So, you would use 360 as the actual value:
.
Advertisement
- For example, you might be measuring the length of a football field. You know that the actual, or accepted length of a professional American football field is 360 feet (including both end zones). So, you would use 360 as the actual value:
-
3
Find the measured value. This will be given to you, or you should make the measurement yourself. Substitute this value for
.
- For example, if you measure the football field and find that it is 357 feet long, you would use 357 as the measured value:
.
- For example, if you measure the football field and find that it is 357 feet long, you would use 357 as the measured value:
-
4
Subtract the actual value from the measured value. Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.[5]
- For example, since
, the absolute error of your measurement is 3 feet.
- For example, since
Advertisement
-
1
Set up the formula for relative error. The formula is
, where
equals the relative error (the ratio of the absolute error to the actual value),
equals the measured value, and
equals the actual value.[6]
-
2
Plug in the value for the relative error. This will likely be a decimal. Make sure you substitute it for
.
- For example, if you know that the relative error is .025, your formula will look like this:
.
- For example, if you know that the relative error is .025, your formula will look like this:
-
3
Plug in the value for the actual value. This information should be given to you. Make sure you substitute this value for
.
- For example, if you know that the actual value is 360 ft, your formula will look like this:
.
- For example, if you know that the actual value is 360 ft, your formula will look like this:
-
4
Multiply each side of the equation by the actual value. This will cancel out the fraction.
-
5
Add the actual value to each side of the equation. This will give you the value of
, giving you the measured value.
-
6
Subtract the actual value from the measured value. Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.[7]
- For example, if the measured value is 369 ft, and the actual value is 360 feet, you would subtract
. So, the absolute error is 9 feet.
- For example, if the measured value is 369 ft, and the actual value is 360 feet, you would subtract
Advertisement
-
1
Determine the measuring unit. This is the “to the nearest” value. This might be explicitly stated (for example, “The building was measured to the nearest foot.”), but it doesn’t have to be. To determine the measuring unit, just look at what place value the measurement is rounded to.
- For example, if the measured length of a building is stated as 357 feet, you know that the building was measured to the nearest foot. So, the measuring unit is 1 foot.
-
2
-
3
Use the maximum possible error as the absolute error.[9]
Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.- For example, if you find the measurement of a building to be
, the absolute error is .5 ft.
- For example, if you find the measurement of a building to be
Advertisement
Add New Question
-
Question
How do I find absolute error of any equation?
An equation does not contain an «absolute error.» Re-read the introduction above.
-
Question
How do I find the root value of a 6-digit number?
-
Question
What is the absolute error in 2.11?
As explained above, the concept of «absolute error» involves both a measured value and an «actual» value.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If the actual value is not given, you can look for the accepted or theoretical value.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate the absolute error, use the formula, “Absolute Error = Measured Value — Actual Value.” Begin by plugging the actual value into the formula, which will either be given to you or is the standardly accepted value. Then, make a measurement and put the measured value into the formula. Finally, subtract the actual value from the measure value to calculate the absolute error. If there are any negative signs, ignore them when you record your answer. To learn how to find the absolute error if you don’t have the measured value, keep reading.
Did this summary help you?
Thanks to all authors for creating a page that has been read 193,656 times.
Did this article help you?
Download Article
Download Article
Absolute error is the difference between the measured value and the actual value.[1]
It is one way to consider error when measuring the accuracy of values. If you know the actual and measured values, calculating the absolute error is a simple matter of subtraction. Sometimes, however, you may be missing the actual value, in which case you should use the maximum possible error as the absolute error.[2]
If you know the actual value and the relative error, you can work backwards to find the absolute error.
-
1
Set up the formula for calculating the absolute error. The formula is
, where
equals the absolute error (the difference, or change, in the measured and actual value),
equals the measured value, and
equals the actual value.[3]
-
2
Plug the actual value into the formula. The actual value should be given to you. If not, use a standardly accepted value. Substitute this value for
.[4]
- For example, you might be measuring the length of a football field. You know that the actual, or accepted length of a professional American football field is 360 feet (including both end zones). So, you would use 360 as the actual value:
.
Advertisement
- For example, you might be measuring the length of a football field. You know that the actual, or accepted length of a professional American football field is 360 feet (including both end zones). So, you would use 360 as the actual value:
-
3
Find the measured value. This will be given to you, or you should make the measurement yourself. Substitute this value for
.
- For example, if you measure the football field and find that it is 357 feet long, you would use 357 as the measured value:
.
- For example, if you measure the football field and find that it is 357 feet long, you would use 357 as the measured value:
-
4
Subtract the actual value from the measured value. Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.[5]
- For example, since
, the absolute error of your measurement is 3 feet.
- For example, since
Advertisement
-
1
Set up the formula for relative error. The formula is
, where
equals the relative error (the ratio of the absolute error to the actual value),
equals the measured value, and
equals the actual value.[6]
-
2
Plug in the value for the relative error. This will likely be a decimal. Make sure you substitute it for
.
- For example, if you know that the relative error is .025, your formula will look like this:
.
- For example, if you know that the relative error is .025, your formula will look like this:
-
3
Plug in the value for the actual value. This information should be given to you. Make sure you substitute this value for
.
- For example, if you know that the actual value is 360 ft, your formula will look like this:
.
- For example, if you know that the actual value is 360 ft, your formula will look like this:
-
4
Multiply each side of the equation by the actual value. This will cancel out the fraction.
-
5
Add the actual value to each side of the equation. This will give you the value of
, giving you the measured value.
-
6
Subtract the actual value from the measured value. Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.[7]
- For example, if the measured value is 369 ft, and the actual value is 360 feet, you would subtract
. So, the absolute error is 9 feet.
- For example, if the measured value is 369 ft, and the actual value is 360 feet, you would subtract
Advertisement
-
1
Determine the measuring unit. This is the “to the nearest” value. This might be explicitly stated (for example, “The building was measured to the nearest foot.”), but it doesn’t have to be. To determine the measuring unit, just look at what place value the measurement is rounded to.
- For example, if the measured length of a building is stated as 357 feet, you know that the building was measured to the nearest foot. So, the measuring unit is 1 foot.
-
2
-
3
Use the maximum possible error as the absolute error.[9]
Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.- For example, if you find the measurement of a building to be
, the absolute error is .5 ft.
- For example, if you find the measurement of a building to be
Advertisement
Add New Question
-
Question
How do I find absolute error of any equation?
An equation does not contain an «absolute error.» Re-read the introduction above.
-
Question
How do I find the root value of a 6-digit number?
-
Question
What is the absolute error in 2.11?
As explained above, the concept of «absolute error» involves both a measured value and an «actual» value.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If the actual value is not given, you can look for the accepted or theoretical value.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate the absolute error, use the formula, “Absolute Error = Measured Value — Actual Value.” Begin by plugging the actual value into the formula, which will either be given to you or is the standardly accepted value. Then, make a measurement and put the measured value into the formula. Finally, subtract the actual value from the measure value to calculate the absolute error. If there are any negative signs, ignore them when you record your answer. To learn how to find the absolute error if you don’t have the measured value, keep reading.
Did this summary help you?
Thanks to all authors for creating a page that has been read 193,656 times.
Did this article help you?
Чтобы оценить степень отклонения, используется показатель абсолютной и относительной погрешности.
В математике, физике и метрологии этот коэффициент может быть использован для округления полученных результатов.
Показатель бывает нескольких видов. Для его определения применяют разные методы.
Понятие и классификация
Под термином погрешность принято понимать степень отклонения реальной величины от вычисленной. Этот показатель служит мерой точности измерения.
Существует несколько разновидностей погрешности:
- Абсолютная — оценка ошибки в абсолютных единицах. Величина ее может быть разной в зависимости от способа расчета.
- Относительная — отношение абсолютной величины к тому значению, которое принято считать истинным. Измеряется в процентах.
- Приведенная — разновидность относительной. Ее вычисляют отношением абсолютной и условной постоянной величины, определяется в процентах.
- Приборная или инструментальная — погрешность, которую дают технические средства измерений. Она обусловлена неточной цифровой градуировкой приборов или недостаточной наглядностью. Класс точности приборов будет равен максимальной приведенной погрешности и выражается в процентах. К примеру, класс точности вольтметра ΔU = ±0,75 В.
- Методическая — связанная с несовершенством метода измерения или его чрезмерным упрощением.
- Субъективная или операторная — погрешность, связанная с личными свойствами оператора — невнимательностью, утомлением, профессиональной подготовленностью.
- Случайная. Погрешность, которая может изменяться при разных измерениях. Изменения возможны по знаку или величине отклонения. Причиной может быть техническое несовершенство приборов отсчета или объекта измерения, неблагоприятные для работы условия или особенности измеряемых единиц.
- Систематическая. Погрешность, изменения которой имеют некоторую закономерность во времени. В качестве частного случая допускают постоянное отклонение, которое не изменяется во времени.
- Прогрессирующая или дрейфовая — медленно изменяется во времени и не может быть предсказана. Такое отклонение относится к случайным.
- Грубая или промах. Значительное отклонение от принятой нормы. Возникает в результате неисправности аппаратуры или ошибки экспериментатора.
Выделяют также отклонения прямых или косвенных измерений. Вторая разновидность учитывается в тех случаях, когда измерить величину напрямую невозможно и ее можно посчитать по формулам исходя из других данных.
Абсолютная и относительная погрешности
Абсолютная погрешность величины — это разница между ней и принятым точным значением. Чтобы определить этот показатель, из большего числа вычитают меньшее. Единицы обозначения такие же, как и для основной величины. В формулах обозначается греческой буквой дельта и исследуемой величиной.
Пример: В пакете находится 478 граммов сахара. Это число можно округлить до 500. В этом случае абсолютная погрешность приближения будет 500 — 478 =22 г
Для вычислений разработана специальная формула: Δа=А-а,
где А — это точная величина,
а — приближенная, это число, которое немного отличается от точного.
Результаты вычисления записывают со знаком ±. Например, длина бумажного рулона составляет 25 м ± 5 см. Наибольшее значение абсолютной погрешности принято называть ее пределом.
Чтобы получить измерения высокой точности, рассчитать абсолютную погрешность недостаточно. Если измерять предмет длиной 30 см и допустить неточность в 1 см, ее величина будет значительной. При измерении 30-метрового участка дороги то же самое отклонение в 1 см допускается, такое измерение будет наиболее точным. При вычислении ускорения свободного падения с помощью маятника неточность не превышает 10 -5 м/с. 2
Относительная погрешность — условная величина, равная отношению абсолютной к самому числу.
Пример: количество сахара в пакете равно 478 граммов, абсолютная погрешность составляет 22 грамма, относительная равняется 22: 478 = 0, 046. Если перевести в проценты, получается 4,6%. Для отрезка длиной 10 см погрешность в 1 см будет составлять 10%, а для отрезка в 1 м такая же абсолютная величина составит всего 1%. Относительная оценка считается наиболее точной.
Относительная погрешность может быть случайной, возникающей под действием внешних факторов. Ее размер зависит от способа нахождения.
Методики расчета
Существует несколько методов определения отклонения. Наиболее простой и доступный способ:
- Необходимые измерения проводят не менее 5 раз. Это дает возможность вычислить наиболее точное значение параметра. Результаты вносят в таблицу excel.
- Полученные величины складывают и делят на количество замеров. В результате получится действительное значение. Его обычно применяют вместо истинного, так как нет возможности вычислить последнее.
- Следующий шаг — определение абсолютной погрешности. Ее считают для каждого измерения. Чтобы узнать величину этого показателя, из результата каждого замера вычитают действительное значение. Для обработки данных неважно, положительная или отрицательная получилась цифра. Используют модули полученных чисел, пренебрегая знаками.
- Чтобы определить относительную погрешность измерения, нужно разделить абсолютную на действительное значение. Полученное число умножают на 100%.
Для определения предельного отклонения выбирают наибольшее значение из всех полученных.
Чтобы получить наиболее точные показатели дискретности цифровых приборов, пользуются средним квадратическим отклонением. Вычислить его можно следующим способом:
- Каждый показатель абсолютной погрешности возводят в квадрат и записывают.
- Полученные результаты складывают между собой.
- Сумму всех квадратов делят на число, которое на единицу меньше количества измерений.
- Из результата вычислений извлекают квадратный корень — это и будет среднее квадратическое отклонение.
Чтобы вычислить, чему равна относительная погрешность измерения, важно придерживаться некоторых правил. Складывая или вычитая числа, учитывают абсолютные отклонения. Если числа нужно разделить или перемножить, прибегают к относительным показателям. Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.
Результаты фиксируются в виде десятичных дробей. Точное значение может быть очень длинным, вплоть до бесконечного. Для удобства используют только среднее значение. При этом важно помнить о существовании верных и сомнительных цифр. У первой категории цифр разряд бывает выше допустимой погрешности, у второй — ниже.
При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%. Эта же закономерность применяется для оценки температуры и других физических величин.
Произвести необходимые расчеты можно с помощью онлайн-калькулятора. В окошки вносятся необходимые данные, после чего программа выдает результат.
Методы Корнфельда и Стьюдента
Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.
Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:
- Предполагается, что имеется ряд результатов измерений от Х1 до Хn.
- Из этих величин выбирают минимальную и максимальную.
- Вычисляют среднее значение Х.
- В пределах от наименьшего до наибольшего показателя выбирают доверительный интервал.
- Чтобы найти абсолютное отклонение, необходимо вычесть из максимального результата измерения величину минимального. Полученную разность делят пополам.
Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.
Эти показатели вычисляются на основе доверительной вероятности и большого количества измерений.
Абсолютная и относительная погрешности (ошибки).
Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x1,
x2,
x3,
…, xn
Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:
Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.
Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:
(13)
Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.
Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):
(14)
Отношения
называются относительными погрешностями
(ошибками) отдельных измерений.
Отношение средней
абсолютной погрешности результата
к среднему арифметическому значению
измеряемой величины называют относительной
ошибкой результата и выражают в процентах:
Относительная
ошибка характеризует точность измерения.
Законы распределения случайных величин.
Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.
Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.
Непрерывная
случайная величина принимает любые
значения в данном интервале.
Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.
Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.
Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.
Два события,
одновременное появление которых
невозможно, называются несовместными.
Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:
называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:
При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:
Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.
Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений хi
на вероятность этих значений рi:
Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:
,
где mi
— число дискретных случайных величин,
имеющих значение хi.
Для непрерывной
случайной величины математическим
ожиданием служит интеграл:
,
где р(х) — плотность
вероятности.
Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:
(15)
(16)
Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:
(17)
Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».
Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:
а) ряд распределения
(для дискретных величин);
б) функция
распределения;
в) кривая распределения
(для непрерывных величин).
Существует
относительно много законов распределения
случайных величин.
Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина
распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:
(18),
где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);
—
среднее квадратичное отклонение;
—
основание натурального логарифма
(неперово число);
f
(x)
– плотность вероятности (функция
распределения вероятностей).
Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).
Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:
(19)
Таким образом,
максимальное значение функции fmax(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом 2>1.
(При увеличении
кривая распределения становится более
пологой, а при уменьшении
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и 3
= 2.
Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал
теоретически была определена в 1860 году
английским физиком Максвеллом
. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т1
< Т2).
Закон распределения Максвелла определяется
формулой:
(20),
где mо
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.
Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:
(21)
Где n(h)
– концентрация молекул газа на высоте
h,
n0
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.
Распределение
Больцмана.
Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному
статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).
n
-
h
Гистограмма
распределения Больцмана.
Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов xi
одинаковой ширины. Для каждого интервала
подсчитывают число mi
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины
для каждого интервала xi
и среднее значение случайной величины
<xi
> в каждом интервале.
Затем по оси абсцисс
откладывают интервалы xi,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой
– плотностью относительной частоты
).
Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).
Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:
(22)
Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:
(23)
Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.
Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.
Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.
Доверительной
вероятностью
(надежностью)
результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.
Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t,n<>,
<x>
+ t,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .
Коэффициент t,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).
Значении коэффициента
Стьюдента t,n
зависит от доверительной вероятности
и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.
Таблица 1
|
n |
|
||||||
|
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
4 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
В таблице 1 в верхней
строке заданы значения доверительной
вероятности
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.
Окончательный
результат измерений записывается в
виде:
(25)
Где
– полуширина доверительного интервала.
Результат серии
измерений оценивается относительной
погрешностью:
(26)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1} triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6 triangle_2=|100,4-101,2|=0,8 triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%} delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%} delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2 S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})
Физические величины и погрешности их измерений — Задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Сразу оговоримся, что при выборе измерительного оборудования часто нужно также знать диапазон измерения и какое именно значение интересует: например, среднеквадратическое значение (СКЗ) измеряемой величины в определённом интервале времени, или требуется измерять среднеквадратическое отклонение (СКО) (для измерения переменной составляющей величины), или требуется измерять мгновенное (пиковое) значение.
- При измерении переменных физических величин (например, напряжение переменного тока) требуется знать динамические характеристики измеряемой физической величины: диапазон частот или максимальную скорость изменения физической величины,
- Эти данные, необходимые при выборе измерительного оборудования, зависят от физического смысла задачи измерения в конкретном физическом эксперименте,
Итак, повторимся: задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Эта задача решается с помощью прямых или косвенных измерений, При прямом измерении осуществляется количественное сравнение физической величины с соответствующим эталоном при помощи измерительных приборов.
- Отсчет по шкале прибора указывает непосредственно измеряемое значение.
- Например, термометр дает значения измеряемой температуры, а вольтметр – значение напряжения.
- При косвенных измерениях интересующая нас физическая величина находится при помощи математических операций над непосредственно измеренными физическими величинами (непосредственно измеряя напряжение U на резисторе и ток I через него, вычисляем значение сопротивления R = U / I ).
Точность прямых измерений некоторой величины X оценивается величиной погрешности или ошибки, измерений относительно действительного значения физической величины X Д, Действительное значение величины X Д (согласно РМГ 29-99 ) – это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
- Различают абсолютную (∆ X) и относительную (δ) погрешности измерений.
- Абсолютная погрешность измерения – это п огрешность средства измерений, выраженная в единицах измеряемой физической величины, характеризующая абсолютное отклонение измеряемой величины от действительного значения физической величины: ∆X = X – X Д,
Относительная погрешность измерения – это п огрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%, При оценке точности косвенных измерений некоторой величины X 1, функционально связанной с физическими величинами X 2, X 3,, X 1 = F (X 2, X 3, ), учитывают погрешности прямых измерений каждой из величин X 2, X 3, и характер функциональной зависимости F (),
Как вычислить погрешность измерений?
Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).
расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. (1). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет (1) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между (9) и (10) метками.
У нас есть два варианта определения длины этого бруска. (1). Если мы заявим, что длина бруска — (9) сантиметров, то недостаток длины от истинной составит более половины сантиметра ((0,5) см (= 5) мм). (2). Если мы заявим, что длина бруска — (10) сантиметров, то избыток длины от истинной составит менее половины сантиметра ((0,5) см (= 5) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет (1) сантиметр. Значит, погрешность этой линейки (1) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. Рис. (2). Деревянная линейка Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления (0,1) мм и (0,05) мм, Рис. (3). Штангенциркуль На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений. Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.
В чем измеряется погрешность?
Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
- Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
- Инструментальные и методические погрешности.
- Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях.
- Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.
Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.
Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.
Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.
Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Как найти абсолютную погрешность измерительного прибора?
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δ и x + Δ о x при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Что такое погрешность метода измерений?
По источнику возникновения — Инструментальная погрешность Эта погрешность определяется несовершенством прибора, возникающим, например, из-за неточной калибровки, Методическая погрешность Методической называют погрешность, обусловленную несовершенством метода измерений.
Что такое погрешность измерительного прибора?
Определение — Проводя измерение параметров рынка, маркетолог получает результаты в виде таблиц, графиков и пр. Эти данные он предоставляет заказчику. Но в отчетах не все специалисты указывают важную величину — погрешность, о которой клиент не подозревает.
Как определить погрешность деления?
Как определить погрешность и объем жидкости — Погрешность равна половине цены деления мензурки. В нашем случае погрешность составляет 2,5 мл. Чтобы определить объем, берем ближайшее число от верхней границы жидкости (на рисунке — это значение 40 мл) и прибавляем количество штрихов (на рисунке — 2 штриха) по 5 мл: V = 40 + 2 × 5 = 50 мл.
Как рассчитывается приведенная погрешность?
Программа КИП и А Дмитрий Бебякин, инженер — метролог, ИЛИМ Позволю себе вначале небольшое отступление. Такие понятия как погрешность, класс точности довольно подробно описываются в нормативной документации ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений», ГОСТ 8.401-80 «Классы точности средств измерений.
- Общие требования» и им подобных.
- Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия.
- Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п.
Попробуем разобраться, а затем свести в одну небольшую, но понятную табличку, что же такое «погрешность» и какая она бывает. Погрешности измерений – отклонения результатов измерения от истинного значения измеряемой величины. Погрешности неизбежны, выявить истинное значение невозможно.
- Абсолютная погрешность: Δ = X д — X изм, выражается в единицах измеряемой величины, например в килограммах (кг), при измерении массы. где X д – действительное значение измеряемой величины, принимаются обычно показания эталона, образцового средства измерений; X изм – измеренное значение.
- Относительная погрешность: δ = (Δ ⁄ X д ) · 100, выражается в % от действительного значения измеренной величины.
- Приведённая погрешность: γ = (Δ ⁄ X н ) · 100, выражается в % от нормирующего значения. где X н – нормирующее значение, выраженное в тех же единицах, что и Δ, обычно принимается диапазон измерения СИ (шкала).
По характеру проявления:
- систематические (могут быть исключены из результатов);
- случайные;
- грубые или промахи (как правило не включаются в результаты измерений).
В зависимости от эксплуатации приборов:
- основная – это погрешность средства измерения при нормальных условиях; (ГОСТ 8.395-80)
- дополнительная погрешность – это составляющая погрешности средства измерения, дополнительно возникающая из-за отклонения какой-либо из влияющих величин от нормативного значения или выход за пределы нормальной области значений. Например: измерение избыточного давления в рабочих условиях цеха, при температуре окружающего воздуха 40 ºС, относительной влажности воздуха 18% и атмосферном давлении 735 мм рт. ст., что не соответствует номинальным значениям влияющих величин при проведении поверки.
| Наимено вание погреш ности | Формула | Форма выражения, записи | Обозначение класса точности | |||||||||||||||
| В докумен тации | На сред стве изме рений | |||||||||||||||||
| Абсолют ная | Δ = X д — X изм | Δ = ±50 мг Примеры: Номинальная масса гири 1 кг ±50 мг Диапазон измерения весов среднего III класса точности от 20 г до 15 кг ±10 г | Класс точности: М 1 Класс точности: средний III Примечание: на многие виды измерений есть свои НД по выражению погрешностей, здесь для примера взято для гирь и весов. | М 1 | ||||||||||||||
| Относи тельная | δ = (Δ ⁄ X д ) · 100 | δ = ±0,5 Пример: Измеренное значение изб.
Как вычислить абсолютную погрешность формула?Поиск: Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ). Чему равна абсолютная погрешность?При измерении каких-либо величин важным понятием является понятие о погрешности. Это связано с тем, что абсолютно точно измерить какую либо величину невозможно. Поэтому вводят понятие погрешности. Есть очень много видов погрешности, связанных с человеческим фактором или процессом измерения. Для чего нужна погрешность измерений?Каждое физическое измерение в исследованиях и промышленности сопровождается определенной погрешностью. Даже незначительные колебания в условиях окружающей среды могут влиять на измерение и вызывать отклонения, которые делают результат измерения ненадежным. Для получения правильных результатов измерений необходимо учитывать связанную с результатами погрешность. Погрешность измерений указывает на недостающую информацию о настоящем значении измеряемой величины. Она определяется параметром, выраженным в процентах и относящимся к результату измерения, который обозначает отклонение значений, которое обоснованно можно присвоить измеряемой величине на основе имеющейся информации. Другими словами, это диапазон, в пределах которого с определенной вероятностью находится истинное значение измеряемой величины. Как найти абсолютную погрешность пример?Абсолютная погрешность — Абсолютной погрешностью числа называют разницу между этим числом и его точным значением. Рассмотрим пример : в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26. Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой.
Границу абсолютной погрешности называют предельной абсолютной погрешностью. Как определить цену деления и погрешность?Найти две соседних отметки шкалы, возле которых написаны величины, соответствующие этим отметкам шкалы; найти разность этих величин; сосчитать количество промежутков между величинами отметок шкалы; полученную разность величин разделить на количество промежутков. Что такое максимальная погрешность измерений?Предельная погрешность измерения в ряду измерений – максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи. Как рассчитывается приведенная погрешность?Программа КИП и А Дмитрий Бебякин, инженер — метролог, ИЛИМ Позволю себе вначале небольшое отступление. Такие понятия как погрешность, класс точности довольно подробно описываются в нормативной документации ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений», ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования» и им подобных. Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия. Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п. Попробуем разобраться, а затем свести в одну небольшую, но понятную табличку, что же такое «погрешность» и какая она бывает. Погрешности измерений – отклонения результатов измерения от истинного значения измеряемой величины. Погрешности неизбежны, выявить истинное значение невозможно.
По характеру проявления:
В зависимости от эксплуатации приборов:
|
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением. Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Видео
Абсолютная и относительная погрешности
Абсолютная погрешность величины — это разница между ней и принятым точным значением. Чтобы определить этот показатель, из большего числа вычитают меньшее. Единицы обозначения такие же, как и для основной величины. В формулах обозначается греческой буквой дельта и исследуемой величиной.
Пример: В пакете находится 478 граммов сахара. Это число можно округлить до 500. В этом случае абсолютная погрешность приближения будет 500 — 478 =22 г
Для вычислений разработана специальная формула: Δа=А-а,
где А — это точная величина,
а — приближенная, это число, которое немного отличается от точного.
Результаты вычисления записывают со знаком ±. Например, длина бумажного рулона составляет 25 м ± 5 см. Наибольшее значение абсолютной погрешности принято называть ее пределом.
Чтобы получить измерения высокой точности, рассчитать абсолютную погрешность недостаточно. Если измерять предмет длиной 30 см и допустить неточность в 1 см, ее величина будет значительной. При измерении 30-метрового участка дороги то же самое отклонение в 1 см допускается, такое измерение будет наиболее точным. При вычислении ускорения свободного падения с помощью маятника неточность не превышает 10 -5 м/с. 2
Относительная погрешность — условная величина, равная отношению абсолютной к самому числу.
Пример: количество сахара в пакете равно 478 граммов, абсолютная погрешность составляет 22 грамма, относительная равняется 22: 478 = 0, 046. Если перевести в проценты, получается 4,6%. Для отрезка длиной 10 см погрешность в 1 см будет составлять 10%, а для отрезка в 1 м такая же абсолютная величина составит всего 1%. Относительная оценка считается наиболее точной.
Относительная погрешность может быть случайной, возникающей под действием внешних факторов. Ее размер зависит от способа нахождения.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.