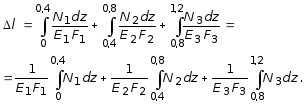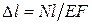Рассмотрим
однородный стержень с одним концом,
жестко заделанным, и другим — свободным,
к которому приложена центральная
продольная сила Р
(рис. 2.2). До нагружения стержня его
длина равнялась l -после
нагружения она стала равной l + Dl
(рис. 2.2). Величину Dl
называют абсолютным удлинением стержня.
Рис. 2.2
Если
в нагруженном стержне напряженное
состояние является однородным, т.е. все
участки стержня находятся в одинаковых
условиях, деформация e
остается одной и той же по длине стержня
и равной

Если
же по длине стержня возникает неоднородное
напряженное состояние, то для
определения его абсолютного удлинения
необходимо рассмотреть бесконечно
малый элемент длиной dz
(рис. 2.2). При растяжении он увеличит
свою длину на величину D dz
и его деформация составит:
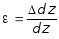
В
пределах малых деформаций при простом
растяжении или сжатии закон Гука
записывается в следующем виде:
s = E e . (2.3)
Величина
Е
представляет собой коэффициент
пропорциональности, называемый
модулем упругости материала первого
рода. Из совместного рассмотрения
уравнений (2.2) и (2.3) получим:
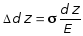
откуда
с учетом того, что
и
,
окончательно
получим:
. (2.4)
Если
стержень изготовлен из однородного
изотропного материала с Е = const,
имеет постоянное поперечное сечение
F = const
и нагружен по концам силой Р,
то из (2.4) получим
. (2.5)
При
решении многих практических задач
возникает необходимость, наряду с
удлинениями, обусловленными действием
механических нагрузок, учитывать
также удлинения, вызванные температурным
воздействием. В этом случае пользуются
принципом независимости действия
сил, и полные деформации рассматривают
как сумму силовой и температурной
деформаций:
, (2.6)
где
a — коэффициент
температурного расширения материала;
t -перепад
температуры тела. Для однородного
стержня, нагруженного по концам
продольными силами Р
и равномерно нагретого по длине, получим:

2.3. Пример расчета (задача № 1)
Для
стального бруса квадратного сечения
сжатого силой Р
с учетом собственного веса при исходных
данных приведенных ниже, требуется
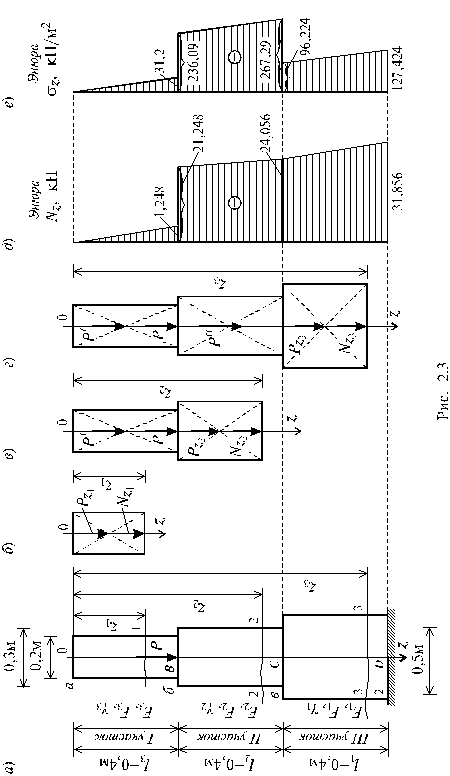
(рис. 2.3, а):
1. Определить
количество расчетных участков;
2. Составить
аналитические выражения для нормальных
сил Nz ,
нормальных напряжений sz
и вычислить их значения для каждого
из участков с учетом их собственных
весов;
3. Построить
эпюры Nz
и sz
;
4. Вычислить
перемещение верхнего конца колонны от
действия силы Р
и собственного веса.
Исходные данные: Р = 20 кН;
l1 = l2 = l3 = 0,4 м;
модуль упругости стали Е = 2,1×108 кН/м2;
F1 = 4×10-2 м2;
F2 = 9×10-2 м2;
F3 = 25×10-2 м2;
g = 78
кН/м3
.
Решение
1. Определение
количества участков.
Так как нормальная сила Nz
зависит от величин внешних сил, в данном
случае включающих в себя и собственный
вес колонны, а последний, в свою очередь,
от размеров поперечного сечения Fi
и
объемного веса g,
то границами участков следует назначать
те сечения, в которых приложены внешние
сосредоточенные силы и где происходит
скачкообразное изменение площади
поперечного сечения или объемного
веса материалов конструкций.
Исходя
из вышесказанного, учитывая g
= const,
брус будет иметь три участка:
1 участок — от
0 до сечения В
(где приложена сила Р);
2 участок — от
сечения
В
до сечения
С;
3 участок — от
сечения
С
до сечения
D.
Следует
заметить, что при определении нормальных
напряжений используются те же участки.
-
Составить
аналитические выражения для нормальных
сил Nz,
нормальных напряжений sz
и вычислить их значения для каждого
из участков, с учетом их собственных
весов.
Для
этого воспользуемся методом сечений.
1 участок
(0 — В)
0 £ z1 £ 0,4
м.
Проведя
сечение 1 — 1
на расстоянии z1
от
начала координат (точка 0), рассмотрим
равновесие верхней части. При этом, к
рассматриваемой части прикладываются
в центре ее тяжести собственный вес
и нормальная сила
,
заменяющую действие отброшенной
нижней части бруса на верхнюю
рассматриваемую (рис. 2.3,б).
Составив уравнение равновесия
рассматриваемой верхней части колонны
по оси z ,
получим:
.
В
свою очередь, собственный вес верхней
части колонны определяется следующим
образом:

Тогда
выражение для нормальной силы будет
иметь вид:
кН,
а
для нормальных напряжений
:
кН/м2.
Так
как,
и
линейно
зависят отz1 ,
то для построения их графиков (эпюр)
достаточно определить значения этих
величин на границах участка, т.е.

z1 = 0

z1 = 0,4 м кН;
кН/м2.
Знаки
минус при
и
указывают
на то, что принятое направление для
этих величин не совпадает с действительным,
т. к. в принятой схеме продольная сила
не растягивает, а сжимает первый участок.

участок (В — С)
0,4 м £ z2 £ 0,8
м.
Аналогично
предыдущему проводим сечение 2-2
на расстоянии z2
(рис. 2.3, в).
Для верхней части составляем уравнение
равновесия åz = 0 .
В
это уравнение войдут: собственный вес
первого участка Р1 =
= g F1 l1;
собственный вес отсеченной части второго
участка

сосредоточенная силаР
= 20 кН, а также сила
.
Тогда
уравнение равновесия примет вид:
Р1 + + P +
= 0,
отсюда
= —P — g F1 l1 —
= -20 — 78×4×10-2×0,4 — 78×9×10-2
(z2 -0,4) =
= -7,02×(z2 + 2,62678)
кН.
Учитывая
постоянство площади поперечного сечения
на втором участке, выражение для
нормального напряжения может быть
записано таким образом:
êÍ/ì2.
Вычислим
значения ординат
и
в граничных сечениях второго участка:

z2 = 0,4 м кН,
кН/м2;

z2 = 0,8 м кН,
кН/м2.

участок (С — D)
0,8 м £ z3 £
1,2 м.
Составив
уравнение равновесия åz = 0
(рис. 2.3, г)
для верхней части бруса, получим:
Р1 + Р2 + + P +
= 0,
откуда
= —P — g F1 l1 — g F2 l2 — g F3 (z3 — l1 — l2)
= -20 — 78×4×10-2×0,4 —
— 78×9×10-2 ×0,4 — 78×25×10-2 (z3 — 0,8) = -19,5×(z3 + 0,43364)
кН.
Выражение
для напряжения:
кН/м2.
Вычислим
значения ординат
и
в граничных сечениях третьего участка:

z3
= 0,8 м (0,8) =-19,5 (0,8 + 0,43364) = -24,056
кН,
(0,8) =-78 (0,8 + 0,43364) = -96,224кН/м2;

z3
= 1,2 м (1,2) =-19,5 (1,2 + 0,43364) = -31,856
кН,
кН/м2.
3. Построение
эпюр Nz
и sz
По причине линейной зависимости
нормальной силы и напряжений от координаты
z
для построения их эпюр достаточно
значений Nz
и
sz
в
граничных сечениях каждого из участков
(см. рис. 2.3, д, е).
Необходимым условием правильности
построения этих графиков является
выполнение следующих требований:
— скачок
в эпюре Nz
должен находиться в точке приложения
сосредоточенного усилия и быть равным
по величине значению этой силы;
— скачки
в эпюре sz
должны
совпадать с точками приложения внешней
силы Р
и изменения площади поперечного сечения
колонны.
После
анализа полученных эпюр (рис. 2.3, д, е)
легко можно убедиться, что построения
выполнены правильно.
4. Вычисление
перемещения верхнего конца колонны
от действия всех сил.
Полное перемещение согласно закону
Гука может быть вычислено по формуле

В
данном случае это выражение принимает
следующий вид:
Так
как величины определенных интегралов
равны площадям, очерченным соответствующими
подынтегральными функциями, то для
вычисления перемещений Dli
достаточно
вычислить площади эпюры Nz
на
каждом из этих участков и разделить их
на Ei
Fi
.
Следовательно,
м.
Соседние файлы в папке 1
- #
- #
- #
25.04.2014747.01 Кб42П1.DOC
- #
- #
- #
- #
- #
Абсолютное удлинение стержня формула
Формула абсолютного удлинения стержня, связывающая продольную силу, длину стержня и жесткость, имеет вид:
Формулу абсолютного удлинения стержня иногда называют законом Гука, но не для материала, а для всего стержня, а стоящее в знаменателе произведение 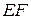
Абсолютное удлинение — показывает на сколько изменилась длина тела (увеличилась или уменьшилась).
Δl=l-l0
Единица измерения абсолютного удлинения метр — [м]
Для того, чтобы было более понятно, что же такое абсолютное удлинение, давайте рассмотрим такой пример. У нас есть металлическая труба длиной 8 метров. К трубе приложили некую силу (сжали ее) и длина трубы стала 7 метров. Тогда абсолютное удлинение будет рассчитываться как: 8м-7м=1м. То есть, длина тела изменилась на 1 метр.
Обозначения:
Δl — абсолютное удлинение тела
l0 — начальная длина тела
l — конечная длина тела, после приложения к нему силы
§1. Продольные силы в поперечных сечениях
§1. Продольные силы в поперечных сечениях
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.
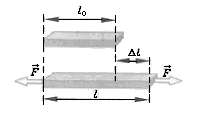
Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 1.
Рис. 1. Растяжение стержня
Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 1, а, б) оказывается единой (рис. 1, в) согласно принципу Сен – Венана.
Если воспользоваться методом сечений (рис. 2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы Nz, равные силе F (рис. 2, б).
Сжатие отличается от растяжения, формально говоря, только знаком силы Nz. При растяжении нормальная сила Nz направлена от сечения (рис. 2, б), а при сжатии – к сечению.
Рис. 2. Нормальная сила N
Растягивающие продольные силы принято считать положительными (рис. 3, а), а сжимающие – отрицательными (рис. 3, б).
Рис. 3. Знак продольной силы N
При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Nz), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.
Продольные силы (Nz), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.
График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. Nz). Он дает наглядное представление о законе изменения продольной силы.
Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.
Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.
На основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.
Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.
§2. Напряжение в поперечных сечениях стержня
При растяжении или сжатии осевыми силами стержней из однородного материала поперечные сечения, достаточно удаленные от точек приложения внешних сил ,остаются плоскими и перемещаются поступательно в направлении деформации. Это положение называют — гипотезой плоских сечений. На основании указанного можно заключить, что все точки какого-либо поперечного сечения стержня находятся в одинаковых условиях и, следовательно, напряжения распределяются по сечению равномерно. Эти напряжения перпендикулярны поперечному сечению, а значит, являются нормальными напряжениями. Их значения найдем, разделив продольную силу N на площадь А: σ=N/A
Продольная сила N с помощью метода сечений всегда может быть выражена через внешние силы. В формулe следует подставлять алгебраическое значение N т.е со знаком плюс в случае растяжения и со знаком минус в случае сжатия
§3. Расчеты на прочность и жесткость при растяжении-сжатии
Прочность стержня при осевом растяжении и сжатии обеспечена, если для каждого его поперечного сечения наибольшее расчетное (рабочее) напряжение σ не превосходит допускаемого [σ] : σ=N/A≤ [σ],
где N — абсолютное продольной силы в сечении;
А — площадь поперечного сечения;
[σ] — допускаемое напряжение пр растяжении или сжатии для материала стержня.
Данное выражение определяет условие прочности при растяжении или сжатии.
С помощью этой формулы решается три вида зада (выполняется три вида расчета):
1. Проверка прочности (проверочный расчет). При заданных продольной силы N и площади поперечного сечения А определяют рабочее (расчетное) напряжение и сравнивают его с допускаемым [σ].
Превышение рабочего (расчетного) напряжения не должно быть больше 5% , иначе прочность рассчитываемой детали считается недостаточной.
В случаях, когда рабочее напряжения значительно ниже допускаемых σ<<[σ], получаются неэкономичные конструкции чрезмерным необоснованным расходом материала. Такие решения являются нерациональными. Следует стремится к максимальному использованию прочности материала и снижения материалоемкости конструкций.
2. Подбор сечения (проектный расчет). Исходя из условия прочности можно определить необходимые размеры сечения, зная продольную силу N и допускаемое напряжение [σ]:
A≥N/[σ]
3. Определение допускаемой продольной силы. Допускаемое значение продольной силы в поперечном сечении стержня можно найти по формуле: [N]≤ [σ]·A
Значения допускаемых напряжение для некоторых материалов приведены в табл. 1.
Допускаемые напряжения назначаются на основе результатов механических испытаний образцов соответствующих материалов.
§4. Деформации и перемещения. Закон Гука
Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим — свободным, к которому приложена центральная продольная сила Р (рис. 4). До нагружения стержня его длина равнялась l — после нагружения она стала равной
(рис. 4). Величину называют абсолютной продольной деформацией (абсолютным удлинением) стержня. В большинстве случаев оно мало по сравнению с его первоначальной длиной l (∆l<<l).
Рис. 4. Абсолютное удлинение стержня
Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация
остается одной и той же по длине стержня и равной ε = Δl/l
Величина ε называется относительной продольной деформацией.
В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде (нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации
): σ=Eε
Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода (модуль продольной упругости). Его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки. Так как величина ε безразмерная, то E — измеряется в тех же единицах измерения то и напряжение, т. е. в Паскалях (Па). Значения модуля упругости E для некоторых конструкционных материалов приведены в табл. 2.
Δl=Nl/EA
Выведенное соотношение показывает, что удлинение (укорочение) при растяжении (сжатии) зависит от величины продольной силы N, поперечного сечения А стержня, его длины l и модуля продольной упругости Е. Произведение ЕА называется жесткостью сечения стержня при растяжении (сжатии).
При растяжении и сжатии изменяются и поперечные размеры стержня. Поперечный размер, первоначально равный a , уменьшается до a1. Изменение поперечно размера Δ a= a- a1, а поперечная деформация равна ε┴= Δ a/ a.
Экспериментально установлено что отношение поперечной деформации к продольной при упругом растяжении или сжатии есть величина постоянная и обозначается µ: µ= ε┴/ ε
Следует учитывать, что продольные и поперечные деформации всегда противоположны по знаку. Иными словами, при растяжении, когда продольный размер стержня увеличивается, его поперечный размер уменьшается, и, наоборот , при сжатии продольный размер уменьшается, а поперечный –увеличивается .
Величина µ называется коэффициентом поперечной деформации, или коэффициентом Пуассона. Коэффициент поперечной деформации для некоторых материалов имеет следующие значения:
сталь ….024-032,
медь….031-035,
бронза..032-035,
резина , каучук…047.