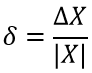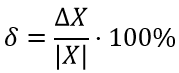Случайные погрешности в лабораторных работах по физике можно оценивать только с использованием калькулятора
О теории случайных погрешностей
Теория случайных погрешностей была создана К.Ф.Гауссом в первой половине XIX в. в связи с его занятиями астрономией и геодезией.
Напомним, что случайные погрешности δi = xi — a проявляются при проведении серии измерений одной и той же физической величины в неизменных условиях одним и тем же методом.
Одним из фундаментальных положений теории Гаусса является «принцип арифметической середины». В соответствии с этим принципом за истинное значение величины а принимается среднее значение
при n → ∞, если метод не сопровождается систематическими погрешностями.
Для случайных погрешностей характерны следующие свойства:
- Положительные и отрицательные случайные погрешности встречаются с одинаковой вероятностью, т. е. одинаково часто.
- Среднее арифметическое из алгебраической суммы случайных погрешностей при неограниченном возрастании числа наблюдений стремится к нулю, т. е.
- Малые по абсолютной величине случайные погрешности встречаются с большей вероятностью, чем большие.
Основная идея теории Гаусса может быть выражена следующим образом
Возможные конкретные значения случайной погрешности, как и сам результат измерения, предсказать невозможно. Однако после того как экспериментатор определил измеряемый параметр и метод его измерения, сразу «возник» объективный закон, неизвестный исследователю. Этот закон определяет совокупность случайных погрешностей, которые возникают в процессе измерений.
Всегда можно эмпирически (на конкретных опытах) выявить закон распределения случайных погрешностей, который обычно выражается в виде так называемой функции распределения f(δ). Этот закон позволяет определить вероятность, с которой погрешность может оказаться в интервале от δ1 до δ2. Вероятность эта равна площади заштрихованной криволинейной трапеции, представленной на графике функции распределения.
Гауссу удалось определить универсальный закон распределения, которому подчиняется огромный класс случайных погрешностей измерений самых разных величин различными методами.
Этот закон носит название нормального закона распределения. Конечно, существуют измерения, погрешность которых не распределена по нормальному закону. Однако всегда можно определить степень их отклонения от нормального закона.
Функция распределения φ(δ), открытая Гауссом, имеет следующие свойства:
1) Функция δ(φ) четная, т. е. δ-(φ-)δ(φ), и в силу этого симметрична относительно оси координат.
2) Функция δ(φ) имеет максимум при значениях случайной погрешности, равных нулю.
3) Функция δ(φ) имеет две точки перегиба, расположенные симметрично относительно оси координат. Координаты точек перегиба равны ±σ.
4) Касательные к кривой δ(φ) в точках перегиба отсекают на оси абcцисс отрезки, равные ±2σ.
5) Максимальное значение функции δ(φ) равно
6) Площадь под всей кривой δ(φ) стремится к 1. Площадь криволинейной трапеции, ограниченной прямыми, проходящими через точки δ1,2 = ±σ, составляет 0,68 от всей площади; если прямые проходят через точки δ3,4 = ±2σ, то площадь составляет 0,95; площадь криволинейной трапеции, ограниченной прямыми δ5,6 = ±3σ, равна 0,99.
Параметр σ, определяющий все фундаментальные свойства нормального закона, называется средним квадратическим отклонением. Этот параметр может быть определен после получения достаточно большой серии результатов измерений x1, х2, х3, …, хn. Тогда
Важность параметра σ состоит в том, что он позволяет определить границы случайных погрешностей. Действительно, вероятность получения случайных погрешностей, превосходящих по абсолютной величине 3σ, равна 1%.
При обычной организации измерений не представляется возможности провести не только бесконечно большое число измерений, но и провести просто большое их число.
Специальные исследования показали, что такая граница может быть определена при небольшом числе опытов в серии.
В такой серии из k измерений находят так называемую среднюю квадратичную погрешность
Затем Δхкв увеличивают в S раз.
Число S называется коэффициентом Стьюдента (коэффициент был предложен в 1908 г. английским математиком В. С. Госсетом, публиковавшим свои работы под псевдонимом Стьюдент — студент). Коэффициент Стьюдента позволяет определить границу случайной погрешности серии: Δхслуч = S Δхкв.
Таблица коэффициентов S для различного числа опытов в серии
Погрешность среднего арифметического
После проведения серии равноточных измерений и нахождения хср и σ легко определяется интервал, к которому с вероятностью 99% принадлежит результат любого следующего измерения. Этот интервал равен [хср ± 3σ], если в серии достаточно много измерений, и имеет вид [хср ± S Δхкв] при небольшом числе опытов. Это означает, что 3σ (или S Δхкв) характеризует погрешность каждого опыта серии. Итак, среднее квадратичное отклонение серии опытов есть погрешность каждого опыта серии. Именно поэтому вводится обозначение σх или ΔSкв.х. Однако среднее арифметическое есть разумная комбинация всех измерений, и поэтому следует ожидать, что истинное значение находится в более узком интервале около хср, чем [xcp ± 3σх].
Понять, почему должно быть именно так, помогут следующие рассуждения
Выполняется N серий по n опытов в каждой. В каждой серии из n опытов определяется среднее значение хср. Таких средних значений получается N: хср1, хср2, …, xcpN. Для этой совокупности средних определяется среднее квадратичное отклонение
Величина σх ср характеризует предельное распределение средних значений, это и есть величина, которая позволяет найти интервал, в котором находится истинное значение измеряемой в опыте величины [хср ± 3σх ср]. На практике такая процедура никогда не реализуется не только потому, что это очень трудоемко, но и потому, что теория погрешностей позволяет по результатам одной серии определить погрешность среднего. Это делается на основе фундаментального результата теории погрешностей:
стандартное отклонение среднего σх ср в раз меньше стандартного отклонения каждого опыта серии σх, т.е.
Итак, если в серии с достаточно большим числом опытов определено хср, то граница случайной погрешности среднего равна
Если в серии небольшое число опытов, то граница случайной погрешности среднего находится по формуле:
Все расчеты случайных погрешностей возможны только с использованием режима статистических расчетов (см. раздел «Статистические расчеты»), следуя методическим рекомендациям, приведенным ниже.
Использование калькулятора CASIO fx-82EX СLASSWIZ для оценки случайных погрешностей
- Включаем калькулятор, клавиша [ON]
- Нажимаем клавишу [SHIFT](SETUP)
- Входим в режим статистики. Нажимаем клавишу [2]
- Выбираем режим 1-Variable. Нажимаем клавишу [1]
- Заполняем таблицу
- Нажимаем клавишу [OPTN]
- Выбираем режим 1-Variable. Нажимаем клавишу [3]
- На дисплее получаем ряд характеристик
8.1. Первая сверху — значение среднего значения
8.2. Вторая снизу — случайная погрешность каждого опыта серии σх - Вычисляем погрешность среднего
- Находим границу случайной погрешности среднего
Пример
Измерялась скорость тела, брошенного горизонтально. В десяти опытах были получены следующие значения дальности полета L (в мм): 250, 245, 250, 262, 245, 248, 262, 260, 260, 248. Дальность полета тела измерялась линейкой с основной погрешностью Δ1 = 1мм. Высота, с которой брошено тело, в опыте равнялась Н = 1 м и измерялась мерной лентой с основной погрешностью Δ2 = 1 см и ценой деления С2 =1 см.
Решение
Сначала определим среднее значение дальности полета тела и вычислим его начальную скорость. Для этого сведем все данные в таблицу и проведем их первичную обработку.
Так как
Легко определить среднее значение скорости по результатам серии опытов:
Граница относительной погрешности измерения скорости:
В этой формуле ΔL — граница абсолютной погрешности измерения дальности полета, Δg — погрешность округления g, ΔН — погрешность прямого однократного измерения высоты.
ΔН = 1 см + 0,5 см = 1,5 см
ΔL складывается из погрешности линейки Δ1 и случайной погрешности ΔLслуч.:
ΔL = Δ1 + ΔLслуч.
Так как ΔLкв = 7мм, то при оценке ΔLслуч. нет смысла учитывать погрешность линейки Δ1 = 1мм.
Определим погрешность измерения скорости в любом однократном опыте, который можно провести на данной установке. В этом случае в формулу для εv следует вместо ∆L подставить его границу ∆L = S ∆Lкв. Здесь S = 3,2 (см. таблицу коэффициентов S для различного числа опытов в серии).
Имеем:
Первое слагаемое в этой сумме равно 0,09; слагаемое в скобках (0,01 + 0,0075) = 0,0175. Следовательно, εv = 0,09. Граница абсолютной погрешности каждого опыта серии не превосходит
εv = ε0 = 0,565 ∙ 0,09 = 0,05 м/с
Это значит, если на данной установке провести еще один опыт, то гарантировать можно, что значение скорости, рассчитанное по его результатам, будет принадлежать интервалу [(0,56 — 0,05)м/с; (0,56 + 0,05)м/с].
Найдем границу случайной погрешности среднего значения скорости тела, брошенного горизонтально. Для этого в формулу для εv следует вместо ∆L подставить границу случайной погрешности среднего:
Таким образом,
Относительная погрешность среднего равна
0,027 + 0,01 + 0,0075
Последним слагаемым в этой сумме можно пренебречь. Итак, ср = 0,04 = 4%. Мы видим, что погрешность среднего в два раза меньше погрешности каждого опыта. Граница абсолютной погрешности среднего равна:
Таким образом, из серии 10 опытов по измерению скорости можно сделать вывод о том, что в любой другой такой серии из 10 опытов на данной установке среднее значение скорости будет находиться в интервале [(0,56 — 0,02)м/с; (0,56 + 0,02)м/с]. Этому же интервалу принадлежит неизвестное значение скорости, которое получится, если проделать серию с очень большим числом опытов, т. е. такое значение, которое можно назвать истинным значением.
Точное значение величины
Приближенное значение величины
Как вычислить относительную погрешность
Относительная погрешность приближенного числа – это отношение абсолютной погрешности к приближенному числу.
Для того чтобы вычислить относительную погрешность необходимо:
1. Вычислить абсолютную погрешность, то есть найти разность между приближенным числом и его точным значением.
2. Разделить абсолютную погрешность на точное значение величины.
3. Для получения округленного результата в процентах разделить абсолютную погрешность на приближенное значение величины и умножить получившееся частное на 100%.
Приведем пример, в помещении 23 человека, округлим это значение до 25. Тогда абсолютная погрешность = 25 – 23 = 2.
Относительная погрешность =
= 0.086956521739
Онлайн инструмент позволяет округлять любые большие числа и вычислять абсолютную и относительную погрешность.
Калькулятор позволяет округлять натуральные числа до целого, десятых, сотых, тысячных, а также дроби — до десятков, сотен, тысяч.
Онлайн калькулятор округления чисел
Округлить число:
Десятичный разделитель:
Запятая (,)
Точка (.)
очистить
Результаты округления
Округлим число: 123.62791
| Точность | Число | Абсолютная погрешность | Относительная погрешность |
|---|---|---|---|
| до целого | 124 | 0,37209 | 0,3010% |
| до десятых | 123,6 | 0,02791 | 0,0226% |
| до сотых | 123,63 | 0,00209 | 0,0017% |
| до тысячных | 123,628 | 0,00009 | 0,0001% |
| до десятитысячных | 123,6279 | 0,00001 | ≈ 0% |
| до стотысячных | 123,62791 | 0 | ≈ 0% |
Правила округления натуральных чисел
Округление целого числа производится заменой его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями:
- Подчеркнуть цифру разряда, до которого надо округлить число.
- Отделить все цифры справа от этого разряда вертикальной чертой.
- Если справа от подчеркнутой цифры следует цифра менее 5, то эту цифру оставляем без изменений, а все последующие цифры заменяем нулями.
- Если справа от подчеркнутой цифры следует цифра 5 или выше, то эту цифру увеличиваем на 1 и все последующие цифры заменяем нулями.
К примеру, округлим число 36972 до тысяч:
36|972 = 36+1|000 ≈ 37000
Теперь, округлим число 36472 до тысяч:
36|472 = 36|000 ≈ 36000
Округлим число 7154 до сотен:
71|54 = 71+1|00 ≈ 7200
Округлим число 961 до сотен:
9|61 = 9+1|00 ≈ 1000
Округлим число 495 до десятков:
49|5 = 49+1|0 ≈ 500
Правила округления десятичных дробей
Округление десятичных дробей производится аналогично округлению целых чисел с тем различием, что дробная часть, следующая после подчеркнутой цифры, отбрасывается. Знак округления чисел — ≈.
Округлим число 435,6278:
до целого числа — 435,6278 = 435+1 ≈ 436
до десятых — 435,6278 ≈ 435,6
до сотых — 435,6278 = 435,62+1 ≈ 435,63
до тысячных — 435,6278 = 435,627+1 ≈ 435,628
Абсолютная погрешность округления числа
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
К примеру, округлим число 689 до целого 700 и вычислим абсолютную погрешность: 700 — 689 = 11
Второй пример — округлим число 43,578 до десятых 43,6 и посчитаем абсолютную погрешность: 43,6 — 43,578 = 0,022
Относительная погрешность округления числа
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу, выраженное в процентах.
Для подсчета относительной погрешности необходимо разделить значение абсолютной погрешности на округляемое число и результат умножить на 100.
Из первого примера относительная погрешность будет равна: 11 / 689 * 100 = 1,6 %
Второй пример: 0,022 / 43,578 * 100 = 0,05 %
Абсолютной погрешностью приближенной величины ∆X называется разность
∆X = |X — X0|
где
X — точное значение измеряемой величины (или истинное значение),
Х0 — приближенное значение (результат измерения)
Относительная погрешность — это отношение абсолютной погрешности этого числа к модулю соответствующего точного числа X
или
Замечание
Относительную погрешность количественно определяют в долях единицы или в процентах.
Погрешность отсчёта обычно принимают равной половине цены деления (или ценой наименьшего деления, если показание прибора происходит скачками, как например у секундомера).
Поправкой называется абсолютная погрешность, взятая с обратным знаком.
43410
1) Абсолютная погрешность.
Абсолютную погрешность принято обозначать прописной греческой буквой дельта (Δ).
Чтобы найти абсолютную погрешность, следует воспользоваться формулой:
Δ = |x – x0|
где
Δ — абсолютная погрешность;
x — приближённое (практическое) значение измеряемой величины;
x0 — точное (истинное/теоретическое) значение измеряемой величины.
Абсолютная погрешность имеет ту же единицу измерения, что и измеряемая величина. Например: если измеряемая величина измеряется в метрах, то и абсолютная погрешность будет измеряться в метрах; если изм. величину мы измеряем в килограммах, то и абсолютную погрешность — тоже в килограммах. И так далее.
2) Относительная погрешность.
Относительная погрешность, как правило, обозначается строчной греческой буквой дельта (δ).
Чтобы найти относительную погрешность, следует воспользоваться формулой:
δ = |x – x0|/x0
где
δ — относительная погрешность;
x — приближённое (практическое) значение измеряемой величины;
x0 — точное (истинное/теоретическое) значение измеряемой величины.
Относительная погрешность является безразмерной величиной. Относительная погрешность либо имеет единицу измерения 1 (доли единицы), либо измеряется в процентах.
Чтобы перевести относительную погрешность из долей единицы в проценты, необходимо умножить её на 100.
δ (%) = δ * 100 = (|x – x0|/x0) * 100
Для примера рассмотрим такую задачу.
Ученик измерял линейкой длину карандаша. В результате измерений ученик получил результат, равный 152 мм. Истинная же длина карандаша, измеренная штангенциркулем, равняется 151,7 мм. Вопрос: чему равна абсолютная и относительная погрешность результата измерений ученика?
Дано:
x = 152 мм;
x0 = 151,7 мм.
Найти:
Δ — ?
δ — ?
Решение.
1) Найдём абсолютную погрешность.
Δ = |x – x0| = |152 мм – 151,7 мм| = |0,3 мм| = 0,3 мм.
2) Найдём относительную погрешность.
δ = |x – x0|/x0 = (|152 мм – 151,7 мм|/151,7 мм) * 100% = (0,3 мм : 151,7 мм) * 100% = 0,198 %.
Ответ: Δ = 0,3 мм; δ = ок. 0,198 % (приближённое значение).