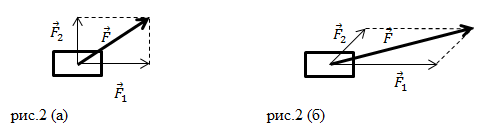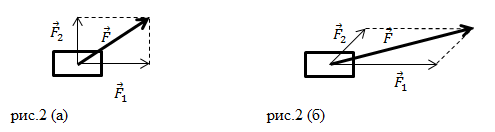Как найти абсолютную величину силы - Исправление недочетов и поиск решений вместе с Examum.ru

Страница 2 из 8

Абсолютная и относительная сила

Абсолютная сила – предельное, максимальное усилие, которое спортсмен может развить в динамическом или статическом режиме. Примером проявления абсолютной силы в динамическом режиме является поднимание штанги или приседание со штангой предельного веса. В статическом режиме абсолютная сила может быть проявлена, например, когда максимальное усилие прилагается к неподвижному объекту («выжимание» неподвижно закрепленной штанги).

Относительная сила — величина силы, приходящаяся на 1 кг веса спортсмена. Этот показатель применяется в основном для того, чтобы объективно сравнить силовую подготовленность различных спортсменов.

Между этими двумя понятиями имеются определенные соотношения, которые выражаются формулой:

Относительная сила = (Абсолютная сила)/(Собственный вес)

Из этой формулы следуют два вывода:

1) с увеличением веса показатели относительной силы у людей примерно равного уровня подготовленности будут различаться, и проигрывать в этом случае будет атлет с большим весом;

2) относительно сильнее спортсмен будет тогда, когда станет развивать абсолютную силу одновременно стремясь удержать свой вес стабильным.

В видах спорта, где приходится иметь дело с перемещением снарядов предельного веса или другими отягощениями, результат особенно или в большей мере зависит от показателей абсолютной силы. Высокие же показатели относительной силы имеют определяющее значение в видах спорта, включающих перемещение спортсменом своего тела в пространстве без дополнительных внешних отягощений, а также в тех видах спорта, где нужно ограничивать свой вес в рамках установленных весовых категорий.

Результаты исследований позволяют утверждать, что уровень абсолютной силы человека в большей степени обусловлен факторами среды (тренировка, самостоятельные занятия и др.). В то же время показатели относительной силы в большей мере испытывают на себе влияние генотипа (В. И. Лях, 1997; цит. по: Ж. К. Холодов, В. С. Кузнецов, 2003).

Источник

Абсолютная сила

Предмет
Физическая культура

Разместил

🤓 ritulya.fomina.95

👍 Проверено Автор24

суммарная сила всех мышечных групп, участвующая в данном движении.

Научные статьи на тему «Абсолютная сила»

Гауссова система единиц (СГС)

Единицей силы в СГС, например, является дина:
$1,дин=frac{гbullet см}{с^{2}}$
В абсолютной электростатической…
Если заряды выразить в абсолютных электростатических единицах, сила будет в динах, расстояние в сантиметрах…
она абсолютной электромагнитной единицей силы тока), то получится система СГСМ….
Абсолютную электромагнитную единицу силы тока обозначают $СГСМ_i.$
$1 СГСМ_i=1sqrt{дин}.$
Единица силы…
Абсолютная электростатическая система и абсолютная электромагнитная система — это две разные системы,

Статья от экспертов

Об абсолютной юридической силе обязательства

В статье рассматриваются последние законодательные изменения, позволяющие расширить общепринятое представление об обязательстве как относительном правоотношении. Основываясь на судебной практике и позициях известных цивилистов, автор приходит к выводу о том, что обязательство не только связывает должника с кредитором, но и порождает у всех субъектов правопорядка пассивную обязанность воздержаться от создания препятствий кредитору в осуществлении его субъективного права. При этом сам кредитор вправе защищать свое субъективное право от нарушений со стороны не только должника, но и любых третьих лиц. Однако в целом ряде установленных законом случаев кредитор может быть лишен возможности ссылаться на обязательство в отношениях с третьими лицами. Подобные юридические последствия наступают, в частности, при неисполнении законодательных предписаний о необходимости государственной регистрации договора, а также при нарушении правил уведомления о залоге движимого имущества. Юридическую значим…

Основные аксиомы статики

С точки зрения статики все тела считаются абсолютно твердыми….
Согласно определению аксиомы, данное положение принимается абсолютно истинным в рамках теории статики…
Если на абсолютно твердое тело действуют два усилия, то такое тело может находиться в равновесии лишь…
нарушено, если тело считать абсолютно твердым….
Третья аксиома может быть применена к абсолютно любым телам.

Статья от экспертов

Исследование путей измерения абсолютного значения силы тяжести в морских условиях

Объект и цель научной работы. Исследование путей измерения абсолютного значения силы тяжести в морских условиях. Материалы и методы. Использован метод проведения экспериментальных исследований. Основные результаты. Исследованы возможности измерения абсолютного значения силы тяжести в морских условиях. Предложена концепция и создан макет морского интегрированного гравиметрического комплекса. Рассмотрены его конструкция и принцип работы. Приведены результаты испытаний макета на стенде имитации морского волнения. Заключение. Показана принципиальная возможность измерения абсолютного значения силы тяжести на слабо качающемся основании. Потенциальная точность морской съемки с использованием интегрированного комплекса может составлять около 0,1 мГал, что в перспективе позволит существенно повысить качество геодезической информации для труднодоступных районов Земли.

Повышай знания с онлайн-тренажером от Автор24!

Напиши термин
Выбери определение из предложенных или загрузи свое
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек

Источник

Формула модуля равнодействующей силы

Сила является вектором, то есть обладает как модулем (величиной) так и направлением. Однако чаще всего приходится иметь дело с телами, на которые действуют не одна, а несколько сил. Тогда рассматривают сумму всех сил, оказывающих действие на тело, такую сумму сил называют равнодействующей силой ():

$[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N qquad(1)]$

Равнодействующая сила – это гипотетический (искусственный) параметр, который вводят для того, чтобы удобнее было производить расчеты. Следует учитывать, что равнодействующая сила (как и любая сила) – это векторная величина, имеющая модуль и направление.

Модуль равнодействующей двух сил

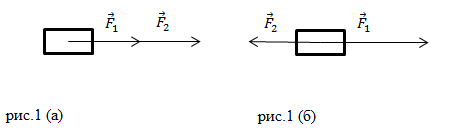
Допустим, тело находится под воздействием двух сил. Они направлены по одной прямой (рис.1).

Если силы имеют одинаковые направления (рис.1 (а)), то модуль равнодействующей вычисляется как:

На рис 1(б) силы направлены по одной прямой, но имеют противоположные направления. Формулой для вычисления модуля равнодействующей в таком случае будет выражение:

Рассмотрим случаи, когда две силы, действующие на тело, направлены под углом друг другу (рис.2).

В случае, который представлен на рис.2 (а) силы ${overline{F}}_1$ и ${overline{F}}_2$ направлены под углом 900 по отношению друг к другу. Модуль равнодействующей силы можно найти по теореме Пифагора:

$[F=sqrt{F^2_1+F^2_2} qquad(3)]$

Если угол между векторами сил ${overline{F}}_1$ и ${overline{F}}_2$ отличен от прямого угла, то модуль равнодействующей силы находят по теореме косинусов:

$[F=sqrt{F^2_1+F^2_2-2F_1F_2{cos alpha } } qquad(4)]$

где – угол между векторами ${overline{F}}_1$ и ${overline{F}}_2.$

Модуль равнодействующей нескольких сил

Пусть на тело действуют силы: ${overline{F}}_1,{overline{F}}_2,dots ,{overline{F}}_N$ , тогда равнодействующая этих сил () находится в соответствии с формулой (1). Для того чтобы вычислить модуль равнодействующей нескольких сил приложенных к телу выполняют следующую последовательность действий:

Вводят декартову систему координат, выбирают направления осей (X,Y).
Записывают проекции сил, действующих на тело на избранные оси:

$[left{ begin{array}{c} X: F_{1x},F_{2x},dots , F_{Nx}; \ Y: F_{1y},F_{2y},dots , F_{Ny} end{array} right. qquad(5)]$

$[left{ begin{array}{c} X: F_x=F_{1x}+F_{2x}+dots ,+ F_{Nx}; \ Y: F_y=F_{1y}+F_{2y}+dots , {+F}_{Ny} end{array} right. qquad(6)]$

$[F=sqrt{F^2_x+F^2_y} qquad(7)]$

Примеры решения задач по теме «Модуль равнодействующей силы»

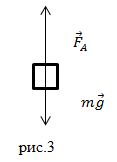
${overline{F}}_p={overline{F}}_A{+m}overline{g}{} left({1.1}right).$ Силы направлены вдоль одной прямой в противоположные стороны. За положительное направление примем направление силы Архимеда ( ${overline{F}}_A$ ) (рис.3), тогда модуль подъемной силы равен:

Величину силы Архимеда найдем как:

$[F_A={rho }_{sh}Vg={rho }_{sh}gfrac{m}{rho } qquad(1.3)]$

где $V=frac{m}{rho }$ . Получаем, что модуль подъемной силы равен:

$[F_p=mgfrac{{rho }_{sh}}{rho } -mg=mgleft(frac{{rho }_{sh}}{rho }-1right)]$

Силой взаимодействия тела и поверхности, по которой оно движется, будем считать равнодействующую ${overline{F}}_{tr}$ и :

$[{overline{F}}_v={overline{F}}_{tr}+overline{N} qquad(2.1)]$

Сила трения и сила реакции опоры направлены под углом по отношению друг к другу, следовательно, модуль силы взаимодействия найдем как:

Модуль силы, скорости, импульса. Что это?!

Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.

Сила и модуль силы

В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.

Что такое модуль силы?

Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.

Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.

Модуль равнодействующих двух сил определяется по формулам:

F=F1 + F2 (в случае сил с одинаковым направлением)
F=F1 — F2 (силы с разным направлением)

Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.

Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).

Что это модуль скорости?

Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.

Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.

Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:

v = S/t = (x — x0)/t.

Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.

Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:

Вычисляется скорость v₂₁ на базе закона сложения скоростей v₂ = v₂₁ + v₁, а значит v₂₁ = v₂ – v₁.
Определяется модуль скорости тела согласно теореме Пифагора.

Модуль импульса и модуль оси

Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается? Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.

Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее. Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.

Как найти модуль силы действующей на тело

На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.

Формула равнодействующей всех сил

Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline $) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:

Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.

Складывают векторы, используя правило треугольника (рис.1)

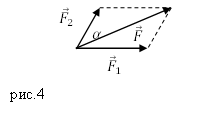
правило параллелограмма (рис.2).

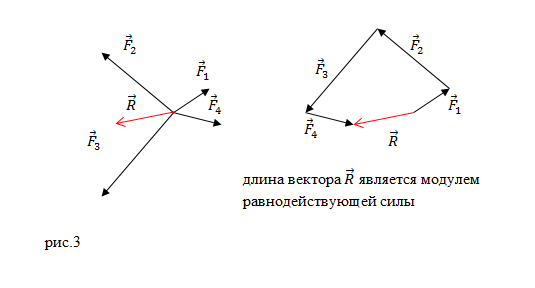
или многоугольника (рис.3):

Второй закон Ньютона и формула модуля равнодействующей

Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:

$overline =0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.

При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.

Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.

Примеры задач с решением

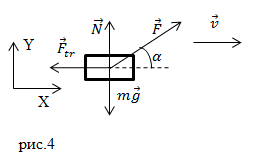
Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?

Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline $ найдем, применяя теорему косинусов:

Вычислим модуль равнодействующей силы:

[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Н
ight).]

Ответ. $F=52,92$ Н

Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?

Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:

Следовательно, модуль силы можно найти как:

Ускорение точки будем искать, используя связь между ним и перемещением точки:

Первая производная от $s$ по времени равна:

Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:

Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:

Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox, изменяется со временем в соответствии с графиком (см. рисунок).

Систему отсчета считать инерциальной. Чему равна равнодействующая всех сил, действующих на автомобиль? (Ответ дайте в ньютонах.)

Согласно второму закону Ньютона, равнодействующая всех сил, действующих на тело, связана с ускорением и массой тела соотношением Из графика определим ускорение, которое остается постоянным на протяжении всего интервала времени:

Таким образом, равнодействующая всех сил равна

а если бы ускорение было отрицательно, то и равнодействующая была бы отрицательной?

Скорость, сила, ускорение — все это векторные величины. Правильно говорить не про их знак, а про знак проекции этих векторов на некоторую ось. Если проекция скорости уменьшается, то ускорение направлено против оси, а значит, так же направлена и равнодействующая. Следовательно, проекции этих величин отрицательны. По графику модуля скорости о знаке проекций судить нельзя. Действительно, имея только график, приведенный в условии, мы не можем сказать, ускоряется тело вдоль оси или против. Проекция ускорения может быть тут как положительной, так и отрицательной.

«Систему отсчета считать инерциальной.» Возможно ошибаюсь, ребят, но, вроде, в ИСО равнодействующая всех сил равна нулю.

ИСО — это система отсчета, в которой тело, на которое не действует никаких внешних сил, двигается равномерно и прямолинейно или покоится.

Равнодействующая сил, конечно, же может и отличаться от нуля, это, согласно второму закону Ньютона, приведет к появлению ускорения.

т.е. в инерциальной системе отсчёта нет силы трения?

и ещё: вы говорите, что тело в ИСО движется равномерно, а в условии задачи дано равноускоренное движение. так бывает?

Я не так говорю, не вырывайте слова и контекста. Я даю определение ИСО: это система отсчета, в которой тело, НА КОТОРОЕ НЕ ДЕЙСТВУЮТ ВНЕШНИЕ СИЛЫ, двигается равномерно и прямолинейно, либо покоится. А вот если СИЛЫ ДЕЙСТВУЮТ, то это приводит к появлению ускорения, о чем нам и говорит второй закон Ньютона.

Наличие силы трения определяется свойством поверхностей, а не выбором системы отсчета. И в данной задаче, она, конечно, присутствует и направлена по скорости движения автомобиля, иначе бы он просто не мог бы разгоняться. Но чему она равна, мы найти из данного графика не можем, так как есть и другие силы, например, сила сопротивления воздуха. Что мы может тут определить, так это равнодействующую всех сил. Именно ей определяется ускорение.

Пыталась найти ускорение как тангенс угла наклона касательной, то есть производную от v по t. Тут угол — 45 град, тангенс = 1, ускорение, стало быть, так же 1 м/с^2.

Подскажите пожалуйста, где в моих рассуждениях ошибка?

Ошибка в том, что тангенс надо считать, учитывая масштаб графика по осям. То есть Вы должны определить катеты прямоугольного треугольника, используя числа на осях, а потом поделить один катет на другой.

Кстати, простое доказательство, почему Ваше решение не верно. Сожмем картинку с графиком по вертикали в два раза. Угол на рисунке изменится, а ускорение, конечно, же останется прежним.

а почему считают ускорение до 8с. а не до 18, если найдем ускорение по всей длине то получается 10-0/18=1,8 и получается другой ответ!

Делить нужно на 20. Масштаб по горизонтальной оси: в одной клеточке 4 с

На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху). Каков модуль равнодействующей этих сил, если (Ответ дайте в ньютонах и округлите до десятых.)

На рисунке обозначена равнодействующая векторов и

Поскольку модуль вектора силы равен 1 Н, заключаем, что масштаб рисунка такой, что сторона одного квадрата сетки соответствует модулю силы 1 Н. Таким образом, модуль равнодействующей равен по теореме Пифагора

А как определили эту равнодействующую трёх сил, я понять не могу?!

Чтобы найти равнодействующую, необходимо сложить вектора всех сил (например, по правилу треугольника или параллелограмма складываем вектора по два).

Если сложить вектор и вектор , получится вектор, направленный вверх длиной в одну клеточку. Теперь осталось прибавить к нему вектор . В результате и получается то, что показано красной стрелкой.

векторы F1 и F3 никак нельзя сложить правилом треугольника! дак как эту задачц решить тут решения совсем непонятные!

Когда Вы складываете параллельные вектора, у Вас просто получается «вырожденный треугольник». Правила все те же, к концу первого вектора прикладываем начало второго. Сумма векторов — это вектор, который начинается в начале первого и заканчивается в конце второго. То есть в данном случае у Вас получится вектор, направленный вверх и длиной в одну клеточку.

Две силы 3 H и 4 H приложены к одной точке тела, угол между векторами сил равен 90°. Чему равен модуль равнодействующей сил? (Ответ дайте в ньютонах.)

Силы и их равнодействующая указаны на рисунке. По теореме Пифагора, модуль равнодействующей сил равен

Под действием одной силы F₁ тело движется с ускорением 4 м/с 2 . Под действием другой силы F₂, направленной противоположно силе F₁, ускорение тела равно 3 м/с 2 . С каким ускорением тело будет двигаться при одновременном действии сил F₁ и F₂? (Ответ дайте в метрах в секундах в квадрате.)

Согласно второму закону Ньютона, ускорение тела пропорционально равнодействующей всех сил, действующих на него: Силы и по условию, направлены противоположно, поэтому при их одновременном действии тело будет двигаться с ускорением

Тело подвешено на двух нитях и находится в равновесии. Угол между нитями равен 90°, а силы натяжения нитей равны 3 H и 4 H. Чему равна сила тяжести, действующая на тело? (Ответ дайте в ньютонах.)

Всего на тело действует три силы: сила тяжести и силы натяжения двух нитей. Поскольку тело находится в равновесии, равнодействующая всех трех сил должна равняться нулю, а значит, модуль силы тяжести равен

в условии написано,что нужно найти вес тела.

а в решении модуль силы тяжести.

Как вес может измеряться в Ньютонах.

В условии ошибка(

Вы путаете понятия массы и веса. Весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Как следует из определения, эта сила приложена даже не к телу, а к опоре. Невесомость — это состояние, когда у тела пропадает не масса, а вес, то есть тело перестает давить на другие тела.

Согласен, в решении была допущена некоторая вольность в определениях, сейчас она поправлена.

Понятие «вес тела» введен в учебную физику крайне неудачно. Если в бытовом понятии вес обозначает массу то в школьной физике, как вы правильно заметили весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Заметим, что речь идет об одной опоре и об одной нити. Если опор или нитей несколько несколько, понятие веса исчезает.

Привожу пример. Пусть в жидкости на нити подвешено тело. Оно растягивает нить и давит на жидкость с силой равной минус сила Архимеда. Почему же, говоря о весе тела в жидкости, мы не складываем эти силы, как Вы делаете в своем решении?

Я зарегистрировался на Вашем сайте, но не заметил, что же изменилось в нашем общении. Прошу извинить мою тупость, но я, будучи человеком старым, недостаточно свободно ориентируюсь на сайте.

Действительно, понятие веса тела весьма расплывчато, когда тело имеет несколько опор. Обычно вес в этом случае определяют как сумму взаимодействий со всеми опорами. При этом воздействие на газообразные и жидкие среды, как правило, исключается. Это как раз подпадает под описанный Вами пример, с подвешенным в воде грузиком.

Здесь сразу вспоминается детская задачка: «Что весит больше: килограмм пуха или килограмм свинца?» Если решать эту задачу по-честному, то нужно несомненно учитывать силу Архимеда. А под весом скорее всего мы будем понимать то, что нам будут показывать весы, то есть силу, с которой пух и свинец давят, скажем, на чашку весов. То есть здесь сила взаимодействие с воздухом как бы из понятия веса исключается.

С другой стороны, если считать, что мы откачали весь воздух и кладем на весы тело, к которому привязана веревочка. То сила тяжести будет уравновешиваться суммой силы реакции опоры и силой натяжения нити. Если мы понимаем вес как силу действия на опоры, препятствующие падению, то вес тут будет равен этой сумме силы растяжения нити и силы давления на чашку весов, то есть совпадать по величине с силой тяжести. Опять возникает вопрос: чем нитка лучше или хуже силы Архимеда?

В целом тут можно договориться до того, что понятие веса имеет смысл только в пустом пространстве, где есть только одна опора и тело. Как тут быть, это вопрос терминологии, которая, к сожалению, у каждого здесь своя, поскольку не столь уж это и важный вопрос И если силой Архимеда в воздухе во всех обычных случаях можно пренебречь, а значит, на величину веса она особо повлиять не может, то для тела в жидкости это уже критично.

Если уж быть совсем честным, то разделение сил на виды весьма условно. Представим себе ящик, который тащат по горизонтальной поверхности. Обычно говорят, что на ящик действуют две силы со стороны поверхности: сила реакции опоры, направленная вертикально, и сила трения, направленная горизонтально. Но ведь это две силы, действующие между одними и теми же телами, почему же мы просто не рисуем одну силу, являющуюся их векторной суммой (так, кстати, иногда и делается). Тут, это, наверное, вопрос удобства

Так что я немного в замешательстве, что делать с данной конкретной задачей. Проще всего, наверное, переформулировать ее и задавать вопрос про величину силы тяжести.

Не переживайте, все в порядке. При регистрации Вы должны были указать e-mail. Если теперь зайти на сайт под своим аккаунтом, то при попытке оставить комментарий в окне «Ваш e-mail» должен сразу появляться тот самый адрес. После этого система будет автоматически подписывать Ваши сообщения.

Задание 2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей приложенных к телу сил.

Сначала сложим силы F1 и F3. Так как они противоположно направлены, то получим результирующую силу, направленную как F3, но на одну клетку меньше (см. синяя линия на рисунке ниже).

Складывая полученную силу с силой F2, имеем результирующую силу, направление которой показано красной линией на рисунке. Модуль этой силы найдем по теореме Пифагора из прямоугольного треугольника с катетами 4 и 3:

Источник

Магнитное поле. Силы

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: сила Ампера, сила Лоренца.

В отличие от электрического поля, которое действует на любой заряд, магнитное поле действует только на движущиеся заряженные частицы. При этом оказывается, что сила зависит не только от величины, но и от направления скорости заряда.

Сила Лоренца

Сила, с которой магнитное поле действует на заряженную частицу, называется силой Лоренца. Опыт показывает, что вектор vec{F} силы Лоренца находится следующим образом.

1. Абсолютная величина силы Лоренца равна:

(1)

Здесь — абсолютная величина заряда, — скорость заряда, — индукция магнитного поля, alpha — угол между векторами vec{v} и vec{B} .

2. Сила Лоренца перпендикулярна обоим векторам vec{v} и vec{B} . Иными словами, вектор vec{F} перпендикулярен плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля.

Остаётся выяснить, в какое полупространство относительно данной плоскости направлена сила Лоренца.

3. Взаимное расположение векторов vec{v} , vec{B} и vec{F} для положительного заряда показано на рис. 1.

Рис. 1. Сила Лоренца

Направление силы Лоренца определяется в данном случае по одному из двух альтернативных правил.

Правило часовой стрелки. Сила Лоренца направлена туда, глядя откуда кратчайший поворот вектора скорости частицы v к вектору магнитной индукции B виден против часовой стрелки.

Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление скорости частицы, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Лоренца.
Для отрицательного заряда направление силы Лоренца меняется на противоположное.

Всё вышеперечисленное является обобщением опытных фактов. Формула (1) позволяет связать размерность индукции магнитного поля с размерностями других физических величин:

$B=frac{displaystyle F}{displaystyle qv sin alpha vphantom{1^a}}$

Сила Ампера

Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.

Происхождение силы Ампера легко понять. Ведь ток в металле является направленным движением электронов, а на каждый электрон действует сила Лоренца. Все эти силы Лоренца, действующие на свободные электроны, имеют одинаковое направление и одинаковую величину; они складываются друг с другом и дают результирующую силу Ампера.

Направление силы Ампера определяется по тем же двум правилам, сформулированным выше.

Правило часовой стрелки . Сила Ампера направлена туда, глядя откуда кратчайший поворот тока к полю виден против часовой стрелки .

Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление тока, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Ампера .

Взаимное расположение тока, поля и силы Ампера vec{F} указано на рис. 2.

Рис. 2. Сила Ампера

На этом рисунке проводник имеет длину , а угол между направлениями тока и поля равен alpha . Мы сейчас выведем выражение для абсолютной величины силы Ампера.

На каждый свободный электрон действует сила Лоренца:

где — скорость направленного движения свободных электронов в проводнике.

Пусть — число свободных электронов в данном проводнике, — их концентрация (число в единице объёма). Тогда:

где — объём проводника, — площадь его поперечного сечения. Получаем:

Мы не случайно выделили скобками четыре сомножителя. Ведь это есть не что иное, как сила тока: (вспомните выражение силы тока через скорость направленного движения свободных зарядов!). В результате приходим к окончательной формуле для силы Ампера:

(2)

Хорошую возможность поупражняться в нахождении направлений магнитного поля и силы Ампера даёт взаимодействие параллельных токов. Оказывается, два параллельных провода отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают (рис. 3).

Рис. 3. Взаимодействие параллельных токов

Обязательно убедитесь в этом самостоятельно! Делаем так. Сначала берём произвольную точку на первом проводе и определяем направление магнитного поля, создаваемого в этой точке вторым проводом (правило вам известно — см. предыдущий листок>). Ну а затем находим направление силы Ампера, действующей на первый провод со стороны магнитного поля второго провода.

Рамка с током в магнитном поле

В листках по термодинамике мы говорили о важности циклически работающих машин: они снабжают нас энергией. Понимание законов термодинамики позволило сконструировать тепловые двигатели, которые исправно служат нам и по сей день.

Понимание же законов электромагнетизма дало возможность создать циклическую машину другого типа — электродвигатель.

Мы рассмотрим один из элементов электродвигателя — рамку с током в магнитном поле. Разобравшись в её поведении, мы сможем уловить основную идею функционирования электродвигателя.

Пусть прямоугольная рамка 1234 может вращаться вокруг горизонтальной оси (рис. 4, слева). Рамка находится в вертикальном однородном магнитном поле vec{B} . Ток течёт по рамке в направлении ; это направление показано соответствующими стрелками.

Рис. 4. Рамка с током в магнитном поле

Вектор vec{n} называется вектором нормали; он перпендикулярен плоскости рамки и направлен туда, глядя откуда ток кажется циркулирующим против часовой стрелки. (Иными словами, вектор vec{n} сонаправлен с вектором индукции магнитного поля, которое создаётся током в рамке.) Поворот рамки измеряется углом alpha между векторами vec{n} и vec{B} .

Теперь определим направления сил Ампера, которые действуют на рамку со стороны магнитного поля. Эти силы расставлены на рисунке; вот вам ещё одно упражнение на правило часовой стрелки (левой руки) — обязательно проверьте правильность указанных направлений!

Силы $vec{F_{12}}$ и $vec{F_{34}}$ , приложенные к сторонам и , действуют вдоль оси вращения. Они лишь растягивают рамку и не вызывают её вращение.

Куда более интересны силы $vec{F_{23}}$ и $vec{F_{14}}$ , приложеные соответственно к сторонам и . Они лежат в горизонтальной плоскости и перпендикулярны оси вращения. Эти силы вращают рамку в направлении по часовой стрелке, если смотреть справа (рис. 4, правая часть). Вычислим момент этой пары сил относительно оси вращения рамки.

Пусть длина стороны равна . Тогда

$F_{14} = F_{23} = IB_a.$

Пусть длина стороны равна . Плечо силы $F_{14}$ , как видно из рис. 4 (справа) равно:

$d=OA=frac{displaystyle b}{displaystyle 2 vphantom{1^a}} sin varphi$

Таким же будет плечо силы $vec{F_{23}}$ . Отсюда получаем момент сил, вращающий рамку:

$M=F_{14}d + F_{23}d=IB_a cdot frac{displaystyle b}{displaystyle 2 vphantom{1^a}} sin varphi + IB_a cdot frac{displaystyle b}{displaystyle 2 vphantom{1^a}} sin varphi=IBab sin varphi$

Теперь заметим, что ab=S — площадь рамки. Окончательно имеем:

(3)

В этой формуле площадь служит единственной геометрической характеристикой рамки.Это наводит на мысль, что только площадь рамки и существенна в выражении для вращающего момента. И действительно, можно доказать (разбивая рамку на бесконечно узкие полоски, неотличимые от прямоугольников), что формула (3) справедлива для рамки любой формы с площадью .

Как видно из формулы (3), максимальный вращающий момент равен:

$M_{max} = IBS.$

Эта максимальная величина момента достигается при $varphi = frac{displaystyle pi}{displaystyle 2 vphantom{1^a}}$ , то есть когда плоскость рамки параллельна магнитному полю.

Вращающий момент становится равным нулю при и . Оба этих положения по-своему интересны.

При плоскость рамки перпендикулярна полю, а векторы и направлены в разные стороны. Данное положение является положением неустойчивого равновенсия: стоит хоть немного шевельнуть рамку, как силы Ампера начнут её вращать в том же направлении, поворачивая вектор vec{n} к вектору vec{B} (убедитесь!).

При плоскость рамки также перпендикулярна полю, а векторы vec{n} и vec{B} сонаправлены. Это — положение устойчивого равновенсия: при отклонении рамки возникает вращающий момент, стремящийся вернуть рамку назад (убедитесь!). Начнутся колебания рамки, постепенно затухающие из-за трения. В конце концов рамка остановится в положении ; в этом положении вектор индукции магнитного поля рамки сонаправлен с вектором vec{B} индукции внешнего магнитного поля (вот почему при намагничивании вещества элементарные токи ориентируются так, что их поля направлены в сторону внешнего магнитного поля). Полезное сопоставление: рамка занимает такое положение, что её положительная нормаль ориентируется в том же направлении, что и северный конец стрелки компаса, помещённой в это магнитное поле.

Таким образом, поведение рамки в магнитном поле становится ясным: если отклонить рамку от положения устойчивого равновесия и отпустить, то рамка будет совершать колебания. С точки зрения совершения механической работы это не очень хорошо: если намотать нить на ось вращения и подвесить к нити груз, то груз будет то подниматься, то опускаться.
Но вот если исхитриться и заставить ток менять направление в нужные моменты, то вместо колебаний рамки начнётся её непрерывное вращение и, соответственно, непрерывный подъём подвешенного груза. Тогда-то и получится полноценный электродвигатель; идея с переменой направления тока реализуется с помощью коллектора и щёток.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Магнитное поле. Силы» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

Содержание

Способ измерения абсолютной силы
Математический маятник
Физический маятник
Баллистический метод
Абсолютная и относительная сила
главная
измерения
метрологическая экспертиза
форум
полезная информация
Измерения. Выбор средств измерений
1. Основные положения
2. Измерение геометрических величин (измерение длины)
3. Измерение физических величин
4. Измерение давления
5. Измерение массы
6. Измерение температуры
7. Измерение твёрдости
8. Измерение силы
9. Измерение электрических величин — напряжения,
силы тока, сопротивления и мощности
10. Измерение. Методы неразрушающего контроля
Измерение силы

Способ измерения абсолютной силы

Среди динамических методов наиболее важными являются:

измерение периода колебаний маятника
измерение периода колебаний маятника под действием силы тяжести и силы, ей противодействующей
измерение времени свободного падения тел
измерение частоты колебаний струны, которая натянута подвешенной на ней массой.

Измерения силы тяжести бывают абсолютными и относительными.

При абсолютных измерениях определяют полную величину силы тяжести. При относительных – определяют не полное значение, а приращение в данном пункте относительно некоторого другого, исходного, поле в котором обычно известно.

Динамические методы могут быть как абсолютными, так и относительными. Статические – только относительными. Приборы, предназначенные для относительных определений силы тяжести, называют гравиметрами.

В настоящее время статические гравиметры являются основными приборами для относительных определений силы тяжести.

Математический маятник

Среди динамических методов измерения силы тяжести долгое время главенствовал маятниковый метод, доведенный до высокой степени совершенства.

Маятником называется любое твердое тело, способное совершать колебания около горизонтальной оси.

В теории колебаний важную роль играет модель математического маятника. Это идеальная модель, то есть модель, которую можно реализовать лишь в некотором приближении.

Математический маятник представляет собой материальную точку, с массой m, подвешенную на нерастяжимой и невесомой нити длиной l (рис18.1).

Дифференциальное уравнение движения имеет вид:

если задать начальные условия , , то его решением является гармоническая функция с периодом колебаний

Интеграл в этом выражении относится к классу эллиптических первого рода и не приводится к элементарным функциям. Обычно чтобы получить решение в явном виде, подынтегральную функцию разлагают в ряд (по φ), а затем почленно интегрируют. В нашем случае такая процедура приводит к выражению

Решение получается сложным, потому, что уравнение (18.1) является нелинейным. Однако при малых начальных отклонениях угла φ можно положить . Тогда уравнение (18.1) примет линейный вид:

Для него период колебаний равен

Как следует из этой формулы, при малых амплитудах период колебаний не зависит от амплитуды. Это свойство маятника называется изохронностью.

Поскольку математический маятник является идеальной моделью, ее, как правило, невозможно реализовать с необходимой степенью точности. Поэтому на практике при определениях силы тяжести используют физический маятник.

Физический маятник

Под физическим маятником понимают любое тяжелое твердое тело, свободно вращающееся вокруг горизонтальной оси.

Обозначим ось вращения как ось x (рис. 18.2).

Уравнение движения имеет вид:

здесь I_x– момент инерции, M_x – сумма моментов сил, ω – угловая скорость вращения.

Пусть центр тяжести маятника находится в точке C на расстоянии a от оси вращения O. Тогда сумма моментов действующих сил равна:

где M – масса тела. Тогда уравнение движения примет вид:

Если ввести новую переменную , то мы получим уравнение, аналогичное уравнению движения математического маятника (18.1):

Иными словами, физический маятник движется по тем же законам, что и математический. Только роль длины маятника играет величина .

Если эту величину отложить на рисунке, вдоль линии, соединяющей точку O и центр тяжести C, получим точку O’, которая называется центром качания, а длина l отрезка OO’ называется приведенной длиной физического маятника. Особенность положения центра качания в том, что физический маятник, подвешенный к нему будет качаться с тем же периодом.

Маятниковые приборы позволяют выполнять как абсолютные, так и относительные определения силы тяжести. При абсолютных определениях измеряют период колебания и приведенную длину маятника. При относительных определениях силы тяжести достаточно измерить только период колебания маятника в двух пунктах.

Действительно, пусть
тогда выражая значение силы тяжести на втором пункте, получим:

Маятниковые позволяют определить период колебаний с точностью , что обеспечивает точность измерения силы тяжести до 0.1 мГал. При этом время наблюдения на одном пункте составляет около 15 минут.

Баллистический метод

В настоящее время измерения малых интервалов и времени падения тел достиг очень высокой точности, поэтому появилась возможность высокоточных абсолютных измерений силы тяжести способом падающего груза, или баллистическим способом.

В вертикальной вакуумной камере высотой примерно 50 см в качестве падающего груза используется стеклянная призма (рис 18.3).

Путь падения призмы измеряют с помощью лазерного интерферометра, а время падения – с помощью атомных часов. Пучок когерентного света от лазера полупрозрачным стеклом разделяется на два пучка. Пучки света проходят разные пути, а затем сводятся вместе. В результате будет наблюдаться интерференционная картина в виде чередования темных и светлы полос (интерференционных полос), ширина и число которых зависят от спектрального состава источника света и разности оптических путей световых пучков.

Число полос N связано с разностью хода лучей Δ и длиной волны света λ соотношением

время и путь свободно падающего тела связаны соотношением

Однако на практике пользуются более сложной формулой

Это связано с тем, что в начале пути призма может получить небольшое дополнительное ускорение. Чтобы избавиться в выражении (18.12) от априорно неизвестной начальной скорости v₀ , измерения проводят дважды. Тогда из системы двух уравнений получим:

Точность абсолютных измерений баллистическим методом на сегодняшний день чрезвычайно высока – порядка одного микрогала (0.001 мГал) при времени одного измерения около 10 с. Для повышения точности выполняются многократные измерения, которые потом статически обрабатываются.

Источник

Абсолютная и относительная сила

Между этими двумя понятиями имеются определенные соотношения, которые выражаются формулой:

Относительная сила = (Абсолютная сила)/(Собственный вес)

Из этой формулы следуют два вывода:

Источник

главная

измерения

метрологическая экспертиза

форум

полезная информация

Измерения. Выбор средств измерений

1. Основные положения

2. Измерение геометрических величин (измерение длины)

3. Измерение физических величин

4. Измерение давления

5. Измерение массы

6. Измерение температуры

7. Измерение твёрдости

8. Измерение силы

9. Измерение электрических величин — напряжения,

силы тока, сопротивления и мощности

10. Измерение. Методы неразрушающего контроля

Измерение силы

Силой называется всякое воздействие на данное тело, сообщающее ему ускорение или вызывающее его деформацию. Сила векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел.

Сила характеризуется числовым значением, направлением в пространстве и точкой приложения.

За единицу силы в СИ принят ньютон (Н). Ньютон — это сила, которая придает массе 1 кг в направлении действия этой силы ускорение 1 м/с 2 .

В технических измерениях допускаются единицы силы:

1 кгс (килограмм-сила) = 9,81 Н;

1 т c (тонна-сила) = 9,81 х 103 Н.

Измерение силы осуществляют посредством динамометров, силоизмерительных машин и прессов, а также непосредственным нагружением при помощи грузов и гирь.

Динамометры — приборы, измеряющие силу упругости.

Динамометры изготовляют трёх типов:

По способу регистрации измеряемых усилий динамометры подразделяют на:

— указывающие — применяют главным образом для измерений статических усилий, возникающих в конструкциях, установленных на стендах, при приложении к ним внешних сил и для измерения силы тяги при плавном передвижении изделия;

— считающие и пишущие динамометры, регистрирующие переменные усилия, применяют чаще всего при определении силы тяги паровозов и тракторов, так как вследствие сильной тряски и неизбежных рывков при ускорении их движения, а также неравномерности загрузок изделия создаются переменные усилия.

Наибольшее распространение имеют динамометры общего назначения пружинные, указывающие.

Основные параметры и размеры динамометров общего назначения, пружинных со шкальным отсчётным устройством, предназначенных для измерений статических растягивающих усилий, устанавливает ГОСТ 13837.

Выбор пружинных динамометров общего назначения в обыкновенном исполнении, применяемых для измерений статических растягивающих усилий, должен осуществляться согласно настоящего документа.

Основные технические параметры пружинных динамометров общего назначения в обыкновенном исполнении, применяемых для измерений статических растягивающих усилий приведены в таблице 12.1.

Пределы измерений и погрешность динамометра должны определяться одним из двух способов:

— по таблицам приложения 2 ОСТ 1 00380.

Для измерения силы тяги двигателей летательных аппаратов при стендовых испытаниях следует применять силоизмерительные системы. Структурные схемы и принцип действия силоизмерительных систем приведены в рекомендуемом приложении 3 ОСТ 1 00380.

Рабочие средства измерений, применяемые в силоизмерительных системах, приведены в справочном приложении 4 ОСТ 1 00380.

Предел допускаемой погрешности измерений системы не должен превышать допускаемого значения по ОСТ 1 01021 и ОСТ1 02512.

Пример — Необходимо определить верхний предел измерений и основную приведенную погрешность динамометра для измерений силы (160± 10) кгс.

наибольший предельный размер параметра

160 кгс+ 10 кгс= 170 кгс;

наименьший предельный размер параметра

160 кгс-10 кгс= 150 кгс;

170 кгс-150 кгс =20 кгс.

основную допустимую абсолютную погрешность измерений (по формуле (7.1)):

0,33 х 20 кгс = | 6,6 | кгс;

нижний предел рабочей части шкалы (по формуле (7.2)):

верхний предел рабочей части шкалы (по формуле (7.3)):

В_ди > 170 кгс + 6,6 кгс = 176,6 кгс.

Выбираем по таблице 12.1 динамометр общего назначения с верхним пределом В_ди= 2,0 Н (204 кгс). Нормирующее значение для определения основной приведенной погрешности динамометра равно конечному значению его шкалы.

Определяем предел допускаемой основной приведённой погрешности динамометра (по формуле (7.10)):

Находим меньшее ближайшее значение погрешности по отношению к найденному значению допускаемой основной приведенной погрешности. Этим значением для динамометров является = ±2 %, поэтому выбираем динамометр класса точности 2.

Способ с использованием таблиц.

В боковике таблицы приложения 2 ОСТ 1 00380 находим строку с диапазоном измерений от 20 до 200 кгс, в котором измеряемая величина может принимать одно из значений.

На этой же строке во второй графе находим значение верхнего предела измерений динамометра. Этим значением является 200 кгс. На этой же строке находим меньшее ближайшее значение допуска по отношению к заданному. Этим значением является 12 кгс.

В оглавлении таблицы, по значению допуска 12 кгс, находим соответствующее ему значение погрешности = 2 %.

Вывод — для измерения силы (160 ± 10) кгс выбираем динамометр с верхним пределом 2,0 Н (204 кгс), класса точности 2.

Таблица 12.1 – Основные технические параметры пружинных динамометров общего назначения в обыкновенном исполнении, применяемых для измерений статических растягивающих усилий

Источник