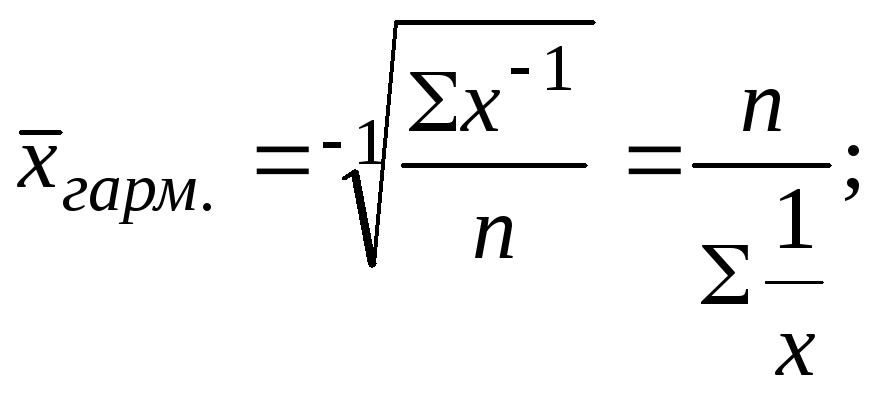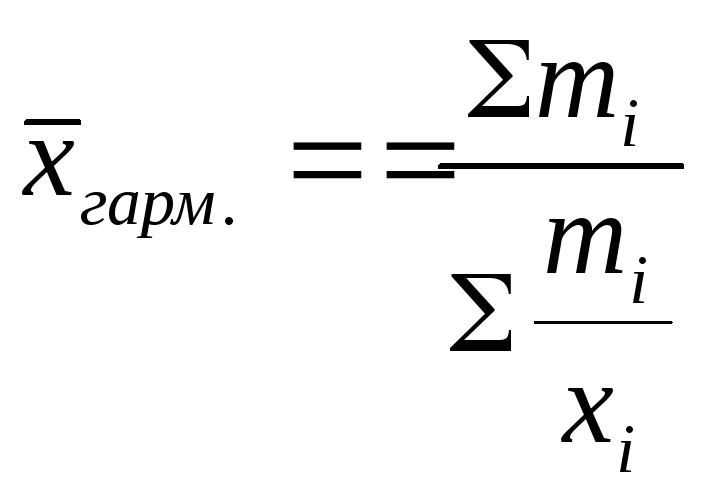Евгения Кузнецова
Эксперт по предмету «Экономический анализ»
преподавательский стаж — 8 лет
Задать вопрос автору статьи
Понятие абсолютных и относительных величин
Замечание 1
Абсолютные и относительные величины — ключевые инструменты статистики и экономики, используемые с целью определения количественных характеристик и динамики изменения показателей.
Абсолютные и относительные величины, отражая соответствующие характеристики, не могут существовать друг без друга.
Абсолютные величины в экономическом анализе
Определение 1
Абсолютная величина выражает количественные размеры определённого явления без отношения его с другими, без оценки происходящих изменений и отклонений.
Абсолютная величина характеризует объем и уровень процесса (явлений), являясь всегда именованными числами.
Абсолютные величины имеют размерность, то есть единицу измерения.
Классификация абсолютных величин:
- натуральные,
- трудовые,
- денежные и др.
Средние и относительные величины
Соотношение нескольких абсолютных величин выражается с помощью средних и относительных величин.
Замечание 2
Это выражение может определяться для нескольких явлений (процессов) или для одного, взятого в другом объеме и в другой период. Данные элементы могут выступать частным от статистических чисел, характеризующих количественное соотношение.
Для определения относительных величин, необходимо один показатель разделить на другой, который принимается в качестве базового.
Базовой величиной могут быть следующие показатели:
- Данные плана,
- Фактические данные,
- Сведения предыдущих лет,
- Показатели других предприятий и др.
Относительные величины сравнения могут выражаться в процентном соотношении (по базе, которая принята за 100) или в виде коэффициентов (в этом случае база — единица).
«Абсолютные и относительные величины в экономическом анализе» 👇
Классификация абсолютных величин
Абсолютные величины могут быть двух типов:
- Индивидуальные абсолютные величины, характеризующие размер признака конкретной единицы Примерами таких величин могут быть размер заработной платы сотрудников или вклад в банке. Данные размеры определяют непосредственно в процессе наблюдения, при этом происходит их фиксация в первичной учетной документации.
- Суммарные абсолютные величины, отражающие итоговый показатель признака в совокупности объектов. Данный размер выступает как сумма числа единиц (численность совокупности) или объем варьирующих характеристик.
Классификация относительных величин
Основное условие расчета относительных величин — сопоставимость единиц и существование реальной связи исследуемых явлений. Величина, с которой проводят сравнение, находящаяся в знаменателе в дроби, выступает базой или основанием соотношения. В соответствии с ее выбором, результат может быть выражен в различных долях единицы, то сеть десятых, сотых (процентов), тысячных (десятая часть процента, промилле), десятитысячные (сотая доля процента продецимилле).
Единицы, которые сопоставляются, могут быть как одноименными, так и разноименными. Если единицы разноименные, то их наименование формируется в зависимости от используемых единиц (ц/га, рублей/чел. и др.).
В экономическом анализе применяются несколько видов относительных величин:
- Динамики,
- Относительная величина структуры, характеризующая долю определенных частей изучаемой совокупности в общем ее объеме;
- Величина планового задания, выражающая отношение запланированных показателей на будущий срок к фактическим сложившимся значениям на текущий период;
- Интенсивности,
- Сравнения,
- Координации,
- Степени экономического развития.
Расчет относительных величин проводят путем определения отношения численности в определенной части на общее их количество (или объемы). Данные единицы выражаются в процентном соотношении или в простом кратном соотношении. Например, расчет удельного веса городского населения.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Для анализа
деятельности предприятий используются
как обобщающие
(синтетические), так и частные
(аналитические)
показатели, в которых отражаются
результаты такой деятельности. Показатели
могут быть представлены абсолютными,
относительными и средними величинами.
Абсолютные
показатели выражают размеры, объемы
и уровни экономических явлений и
процессов, например, численность
работающих на предприятии, объем
реализованной продукции, величина
заработной платы конкретного работника
и т.д. Они имеют большое практическое и
познавательное значение. При помощи
абсолютных величин выражаются размеры
, наличие и движение трудовых , материальных
ресурсов, денежных средств и т.д.
Абсолютные величины служат исходной
базой для всех форм и приемов количественной
характеристики экономических явлений.
Кроме абсолютных
показателей, полученных непосредственно
в результате сводки исходных данных, в
анализе применяются абсолютные
показатели, полученные расчетным путем.
Расчетным путем определяется целый ряд
показателей, характеризующих конечные
результаты деятельности предприятий,
таких как прибыль, рентабельность и
т.д.
В тех случаях,
когда знания абсолютных величин
недостаточно для выявления характерных
черт, особенностей изучаемых явлений,
их дополняют относительными и средними
величинами.
Для сравнения
одних объемных показателей с другими,
выявления типичных их сторон используют
– относительные
величины.
Познание экономических процессов и
явлений состоит не только в том, что
измеряются их достигнутые уровни в
результате деятельности предприятия,
но и в том, что эти уровни и результаты
сравниваются с аналогичными показателями
других предприятий или с показателями
других периодов.
Относительные
величины получают в результате деления
одной величины на другую, которая
принимается за базу сравнения, или за
100%. Относительные величины выражаются
в форме коэффициентов (при базе 1) или
процентов (при базе 100).
В экономическом
анализе нашли применение следующие
виды относительных величин: динамики;
выполнения плана; планового задания;
структуры; координации; интенсивности;
эффективности.
Относительные
величины динамики
представляют собой отношение значений
показателей одного периода к их значениям
в предшествующих (базисных периодах).
Предшествующие (базисные) периоды для
сравнения отчетных данных могут быть
смежными и отдаленными. Сравнение с
этими периодами имеет разный смысл.
Следует иметь в виду, что чем отдаленнее
период, используемый в качестве базы
сравнения, тем более базисные данные
могут отличаться от отчетных по содержанию
(соотношение цен, структуры и т.д.).
Поэтому, проводя сравнения с отдаленной
базой, следует помнить о сопоставимости
показателей.
Относительные
показатели динамики называют обычно
темпами
роста, они
могут быть рассчитаны за два и более
периодов и могут быть определены двумя
способами — базисным
и цепным.
Базисные темпы
роста
определяются как отношение значения
показателя в отчетном (сравниваемом)
периоде (Уi)
к базисному значению (У0).
Цепные темпы
роста – это
отношение значения показателя отчетного
(сравниваемого) периода к значению в
предыдущем периоде (Уi
– 1).
В табл. 2.8 определены
относительные величины динамики
производства продукции ОАО «Прогресс».
Таблица 2.8
Динамика производства
продукции ОАО «Прогресс»
|
ПОКАЗАТЕЛИ |
ГОДЫ |
||||
|
1998 |
1999 |
2000 |
2001 |
2002 |
|
|
У0 |
У1 |
У2 |
У3 |
У4 |
|
|
Объем Темпы (
Темпы роста ( |
577 1,0 1,0 |
570 0,988 0,988 |
565 0,979 0,991 |
566 0,981 1,002 |
578 1,002 1,021 |
Так, например, для
2001 года базисный темп роста был рассчитан
следующим образом: У3/
У0
= 566/ 577 = 0,981, т.о. объем производства
продукции в ОАО «Прогресс» в 2001 году по
сравнению с 1998 годом снизился на 1,9% (1-
0,981)х100%. Цепной темп роста в 2001 году к
уровню 2000 года будет составлять: У3/
У2
= 566/565 = 1.002, т.о. объем производства
продукции ОАО «Прогресс» в 2001 году по
сравнению с 2000 годом возрос в 1.002 раза
или на 0,2% (1,002-100)х100%.
Между базисными
и цепными темпами роста существует
определенная взаимосвязь. Она заключается
в том, что произведение цепных темпов
роста равно базисному темпу роста
последнего анализируемого периода.
Используя символику темпов роста (табл.
2.8), указанную взаимосвязь можно
представить в следующем виде:
У1
х У2
х У3
х У4
= У4 .
У0
х У1 х
У2
х У3 =
У0
Проверим эту
взаимосвязь, используя данные табл.2.8:
0,988 х 0,991 х 1,002 х 1,021=1,002.
Применение
относительных
величин выполнения плана
обусловлено необходимостью контроля
над ходом хозяйственных процессов, они
помогают определять недостатки в работе
и своевременно принимать необходимые
решения.
Относительные
величины выполнения плана характеризуют
степень его выполнения за определенный
период времени и определяются как
отношение значения показателя отчетного
периода (уф)
к его плановому значению на данный
период (упл).
В табл. 2.9 проведен расчет относительных
величин выполнения плана по месяцам
отчетного периода и с нарастающим итогом
за второе полугодие.
Таблица 2.9
Анализ выполнения
плана по товарной продукции
|
Период |
Объем товарной |
Объем продукции |
Степень выполнения |
|||
|
план |
факт |
план |
факт |
по месяцам (гр.3:гр.2)х 100% |
с нарастающим |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Июль Август Сентябрь Октябрь Ноябрь Декабрь |
1800 1850 1920 1910 1870 2100 |
1770 1865 2010 1920 1890 2070 |
1800 3650 5570 7480 9350 11450 |
1770 3635 5445 7565 9455 11525 |
98,3 100,8 104,7 100,5 101,1 99,6 |
98,3 99,6 101,4 101,1 101,1 100,7 |
Анализ табл.2.9
(гр.6) показал, что в июле и декабре план
по товарной продукции был не выполнен
на 1.7% и 0.4% соответственно, с августа по
ноябрь месяц включительно план
перевыполнялся. Однако если рассматривать
работу предприятия с нарастающим итогом
(гр.7), то можно отметить, что в июле и
августе план предприятием был не
выполнен, а начиная с сентября и по конец
года план перевыполнялся. В целом за
второе полугодие план перевыполнен на
на 0,7% или на 75тыс грн.(11525-11450).
Относительные
величины планового задания
представляют собой отношение планового
уровня показателя текущего периода
(упл)
к его фактическому уровню в прошлом
периоде (уо).
Например, фактический объем реализации
продукции предприятия в 2001 году составлял
2300 тыс.грн. В 2002году планировалось
увеличить его до 2500 тыс.грн. Относительная
величина планового задания на 2002год
составит 108.7% ((2500:2300)х100%.)
Между тремя
относительными показателями, рассмотренными
выше, существует следующая взаимосвязь:
относительная величина выполнения
плана равна частному от деления
относительной величины динамики и
относительной величины планового
задания.
Например, плановое
задание по продукции на 2002 год (в % к
предыдущему 2001году) составляет 106.1%,
относительная величина динамики
продукции в 2002 году по сравнению с 2001
годом составила 107.3%, тогда план по
продукции в 2002 году был фактически
выполнен на 101,1% ((1,073:1,061)х100%).
Относительная
величина структуры –
это относительная доля (удельный вес)
части в целом, выраженная в процентах
или коэффициентах. В табл. 2.10 показан
структурный состав работников основной
деятельности предприятия предприятия
по категориям.
Таблица 2.10
Структура персонала
ОАО «Юность»
|
Категории |
Количество, чел |
в % к общей |
|
Рабочие Служащие -руководители -специалисты |
2000 260 100 160 |
88,5 11,5 4,4 7,1 |
|
Итого |
2260 |
100,0 |
Вертикальный
анализ показывает, что наибольший
удельный вес (88.5%) в составе персонала
основной деятельности предприятия
занимают рабочие,11,5%- служащие.
При глубоком
анализе некоторых экономических
процессов относительные величины
структуры нуждаются в совместном
использовании с относительными
показателями интенсивности.
Относительные
величины интенсивности
характеризуют степень распространения
или развития какого-либо явления в
определенной среде. Учитывая экономическую
сущность относительных величин
интенсивности, их можно было бы назвать
показателями уровня экономического
развития. Так, в практике экономической
работы находят широкое применение
показатели технической оснащенности
труда, электроемкости, энергоемкости
и фондоемкости. Примерами относительных
величин, характеризующих интенсивность
процессов в сфере производства и
потребления, являются и другие показатели,
широко применяемые в экономическом
анализе, такие как производство
национального дохода на душу населения,
уровень потребления, определенный как
отношение количества потребленных
продуктов к среднегодовой численности
населения и др.
Относительная
величина координации
представляет соотношение частей целого
между собой, например, активной и
пассивной части основных фондов, служащих
и рабочих предприятия и т.д.
Относительные
величины эффективности
показывают
соотношение эффекта с ресурсами или
затратами, например, производство
продукции на одного рабочего, прибыль
на гривну затрат и т.д.
В отличие от других
видов относительных величин показатели
интенсивности и эффективности являются
обычно именованными величинами и имеют
размерность тех абсолютных величин,
соотношения которых они выражают.
Средние величины
являются
обобщенной характеристикой множества
индивидуальных значений определенного
показателя. На величину индивидуального
значения показателя оказывают действие
некоторые общие причины, а также и
индивидуальные условия. Например,
фрезеровщики машиностроительного
предприятия имеют неодинаковый тарифный
разряд, получают различную заработную
плату. В этих условиях для того чтобы
дать обобщающую характеристику уровня
их заработной платы, нельзя взять
индивидуальную зарплату любого
фрезеровщика. Не может характеризовать
этот уровень и общая сумма заработной
платы, начисленная всем рабочим.
Свойство средней
характеризовать не отдельные единицы,
а выразить уровень показателя в расчете
на каждую единицу совокупности является
её отличительной особенностью. Эта
особенность делает среднюю обобщающим
показателем уровня варьирующего
признака.
Размеры вариации
показателей складываются под влиянием
целого ряда условий и факторов. Так,
например, у всех фрезеровщиков
машиностроительного объединения,
имеющих данный тарифный разряд,
установлена единая тарифная ставка, а
при выполнении одной и той же работы –
одинаковые нормы выработки. Однако
размеры месячной заработной платы у
отдельных фрезеровщиков данного разряда,
даже выполняющих одинаковую работу,
как правило, неодинаковы, так как наряду
с общими условиями на величину заработной
платы влияют также индивидуальные и
чисто случайные факторы: состояние
орудий труда, интенсивность труда,
количество отработанного за месяц
рабочего времени, физиологическое
состояние и др.
Без определения
средней невозможно выяснить, например,
на каком из предприятий выше
производительность труда или заработная
плата рабочих или ниже себестоимость
однотипной продукции.
Средние величины
широко применяются при сравнении
показателей во времени, что даёт
возможность характеризовать важнейшие
закономерности развития показателей,
например, закономерность снижения
себестоимости единицы продукции при
увеличении объёмов производства. В
указанных выше и многих других случаях
в изменении средних показателей
проявляется основная тенденция, под
влиянием которой складывается процесс
развития показателя в целом. В отдельных
же индивидуальных случаях эта тенденция
может и не проявляться. Так, при общем
росте производительности труда в
машиностроении на отдельных предприятиях
этой отрасли под влиянием тех или иных
причин производительность труда может
и не повышаться. Поэтому важно, чтобы
средние характеристики были основаны
на массовом обобщении фактов. Только
при этом условии они выявят общую
тенденцию, лежащую в основе процесса в
целом, и покажут её типичный для данного
периода времени уровень закономерности.
В анализе важное
значение имеет качество средних величин,
которое целиком зависит от однородности
усредняемых объектов. Средняя величина
только тогда отражает действительно
типовой, обобщающий уровень анализируемого
показателя, когда она рассчитана исходя
из однородной совокупности, – в
противоположном случае можно говорить
о «некачественной» средней величине.
Так, нецелесообразно определять с
какой-либо целью среднюю цену единицы
продукции предприятия, которое выпускает,
например, стиральные машины и дверные
замки. Классическим в этом плане является
пример расчета средней температуры
больного в больничной палате, когда,
например, из четырех больных с температурой
тела 34.5; 35.0; 37.2; 40.0 градусов выводится
средняя на одного больного – 36.6 градуса.
Для выявления
качественно однородных совокупностей
при анализе используется метод
группировок. Только после того как в
результате качественного экономического
анализа образованы типически однородные
группы, имеет смысл характеризовать их
средними величинами. Вне метода
группировок по отношению к массе
неоднородных единиц средние величины
приобретают огульный, фиктивный характер.
В экономическом
анализе средним величинам принадлежит
важная роль во вскрытии внутрипроизводственных
резервов, в обосновании экономической
эффективности новых материалов,
технологий, финансовых результатов
деятельности предприятий и организаций.
Однако не следует забывать, что средними
характеристиками нужно пользоваться
с большой осторожностью, не преувеличивая
их значения.
Аналитик, использующий
средние для экономического анализа
должен четко представлять себе характер
исходной совокупности, для которой
рассчитаны средние, и цель, которую он
преследует, так как именно этим условием
определяется вид используемых средних
величин.
Наиболее часто в
экономическом анализе применяются
следующие виды средних: средняя
арифметическая; средняя гармоническая;
средняя квадратическая ; средняя
геометрическая.
Общей формулой
перечисленных выше средних является:
|
|
(2.2) |
где x
– усредняемый признак (индивидуальные
значения показателя) или варианты;
— среднее значение показателя;
и
— взаимообратные функции;n
– число единиц в совокупности.
Равенство (2.2)
называется уравнением средней. Вид
функции
определяет вид средней. Он зависит от
качественной природы совокупности и
поставленной перед средней задачей.
В экономическом
анализе особенно важны различные
модификации степенной средней, т.е.
средней, построенной из различных
степеней вариантов: арифметическая,
гармоническая, квадратическая,
геометрическая и др., для которых (х)=хm.
Общий вид степенной
средней (простой):
|
|
(2.3) |
где k
– показатель степени, определяющий вид
средней.
По формуле 2.3
степенная средняя рассчитывается, если
каждое значение показателя встречается
в совокупности один раз. Если же значения
вариантов повторяются с определенной
для каждого из них частотой «m»,
то формула степенной (взвешенной)
принимает вид:
|
|
(2.4) |
где m
– частота.
В формуле 2.4
каждый вариант «взвешивается» по своей
частоте, т.е. умножается на неё. Частоты
при этом часто называются весами.
Подставляя
различные значения показателя степени
«k»
в формулу 2.3, можно получать различные
виды средних величин.
При k=1
— среднюю арифметическую (простую):
|
|
(2.5) |
при k=2
— среднюю квадратическую (простую):
|
|
(2.6) |
при k=-1
— среднюю гармоническую (простую):
|
|
( 2.7) |
при k=0
— среднюю геометрическую:
|
|
(2.8) |
Для раскрытия
неопределенности используют правило
Лапиталя, в конечном виде получим части
средней степенной:
(2.9)
где
— знак умножения.
При подстановке
различных значений «k»
в формулу 2.4 получают так называемые
взвешенные средние:
|
|
(2.10) |
|
|
(2.11) |
|
|
(2.12) |
|
|
(2.13) |
Естественно,
что различные значения степени средней,
рассчитанные для одной и той же
совокупности с одними и теми же весами,
имеют различное числовое значение. Их
величины при этом возрастают в соответствии
с показателем степени, на основании
которого получена степенная средняя.
В общем виде соотношение между этими
средними такое:
,
т.е. средняя квадратическая больше
средней арифметической, которая в свою
очередь больше средней геометрической,
а та больше средней гармонической.
При анализе
хозяйственной деятельности правильную
характеристику совокупности по
варьирующему показателю в каждом
отдельном случае дает только вполне
определенный вид средней. Так, например,
средняя геометрическая применяется
только при определении средних темпов
роста, а средняя квадратическая — только
при определении показателей вариации.
Для определения средней арифметической
простой, взвешенной и гармонической
необходимо составлять логическую схему,
т.е. описание изучаемого процесса. В
соответствии с задачей, стоящей в каждом
конкретном случае, должно быть найдено
единственное значение средней путем
использования определенной её формы.
Так, при изучении уровня заработной
платы рабочих предприятия должна быть
получена ее обобщающая характеристика
в виде средней заработной платы. При
этом для имеющихся исходных данных эта
средняя должна иметь вполне определенное
значение, быть однозначной. Например,
средняя заработная плата в бригаде
выражается как отношение суммы заработной
платы всех членов бригады к числу
рабочих в бригаде:
Приведем ещё один
пример:
Подобного рода
соотношения, выражающие смысл средних
величин и их зависимость от других
показателей, являются исходной базой
(логической схемой) и критерием
правильности выбора вида средней.
Наиболее
распространенным видом средней,
применяемой в экономических расчетах,
является средняя арифметическая. Расчет
средней арифметической рассмотрим на
примере данных табл.2.11.
Таблица 2.11
Данные о выработке
продукции рабочих
|
Порядковый |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Изготовлено |
13 |
12 |
14 |
16 |
18 |
12 |
19 |
14 |
18 |
14 |
Если обозначить
индивидуальные значения показателя
(т.е. выработку отдельных токарей за
смену) через х1,
х2,
х3…хn
(в данном случае n
= 10), то среднюю арифметическую можно
рассчитать по формуле 2.5 (средней
арифметической простой). При её определении
делают две операции: суммируют
индивидуальные значения признаков;
полученную сумму делят на число значений.
В табл.2.11 некоторые
варианты (12, 14, 18) повторяются несколько
раз, поэтому целесообразно в данном
случае использовать для расчета средней
выработки одного рабочего среднюю
арифметическую взвешенную (формула
2.10). Взяв различные по величине варианты
и указав число случаев их повторения
(частоты), получим табл.2.12.
Таблица 2.12
Выработка рабочих
по числу изготовленных деталей в смену
|
Исходные данные |
Расчет |
|
|
Выработка деталей |
Число рабочих, |
Хm |
|
1 |
2 |
3 |
|
12 |
2 |
24 |
|
13 |
1 |
13 |
|
14 |
3 |
42 |
|
16 |
1 |
16 |
|
18 |
2 |
36 |
|
19 |
1 |
19 |
|
Итого: |
10 |
150 |
В графе 3 табл.2.12
произведено взвешивание выработки
рабочих по числу рабочих. В нашем примере
вариантами являются отдельные значения
выработки рабочих, а весами – число
рабочих. Средняя выработка на одного
рабочего равна:
.
Рассмотрим расчет
средней арифметической , когда
анализируемые данные заданы интервальным
вариационным рядом (табл. 2.13) .
Таблица 2.13
Расчет средней
заработной платы
|
Размер заработной |
Середина |
Число рабочих, |
xm |
|
1 |
2 |
3 |
4 |
|
80-90 |
85 |
10 |
850 |
|
90-100 |
95 |
20 |
1900 |
|
100-110 |
105 |
40 |
4200 |
|
110-120 |
115 |
60 |
6900 |
|
120-130 |
125 |
130 |
16250 |
|
130-140 |
135 |
120 |
16200 |
|
140-150 |
145 |
80 |
11600 |
|
150-160 |
155 |
35 |
5425 |
|
160-170 |
165 |
5 |
825 |
|
Итого: |
х |
500 |
64150 |
В интервальных
рядах значения показателя даны в виде
интервала «от…до». Поэтому для расчета
средней необходимо прежде всего перейти
к дискретному ряду, т.е. по каждой группе
определить середину интервала. Середину
интервала находят как сумму его верхней
и нижней границ. Так, для первой группы
середина интервала будет равна 85 грн.
((80+90):2); для второй – 95 грн.((90+100):2) и т.д.
Затем расчет средней производят так
же, как и в дискретном ряду, т.е. по формуле
2.10. Для нашего случая среднемесячная
заработная плата одного рабочего
составит:
Средние, рассчитанные
из интервальных рядов, являются
приближенными. Степень их приближения
зависит от того, в какой мере фактическое
распределение показателей внутри
интервала приближается к равномерному.
При более равномерном распределении
погрешность средней, рассчитанной из
интервальных рядов, будет меньше.
Точность средней интервального ряда
зависит от величины интервала. Чем
меньше величина интервала, тем точнее
средняя. Средняя, вычисленная из ряда
с равномерными интервалами, будет точнее
средней, вычисленной из ряда с неравными
интервалами, потому что середины равных
интервалов ближе расположены к серединам
данных групп, чем при неравных интервалах.
В случаях, когда
при построении логической схемы имеются
данные только числителя , используется
не средняя арифметическая, а средняя
гармоническая. К средней гармонической
следует прибегать в тех случаях, когда
в качестве весов применяют произведения
единиц совокупности на значение
показателя.
Например, необходимо
определить среднюю себестоимость
единицы однотипной продукции по трем
предприятиям. Известны значения
себестоимости единицы продукции и общих
затрат на производство продукции.
Таблица 2.14
Затраты на
производство однотипной продукции по
предприятиям
|
Номер пред-прия-тия |
Себестоимость |
Затраты на |
Количество |
|
1 |
2 |
3 |
4 |
|
№1 |
320 |
32000 |
100 |
|
№2 |
350 |
33250 |
95 |
|
№3 |
380 |
39900 |
105 |
|
Итого |
х |
105150 |
300 |
Составим логическую
схему:
Числитель логической
схемы задан исходными данными – 105150
грн. (32000+33250+39900), знаменатель можно
определить для каждого предприятия как
отношение затрат на производство (m)
к себестоимости единицы продукции ,
тогда средняя себестоимость единицы
продукции для трех предприятий составит:
Обозначив
себестоимость единицы продукции по
каждому предприятию через хi,
а затраты на производство продукции
через mi,
действия по расчету средней себестоимости
по предприятиям можно провести по
формуле 2.12 — средней гармонической
взвешенной.
Средняя
квадратическая (
формулы 2.11,2.6) чаще всего используется
для расчета среднего квадратического
отклонения при решении задач стохастического
факторного анализа ( см. гл. 5), задач
комплексной оценки деятельности
предприятий ( см. гл. 6) и в ряде других
случаев .
Средняя
геометрическая (
формулы 2.13,2.8) используется при анализе
динамических рядов для расчета средних
темпов роста .
Для изучения социально-экономических явлений и для их количественной оценки в статистике используются величины, которые условно делятся на абсолютные и относительные.
Каждый статистический показатель обладает рядом признаков, по которым его можно отнести к одному из видов.
Читайте также статью “Объект и предмет исследования, задачи и основные методы статистики “.
Понятие “абсолютные величины”
Абсолютные величины – это показатели, которые выражают размеры социально-экономических явлений и процессов в определенных границах времени и места (объем товарооборота, численность предприятий, численность работников).
Абсолютные величины выражены в натуральных единицах, их получают в результате проведения статистического наблюдения и сводки исходной информации.
Абсолютные величины являются основой для расчета аналитических и обобщающих показателей, а также относительных статистических величин. Они являются исходной базой для любого статистического анализа.
Виды абсолютных величин
По способу выражения размеров исследуемых явлений абсолютные величины подразделяются на:
- индивидуальные – характеризуют размеры количественного признака единиц совокупности (например, количество магазинов в определенном жилом районе),
- общие (суммарные, итоговые) – характеризуют размеры количественного признака по отношению ко всей совокупности или группе (объем товарооборота).
Единицы измерения абсолютных величин
В зависимости от цели и задач анализа используются разные единицы измерения абсолютных величин:
[quads id=2]
- натуральные – отвечают природным или физическим свойствам объекта, выражаются в единицах массы, длины, площади, объема, времени (метры, штуки, гектары, литры),
- условно-натуральные – используются в том случае, когда какой-нибудь товар имеет несколько разновидностей и суммарный объем можно определить на основании общего потребительского свойства, присущего для всех разновидностей (например, количество произведенного молока переводится в базисную жирность),
- денежные (стоимостные) – для измерения стоимостной характеристики показателя (цена единицы продукции, выручка от продажи),
- трудовые – используются для измерения трудозатрат, для определения величины трудовых ресурсов, рациональности их использования и пр. (человеко-час, человеко-день и т.д.).

Понятие “относительные статистические величины”
Относительными статистическими величинами называются показатели, которые выражают количественные соотношения между социально-экономическими явлениями.
Рассчитываются относительные величины путем деления двух одноименных или разноименных абсолютных (или других относительных) величин, которые относятся к одним и тем же или взяты из разных периодов времени, территорий, объектов, частей совокупности. То есть относительные величины представляют собой отношение количества единиц одного показателя, приходящееся на единицу другого показателя.
Виды относительных статистических величин
Относительные величины делятся на две группы:
- Величины, которые получены при помощи деления одноименных статистических показателей.
- Величины, которые получены путем деления разноименных статистических показателей.
К 1-й группе относятся следующие виды относительных величин:
- Относительные величины динамики.
- Относительные величины выполнения плана.
- Относительные величины планового задания.
- Относительные величины структуры.
- Относительные величины координации.
- Относительные величины пространственного сравнения (наглядности).
Результат сопоставления представляется в виде коэффициента, когда база сравнения принята за единицу, или в процентах и показывает, во сколько раз и насколько сравниваемый показатель больше или меньше базисного.
Ко 2-й группе относительных величин относятся относительные величины интенсивности.
Рассмотрим каждый из видов относительных статистических величин подробнее.
[quads id=4]
Относительные величины динамики
Относительными величинами динамики называются показатели, которые характеризуют степень изменения уровней одноименных явлений во времени, скорость изменения уровней явлений, темпы их развития.
Относительная величина динамики рассчитывается путем соотношения значений показателя за два периода или момента времени.
Данную величину еще называют коэффициентом роста, так как показывает, во сколько раз увеличился или уменьшился объем социально-экономического явления за определенный период времени:
Коэффициент динамики = П1/П0 (в долях единицы),
где П1 – значение показателя в отчетном периоде,
П0 – значение показателя в базисном периоде.
Коэффициент роста, выраженный в процентах, называется темпом роста:
Темп роста = П1/П0 * 100%
Относительные величины выполнения плана
Относительные величины выполнения плана (выполнение договорных обязательств) вычисляются путем деления фактического (Рф) и планового (Рп) уровней показателей и объема выполненных обязательств (например, Рф) и объема обязательств по договору (Рд)). Выражает отношение фактического значения показателя к плановому.
Относительная величина планового задания
Относительная величина планового задания рассчитывается путем соотношения показателя у соответствия с плановым заданием на будущий период (Рз) и фактического уровня показателя за базисный период (Рф).
Как правило, относительная величина планового задания выражается в процентах.
Относительные величины структуры
Относительными величинами структуры называются показатели, которые характеризуют состав исследуемой совокупности.
[quads id=2]
Они рассчитываются путем соотношения абсолютной величины каждого составного элемента совокупности к абсолютной величине всей совокупности (по какому-то признаку, который изучается), то есть путем соотношения части к целому.
Относительные величины структуры называют удельным весом или долей. Преимущественно выражаются в процентах, но можно выражать их и в коэффициентной форме.
Относительная величина координации
Относительными величинами координации называются показатели, которые характеризуют соотношение отдельных частей определенной совокупности.
Относительные величины координации показывают, во сколько раз часть совокупности, которая сравнивается, больше или меньше части совокупности, которая избрана за базу сравнения.
Примерами таких величин могут быть соотношение между численностью управленческого персонала организации и общей численности работников, соотношение собственного капитала предприятия и заемного.
Относительные величины пространственного сравнения
Относительные величины пространственного сравнения (наглядности) – это показатели, которые характеризуют соотношение одноименных величин, взятых за один и тот же период или момент времени, но которые относятся к разным объектам или территориям.
Такие относительные величины часто используются при сравнении результатов деятельности организаций различных форм собственности, в международных сопоставлениях, при сравнении цен, величин капитала и пр.
Относительные величины интенсивности
Относительными величинами интенсивности называют показатели, которые характеризуют степень распространения, развития явлений в определенной среде.
[quads id=4]
Относительные величины интенсивности рассчитываются путем соотношения разноименных абсолютных величин.
В числителе – величина явления (показатель), степень распространения которого изучается, а в знаменателе – величина той среды, в которой развивается (распространяется) это явление.
Относительная величина интенсивности показывает, сколько единиц одной совокупности приходится на единицу другой совокупности.
Относительная величина интенсивности всегда является именуемой. Чаще исчисляются в долях единицы, чем в процентах.
К относительным величинам интенсивности относятся такие показатели, как коэффициенты деловой активности, фондовооруженность, фондоотдача, материалоотдача, рентабельность, доходность различных видов деятельности.
Изображение – freepik.com
P. S.: Если Вам понравилась статья, поделитесь ссылкой в социальных сетях! Спасибо, и хорошего Вам дня!
Аннотация: Каждое статистическое исследование начинается со сбора первоначальных сведений об отобранных единицах наблюдения. На основе этих сведений определяются статистические показатели, которые дают количественную характеристику изучаемых экономических и социальных явлений и процессов. В зависимости от способа расчета статистические показатели могут быть абсолютными, относительными и средними величинами. Статистический показатель может быть индивидуальным, если он относится к отдельно взятой единице наблюдения, или же обобщающим, если характеризует всю статистическую совокупность или ее часть.
5.1. Абсолютные статистические величины
Абсолютные статистические величины характеризуют абсолютные размеры (уровни) социально-экономических явлений, например: численность населения, объем продукции, абсолютный прирост вкладов населения, площадь под зерновыми культурами, число страховых компаний и т.д.
Индивидуальные показатели в форме абсолютных величин получают в процессе самого статистического наблюдения в результате подсчета, определения значения количественного признака у каждой конкретной единицы наблюдения.
Обобщающие (сводные) показатели в форме абсолютных величин определяют путем суммирования зарегистрированных значений признака по всем единицам наблюдения или их части в процессе сводки и группировки результатов наблюдения. Сводные абсолютные показатели характеризуют, во-первых, число единиц по группе или совокупности в целом, во-вторых, общий размер признака по группе или совокупности в целом.
На основе абсолютных показателей исчисляются относительные и средние величины. Абсолютные показатели всегда имеют единицы измерения: либо натуральные, либо стоимостные, либо трудовые.
Натуральные единицы измерения бывают простыми, составными и условными.
Простые натуральные единицы измерения — это штуки, километры, килограммы, тонны, метры, литры, мили, дюймы и т.д. В простых натуральных единицах также измеряется объем статистической совокупности или объем отдельной ее части (количество предприятий, из них количество малых предприятий; число объектов страхования, из них число пострадавших объектов; численность работников банка и т.д.).
Составные натуральные единицы измерения имеют расчетные показатели, получаемые как произведение двух или нескольких показателей, имеющих простые единицы измерения, например: объем произведенной энергии учитывается в киловатт-часах (мощность электростанции умножается на количество часов работы), грузооборот — в тонно-километрах (масса перевезенных грузов умножается на расстояние перевозки).
Условные натуральные единицы измерения широко используют в анализе производственной деятельности, когда требуется найти итоговое значение (сумму) однотипных показателей, которые напрямую несопоставимы, но характеризуют одни и те же свойства объектов. Например, в топливной промышленности для определения суммарного объема произведенного топлива его различные виды пересчитываются в условное топливо, единица которого имеет теплоту сгорания 29,3 МДж/кг.
Пример 5.1 Найдем общий объем потребления топлива предприятием за год по данным таблицы:
| Вид топлива | Объем потребления в натуральных единицах измерения | Теплота сгорания единицы топлива, МДж/кг | Коэффициент перевода в условное топливо | Объем потребления в условно натуральных единицах измерения, тыс. т условного топлива |
|---|---|---|---|---|
| Природный газ, тыс. м3 | 5,6 | 35,2 | 35,2 : 29,3 = 1,20 | 5,6 х 1,2 = 6,72 |
| Каменный уголь, тыс. т | 4,2 | 25,2 | 25,2 : 29,3 = 0,86 | 4,2 х 0,86 = 3,612 |
| Торф, тыс. т | 8,3 | 24,0 | 24,0 : 29,3 = 0,82 | 8,3 х 0,82 = 6,806 |
| Итого | — | — | — | 17,138 |
Итак, общий объем потребления топлива предприятием составил 17,138 тыс. т условного топлива.
Помимо топливной промышленности условно-натуральные единицы измерения используются и в других отраслях, в основном при учете производства и потребления различных видов продукции, например: при производстве консервов их общий объем пересчитывается в условные консервные банки объемом 353,4 см3; мыла — в условное мыло с 40%-ным содержанием жирных кислот и т.д.
При анализе социально-экономических явлений наибольшее распространение получили стоимостные единицы измерения: рубли, доллары, евро, валюта других стран. Аналитическая ценность стоимостных единиц заключается в том, что они позволяют суммировать либо сравнивать показатели, которые не сопоставимы в натуральных единицах измерения, например, определить общий объем производства различных видов продукции, общий объем всех затрат, связанных с производством продукции. Однако в некоторых случаях могут возникнуть сложности, например, нельзя напрямую сравнивать валовой внутренний продукт России в 2000 г. и 2004 г.: следует ввести корректирующий коэффициент, учитывающий инфляцию. Также нельзя напрямую сравнивать размеры пенсий за эти периоды — они несопоставимы из-за изменения цен.
Абсолютные показатели могут выражаться в трудовых единицах измерения. Так, учет затрат труда на предприятиях выражается в отработанных человеко-днях (число работников предприятия умножается на количество отработанных за период дней) или человеко-часах (число работников предприятия умножается на среднюю продолжительность одного рабочего дня и количество рабочих дней в периоде).
5.2. Относительные статистические величины
Для статистического анализа недостаточно иметь только абсолютные величины. Например, прибыль от реализации продукции предприятия в 2005 г. составила 1200 тыс. руб. Сложно оценить, много это или мало? Но если сказать по-другому, а именно: прибыль предприятия от реализации продукции возросла на 25% по сравнению с предыдущим годом, то становится понятным — финансовые результаты деятельности предприятия улучшились. Таким образом, при анализе статистических данных необходимо проводить сопоставления статистических показателей во времени, в пространстве, сравнивать фактические показатели с планом, изучать структуру совокупности по тому или иному признаку, сопоставлять уровень развития одного явления на фоне развития другого, связанного с ним, явления.
Для решения этих задач используются относительные величины.
Относительные величины представляют собой меру количественного соотношения статистических показателей. Они всегда получаются как частное от деления двух сравниваемых величин. При этом если сравниваемые величины являются одноименными и имеют одну размерность, то получаемая относительная величина выражается в виде простого кратного отношения (коэффициента). Она показывает, во сколько раз величина, находящаяся в числителе, больше величины, находящейся в знаменателе, — базы сравнения, принимаемой за единицу. Если частное от деления двух сравниваемых величин умножить на 100, то относительная величина выражается в процентах (%), т.д. величина, находящаяся в знаменателе, принимается за 100 единиц; если на 1000 — то в промилле (‰, т.д. величина в знаменателе принимается за 1000 единиц).
Если сравниваемые величины разноименны, то их отношение будет представлять собой относительную величину, имеющую сложную единицу измерения, образуемую от наименований единиц измерения сравниваемых показателей: ц/га, руб./шт., м2/чел., дол./чел. и т. п.
В зависимости от целей статистического анализа различают следующие виды показателей в форме относительных величин:
- относительный показатель плана;
- относительный показатель выполнения плана;
- относительный показатель динамики;
- относительный показатель структуры;
- относительный показатель координации;
- относительный показатель интенсивности;
- относительный показатель сравнения.
Исходной, первичной формой выражения статистических показателей являются показатели в абсолютном выражении или абсолютные величины. Статистические показатели в форме абсолютных величин характеризуют абсолютные размеры изучаемых статистикой процессов и явлений, а именно их массу, площадь, объем, протяженность, отражают их временные характеристики, а также могут представлять объем совокупности, т.е. число составляющих ее единиц.
Индивидуальные абсолютные показатели (величины), как правило, получают непосредственно в процессе статистического наблюдения как результат замера, взвешивания, подсчета и оценки интересующего количественного признака. В ряде случаев индивидуальные абсолютные показатели имеют разностный характер: разность между численностью работников предприятия на конец и на начало года, разность между выручкой от реализации предприятия и общей суммой затрат и т.п.
Сводные абсолютные показатели, характеризующие объем признака или объем совокупности как в целом по изучаемому объекту, так и по какой-либо его части, получают в результате сводки и группировки индивидуальных значений. К таким показателям относятся общая численность занятых в отрасли, совокупные активы коммерческих банков региона и т.п.
Абсолютные статистические показатели всегда являются именованными числами. В зависимости от социально-экономической сущности исследуемых явлений, их физических свойств они выражаются в натуральных, стоимостных или трудовых единицах измерения.
В международной практике используются такие натуральные единицы измерения, как тонны, килограммы, квадратные, кубические и простые метры, мили, километры, галлоны, литры, штуки и т.д.
Пример: согласно данным по международным стандартам финансовой отчетности (МСФО), “Роснефть” в 2018 году увеличила добычу нефти на 2,6% – до 216,3 млн т.; по данным (ТАСС) фактическое потребление электроэнергии в Российской Федерации в 2018 г. составило 1076,2 млрд кВт∙ч (по ЕЭС России 1055,6 — млрд кВт∙ч); экспорт сжиженного природного газа (СПГ) из России в страны Азиатско-Тихоокеанского региона (АТР) вырос в 2018 году на 58,6% год к году и составил 26 млрд куб. м.
В группу натуральных также входят условно-натуральные измерители, используемые в тех случаях, когда какой-либо продукт имеет несколько разновидностей и общий объем можно определить только исходя из общего для всех разновидностей потребительского свойства. Например, различные виды органического топлива переводятся в условное топливо ((у.т.) – единица учёта органического топлива, применяемая для сопоставления эффективности различных видов топлива и суммарного учёта их. В качестве единиц у.т. принимается 1 кг топлива с теплотой сгорания 7000 ккал/кг (29,3 Мдж/кг)); мыло разных сортов ‑ в условное мыло с 40%-ным содержанием жирных кислот; консервы различного объема ‑ в условные консервные банки объемом 353,4 куб. см и т.д.
Перевод в условные единицы измерения осуществляется на основе специальных коэффициентов, рассчитываемых как отношение потребительских свойств отдельных разновидностей продукта к эталонному значению. Так, например, 100 т торфа, теплота сгорания которого ‑ 24 МДж/кг, будут эквивалентны 81,9 т условного топлива (100 × 24,0/29,3), а 100 т нефти при теплоте сгорания 45 МДж/кг будут оцениваться в 153,6 т условного топлива (100 × 45,0/29,3).
В отдельных случаях для характеристики какого-либо явления или процесса одной единицы измерения недостаточно, и используется произведение двух единиц. Примером этому могут служить такие показатели, как грузооборот и пассажирооборот, оцениваемые соответственно в тонно-километрах и пассажиро-километрах, производство электроэнергии, измеряемое в киловатт-часах и т.д.
В условиях рыночной экономики наибольшее значение и применение имеют стоимостные единицы измерения, позволяющие получить денежную оценку социально-экономических явлений и процессов. Так, одним из важнейших стоимостных показателей в системе национальных счетов, характеризующим общий уровень развития экономики страны, является валовой внутренний продукт, который в России по данным Федеральной службы государственной статистики за 2018 года составил 103875,8 млрд. рублей.
При анализе и сопоставлении стоимостных показателей необходимо иметь в виду, что в условиях высоких или относительно высоких темпов инфляции они становятся несопоставимыми. Так, сравнивать экспорт ВПК России за 2018 год с его величиной, например, за 1998 год вряд ли целесообразно, так как содержание рубля за этот период существенно изменилось. Для того, чтобы произвести подобные сравнения, там где это возможно, осуществляют пересчет в сопоставимые цены.
К трудовым единицам измерения, позволяющим учитывать как общие затраты труда на предприятии, так и трудоемкость отдельных операций технологического процесса, относятся человеко-дни и человеко-часы.