Sometimes we come across functions that have hills and valleys. Polynomial functions usually have more than one hill and valley point. We know that these points are critical points of the function and can be classified into maxima or minima. Hill points are called maxima and the valley points are called minimas. Since there are multiple maxima and minimas, it becomes essential for us to identify the points where the function takes up the minimum value and the maximum value are called global maxima and global minima.
Critical Points and Extrema Value Theorem
Let’s say we have a function f(x), critical points are the points where the derivative of the function becomes zero. These points can either be maxima or minima. A critical point is minima or maxima is determined by the second derivative test. Since there can be more than one point where the derivative of the function is zero, more than minima or maxima is possible. The figure below shows a function that has multiple critical points.
Notice that points A, C are minimas, and points B, D are maximas. B and C are called local maxima and local minima respectively. This means that these points are maximum and minimum in their locality but not necessarily on a global level. Points A and D are called global minima and global maxima.
Let’s say we have a function f(x) which is twice differentiable. Its critical points are given by the f'(x) = 0. Second Derivative Test allows us to check whether the calculated critical point is minima or maxima.
- If f”(x) > 0, then the point x is a maxima.
- If f”(x) < 0, then the point x is a minima.
Now, this test tells us which point is a minimum or a maximum, but it still fails to give us information about the global maxima and global minima. Extrema value Theorem comes to our rescue.
Extrema Value Theorem
Extrema value theorem guarantees both the maximum and minima for a function under certain conditions. This theorem does not tell us where the extreme points will exist, this theorem tells us that they will exist. The theorem states that,
If a function f(x) is continuous on a closed interval [a, b], then f(x) has both at least one maximum and minimum value on [a, b].
Absolute Minima and Maxima in a closed Interval
Now to find the extreme points in any interval, we need to follow some basic steps. Let’s say we have a function f(x) and a region D. We want to find the extreme value of the function in this interval.
Step 1: Find the critical points of the function in the interval D,
f'(x) = 0
Step 2: Find the value of the function at the extreme points of interval D.
Step 3: The largest value and smallest value found in the above two steps are the absolute maximum and absolute minimum of the function.
Absolute Minima and Maxima in the entire domain
Absolute minimum and maximum values of the function in the entire domain are the highest and lowest value of the function wherever it is defined. A function can have both maximum and minimum values, either one of them or neither of them. For example, a straight line extends up to infinity in both directions so it neither has a maximum value nor minimum value. We need to follow some steps similar to the previous case to find out the absolute maxima and minima for the entire domain.
Step 1: Find the critical points of the function wherever it is defined.
Step 2: Find the value of the function at these extreme points.
Step 3: Check for the value of the function when x tends to infinity and negative infinity. Also, check for the points of discontinuity.
Step 4: Maximum and minimum of all these values give us the absolute maximum and absolute minimum for the function in its entire domain.
Let’s see some sample problems
Sample Problems
Question 1: Find the absolute maximum and absolute minimum values of the function f(x) = 5x + 2 in the interval [0,2].
Solution:
The first step is to find the critical points by differentiating the function f(x),
f'(x) = 5
This equation has no roots, therefore there are no critical points which means no maxima or minima. This function is continuously increasing. Thus, the maxima and minima will occur at the end points of the interval.
f(0) = 2
f(2) = 12
Thus, f(0) is the minimum and f(2) is the maximum value of the function.
Question 2: Find the absolute maximum and absolute minimum values of the function f(x) = x2 – 2x + 5 in the interval [0,2].
Solution:
The first step is to find the critical points by differentiating the function f(x),
f'(x) = 2x – 2
f'(x) = 0
⇒ 2x – 2 = 0
⇒ x = 1
This, x = 1 is the critical point of the function.
f(1) = (1)2 – 2(1) + 5
⇒f(1) = 1 – 2 + 5
⇒f(1) = 4
Checking the end points of the interval,
f(0) = 5
f(2) = 5
Out of all these values, we can conclude that,
x = 1 is the minima and x = 2,0 is the maxima.
Thus, absolute maximum and absolute minimum values of the function are 5 and 4 respectively.
Question 3: Find the absolute maximum and absolute minimum values of the function f(x) = x3 – 2x2+ 5 in the interval [-2,2].
Solution:
The first step is to find the critical points by differentiating the function f(x),
f'(x) = 3x2 – 4x
f'(x) = x(3x – 4)
⇒ x(3x – 4) = 0
⇒ x = 0 and

This, x = 0 and
are the critical points of the function.
f(0) = 5
⇒f(1) =

⇒f(1) =
⇒f(1) =
⇒f(1) =
⇒f(1) =
⇒f(1) =
Checking the end points of the interval,
f(-2) = (-2)3 – 2(-2)2+ 5
⇒ f(-2) = -8 -2(4) + 5
⇒f(-2) = -16 + 5
⇒f(-2) = -11
f(2) = (2)3 – 2(2)2+ 5
⇒ f(2) = 5
Out of all these values, we can conclude that,
x = -2 is the minima and x = 0, 2 is the maxima.
Thus, absolute maximum and absolute minimum values of the function are 5 and 4 respectively.
Question 4: Find the absolute maximum and absolute minimum values of the function f(x) = in the interval [0,1].
Solution:
The first step is to find the critical points by differentiating the function f(x),
f'(x) =
This equation will not be zero for any value of x in the interval. So, it is monotonically increasing or decreasing in the interval. Checking at the boundary points.
f(0) =
f(1) =
Out of all these values, we can conclude that,
x = 1 is the minima and x = 0 is the maxima.
Thus, absolute maximum and absolute minimum values of the function are
and
respectively.
Question 5: Find the absolute maximum and absolute minimum values of the function f(x) = 2ex – 2 in the interval [0,1].
Solution:
The first step is to find the critical points by differentiating the function f(x),
f'(x) = 2ex
This equation will not be zero for any value of x in the interval. So, it is monotonically increasing or decreasing in the interval. Checking at the boundary points.
f(1) = 2e1 – 2
⇒f(1) = 2e – 2
f(0) = 2(1) – 2
⇒f(0) = 0
Out of all these values, we can conclude that,
x = 0 is the minima and x = 1 is the maxima.
Thus, absolute maximum and absolute minimum values of the function are 2e – 2 and 0 respectively.
Question 6: Find the absolute maximum and absolute minimum values of the function f(x) = x2 – x in the interval [0,1].
Solution:
The first step is to find the critical points by differentiating the function f(x),
f'(x) = 2x – 2
f'(x) = 0
⇒ 2x – 1 = 0
⇒ x =
This, x =
is the critical point of the function.
f(
) =
⇒f(
) =
⇒f(
) =
Checking the end points of the interval,
f(0) = 0
f(1) = 0
Out of all these values, we can conclude that,
x =
is the minima and x = 1,0 is the maxima.
Thus, absolute maximum and absolute minimum values of the function are 0 and
respectively.
Question 7: Find the absolute maxima and the minima for the function f(x) = x4 + 2x2.
Solution:
Since no interval is given, we need to calculate the minimum and the maximum value of the function on it’s domain which is R. First let’s check for the critical points.
f(x) = x4 – 2x2
⇒ f'(x) = 4x3 – 4x
f'(x) = 0
⇒ 4x3 – 4x = 0
⇒ 4x(x2 – 1) = 0
The critical points are x = 0, 1, -1.
Now since it’s a polynomial function there are no discontinuities. Let’s check for the asymptomatic values of the function.
When x ⇢ ∞, f(x) ⇢ ∞ similarly,
x ⇢ -∞, f(x) ⇢ ∞
So, there is no maximum value for the function. For minimum value, let’s check on the critical points.
x = 0,-1 and 1
f(0) = 0
f(1) = 3
f(-1) = 3
Thus, minimum value is f(0) = 0.
Question 8: Find the absolute minimum and maximum value of the function f(x) = .
Solution:
Since no interval is given, we need to calculate the minimum and the maximum value of the function on its domain which is R – {-3}. First let’s check for the critical points.
f(x) =
f'(x) =
There is no point in the function’s domain where f'(x) = 0.
So now we need to check for the values of the function when x tends to infinity.
As x ⇢ -∞ or x ⇢ ∞. f(x) ⇢ 0. And as x ⇢ -3, f (x) ⇢ ∞
Thus, there is no maximum value and the minimum value exists when x ⇢ ∞ or -∞ and f(x) ⇢ 0.
Точка
М называется внутренней для некоторого
множества G,
если она принадлежит этому множеству
вместе с некоторой своей окрестностью.
Точка N
называется граничной для множества G,
если в любой ее полной окрестности
имеются точки, как принадлежащие G,
так и не принадлежащие ему.
Совокупность
всех граничных точек множества G
называется границей Г.
Множество
G
будет называться областью, если все его
точки – внутренние (открытое множество).
Множество G
с присоединенной границей Г
называется замкнутой областью. Область
называется ограниченной, если она
целиком содержится внутри круга
достаточно большого радиуса.
Наименьшее
и наибольшее значения функции в данной
области называются абсолютными
экстремумами функции в этой области.
Теорема
Вейерштрасса: функция, непрерывная в
ограниченной и замкнутой области,
достигает в этой области своего
наименьшего и своего наибольшего
значений.
Следствие.
Абсолютный экстремум функции в данной
области достигается либо в критической
точке функции, принадлежащей этой
области, либо на Д
отыскания наибольшего и наименьшего
значений функции в замкнутой областиG
необходимо найти все ее критические
точки в этой области, вычислить значения
функции в этих точках (включая граничные)
и путем сравнения полученных чисел
выбрать наибольшее и наименьшее из них.
Пример
4.1. Найти
абсолютный экстремум функции (наибольшее
и наименьшее значения)
в треугольной областиD
с вершинами
,
,
(рис.1).
-
Найдем
критические точки:
;
,
то
есть точка О(0, 0) – критическая точка,
принадлежащая области D.
z(0,0)=0.
-
Исследуем границу:
а)
ОА: y=0
;z(x,
0)=0; z(0,
0)=0; z(1,
0)=0,
б)
ОВ: х=0
z(0,y)=0;
z(0,
0)=0; z(0,
2)=0,
в)
АВ:
;
,
,
.
Пример
4.2. Найти
наибольшее и наименьшее значения функции
в замкнутой области, ограниченной осями
координат и прямой.
1) Найдем критические
точки, лежащие в области:
,
,
.
-
Исследуем
границу. Т.к. граница состоит из отрезка
ОА оси Ох, отрезка ОВ оси Оу и отрезка
АВ, то определим наибольшее и наименьшее
значения функции z
на каждом из этих отрезков.
а)
ОА:
.
б)
ОВ:
,
z(0,
2)=–3, z(0,
0)=5, z(0,
4)=5.
в)
АВ:
M3(5/3,7/3),
z(5/3,
7/3)=–10/3.
Среди
всех найденных значений выбираем
zнаиб=z(4,
0)=13; zнаим=z(1,
2)=–4.
5. Условный экстремум. Метод множителей Лагранжа
Рассмотрим задачу,
специфическую для функций нескольких
переменных, когда ее экстремум ищется
не на всей области определения, а на
множестве, удовлетворяющему некоторому
условию.
Пусть рассматривается
функция
,
аргументыи
которой удовлетворяют условию
,
называемому уравнением связи.
Точка
называется точкой условного максимума
(минимума), если существует такая
окрестность этой точки, что для всех
точекиз этой окрестности удовлетворяющих
условию,
выполняется неравенствоили
.
На рис.2 изображена
точка условного максимума
.
Очевидно, что она не является точкой
безусловного экстремума функции(на рис.2 это точка
).
Наиболее простым
способом нахождения условного экстремума
функции двух переменных является
сведение задачи к отысканию экстремума
функции одной переменной. Допустим
уравнение связи
удалось разрешить относительно одной
из переменных, например, выразитьчерез
:
.
Подставив полученное выражение в функцию
двух переменных, получим
Рис.
2
т.е. функцию одной
переменной. Ее экстремум и будет условным
экстремумом функции
.
Пример 5.1. Найти
точки максимума и минимума функциипри условии
.
Решение. Выразим
из уравнения
переменную
через переменную
и подставим полученное выражение
в функцию
.
Получимили
.
Эта функция имеет единственный минимум
при.
Соответствующее значение функции.
Таким образом,– точка условного экстремума (минимума).
В рассмотренном
примере уравнение связи
оказалось линейным, поэтому его легко
удалось разрешить относительно одной
из переменных. Однако в более сложных
случаях сделать это не удается.
Для отыскания
условного экстремума в общем случае
используется метод множителей Лагранжа.
Рассмотрим функцию трех переменных
.
Эта функция называется функцией Лагранжа,
а–
множитель Лагранжа. Верна следующая
теорема.
Теорема.Если
точкаявляется точкой условного экстремума
функциипри
условии,
то существует значениетакое, что точка
является точкой экстремума функции
.
Таким образом, для
нахождения условного экстремума функции
при
условиитребуется
найти решение системы
П
из этих уравнений совпадает с уравнением
связи. Первые два уравнения системы
можно переписать в виде,
т.е. в точке условного экстремума
градиенты функцийи
коллинеарны. На рис. 3 показан геометрический
смысл условий Лагранжа. Линияпунктирная, линия уровня
функции
сплошные. Из рис. следует, что в точке
условного экстремума линия уровня
функциикасается линии
.
Пример 5.2.Найти точки экстремума функциипри условии
,
используя метод множителей Лагранжа.
Решение. Составляем
функцию Лагранжа
.
Приравнивая к нулю ее частные производные,
получим систему уравнений:
Ее единственное
решение
.
Таким образом, точкой условного экстремума
может быть только точка (3; 1). Нетрудно
убедиться в том, что в этой точке функцияимеет условный минимум. В случае, если
число переменных более двух, моет
рассматриваться и несколько уравнений
связи. Соответственно в этом случае
будет и несколько множителей Лагранжа.
Задача нахождения
условного экстремума используется при
решении таких экономических задач, как
нахождение оптимального распределения
ресурсов, выбор оптимального портфеля
ценных бумаг и др.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Абсолютные экстремумы функции двух переменных
Как и в случае одной переменной, функция 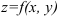
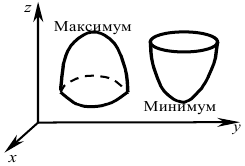
Функция 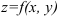
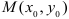
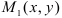
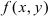
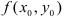
Процедура отыскания экстремумов функции 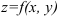
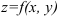
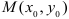
Таким образом, возможные точки экстремума (или стационарные точки) определятся из системы уравнений:
Так же, как и в случае функции одной переменной, если в области определения первых производных имеются точки, где производные равны бесконечности (или не существуют), то их следует включить в состав стационарных точек. Необходимое условие экстремума можно переформулировать также следующим образом: в точке минимума или максимума дифференцируемой функции градиент равен нулю.
Для определения фактического наличия экстремума и его типа необходимо применить достаточное условие. Аналог первого достаточного условия экстремума (по изменению знака производных при переходе через стационарную точку) на практике используется редко, из-за громоздкости вычислений и недостаточной наглядности. В связи с этим обычно используется аналог второго достаточного условия, который формулируется следующим образом:
Пусть функция 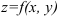
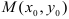
Здесь 
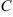
- если
, то в точке
функция
имеет экстремум, причем при
— максимум, при
— минимум;
- если
, то в точке
функция
экстремума не имеет;
- если
, то в точке
вопрос об экстремуме остается открытым и требуется дополнительное исследование — графическое или с применением первых частных производных (аналог первого достаточного условия).
Исследование функции двух переменных на экстремум рекомендуется проводить по следующей схеме:
- Найти частные производные
и
функции
.
- Найти стационарные точки функции.
- Найти частные производные второго порядка, вычислить их значения в каждой стационарной точке и с помощью достаточного условия сделать вывод о наличии экстремумов.
- Вычислить экстремумы (экстремальные значения) функции:
.
Заметим, что в стационарных точках, в которых исследование устанавливает отсутствие экстремума или оставляет вопрос открытым, может действительно не быть экстремума, но вполне может быть и случай, показанный на рисунке:
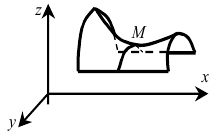
В точке 
Кроме того, отметим, что, так же как и в случае функции одной переменной, если 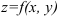
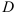
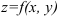
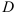
Остальные темы находится на этой странице и там же можно заказать любые работы по высшей математике:
Помощь по высшей математике
Обратите внимание на эти страниц, возможно они вам будут полезны:




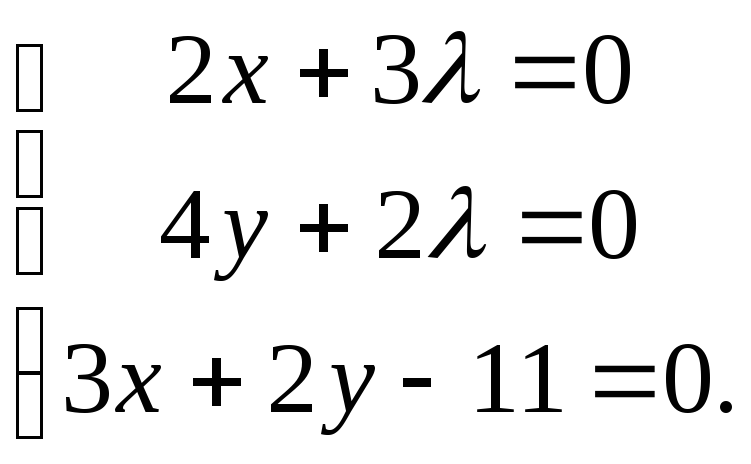

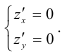
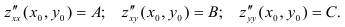
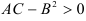 , то в точке
, то в точке 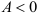 — максимум, при
— максимум, при 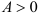 — минимум;
— минимум;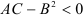 , то в точке
, то в точке 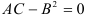 , то в точке
, то в точке 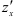 и
и 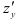 функции
функции 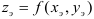 .
.