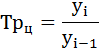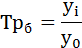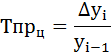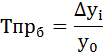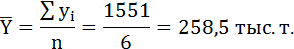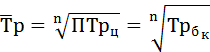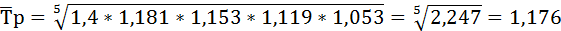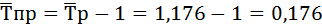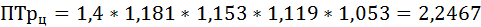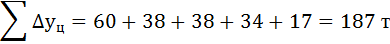Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Как найти абсолютный прирост
Абсолютными величинами в статистике называются обобщенные показатели, характеризующие размеры общественных явлений в конкретных условиях места и времени. Абсолютный размер — его величина, взятая сама по себе безотносительно к размерам других явлений. Абсолютные величины — это именованные числа, которые выражают размеры явлений в определенных единицах измерения (человеках, рублях, штуках, человекоднях и т.д.). Абсолютный прирост относится к показателям рядов динамики. Ряды динамики (временные ряды) — это ряды статистических величин, характеризующие изменения явлений во времени.

Вам понадобится
- Калькулятор, данные о динамике производства продукции анализируемого предприятия.
Инструкция
Определите показатель абсолютного прироста на базисной основе как разность между текущем и начальным уровнем ряда по формуле:
Δi = yi – yo,
где yi — текущий уровень ряда,
yo — начальный уровень ряда.
Пример:
В 1997 году произведено продукции на 10 млн.т., в 1998 году — 12 млн.т., в 1999 году — 16 млн.т., в 2000 году — 14 млн.т.
Δi = 12 — 10 = 2 млн.т.
Δi = 16 — 10 = 6 млн.т.
Δi = 14 — 10 = 4 млн.т.
Рассчитайте показатель абсолютного прироста на цепной основе как разность между текущем и предыдущим уровнем ряда по формуле:
Δi = yi – yi-1,
где yi — текущий уровень ряда,
yi-1 — предыдущий уровень ряда.
Пример:
В 1997 году произведено продукции на 10 млн.т., в 1998 году — 12 млн.т., в 1999 году — 16 млн.т., в 2000 году — 14 млн.т.
Δi = 12 — 10 = 2 млн.т.
Δi = 16 — 12 = 4 млн.т.
Δi = 14 — 16 = -2 млн.т.
Вычислите средний показатель абсолютного прироста по формуле:
_
Δ = yn – y1/n-1,
где y1 — первый уровень ряда,
n — число уровней ряда,
yn — конечный уровень ряда.
Пример:
В 1997 году произведено продукции на 10 млн.т., в 1998 году — 12 млн.т., в 1999 году — 16 млн.т., в 2000 году — 14 млн.т.
_
Δ = 14-10/4-1 = 1,3 млн.т.
Видео по теме
Обратите внимание
Вычисление среднего показателя абсолютного прироста необходимо для обобщения итогов развития явления за единичный интервал или момента из имеющейся временной последовательности.
Полезный совет
Показатели динамики рассчитываются на базисной и цепной основе. Базисные показатели динамики получают путем сравнения всех уровней ряда с одним и тем же первоначальным уровнем. Цепные показатели динамики получают путем сравнения каждого уровня ряда с предыдущим.
Источники:
- Статистика государственного бюджета
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Определение среднего абсолютного прироста, средних темпов роста и прироста
По
показателям изменения уровней ряда
динамики (абсолютные приросты, темпы
роста и прироста), полученным в результате
анализа исходного ряда, могут быть
рассчитаны обобщающие показатели в
виде средних величин — средний абсолютный
прирост, средний темп роста, средний
темп прироста.
Средний
абсолютный прирост может быть получен
по одной из формул:
или
,
где n — число уровней
ряда динамики;
—
первый уровень ряда динамики;
—
последний уровень ряда динамики;
—
цепные абсолютные приросты.
Средний темп роста
можно определить, пользуясь формулами:
где n — число
рассчитанных цепных или базисных темпов
роста;
—
уровень ряда, принятый за базу для
сравнения;
—
последний уровень ряда;
—
цепные темпы роста (в коэффициентах);
—
первый базисный темп роста;
—
последний базисный темп роста.
Между
темпами прироста
и темпами роста К существует соотношение
=
К — 1, аналогичное соотношение верно и
для средних величин.
Определение в рядах динамики общей тенденции развития
Определение
уровней ряда динамики на протяжении
длительного периода времени обусловлено
действием ряда факторов, которые
неоднородны по силе и направлению
воздействия, оказываемого на изучаемое
явление.
Рассматривая
динамические ряды, пытаются разделить
эти факторы на постоянно действующие
и оказывающие определяющее воздействие
на уровни ряда, формирующие основную
тенденцию развития, и случайные факторы,
приводящие к кратковременным изменениям
уровней ряда динамики. Наиболее важна
при анализе ряда динамики его основная
тенденция развития, но часто по одному
лишь внешнему виду ряда динамики ее
установить невозможно, поэтому используют
специальные методы обработки, позволяющие
показать основную тенденцию ряда. Методы
обработки используются как простые,
так и достаточно сложные. Простейший
способ обработки ряда динамики,
применяемый с целью установления
закономерностей развития — метод
укрупнения интервалов.
Суть
метода укрупнения интервалов в том,
чтобы от интервалов, или периодов
времени, для которых определены исходные
уровни ряда динамики, перейти к более
продолжительным периодам времени и
посмотреть, как уровни ряда изменяются
в этом случае.
Пример.
Данные о реализации молочной продукции
в магазинах города по месяцам представлены
таблицей 1.27 (в тоннах).
Таблица
8.2
|
месяц |
2004 |
2005 |
2006 |
|
январь |
5,3 |
5,3 |
5,4 |
|
февраль |
5,3 |
5,1 |
5,2 |
|
март |
7,9 |
8,3 |
8,2 |
|
апрель |
8,2 |
9,0 |
9,3 |
|
май |
9,8 |
9,5 |
10,1 |
|
июнь |
12,5 |
13,0 |
13,1 |
|
июль |
11,8 |
12,2 |
12,5 |
|
август |
10,3 |
10,4 |
10,8 |
|
сентябрь |
8,2 |
8,0 |
8,3 |
|
октябрь |
6,5 |
6,6 |
6,8 |
|
ноябрь |
5,4 |
5,5 |
5,7 |
|
декабрь |
5,5 |
5,5 |
5,6 |
|
итого за год |
96,7 |
98,4 |
101 |
Исходные
уровни ряда динамики подвержены сезонным
изменениям; для определения общей
тенденции развития переходят от
ежемесячных уровней к годовым уровням:
2004 г. — 96,7 тонн; 2005 г. — 98,4 тонн; 2006 г. — 101
тонна. Эти цифры, полученные в результате
перехода к годовым уровням ряда динамики,
показывают общую тенденцию роста
реализации молочной продукции.
Другой
способ определения тенденции в ряду
динамики – метод скользящих средних.
Суть метода заключается в том, что
фактические уровни ряда заменяются
средними уровнями, вычисленными по
определённому правилу, например:
– исходные или фактические уровни ряда
динамики заменяются средними уровнями:;
;
;
…….
В
результате получается сглаженный ряд,
состоящий из скользящих пятизвенных
средних уровней
.
Между расположением уровнейи
устанавливается соответствие:
,
– –– – , сглаженный ряд короче исходного
на число уровней,
гдеk
— число уровней, выбранных для определения
средних уровней ряда.
Сглаживание
методом скользящих средних можно
производить по четырём, пяти или другому
числу уровней ряда, используя
соответствующие формулы для усреднения
исходных уровней. Полученные при этом
средние уровни называются четырёхзвенными
скользящими средними, пятизвенными
скользящими средними и т.д.
При
сглаживании ряда динамики по чётному
числу уровней выполняется дополнительная
операция, называемая центрированием,
поскольку, при вычислении скользящего
среднего, например по четырём уровням,
относится к временной точке между
моментами времени, когда были зафиксированы
фактические уровнии
.
Схема вычислений и рас положений уровней
сглаженного ряда становится сложнее:
…
– исходные уровни;
– –
…
– сглаженные уровни;
– –
…
– центрированные сглаженные уровни;
.
Метод
скользящих средних не позволяет получить
численные оценки для выражения основной
тенденции в ряду динамики, давая лишь
наглядное графическое представление.
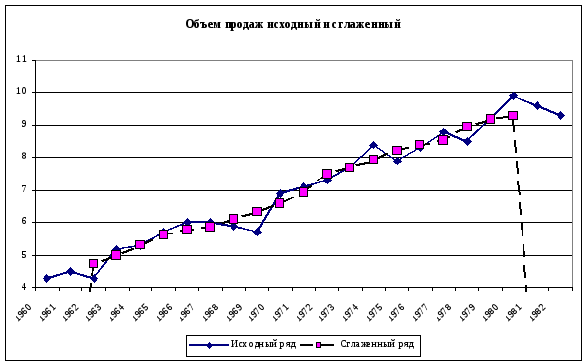
Пример.
Таблица
|
Годы |
Объем продаж, |
Скользящая |
|
1960 |
4,3 |
– |
|
1961 |
4,5 |
– |
|
1962 |
4,3 |
4,72 |
|
1963 |
5,2 |
5,00 |
|
1964 |
5,3 |
5,30 |
|
1965 |
5,7 |
5,64 |
|
1966 |
6,0 |
5,78 |
|
1967 |
6,0 |
5,86 |
|
1968 |
5,9 |
6,10 |
|
1969 |
5,7 |
6,32 |
|
1970 |
6,9 |
6,58 |
|
1971 |
7,1 |
6,94 |
|
1972 |
7,3 |
7,48 |
|
1973 |
7,7 |
7,68 |
|
1974 |
8,4 |
7,92 |
|
1975 |
7,9 |
8,22 |
|
1976 |
8,3 |
8,38 |
|
1977 |
8,8 |
8,54 |
|
1978 |
8,5 |
8,94 |
|
1979 |
9,2 |
9,18 |
|
1980 |
9,9 |
9,30 |
|
1981 |
9,6 |
– |
|
1982 |
9,3 |
– |
На
рис. показан график, построенный по
данным о объеме продаж представленных
в таблице 8.2.

8.1. Объем продаж исходный и сглаженный
Наиболее
совершенным способом определения
тенденции развития в ряду динамики
является метод аналитического
выравнивания. При этом методе исходные
уровни ряда динамики
заменяются теоретическими или расчетными
,
которые представляют из себя некоторую
достаточно простую математическую
функцию времени, выражающую общую
тенденцию развития ряда динамики. Чаще
всего в качестве такой функции выбирают
прямую, параболу, экспоненту и др.
Например,
,
где
— коэффициенты, определяемые в методе
аналитического выравнивания;
—
моменты времени, для которых были
получены исходные и соответствующие
теоретические уровни ряда динамики,
образующие прямую, определяемую
коэффициентами
.
Расчет
коэффициентов
ведется на основе метода наименьших
квадратов:
Если
вместо
подставить
(или соответствующее выражение для
других математических функций), получим:
Это
функция двух переменных
(все
и
известны), которая при определенных
достигает минимума. Из этого выражения
на основе знаний, полученных в курсе
высшей математики об экстремуме функций
n переменных, получают значения
коэффициентов.
Для прямой:
где
n – число моментов времени, для которых
были получены исходные уровни ряда
.
Если
вместо абсолютного времени
выбрать
условное время таким образом, чтобы,
то записанные выражения для определенияупрощаются:
Пример. Нечетное
число уровня ряда.
|
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
абсолютное время |
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
условное время |
Чётное число
уровней ряда.
|
1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
абсолютное время |
|
-7 |
-5 |
-3 |
-1 |
1 |
3 |
5 |
7 |
условное время |
В
обоих случаях
.
Пример.
Выполняется аналитическое выравнивание
ряда, отражающего производство стали
в стране по годам (млн. т).
|
1985 |
1986 |
1987 |
1988 |
1989 |
|
141,3 |
144,8 |
146,7 |
151,5 |
149,0 |
В
качестве математической функции,
отражающей тенденцию развития, выбирается
прямая
,
определениепроизводится для условного времени, в
результате,
.
|
Год |
Производство |
Условное |
Теоретические
|
|
1985 |
141,3 |
-2 |
142,2 |
|
1986 |
144,8 |
-1 |
144,4 |
|
1987 |
146,7 |
0 |
146,7 |
|
1988 |
151,5 |
1 |
148,9 |
|
1989 |
149,0 |
2 |
151,1 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
![Определить базисным и цепным способами абсолютный прирост [18.05.13]](https://studrb.ru/files/works_screen/1/44/43.png)
Тема: Определить базисным и цепным способами абсолютный прирост
Раздел: Бесплатные рефераты по статистике
Тип: Задача | Размер: 12.01K | Скачано: 233 | Добавлен 18.05.13 в 22:51 | Рейтинг: 0 | Еще Задачи
Задача
Имеются следующие данные:
|
Год |
Наличие в городе Архангельске цветочных клумб |
|
1990 |
16226 |
|
1991 |
17159 |
|
1992 |
15833 |
|
1993 |
11455 |
|
1994 |
12668 |
|
1995 |
13126 |
|
1996 |
14553 |
|
1997 |
14120 |
|
1998 |
15663 |
|
1999 |
17290 |
|
2000 |
18115 |
|
2001 |
19220 |
Определить базисным и цепным способами:
- Абсолютный прирост;
- Темп роста (%);
- Темп прироста (%);
- Среднегодовой темп роста.
Привести расчёты всех показателей, результаты расчётов свести в таблицу. Сделать выводы, описав в них каждый показатель таблицы в сравнении с предыдущим и базисным показателем. Результатом данной работы является подробный вывод.
Вычисления
- Абсолютный прирост (снижение) (Апр)
- Абсолютный прирост (снижение) «цепным» способом.
Если определять абсолютный прирост (снижение) наличия в городе Архангельске цветочных клумб каждый раз к предыдущему году, то он составит:
В 1991 году: 17159 – 16226 = 933 единицы.
В 1992 году: 15833 – 17159 = — 1326 единиц.
В 1993 году: 11455 – 15833 = — 4378 единиц.
В 1994 году: 12668 – 11455 = 1213 единиц.
В 1995 году: 13126 – 12668 = 458 единицы.
В 1996 году: 14553 – 13126 = 1427 единиц.
В 1997 году: 14120 – 14553 = — 433 единицы.
В 1998 году: 15663 – 14120 = 1543 единиц.
В 1999 году: 17290 – 15663 = 1627 единиц.
В 2000 году: 18115 – 17290 = 825 единиц
В 2001 году: 19220 – 18115 = 1105 единиц.
- Абсолютный прирост (снижение) «базисным» способом.
Если 1990 год принять за базу сравнения, то по отношению к нему абсолютный прирост (снижение) наличия в городе Архангельске цветочных клумб в последующие годы будет составлять:
В 1991 году: 17159– 16226 = 933 единицы.
В 1992 году: 15833 – 16226 = — 393единиц.
В 1993 году: 11455 – 16226 = — 4771 единиц.
В 1994 году: 12668 – 16226 = 3558 единиц.
В 1995 году: 13126 – 16226 = — 3100 единицы.
В 1996 году: 14553 – 16226 = — 1673 единиц.
В 1997 году: 14120 – 16226 = — 2106 единицы.
В 1998 году: 15663 – 16226 = — 563 единиц.
В 1999 году: 17290 – 16226 = 1064 единиц.
В 2000 году: 18115 – 16226 = 1889 единиц
В 2001 году: 19220 – 16226 = 2994 единиц.
- Темп роста (снижения) (Тр)
- Темп роста (снижения) «цепным» способом.
Если определять темп роста (снижения) наличия в городе Архангельске цветочных клумб каждый раз к предыдущему году, то он составит:
В 1991 году: 17159 / 16226 * 100% = 105,7(%)
В 1992 году: 15833 / 17159 * 100% = 92,3 (%)
В 1993 году: 11455 / 15833 * 100% = 72,3 (%)
В 1994 году: 12668 / 11455 * 100% = 110,6 (%)
В 1995 году: 13126 / 12668 * 100% = 103,6 (%)
В 1996 году: 14553 / 13126 * 100% = 110,8 (%)
В 1997 году: 14120 / 14553 * 100% = 97,0 (%)
В 1998 году: 15663 / 14120 * 100% = 110,9 (%)
В 1999 году: 17290 / 15663 * 100% = 110,4 (%)
В 2000 году: 18115 / 17290 * 100% = 104,8 (%)
В 2001 году: 19220 / 18115 * 100% = 106,1 (%)
- Темп роста (снижения) «базисным» способом.
Если 1990 год принять за базу сравнения, то по отношению к нему темп роста (снижения) наличия в городе Архангельске цветочных клумб в последующие годы будет составлять:
В 1991 году: 17159 / 16226 * 100% = 105,7(%)
В 1992 году: 15833 / 16226 * 100% = 97,6 (%)
В 1993 году: 11455 / 16226 * 100% = 70,6 (%)
В 1994 году: 12668 / 16226 * 100% = 78,0 (%)
В 1995 году: 13126 / 16226 * 100% = 80,9 (%)
В 1996 году: 14553 / 16226 * 100% = 89,7 (%)
В 1997 году: 14120 / 16226 * 100% = 87,0 (%)
В 1998 году: 15663 / 16226 * 100% = 96,5 (%)
В 1999 году: 17290 / 16226 * 100% = 106,5 (%)
В 2000 году: 18115 / 16226 * 100% = 111,6 (%)
В 2001 году: 19220 / 16226 * 100% = 118,5 (%)
- Темп прироста (снижения) (Тпр)
- Темп прироста (понижения) «цепным» способом.
Если определять темп прироста (снижения) наличия в городе Архангельске цветочных клумб каждый раз к предыдущему году, то он составит:
В 1991 году: (17159 – 16226) / 16226 * 100% = 5,8(%)
В 1992 году: (15833 – 17159) / 17159 * 100% = — 7,7(%)
В 1993 году: (11455 – 15833) / 15833 * 100% = — 27,7(%)
В 1994 году: (12668 – 11455) / 11455 * 100% = 10,6(%)
В 1995 году: (13126 – 12668) / 12668 * 100% = 3,6(%)
В 1996 году: (14553 – 13126) / 13126 * 100% = 10,9(%)
В 1997 году: (14120– 14553) / 14553 * 100% = -3,0(%)
В 1998 году: (15663 – 14120) / 14120 * 100% = 10,9(%)
В 1999 году: (17290 – 15663) / 15663 * 100% = 10,4(%)
В 2000 году: (18115 – 17290) / 17290 * 100% = 4,8(%)
В 2001 году: (19220 – 18115) / 18115 * 100% = 6,1(%)
- Темп прироста (снижения) «базисным» способом.
Если 1990 год принять за базу сравнения, то по отношению к нему темп прироста (понижения) наличия в городе Архангельске цветочных клумб в последующие годы будет:
В 1991 году: (17159 – 16226) / 16226 * 100% = 5,8(%)
В 1992 году: (15833 – 16226) / 16226 * 100% = — 2,4(%)
В 1993 году: (11455 – 16226) / 16226 * 100% = — 29,4(%)
В 1994 году: (12668 – 16226) / 16226 * 100% = — 21,9(%)
В 1995 году: (13126 – 16226) / 16226 * 100% = — 19,1(%)
В 1996 году: (14553 – 16226) / 16226 * 100% = — 10,3(%)
В 1997 году: (14120– 16226) / 16226 * 100% = — 13,0(%)
В 1998 году: (15663 – 16226) / 16226 * 100% = — 3,5(%)
В 1999 году: (17290 – 16226) / 16226 * 100% = 6,6(%)
В 2000 году: (18115 – 16226) / 16226 * 100% = 11,6(%)
В 2001 году: (19220 – 16226) / 16226 * 100% = 18,5(%)
Среднегодовой темп роста (Тр)
- Среднегодовой темп роста, определяемый «цепным» способом составит:
1,057*0,923*0,723*1,106*1,036*1,108*0,970*1,109*1,104*1,048*1,061 = 1,183
- Среднегодовой темп роста, определяемый «базисным» способом составит:
1,057*0,976*0,706*0,780*0,809*0,897*0,870*0,965*1,065*1,116*1,185 = 0,487
Динамика показателей абсолютного прироста (снижения), темпа роста (снижения), темпа прироста (понижения) наличия в городе Архангельске цветочных клумб в период с 1990 по 2001 год, исчисленных «цепным» и «базисным» способами
|
№ п/п |
Год |
Наличие в городе Архангельске цветочных клумб, единиц |
Абсолютный прирост (снижение) Наличия в городе Архангельске цветочных клумб, единиц |
Темп роста (снижения) Наличия в городе Архангельске цветочных клумб, % |
Темп прироста (понижения) наличия в городе Архангельске цветочных клумб, % |
|||
|
Цепной способ |
Базисный способ |
Цепной способ |
Базисный способ |
Цепной способ |
Базисный способ |
|||
|
1 |
1990 |
16226 |
100,0 |
100,0 |
||||
|
2 |
1991 |
17159 |
933 |
933 |
105,7 |
105,7 |
5,8 |
5,8 |
|
3 |
1992 |
15833 |
— 1326 |
— 393 |
92,3 |
97,6 |
— 7,7 |
— 2,4 |
|
4 |
1993 |
11455 |
— 4378 |
— 4771 |
72,3 |
70,6 |
— 27,7 |
— 29,4 |
|
5 |
1994 |
12668 |
1213 |
3558 |
110,6 |
78,0 |
10,6 |
— 21,9 |
|
6 |
1995 |
13126 |
458 |
— 3100 |
103,6 |
80,9 |
3,6 |
— 19,1 |
|
7 |
1996 |
14553 |
1427 |
— 1673 |
110,8 |
89,7 |
10,9 |
— 10,3 |
|
8 |
1997 |
14120 |
— 433 |
— 2106 |
97,0 |
87,0 |
— 3,0 |
— 13,0 |
|
9 |
1998 |
15663 |
1543 |
— 563 |
110,9 |
96,5 |
10,9 |
— 3,5 |
|
10 |
1999 |
17290 |
1627 |
1064 |
110,4 |
106,5 |
10,4 |
6,6 |
|
11 |
2000 |
18115 |
825 |
1889 |
104,8 |
111,6 |
4,8 |
11,6 |
|
12 |
2001 |
19220 |
1105 |
2994 |
106,1 |
118,5 |
6,1 |
18,5 |
Выводы
В 1990 году наличие в городе Архангельске цветочных клумб составило 16226.
В 1991 году наличие в городе Архангельске цветочных клумб составило 17159 еденицы. Абсолютный прирост наличия в городе Архангельске цветочных клумб по сравнению с 1990 годом составил 933 единицы. Темп роста наличия в городе Архангельске цветочных клумб в 1991 году по сравнению с 1990 годом составил 105,7 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1991 году по сравнению с 1990 годом составил 5,8 процента.
В 1992 году наличие в городе Архангельске цветочных клумб составило 15833 единицы. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1991 составил 1326 единицы. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1990 годом составило 393 единицы. Темп снижения наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1991 составил 92,3 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1990 годом составило 97,6 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1991 составил 7,7 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1990 годом составил 2,4 процента.
В 1993 году наличие в городе Архангельске цветочных клумб составило 11455 единиц. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1992 составило 4378 единицы. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1990 годом составил 4771 единиц. Темп снижения наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1992 составил 72,3 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1990 годом составил 70,6 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1992 составил 27,7 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1990 годом составил 29,4 процента.
В 1994 году наличия в городе Архангельске цветочных клумб составило 12668 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1993 составило 1213 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1990 годом составил 3558 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1993 составил 110,6 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1990 годом составил 78,0 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1993 составил 10,6 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1990 годом составил 21,9 процента.
В 1995 году наличие в городе Архангельске цветочных клумб составило 13126 единиц. Абсолютный рост наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1994 составило 458 единиц. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1990 годом составил 3100 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1994 составил 103,6 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1990 годом составил 80,9 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1994 составил 3,6 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1990 годом составил 19,1 процента.
В 1996 году наличие в городе Архангельске цветочных клумб составило 14553 единицы. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1995 составил 1427 единиц. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1990 годом составил 1673 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1995 составил 110,8 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1990 годом составил 89,7 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1995 составил 10,9 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1990 годом составил 10,3 процента.
В 1997 году наличие в городе Архангельске цветочных клумб составило 14120 единиц. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1996 составил 433 единицы. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1990 годом составил 2106 единиц. Темп снижения наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1996 составил 97,0 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1990 годом составил 87,0 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1996 составил 3,0 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1990 годом составил 13,0 процента.
В 1998 году наличие в городе Архангельске цветочных клумб составило 15663 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1997 составил 1543 единицы. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1990 годом составил 563 единицы. Темп роста наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1997 составил 110,9 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1990 годом составил 96,5 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1997 составил 10,9 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1990 годом составил 3,5 процента.
В 1999 году наличие в городе Архангельске цветочных клумб составило 17290 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1998 составил 1627 единицы. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1990 годом составил 1064 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1998 составил 110,4 процента. Темп роста наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1990 годом составил 106,5 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1998 составил 10,4 процента. Темп роста наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1990 годом составил 6,6 процента.
В 2000 году наличие в городе Архангельске цветочных клумб составило 18115 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1999 составил 825 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1990 годом составил 1889 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1999 составил 104,8 процента. Темп роста наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1990 годом составил 111,6 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1999 составил 4,8 процента. Темп роста наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1990 годом составил 11,6 процента.
В 2001 году наличие в городе Архангельске цветочных клумб составило 19220 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 2000 составил 1105 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 1990 годом составил 2994 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 2000 составил 106,1 процента. Темп роста наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 1990 годом составил 118,5 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 2000 составил 6,1 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 1990 годом составил 18,5 процента.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Бесплатная оценка
0
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Добавить работу
Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
Похожие работы
- Решение задач по статистике для каждой темы
- Задачи по статистике с расчетами
- Задача с решением по статистике
- Определить цепным и базисным способами
- Контрольные задачи по Статистике
- Задачи по статистике с расчетами (6 задач)
- Задачи по статистике на экзамен с решением
- Расчетно-графическая работа по статистике
- Примеры решения задач по статистике
- Решение задачи по статистике с пояснением
- Типовые экзаменационные задачи по статистике
- Задачи по статистике с решением (5 задач)
- Решение задач по статистике (4 задачи)
- Решение задач по статистике в Excele
- Решение задач по статистике с подробным описанием решения
- Решение задач по статистике (5 задач)
- Решение задач по статистике (2 задачи)
- Решение задач по Статистике
- Задачи к экзаменационным билетам по статистике
- Задачи по статистике с решением и выводом
Добыча нефти характеризуется следующими данными:
| Годы | Добыча нефти, тыс. т |
|---|---|
| 1-ый | 150 |
| 2-ой | 210 |
| 3-ий | 248 |
| 4-ый | 286 |
| 5-ый | 320 |
| 6-ой | 337 |
Произвести анализ ряда динамики по:
1) показателям, характеризующим рост добычи нефти (на цепной и базисной основе): абсолютный прирост, темпы роста и прироста (по годам к базисному году); результаты расчетов изложить в табличной форме;
2) средний уровень и среднегодовой темп ряда динамики;
3) показать взаимосвязь между цепными и базисными показателями.
Сделайте выводы.
Решение:
Абсолютный прирост цепной (Δyц) – это разность между текущим уровнем ряда и предыдущим:
Δyц =yi – yi-1
Так, во 2-ом г. прирост добычи нефти в сравнении с первым годом составит:
Δyц 2-й год = y2 – y1 =
= 210 – 150 = 60 тыс. т.
В 3-ем году прирост добычи нефти в сравнении со 2-м годом составит:
Δyц 3-й год = 248 – 210 = 38 тыс. т.
Аналогично исчисляются абсолютные приросты за последующие годы. Результаты расчётов занесём в таблицу.
Абсолютный прирост базисный (Δyб) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения:
Δyб = yi – y0
Так как в задании не указано, какой год взять в качестве базисного года, по умолчанию будем считать базисным 1-й год.
Абсолютный прирост базисный во 2-ом г. совпадает с цепным абсолютным приростом в этом году:
Δyб = 210 – 150 = 60 тыс. т
в 3-ем году базисный абсолютный прирост равен:
Δyб = y3 – y2 = 248 – 150 = 98 тыс. т и т.д (гр. 3 расчётной таблицы).
Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.
Цепной темп роста исчисляют отношением текущего уровня к предыдущему:
(гр. 5 расчётной таблицы);
базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения:
(гр. 4 расчётной таблицы).
Темп прироста (Тпр) так же может быть цепной или базисный.
Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики:
Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики:
Если предварительно был вычислен темп роста, то темп прироста можно рассчитать как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:
Тпр= Тр – 1;
или как разность между темпами роста и 100%, если темпы роста выражены в процентах:
Тпр= Тр – 100% (гр. 6 и 7 расчётной таблицы).
Расчётная таблица
| Годы | Добыча нефти, тыс. т | Абсолютный прирост базисный, тыс. т | Абсолютный прирост цепной, тыс. т | Темп роста базисный, % | Темп роста цепной, % | Темп прироста базисный, % | Темп прироста цепной, % |
|---|---|---|---|---|---|---|---|
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1-ый | 150 | 0 | — | 100,00 | — | — | — |
| 2-ой | 210 | 60 | 60 | 140,00 | 140,0 | 40,00 | 40,0 |
| 3-ий | 248 | 98 | 38 | 165,33 | 118,1 | 65,33 | 18,1 |
| 4-ый | 286 | 136 | 38 | 190,67 | 115,3 | 90,67 | 15,3 |
| 5-ый | 320 | 170 | 34 | 213,33 | 111,9 | 113,33 | 11,9 |
| 6-ой | 337 | 187 | 17 | 224,67 | 105,3 | 124,67 | 5,3 |
Из таблицы видно, что добыча нефти росла от года к году. Однако прирост добычи с каждым годом становился меньше.
2) Средний уровень ряда определяется в данном случае по формуле средней арифметической простой, где в числителе сумма уровней динамического ряда, а в знаменателе их число:
Среднегодовой темп роста ряда динамики рассчитывается по формуле средней геометрической
где ПТр – произведение цепных темпов роста (в коэффициентах),
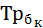
n – число темпов.
Среднегодовой темп прироста ряда динамики:
Добыча нефти ежегодно возрастала в среднем на 17,6%.
3) Между цепными и базисными темпами роста имеется взаимосвязь:
произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста.
Сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту:
Выводы: С 1 по 6 годы добыча нефти росла от года к году. Объём добычи нефти за эти годы вырос на 124,7%, что в абсолютном выражении составило 187 т. Однако ежегодный прирост добычи с каждым годом снижался. В среднем добыча нефти ежегодно возрастала на 17,6%.