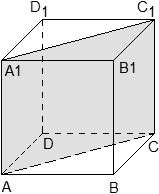
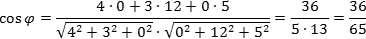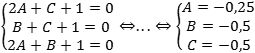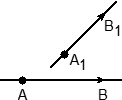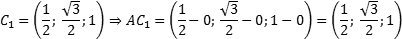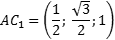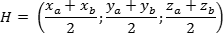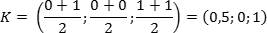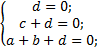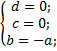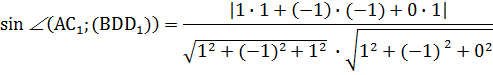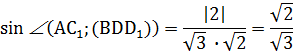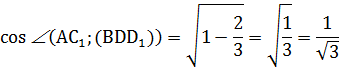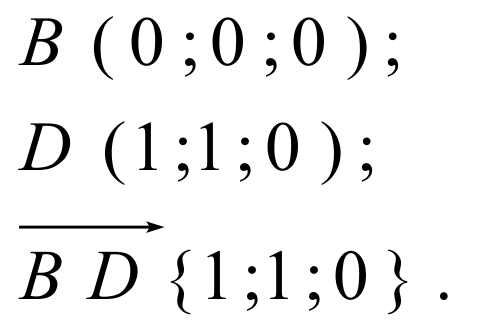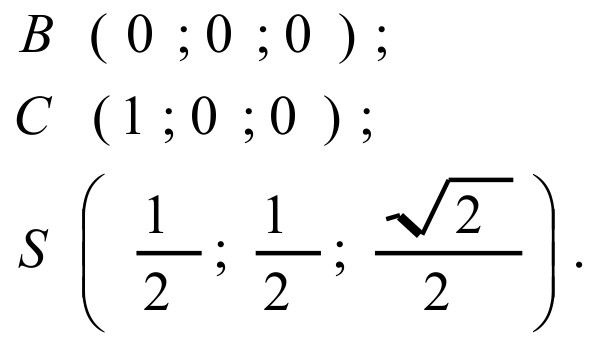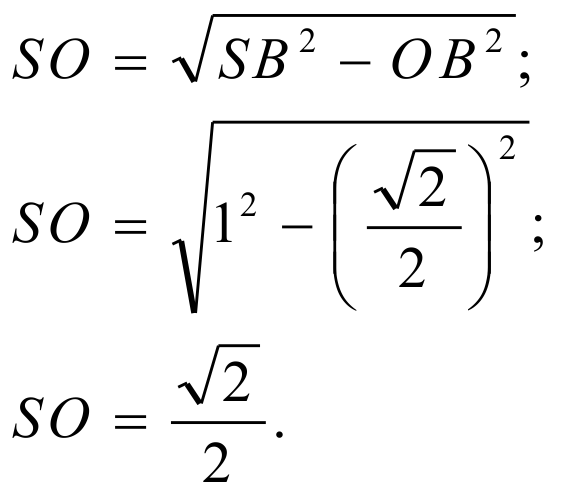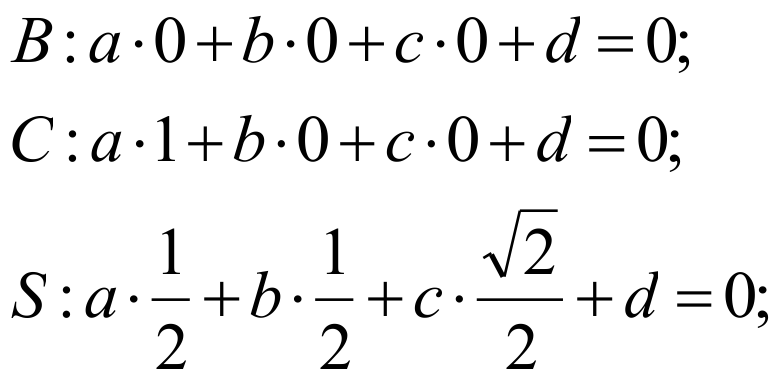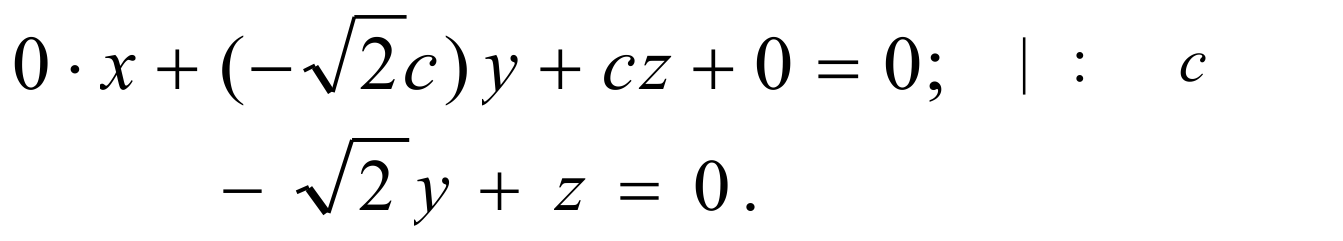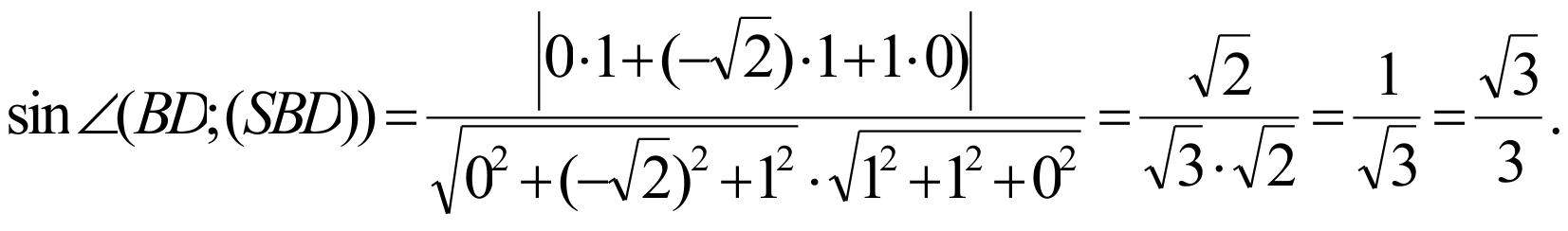Метод координат в пространстве
Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:
Главная формула — косинус угла φ между векторами a = (x1; y1; z1) и b = (x2; y2; z2):
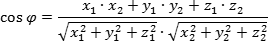
На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.
Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).
Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:
Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.
Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.
Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;
Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;
Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:
Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.
Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.
Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!
Вычисление координат векторов
А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.
Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.
Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:
Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.
Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).
Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).
Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).
Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)
Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!
Вычисление направляющих векторов для прямых
Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.
Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую.
Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый для прямой:
Зачем нужен этот вектор? Дело в том, что — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:
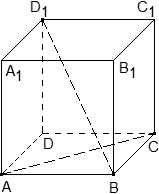
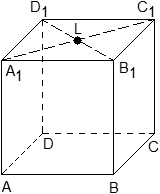
Задача. В кубе ABCDA1B1C1D1 проведены прямые AC и BD1. Найдите координаты направляющих векторов этих прямых.
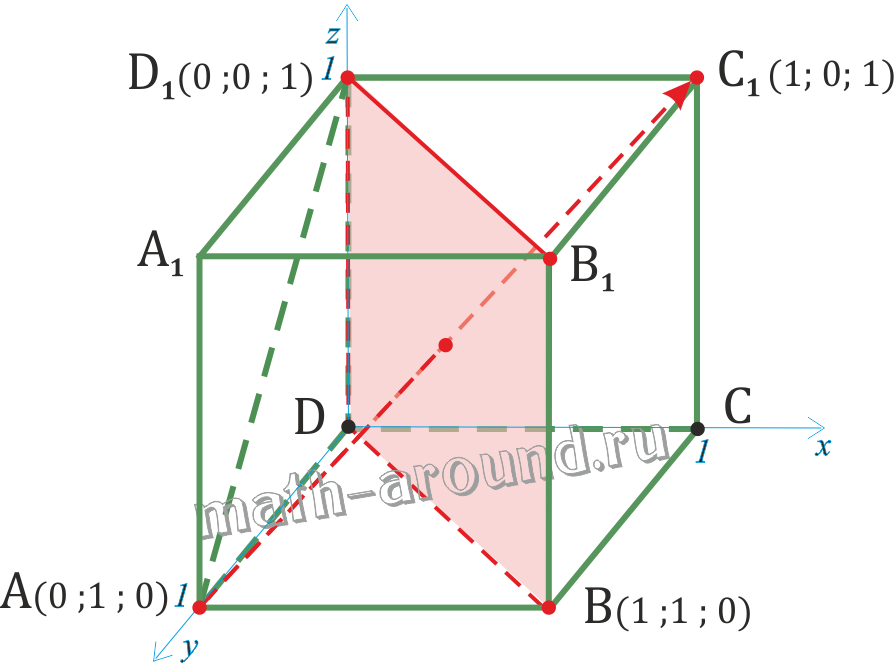
Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA1 соответственно. Единичный отрезок равен AB = 1.
Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.
Теперь разберемся с прямой BD1. На ней также есть две точки: B = (1; 0; 0) и D1 = (0; 1; 1). Получаем направляющий вектор BD1 = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).
Ответ: AC = (1; 1; 0); BD1 = (− 1; 1; 1)
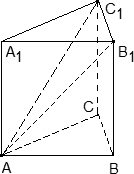
Задача. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, проведены прямые AB1 и AC1. Найдите координаты направляющих векторов этих прямых.
Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA1, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.
Для начала разберемся с прямой AB1. Тут все просто: у нас есть точки A = (0; 0; 0) и B1 = (1; 0; 1). Получаем направляющий вектор AB1 = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).
Теперь найдем направляющий вектор для AC1. Все то же самое — единственное отличие в том, что у точки C1 иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:
Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.
Вычисление нормальных векторов для плоскостей
Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.
Другими словами, — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.
Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).
Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:
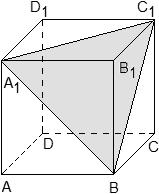
Задача. В кубе ABCDA1B1C1D1 проведено сечение A1BC1. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.
Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A1, B и C1, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.
Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;
Аналогично, для точек B = (1; 0; 0) и C1 = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;
Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.
Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).
Задача. В кубе ABCDA1B1C1D1 проведено сечение AA1C1C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.
В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A1 и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.
Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;
Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;
Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).
Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.
Координаты середины отрезка
Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.
Итак, пусть отрезок задан своими концами — точками A = (xa; ya; za) и B = (xb; yb; zb). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:
Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.
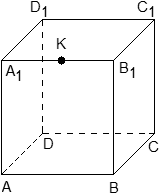
Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A1B1. Найдите координаты этой точки.
Поскольку точка K — середина отрезка A1B1, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A1 = (0; 0; 1) и B1 = (1; 0; 1). Теперь найдем координаты точки K:
Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A1B1C1D1.
Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A1L = C1L, т.е. точка L — это середина отрезка A1C1. Но A1 = (0; 0; 1), C1 = (1; 1; 1), поэтому имеем:
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
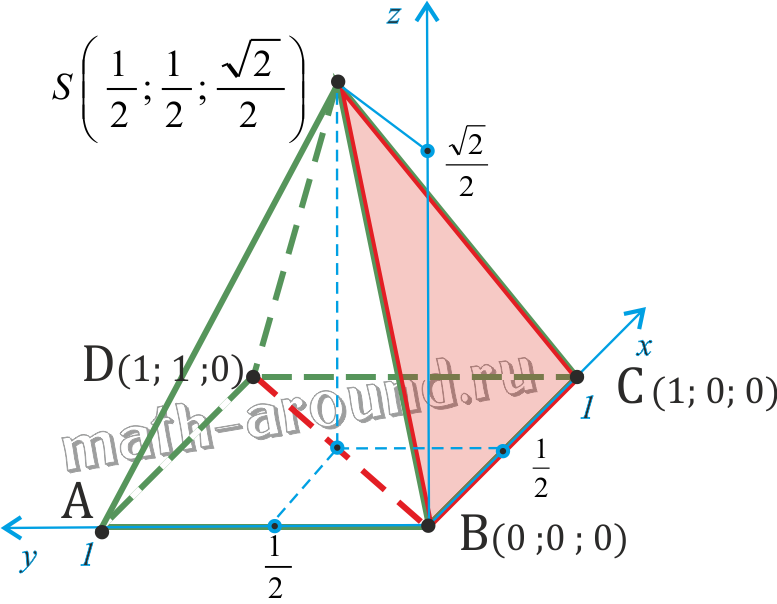
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Геометрия
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Понятие вектора в пространстве
Напомним, что в курсе планиметрии мы уже подробно изучали вектора и действия с ними. При этом предполагалось, что все вектора располагаются в одной плоскости. Однако можно расширить понятие вектора так, чтобы они использовались и в стереометрии. В таком случае вектора уже могут располагаться в различных плоскостях.
Начнем с определения вектора:
Конец вектора обозначают с помощью стрелки. Посмотрим на рисунок:
Здесь показаны сразу три вектора:
У вектора АВ начало находится в точке А, а конец – в точке В. Аналогично у вектора С D точка С – это начало, а D – это конец. В обоих случаях начало и конец – это различные точки, поэтому АВ и CD именуют ненулевыми векторами. Если же начало и конец находятся в одной точке, например в Т, то получается нулевой вектор ТТ. Всякую точку в пространстве можно рассматривать как нулевой вектор:
Длина вектора АВ – это длина соответствующего ему отрезка АВ. Для обозначения длины используют квадратные скобки:
Естественно, что нулевой вектор имеет нулевую длину.
Далее напомним понятие коллинеарных векторов:
Коллинеарные вектора могут быть либо сонаправленными, либо противоположно направленными. Сонаправленные вектора находятся на сонаправленных лучах. Рассмотрим пример с кубом:
Здесь показаны вектора AD и ВС. Они сонаправленные, этот факт записывается так:
Вектора AD и FE располагаются на скрещивающихся прямых, поэтому они не коллинеарны. Их нельзя считать ни сонаправленными, ни противоположно направленными.
Сонаправленные вектора, имеющие одинаковую длину, именуются равными.
Рассмотрим несколько простейших задач.
Задание. В прямоугольном параллелепипеде АВС DA 1 B 1 C 1 D 1 известны три его измерения:
Решение. Для нахождения длин этих векторов достаточно вычислить длину отрезков СВ, DB и DB 1. Проще всего вычислить СВ, ведь отрезки СВ и AD одинаковы как стороны прямоугольника АВ CD :
Задание. На рисунке показан правильный тетраэдр АВС D . Точки M , N , P и Q являются серединами тех сторон, на которых они располагаются. Какие вектора из отмеченных на рисунке равны между собой?
Решение. Легко заметить, что вектора DP и PC находятся на одной прямой DC и сонаправлены, при этом их длина одинакова, ведь Р – середина DC . Тогда эти вектора по определению равны:
Вектора АМ и МВ также коллинеарны и имеют одинаковую длину, но они противоположно направлены, а потому равными не являются.
Теперь заметим, что отрезки MN , MQ , PQ и NP – это средние линии в ∆ ABD , ∆ АВС, ∆ BCD и ∆ ACD соответственно. По свойству средней линии получаем, что MN || BD , PQ || BD , MQ ||АС и NP ||АС. Отсюда по свойству транзитивности параллельности получаем, что MN || PQ и MQ || NP . Это значит, что четырехугольник MQPN – это параллелограмм, а у него противоположные стороны одинаковы:
Операции над векторами
Правила сложения векторов в стереометрии не отличаются от правил в планиметрии. Пусть надо сложить два вектора, а и b . Для этого отложим вектор а от какой-нибудь точки А, тогда его конец окажется в некоторой точке В. Далее от В отложим вектор b , его конец попадет в какую-то точку С. Тогда вектор АС как раз и будет суммой a и b :
Такой метод сложения векторов именуется правилом треугольника. Если нужно сложить больше двух векторов, то используют правило многоугольника. В этом случае необходимо каждый следующий вектор откладывать от конца предыдущего. При этом в стереометрии вектора могут располагаться в различных плоскостях, то есть они на самом деле многоугольник не образуют:
Напомним, что в планиметрии существовали так называемые противоположные вектора. Есть они и в стереометрии:
Главное свойство противоположных векторов заключается в том, что в сумме они дают нулевой вектор:
Заметим, что для получения противоположного вектора достаточно поменять его начало и конец, то есть в записи вектора обозначающие его буквы надо просто записать в обратном порядке:
C помощью противоположного вектора легко определить операцию вычитания векторов. Чтобы из вектора а вычесть вектор b , надо всего лишь прибавить к a вектор, противоположный b :
Далее рассмотрим умножение вектора на число. Пусть вектор а умножается на число k . В результате получается новый вектор b , причем
1) b и a будут коллинеарными векторами;
2) b будет в k раз длиннее, чем вектор a .
Если k – положительное число, то вектора a и b будут сонаправленными. Если же k a и b будут направлены противоположно.
Уточним, что если | k | b будет не длиннее, а короче вектора a . Наконец, если k = 0, то и b будет иметь нулевую длину, то есть b окажется нулевым вектором.
Задание. Дан параллелепипед АВС D А1В1С1 D 1. Постройте вектор, который будет являться суммой векторов:
Решение. В каждом случае необходимо заменить один из векторов в сумме на другой равный ему вектор так, чтобы можно было применить правило треугольника.
В задании а) вектор А1 D 1 заменить равным ему вектором ВС. В итоге получится вектор АС.
В задании б) заменяем А D 1 на вектор ВС1. Также можно было бы заменить АВ на D 1 C 1. В обоих случаях сумма окажется равной АС1.
В задании в) удобно DA заменить на C 1В1, тогда искомой суммой будет вектор С1В.
В задании г) производим замену DD 1 на равный ему вектор BB 1. Тогда сумма DB и BB 1– это вектор DB 1.
В задании д) необходимо заменить ВС на В1С1. В итоге получаем вектор DC :
Задание. В пространстве отмечены точки А, В, С и D . Выразите вектор АВ через вектора:
Решение. В случае а) сначала запишем очевидное равенство векторов, вытекающее из правило многоугольника:
Обратите внимание, что здесь у каждого следующего слагаемого начальная точка совпадает с конечной точкой предыдущего слагаемого, поэтому равенство и справедливо:
Однако по условию а) нам надо использовать другие вектора для выражения АВ. Мы можем просто заменить вектора CD и DB на противоположные:
Теперь можно составить и выражение для АВ:
Аналогично решаем и задания б) и в):
Задание. Р – вершина правильной шестиугольной пирамиды. Докажите, что сумма векторов, совпадающих с ребрами этой пирамиды и начинающихся в точке Р, в точности равна сумме векторов, которые совпадают с апофемами пирамиды и при этом также начинаются в точке Р.
Решение. Обозначим вершины буквами А1, А2, … А6, а середины сторон шестиугольника, лежащего в основании, буквами Н1, Н2, … Н6, как это показано на рисунке:
Нам надо показать, что сумма красных векторов равна сумме черных векторов:
Теперь отдельно построим правильный шестиугольник, лежащий, в основании пирамиды:
Ясно, что вектора, образованные сторонами этого шестиугольника, в сумме дают нулевой вектор (по правилу многоугольника):
Так как точки Н1, Н2, … Н6 – середины сторона, то вектора Н6А6, Н5А5,…Н1А1 будут вдвое короче векторов А1А6, А6А5, … А2А1. При этом они находятся на одних прямых, поэтому справедливы равенства:
Таким образом нам удалось из верного равенства (3) доказать (2), из которого в свою очередь следует справедливость и (1), ч. т. д.
Задание. Упростите выражения:
Решение. Здесь надо просто применить законы сложения и умножения векторов, как это делалось и в курсе планиметрии. Сначала раскрываем скобки, а потом приводим подобные слагаемые:
Компланарные векторы
Если мы отложим несколько векторов от одной точки, то они либо будут находиться в одной плос-ти, либо располагаться в различных плос-тях. В первом случае их именуют компланарными векторами, а во втором – некомпланарными.
Любые два вектора будут компланарны, ведь при их откладывании от одной точки мы получаем две пересекающихся прямых, а через них всегда можно провести плос-ть. Однако если векторов более двух, то они могут быть как компланарны, так и некомпланарны.
Рассмотрим для примера параллелепипед:
Здесь вектора АС, АВ и АD компланарны, так как все они принадлежат одной грани (то есть плос-ти) АВСD. А вектора АВ, АD и АА1 некомпланарны, ведь через них нельзя провести одну плос-ть.
Очевидно, что если из трех векторов любые два коллинеарны, то вся тройка векторов компланарна, ведь при откладывании векторов от одной точки коллинеарные вектора окажутся на одной прямой.
Существует признак компланарности векторов:
Напомним, что подразумевается под разложением вектора. Пусть есть вектора а, b и c. Если существуют такие числах и y, при которых выполняется равенство
то говорят, что вектор с разложен по векторам а и b, причем числа xи y называются коэффициентами разложения.
Докажем сформулированный признак. Пусть есть три вектора а, b и c, а также числа xи y, такие, что
Эти вектора находятся в одной плос-ти ОАВ. Теперь от той же точки О отложим вектора ха и уb, концы которых окажутся в точках А1 и В1:
Естественно, что вектора ОА1 и ОВ1 также окажутся в плос-ти ОАВ. Тогда и их сумма будет принадлежать этой плос-ти, а эта сумма как раз и есть вектор с:
В итоге получили, что а, b и с располагаются в одной плос-ти, то есть они компланарны.
Справедливо и обратное утверждение. Если вектора а, b и с компланарны, но а и b неколлинеарны, то вектор с можно разложить на вектора a и b. Это утверждение прямо следует из изученной в 9 классе теоремы о разложении векторов. Важно отметить, что коэффициенты такого разложения определяются однозначно.
Для сложения тройки некомпланарных векторов можно применить так называемое правило параллелепипеда. Если есть три некомпланарных вектора, то можно отложить их от одной точки О и далее построить параллелепипед, в котором эти вектора будут ребрами. Тогда диагональ этого параллелепипеда, выходящая из точки О, и будет суммой этих трех векторов:
Разложение вектора на некомпланарные вектора
Иногда вектор можно разложить не на два, а на три вектора. Выглядит такое разложение так:
Для доказательства рассмотрим три некомпланарных вектора а, bи c, а также произвольный вектор р. Отложим их от одной точки О. Обозначим концы этих векторов большими буквами А, В, С и Р:
Через ОВ и ОА можно провести некоторую плос-ть α. Точка С ей принадлежать не может, ведь ОА, ОВ и ОС – некомпланарные вектора. Проведем через Р прямую, параллельную ОС. Так как ОС пересекает α, то и параллельная ей прямая также пересечет α в некоторой точке Р1. (Примечание. Если Р принадлежит α, то точки Р и Р1 совпадут, то есть вектор Р1Р будет нулевым).
Далее через точку Р1 в плос-ти α проведем прямую, параллельную ОВ, которая пересечет ОА в точке Р2. Заметим, что вектор ОР2 находится на той же прямой, что и вектор ОА, то есть они коллинеарны, поэтому существует такое число х, что
Итак, мы показали, что у произвольного вектора p есть разложение на заранее заданные некомпланарные вектора. Осталось показать, что существует только одно такое разложение. Докажем это методом от противного. Пусть есть второе разложение с другими коэффициентами х1, у1 и z1:
В правой части находятся три вектора, которые в сумме нулевой вектор. По правилу сложения векторов это означает, что эти вектора образуют треугольник, то есть находятся в одной плос-ти:
Значит, они компланарны. Тогда компланарны и вектора a, b и с, что противоречит условию теоремы. Значит, второго разложения р на заданные некомпланарные векторы не существует, ч. т. д.
Задание. АВСD и А1В1С1D1 – параллелограммы, располагающиеся в разных плос-тях. Докажите, что тройка векторов ВВ1, СС1 и DD1 компланарна.
Решение. Сначала построим рисунок по условию задачи:
Для доказательства используем признак компланарности векторов. Для этого надо один из векторов, отмеченных на рисунке красным, разложить на два других вектора.
В результате нам удалось разложить СС1 на вектора BB1 и CC1. Значит, эти три вектора коллинеарны.
Задание. В параллелепипеде АВСDA1B1C1D1 запишите разложение вектора BD1 по векторам ВА, ВС и ВВ1.
Решение. Сначала представим вектор BD1 как сумму трех векторов:
Теперь заметим, что вектора С1D1 и ВА соответствуют ребрам параллелепипеда. Эти ребра одинаковы по длине и параллельны, поэтому и вектора будут равными. Аналогично равны вектора СС1 и ВВ1:
Задание. АВСD – тетраэдр, а точка К делит его ребро ВС пополам. Разложите вектор DK по векторам DA, AB и AC.
Решение. Сначала запишем очевидное выражение для вектора DK:
Задание. В точке М пересекаются медианы треугольника АВС, а О – произвольная точка в пространстве. Разложите вектор ОМ по векторам ОА, ОВ и ОС.
Решение. Медиану, проходящую через точку А, мы обозначим как АА1, то есть А1 – это середина отрезка ВС. Также буквой К обозначим середину ОВ:
Сначала разложим вектор ОА1 на ОВ и ОС. Это можно сделать, ведь они компланарны. КА1 – это средняя линия ∆ОСВ, поэтому КА1||ОС и КА1 вдвое короче ОС. Это значит, что
Так как АА1 – медиана, то точка М делит ее в отношении 2:1. Отсюда вытекает следующее соотношение:
Только что решенная задача может быть использована и при решении другого, более сложного задания.
Задание. Докажите, что в параллелепипеде АВСDА1В1С1D1 плос-ти А1ВD и СB1D1 делят диагональ АС1 на три равных отрезка.
Решение. Обозначим точкой K точку пересечения медиан ∆А1ВD. Тогда по формуле, выведенной в предыдущей задаче, мы получаем, что
Это соотношение означает, что вектора АК и АС1 коллинеарны, поэтому они располагаются на одной прямой (они не могут находиться на параллельных прямых, ведь у них есть общая точка А). Значит, точка K принадлежит диагонали АС1, и отрезок АК втрое короче диагонали.
Аналогично можно показать, что и
Из этого также вытекает, что М принадлежит диагонали АС1, и МС1 втрое короче АС1. Значит, точки М и К делят диагональ на три равных отрезка, ч. т. д.
Сегодня мы расширили понятие векторов и научились их применять не только в планиметрических, но и в стереометрических задачах. При сохраняются все правила, по которым выполняются действия над векторами. Также в стереометрии появляется новое понятие компланарных и некомпланарых векторов.
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
http://100urokov.ru/predmety/vektora-v-prostranstve
Нахождение угла между прямой и плоскостью.
Давайте повторим определение угла между прямой и плоскостью.
Определение. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
Пусть даны плоскость γ и прямая a, которая пересекает эту плоскость и не перпендикулярна к ней.
Построим угол между прямой a и плоскостью γ:
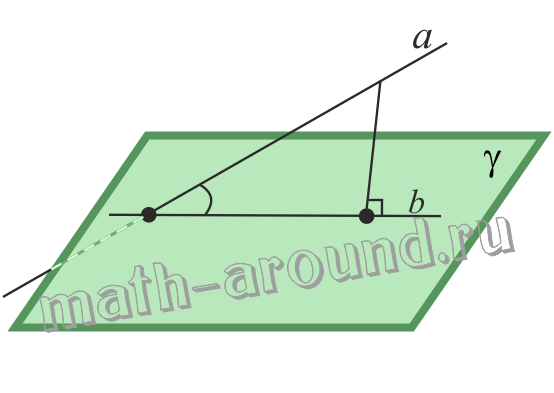
- Из любой удобной для нас точки прямой a опустим перпендикуляр к плоскости γ;
- Через точки оснований наклонной и перпендикуляра проведем прямую b . Прямая b — проекция прямой a на плоскость γ;
- Острый угол между прямыми a и b – это угол между прямой a и плоскостью γ, т.е. ∠(a;b)= ∠(a;γ) , где ∠(a;b) — угол между прямыми а и b; ∠(a;γ) — угол между прямой а и плоскостью γ.
Для решения задач с помощью метода координат нам необходимо вспомнить следующее:
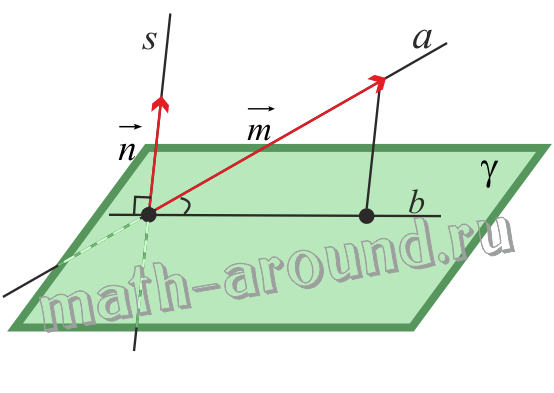
3. Если известны координаты направляющего вектора { a1; b1; c1} и вектора нормали
{a; b; c}, то угол между прямой а и плоскостью γ вычисляется по формуле, которую сейчас выведем.
Нам известна формула нахождения угла между прямыми:
; (1)
∠(s; a) = 90°-∠(a;b), тогда cos∠(s;a)=cos (90°-∠(a;b))=sin ∠(a;b) ; (2)
Из (1) и (2) => ; (3)
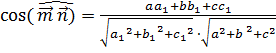
– угол между векторами m и n; (4)
Подставляем (4) в (3) и т.к. ∠(a;b)= ∠(a;γ), то получаем:
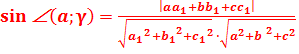
4. Если координаты вектора нормали неизвестны, то нам необходимо знать уравнение плоскости.
Любая плоскость в прямоугольной системе координат может быть задана уравнением
ax + by + cz + d = 0,
где хотя бы один из коэффициентов a, b, c отличен от нуля. Эти коэффициенты и будут координатами вектора нормали, т.е. {a; b; c}.
Алгоритм решения задач на нахождение угла между прямой и плоскостью с помощью метода координат:
- Делаем рисунок, на котором отмечаем прямую и плоскость;
- Вводим прямоугольную систему координат ;
- Находим координаты направляющего вектора по координатам его начала и конца ;
- Находим координаты вектора нормали к плоскости;
- Подставляем полученные данные в формулу синуса угла между прямой и плоскостью;
- Находим значение самого угла.
Рассмотрим задачу:
1. В кубе ABCDA1B1C1D1 найдите тангенс угла между прямой AC1 и плоскостью BDD1 .
Решение:
1. Введем прямоугольную систему координат с началом координат в точке D.
2. Найдем координаты направляющего вектора АС1. Для этого сначала определим координаты точек А и С1:
А(0; 1; 0);
С1(1; 0; 1).
{1; -1; 1}.
3. Найдем координаты вектора нормали к плоскости BB1D1. Для этого найдем координаты трех точек плоскости, не лежащих на одной прямой, и составим уравнение плоскости:
D(0; 0; 0);
D1(0; 0; 1);
В(1; 1; 0);
Уравнение плоскости имеет вид ax+by+cz+d=0. Подставим в это уравнение координаты точек:
D: a⋅0+b⋅0+c⋅0+d=0;
D1: a⋅0+b⋅0+c⋅1+d=0;
B: a⋅1+b⋅1+c⋅0+d=0.
Получили систему из трех уравнений:
Подставим в уравнение: a⋅x+(-a)⋅y+0⋅z+0 = 0;
a⋅x-a⋅y = 0; |:a
x-y = 0.
Т.о., вектор нормали к плоскости BDD1 имеет координаты:
{1;-1; 0}.
4. Найдем синус между прямой АС1 и плоскостью BDD1:
5. Воспользуемся основным тригонометрическим тождеством и найдем косинус угла между прямой АС1 и плоскостью BDD1:
6. Найдем тангенс угла между прямой АС1 и плоскостью BDD1:
;
.
Ответ: .
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между прямой BD и плоскостью SBC.
Решение:
1. Введем прямоугольную систему координат с началом координат в точке B.
2. Найдем координаты направляющего вектора BD. Для этого сначала определим координаты точек B и D:
3. Найдем координаты вектора нормали к плоскости SBC. Для этого найдем координаты трех точек плоскости, не лежащих на одной прямой, и составим уравнение плоскости SBC:
Как получили координаты точки S ?
Из точки S опустили перпендикуляр к плоскости основания ABC. Точку пересечения обозначили О. Точка О — проекция точки S на плоскость ABC. Ее координаты по осям х и у будут первыми двумя координатами точки S.
Узнав значение высоты пирамиды, мы нашли третью координату точки S (по оси z)
Треугольник SOB — прямоугольный, следовательно, по теореме Пифагора:
Уравнение плоскости имеет вид ax+by+cz+d=0. Подставим в это уравнение координаты точек:
Получили систему из трех уравнений:
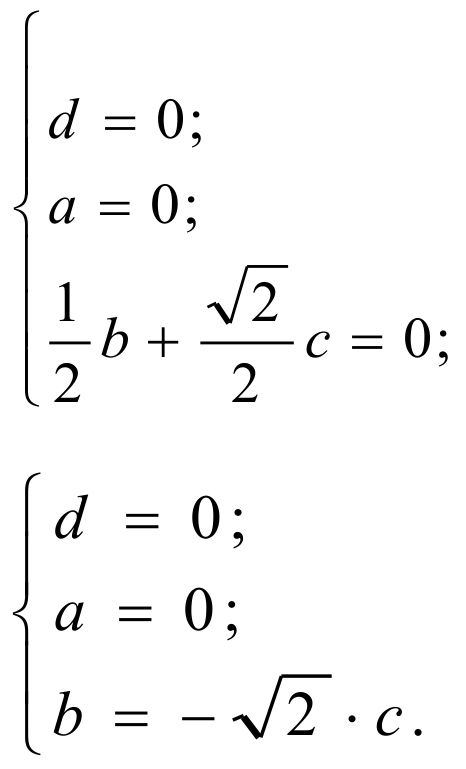
Подставим в уравнение:
Т.о., вектор нормали к плоскости SBD имеет координаты:
.
4. Найдем синус между прямой BD и плоскостью SBD:
Ответ: .
Если Вам понравилась информация и появилось желание поддержать нас, Вы можете:
- отправить денежный перевод с карты на карту мгновенно и без комиссий по ссылке . Ссылка на перевод . В поле «Добавьте комментарий» необходимо указать «в дар» или «подарок».
- оставить комментарий ниже.
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
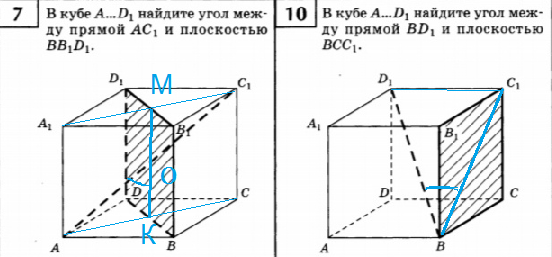
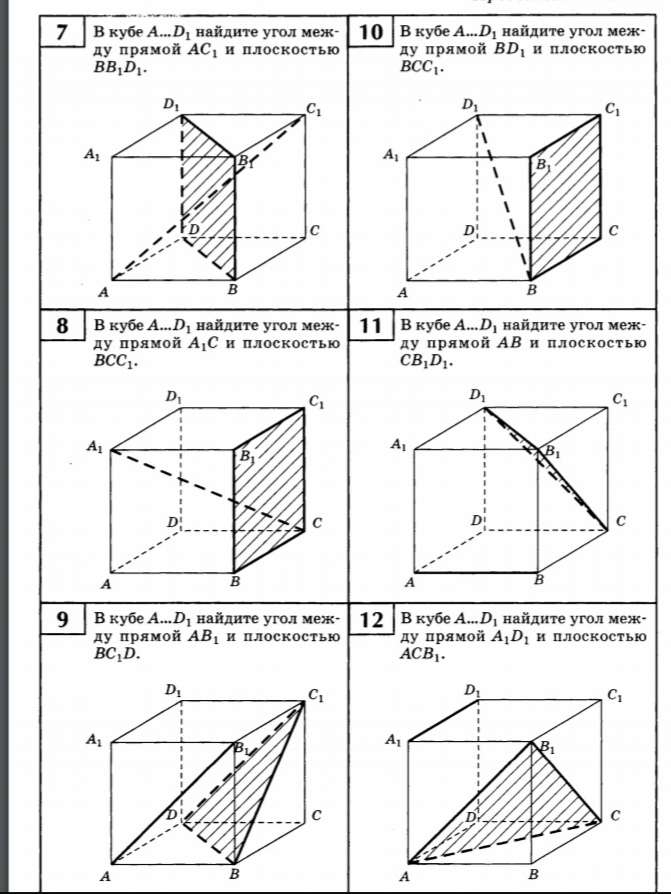
7. В кубе А…D1, найдите угол между прямой АС1, и плоскостью BB1D1
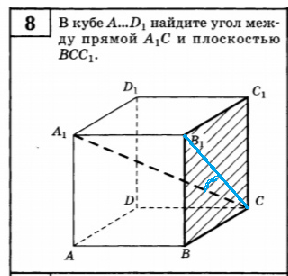
8. В кубе A…D1, найдите угол между прямой А1С и плоскостью BCC1.
9. В кубе А…D1, найдите угол между прямой АВ1, и плоскостью BC1D
10. В кубе А…D1, найдите угол между прямой BD1 и плоскостью ВСС1.
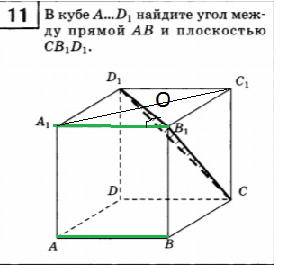
11. В кубе А…D1, найдите угол между прямой АВ и плоскостью СВ1D1.
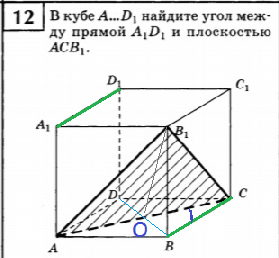
12. В кубе А…D1, найдите угол между прямой А1D1 и плоскостью АСВ1.
математика 10-11 класс
34191
★
7.
Угол между прямой и плоскостью — угол между прямой и ее проекцией на плоскость.
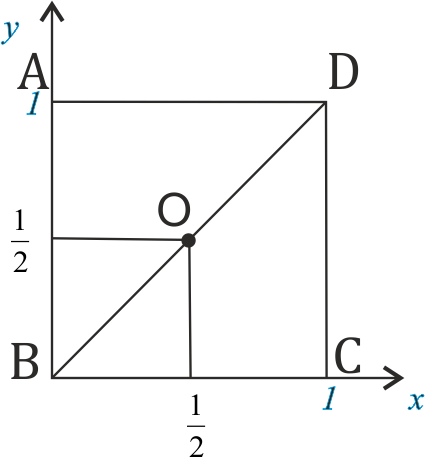
Проводим A_(1)C_(1) ⊥ B_(1)D_(1)
и АС ⊥ BD
Проекцией АС_(1) является MK
Угол АОК — искомый, находим из треугольника AOK
[b]tg ∠ AOK[/b]=AK/OK=sqrt(2)/2/1/2= [b]sqrt(2)[/b]
АК=AC/2=sqrt(2)/2
ОК=(1/2)МК=1/2
О т в е т. ∠ AOK= arctg(sqrt(2))
10.
Угол между прямой и плоскостью — угол между прямой и ее проекцией на плоскость.
Проекцией BD_(1) является BС_(1).
Угол C_(1)BD_(1) — искомый, находим из треугольника C_(1)BD_(1)
tg ∠ C_(1)BD_(1)=C_(1)D_(1)/BC_(1)=1/sqrt(2)=sqrt(2)/2
∠ C_(1)BD_(1)=arctg (sqrt(2)/2)
О т в е т. ∠ C_(1)BD_(1)=arctg (sqrt(2)/2)
8.
Угол между прямой и плоскостью — угол между прямой и ее проекцией на плоскость.
Проекцией A_(1)C является B_(1)C.
Угол A_(1)BC_(1) — искомый, находим из треугольника A_(1)BC_(1)
tg ∠ A_(1)BC_(1)=A_(1)B_(1)/B_(1)C=1/sqrt(2)=sqrt(2)/2
∠∠ A_(1)BC_(1)=arctg (sqrt(2)/2)
О т в е т. ∠ A_(1)BC_(1)=arctg (sqrt(2)/2)
12.
BD ⊥ AC
AC⊥ BO
B_(1)O — медиана равнобедренного треугольника АВ_(1)С
Значит, B_(1)O⊥ AC
АС ⊥ пл. В_(1)ОВ, так как перпендикулярна двум пересекающимся прямым этой плоскости BO и B_(1)O.
пл. АВ_(1)С ⊥ пл. В_(1)ОВ
⇒ ОС- проекция ВС,
угол между ОС и ВС — это угол АСВ он равен 45 градусов
ВС || A_(1)D_(1)
Значит угол между A_(1)D_(1) и пл. АВ_(1)С равен 45 градусов
11.
Как в 12.
∠ А_(1)В_(1)О= 45 градусов.
9. AB_(1)|| DС_(1)
AB_(1) || пл. DС_(1)B
Значит угол между ними 0 градусов.
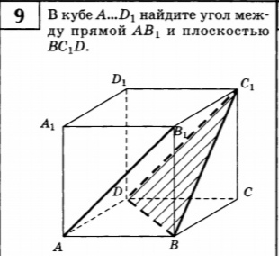
а) Примем ребро куба за а.
Сечение куба плоскостью, проходящей через точки A,B и C1, представляет собой прямоугольник с одной стороной, равной а, и другой, равной а√2.
б) АС1 — это диагональ куба. Её длина равна √(а²+а²+а²) = а√3.
Угол между прямой AC1 и плоскостью BCC1 — это угол АС1В.
sin(AC1B) = a/(a√3) = 1/√3 ≈
0.57735.
Этому синусу соответствует угол
0,61548 радиан или 35,26439°.