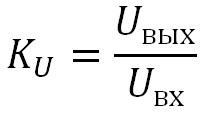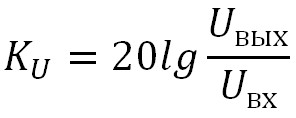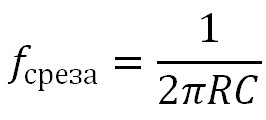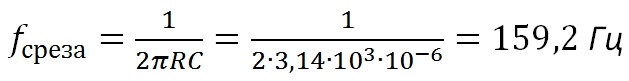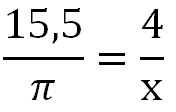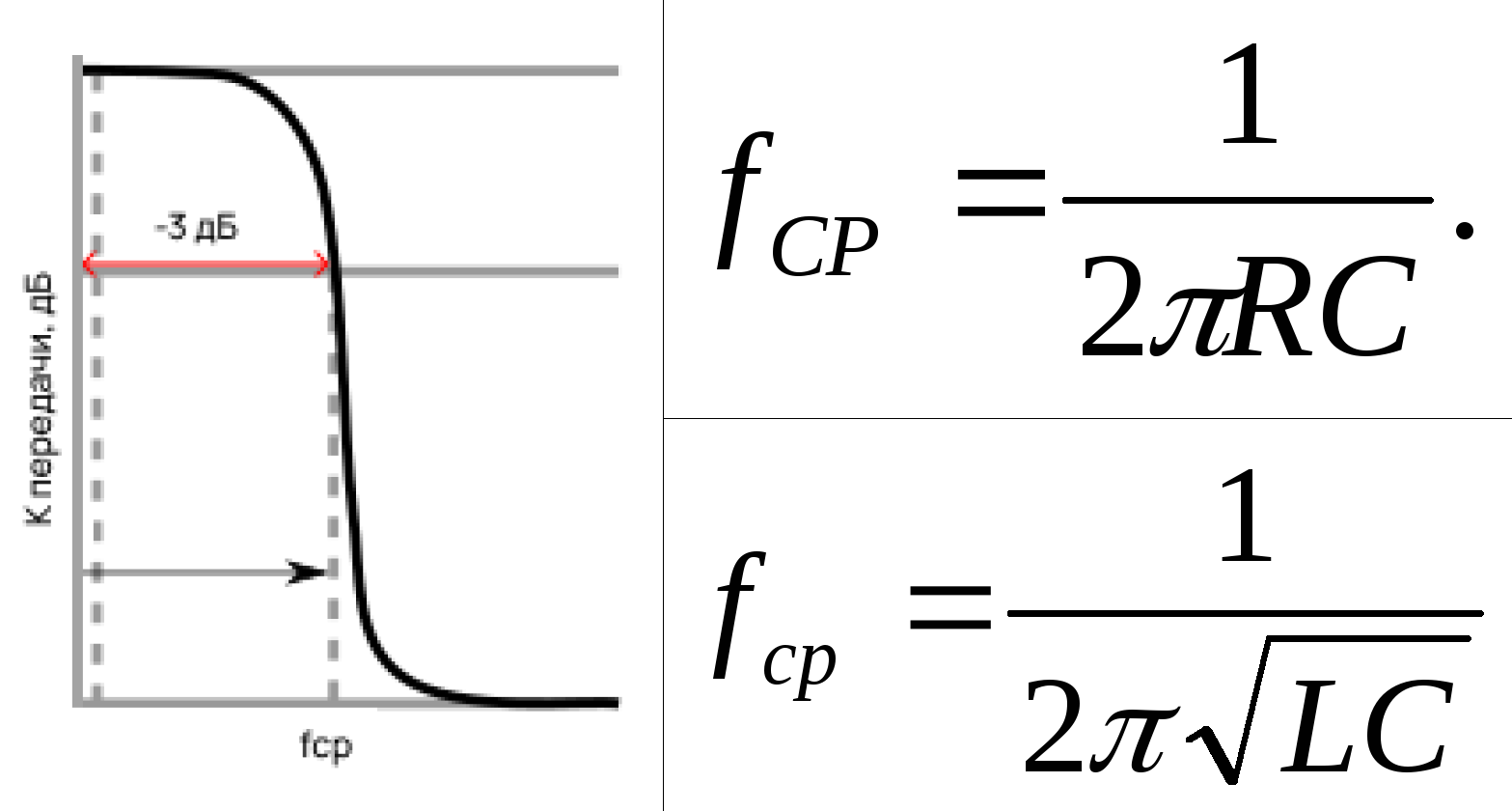Как найти ачх фильтра

Амплитудно-частотная характеристика

Аббревиатура АЧХ расшифровывается как амплитудно-частотная характеристика. На английском этот термин звучит как «frequency response», что в дословном переводе означает «частотный отклик». Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства. АЧХ может быть определена аналитически через формулы, либо экспериментально. Любое устройство предназначено для передачи (или усиления) электрических сигналов.  АЧХ устройства определяется по зависимости  коэффициента передачи (или коэффициента усиления) от частоты.

Коэффициент передачи

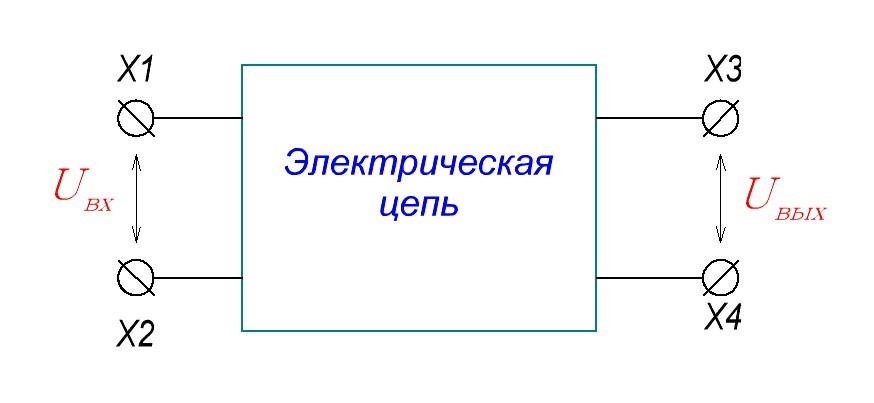
Что такое коэффициент передачи? Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Или формулой:

где

U_вых   — напряжение на выходе цепи

U_вх  — напряжение на входе цепи

В усилительных устройствах коэффициент передачи больше единицы. Если устройство вносит ослабление передаваемого сигнала, то коэффициент передачи меньше единицы.

Коэффициент передачи может быть выражен через децибелы:

Строим АЧХ RC-цепи в программе Proteus

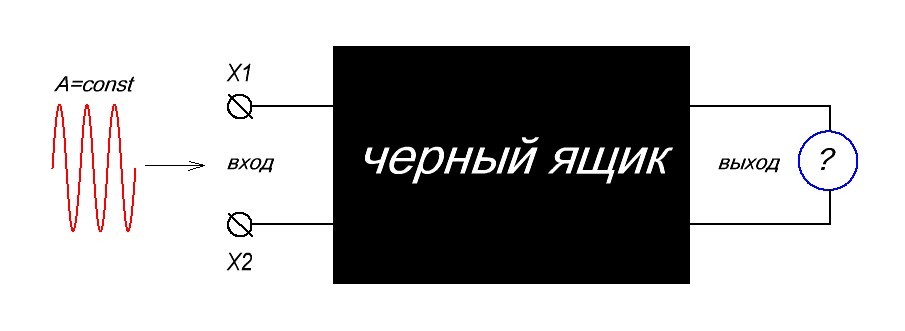
Для того, чтобы досконально разобраться, что такое АЧХ, давайте рассмотрим рисунок ниже.

Итак, имеем «черный ящик», на вход которого мы будем подавать синусоидальный сигнал, а на выходе черного ящика мы будем снимать сигнал. Должно соблюдаться условие: нужно менять частоту входного синусоидального сигнала, но его амплитуда должна быть постоянной.

Что нам  делать дальше? Надо измерить амплитуду сигнала на выходе после черного ящика при интересующих нас значениях частоты входного сигнала. То есть мы должны изменять частоту входного сигнала от 0 Герц (постоянный ток) и до какого-либо конечного значения, которое будет удовлетворять нашим целям, и смотреть, какая амплитуда сигнала будет на выходе при соответствующих значениях на входе.

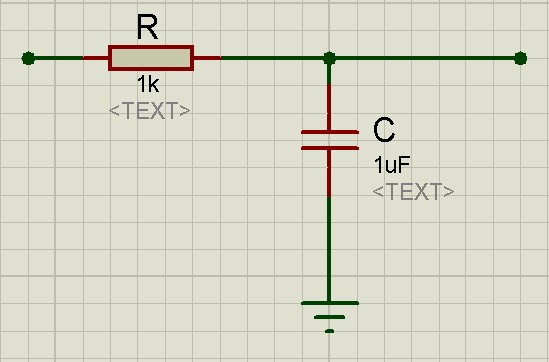
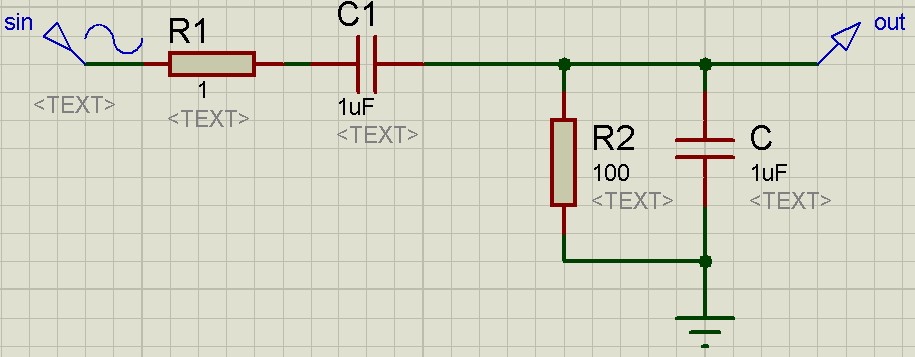
Давайте разберем все это дело на примере. Пусть в черном ящике у нас будет самая простая RC-цепь с уже известными номиналами радиоэлементов.

Как я уже говорил, АЧХ может быть построено экспериментально, а также с помощью программ-симуляторов. На мой взгляд, самый простой и мощный симулятор для новичков — это Proteus. С него и начнем.

Собираем данную схему в рабочем поле программы Proteus

Для того, чтобы подать на вход схемы синусоидальный сигнал, мы кликаем на кнопочку «Генераторы», выбираем SINE, а потом соединяем его со входом нашей схемы.

Для измерения выходного сигнала достаточно кликнуть на значок  с буквой «V»  и соединить выплывающий значок с выходом нашей схемы:

Для эстетики, я уже поменял название входа и выхода на sin и out. Должно получиться как-то вот так:

Ну вот, пол дела уже сделано.

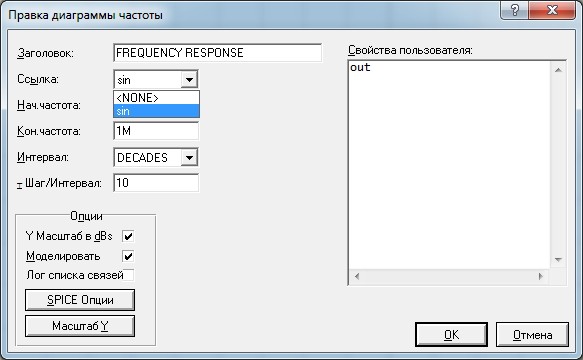
Теперь осталось добавить важный инструмент. Он называется «frequency response», как я уже говорил, в дословном переводе с английского — «частотный отклик». Для этого нажимаем кнопочку «Диаграмма» и в списке выбираем «frequency»

На экране появится что-то типа этого:

Кликаем ЛКМ два раза и открывается вот такое окошко, где в качестве входного сигнала мы выбираем наш генератор синуса (sin), который у нас сейчас задает частоту на входе.

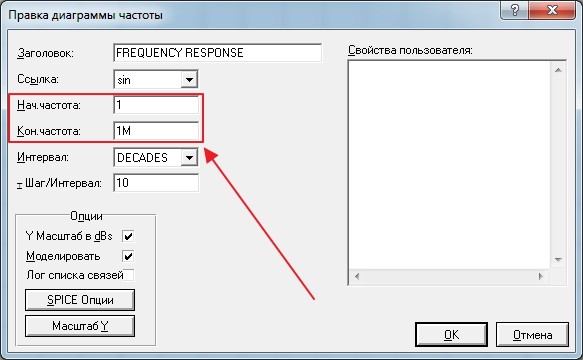
Здесь же выбираем диапазон частоты, который будем «загонять» на вход нашей цепи. В данном случае это диапазон от 1 Гц и до 1 МГц. При установке начальной частоты в 0 Герц Proteus выдает ошибку. Поэтому, ставьте начальную частоту близкую к нулю.

Нажимаем ОК.

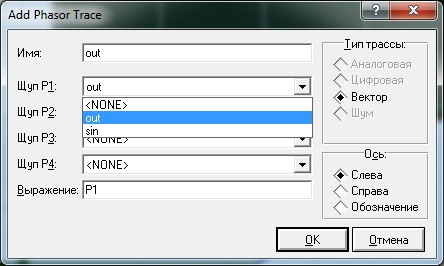
Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»

Долго не думая, выбираем в первом же окошке наш выход out

и в результате должно появится окошко с нашим выходом

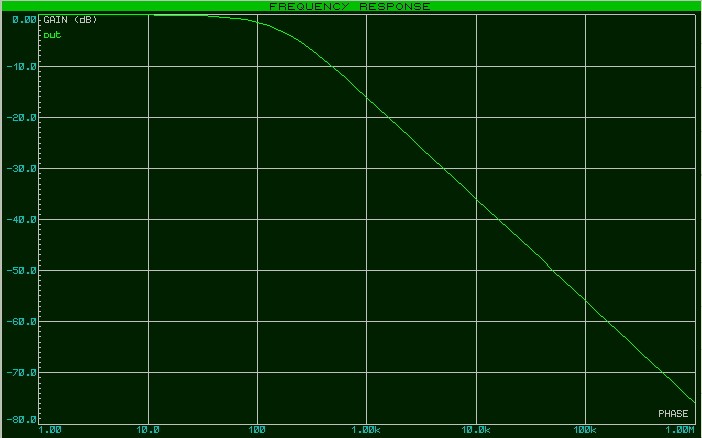
Нажимаем пробел и радуемся результату

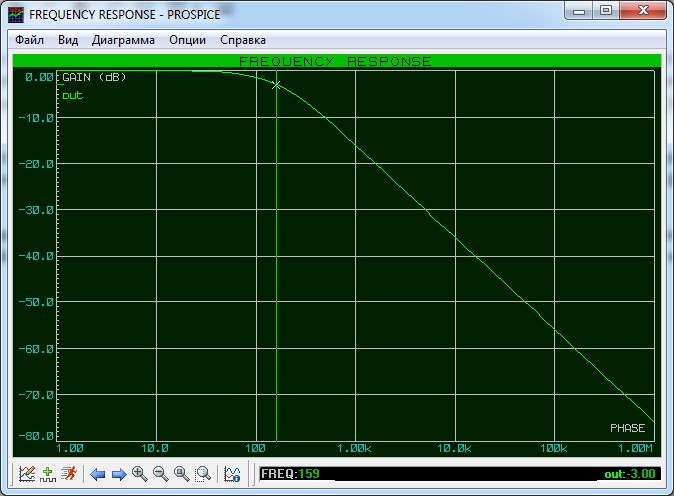
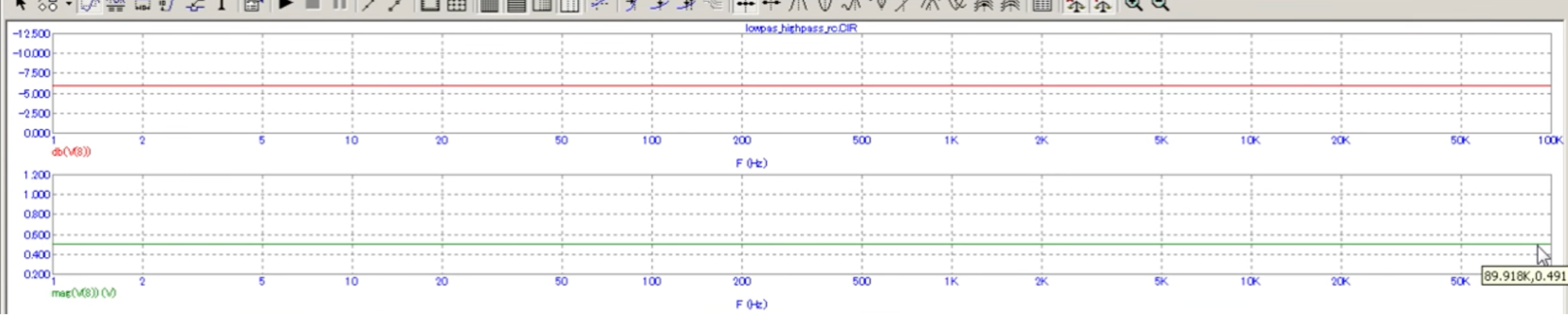
Итак, что интересного можно обнаружить, если взглянуть на нашу АЧХ? Как вы могли заметить, амплитуда на выходе цепи падает с увеличением частоты. Это означает, что наша RC-цепь является своеобразным частотным фильтром. Такой фильтр пропускает низкие частоты, в нашем случае до 100 Герц, а потом с ростом частоты начинает их «давить». И чем больше частота, тем больше он ослабляет амплитуду выходного сигнала. Поэтому, в данном случае, наша  RC-цепь является самым простейшим фильтром низкой частоты (ФНЧ).

Полоса пропускания

В среде радиолюбителей и не только встречается также такой термин, как полоса пропускания. Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы.

Как же определить полосу пропускания? Это сделать довольно легко. Достаточно на графике АЧХ найти уровень в -3 дБ от максимального значения АЧХ и найти точку пересечения прямой с графиком. В нашем случае это можно сделать легче пареной репы. Достаточно развернуть нашу диаграмму на весь экран и с помощью встроенного маркера посмотреть частоту на уровне в -3 дБ в точке пересечения с нашим графиком АЧХ. Как мы видим, она равняется 159 Герц.

Частота, которая получается на уровне в -3 дБ, называется частотой среза. Для RC-цепи ее можно найти по формуле:

Для нашего случая расчетная частота получилась 159,2 Гц, что подтверждает и Proteus.

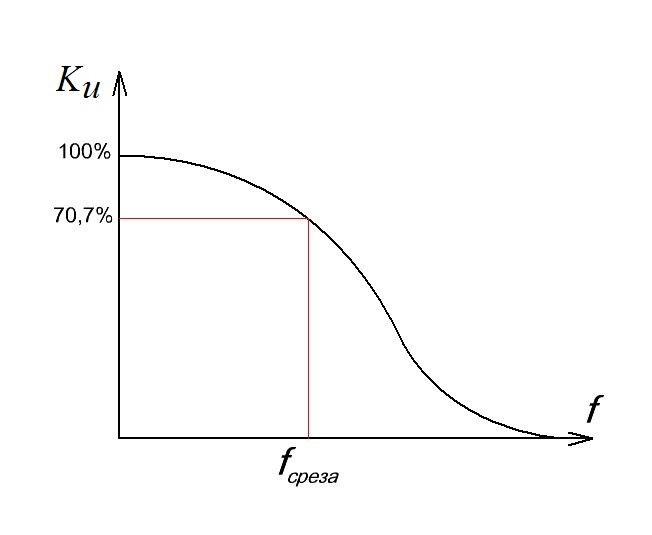
Кто не желает связываться  с децибелами, то можно провести линию на уровне 0,707 от максимальной амплитуды  выходного сигнала и смотреть пересечение с графиком. В данном примере, для наглядности, я взял максимальную амплитуду за уровень в  100%.

Как построить АЧХ на практике?

Как построить АЧХ на практике, имея в своем арсенале генератор частоты и осциллограф?

Итак, поехали. Собираем нашу цепь в реале:

Ну а теперь цепляем ко входу схемы генератор частоты, а с помощью осциллографа следим за амплитудой выходного сигнала, а также будем следить за амплитудой входного сигнала, чтобы мы были точно уверены, что на вход RC-цепи подается синус с постоянной амплитудой.

Для экспериментального изучения АЧХ  нам потребуется собрать простенькую схемку:

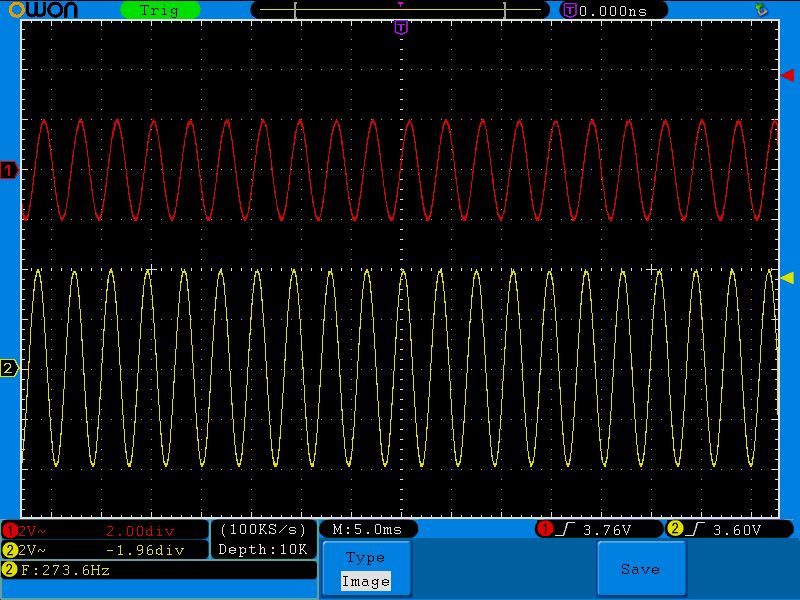
Наша задача состоит в том, чтобы менять частоту генератора и уже наблюдать, что покажет осциллограф на выходе цепи. Мы будем прогонять нашу цепь по частотам, начиная от самой малой. Как я уже сказал, желтый канал предназначен для визуального контроля, что мы честно проводим опыт.

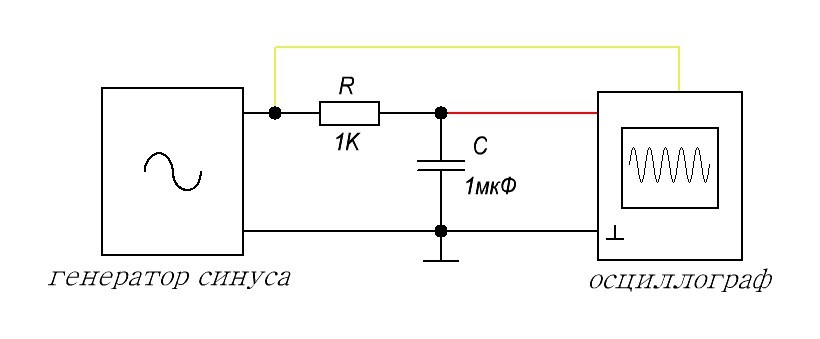
Постоянный ток, проходящий через эту цепь,  на выходе будет давать амплитудное значение входного сигнала, поэтому первая точка будет иметь координаты (0;4), так как амплитуда нашего входного сигнала 4 Вольта.

Следующее значение смотрим на осциллограмме:

Частота 15 Герц, амплитуда на выходе 4 Вольта. Итак, вторая точка (15;4)

Третья точка (72;3.6). Обратите внимание на амплитуду выходного красного сигнала. Она начинает проседать.

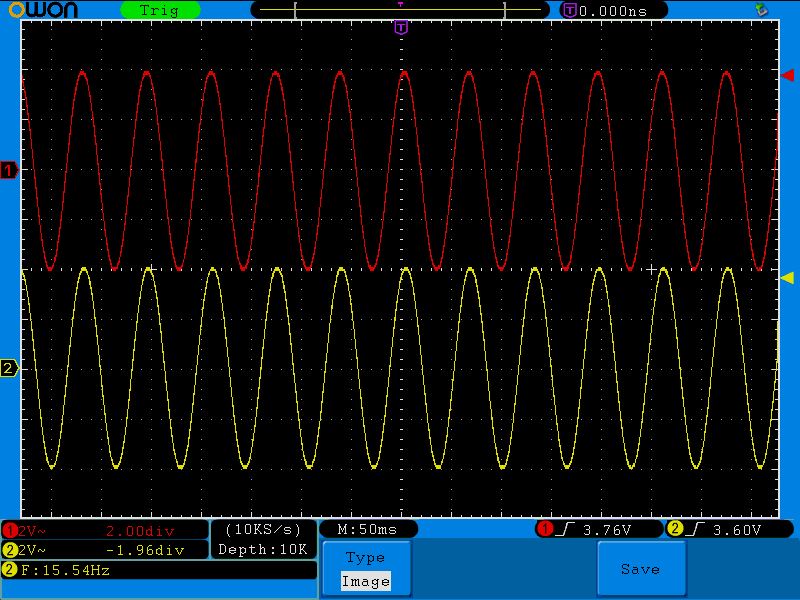
Четвертая точка (109;3.2)

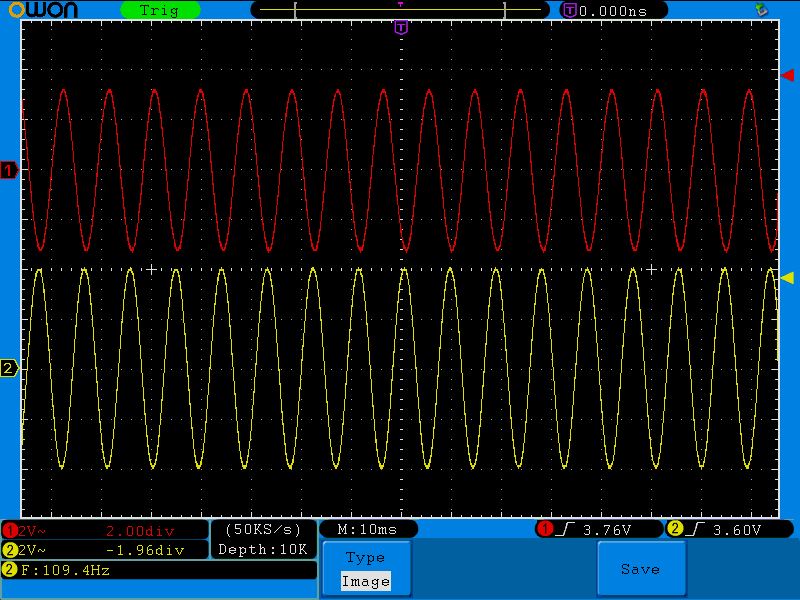
Пятая точка (159;2.8)

Шестая точка (201;2.4)

Седьмая точка (273;2)

Восьмая точка (361;1.6)

Девятая точка (542;1.2)

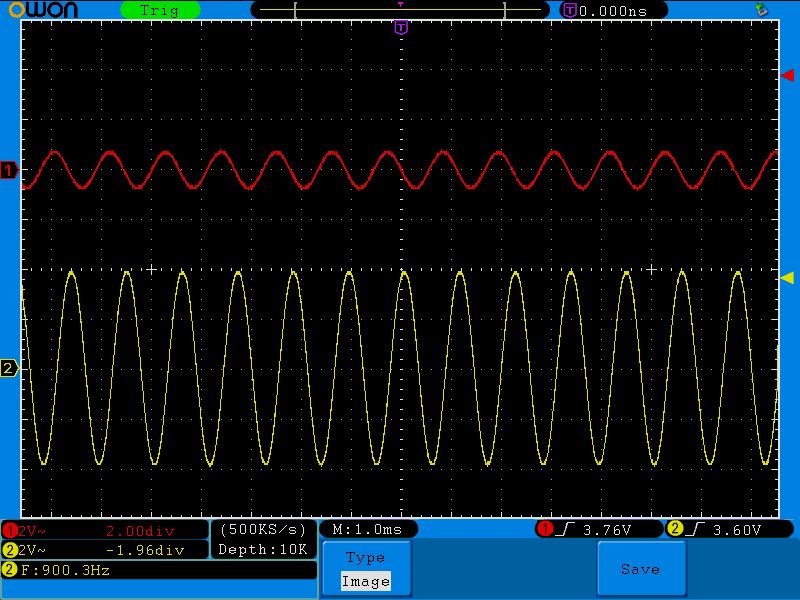
Десятая точка (900;0.8)

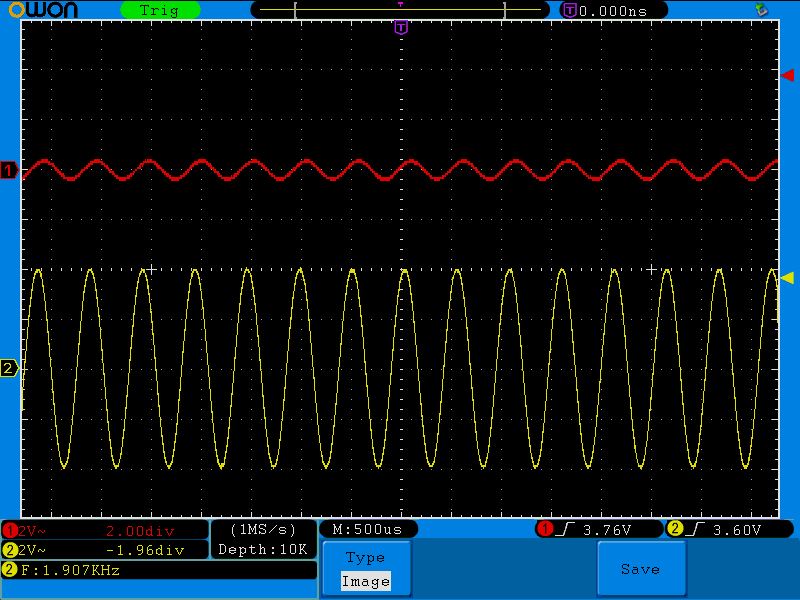
Ну и последняя одиннадцатая точка (1907;0.4)

В результате измерений у нас получилась табличка:

Строим график по полученным значениям и получаем нашу экспериментальную АЧХ 

Получилось не так, как в технической литературе. Оно и понятно, так как по Х берут логарифмический масштаб, а не линейный, как у меня на графике. Как вы видите, амплитуда выходного сигнала будет и дальше понижаться с увеличением частоты. Для того, чтобы еще более точно построить нашу АЧХ, требуется взять как можно больше точек.

Давайте вернемся к этой осциллограмме:

Здесь на частоте среза амплитуда выходного сигнала получилась ровно 2,8 Вольт, которые как раз и находятся на уровне в 0,707. В нашем случае 100% это 4 Вольта. 4х0,707=2,82 Вольта.

АЧХ полосового фильтра

Существуют также схемы, АЧХ которых имеет вид холма или ямы. Давайте рассмотрим один из примеров. Мы будем рассматривать так называемый полосовой фильтр, АЧХ которого имеет вид холма.

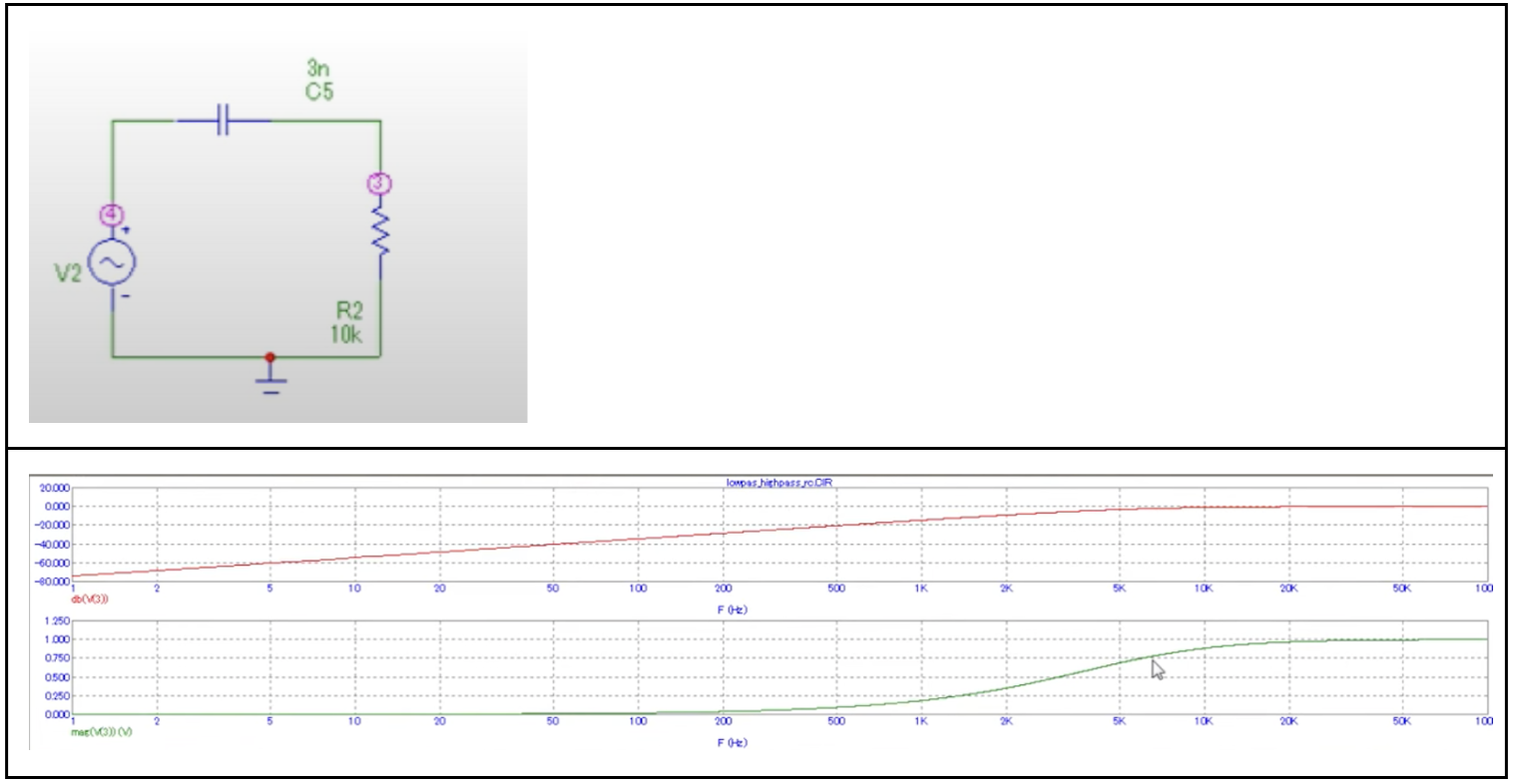
Собственно сама схема:

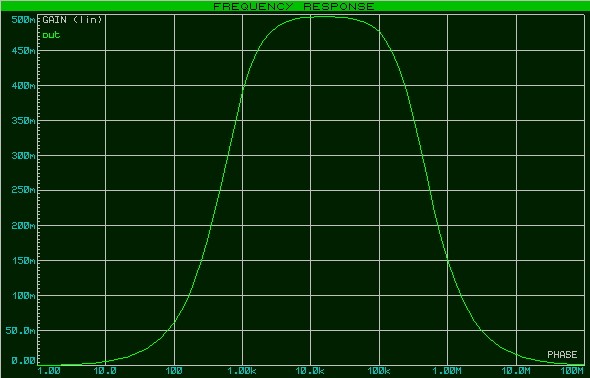
А вот ее АЧХ:

Особенность таких фильтров, что они имеют две частоты среза. Определяются они также на уровне в -3дБ  или на уровне в  0,707 от максимального значения коэффициента передачи, а еще точнее K_{u max}/√2.

Так как в дБ смотреть график неудобно, поэтому я переведу его в линейный режим по оси Y, убирая маркер

В результате перестроения получилась такая АЧХ:

Максимальное значение на выходе составило 498 мВ при амплитуде входного сигнала в 10 Вольт. Мдя, неплохой «усилитель») Итак, находим значение частот на уровне в 0,707х498=352мВ. В результате получились две частоты среза — это частота в 786 Гц и в 320 КГц. Следовательно, полоса пропускания данного фильтра от 786Гц и до 320 КГц.

На практике для получения АЧХ используются приборы, называемые характериографами для исследования АЧХ. Вот так выглядит один из образцов Советского Союза

Фазо-частотная характеристика

ФЧХ расшифровывается как фазо-частотная характеристика, phase response — фазовый отклик. Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.

Разность фаз

Думаю, вы не раз слышали такое выражение, как » у него произошел сдвиг по фазе». Это выражение не так давно пришло в наш лексикон и обозначает оно то, что человек слегка двинулся умом. То есть было все нормально, а потом раз! И все :-). И в электронике такое тоже часто бывает)  Разницу между фазами сигналов в электронике называют разностью фаз. Вроде бы «загоняем» на вход  какой-либо сигнал, а выходной сигнал ни с того ни с сего взял и сдвинулся по времени, относительно входного сигнала.

Для того, чтобы определить разность фаз, должно выполняться условие: частоты сигналов должны быть равны. Пусть даже один сигнал будет с амплитудой в Киловольт, а другой в милливольт. Неважно! Лишь бы соблюдалось равенство частот. Если бы  условие равенства не соблюдалось, то сдвиг фаз между сигналами все время бы изменялся.

Для определения сдвига фаз используют двухканальный осциллограф. Разность фаз чаще всего обозначается буквой φ и на осциллограмме это выглядит примерно так:

Строим ФЧХ RC-цепи в Proteus

Для нашей исследуемой цепи

Для того, чтобы отобразить ее в Proteus мы снова открываем функцию «frequency response»

Все  также выбираем наш генератор

Не забываем проставлять испытуемый диапазон частот:

Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»

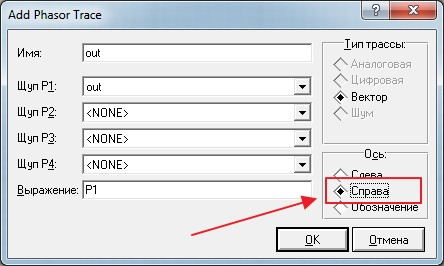
Долго не думая, выбираем в первом же окошке наш выход out

И теперь главное отличие: в колонке «Ось» ставим маркер на «Справа»

Нажимаем пробел и вуаля!

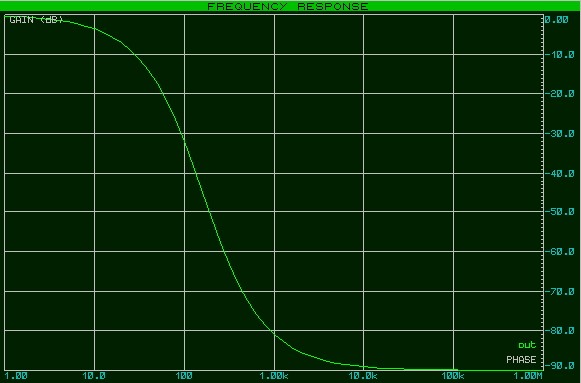
Можно его развернуть на весь экран

При большом желании эти две характеристики можно объединить на одном графике

Обратите внимание, что на частоте среза сдвиг фаз между входным и выходным сигналом составляет 45 градусов или в радианах п/4 (кликните для увеличения)

В данном опыте при частоте более 100 КГц разность фаз достигает значения в 90 градусов (в радианах π/2) и уже не меняется.

Строим ФЧХ на практике

ФЧХ на практике можно измерить также, как и АЧХ, просто наблюдая разность фаз и записывая показания в табличку. В этом опыте мы просто убедимся, что на частоте среза у нас действительно разность фаз между входным и выходным сигналом будет 45 градусов или  π/4 в радианах.

Итак, у меня получилась вот такая осциллограмма на частоте среза в 159,2 Гц

Нам надо узнать разность фаз между этими двумя сигналами

Весь период — это 2п, значит половина периода — это π. На полупериод у нас приходится где-то 15,5 делений. Между двумя сигналами разность в 4 деления. Составляем пропорцию:

Отсюда х=0,258п или можно сказать почти что 1/4п. Следовательно, разница фаз между двумя этими сигналами равняется п/4, что почти в точности совпало с расчетными значениями в Proteus.

Если Вы лучше воспринимаете информацию через видео, то к Вашему вниманию:

Резюме

Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства.

И еще интересная статья — последовательное и параллельное соединение проводников.

Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.

Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Если коэффициент передачи больше единицы, то электрическая цепь усиливает входной ссигнал, если же меньше единицы, то ослабляет.

Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы. Определяется по уровню 0,707 от максимального значения АЧХ.

В данном посте освещены 3 темы по основам цифровой обработки сигналов:

• АЧХ и ФЧХ,
• Цифровые фильтры,
• КИХ и БИХ фильтры.

АЧХ и ФЧХ

В этом видео мы поговорим о таких характеристиках линейных стационарных систем, как амплитудно-частотная характеристика (АЧХ) и фазо-частотная характеристика (ФЧХ). В предыдущей публикации мы рассмотрели различные способы описания линейных стационарных дискретных систем. Разностное уравнение показывает, как вычислять значения отсчётов на выходе системы, передаточная функция описывает динамику в зэд области, импульсная характеристика нужна для свёртки с входным сигналом. Но ни одно из рассмотренных описаний не даёт нам понимания, как же именно наша система будет преобразовывать сигнал. А это хотелось бы знать до того, как мы подадим входное воздействие. 

Именно поэтому для описания систем используют частотные характеристики. А именно – амплитудно-частотную характеристики (АЧХ) и фазочастотную характеристику (ФЧХ). Как вы уже поняли, это характеристики системы, но для их лучшего понимания мы можем обратиться к характеристикам сигнала.

Давайте для простоты начнём с АЧХ. У сигнала есть амплитудный спектр, то есть зависимость энергии сигнала в зависимости от частоты. А у системы есть АЧХ, говоря простыми словами, зависимость коэффициента усиления от частоты.

В частотной области спектр сигнала должен пройти через АЧХ системы, при этом его спектр исказится, подобно тому, как брусок пластилина изменит своё сечение при прохождении через определённую формочку. 

Давайте рассмотрим влияние АЧХ и ФЧХ на отдельные спектральные составляющие сигнала, или синусоиды. Допустим, у нас есть сигнал, состоящий из двух отдельных синусоид. При прохождении через систему с АЧХ представленной формы, синусоида меньшей частоты не изменит своей амплитуды, в то время как синусоида большей частоты станет меньше по уровню, так как этой частоте соответствует коэффициентт усиления меньше единицы. АЧХ системы может усиливать сигнал в одних полосах и подавлять в других.

Фазочастотная характеристика показывает зависимость фазового сдвига от частоты. Подобно тому, как мы можем отразить фазовый спектр сигнала. Но в случае с ФЧХ, к начальной фазе сигнала на конкретной частоте добавится сдвиг, определяемый ФЧХ. Проще говоря, синусоида не только изменит свою амплитуду, но и сдвинется на временной оси.

АЧХ и ФЧХ наглядно демонстрируют нам, как система изменяет проходящий через неё сигнал. Но откуда мы получаем эти характеристики, и связанны ли они с разностным уравнением, или передаточной функцией? На самом деле да, связаны.

Если мы отобразим передаточную функцию на комплексной плоскости в виде трёхмерной поверхности, с учётом нулей и полюсов, и наложим на неё окружность единичного радиуса, то проекция или разворот этой кривой с учётом всех взлётов и падений и есть ни что иное, как форма амплитудно-частотной характеристики системы.

Как вы видите, кривая строится также и в области отрицательных частот. А о способах определения АЧХ системы я рекомендую Вам поискать дополнительную информацию самостоятельно.

Мы же подошли к основному смыслу рассматриваемых систем. Задачи линейных стационарных систем – изменять амплитуду и фазу входных сигналов. И процесс этот называется фильтрацией. К примеру, удаление нежелательной высокочастотной составляющей в сигнале и усиление полезной низкочастотной – типичная задача для линейной стационарной системы. Отныне и в дальнейшем мы будем называть такие системы фильтрами. И в следующих публикациях мы познакомимся с различными типами дискретных фильтров. Пока что нам важно усвоить, что для описания фильтра нам достаточно знать его коэффициенты a и b.

Давайте перейдём в MATLAB и проанализируем фильтр с коэффициентами из прошлой публикации.

Начнем мы с формирования входного воздействия. В нашем случае, это будет ЛЧМ сигнал, то есть так называемый сигнал с линейной частотной модуляцией. Давайте запустим секцию и посмотрим как он выглядит во временной области.

Вы видите, что это сигнал, у которого частота нарастает с ростом времени. Подобный тип сигнала позволит нам достаточно наглядно во временной области посмотреть на работу нашего фильтра.

Теперь давайте посмотрим, как же выглядит амплитудно-частотные и фазо-частотные характеристики при заданных коэффициентах b и a. Для этого мы воспользуемся встроенной функцией freqz. Это функция отображает сразу АЧХ и ФЧХ, также в этой секции мы высчитываем нули и полюса нашей передаточной функции и отображаем их на нуль-полюсной диаграмме. Из форм АЧХ мы сразу можем понять, что данный фильтр представляет собой фильтр нижних частот, то есть он пропускает частоты меньше 2 кГц, а начиная с 2 кГц он начинает постепенно подавлять, и высокочастотные компоненты будут уже гораздо меньше по уровню нежели низкочастотные. Нуль-полюсная диаграмма конечно не настолько наглядно показывает нам, что же будет происходить с сигналом при прохождении через наш фильтр.

В следующей секции мы будем строить трёхмерный вид передаточной функции на комплексной плоскости. Все длинные формулы вычисления я убрал в функцию helperfunk2, мы также будем прилагать её в описании к этому видео. Так что если хотите проанализировать ее, можете это сделать, но сейчас я на это время тратить не буду. Я просто запущу эту секцию, и мы посмотрим на вид нашей передаточной функции на комплексной плоскости.

Я специально отразил здесь 2 версии этой проекции, то есть в данном случае у нас здесь просто показаны 2 явных полюса и 1 ноль.

Если приблизить передаточную функцию, то мы явно увидим нашу кривую, которая при развороте даёт нам уже форму нашей АЧХ.

Если мы посмотрим на вид этого разворота, конкретно в области положительных частот, то он по форме очень напоминает то, что выдавала нам функция freqz. То есть здесь мы также наблюдаем АЧХ фильтра нижних частот. 

Пришло время отфильтровать наш сигнал. Для этого мы воспользуемся встроенной функцией filter, которой мы просто передаём наши наборы коэффициентов фильтра и входное воздействие х. Затем мы отобразим отфильтрованный сигнал на одном графике с исходным. Давайте запустим эту секцию.

И как мы видим в момент времени t=1 сек, когда частота нашего сигнала доходит до 4 кГц, его амплитуда становится минимальной. Ну и завершении этого скрипта давайте попробуем вычислить выход нашего фильтра при помощи свертки. Для этого сперва мы вычисляем нашу импульсную характеристику фильтра при помощи встроенной функций impz, а затем при помощи функции conv определяем выход нашего фильтра.

В данном случае я накладываю выход функции filter и выход функции conv друг на друга. Как видите, они точно совпадают. 

Наверх

Цифровые фильтры

В этой публикации мы начинаем знакомиться с цифровыми фильтрами. В прошлых публикациях мы познакомились с описанием линейных стационарных дискретных систем, в данном и последующих видео мы будем знакомиться с применением подобных систем для задач цифровой обработки сигналов и фильтрации, в частности.

Для начала давайте вспомним, что делает фильтр в соответствии с задачами цифровой обработки. Например, он может пропускать сигналы в определённой полосе частот, и подавлять в других полосах. Он может быть частью эквалайзера, усиливая или подавляя сигнал в выбранной полосе. Помимо этого, фильтры могут быть использованы для изменения фазы сигнала, дифференцирования, изменения частоты дискретизации, но об этом мы пока не говорим. А сосредоточимся мы именно на свойствах частотной избирательности цифровых фильтров. 

Давайте вспомним знакомый нам пример фильтра из предыдущих публикаций – скользящее среднее. Только в этот раз мы представим осредняющие коэффициенты как импульсную характеристику нашей линейной дискретной системы. Как ведёт себя подобный фильтр с точки зрения частотной избирательности? Давайте разберёмся в MATLAB.

В данном скрипте мы будем осуществлять осреднение входного сигнала, но теперь – через операцию свёртки сигнала с импульсной характеристикой линейной дискретной системы. Длина импульсной характеристики h может варьироваться через переменную num. Создаём сумму двух синусоид, медленной, которую мы считаем полезным сигналом, и быстрой, большей частоты и меньшей амплитуды, которая будет зашумлять первую. Сумму s мы затем сворачиваем с вектором h. Запускаем секцию скрипта и наблюдаем эффект осреднения входного сигнала.

Если импульсную характеристику сделать длиннее, то сигнал осредняется ещё сильнее, и задержка выхода относительно входа  также увеличивается.

Но что здесь происходит с точки зрения частотной избирательности? Быстро меняющаяся синусоида подавляется, так как близко расположенные отсчёты входного сигнала приравниваются к среднему значению попавших в окно осреднения. Медленно изменяющийся сигнал при подобной операции искажается меньше, а это значит, что относительно плавно изменяющаяся первая синусоида на выходе подобного фильтра будет иметь большую амплитуду. С точки зрения частотной избирательности, подобная система пропускает сигналы меньшей частоты, и подавляет сигналы большей частоты.

Давайте убедимся в этом, оценив АЧХ фильтра. Воспользуемся функцией freqz. Как мы видим по форме АЧХ, это действительно фильтр нижних частот. В данной публикации мы рассмотрим параметры частотно-избирательных цифровых фильтров, и очертим основные этапы проектитования фильтров. И тут нужно сделать одно пояснение. Несмотря на то, что в предыдущих публикациях я говорил, что линейные дискретные системы мы можем смело называть фильтром, и часто в инженерных кругах так и делают, между ними всё же есть различие. Формально, линейной дискретной системой мы называем математическое описание, а фильтром – устройство. Фильтры строятся на основе описания линейной дискретной системы, но, помимо этого, также определяются способом их реализации – архитектурой, квантованием, платформой – например, цифровой фильтр может быть реализован программно, в виде кода, или аппаратно, как цифровая схема.

Давайте попробуем очертить основные параметры цифровых фильтров.  Во-первых, сюда относятся параметры линейной дискретной системы, такие как передаточная функция или разностное уравнение, то есть по сути – коэффициенты фильтра. Тесно связанные с коэффициентами АЧХ и ФЧХ определяют функцию фильтра, например, тип его частотной избирательности, и об этом мы подробно поговорим в этом видео.

Импульсная характеристика также относится к параметрам линейной системы, но мы чаще говорим о классификации фильтров в зависимости от их импульсной характеристик. Мы различаем фильтры с конечной импульсной хар-кой – КИХ фильтры, и фильтры с бесконечной импульсной характеристикой – БИХ фильтры. О разнице между ними я расскажу с следующей публикации.

Помимо этого, у фильтров есть дополнительные характеристики, вытекающие из вышеперечисленных – например, переходная функция, групповая и фазовые задержки, нуль-полюсная диаграмма и прочие.

Фильтры могу различаться по своей архитектуре, а она тесно связана с реализацией устройства в железе. Также, большинство реальных фильтров работают в целочисленной арифметике, и при их реализации надо обязательно учитывать эффекты квантования.

Цифровые фильтры могут быть классифицированы по перечисленным характеристикам.

Давайте рассмотрим классификацию фильтров по их частотной избирательности, то есть по АЧХ. С точки зрения своей функции частотно-избирательной цепи, фильтры могут разделяться на множество типов. Рассмотрим основные, наиболее распространённые типы.

Во-первых, это фильтры нижних и верхних частот. Как вы понимаете из названия, фильтр нижних частот пропускает низкие частоты, до определённой частоты среза, и подавляет высокие частоты. Фильтр верхних частот исполняет обратную функцию.

Также существуют полосно-пропускающие и полосно-заграждающие фильтры. Первые пропускают сигнал только в определённой полосе частот, вторые могут подавлять сигнал в определённой полосе частот, и пропускать во всех остальных.

Ну и частным случаем полосовых фильтров могут считаться резонансные фильтры, пропускающие или подавляющие сигнал только на одной конкретной частоте.

Требования к частотной избирательности фильтра в зависимости от накладываемой на него задачи можно записать в виде спецификации к его частотным характеристикам.

Давайте познакомимся со спецификацией на примере фильтра нижних частот. У АЧХ подобного фильтра можно выделить три основные полосы, а именно – полосу пропускания, полосу перехода, и полосу заграждения.

Полоса пропускания фильтра, или passband, – это тот диапазон частот, в котором в идеале находится наш полезный сигнал. Его мы хотим пропустить по возможности без искажений. Границей полосы пропускания для ФНЧ является частота Fp, или Fpass. Она отсчитывается по уровню минус три децибела от максимума.

Усиление сигнала в полосе пропускания, опять-таки в идеале, должно быть постоянным. Но на практике зачастую присутствуют определённые нестабильности усиления, или пульсации. Уровень допустимых пульсаций в полосе пропускания определяется параметром Apass, и измеряется в децибелах.

Полоса заграждения, или stopband, – это тот диапазон частот, в котором сигнал должен гарантированно ослабляться не менее чем на Ast децибел. Начинается полоса заграждения с частоты Fst.

А между этими полосами находится переходная полоса, или transition band, усиление в этой полосе плавно спадает. Кстати, чем более резкий переход у фильтра от полосы пропускания к полосе заграждения, то есть чем уже полоса перехода, тем больший порядок должен иметь фильтр. А порядок – это количество коэффициентов фильтра, и оно связано с количеством умножителей, необходимых для реализации.

Так что фильтры с крутыми спадами обычно более сложные и дорогие, поэтому перед проектировщиком всегда стоит задача поиска компромисса между соответствием формы частотной характеристики некой идеальной, и стоимостью реализации устройства.

Давайте также рассмотрим этапы проектирования того самого устройства – цифрового фильтра. Начинаем мы с определения спецификации фильтра, исходя из его задачи. Затем нам надо понять, хотим мы использовать для этого КИХ или БИХ фильтр. Как и говорил, о разнице между ними – в следующей публикации. Затем нам необходимо на основе спецификации и типа фильтра подсчитать коэффициенты, то есть те значения, на которые мы будем умножать отсчёты входного и, возможно, выходного сигналов.

Процесс, который является ключевым здесь – переход от спецификации к коэффициентам! Сложная в прошлом вычислительная задача в современном мире решается очень просто – при помощи MATLAB. Большинство инженеров занимаются расчётом коэффициентов фильтров именно в MATLAB с использованием средств Signal Processing Toolbox.

Давайте пройдём путь до подсчёта коэффициентов по заданной спецификации в livescript, пока что не затрагивая реализацию. Для начала импортируем и прослушаем аудиофайл, который будет нашим входным сигналом.

Затем перейдём к спецификации.

Я хочу попробовать создать полосно-заграждающий фильтр, который слегка подавит так называемую середину. Полоса заграждения будет лежать в пределах от 1000 до 4000 Гц. Подавление в полосе будет всего лишь 10 дБ, а уровень допустимых пульсаций в полосах пропускания составит 1 дБ. Для аудио-фильтра это весьма много, но для нашего примера это не так критично.

Затем мы формируем объект спецификации d. Для этого мы передаём функции fdesign тип отклика – bandstop, и все наши значения параметров.

Затем на основе объекта спецификации мы уже будем счиать коэффициенты, которые будут храниться в объекте фильтра Hd . Подсчитываем мы их командой design. Ей мы передаём объект спецификации и тип фильтра. У нас это КИХ фильтр типа equiripple.

На основе подсчитанных коэффициентов MATLAB вычисляет характеристики фильтра и мы можем их посмотреть в программе Filtel Visualization Tool.

Здесь мы сразу наглядно оцениваем АЧХ фильтра и соответствие её спецификации. Маска спецификации отрисовывается красными пунктирными линиями. Так же нам доступны выизуализации фазочастотной характеристики, групповой и фазовой задержек, импульсной и переходной характеристик, нуль-полюсная диаграмма, значения коэффициентов и сводная информация, включающая также стоимость реализации фильтра.

Если мы отразим значения коэффициентов числителя передаточной функции фильтра на графике, то мы можем заметить, что это – импульсная характеристика.

Для КИХ-фильтров это всегда так, но подробнее об этом мы поговорим в следующей публикации.

А сейчас нам осталось только применить фильтр к входному аудиофайлу и прослушать результат. Ну а если вам интересно посмотреть на спектр сигнала до и после фильтрации – попробуйте сделать это самостоятельно, команды вы знаете. Просто добавьте их в livescript.

Наверх

КИХ и БИХ фильтры

В данной публикации мы поговорим о КИХ и БИХ фильтрах, о разнице между ними и мотивациях применения. Начнём с КИХ-фильтров. По определению, КИХ – это фильтр с конечной импульсной характеристикой. По английский это произносится как FIR Filter, от final impulse response. КИХ фильтры – нерекурсивные, а это значит, что для вычисления значения на выходе фильтра используются только текущее и задержанные значения входа. В разностном уравнении есть только коэффициенты при x. Передаточная функция в знаменателе имеет константу, часто единицу.  А схема фильтра не имеет обратных связей.

Если вы вспомните схему для подсчёта дискретной свёртки из предыдущих публикаций, то она очень похожа на представленную схему КИХ-фильтра. Вектор входных отсчётов формируется при помощи линий задержки, или регистров, перемножение отсчётов сигнала на отсчёты импульсной характеристики осуществляется в умножителях, а сумматоры потом объединяют всё в отсчёт выходного сигнала. Отсчёты импульсной характеристики КИХ-фильтра – это и есть вектор коэффициентов b. То есть мы указываем импульсную характеристику явно, и она по понятным причинам конечна.

Теперь поговорим о преимуществах и недостатках применения КИХ-фильтров.

Начнём с преимуществ:

• они могут обладать линейной фазой, и это очень важно, так как задача компенсации фазового набега заметно упрощается;
• они всегда устойчивы, то есть даже при очень большом уровне входного сигнала при его выключении через некоторое время сигнал на выходе гарантированно затухнет. Это прямое следствие того, что схемы КИХ-фильтров не содержат обратных связей
• ну и фактически имея достаточный порядок фильтра, мы можем сформировать произвольный частотный или фазовый отклик

Основной существенный недостаток КИХ-фильтров:

• Они до роже в реализации, чем БИХ-фильтры со схожей АЧХ.

Мы говорим, что КИХ-фильтры обычно бывают больших порядков, а порядок фильтра влияет на количество ресурсов, требуемых для его реализации. О каких ресурсах мы говорим? Когда мы рассматриваем аппаратную реализацию, то есть цифровую схему, то речь идёт о базовых блоках для построения фильтров – умножителях, сумматорах и регистрах, или линиях задержки. Иногда там ещё используются мультиплексоры.

Кратко расскажу об одном из методов синтеза КИХ-фильтров, наиболее наглядном. Под синтезом мы понимаем процесс получения коэффициентов. И так как коэффициенты КИХ-фильтра – это его импульсная характеристика, то мы можем нарисовать идеальную форму АЧХ, (к примеру, здесь мы идём от идеальной АЧХ фильтра нижних частот) и при помощи обратного быстрого преобразования Фурье  получить соответствующую ей идеальную импульсную характеристику. Она получится бесконечная.

Затем эту импульсную характеристику мы перемножаем с оконной функцией конечной длительности, то есть формируем конечную импульсную характеристику. При ограничении количества отсчётов, форма АЧХ отклоняется от идеальной, появляются пульсации и переходные полосы. Вспоминаем эффект Гиббса. А вообще методы синтеза фильтров – это отдельная наука, в рамках данного курса мы её не охватим.

А в рамках этой публикации мы познакомимся с БИХ-фильтрами, фильтрами с бесконечной импульсной характеристикой. По-английски они называются IIR (Infinite impulse response). Кстати, БИХ-фильтры могут быть как аналоговые, так и цифровые. КИХ-фильтры могут быть только цифровыми.

БИХ фильтры – рекурсивные, для вычисления значения на выходе фильтра используются как  значения входа, так и задержанные значения выхода. Передаточная функция представляется в стандартном дробно-рационально виде, а схема фильтра содержит обратные связи.

Из преимуществ БИХ-фильтров можно отметить:

• относительную простоту реализации по сравнению с КИХ-фильтрами (мы убедимся в этом на примере),
• относительную простоту синтеза на основе аналоговых прототипов.

В качестве недостатков:

• могут быть неустойчивыми. Если коэффициент в цепи обратной связи будет больше единицы, может образоваться положительная обратная связь, фильтр может завестись, и сигнал на его выходе может продолжаться и усиливаться даже после выключения входного воздействия,
• они не могут обладать линейной фазой,
• мы не можем сформировать произвольную АЧХ и ФЧХ, по сути, мы выбираем АЧХ из типов, основывающихся на аналоговых прототипах, чаще всего это стандартные фильтры нижних и верхних частот, полосовые и так далее. Частотно-избирательные фильтры, с полосами пропускания и заграждения и без какого-либо контроля над фазой сигнала.

Синтезируются БИХ-фильтры при помощи преобразования непрерывной передаточной характеристики аналогового прототипа в дискретную характеристику цифрового фильтра. В детали билинейного преобразования тоже не лезем.

А поговорим мы про автоматизацию задания спецификации и синтеза самых разнообразных фильтров в  MATLAB. Конкретно – про интерактивное приложение Filter Designer App, ранее называлось FDA Tool. Это приложение в составе Signal Processing Toolbox для анализа, синтеза, квантования фильтров, создания многоскоростных систем, импорта и экспорта коэффициентов и многого другого. Инженеры по всему миру не один десяток лет используют именно это приложение для быстрого проектирования цифровых фильтров, очень его любят и уважают, вполне заслуженно.

Давайте воспользуемся им для фильтрации зашумлённого музыкального файла.  Во-первых, загрузим аудиоданные. Я это сделаю, просто кликнув дважды по mp3-файлу. Именя переменных оставляем по-умолчанию. Ну и сразу прослушаем аудио. Мы слышим Дебюсси с наложенными на него ударными из другой композиции.

Посмотрим на этот сигнал в Signal Analyzer. Выберем наш вектор, отобразим его во временной области, укажем частоту дискретизации, чтобы наблюдать сигнал в реальных секундах и герцах. И отобразим спектр.

Курсор поможет нам понять, где проходит граница полезного сигнала и помехи. Граница расположена в районе 2.2 кГц. Свернём Signal Analyzer и откроем инструмент Filter Designer. Попробуем разработать в нём подходящий цифровой фильтр.

Выбираем тип отклика мы оставляем lowpass, то есть фильтр нижних частот. Пока что попробуем реализовать его в виде КИХ-фильтра equiripple.  Указываем частоту дискретизации, границу полосы пропускания и начало полосы заграждения. На переходную полосу мы оставляем всего лишь 200 Герц, это достаточно крутой спад. Пульсации для аудио-фильтра мы зададим не более 0.1 децибела, а подавление оставим на уровне 80. Нажимаем кнопку Design Filter.

И наблюдаем АЧХ. Форма вполне соответствует спецификации, фазочастотная характеристика линейна в полосе пропускания, групповая и фазовая задержки – константы, тут же можем оценить форму импульсной характеристики и переходной функции,

Но на вкладке информации мы можем увидеть, что фильтр требует очень много ресурсов, более семи сотен умножителей, сумматоров  и регистров.

Проверим, будет ли БИХ-фильтр экономичнее. Выберем самый экономичный вариант, эллиптический БИХ-фильтр, наблюдаем форму его АЧХ, и в информации видим, что ресурсов подобный фильтр требует в тридцать раз меньше! Это серьёзная разница.

Но за неё придётся поплатиться нелинейностью фазы, а также зависящими от частоты групповой и фазовой задержками. Но наш БИХ-фильтр устойчив, все его полюса находятся внутри окружности единичного радиуса на нуль-полюсной диаграмме.

И в информации о структуре фильтра мы видим надпись Second Order Sections. Покажем структуру в центре документации.

Секции второго порядка – это каскадный способ построения БИХ-фильтров из меньших фильтров второго порядка. Оставим всё как есть, убедимся, что форма АЧХ нас устраивает, а фаза для задачи фильтрации аудио не так критична.

И теперь мы экспортируем вычисленные коэффициенты фильтра в рабочее пространство  MATLAB в виде так называемой sos матрицы и вектора усилений для каждого каскада. Каждая секция содержит шесть коэффициентов, они объединяются в матрицу размером n на 6. При желании мы можем преобразовать такую форму преставления в привычные нам коэффициенты передаточной функции. Воспользуемся функцией sos2tf и получим общую дробь для всего фильтра. Теперь отфильтруем входной сигнал data, и оценим результат в Signal Analyzer. Добавим вектор y, укажем ему частоту дискретизации, чтобы на временной оси его можно было отрисовать.

Видим явное уменьшение амплитуды на всём промежутке, и на спектре после 2,2 кГц мы наблюдаем серьёзное подавление. Проверим, удалось ли нам освободить Дебюсси. Прослушаем выход фильтра командой sound. В целом, получилось неплохо.

Федеральное
агентство по образованию

Государственное
образовательное учреждение

высшего
профессионального образования

Уфимский
государственный авиационный технический
университет

Методические
указания к лабораторной работе №1

по
дисциплине «Математические основы

цифровой
обработки сигналов»

Исследование частотных характеристик цифровых фильтров

Уфа
2006

Лабораторная работа №1 Исследование частотных характеристик цифровых фильтров

Цель работы:
освоение методов нахождения АЧХ цифровых
ФНЧ

Частотные
характеристики ЦФ

Пусть:

Тогда ЧХ – частотная
характеристика

При

ПФ
ЧХ

ЧХ – комплексная
величина

—
АЧХ

—
ФЧХ

.

Групповое время
задержки (групповое время замедления)
ГВЗ

Физический смысл
ГВЗ – это мера средней задержки, вносимой
фильтром в зависимости от частоты.

Основные
свойства ЧХ:

1. Все ЧХ – непрерывные
функции частоты.

2.
Все ЧХ – периодические функции частоты,
с периодом равным

3.
Для фильтров, ПФ которых имеют только
вещественные коэффициенты:

и

— чётные функции частоты

—
нечётные функции

Из
2 и 3 следовательно требования к ЧХ
фильтров с вещественными коэффициентами
достаточно задавать на интервале от

Пример 1:

;

Найти: АЧХ, ФЧХ,
ГВЗ.

Рис. 10

Пример
2:

Найти ФЧХ и ГВЗ.

Рис. 11

Нормирование
частоты

Для того чтобы
частотные характеристики разных фильтров
легче было сравнивать друг с другом,
частоту нормируют.

Т.к.
все частотные характеристики зависят
при постоянном периоде от произведения

,
вместо

вводят одну переменную.

Как правило
используют два способа нормирования
частоты:

1)

—
требования к ЧХ на этом интервале.

2)

а)	— Гольденберг
б)	— MATLAB

Формулировка
требований

к частотным характеристикам
фильтра

Избирательный
фильтр служит для выделения частотных
составляющих входного сигнала,
расположенных в полосе пропускания
фильера, и подавления частотных
составляющих, расположенных в полосе
задерживания. В зависимости от того,
каким образом указанные полосы расположены
относительно друг друга на частотной
оси, различают следующие типы фильтров:
нижних частот (ФНЧ), верхних частот
(ФВЧ), полосовые (ПФ) и режекторные
(РФ). На рис.1 приведены идеализированные
амплитудно-частотные характеристики
соответствующих фильтров.

Рис.1

Естественно,
что фильтры с такими характеристиками
построить невозможно, к идеализированным
характеристикам можно только приблизиться.
На этапе решения аппроксимационной
задачи определяют передаточную функцию
H(z)
фильтра, которая воспроизводила бы
заданную АЧХ A(w)
с требуемой точностью. Отсюда следует,
что в качестве исходных данных для
решения аппроксимационной задачи должны
быть заданы допуски на максимальное
значение неравномерности АЧХ в полосе
пропускания (А_п)
и максимальное отклонение АЧХ от нуля
в полосе задерживания (А_з).

Требования
к фазочастотной характеристике фильтра
при проектировании избирательных
БИХ-фильтров описанными ниже методами
не могут быть заданы, ФЧХ получается
нелинейной. Степень нелинейности ФЧХ
можно лишь проконтролировать путем
расчета фазочастотной характеристики
или группового времени замедления для
определенной (рассчитанной) передаточной
функции БИХ-фильтра. Методы построения
БИХ-фильтров с заданными требованиями
как к АЧХ, так и к ФЧХ достаточно сложны,
базируются, как правило, на использовании
дополнительного корректора ФЧХ и здесь
не рассматриваются.

Таким
образом, исходными данными для решения
аппроксимационной задачи являются
граничные частоты полос пропускания и
задерживания, а также величины А_п
и А_з.

Пример 1.
Разрабатывается цифровой фильтр нижних
частот с полосой пропускания от 0 до 0,2
(частота нормирована) и полосой
задерживания от 0,4 до 0,5. Частотные
составляющие входного сигнала в полосе
пропускания должны быть ослаблены не
более чем в

раза, а в полосе задерживания подавлены
не менее чем в 100 раз. Необходимо задать
требования к АЧХ фильтра.

Соответствующие
требования показаны на рис. 2,а, где
нормированная граничная частота полосы
пропускания w_г.п=0,2,
нормированная граничная не требования
к АЧХ частоты полосы задерживания
w_г.з=0,4, А_п=1-

= 0,293, А_з=0.01.
Обратите внимание, что между полосой
пропускания и полосой задерживания
существует переходная полоса, для
которой требования к АЧХ, как правило,
не задаются.

Рис.2

В качестве исходных
данных при решении аппроксимационной
задачи часто задаются A(w),
а требования к характеристике затухания
a(w).
Эти характеристики связаны между собой
простым соотношением

a(w)=-20lgA(w).
(1)

П
ри
этом в качестве исходных данных должны
быть заданы верхняя граница рабочего
затухания в полосе пропускания а
и нижняя
граница затухания в полосе задерживания
а₀.

Связь между
параметрами А_п
и а,
а также А_з
и а₀
можно установить, используя (1):

а
= — 20lg
(1-А_п);

а₀
= -20lg(А_з).

Следует заметить,
что амплитудно-частотная характеристика
A(w)
не имеет размерности, а характеристика
затухания a(w)
определена в децибелах.

Пример 2. Необходимо
задать требования к характеристике
затухания a(w)
для ФНЧ, аналогично рассмотренному в
примере 1. Соответствующие требования
показаны на рис. 2,б. Действительно,
используя (1), получаем а
= — 20lg
(1-0,293) = 3 дБ,
а₀
= -20lg
0,01 = 40 дБ.

Схемы допусков на
амплитудно-частотную характеристику
A(w)
и характеристику затухания a(w)
приведены на рис. 3 и 4 соответственно
для фильтров
нижних частот
(а), верхних частот (б), полосовых
(в) и режекторных
(г).

Рис.3
Рис.4

В заключение надо
отметить, что указанные параметры
(граничные частоты и А_п(а),
А_з(а₀))
являются основными при постановке
аппроксимационной задачи и часто
дополняются некоторыми более частными
требованиями. Например, в ряде случаев
требуется обеспечить монотонность АЧХ
(затухания) в полосе пропускания. Могут
также задаваться требования к допустимому
отклонению фазочастотной характеристики
от заданной (например, линейной). Наконец,
могут задаваться требования и к
реализационным параметрам разрабатываемого
фильтра. Все эти требования так или
иначе влияют на формулировку и решение
аппроксимационной задачи. Мы, однако,
вначале будем рассматривать методику
решения аппроксимационной задачи в
наиболее простом виде – при задании в
качестве исходных данных только основных
параметров (w_г.п
,w_г.з,
А_п(а)
и
А_з(а₀)).

КРАТКИЙ
ОБЗОР МЕТОДОВ РЕШЕНИЯ АППРОКСИМАЦИОННОЙ
ЗАДАЧИ.

При определении
передаточных функций БИХ-фильтров
используется три класса методов:

— методы преобразования
аналоговых фильтров в цифровые;

— прямые методы
расчета БИХ-фильтров;

— методы, использующие
алгоритмы оптимизации.

Для расчета
избирательных БИХ-фильтров со стандартными
характеристиками (ФНЧ, ФВЧ, ПФ, РФ)
наиболее простым и широко используемым
является метод билинейного
преобразования.
С помощью этого метода передаточная
функция T(s)
аналогового фильтра-прототипа
преобразуется в передаточную функцию
H(z)
цифрового БИХ-фильтра. Достоинством
метода билинейного преобразования
является то, что передаточная функция
цифрового фильтра определяется с помощью
простых формул из передаточной функции
аналогового фильтра, для которых
существуют подробные таблицы и
справочники. Это, в свою очередь, позволяет
решать аппроксимационную задачу даже
в достаточно сложных случаях без
использования ЭВМ.

Достоинством
метода билинейного преобразования по
сравнению с другими методами преобразования
аналоговых фильтров в цифровые
(инвариантности импульсной характеристики
и согласованного z-преобразования)
является то, что данный метод обеспечивает
построение такого БИХ-фильтра, выходной
сигнал которого приближенно совпадает
с выходным сигналом аналогового
фильтра-прототипа при одинаковых
произвольных входных сигналах.

БИЛИНЕЙНОЕ
ПРЕОБРАЗОВАНИЕ.

Билинейное
преобразование представляет собой
конформное
отображение
точек s-плоскости
в точки z-плоскости
и использует замену переменной вида

s
= [(1-z^-1)/(1+z^-1)]
=
[(z-1)/(z+1)],

(3)

где

— постоянный множитель, значение которого
не меняет формы преобразования (о выборе
величины 
поговорим позже). Из (3) можно найти
обратное соотношение

z
=
(+s)/(-s).
(4)

Использование
подстановки (3) обеспечивает однозначное
преобразование передаточной функции
T(s)
аналогового фильтра-прототипа
(АФ-прототипа) в передаточную функцию
H(z)
цифрового фильтра:

H(z)
= T(s)

Рассмотрим
преобразование (3). Каждой точке комплексной
s—плоскости
(s=+јΩ)
ставится в соответствие определенная
точка z-плоскости
(z=exp
(σ+јω)T).

Мнимая ось
s-плоскости
(s=јΩ
для -∞
Ω
∞) отображается в единичную окружность
z-плоскости
(z=exp(јωT)).
Действительно, при s=јΩ
из (4) получаем

z=(+јω)/(-јω).

Представим теперь
последнее выражение в показательной
форме, т.е выделим модуль r
и аргумент θ:

(6)

Из (6) видно, что
r=|z|=1.
При монотонном изменении Ω от -∞ до ∞
фазовый угол θ
(Ω) монотонно изменяется от -
до ,
т.е точка јΩ₁,
расположенная на мнимой оси в s-плоскости,
отображается в соответствующую точку
ехр (ј2arctg
(Ω₁/)).

В частности, для
Ω=0 имеем z=exp(ј0)=1,
для Ω=∞ получаем z=exp
(ј)=
-1 и для Ω=-∞ имеем z=exp(ј)=-1.

Левая половина
s-плоскости
(Re(s)
= Re(+јΩ)0)
отображается в часть z-плоскости
внутри единичного круга (z1).
Действительно, при Re(s)0
имеем 0.
Тогда из (4) можно получить

z=[(+)+јΩ]/[(-)-јΩ].

(7)

Теперь поступив
точно так же, как при выводе (6), получим

z=r
exp(јθ(Ω)),
(8)

где

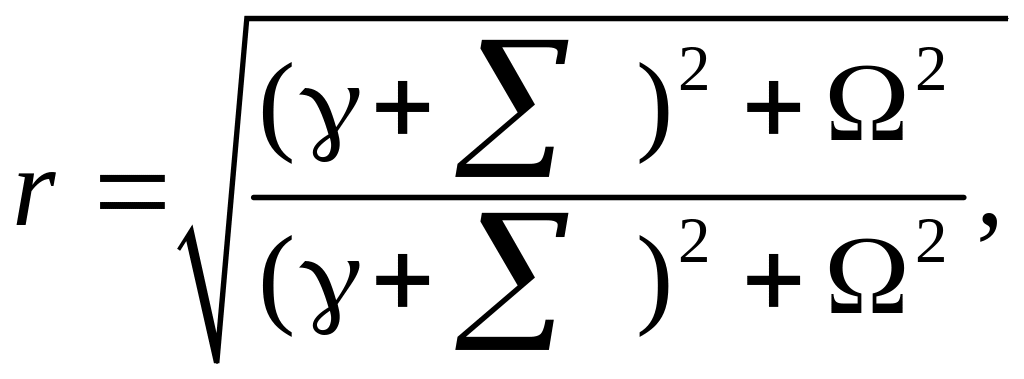
Поскольку 0,
то модуль числителя в (7) всегда меньше
модуля знаменателя, т.е r=z1.

Пример 4. Расположение
точек в s-плоскости
показано на рис. 7. Определить соответствующие
точки z-плоскости
(положить =1),
если s₁=-2+ј0;s₂=0+ј1,0;
s₃=0-ј1,0.

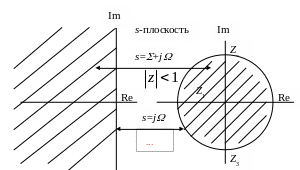
Рис.7

Используя
(7), получаем
z₁=(1-2)/(1+2)=-0,333,
а
из
(6) имеем
z₂=1
exp(ј2
arctg 1)=exp (ј/2)
и
z₃=1
exp (ј2
arctg (-1))=exp (-ј/2).
Расположение
точек в z-плоскости,
а также правила отображения мнимой оси
и левой половины s-плоскости
в единичную окружность и часть z-плоскости
внутри единичного круга показаны на
рис. 7.

Очень важными
являются два обстоятельства. Во-первых,
поскольку все полюсы устойчивого
аналогового фильтра расположены в левой
половине s-плоскости,
он при преобразовании к цифровому
фильтру будет давать устойчивый фильтр.
Во-вторых, так как мнимая ось s-плоскости
отображается на единичную окружность
z-плоскости,
то все максимумы и минимумы АЧХ Т(јΩ)
аналогового фильтра сохраняются и в
АЧХ H(e^jωT)
цифрового фильтра. Сохраняется также
и неравномерность АЧХ для соответствующих
диапазонов частот. Таким образом,
избирательные аналоговые фильтры
преобразуются в соответствующие цифровые
фильтры (например, если аналоговый
фильтр есть фильтр нижних частот с
неравномерностью АЧХ в полосе пропускания
А_п
и отклонением АЧХ от нуля в полосе
задерживания А_з,
то соответствующий цифровой фильтр
будет также фильтром нижних частот с
параметрами А_з
и А_п).

Но не все так
хорошо. Так, соотношение между «аналоговыми»
частотами Ω и «цифровыми» частотами ω,
которое можно получить из (3), является
нелинейным:

Ω=
tg (ωT/
2)=

tg (w),
(9)

Где
w=ω/ω_д
нормированная цифровая частота. Таким
образом, имеет место деформация
шкалы частот при
переходе от аналогового фильтра к
цифровому. На рис.8 изображена зависимость
(9) и проиллюстрировано явление деформации
частотной шкалы.

Рис.8

Слева показана
идеализированная АЧХ полосового фильтра
с двумя полосами пропускания, равными
по величине, но расположенными в разных
частотных диапазонах. Полученный
цифровой фильтр будет иметь также две
полосы пропускания, но ширина последней
в области верхних частот будет существенно
меньше ширины полосы пропускания в
области нижних частот.

Выход, однако,
чрезвычайно прост. Деформация шкалы
частот для частотно-избирательных
фильтров (ФНЧ, ФВЧ, ПФ, РФ), аппроксимируемая
АЧХ которых имеет вид кусочно-постоянной
функции, не приводит к нарушению
избирательных свойств фильтра при
билинейном преобразовании (и это
главное!). А деформацию шкалы частот
можно скомпенсировать с помощью
предыскажений в аналоговом фильтре.

Рассмотрим, наконец,
вопрос о выборе параметра 
в подстановке (3). Если использовать
соотношение

=ctg
(ω_г.п
T/
2)=ctg
(
w_г.п),
(10)

то
для получения цифрового фильтра нижних
частот с граничной частотой полосы
пропускания ω_г.п
(w_г.п)
надо в качестве прототипа использовать
нормированный аналоговый фильтр с
частотой среза Ω_с=1,
а именно такие фильтры и приводятся в
справочниках.

Пример 5. Рассмотрим
порядок действий при определении
передаточной функции H(z)
цифрового
ФНЧ по заданным требованиям к
неравномерности АЧХ в полосе пропускания
А_п,
отклонению от нуля в полосе задерживания
А_з,
а также граничным нормированным частотам
полос пропускания w_г.п
и задерживания w_г.з
(рис.9).

Рис.9

Вначале определим
соответствующие граничные частоты
полосы пропускания Ω_с
и полосы задерживания Ω_к
аналогового фильтра с помощью нелинейного
соотношения (9). Графически этот процесс
показан на рис. 9. Теперь надо определить
передаточную функцию T(s)
аналогового фильтра-прототипа с
неравномерностью АЧХ в полосе пропускания
[0, Ω_с],
равной А_п,
и отклонением от нуля в полосе задерживания
[Ω_к,∞],
равным А_з.
Это можно сделать с помощью справочника
по расчету аналоговых фильтров [6]. Работу
со справочником мы рассмотрели выше.
Доустим, АФ найден и его АЧХ показана
на рис. 9. Теперь надо выполнить билинейное
преобразование (5), т.е в определенной
из справочника передаточной функции
T(s)
выполнить замену переменной s
в
соответствии с (3). В результате получим
БИХ-фильтр, удовлетворяющий поставленным
требованиям.

Билинейное
преобразование можно выполнить как
вручную (с помощью калькулятора), так и
на ЭВМ.

Расчет
частотной характеристики

Частотная
характеристика дискретного фильтра
рассчитывается с помощью функции freqz,
которая очень похожа на функцию freqs,
выполняющую
аналогичные расчеты для аналоговых
цепей.

В
простейшем виде функция freqz
используется следующим образом:

freqz(b,
a)

Входные
параметры b
и а — векторы коэффициентов полиномов
числителя и знаменателя функции передачи
фильтра.

При
расчете используются нормированные
значения частот, измеряемые в ра­дианах
на отсчет (при такой нормировке частота
дискретизации равна

,
а частота Найквиста —

).
По
умолчанию выбирается 512 частотных точек,
равномерно распределенных в диапазоне
0…
.

При
отсутствии выходных параметров функция
freqs
строит графики АЧХ (в децибелах) и ФЧХ
(в градусах) фильтра.

Построим
графики частотных характеристик фильтра,
использованного при демонстрации
дискретной свертки, но добавим к этому
фильтру рекурсивную ветвь с коэффициентом
передачи 0,1. Результат показан на рис.
10:

>>
b
= [1 2 3 4];

>>
a
= [1 2 3 4];

>>
freqz(b,
a)

Рис.
10.
Частотная
характеристика дискретного фильтра,
построенная функцией freqz

Если при вызове
функции указаны выходные параметры,
построение графика не производится:

[h,
w]
= freqz(b,
a);

В
векторе h
возвращаются рассчитанные значения
комплексного коэффициента передачи, а
в векторе w
– использованные
при расчете значения нормированных
частот.

Чтобы
задать количество частотных точек для
расчета, используется третий входной
параметр n
(частоты при этом по-прежнему равномерно
распределяют­ся в диапазоне

):

freqz(b,
a,
n);

Можно
заставить функцию freqz
использовать ряд частот, равномерно
распреде­ленных на интервале

,
то есть вплоть до частоты дискретизации.
Это может быть необходимо при анализе
фильтров с комплексными коэффициентами,
частотные характе-ристики которых не
являются симметричными. Такое указание
дается функции freqz
c
помощью четвертого входного параметра
– строки

‘whole’:

freqz(b,
a, n, ‘whole’);

Наконец
можно задать вектор нормированных
круговых частот w
для расчета частотной характеристики:

h=
freqz(b,
a,
w);

Использование
второго выходного параметра в этом
случае не имеет смысла, поскольку вектор
частот задан на входе.

При
выводе графиков ФЧХ фильтров функция
freqz
применяет к вектору рассчитанных фазовых
сдвигов функцию unwrap,
чтобы устранить «фиктивные» разрывы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уровень сложности
Средний

Время на прочтение
7 мин

Количество просмотров 11K

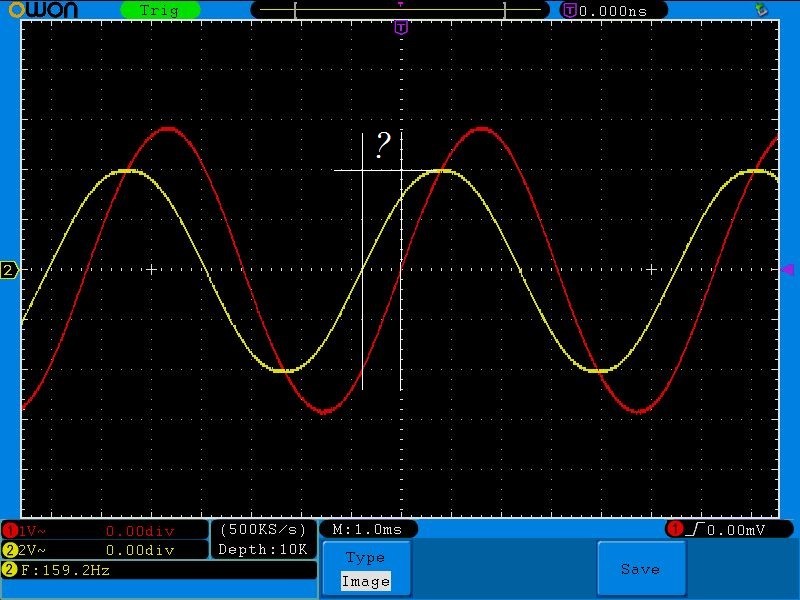
Представьте: вы принимаете аналоговый сигнал, смотрите на результаты показаний и видите, что синусоиду «перекосило». Все из-за плохой селективности вашего приемника и шумов, которые он принимает. Чтобы выделить и выровнять полезный сигнал и не слушать бесконечное шипение, в радиоприемнике должны быть качественные фильтры. Но что это такое, как они работают и какими бывают? Давайте разбираться.

Используйте навигацию, если не хотите читать текст полностью:

→ Что такое частотный фильтр
→ Очередной резистивный делитель, или из чего состоят фильтры
→ Немного о параметрах частотных фильтров
→ Рассчитывать фильтры — это сложно
→ Собираем фильтр Чебышева

Что такое частотный фильтр

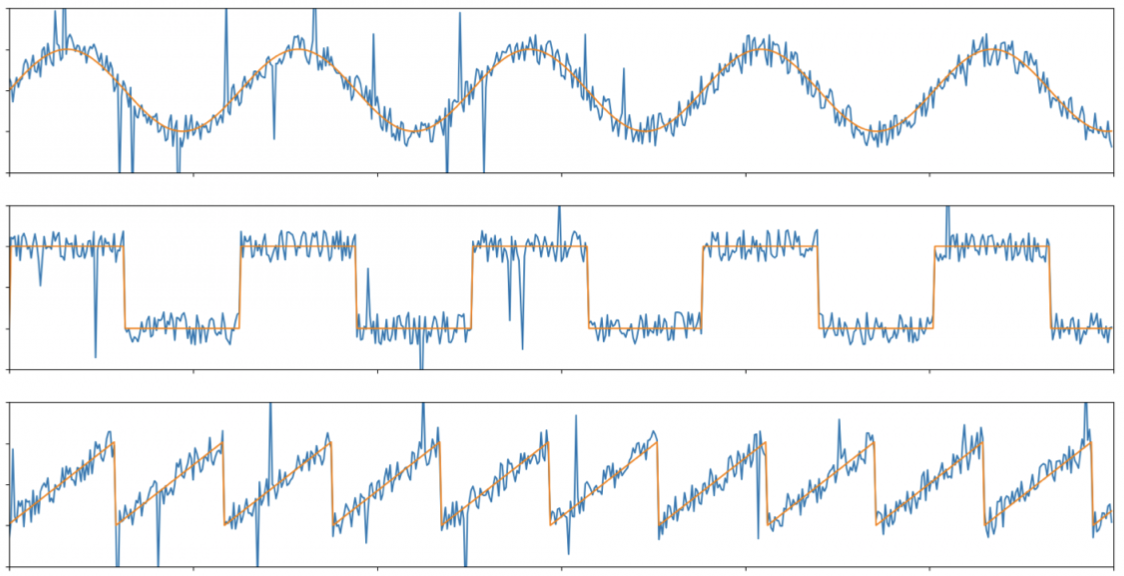
Синий сигнал — с шумами, оранжевый — идеальный, абсолютно чистый. Фильтр не может на 100% выпрямить сигнал, флуктуации все равно будут (см. пример, зеленый — отфильтрованный сигнал).

Частотный фильтр — это электрическая цепь, которая эффективно пропускает только одну область частот. Устройство позволяет «игнорировать» лишние частоты. Тем самым выделять и выравнивать сигналы любой формы — квадратные, синусоидальные, треугольные и другие.

Пример диапазона частот усиливаемого сигнала. Зависимость коэффициента пропускания по напряжению от частоты сигнала.

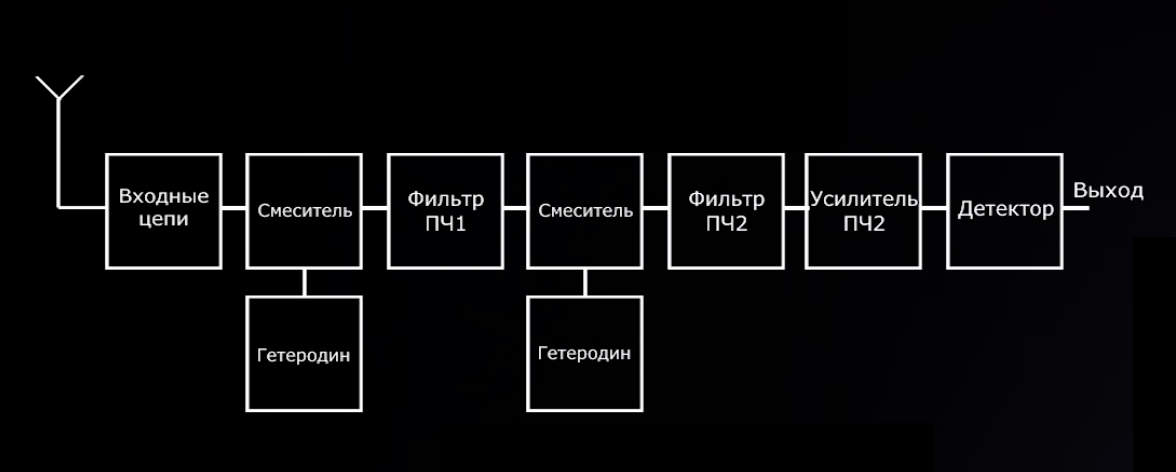
Фильтры широко применяют в измерительной, электронно вычислительной и радиотехнике. Яркий пример из схемотехники приемно-передающих устройств — ФНЧ/ ФПЧ в супергетеродинах и приемниках прямого преобразования, которые помогают выделить определенную частоту из диапазона.

Типичная схема супергетеродина.

Фильтры используют не только в радиостанциях, усилителях и другой профессиональной технике. Их можно встретить в любом приемно-передающем устройстве — например, в смартфоне или роутере. Если говорить о более «прекрасном», то фильтры используют в эквалайзерах для обработки аудиосигналов.

Эквалайзер FabFilter Pro-Q2.

Какие бывают фильтры

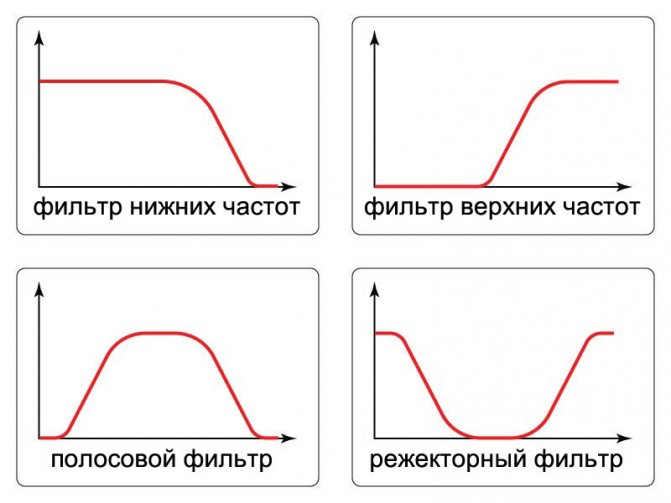
Чаще всего можно встретить фильтры нижних частот (ФНЧ) и верхних (ФВЧ), а также полосовые и заградительные.

Фильтр верхних частот — пропускает частоты выше частоты среза.

Фильтр нижних частот — пропускает частоты ниже частоты среза.

Полосовой фильтр — пропускает определенную полосу.

Заградительный фильтр — не пропускает частоты определенной полосы, но пропускает колебания, выходящие за ее пределы.

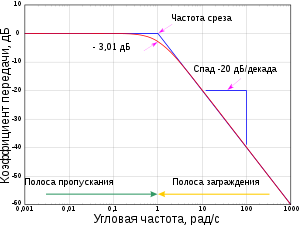
Частота среза — это такая частота, после которой идет фронт (спад) с полосы пропускания на полосу заграждения. Посмотрим, как это выглядит на АЧХ ФНЧ:

Видно, что с увеличением частоты падает коэффициент передачи.

И вот простое правило: чем круче спад, тем круче фильтр.

Соответственно, для названных видов фильтров АЧХ будут следующими:

АЧХ для ФНЧ, ФВЧ, полосового и режекторного (заградительного) фильтров.

Согласитесь — красивые рисунки! Но как получить это на

плате

практике?

Очередной резистивный делитель, или из чего состоят фильтры

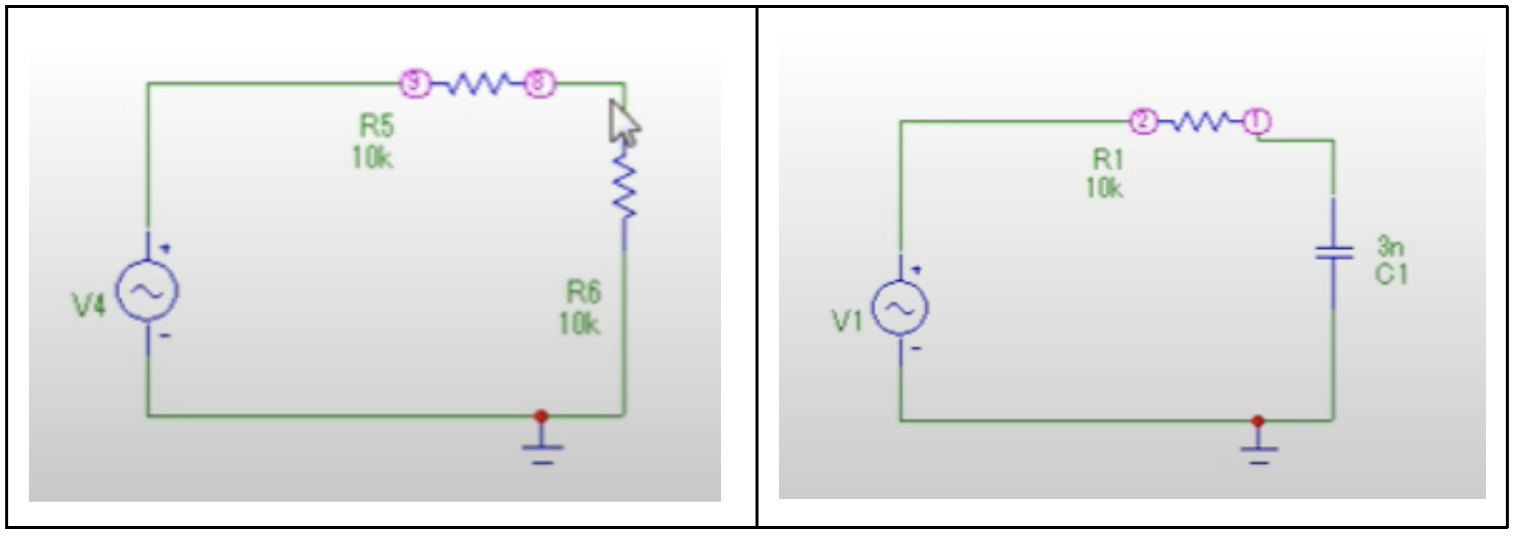
На самом деле, схема фильтра напоминает резистивный делитель (делитель напряжения на резисторах). Посмотрите сами:

Слева — резистивный делитель, справа — электрический фильтр.

Разница буквально в одном элементе: вместо резистора стоит конденсатор. Но на АЧХ это влияет очень сильно. При включении делителя АЧХ будет стабильна, то есть частота источника на выходную амплитуду никак влиять не будет. Другая ситуация с фильтром: на определенной частоте появляется явный срез.

АЧХ резистивного делителя.

АЧХ ФНЧ.

Это связано с тем, что при увеличении частоты тока сопротивление на конденсаторе уменьшается и напряжение падает — по такому принципу работают ФНЧ.

Запомните правило. Емкостное сопротивление обратно пропорционально частоте тока и емкости конденсатора — чем больше их величины, тем меньше емкостное сопротивление.

АЧХ можно «отразить», если поменять емкость и резистор местами — превратить ФНЧ в ФВЧ. Но это не все варианты схемотехнического многообразия

Схема и АЧХ для RC-ФВЧ.

LC-фильтры

Вместо резистора можно поставить индуктивность, и тогда вместо привычного ФНЧ (RC-ФНЧ) получим LC-ФНЧ. Суть та же: у него будет своя частота среза и так далее. Но добротность фильтра будет выше — соответственно, область частот, которую пропускает фильтр (она же полоса пропускания), будет меньше, а спад АЧХ — круче. Именно LC-контуры используются в фильтрах для работы с высокочастотным диапазоном.

LC-фильтры.

Принцип построения LC-фильтров основан на свойствах емкостей и индуктивностей по-разному вести себя в цепях переменного тока.

Индуктивное сопротивление катушки прямо пропорционально частоте тока, проходящего через нее. Следовательно, чем выше частота тока на катушке, тем большее реактивное сопротивление она этому току оказывает — сильнее задерживает переменные токи на более высоких частотах и легче пропускает на более низких.

У конденсатора наоборот: чем выше частота тока, тем легче протекает переменный ток. А чем ниже его частота, тем большим препятствием для тока оказывается этот конденсатор.

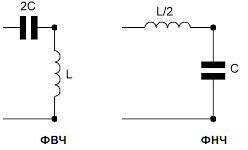
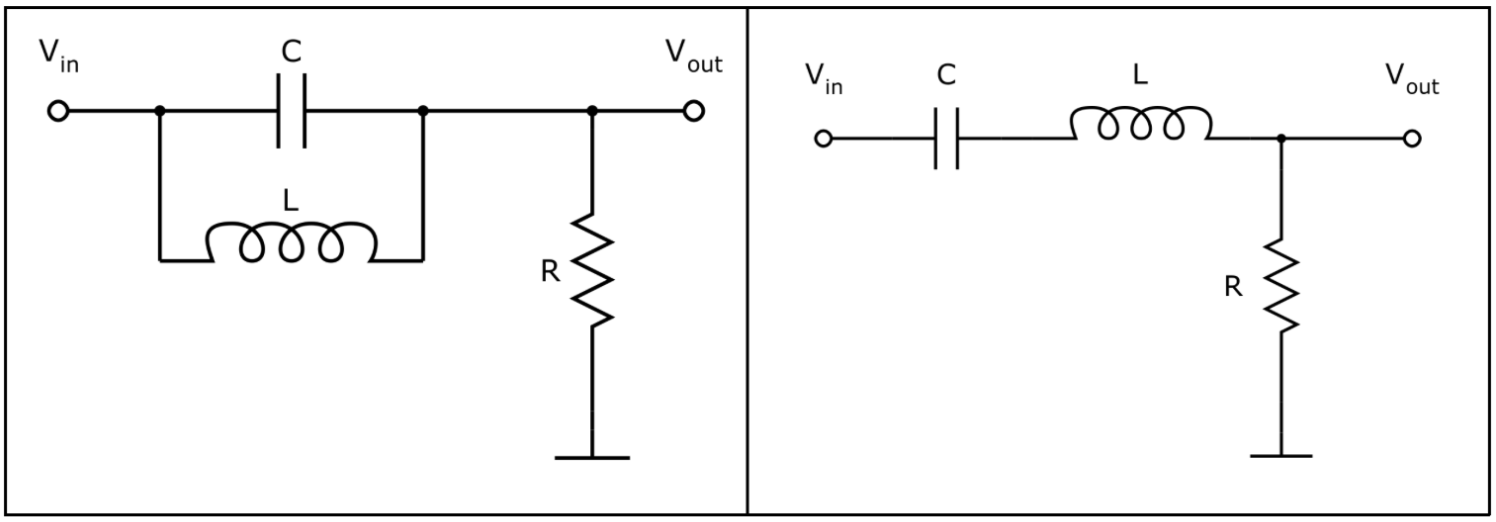
Схемы режекторного и полосового фильтров чуть сложней. Режекторный фильтр — это цепь с параллельно соединенными индуктивностью и емкостью, а полосовой — с последовательно соединенными.

Слева — режекторный фильтр, справа — полосовой.

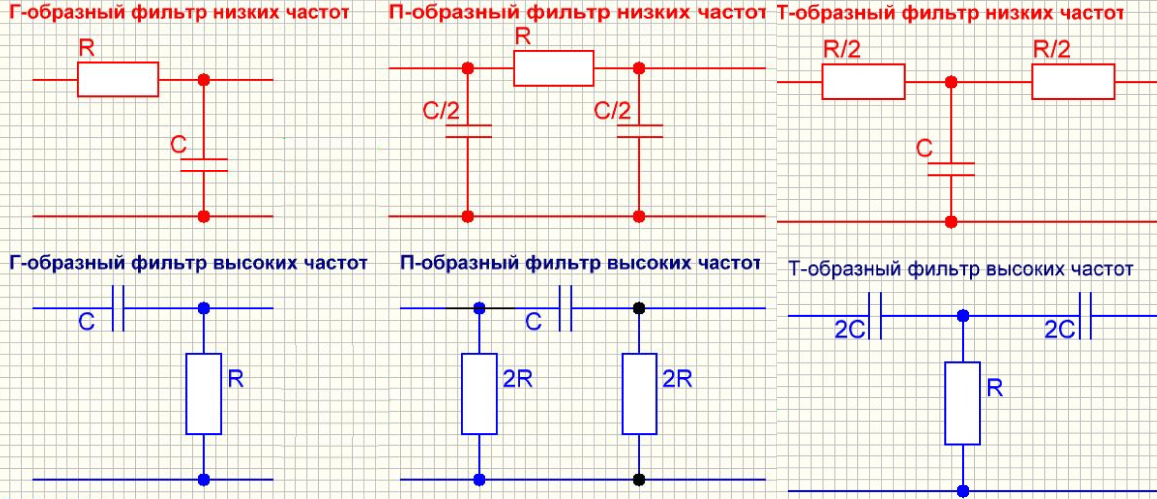
Г-, Т- и П-образные фильтры

Схематически ФНЧ и ФВЧ бывают Г-образными, Т-образными и П-образными (многозвенными).

Г-образные — это схемы ФНЧ и ФВЧ, которые мы рассмотрели выше. Их входные сопротивления всегда меньше выходных. Г-образные фильтры часто применяют в качестве трансформаторных сопротивлений. В качестве фильтров обычно используют П- и Т-образные схемы.

Г-, П- и Т-образные RC-фильтры.

Тип схемы обычно выбирают из экономических соображений. Например, для сборки LC-ФНЧ лучше использовать П-образную схему, чтобы сэкономить катушки индуктивности, а для LC-ФВЧ — Т-образную.

Немного о параметрах частотных фильтров

Вот мы упомянули, что у фильтров есть ширина полосы пропускания, добротность, частота среза. Но все ли это параметры и как они связаны? Давайте разбираться.

Ключевые параметры

При проектировании частотных фильтров учитывают следующие параметры:

• наклон АЧХ — чем круче, тем лучше,
• частота среза — выбирается разработчиком,
• неравномерность АЧХ — чем меньше, тем лучше,
• отношение входного и выходного сопротивлений — особенно важный параметр для ВЧ-фильтров,
• ослабление в полосе задержания — оно же ослабление в полосе заграждения, но без учета переходного участка (длительности фронта).

Самый важный параметр — это частота среза. С помощью нее мы можем регулировать, какую долю частотного диапазона «проигнорировать», а какую — оставить. Поговорим о ней чуть подробнее.

Подробнее о частоте среза

Частота среза — это такая частота, на которой ослабление фильтра равно -3 дБ в логарифмическом масштабе (в линейном это 0,707).

Важно отметить, что частота среза для ФНЧ и ФВЧ вычисляется по одному выражению:

Зная сопротивление/ индуктивность и емкость, можно определить, на какой частоте случится ослабление на -3 дБ. То есть, опираясь на нужную частоту среза, мы можем рассчитать и спроектировать фильтр. Или не все так просто?

Что такое порядок фильтра

Допустим, вы знаете частоту среза и хотите спроектировать фильтр. Но что такое R, C и L? Обычные номиналы для сопротивления, емкости и индуктивности? Вы можете ответить «да» и будете правы: для ФНЧ и ФВЧ второго порядка (самых обычных Г-образных RC- и LC-фильтров) достаточно подобрать резистор, конденсатор и катушку с нужными параметрами. Но для фильтров больших порядков ответ неоднозначный.

Наклон АЧХ удовлетворяет не всегда: если он сильно пологий, то радиоприемное устройство может поймать лишние частоты. Чтобы избавиться от такого эффекта, разработчики стараются делать фильтры с крутым наклоном АЧХ.

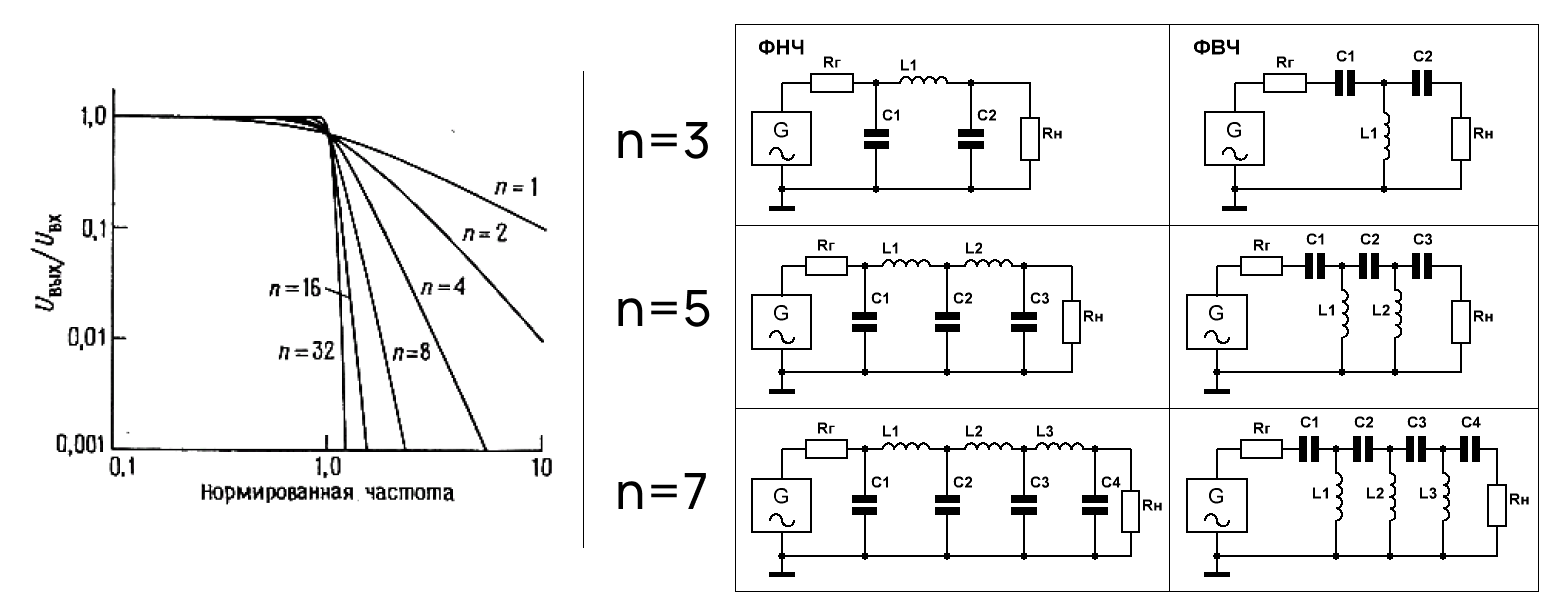
Наклон АЧХ тем круче, чем больше ослабление в полосе задержания и выше порядок фильтра. Последнее указывает на количество L- и C- элементов: в фильтре пятого порядка будет, например, три емкости и две индуктивности.

Зависимость крутизны наклона АЧХ от количества порядков (n).

Можно сказать, что каждый LC-элемент — индуктивность или емкость — дает уклонение АЧХ на 12 дБ на октаву, тогда как RC — всего 6 дБ на октаву.

Октава — это область частотного диапазона, на которой значение частоты увеличивается в два раза. Иногда в литературе предпочитают измерять в декадах, которые обозначают область с увеличением частоты в десять раз.

Рассчитывать фильтры — это сложно

Теперь вы знаете, что означают те самые R, C и L в формулах для частоты среза: это «суммы» номиналов для элементов фильтра. Стало ли от этого проще рассчитывать фильтры под определенную частоту среза? Не особо.

Расчет фильтров — это отдельная наука, объединяющая теорию электрических цепей, электротехнику и математические методы.

Чтобы рассчитать фильтр большого порядка по заданным условиям, применяют специальные методики. Среди них — формулы на базе полиномов Баттерворта и Чебышева, функций Бесселя.

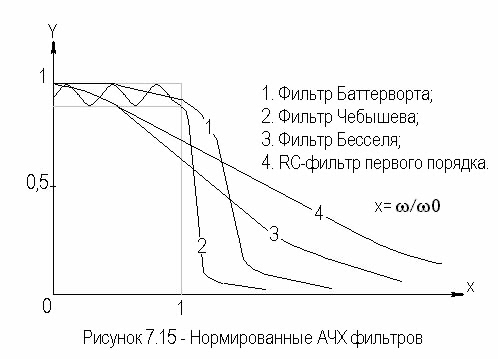
Нормированные АЧХ фильтров.

По сути, выбирая конкретную методику, вы выбираете фильтр:

• Фильтр Баттерворта — обладает самой плоской характеристикой затухания в полосе пропускания, за счет этого имеет плавный спад.
• Фильтр Чебышева — обладает самым крутым спадом, но у него самые неравномерные характеристики в полосе пропускания.
• Фильтр Бесселя — имеет хорошую фазочастотную характеристику и крутой спад.

Чтобы понять теорию расчета фильтров, рекомендую почитать книгу «Аналоговые и цифровые фильтры». Если хотите утонуть в полиномах, аналитических вычислениях комплексных расчетах, сохраняйте в закладки.

Но рассчитать фильтр можно проще, если «схитрить» и использовать онлайн-калькулятор. Так можно узнать, например, номиналы для фильтра Чебышева пятого порядка с частотой среза 4 МГц. Проверим, работает ли он на практике.

Возможно, эти тексты тоже вас заинтересуют:

→ Как геймифицировать аренду серверов со скидкой, связав сайт с внутренней панелью администрирования
→ Первая «зеркалка» от Polaroid, робот-пылесос iRobot, гомеопатия начала XX века и кое-что еще: новые находки на барахолке
→ Проблемы безопасности SNMP на практике: имитация атак и меры профилактики

Собираем фильтр Чебышева

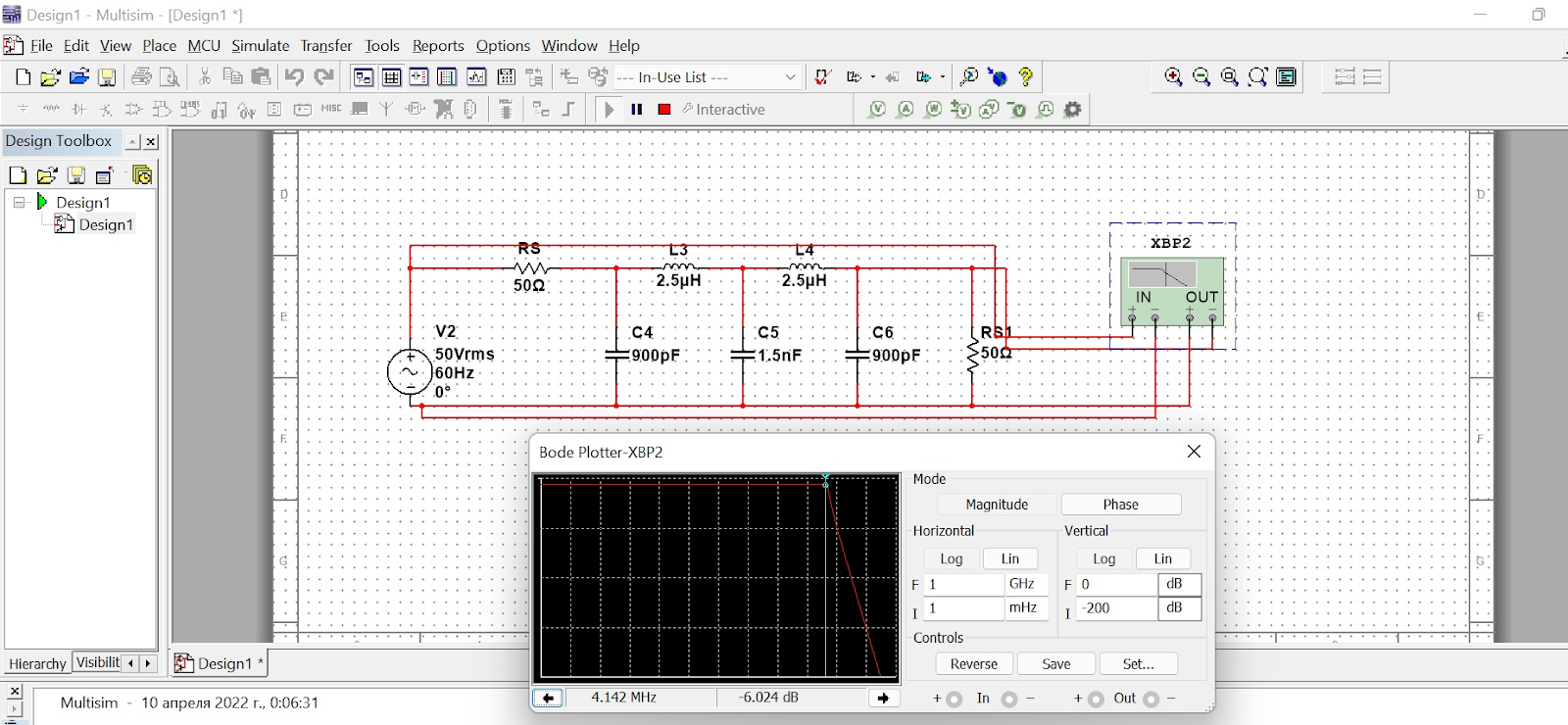
Предварительно я узнал номиналы через онлайн-калькулятор и проверил фильтр в Multisim. Если подключить параллельно Bode Plotter и правильно установить масштабы, программа покажет идеальную АЧХ фильтра Чебышева.

Multisim, схема ФНЧ Чебышева пятого порядка.

Супер — схему можно «перенести» на макетную плату.

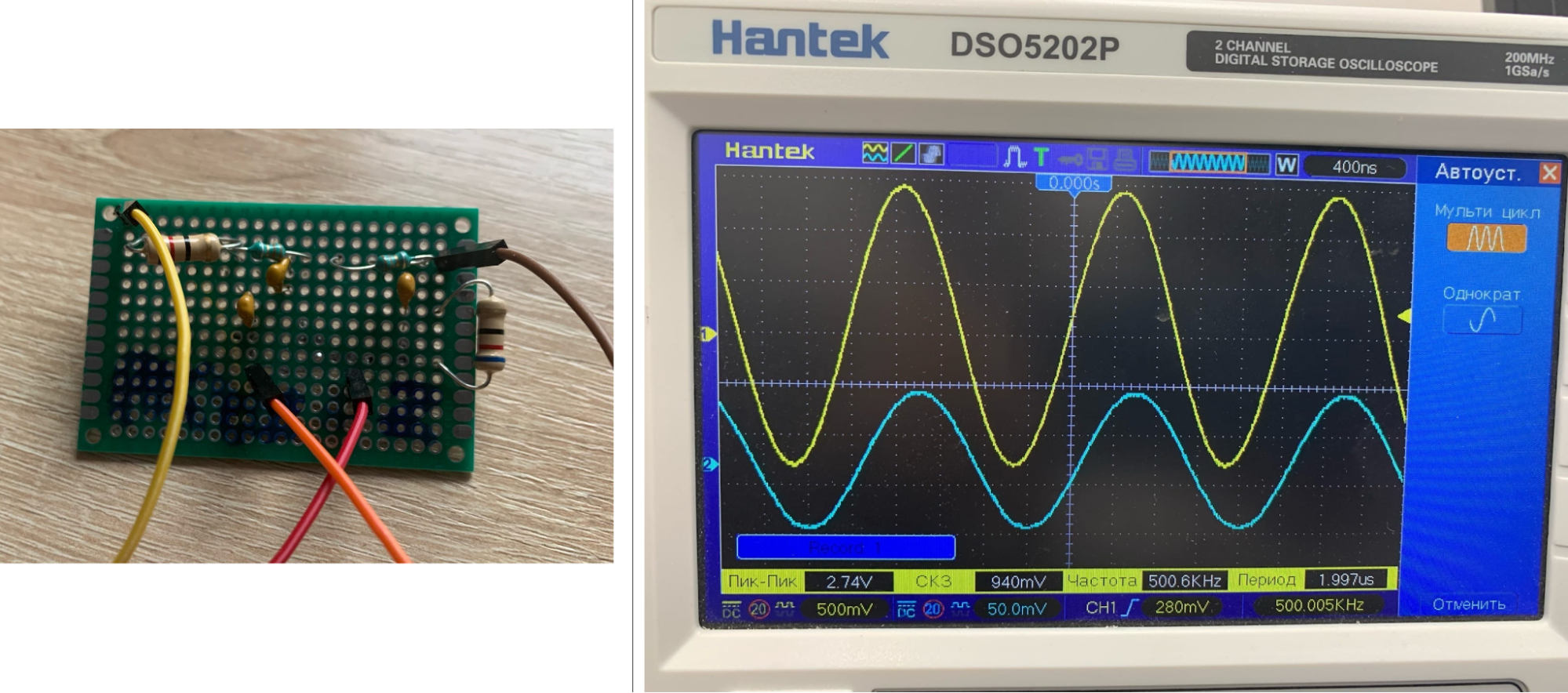
Понадобится генератор гармонических колебаний и осциллограф, подключенный к выходам фильтра. Если у вас есть анализатор цепей, можно использовать его.

Синусоида синего цвета — выходной сигнал, желтого — входной.

Обратите внимание. Электрическая схема может отличаться по номиналам от идеальной, которую вы рассчитали под свою частоту среза. Не всегда возможно точно повторить значения емкостей и индуктивностей, потому что элементов с такими номиналами может просто и не быть.

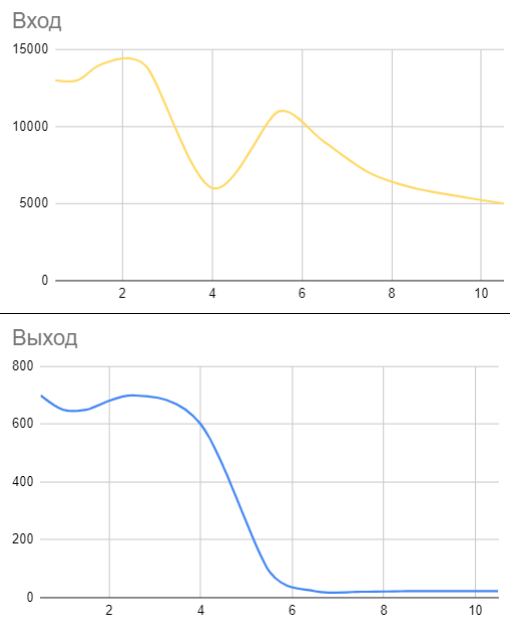
Постепенно увеличивая частоту входного сигнала, можно составить таблицу для построения графика.

Если отразить значения на системе координат, получится график для фильтра Чебышева.

Готово — у нас получилось добиться вполне крутого спада на частоте 4 МГц, ФНЧ Чебышева работает.

В статье рассмотрена лишь малая часть теоретических и практических аспектов. Фильтров гораздо больше: есть активные на базе операционных усилителей, микроконтроллеров, рассчитанные топологии Саллена-Ки и программные фильтры. Обо всем этом — в следующей статье.