При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.
Адиабатический процесс
Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:
- теплопроводность между внешней средой и системой по той или иной причине является низкой;
- скорость процесса велика, поэтому обмен теплом не успевает происходить.
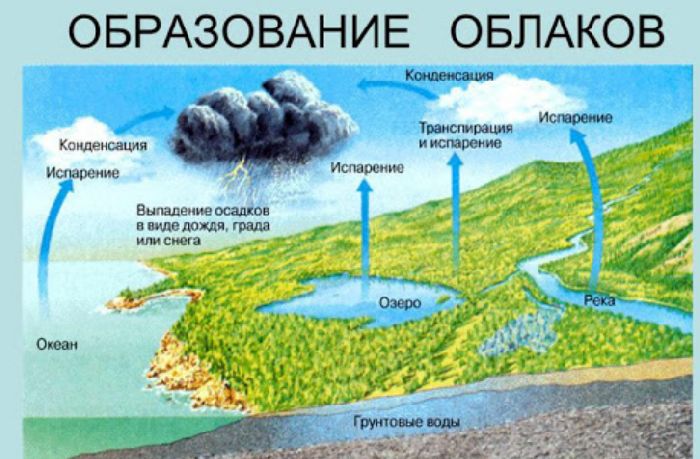
В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.
Уравнение Пуассона для адиабаты идеального газа
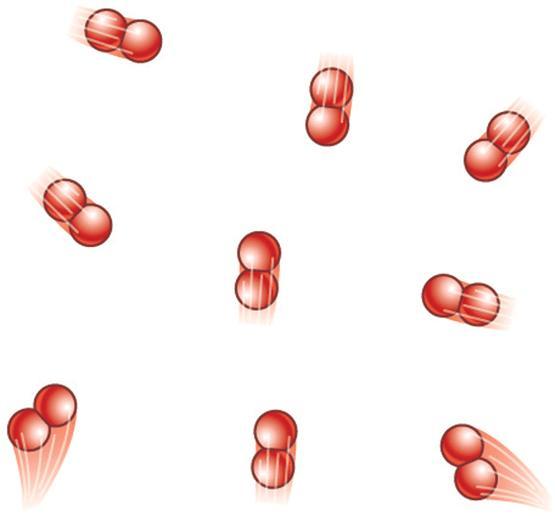
Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.
Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:
dU = -P*dV.
Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.
В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:
P*Vγ = const.
Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.
Что такое показатель адиабаты?
Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом CP изобарную теплоемкость, а символом CV — изохорную. Тогда для γ справедливо равенство:
γ = CP/CV.
Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.
Теплоемкости CP и CV
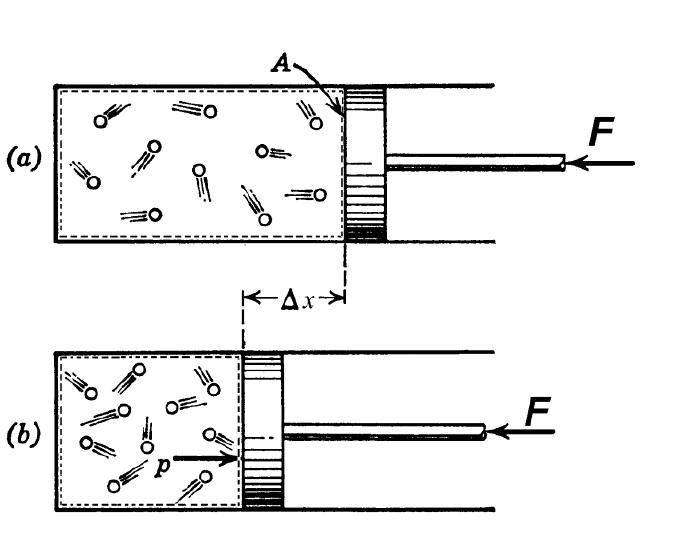
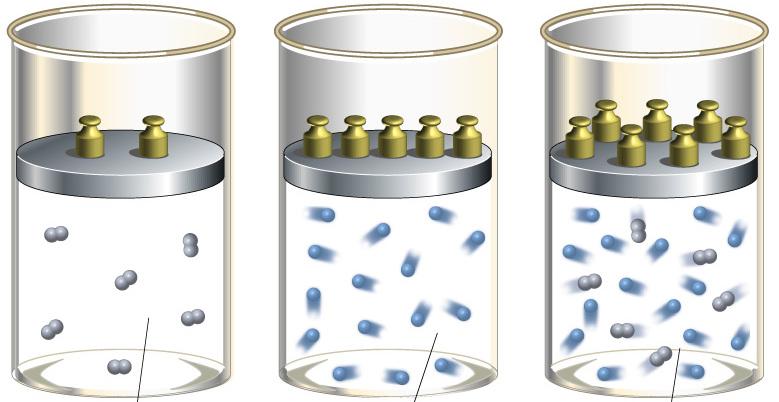
Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин CP и CV. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:
dU = CV*dT.
Величина CV определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.
Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:
CP*dT = CV*dT + P*dV.
Отсюда видно, что CP>CV, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.
Величина γ для газа идеального одноатомного
Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:
CP = CV + R.
Откуда можно определить значение изохорной теплоемкости CV:
γ = CP/CV;
CV = R/(γ-1).
Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:
CV = 3/2*R.
Из последних двух равенств следует значение показателя адиабаты:
3/2*R = R/(γ-1) =>
γ = 5/3 ≈ 1,67.
Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.
Зависимость γ от числа степеней свободы
Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.
Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для CV приобретает вид:
CV = 5/2*R.
Тогда значение γ будет равно:
γ = 7/5 = 1,4.
Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.
Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:
γ = 4/3 ≈ 1,33.
Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.
Показатель адиабаты для смеси газов
Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна ai. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:
γ = ∑i=1N(ai*γi).
Где γi — это величина γ для i-го компонента.
Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.
Определение показателя адиабаты
Цель
работы:
познакомиться с адиабатическим процессом,
определить показатель адиабаты для
воздуха.
Оборудование:
баллон с клапанома, компрессор, манометр.
Теоретическое введение
Адиабатический
процесс – это
процесс, протекающий в термодинамической
системе без теплообмена с окружающей
средой. Термодинамической системой
является система, содержащая огромное
количество частиц. Например газ, число
молекул которого сравнимо с числом
Авагадро 6,02∙1023
1/моль. Хотя движение каждой частицы
подчиняется законам Ньютона, но их так
много, что состояние системы характеризуют
макроскопическими параметрами, такими
как давление
P,
объем V,
температура
T.
Согласно
первому началу термодинамики, являющемуся
законом сохранения энергии в
термодинамических процессах, теплота
Q,
подводимая к системе, расходуется на
совершение работы А
и на изменение внутренней энергии Δ
U
Q
= A
+
U.
(1)
В
применении к идеальному газу теплота,
подводимая к газу приводит к изменению
температуры:
,
где
= m/M
– количество газа, равное отношению
массы к массе одного моля, С
− молярная теплоемкость, зависящая от
вида процесса. Внутренняя энергия
идеального газа − это кинетическая
энергия всех молекул, она равна
,
гдеCv
– молярная
теплоемкость при изохорическом
нагревании. Работа элементарного
изменения объема силами давления равна
произведению давления на изменение
объема: dA=
PdV.
Для
адиабатического процесса, происходящего
без теплообмена (Q
= 0), работа совершается за счет изменения
внутренней энергии, A
= −
U.
При адиабатическом расширении работа
газа положительна, поэтому внутренняя
энергия и температура понижаются. При
сжатии – наоборот. Все
быстро протекающие процессы можно
достаточно точно считать адиабатическими.
Выведем
уравнение
адиабатического
процесса идеального газа. Для этого
применим уравнение первого начала
термодинамики для элементарного
адиабатического процесса
dA=
− dU,
которое
принимает
вид
РdV
=−
СvdT
. Применим еще одно уравнение, полученное
дифференцированием уравнения Менделеева
– Клапейрона (PV=νRT):
PdV
+VdP
=R
dT.
Исключая один из параметров, например,
температуру, получим соотношение для
двух других параметров
.
Интегрируя и потенцируя, получим
уравнение адиабаты черездавление
и объем: P
V
= const.
Аналогично
для других пар параметров:
T
V
-1
= const, P
-1
T—
= const.
(2)
Здесь
– показатель адиабаты, равный отношению
теплоемкостей газа при изобарическом
и изохорическом нагревании.
Получим формулу для показателя адиабаты
в молекулярно-кинетической теории.
Молярная теплоемкость по определению
это количество теплоты, необходимое
для нагревания одного моль вещества на
один Кельвин
.
При изохорическом нагревании теплота
расходуется на повышение внутренней
энергии.
Подставив теплоту, получим.
Тогда показатель адиабаты может быть
определен теоретически по формуле
.
(3)
Здесь
i
– число степеней свободы молекул газа.
Это число координат, достаточное для
определения положения молекулы в
пространстве или число составляющих
компонентов энергии молекулы. Например,
для одноатомной молекулы кинетическая
энергия может быть представлена как
сумма трех компонентов энергии,
соответствующих движению вдоль трех
осей координат, i
= 3. Для жесткой двухатомной молекулы
следует добавить еще два компонента
энергии вращательного движения, так
как энергия вращения относительно
третьей оси, проходящей через атомы,
отсутствует. Итак, для двухатомных
молекул i
= 5. Для воздуха как для двухатомного
газа теоретическое значение показателя
адиабаты будет равно
= 1,4.
Показатель
адиабаты можно определить экспериментально
методом Клемана – Дезорма. В баллон
нагнетают
воздух, сжимая до некоторого давления
Р1,
немного
больше
атмосферного.
При сжатии воздух несколько нагревается.
После установления теплового равновесия
баллон на короткое время открывают.
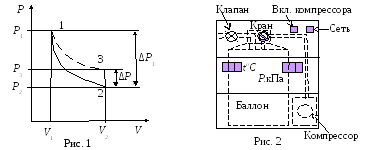
В этом
процессе расширения 1–2 давление падает
до атмосферного Р2=Ратм,
а исследуемая масса газа, которая до
этого занимала часть объема баллона
V1,
расширяется, занимая весь баллон V2
(рис.1).
Процесс расширения воздуха (1−2) происходит
достаточно быстро, его можно считать
адиабатическим, происходящим по уравнению
(2)
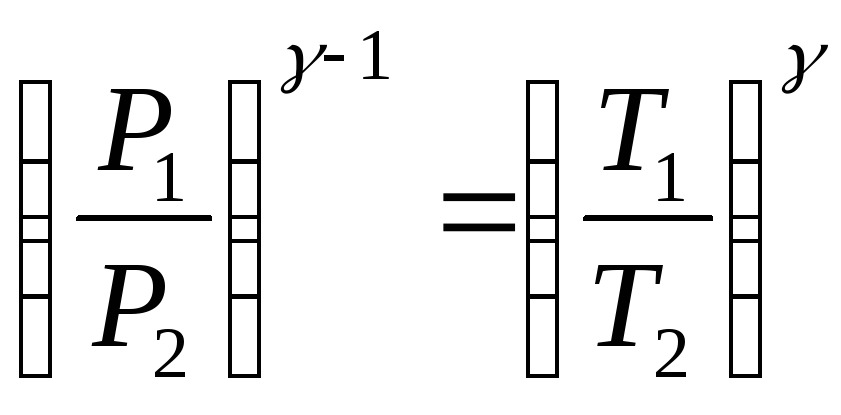
( 4)
В
адиабатическом процессе расширения
воздух охлаждается. После закрытия
клапана охлажденный воздух в баллоне
через стенки баллона нагревается до
температуры лаборатории Т
3
= Т1.
Это изохорический процесс 2–3
.
(5)
Решая совместно
уравнения (4) и (5), исключая температуры,
получим уравнение, связывающее давления:
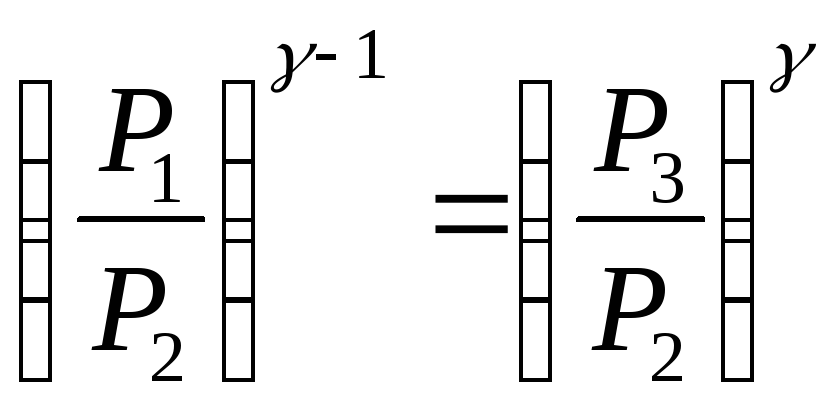
из которого следует определить показатель
адиабатыγ.
Датчик давления измеряет не абсолютное
давление, которое записано в уравнениях
процессов, а избыточное над атмосферным
давлением. То есть Р1
= ΔР1+
Р2,
и Р3
=
ΔР3+Р2.
Переходя к избыточным давлениям, получим
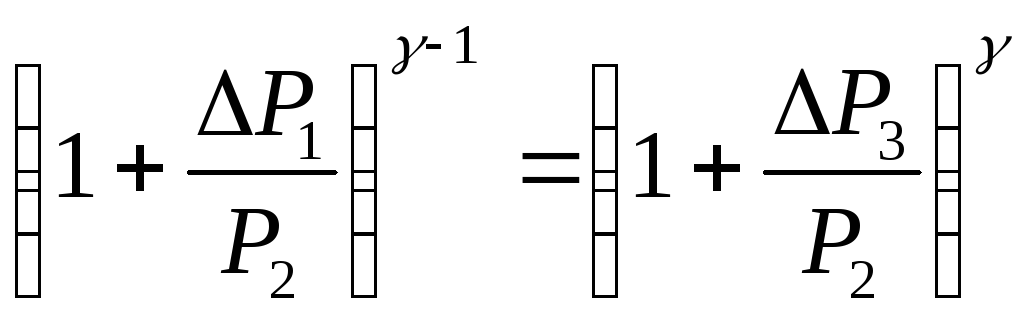
Избыточные давления невелики по
сравнению с атмосферным давлениемР2
. Разложим члены уравнения в ряд по
соотношению
.
После сокращения наР2
получим для показателя адиабаты расчетную
формулу
.
(6)
Лабораторная
установка
(рис.2) состоит из стеклянного баллона,
который сообщается с атмосферой через
клапан «Атмосфера». Воздух накачивается
в баллон компрессором при открытом
кране «К». После накачивания, во избежание
утечки воздуха, кран закрывают.
ВЫПОЛНЕНИЕ РАБОТЫ
1.
Включить установку в сеть 220 В.
Открыть
кран баллона. Включить компрессор,
накачать воздух до избыточного давления
в диапазоне 4 –11 кПа. Закрыть кран
баллона. Выждать 1,5 –2 мин, записать
величину давления ΔР1
в таблицу.
|
ΔР1, |
|||||
|
ΔР3, |
|||||
|
γ |
2. Повернуть клапан
«Атмосфера» до щелчка, клапан откроется
и захлопнется. Произойдет адиабатический
сброс воздуха с понижением температуры.
Следить за повышением давления в баллоне
по мере нагрева. Измерить наивысшее
давление ΔР3
после установления
теплового равновесия. Записать в таблицу.
Повторить
опыт не менее пяти раз, изменяя исходное
давление в диапазоне 3–11 кПа.
Выключить
установку.
3.
Произвести расчеты. Определить показатель
адиабаты в каждом опыте по формуле (6).
Записать в таблицу. Определить среднее
значение показателя адиабаты <γ>
4.
Оценить случайную погрешность измерения
по формуле для прямых измерений
.
(7)
5.
Записать результат в виде:
=
.
Р =
0,9. Сравнить результат с теоретическим
значением показателя адиабаты двухатомного
газа
теор
= 1,4.
Сделать
выводы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Адиабатный процесс

4.7
Средняя оценка: 4.7
Всего получено оценок: 149.
4.7
Средняя оценка: 4.7
Всего получено оценок: 149.
Среди различных явлений, происходящих с газами, важную роль играет адиабатный процесс. Он широко используется в технике и часто встречается в Природе. Рассмотрим его суть более подробно.
Адиабатный процесс
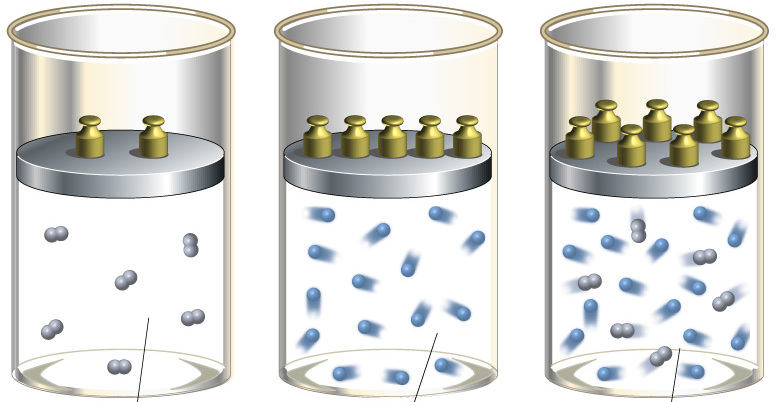
При изучении законов газовых процессов (изопроцессов) для изменения внутренней энергии газа используется обмен теплом с внешними источниками. Например, в изохорическом процессе, когда объем газа не меняется, увеличение внутренней его энергии возможно за счет внешнего нагрева. Обмен теплом также происходит и в изобарическом и изотермическом процессах.
Однако, состояние газа и его внутренняя энергия могут меняться и без теплового обмена с внешними источниками. Такой процесс, для которого количество подведенного тепла равно нулю ($Q=0$), называется адиабатным.
Для того, чтобы газовый процесс был приближен к адиабатному в реальных условиях, существует два способа (и их комбинация). Во-первых, можно окружить систему толстой теплоизолирующей оболочкой, сильно замедляющей обмен теплом. Во-вторых, процесс можно проводить очень быстро, при этом теплообмен просто не успеет произойти.
На первый взгляд, может показаться, что если к системе не подводится тепло, то она не может совершать работу. Однако, это не так. Согласно Первому Закону термодинамики, изменение внутренней энергии системы равно сумме работы внешних сил и количества тепла переданного системе:
$$ΔU=A+Q$$
А это значит, что в адиабатном процессе совершение работы возможно. Но вся эта работа будет произведена за счет изменения внутренней энергии газа.
График адиабаты
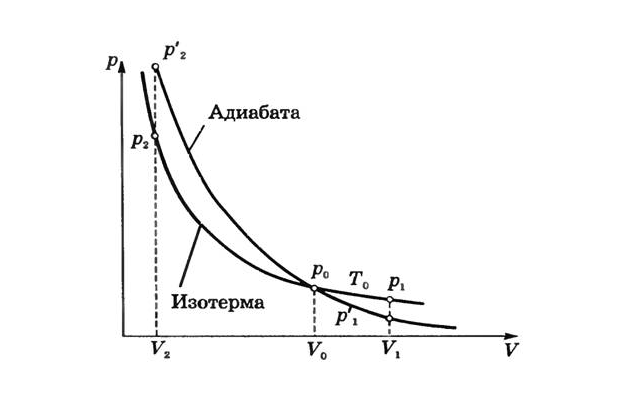
Характеристикой внутренней энергии газа является его температура. То есть, если в адиабатном процессе производится работа, то это происходит с обязательным изменением температуры. Например, если работа положительна, и внешние силы сжимают газ, то его температура увеличится, газ нагреется.
Отсюда следует, что давление газа при сжатии в адиабатном процессе будет расти быстрее, чем в изотермическом. В адиабатном процессе давление будет повышаться не только за счет уменьшения объема, но и за счет увеличения температуры. То есть, график адиабаты в координатах $p-V$ внешне будет похож на график изотермы, но пройдет более круто.
Можно вывести математические уравнения данных процессов:
- Изотерма: $pV=const$;
- Адиабата: $pV^gamma=const$.
Параметр $gamma$ в формуле адиабатного процесса называется показателем адиабаты. Для реальных газов в нормальных условиях показатели адиабаты несколько больше единицы, и равны:
|
Газ |
Показатель |
|
Пропан |
1.13 |
|
Метан |
1.32 |
|
Воздух |
1.40 |
|
Аргон |
1.67 |
Фактически, изотерму можно представить адиабатой, с показателем адиабаты $gamma=1$.
Адиабатные процессы в Природе и технике
Поскольку при быстром сжатии и расширении газа теплообмен очень невелик, адиабатные процессы широко используются в технике, и играют большую роль в атмосферных явлениях в Природе.
Например, в двигателях внутреннего сгорания горючая смесь после впуска в цилиндр в течение короткого времени сжимается, а затем, после воспламенения смеси в течении короткого времени расширяется. Таким образом, такты сжатия и рабочего хода в двигателях являются хорошими примерами адиабатного процесса.
Значительный нагрев газа при адиабатном процессе используется в дизельных двигателях. В этих двигателях нет систем для поджигания сжатой топливовоздушной смеси. В дизеле происходит сжатие атмосферного воздуха, сильнее, чем в бензиновом карбюраторном двигателе. А в конце сжатия топливо впрыскивается в цилиндр с помощью специальной форсунки. В этот момент воздух имеет температуру, достаточную для самовоспламенения впрыснутой горючей смеси, температура сгоревшей топливовоздушной смеси резко возрастает, смесь расширяется, толкая поршень и совершая полезную работу.
Природные адиабатные процессы играют значительную роль в формировании погоды. Нагретые массы воздуха быстро поднимаются вверх и расширяются. В результате их температура падает ниже точки росы, и влага, содержащаяся в воздухе, конденсируется в облака. Однако, при снижении снова происходит адиабатное сжатие, температура повышается, и облачные капли у нижней границы облаков снова превращаются в пар.
Что мы узнали?
Адиабатный процесс – это газовый процесс, при котором не происходит теплообмена с внешней средой. Работа при адиабатном процессе может быть совершена только за счет изменения внутренней энергии. На графике $p-V$ график адиабаты похож на график изотермы, но пройдет более круто.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 149.
А какая ваша оценка?
Уравнение Пуассона для адиабатного процесса
Содержание:
- Описание адиабатного процесса
- Уравнение Пуассона
- Коэффициент Пуассона
- Применение уравнения в расчетах ДВС и холодильных установок
Описание адиабатного процесса
Определение
Адиабатный или адиабатический процесс – это процесс, который протекает с небольшой скоростью при отсутствии теплового обмена с окружающей средой.
Адиабатный процесс является разновидностью термодинамического процесса. Важными условиями его возникновения являются теплоизолированная система и условия, при которых полностью исключается теплообмен с окружающей средой. При проведении практических исследований Q = 0. По первому закону термодинамики требуется полный расход выполненной работы для изменения внутренней энергии системы:
(A=Delta U)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Такие результаты практически недостижимы при реальных условиях. Причина заключается в отсутствии идеальных теплоизоляционных материалов. Однако ученым удалось максимально приблизиться к созданию подходящих условий.
Например, благодаря применению оболочек, которые характеризуются низкими параметрами теплопроводности, создаются условия, как в термосе. Другим способом выступает достижение достаточно большой скорости протекания адиабатного процесса. В этом случае система обменивается теплом с окружающей средой в течение короткого промежутка времени, которым можно пренебречь при расчетах.
Уравнение Пуассона
При возникновении адиабатного процесса наблюдается одновременное изменение трех характеристик, которыми обладает газообразное вещество: V, p, Т. Величины зависят друг от друга, что выражается в уравнении Клапейрона-Менделеева. Корректно представить описание процесса можно, дополняя формулу уравнением Пуассона.
Формулировка отражает наличие зависимости между объемом и давлением газа. Исходя из первого принципа термодинамики, уравнение для адиабатного процесса в случае идеального газа будет выглядеть следующим образом:
(0 = CVDt + pdV)
Удаляя из уравнения выражение dT по уравнению Клапейрона-Менделеева, получается следующее равенство:
(pV = RT)
Таким образом:
(dT=frac{1}{R}left(pdV+V dp right))
В результате будет записана формула:
(frac{C_{V}}{R}left(pdV+V dp right)+pdV=0)
Исходя из уравнения Майера,
(R = CP – CV)
Необходимо подставить эту формулу, а также поделить числитель и знаменатель дроби перед скобками на (CV) и обозначить (CP/CV) – (gamma)
(frac{1}{gamma -1}left(pdV+V dp right)+pdV=0)
Можно сделать следующий вывод:
(V dp + gamma pdV=0)
Почленно поделив уравнение на произведение (pV), формула будет записана следующим образом:
(frac{dp}{p}+gamma frac{dV}{V}=0)
В результате интеграции данного уравнения получается следующее соотношение:
(ln p+gamma ln V=ln C)
где С является постоянной величиной интегрирования.
Если пропотенциировать последнюю формулу, то в итоге получается уравнение Пуссона:
(pVgamma =const)
Важно отметить, что (gamma) определяется природой газообразного вещества. К примеру, в случае воздуха (gamma=1,42).
Коэффициент Пуассона
Определение
Показатель адиабаты равен отношению теплоемкости в условиях постоянного давления к теплоемкости в условиях постоянного объема.
Показатель адиабаты по-другому называют коэффициентом Пуассона или фактором изоэнтропийного расширения. Для обозначения этой величины используют греческую букву γ (гамма) или κ (каппа). Такие специальные символы применимы для решения задач химических инженерных дисциплин. Если решается задача по теплотехнике, целесообразно изображать коэффициент Пуассона в виде латинской буквы k.
Показатель адиабаты рассчитывают из отношения между изобарной теплоемкостью газообразного вещества и его изохорной теплоемкостью. Формула имеет следующий вид:
(k=frac{C_{p}}{C_{V}})
В разных газах показатель адиабаты будет неодинаковым. Для идеального газообразного вещества коэффициент Пуассона составляет 5/3, для двухатомного – 7/3, для трехатомного – 4/3.
Применение уравнения в расчетах ДВС и холодильных установок
В условиях реальных газов имеют значения силы, которые возникают при взаимодействии молекул друг с другом. Для расчета показателя адиабаты исследованных газообразных веществ требуется проводить эксперименты. В 1819 году учеными Клеманом и Дезормом были предложены методики определения коэффициента Пуассона. Описание эксперимента:
- резервуар наполнили охлажденным газом;
- достижение давлением величины Р1;
- открытие крана;
- адиабатическое расширение газа;
- понижение давления до значения атмосферного РА;
- изохорное прогревание газообразного вещества до температуры окружающей среды;
- повышение давления в баллоне до Р2.
В этом случае показатель адиабаты будет иметь следующий вид:
(k=frac{P_{1}-P_{A}}{P_{1}- P_{2}})
После расчетов показатель адиабаты будет больше 1. Это объясняет постоянное возрастание температуры во время адиабатического сжатия идеального или реального газа. В случае расширения газообразного вещества, температурные показатели снижаются. Описанное явление носит название пневматического огнива. Это свойство адиабатического процесса применяют при конструировании двигателей, функционирующих на дизельном топливе. Горючая смесь в агрегате сжимается, находясь в специальном цилиндре, и воспламеняется под действием высокой температуры.
Уравнение Пуассона применимо не только для разработки двигателей внутреннего сгорания, но и активно применяется для осуществления расчетов в проектировании холодильного оборудования. Формула Пуассона позволяет с максимальной точностью описать равновесный адиабатный процесс, при условии которого состояния равновесия непрерывно сменяют друг друга. Если в реальных обстоятельствах открыть кран в баллоне, что приведет к адиабатному расширению газа, можно будет наблюдать нестационарный переходный процесс, сопровождающийся завихрениями газообразного вещества, которые со временем затухают по причине макроскопического трения.
Насколько полезной была для вас статья?
Рейтинг: 2.00 (Голосов: 8)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Показатели адиабаты: определение и процесс
При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.
Адиабатический процесс

Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:
- теплопроводность между внешней средой и системой по той или иной причине является низкой;
- скорость процесса велика, поэтому обмен теплом не успевает происходить.
В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.
Уравнение Пуассона для адиабаты идеального газа

Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.
Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:
Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.
В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:
Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.
Что такое показатель адиабаты?
Показатель γ, который появляется в уравнении Пуассона для газа идеального, представляет собой отношение теплоемкости при постоянном давлении к аналогичной величине, но уже при постоянном объеме. В физике теплоемкостью называют величину теплоты, которую нужно передать данной системе или забрать у нее, чтобы она изменила свою температуру на 1 Кельвин. Будем обозначать символом CP изобарную теплоемкость, а символом CV — изохорную. Тогда для γ справедливо равенство:
Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.
Теплоемкости CP и CV
Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин CP и CV. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:
Величина CV определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.
Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:
CP*dT = CV*dT + P*dV.
Отсюда видно, что CP>CV, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.
Величина γ для газа идеального одноатомного
Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:
Откуда можно определить значение изохорной теплоемкости CV:
Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:
Из последних двух равенств следует значение показателя адиабаты:
Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.
Зависимость γ от числа степеней свободы
Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.
Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для CV приобретает вид:
Тогда значение γ будет равно:
Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.
Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:
Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.
Показатель адиабаты для смеси газов
Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна ai. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:
Где γi — это величина γ для i-го компонента.
Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.
Адиабатический процесс — справочник студента

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Не можете решить контрольную?! Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
К адиабатическим часто относят процессы, которые происходят с большой скоростью. Адиабатические процессы используют, например, в двигателях внутреннего сгорания, в холодильных приборах. Рассмотрим адиабатический процесс в идеальном газе. Запись первого начала термодинамики для адиабатического процесса выглядит как:
Уравнение адиабатического процесса
- Подставим вместо в формулу (6) правую часть выражения (4):
- где для идеального газа – показатель адиабаты (или коэффициент Пуассона).
Из полученного дифференциального уравнения имеем:
Уравнение (7) называют уравнением адиабатического процесса (уравнением адиабаты, уравнением Пуассона).
Уравнение адиабаты можно легко получить в других параметрах: (p (T) или V(T)). Диаграмма адиабатического процесса в осях p(V) отображается гиперболой.
Адиабатический процесс как и изохорный, изобарный и изотермический процессы происходят при постоянной теплоемкости. В адиабатном процессе теплоемкость равна нулю.
Примеры решения задач
Понравился сайт? Расскажи друзьям!
Адиабатный процесс, его суть и и формулы :
Адиабатный процесс (в некоторых источниках упоминается как адиабатический) — это термодинамический процесс, который происходит при отсутствии теплообмена с окружающей средой. Есть несколько факторов, которые характеризуют этот класс. Например, адиабатный процесс происходит динамично и укладывается в короткий срок времени. Происходят процессы данного класса, как правило, мгновенно.
Связь с первым началом термодинамики
Адиабатный процесс (адиабатический) можно напрямую связать с первым законом термодинамики. Его формулировка “по умолчанию” звучит следующим образом: изменение количества теплоты в системе при протекании в ней термодинамического процесса будет численно равно сумме изменения внутренней энергии идеального газа и работы, совершаемой этим газом.
Если мы попытаемся записать первое начало термодинамики в его стандартном виде, то получим следующее выражение: dQ = dU + dA. А теперь постараемся видоизменить эту формулу применительно к адиабатическому процессу. Как было сказано ранее, подобные процессы протекают при условии отсутствия теплообмена с окружающей (внешней, как ее называют некоторые литературные источники) средой.
В таком случае формула, описывающая первое начало термодинамики, примет следующий вид: dA = -dU. Теперь несколько подробнее о видоизменении.
Если мы говорим о том, что теплообмена в системе не происходит, изменение количества теплоты (обозначенное в формуле первого закона термодинамики через dQ) будет равно нулю.
Следовательно, мы можем перенести одно из слагаемых из правой части в левую, после чего получим формулу, приведенную к описанному ранее виду.
Следствие из первого начала термодинамики для адиабатического процесса
Допустим, что в системе произошел адиабатный процесс. В этом случае можно, не вдаваясь в мельчайшие детали, говорить о том, что газ при расширении совершает работу, но при этом он теряет свою внутреннюю энергию. Иными словами, работа, совершаемая при адиабатном расширении газа, будет осуществляться за счет убыли внутренней энергии. Следовательно, в качестве исхода этого процесса мы будем рассматривать понижение температуры самого вещества.
Абсолютно логично можно предположить, что если газ будет адиабатически сжат, его температура вырастет. Несложно заметить, что в ходе процесса будут изменяться все главные характеристики идеального газа. Речь идет о его давлении, объеме и температуре. Следовательно, грубой ошибкой стало название адиабатического процесса изопроцессом.
Адиабатный процесс. Формулы
Ранее была записана формула, выведенная из первого начала термодинамики. Используя ее, мы без особого труда можем вычислить работу в общем виде, которую будет выполнять газ при течении адиабатного процесса. Как вы уже могли догадаться, делать это мы будет при помощи интегрирования.
Итак, чтобы получить общую формулу работы для x молей газа, проинтегрируем выражение первого закона термодинамики для адиабатного процесса. Выглядеть все это будет следующим образом: A = — (интеграл) от dU. Раскроем это выражение, получим: A = — xCv (интеграл в пределах от T1 до T2) dT.
Теперь, когда мы привели интеграл к конечному виду, мы можем его упростить. На выходе получим формулу следующего вида: A = — xCv (T2 – T1). Ну и последним шагом станет небольшое упрощение. Избавимся от минуса перед формулой. Для этого сделаем в скобках небольшую перестановку, поменяв конечную температуру с начальной местами. В итоге получим: A = xCv (T1 – T2).
Уравнение адиабаты
Используя первое начало термодинамики для адиабатного процесса, мы можем найти уравнение адиабаты. При этом оно будет записано для произвольного числа молей идеального газа. Итак, запишем первоначальную формулу. Она имеет такой вид: dA + dU = 0. Но ведь мы прекрасно знаем, что работа идеального газа представляет численно собой не что иное, как произведение давления на изменение объема.
В то же время изменение внутренней энергии будет равно работе, взятой с обратным знаком. А ее-то мы уже нашли при помощи интегрирования.
Значит, первое начало термодинамики для адиабатического процесса может принять следующий вид: pdV + xCvdT = 0. Из этого уравнения нам нужно исключить один показатель, а именно, температуру. Вернее, ее изменения.
Чтобы сделать это, мы обратимся к достаточно часто используемому в молекулярной физики уравнению. А именно к уравнению Менделеева-Клапейрона.
Первичное выражение
Его нам нужно продифференцировать, чем мы и займемся. Итак, в общем виде уравнение выглядит следующим образом: PV = XRT. Вследствие дифференцирования оно будет приведено к такой форме: pdV + Vdp = xRdT. Отсюда мы можем выразить изменение энергии. Оно будет равно левой части, деленной на произведение количества вещества на универсальную газовую постоянную. Иными словами, формула будет такой: (pdV + Vdp)/xR. Остается только упростить ее. В итоге получим следующее выражение: dT = (pdV + Vdp)/x(Cp — Cv)
По сути дела, первая часть задачи выполнена. Остается только довести все до ума.
Вторичное выражение. Подстановка значения
Возьмем полученную в результате дифференцирования формулу Менделеева-Клапейрона и подставим ее в выражение, выведенное нами ранее для первого закона термодинамики по отношению к адиабатному процессу. Итак, что мы получим? Все это громоздкое выражение примет следующий вид: pdV + xCv ((pdV + Vdp)/x(Cp-Cv)) = 0.
Чтобы упростить все это, мы должны принять во внимание пару фактов. Во-первых, упростить выражение можно за счет приведения к общему знаменателю.
Когда мы получим одну дробь, мы можем воспользоваться старым добрым правилом, которое гласит, что дробь равна нулю, когда ее числитель равен нулю, а знаменатель от нуля отличен.
В результате совокупности всех этих действий мы получим следующее выражение: pCpdV – pCvdV + pCvdV + VCvdp = 0.
Теперь следующим шагом мы можем разделить данное выражение на pVCv. Получим сумму двух частей, дающих в итоге ноль. Это будет Cp/Cv * dV/V + dp/p = 0. Эту формулу необходимо проинтегрировать. Тогда мы получим следующее выражение: y (интеграл) dV/V + (интеграл) dp/p = (интеграл) 0.
Ну а дальше все достаточно просто. Воспользовавшись формулами интегрирования (можно использовать табличные интегралы, чтобы все было проще), получим в итоге следующую запись: y ln V + ln p = ln (const). Получается, что p(V)y = const. Данное выражение называется в молекулярной физике уравнением Пуассона.
Многие литературные источники научной направленности также называют эту формулу уравнением адиабаты. В то же время величина y, которая имеет место в данной записи, называется показателем адиабаты. Она равна (i+2)/i. Нужно отметить, что показатель адиабаты всегда больше единицы, что, в принципе, логично.
Примеры адиабатных процессов
Вскоре после того, как был открыт адиабатический процесс, стартовало огромное количество различных исследований. Так, была создана первая теоретическая модель, имеющая отношение к циклу Карно. Именно она позволила установить условные пределы, ограничивавшие развитие тепловых машин. Но в случае некоторых реальных процессов осуществлять цикл Карно достаточно трудно. Все дело в том, что в его состав входят изотермы. А они, в свою очередь, требуют задания определенной скорости термодинамических процессов.
Заключение
С целью обойти подобные проблемы был придуман цикл Отто, а также цикл сжижения газа. Они стали широко применяться при решении конкретных задач на практике.
Стартовавшие исследования показали возможность описания некоторых природных процессов в адиабатическом плане, что позволило выявлять общие закономерности соответствующих процессов.
Примером адиабатического процесса можно смело назвать химическую реакцию, которая происходит внутри некоторого объема газа, если система является замкнутой, а обмен с внешней средой теплом отсутствует.
Адиабатный процесс в термодинамике
Адиабатный процесс или адиабатический — это термодинамический процесс, происходящий при отсутствии теплообмена с окружающей средой.
Рисунок 1. Адиабатический процесс. Автор24 — интернет-биржа студенческих работ
Есть несколько основных факторов, которые характеризуют данный класс. Например, адиабатный процесс может происходит динамично и укладывается в достаточно короткий период времени. Происходят все адиабатные процессы в термодинамике, как правило, мгновенно.
Уравнение первого закона термодинамики для исследуемого класса имеет следующий вид: $du = -dl = -pdv$.
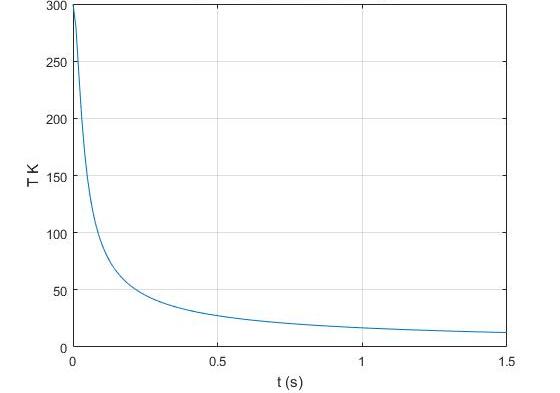
Из этой формулы видно, что работа адиабатического процесса расширения совершается в результате постепенного уменьшения внутренней энергии идеального газа и, следовательно, температура самого элемента уменьшается.
Работа адиабатного сжатия всегда идет на только увеличение внутреннего энергетического потенциала, то есть на повышение температурных параметров. Таким образом, изменения условий работы системы в адиабатном процессе эквивалентны по величине и противоположны по знаку.
Попробуй обратиться за помощью к преподавателям
В реальных условиях указанное термодинамическое явление возможно осуществить двумя методами:
- провести физический процесс так быстро, чтобы теплообмен не успел произойти;
- полностью изолировать систему от факторов внешней среды.
После введения в эксперименты вышеуказанных способов получаем такое уравнение: $dU + dA = 0$.
Графически на координатной плоскости адиабатный процесс практически всегда изображается кривой, которая называется в физике адиабатой.
Она падает намного круче, чем более постоянная изотерма, поскольку при этом явлении изменение давления происходит с помощью одновременного уменьшения температуры и увеличения объема.
Этот вывод теоретически подтверждает формула: $p = nkT$, ведь увеличение общего объема идеального газа ведет автоматически к уменьшению концентрации молекул изучаемого вещества, следовательно, уменьшение давления обусловливают два показателя — концентрация молекул $n$ и температура газа $T$.
Связь с первым началом термодинамики
Рисунок 2. Адиабатический процесс. Автор24 — интернет-биржа студенческих работ
Адиабатный процесс возможно легко связать с первым законом термодинамики. Его определение “по умолчанию” звучит следующим образом: изменение количества тепловой энергии в системе при протекании в ней определенного термодинамического процесса будет прямо пропорционально сумме изменения тепла идеального газа и работы, которая совершается данным элементом.
Если записывать первое начало термодинамики в его первоначальном, стандартном виде, то получим такое выражение: $dQ = dU + dA$. А теперь попробуем видоизменить это уравнение применительно к действию адиабатического процесса. Как было сказано ранее, подобные явление протекают только при условии отсутствия теплообмена с окружающей средой.
В таком случае новая формула, описывающая более детально первое начало термодинамики, примет уже совершенно иной вид: $dA = -dU$. Теперь немного подробнее о самом видоизменении.
Если говорить о том, что теплообмена между активно действующими в конкретной системе телами не происходит, тогда изменение количества тепловой энергии (обозначенное в уравнении первого термодинамического закона через $dQ$) будет в обязательно порядке равно нулю. Следовательно, можно перенести одну из слагаемых частей из правой части в левую, после чего получить модернизированную формулу, приведенную к описанному ранее виду.
Влияние первого начала термодинамики на адиабатический процесс
Рисунок 3. Первый закон термодинамики к различным процессам. Автор24 — интернет-биржа студенческих работ
Чтобы определить воздействие первого закона термодинамики на адиабатный процесс, необходимо чисто теоретически предположить, что в системе произошло уже данное явление.
В этом случае возможно, не вдаваясь в мельчайшие нюансы и детали, утверждать, что газ при постепенном расширении совершает работу, но при этом теряет собственную внутреннюю энергию.
Другими словами, совершаемая при адиабатном расширении газа работа будет осуществляться только посредством убыли энергетического потенциала.
Следовательно, в качестве недопущение такого исхода лучше применять понижение температуры действующего в системе вещества. Абсолютно логично можно определить, что, если газ будет адиабатически сжат, его тепловая энергия вырастет в несколько раз.
Несложно заметить, что в ходе этого процесса будут изменяться все ключевые характеристики исследуемого вещества. Речь идет о его объеме, давлении и температуре.
Поэтому, грубой ошибкой исследователей стало название адиабатического процесса изопроцессом.
Вскоре после того, как был открыт и описан адиабатический процесс, физики начали проводить огромное количество различных исследований. Так, была разработана первая теоретическая модель, которая имеет непосредственное отношение к универсальному циклу Карно.
Именно она позволила ученым установить условные границы, ограничивавшие дальнейшее развитие тепловых машин. Однако в случае некоторых природных явлений осуществлять данную модель достаточно трудно.
Все дело в том, что в его состав в основном входят изотермы, которые требуют изначального задания определенной скорости термодинамических процессов.
Использование адиабатного процесса в теоретических циклах тепловых машин
На самом деле на сегодняшний день более 90% электроэнергии вырабатывается только на тепловых электростанциях. В них в качестве рабочего тела применяется водяной пар, который возможно получают при кипении воды в адиабатном процессе.
По аналогии с устаревшими поршневыми автомобилями работают и турбинные. Но в них адиабатический процесс отвода тепловой энергии по завершении постепенного расширения газа выполняется исключительно по изобаре. На самолетах с турбовинтовым и газотурбинным двигателями изучаемое явление совершается дважды: при расширении и сжатии.
Чтобы обосновать все основополагающие и применяемые в науке понятия адиабатического процесса, ученые вывели расчетные формулы.
Здесь фигурирует одна основная величина, которая получила название параметр адиабаты. Его значение для двухатомного газа при любых условиях равно 1,4. Для расчета этого показателя адиабаты применяются две характеристики, а именно: изохорная и изобарная теплоемкости физического тела. Отношение их $k=frac$ – и есть показатель действующей в системе адиабаты.
Чтобы повысить и удержать рабочий потенциал пара, его желательно перегреть. Затем при максимально высоком давлении данный элемент подается на паровую турбину. Здесь также совершается адиабатический процесс расширения идеального пара. Турбина получает необходимое вращение, которое передается на электрогенератор.
Тот, в свою очередь, вырабатывает электроэнергию для потребителей. В идеале увеличение эффективности лучше связать с повышением давления и температуры водяного пара. Как видно из вышесказанного, адиабатный процесс в термодинамике является достаточно распространенным в производстве электрической и механической энергий.
Адиабатный (адиабатический) процесс
Согласно первому закону термодинамики ΔU = Q + A.
Изотермический, изохорный и изобарный изопроцессы широко применяются в технике.
Так, закон Гей-Люссака положен в основу строения газовых термометров; закон Шарля «работает» в устройствах, которые называются автоклавами, и т. п.
Термодинамика изучает еще один процесс, широко применяющийся на практике, в частности в тепловых двигателях. Это так называемый адиабатный процесс.
Адиабатный процесс — это термодинамический процесс, который происходит в теплоизолированной системе, то есть при отсутствии теплообмена с окружающими телами.
Поскольку в таком случае Q = 0, то в соответствии с первым законом термодинамики вся выполненная работа идет на изменение внутренней энергии системы: A = ΔU.
Конечно, в реальных условиях достичь такого результата практически невозможно, поскольку не существует идеальных изоляторов тепла. Но приблизиться к этому условию можно несколькими способами.
Например, создать оболочки с низкой теплопроводностью (по принципу термоса) или осуществить процесс настолько быстро, чтобы теплообмен между системой и окружающими телами был непродолжительным и им можно было пренебречь.
При адиабатном сжимании газа вся выполненная работа идет на увеличение внутренней энергии тела: A = ΔU. При адиабатном расширении газа A’ = —ΔU, то есть газ выполняет работу за счет уменьшения собственной внутренней энергии.
 |
| Рис. 2.5. Графическое изображение адиабаты |
Например, быстрое сжатие газа вызывает возрастание внутренней энергии, которая равняется количеству выполненной работы A, и газ нагревается. На этом явлении, в частности, построено самовозгорание топливной смеси в дизельных двигателях.
И наоборот, если газ сам выполняет работу вследствие стремительного расширения, то его внутренняя энергия уменьшается, и температура газа снижается. Это свойство адиабатного процесса положено в основу сжижения газа.
Примером адиабатного процесса является также взрыв, плавление предохранителя при коротком замыкании и т. п.
Адиабаты, как и изотермы, не перекрещиваются между собой. Материал с сайта http://worldofschool.ru
Графически на координатной плоскости pV адиабатный процесс изображается кривой, которая называется адиабатой (рис. 2.5).
Она падает круче, чем изотерма, поскольку при адиабатном процессе изменение давления происходит за счет одновременного увеличения объема и уменьшения температуры.
Этот вывод подтверждает также формула (24): p = nkТ, ведь увеличение объема газа ведет к уменьшению концентрации молекул газа, и потому уменьшение давления обусловливают два параметра — температура газа T и концентрация молекул n.
Вследствие адиабатного расширения газа происходит изменение его состояния, которое характеризуется уменьшением внутренней энергии; при адиабатном сжимании газа его внутренняя энергия возрастает.
На этой странице материал по темам: Вопросы по этому материалу:
ПОИСК
Термодинамические функции Изохорический процесс Изобарический процесс Изотермический процесс Адиабатический процесс Политропный процесс [c.65]
Температура газа в конце процесса адиабатического сжатия [c.423]
| Рис. 1.14. Процесс адиабатического сжатия в S, -диаграмме |  |
Процесс адиабатического сжатия газа характеризуется полным отсутствием теплообмена между газом и окружающей средой. При адиабатическом сжатии газа dQ = О и из уравнения (IV,2) следует, что dS = 0. [c.154]
Реакторы можно классифицировать также в зависимости от других параметров, например, природы и числа реагентов, метода из контактирования, характера процесса (адиабатический или изотермический), способа передачи тепла и т. д. [c.30]
Количество воды для увлажнения определяется изменением относительной влажности ф и снижением температуры охлаждающего воздуха на входе в теплообменные секции.
Количественная оценка изменения ф на входе и выходе охлаждающего воздуха, степень использования воды в процессе адиабатического снижения температуры воздуха, показатели испарения воды с оребренной поверхности и потерь в дренаж являются предметом специальных исследований системы увлажнения воздуха на входе в АВО. [c.74]
Если можно предсказать, как будут изменяться характеристики реакционной системы в различных условиях (скорость реакции и равновесные состояния при изменении температуры и давления), то удается сравнить результаты различного аппаратурного оформления процесса (адиабатический или изотермический процесс, единичный реактор или комбинация реакторов, проточная или периодически действующая система) и экономически оценить эффективность указанных вариантов. Только в этом случае можно надеяться, что достигнуто наилучшее оформление процесса для данных условий. К сожалению, в практике создания химических реакторов редко все бывает так просто. Часто мы не располагаем достаточными данными для сопоставления результатов расчета, не всегда можем преодолеть математические трудности или, что более вероятно, не имеем возможности тратить слишком много времени и усилий для решения математических задач. Кроме того, нельзя достаточно уверенно рассчитать реактор в отрыве от всего производства в целом. Таким образом, расчет реак/ора представляет собой некоторый компромисс между недопустимостью больших затрат труда и времени, с одной стороны, и экономическим риском принять плохое технологическое решение, с другой стороны. [c.105]
Допустим, что состоя51ие сжатого газа перед детандером характеризуется температурой Т, = 205 К и давлением = 100 ат — точка 1. Процесс адиабатического расширения газа с отдачей пненшей работы осушествляется при S = onst. Поэтому опустив из точки 1 вертикаль вниз до пересечения с изобарой, отвечающей заданному конечному давлению Рз = сип, найдем точку 4, характеризующую состояние газа в конце детандирования. Этой точке соответствует температура Т4 = 82 К и, следовательно, понижение температуры газа ЛГ [c.653]
Пример VI-6. При тех же начальных условиях, что и в двух предыдущих примерах, газ расширяется до давления 30 ат в открытой системе, процесс адиабатический обратимый с выполнением внешней работы. Определить конечную температуру газа и его энтальпию. [c.141]
Наряду с изучением и усовершенствованием состава катализатора и условий проведения реакции димеризации ацетилена было разработано технологическое оформление процесса адиабатическим методом путем регулирования теплового режима сильно экзотермической реакции и поддержания необходимой температуры за счет испарения воды и продуктов реакции при циркуляции через раствор катализатора избытка ацетилена. Постоянство состава и концентрации компонентов раствора катализатора поддерживали добавлением подкисленной воды в количествах, необходимых для компенсации ее уноса. [c.710]
Вводят еще понятие критической скорости звука а р.
Разница между йкр и а заключается в том, что а — скорость звука при действительной температуре в данной точке, а р — скорость потока, равная скорости звука при температуре, которая установилась бы после того, как газ в процессе адиабатического расширения из состояния покоя получил бы скорость, равную скорости звука. Эта температура меньше температуры торможения [c.13]
Если = О, процесс адиабатический. Для адиабатического процесса [c.93]
Полагаем, что процесс адиабатический (Q = 0), так как оборудование хорошо изолировано и потери тепла в таких случаях редко достигают 5% от общего количества энергии. Тогда [c.107]
По конечной температуре в процессе адиабатического сжатия реального газа, определяемой по s, Т- или s, -диаграммам, можно вычислить величину kj для газов, не указанных в табл. 1.2. Из выражения (1.41) [c.33]
Рассмотрим сначала соотношение между принципами Каратеодори и Клаузиуса (соответственно Томсона) ( 4). Сразу видно, что принцип Каратеодори вытекает из принципа Клаузиуса.
Обратное несправедливо, так как принцип Каратеодори ограничивается утверждением, что существуют вообще нереализуемые адиабатические процессы, в то время как принцип Клаузиуса указывает, какие процессы адиабатически нереализуемы. [c.46]
Процессы адиабатические. Это тоже не правильно, так как тепло будет проникать из окружающей среды. Однако процесс мгновенного испарения протекает очень быстро, и, следовательно, притоком тепла от окружающей среды скорее всего можно пренебречь.
Намного существеннее здесь степень влияния пены и брызг на количество жидкости, выброшенной в окружающую среду. Эти вопросы будут обсуждаться чуть ниже.
Как и в случаи с криогенными жидкостями, можно ожидать дифференцированного испарения более низкокипящих компонентов смеси, что является основой «однократной равновесной перегонки». [c.79]
По энтальпийной диаграмме можно определить также ход процесса адиабатической абсорбции. [c.449]
Цикл идеальной машины. В илеальнон компрессионной холодильной машине (рис. ХУП-5, а), цикл работы которой соответствует обратному пиклу Карно, компрессор 1 засасывает пары холодильного агента, сжи- aeт их до заданного давления, прн котором они могут быть сжижены охлаждением водой, и нагнетает пары в конденсатор II. На диаграмме Т—5 (рис.
ХУП-5, б) процесс адиабатического сжатия паров изображается вертикальной линией (адиабатой) /—2. Сжатие сопровождается нагреванием паров от температуры 7 (точка /) до температуры Т (точка 2). Лля того чтобы процесс сжижения в конденсаторе II происходил при [1ССТ0ЯН1ЮЙ температуре Т, процесс сжатия паров, как показано на [c.
Для расчета объемных коэффициентов тепло-. и массопередачи в процессе адиабатического охлаждения воздуха (путем испарения воды в потоке воздуха), характерного, например, для кондиционирования воздуха, можно использовать упрощенные формулы [c.258]
Линия /—2 характеризует процесс адиабатического расширения сухого рабочего пара в сопле эжектора от давления пара в котле до давления в испарителе ро, линия 3—6 — процесс испарения жидкости в испарителе.
Точка 3 характеризует состояние смеси рабочего пара с сухим насыщенным холодным паром давления ро.
Линия 3—4 соответствует процессу адиабатического сжатия смеси рабочего и холодного паров в диффузоре до давления конденсации р, линия 4—5 — процессу конденсации водяных паров в конденсаторе, линия 5—6 — дросселированию части конденсата в регулирующем вентиле. [c.409]
Выбор типа реактора для осуществления данного химического процесса зависит от многих факторов, из которых важнейшими являются необходимость использования катализатора, его свойства и расход термодинамические особенности процесса — адиабатические, изотермические или политропические условия проведения химической реакции методы теплообмена, используемые для обеспечения заданного температурного режима в зоне реакции свойства используемых теплоагентов периодическое или непрерывное осуществление процесса. [c.631]
Величины давлений и удельных объемов в процессе адиабатического сжатия, как видно из уравнения (1.32), связаны следующей зависимостью с начальными параметрами газа [c.18]
Известна схема совмещенного процесса испарения и конденсации, в которой реализован процесс адиабатического разделения смеси. В этой схеме величины теплоподвода и теплоотвода в совмещенной ступени равны.
Поэтому исключается возможность регулирования подвода и отвода тепла по ступеням. В связи с этим отсутствует возможность управления качеством продуктов разделения.
При неадиабатическом же разделении имеется возможность регулирования как отводимого, так и подводимого тепла в каждую смежную ступень. [c.54]
Для процесса адиабатического сжатия в идеально изолированном цилиндре, учитывая, что dQ = 0, дифференциал работы процесса адиабатического сжатия газа в соответствии с зависимостями (111-120) и (111-22) равен [c.248]
Сущность эксперимента заключается в следующем. Теорией теплового взрыва установлена связь между характеристиками рассматриваемого явления, с одной стороны, и кинетическими параметрами и условиями протекания процесса, с другой.
Если известны условия процесса и экспериментально измерены характеристики, то по теоретическим формулам, решая обратную задачу, можно определить кинетические параметры.
В нашем случае условия процесса адиабатические — езуаьтате экспери -мента мы снимаем конкретные характеристики — время индукции теплового взрыва и характер изменения температуры, т. е. исходные данные для решения указанной обратной задачи.
Полученная в результате опыта информация в виде кривых температура — время несет в себе данные о периоде индукции теплового взрыва и о критической температуре. Серия экспериментов с различными исходными температурами реакционной массы дает зависимость периода индукции теплового взрыва от температуры.
Информацию об изменениях концентрации реагентов в реакционной массе несут полученные кривые электропроводность — время . Важные стороны характера физико-химического превращения раскрывает записанный во времени расход смеси газов и паров из реактора. [c.177]
Для сушильной практики большое значение имеет понятие о теоретическом процессе адиабатического испарения в системе поверхность испарения—воздух. В этом процессе воздух только испаряет, [c.589]
Так как система изолирована, то процесс адиабатический, следовательно, ДР=0. Таким образом, единственным источником работы является изменение внутренней энергии газа, т. е. [c.34]
Так как условная теплоемкость паровоздушной смеси в процессе адиабатического сжатия претерпевает значительные изменения, в практических расчетах предлагается пользоваться средними значениями Срту, определяемой по формуле [c.142]
Учитывая условпя теплообмена, было решено в первом реакторе провестп процесс адиабатически, а во втором и третьем реакторах включить охлаждающие змеевики. Чтобы рассчитать требуемую температуру на входе в первый реактор, используем уравненпе (IV,14) без последнего члена [c.122]
Доля вещества, участвующего в процессе адиабатического мгновенного испарения, согласно [Сгетег,1974а], определяется следующим выражением [c.346]
Физические характеристики. Важнейшая характеристика процесса — адиабатический разогрев смеси АГад- Для газов, получаемых после обжига колчедана пли сжигания серы, ДГад = = 200—280°С.
Это соответствует оптимальному соотношению концентраций кислорода (10—13%) и диоксида серы (7—11%). Далее будут рассматриваться также металлургические газы, содержащие 1,5—5% SO2 и 9—16% О2. Для этих газов ДГад = 45—145°С.
Газы, идущие на вторую стадию двойного контактирования, имеют такой состав so = 0,6 — 1,2%, со = 5 —8%.Для них А7 ад = [c.188]
Здесь ( ( = 12 — 1—работа адиабатического сжатия на единицу массы холодильного агента, вт кг ь ь — энтальпия хладагента в начале и в конце процесса адиабатического сжатия, вт1кг-, 15 — энтальпия хладагента при входе и выходе из испарителя, вт/кг. Значения I находятся из диаграмм (см. рис. ХПЫ.б и Х1П-12). [c.789]
Выбор типа реакционного аппарата для осуществления данного химического процесса зависит от многих факторов, из которых важнейшими япляются необходимость использования катализатора, его свойства и расход термодинамические особенности процесса — адиабатические, изотермические или политропическио условия проводе- [c.618]
Рассмотрим поток воздуха над жидкостью в закрытом сосуде (рис. VHI-2). Входящий воздух имеет параметры t, X (Р = onst), насыщается при протекании над жидкостью и уходит в состоянии насыщения (ф=100%, 4ас, Хнас).
Процесс адиабатический, испарение воды, насыщающей воздух, происходит за счет тепла воздуха. Для покрытия расхода тепла в сосуд вводится вода в количестве Хнао — X на 1 кг сухого воздуха. Температура [c.
Для адиабатического течения вскипающей жидкости и равновесного течения газонасыщенной жидкости предложены баротропические уравнения состояния.
Установлены критические условия, разделяющие начальную стадию, когда интенсивность опорожнения полубесконечного трубчатого канала определяется чисто газодинамическими явлениями (инерционными эффектами и процессом адиабатического расширения вскипающей и равновесного расширения газонасыщенной жидкостей) с последующим этапом, когда инерция несущественна. Для двух предельных режимов истечения, когда сила гидравлического трения от скорости потока зависит линейно, и по квадратическому закону система уравнений движения сводится к одному нелинейному уравнению. Построены автомодельные решения для задачи о внезапной разгерметизации канала на одном конце. Кроме того, получены решения, описывающие стационарное истечение кипящей жидкости чере З цилиндрические насадки, а также опорожнение конечного объема через щель. [c.12]
Процесс адиабатический 5 = onst. На сколько градусов изменится температура куска меди при сжатии [c.35]
Адиабатный процесс в термодинамике
- Связь с первым началом термодинамики
- Влияние первого начала термодинамики на протекающий адиабатический процесс
- Применение адиабатного процесса для расчета тепловых машин
- Термодинамический процесс, происходящий в теплоизолированной системе, либо протекающий с большой (взрывной) скоростью, исключающей передачу тепла в окружающую среду, называется адиабатическим (адиабатным).
Этот процесс характеризуют несколько основных моментов. Например, адиабатический процесс обычно развивается энергично и быстро. В термодинамике все адиабатные процессы протекают, обычно, мгновенно.
В результате обобщения опытных фактов был создан первый закон термодинамики.
Адиабатный процесс производится с большой скоростью, исключающей теплообмен с окружающей средой.
Осуществляется полная теплоизоляция системы от влияния внешней среды.
Связь с первым началом термодинамики
Между первым законом термодинамики и адиабатным процессом прослеживается четкая связь. Первый закон термодинамики гласит – изменение внутренней энергии системы, связанной с развитием термодинамического процесса пропорционально работе, совершаемой данным элементов и изменением количества тепла идеального газа.
Влияние первого начала термодинамики на протекающий адиабатический процесс
Для определения взаимосвязи первого закона термодинамики на адиабатный процесс, нужно представить, что в замкнутой, теплоизолированной системе процесс уже завершился.
Не вдаваясь в незначительные детали и нюансы можно с уверенностью утверждать – газ, расширяясь, совершает работу, при этом уменьшается его внутренняя энергия.
Следовательно, работа, совершаемая при адиабатном расширении газа, производится посредством энергетического потенциала газа.
С другой стороны, при адиабатическом сжатии газа его тепловая энергия возрастает, при этом в ходе этого процесса изменяются основные характеристики вещества – объем, давление, температура. Поэтому, называя адиабатический процесс изопроцессом, исследователи совершают грубую ошибку.
После открытия и четкого описания адиабатического процесса, физиками произведено большое количество практических экспериментов, приведших к разработке первой теоретической модели, связавшей адиабатный процесс с универсальным циклом Карно.
Эта модель помогла ученым-физикам установить предельные возможности тепловых машин.
У модели есть некоторые недостатки, например с ее помощью сложно описать некоторые природные явления из-за отсутствия изотерм, требующих предварительного определения скорости термодинамических процессов.
Применение адиабатного процесса для расчета тепловых машин
В современной энергетике свыше 90% электрической энергии производится на ТЭС (тепловых электростанциях). Рабочим телом, заставляющим вращаться турбины, является перегретый водяной пар, получаемый при кипении воды.
Отвод тепла в ходе адиабатического процесса при расширении пара, передающего накопленную энергию турбине, осуществляется по изобаре. На реактивных и турбовинтовых двигателях самолетов это явление происходит дважды – при сжатии воздуха и последующем расширении.
Для теоретического обоснования понятия адиабатического процесса, физики-теоретики вывели расчетные формулы.
Для увеличения и стабилизации рабочего потенциала пара осуществляется его перегрев. Перегретый пар под максимально возможным давлением подается на паровую турбину. В результате происходящего адиабатического процесса расширения идеального пара совершается работа, и турбина начинает вращаться.
Ее вращение передается на электрогенератор, вырабатывающий электрическую энергию. КПД системы связан с увеличением давления и температуры перегретого водяного пара.
Из вышесказанного можно сделать вывод, что адиабатный процесс в термодинамике активно используется для производства механической и электрической энергий.
Вывод по ответу (шаблон):
- Полученное экспериментально значение
величины _________________, - полное название
словами - равное _________________, с точностью до ошибки
измерений, - число, единица
измерения - составляющей ________________ , совпадает (не
совпадает) с табличным - число, единица
измерения - (теоретическим) значением данной
величины, равным ________________ . - число, единица
измерения
4. Молекулярная физика и термодинамика
ЛАБОРАТОРНАЯ
РАБОТА № 4_1
Адиабатический процесс
Ознакомьтесь с теорией
в конспекте и учебнике. Запустите
программу. Выберите «Термодинамика и
молекулярная физика», «Адиабатический
процесс». Нажмите кнопку с изображением
страницы во внутреннем окне. Прочитайте
теорию и запишите необходимое в свой
конспект лабораторной работы. Закройте
окно теории, нажав кнопку с крестом в
правом верхнем углу внутреннего окна.
Знакомство с компьютерной моделью, описывающей адиабатический процесс в идеальном газе.
Экспериментальное подтверждение закономерностей адиабатического процесса.
Экспериментальное определение показателя адиабаты, количества степеней свободы и структуры молекул газа в данной модели.
СОСТОЯНИЕ системы
имеет фиксированныезначениямакроскопическихпараметров,
описывающих систему в целом. Параметры,
характеризующие систему в целом,
называются ПАРАМЕТРАМИ СОСТОЯНИЯ.
Примерами являются температура, давление,
объем и т.д.
РАВНОВЕСНЫМ называется
такое состояние системы, при котором
все параметры системы имеют определенные
значения, остающееся неизменнымисколь угодно долго при неизменных
внешних условиях.
ОБРАТИМЫМ называется
процесс, при реализации которого в
обратном направлении система проходит
через те же состояния, что и при
прямом ходе, но в обратной последовательности.
Равновесные процессы всегда обратимы.
КРУГОВЫМ процессом
(ЦИКЛОМ) называется процесс, при котором
система после ряда изменений возвращается
в исходноесостояние.
УРАВНЕНИЕ СОСТОЯНИЯ
идеального газа (уравнение
Менделеева-Клапейрона)
- ТЕПЛОЕМКОСТЬ тела
численно равна отношению количества
тепла d’Q,
сообщенного телу, к изменению температуры
телаdT, которое при этом
произошло: - СТЕЛА =.
- УДЕЛЬНОЙ теплоемкостью
вещества называется отношение теплоемкости
к массе тела. - Если тело нем меняет
свой объем, то оно не совершает работы,
поэтому при постоянном объеме тела
переданное телу тепло dQ’
идет на изменение его внутренней энергииdU. - ТЕПЛОЕМКОСТЬ ПРИ
ПОСТОЯННОМ ОБЪЕМЕ - СV=
. - ТЕПЛОЕМКОСТЬ ПРИ
ПОСТОЯННОМ ДАВЛЕНИИ идеального газа,
молекулы которого имеют iстепеней свободы - CP=
(1).
- ЧИСЛО (количество)
СТЕПЕНЕЙ СВОБОДЫ есть минимальное
количество независимых координат,
необходимых для однозначного описания
положения молекулы в пространстве ИЛИ
минимальное количество независимых
движений, суперпозиция которых дает
любое движение молекулы. - ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
всегда дает 3 степени свободы. - ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
дает 2 степени свободы для линейной
молекулы и 3 степени свободы, если атомы
в молекуле не расположены на одной
линии. - КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
дает 2nКОЛстепеней
свободы, гдеnКОЛ–
количество независимых колебаний атомов
в молекуле (у двухатомной молекулыnКОЛ= 1). - АДИАБАТИЧЕСКИМ
называется процесс, происходящий без
теплообмена с внешней средой (d’Q= 0). Уравнение адиабаты - PV=const(3).
- Принято также выделять
ИЗОТЕРМИЧЕСКИЙ, ИЗОБАРИЧЕСКИЙ и
ИЗОХОРИЧЕСКИЙ процессы. - МЕТОДИКА
и ПОРЯДОК ИЗМЕРЕНИЙ
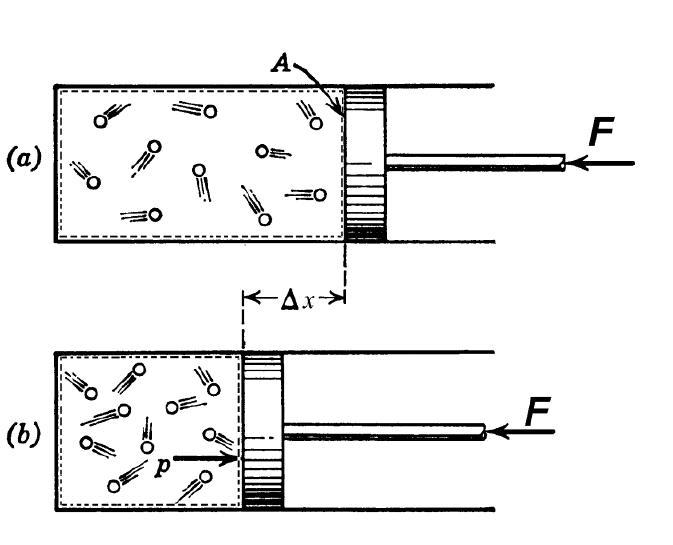
Внимательно рассмотрите
картинку на рисунке, найдите рисунок
элемента, в котором реализуется
адиабатический процесс, обратите
внимание на его теплоизоляцию. Найдите
математическую формулировку условия
теплоизоляции. Ознакомьтесь с графиками
в правой части изображения.
Зарисуйте необходимое
в свой конспект лабораторной работы.
Получите у преподавателя
допуск для выполнения измерений.
Установите начальное значение объема Vнач= 40 дм3 и начальную температуру Т1 газа, близкую к числам из табл.1. Для этого нажмите кнопку «ВЫБОР», переместите маркер мыши так, чтобы его острие находилось в указанной точке вблизи границы столбика на градуснике, и коротко нажмите и удерживая левую кнопку мыши двигайте столбик.
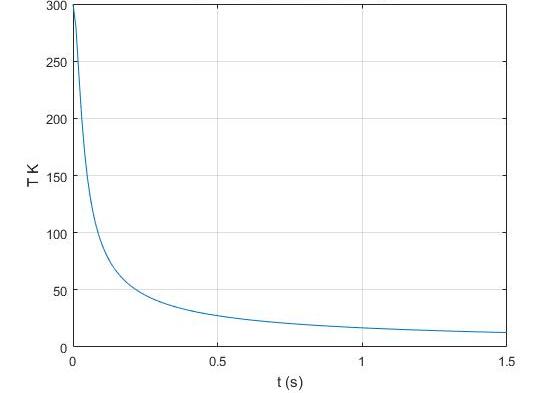
Нажмите мышью кнопку «Старт»на экране и наблюдайте перемещение поршня на левой картинке модели и перемещение точки по красной кривой теоретической адиабаты. Попробуйте останавливать процесс нажатием кнопки «СТОП». Последующий запуск процесса осуществляется нажатием кнопки «Старт».
После автоматической остановки процесса запустите его снова, нажав кнопку «Старт», и останавливайте, нажимая кнопку «Стоп», когда крестик на теоретической адиабате (красная кривая) будет находиться вблизи следующих значений объема: 15, 20, 25, 30, 35 и 40 дм3 (6 значений), записывая при остановке значения объема, температуры и давления в таблицу 2.
Установите новое значение температуры Т2, взяв его из таблицы 1, задавая Vнач= 40 дм3и повторите измерения, записывая результаты в таблицу 3.
ТАБЛИЦА
1. Начальные значения температуры (не
перерисовывать)
| Бригада | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Т1 | 50 | 70 | 100 | 120 | 140 | 170 | 200 | 220 |
| Т2 | 230 | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
ТАБЛИЦЫ
2,3 Результаты измерений
ОБРАБОТКА РЕЗУЛЬТАТОВ
И ОФОРМЛЕНИЕ ОТЧЕТА:
Постройте на одном рисунке графики экспериментальных зависимостей логарифма давления от логарифма объема для обеих адиабат (указав на них начальные температуры).
Определите число степеней свободы молекулы газа, исследуемого в данной компьютерной модели, используя формулу (2).
Подберите распространенный газ, структура молекулы которого близка к наблюдаемой.
Запишите ответы и проанализируйте ответы и графики.
Определение показателя адиабаты для воздуха
Федеральное агентство по образованию
Саратовский государственный технический университет
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ
Методические указания к выполнению лабораторной работы
по курсам «Теплотехника», « Техническая термодинамика
и теплотехника », «Гидравлика и теплотехника» для студентов
дневной и заочной форм обучения
Саратовс кого государственного
Цель работы : ознакомление с методикой и экспериментальное определение показателя адиабаты для воздуха, изучение основных закономерностей для адиабатного, изохорного и изотермического процессов изменения состояния рабочих тел.
Адиабатными называются процессы изменения состояния рабочего тела (газа или пара), происходящие без подвода и отвода теплоты от него.
Необходимым и достаточным условием адиабатного процесса является аналитическое выражение dq =0, означающее, что в процессе совершенно отсутствует теплообмен, т. е. q =0. При dq =0 для обратимых процессов Tds =0, т. е. ds =0; это значит, что для обратимых адиабатных процессов s = const . Иными словами, обратимый адиабатный процесс является в то же время и з о э н т р о п н ы м.
Уравнение, связывающее между собой изменение основных термодинамических параметров в адиабатном процессе, т. е. уравнение адиабаты имеет вид:

где k — показатель адиабаты (изоэнтропы):

Уравнение адиабаты можно получить в другом виде, используя связь между основными термодинамическими параметрами:

Аналогично получается зависимость:

Работа в адиабатном процессе может быть определена из уравнения первого закона термодинамики:




Заменяя в этом уравнении 




Используя связь между термодинамическими параметрами, можно получить другое выражение для работы адиабатного процесса. Вынося в уравнении (4) 



Графическое отображение адиабатного процесса в p — v — и T — s -координатах показано на рис.1.
В p — v — координатах кривая адиабаты представляет собой показательную функцию 

В p — v — координатах адиабата всегда идет круче изотермы, поскольку 
В T — s -координатах кривая адиабаты представляет собой вертикальную линию с 
Рис.1. Адиабатный процесс изменения состояния газа
в p — v — и T — s — диаграммах
К адиабатному процессу близки реальные процессы, происходящие с рабочими телами в тепловых машинах. Например, расширение газов и паров в турбинах и цилиндрах тепловых двигателей, сжатие газов и паров в компрессорах тепловых двигателей и холодильных машин.
Приближенно величину k можно оценить по атомности газа (или основных газов в смеси), пренебрегая зависимостью от температуры:
для одноатомных газов: 
для двухатомных газов: 
для трех — и многоатомных газов: 
При известном составе газа показатель адиабаты 
Показатель адиабаты также может быть определен из дифференциальных соотношений термодинамики. В отличие от теории идеального газа дифференциальные уравнения термодинамики дают возможность получить общие закономерности изменения параметров для реальных газов. Дифференциальные уравнения термодинамики получают путем частного дифференцирования объединенного уравнения первого и второго законов термодинамики:
сразу по нескольким параметрам состояния.
Аппарат дифференциальных уравнений термодинамики позволяет, в частности, установить ряд важнейших соотношений для теплоемкостей реальных газов.
Одним из них является соотношение вида:

Соотношение (7) устанавливает связь между теплоемкостями cp , cv и элементарным изменением параметров p и v в адиабатном процессе 

Учитывая, что показатель адиабаты 

Последнее выражение можно использовать для экспериментального определения показателя адиабаты.
Для определения истинного показателя адиабаты достаточно разреженных реальных газов с использованием уравнения (8) необходимы точные измерения термодинамических параметров р, v , T и их частных производных. Но если в уравнение (8) подставить малые конечные приращения, то при 

При р2=рбар, то есть равном барометрическому давлению,

где р u 1 , р u 3 – избыточное давление в состояниях 1, 3.
Очевидно, что с уменьшением избыточного давления р u 1 значение km будет приближаться к истинному для атмосферного воздуха.
Лабораторная установка (рис.2) имеет сосуд постоянного объема 1, краны 2, 3. Воздух нагнетается в сосуд компрессором 4. Давление воздуха в сосуде измеряется U -образным манометром 5. Сосуд не изотермический, поэтому воздух, который находится в нем, принимает равновесное температурное состояние с окружающей средой в результате теплообмена. Контроль температуры воздуха в сосуде осуществляется с помощью ртутного термометра 6 с ценой деления 0,01 ° С.

Рис.2. Схема лабораторной установки для определения показателя
адиабаты воздуха: 1 – сосуд; 2, 3 – краны; 4 – компрессор;
5 — U -образный манометр; 6 – термометр
На рис.3 показаны термодинамические процессы, происходящие в воздухе при проведении эксперимента: процесс 1-2 – адиабатное расширение воздуха при частичном его выпуске из сосуда; 2-3 – изохорный нагрев воздуха до температуры окружающей среды; 1-3 — эффективный (результирующий) процесс изотермического расширения воздуха.














Рис.3. Термодинамические процессы в воздухе при проведении эксперимента
ТРЕБОВАНИЯ БЕЗОПАСНОСТИ ТРУДА
При выполнении настоящей работы отсутствуют и не могут возникнуть опасные и вредные факторы. Однако подъем давления в сосуде компрессором с ручным приводом следует производить постепенно, вращая маховик компрессора. Это предотвратит возможность выбивания воды из манометра.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Ознакомиться со схемой установки и произвести ее осмотр для определения готовности ее к работе.
Определить по барометру и записать в протокол измерений атмосферное давление рбар, температуру t и относительную влажность воздуха в лаборатории. Открыть кран 2 (рис.2) и при закрытом кране 3, вращая маховик компрессора 4, накачать воздух в сосуд 1. Как отмечалось выше, р u 1 должно быть возможно меньше. Поэтому, создав небольшое избыточное давление в сосуде, прекратить подачу воздуха, закрыть кран 2.
Давление выдерживается в течение некоторого времени, необходимого для установления термического равновесия с окружающей средой, о чем должна свидетельствовать неизменность показаний манометра 5. Записать значение р u 1. Затем открыть и при достижении атмосферного давления немедленно закрыть кран 3. Воздух, оставшийся в сосуде в результате адиабатного расширения и охлаждения при истечении, начнет нагреваться за счет изохорного подвода теплоты из окружающей среды. Этот процесс наблюдается по заметному увеличению давления в сосуде до р u 3. Опыт повторить 5 раз.
Полученные результаты заносятся в протокол измерений по форме табл.1.
http://school16rostov.ru/gumanitarnye/adiabaticheskij-protsess-spravochnik-studenta.html
http://pandia.ru/text/79/436/56473.php