Вычисление приближенного значения активности ионов в растворе электролита
Задача 529.
Вычислить приближенное значение активности ионов K+ и SO42- в 0,01 М растворе K2SO4.
Решение:
Уравнение диссоциации K2SO4 имеет вид:
K2SO4 ⇔ 2K+ + SO42-.
Активность иона 

Здесь f — коэффициент активности иона (безразмерная величина), СМ – концентрация иона. Коэффициент активности иона зависит от заряда иона и ионной силы раствора, которая равна полусумме произведений концентрации каждого иона на квадрат заряда иона:
Ионная сила раствора равна:
I = 0,5[CM(2K+) . 12 + CM(SO42-) . 22] = 0,5(0,02 . 12) + (0,01 . 22) = 0,03.
Коэффициент активности ионов K+ и SO42- найдём по формуле, получим:
Теперь рассчитаем активность ионов K+ и SO42- из соотношения 


Ответ: 

Задача 530.
Вычислить приближенное значение активности ионов Ba2+ и Cl— в 0,002 н. растворе BaCl2.
Решение:
M(BaCl2) = CЭ(BaCl2)
СМ = СН = 2 . 0,002 = 0,004 моль/л.
Уравнение диссоциации хлорида бария имеет вид:
BaCl2 ⇔ Ba2+ + 2Cl— .
Активность иона 

Здесь f — коэффициент активности иона (безразмерная величина), СМ – концентрация иона. Коэффициент активности иона зависит от заряда иона и ионной силы раствора, которая равна полусумме произведений концентрации каждого иона на квадрат заряда иона:
Ионная сила раствора равна:
I = 0,5[CM(Ba2+) . 22 + CM(Cl—) . 12] = 0,5(0,004 . 22) + (0,008 . 12) = 0,024.
Коэффициент активности ионов Ba2+ и Cl– найдём по формуле, получим:
Теперь рассчитаем активность ионов Ba2+ и Cl— из соотношения 


Ответ: 

Задача 531.
Найти приближенное значение коэффициента активности иона водорода в 0,0005 М растворе H2SO4, содержащем, кроме того, 0,0005 моль/л НСI. Считать, что серная кислота полностью диссоциирует по обеим ступеням.
Решение:
Общая концентрация ионов водорода составляет сумму от концентрации H2SO4 и концентрации НСI. Кислоты диссоциируют по схеме:
H2SO4 ⇔ 2H+ + SO42-;
HCl ⇔ H+ + Cl—
Из уравнений вытекает, что концентрация ионов водорода в серной кислоте в 2 раза выше, чем кислоты и составит: 2 . 0,0005 = 0,001 моль/л. Общая концентрация ионов водорода в растворе составит:
0,001 + 0,0005 = 0,0015 моль/л.
Коэффициент активности иона рассчитывается по формуле:
где f — коэффициент активности иона (безразмерная величина), I — ионная сила раствора, Z — заряд иона. Ионная сила раствора рассчитаем по уравнению:
Здесь концентрация иона в растворе, получим:
I = 0,5[CM(H+) . 12 + CM(SO42-) . 22 + CM(Cl—) . 1 =
= 0,5[(0,0015 . 12) + (0,0005 . 22) + (0,0005 . 12)] = 0,002.
Рассчитаем коэффициент активности иона водорода:
Ответ: 0,95.
Влияние электростатических взаимодействий на поведение ионов в растворе. Ионная сила раствора. Коэффициент активности
Характеристикой электростатического поля в растворе и мерой электростатических взаимодействий ионов является ионная сила раствора I, связанная с концентрацией ионов 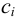
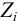
Ионной силой раствора определяется коэффициент активности иона 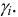
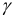
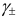
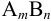
Например, для 0,01 М раствора 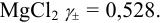
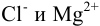
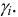
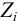
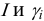
В практических расчетах для оценки коэффициентов активности используют ряд постулатов, упрощающих расчеты:
- Коэффициенты активности ионов равного заряда, независимо от знака и размера, приблизительно равны.
- Растворы, содержащие только нейтральные молекулы, можно считать идеальными
.
- Разбавленные растворы электролитов (особенно — слабых!) приближаются к идеальным
.
Поэтому при расчете величины 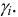
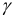
Коэффициент активности является мерой отклонения реальной системы от идеальной. Он связывает концентрацию иона и его активность 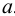
где [А] — равновесная концентрация иона А. Активность имеет размерность концентрации (моль/л).
Следует помнить, что при расчетах любого из четырех видов химических равновесий с применением табличных (термодинамических) констант равновесия получают значения активностей частиц, а не их равновесные концентрации. Расчет равновесных концентраций при I > 0 проводится с учетом у с использованием уравнения (2.11), связывающего различные константы.
Пример 2.1.
Вычислить ионную силу, коэффициенты активности и активность ионов в 0,010 М растворе 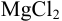
Решение:
Уравнение диссоциации сильного электролита
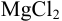
Начальная концентрация (моль/л) с: 0,010
Равновесные концентрации (моль/л) […]: — 0,010 0,020.
По формуле (2.1) вычисляют ионную силу раствора:
Коэффициенты активности можно найти в табл. 1 приложения: при / = 0,03 для двухзарядного иона 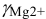
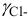
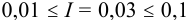
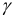
Активности ионов соответственно равны:
Пример 2.2.
Во сколько раз изменится активность ионов водорода в 0,010М растворе 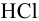
Решение:
Для 0,010 М раствора 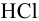
Молярная концентрация раствора 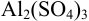
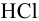
В полученном растворе сильных электролитов устанавливаются равновесия:
В величину I (формула 2.1) вносят вклад все ионы, находящиеся в растворе:
При
Отношение полученных активностей (0,0091/0,0080) показывает, что при введении в раствор 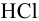
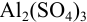
Пример 2.3.
Вычислить ионную силу и активности ионов в растворе, полученном при сливании по 100 мл 0,050 М раствора 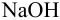
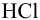
Решение:
При сливании растворов протекает реакция нейтрализации с образованием достаточно слабого электролита — воды, диссоциацией которой пренебрегаем. Данные указывают на избыток взятой щелочи.
С учетом разбавления
и после расчета
В растворе присутствуют ионы 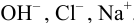
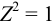
Соответственно 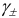
Проверкой решения может быть выполнение принципа электронейтральности раствора в целом:
Эти примеры взяты со страницы примеров решения задач по аналитической химии:
Решение задач по аналитической химии
Возможны вам будут полезны эти страницы:
Мерой
электростатического взаимодействия
ионов в растворе является ионная
сила раствора (µ),
равная
полусумме произведений молярных
концентраций всех присутствующих в
растворе ионов на квадраты их зарядов:
µ
=
0,5 ΣCi
Zi
где:
Ci
– молярная концентрация i-го
иона, Zi
— заряд i
-го иона.
На
величину электростатического
взаимодействия ионов в растворе не
влияют электронейтральные молекулы
(неэлектролиты или слабые электролиты),
поэтому их не учитывают при вычислении
ионной силы раствора.
Легко
показать, что для бинарных электролитов
с однозарядными ионами (NaCl, HCl, HI, HNO3)
ионная сила раствора равна молярной
концентрации этого электролита, т.е. µ
(NaCl) =
С(NaCl).
В случае бинарных электролитов с
двухзарядными ионами (FeSO4,
MgSO4)
ионная сила раствора в четыре раза
больше концентрации этого электролита,
т.е. µ (FeSO4)
=
4С(FeSO4).
Для трехионных электролитов (K2SO4,
MgCl2)
ионная сила раствора в три раза больше
концентрации этого электролита, т.е.
µ(K2SO4)
=
3С(K2SO4).
Ионная
сила раствора, содержащего несколько
сильных электролитов, равна сумме ионных
сил, создаваемых каждым из них.
Например,
ионная сила раствора, содержащего хлорид
и сульфат натрия, равна: µ (NaCl + Na2SO4)
=
С(NaCl)
+ 3С(Na2SO4).
Акти́вность
компонентов раствора — эффективная
(кажущаяся) концентрация компонентов
с учётом различных взаимодействий между
ними в растворе, то есть с учётом
отклонения поведения системы от модели
идеального раствора.
С
увеличением ионной силы раствора
коэффициент активности уменьшается.
Однако, достигнув определенного
минимального значения, коэффициент
активности при дальнейшем увеличении
ионной силы возрастает.
Активность
отличается от общей концентрации на
некоторую величину. Отношение активности
()
к общей концентрации вещества в растворе
называется коэффициентом активности:
Коэффициент
активности служит мерой отклонения
поведения раствора (или компонента
раствора) от идеального. Отклонения от
идеальности могут быть обусловлены
различными химическими и физическими
причинами — дипольные взаимодействия,
поляризация, образование водородных
связей, ассоциация, диссоциация,
сольватация и др
Зависимость
коэффициента активности иона от ионной
силы очень разбавленного водного
раствора электролита выражается
следующей формулой Дебая и Хюккеля:
где
z — заряд иона.
14. Потенциометрический метод определения рН. Электроды с водородной функцией.
В
настоящее время наиболее распространен
потенциометрический метод определения
рН, поскольку он является наиболее
точным и быстрым. Метод основан на
измерении ЭДС гальванической цепи,
составленной из электрода, обладающего
водородной функцией, и электрода
сравнения. Электродами с водородной
функцией называю электроды, чей потенциал
полностью обусловлен активностью ионов
водорода в растворе. Существует ряд
электродов, обладающих водородной
функцией (водородный, хингидронный,
стеклянный), но в настоящее время в
лабораторной практике широко применяется
стеклянный электрод с водородной
функцией, т.к. он обладает рядом
преимуществ. Например, одним из преимуществ
стеклянного электрода является то, что
он позволяет определять рН раствора
любого химического соединения в
достаточно широком диапазоне значений.
Схематически
стеклянный электрод, обладающий
водородной функцией, записывается
следующим образом:
Ag
| AgCl,
0,1н HCl
|


измерения рН раствора составляют цепь
из стеклянного и хлорсеребряного
электродов. Хлорсеребряный электрод
является электродом сравнения. Таким
образом, стеклянно-хлорсеребряная цепь
записывается так:
Ag
| AgCl,
0,1н НСl
|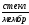
|KClнасыщ,
AgCl|
Ag.
Величина
потенциала стеклянного электрода (ст)
связана с концентрацией Н+—
ионов исследуемого раствора уравнением
Нернста:

Н+ст.
= Н+ст.
+ 0,0579 lgаН+
где:
0ст
– потенциал асимметрии стеклянного
электрода, величина переменная (в отличие
от металлов) и поэтому требующая
корректировки по буферным растворам.
Расчет
рН растворов при использовании
стеклянно-хлорсеребряной цепи
потенциометрическим методом заключается
в следующем. ЭДС любой гальванической
цепи равна разности электродных
потенциалов:
Е
= Н+ст.
— хл.
подставим
в данное уравнение значение электродного
потенциала стеклянного электрода:
Е
= Н+ст.
+ 0.0579 lgаН+
— хл.
решим
данное уравнение относительно рН:
-0.0579
lgаН+
= Н+ст.
— хл.
– Е
а
т.к. -lgаН+
= рН , то
рН
= Н+ст.
— хл.
– Е / 0,0579
15.Буферные
системы, буферная ёмкость.
Одним
из характерных свойств внутренней
системы организмов является постоянство
концентрации водородных ионов (изогидрия).
Так, например, рН крови человека – 7,36.
Сохранение этого показателя обеспечивается
совместным действием ряда физико-химических
и физиологических механизмов, из которых
очень важная роль принадлежит буферным
системам.
Буферными
системами называются растворы,
обладающие
свойством достаточно стойко сохранять
постоянство концентрации водородных
ионов как при добавлении к ним небольшого
количества сильных кислот или щелочей,
так и при разведении.
Буферные
системы (смеси или растворы) по составу
бывают двух основных типов:
а)
кислотные
— слабая
кислота и ее соль, образованная этой
кислотой с сильным основанием;
б)
основные
— слабое
основание и его соль, образованная этим
основанием и сильной кислотой.
На
практике часто применяются следующие
буферные смеси:
СН3
СООН
СН3СООNa
— ацетатный
буфер;
Н2СО3
NaHCO3
— бикарбонатный
буфер;
NH4OH
NH4Cl
— аммиачный
буфер
КН2PO4
Na2HPO4
— фосфатный буфер
Pt
– COOH
– белок-кислота
Pt
– COONa
– белок-соль
— белковый
буфер (Pt
– протеин-белок).
Каждая
из буферных смесей характеризуется
определенной концентрацией водородных
ионов, которую буферная система и
стремится сохранить при добавлении
кислот или щелочей. Рассмотрим, что
определяет постоянство рН, например,
ацетатной буферной смеси
СН3СООН
Н+
+
СН3СОО
—
СН3СООNa
СН3СОО—
+ Na+
В
ацетатном буферном растворе концентрация
водородных ионов будет зависеть от
степени диссоциации молекул кислоты.
Согласно закону действия масс, константа
диссоциации уксусной кислоты будет:
К
=

откуда
[H+
]
= К×
При
добавлении к слабодиссоциированной
уксусной кислоте (К = 1,86× 10-5)
ее сильнодиссоциированной соли происходит
резкое увеличение концентрации общего
аниона (СН3СОО
—).
В соответствие с законом действия масс
это вызывает смещение равновесия влево,
т.е. приводит к увеличению недиссоциированных
молекул кислоты:
СН3СООН
СН3СОО
— +
Н+
Слабая
диссоциация уксусной кислоты еще в
большей степени будет подавлена и
концентрация недиссоциированных молекул
кислоты может быть принята равной общей
концентрации кислоты. Так как соль
полностью диссоциированна на ионы, то
общая концентрация анионов может быть
принята за общую концентрацию соли в
буферном растворе. Исходя из этого,
концентрацию ионов водорода в буферной
смеси можно представить в следующем
виде:
[H+
]
= Кк×
Для
основного буфера, каким является,
например аммиачный, соответственно
будет
[OH
—]
= Ко×
Данные
выражения являются основным
уравнением буферных
растворов.
В логарифмической форме эти уравнения
принимают вид:
pH
= pKк
+ lg[соль]
– lg[кислота].
рH
= pKо
+ lg[основание]
— lg[соль].
Таким
образом, рН буферных смесей зависит от
константы диссоциации кислоты или
основания и от соотношения концентрации
компонентов буферных смесей. Используя
основное уравнение буферного раствора,
можно вычислить рН любого буферного
раствора, зная константу электролитической
диссоциации кислоты или основания и
концентрации кислоты и соли, а при
одинаковых концентрациях их объемные
отношения.
Предел,
в котором проявляется буферное действие
буферной системы характеризуется
буферной емкостью. Численное
значение буферной емкости (Б) определяется
числом моль сильной кислоты или сильного
основания, которое необходимо добавить
к 1 л буферной смеси, чтобы изменить
значение рН на 1:
где:
рН
– изменение рН при титровании буфера
кислотой или щелочью, наиболее близкое
к 1 (рН
= рН1
– рН0).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In thermodynamics, an activity coefficient is a factor used to account for deviation of a mixture of chemical substances from ideal behaviour.[1] In an ideal mixture, the microscopic interactions between each pair of chemical species are the same (or macroscopically equivalent, the enthalpy change of solution and volume variation in mixing is zero) and, as a result, properties of the mixtures can be expressed directly in terms of simple concentrations or partial pressures of the substances present e.g. Raoult’s law. Deviations from ideality are accommodated by modifying the concentration by an activity coefficient. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressures by a fugacity coefficient.
The concept of activity coefficient is closely linked to that of activity in chemistry.
Thermodynamic definition[edit]
The chemical potential, 
,
where μo
B is the chemical potential of a pure substance 

This is generalised to include non-ideal behavior by writing
when 
,
where 





In many cases, as 
Note that in general activity coefficients are dimensionless.
In detail: Raoult’s law states that the partial pressure of component B is related to its vapor pressure (saturation pressure) and its mole fraction 
with the convention
In other words: Pure liquids represent the ideal case.
At infinite dilution, the activity coefficient approaches its limiting value, 
immediately gives
In other words: The compound shows nonideal behavior in the dilute case.
The above definition of the activity coefficient is impractical if the compound does not exist as a pure liquid. This is often the case for electrolytes or biochemical compounds. In such cases, a different definition is used that considers infinite dilution as the ideal state:
with
and
The 
Modifying mole fractions or concentrations by activity coefficients gives the effective activities of the components, and hence allows expressions such as Raoult’s law and equilibrium constants to be applied to both ideal and non-ideal mixtures.
Knowledge of activity coefficients is particularly important in the context of electrochemistry since the behaviour of electrolyte solutions is often far from ideal, due to the effects of the ionic atmosphere. Additionally, they are particularly important in the context of soil chemistry due to the low volumes of solvent and, consequently, the high concentration of electrolytes.[3]
Ionic solutions[edit]
For solution of substances which ionize in solution the activity coefficients of the cation and anion cannot be experimentally determined independently of each other because solution properties depend on both ions. Single ion activity coefficients must be linked to the activity coefficient of the dissolved electrolyte as if undissociated. In this case a mean stoichiometric activity coefficient of the dissolved electrolyte, γ±, is used. It is called stoichiometric because it expresses both the deviation from the ideality of the solution and the incomplete ionic dissociation of the ionic compound which occurs especially with the increase of its concentration.
For a 1:1 electrolyte, such as NaCl it is given by the following:
where 

More generally, the mean activity coefficient of a compound of formula 
Single-ion activity coefficients can be calculated theoretically, for example by using the Debye–Hückel equation. The theoretical equation can be tested by combining the calculated single-ion activity coefficients to give mean values which can be compared to experimental values.
The prevailing view that single ion activity coefficients are unmeasurable independently, or perhaps even physically meaningless, has its roots in the work of Guggenheim in the late 1920s.[5] However, chemists have never been able to give up the idea of single ion activities, and by implication single ion activity coefficients. For example, pH is defined as the negative logarithm of the hydrogen ion activity. If the prevailing view on the physical meaning and measurability of single ion activities is correct then defining pH as the negative logarithm of the hydrogen ion activity places the quantity squarely in the unmeasurable category. Recognizing this logical difficulty, International Union of Pure and Applied Chemistry (IUPAC) states that the activity-based definition of pH is a notional definition only.[6] Despite the prevailing negative view on the measurability of single ion coefficients, the concept of single ion activities continues to be discussed in the literature, and at least one author presents a definition of single ion activity in terms of purely thermodynamic quantities and proposes a method of measuring single ion activity coefficients based on purely thermodynamic processes.[7]
Concentrated ionic solutions[edit]
For concentrated ionic solutions the hydration of ions must be taken into consideration, as done by Stokes and Robinson in their hydration model from 1948.[8] The activity coefficient of the electrolyte is split into electric and statistical components by E. Glueckauf who modifies the Robinson–Stokes model.
The statistical part includes hydration index number h, the number of ions from the dissociation and the ratio r between the apparent molar volume of the electrolyte and the molar volume of water and molality b.
Concentrated solution statistical part of the activity coefficient is:
[9][10][11]
The Stokes–Robinson model has been analyzed and improved by other investigators as well.[12][13]
Experimental determination of activity coefficients[edit]
Activity coefficients may be determined experimentally by making measurements on non-ideal mixtures. Use may be made of Raoult’s law or Henry’s law to provide a value for an ideal mixture against which the experimental value may be compared to obtain the activity coefficient. Other colligative properties, such as osmotic pressure may also be used.
Radiochemical methods[edit]
Activity coefficients can be determined by radiochemical methods.[14]
At infinite dilution[edit]
Activity coefficients for binary mixtures are often reported at the infinite dilution of each component. Because activity coefficient models simplify at infinite dilution, such empirical values can be used to estimate interaction energies. Examples are given for water:
| X | γx∞ (K) | γW∞ (K) |
|---|---|---|
| Ethanol | 4.3800 (283.15) | 3.2800 (298.15) |
| Acetone | 6.0200 (307.85) |
Theoretical calculation of activity coefficients[edit]
Activity coefficients of electrolyte solutions may be calculated theoretically, using the Debye–Hückel equation or extensions such as the Davies equation,[16] Pitzer equations[17] or TCPC model.[18][19][20][21] Specific ion interaction theory (SIT)[22] may also be used.
For non-electrolyte solutions correlative methods such as UNIQUAC, NRTL, MOSCED or UNIFAC may be employed, provided fitted component-specific or model parameters are available. COSMO-RS is a theoretical method which is less dependent on model parameters as required information is obtained from quantum mechanics calculations specific to each molecule (sigma profiles) combined with a statistical thermodynamics treatment of surface segments.[23]
For uncharged species, the activity coefficient γ0 mostly follows a salting-out model:[24]
This simple model predicts activities of many species (dissolved undissociated gases such as CO2, H2S, NH3, undissociated acids and bases) to high ionic strengths (up to 5 mol/kg). The value of the constant b for CO2 is 0.11 at 10 °C and 0.20 at 330 °C.[25]
For water as solvent, the activity aw can be calculated using:[24]
where ν is the number of ions produced from the dissociation of one molecule of the dissolved salt, b is the molality of the salt dissolved in water, φ is the osmotic coefficient of water, and the constant 55.51 represents the molality of water. In the above equation, the activity of a solvent (here water) is represented as inversely proportional to the number of particles of salt versus that of the solvent.
Link to ionic diameter[edit]
The ionic activity coefficient is connected to the ionic diameter by the formula obtained from Debye–Hückel theory of electrolytes:
where A and B are constants, zi is the valence number of the ion, and I is ionic strength.
Dependence on state parameters[edit]
The derivative of an activity coefficient with respect to temperature is related to excess molar enthalpy by
Similarly, the derivative of an activity coefficient with respect to pressure can be related to excess molar volume.
Application to chemical equilibrium[edit]
At equilibrium, the sum of the chemical potentials of the reactants is equal to the sum of the chemical potentials of the products. The Gibbs free energy change for the reactions, ΔrG, is equal to the difference between these sums and therefore, at equilibrium, is equal to zero. Thus, for an equilibrium such as
Substitute in the expressions for the chemical potential of each reactant:
Upon rearrangement this expression becomes
The sum
σμo
S + τμo
T − αμo
A − βμo
B is the standard free energy change for the reaction, 
Therefore,
where K is the equilibrium constant. Note that activities and equilibrium constants are dimensionless numbers.
This derivation serves two purposes. It shows the relationship between standard free energy change and equilibrium constant. It also shows that an equilibrium constant is defined as a quotient of activities. In practical terms this is inconvenient. When each activity is replaced by the product of a concentration and an activity coefficient, the equilibrium constant is defined as
where [S] denotes the concentration of S, etc. In practice equilibrium constants are determined in a medium such that the quotient of activity coefficient is constant and can be ignored, leading to the usual expression
which applies under the conditions that the activity quotient has a particular (constant) value.
References[edit]
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the «Gold Book») (1997). Online corrected version: (2006–) «Activity coefficient». doi:10.1351/goldbook.A00116
- ^ DeHoff, Robert (2018). «Thermodynamics in materials science». Entropy (2nd ed.). 20 (7): 230–231. Bibcode:2018Entrp..20..532G. doi:10.3390/e20070532. ISBN 9780849340659. PMC 7513056. PMID 33265621.
- ^ Ibáñez, Jorge G.; Hernández Esparza, Margarita; Doría Serrano, Carmen; Singh, Mono Mohan (2007). Environmental Chemistry: Fundamentals. Springer. ISBN 978-0-387-26061-7.
- ^ Atkins, Peter; dePaula, Julio (2006). «Section 5.9, The activities of ions in solution». Physical Chemisrry (8th ed.). OUP. ISBN 9780198700722.
- ^ Guggenheim, E. A. (1928). «The Conceptions of Electrical Potential Difference between Two Phases and the Individual Activities of Ions». The Journal of Physical Chemistry. 33 (6): 842–849. doi:10.1021/j150300a003. ISSN 0092-7325.
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the «Gold Book») (1997). Online corrected version: (2006–) «pH». doi:10.1351/goldbook.P04524
- ^ Rockwood, Alan L. (2015). «Meaning and Measurability of Single-Ion Activities, the Thermodynamic Foundations of pH, and the Gibbs Free Energy for the Transfer of Ions between Dissimilar Materials». ChemPhysChem. 16 (9): 1978–1991. doi:10.1002/cphc.201500044. ISSN 1439-4235. PMC 4501315. PMID 25919971.
- ^ Stokes, R. H; Robinson, R. A (1948). «Ionic Hydration and Activity in Electrolyte Solutions». Journal of the American Chemical Society. 70 (5): 1870–1878. doi:10.1021/ja01185a065. PMID 18861802.
- ^ Glueckauf, E. (1955). «The influence of ionic hydration on activity coefficients in concentrated electrolyte solutions». Transactions of the Faraday Society. 51: 1235. doi:10.1039/TF9555101235.
- ^ Glueckauf, E. (1957). «The influence of ionic hydration on activity coefficients in concentrated electrolyte solutions». Transactions of the Faraday Society. 53: 305. doi:10.1039/TF9575300305.
- ^ Kortüm, G. (1959). «The Structure of Electrolytic Solutions». Angewandte Chemie. London: Herausgeg. von W. J. Hamer; John Wiley & Sons, Inc., New York; Chapman & Hall, Ltd. 72 (24): 97. doi:10.1002/ange.19600722427. ISSN 0044-8249.
- ^ Miller, Donald G. (1956). «On the Stokes-Robinson Hydration Model for Solutions». The Journal of Physical Chemistry. 60 (9): 1296–1299. doi:10.1021/j150543a034.
- ^ Nesbitt, H. Wayne (1982). «The stokes and robinson hydration theory: A modification with application to concentrated electrolyte solutions». Journal of Solution Chemistry. 11 (6): 415–422. doi:10.1007/BF00649040. S2CID 94189765.
- ^ Betts, R. H.; MacKenzie, Agnes N. (1952). «Radiochemical Measurements of Activity Coefficients in Mixed Electrolytes». Canadian Journal of Chemistry. 30 (2): 146–162. doi:10.1139/v52-020.
- ^ «Activity Coefficients at Infinite Dilution of 30 Important Components from Dortmund Data Bank». Dortmund Data Bank. DDBST GmbH. Retrieved 13 December 2018.
- ^ King, E. L. (1964). «Book Review: Ion Association, C. W. Davies, Butterworth, Washington, D.C., 1962». Science. 143 (3601): 37. Bibcode:1964Sci…143…37D. doi:10.1126/science.143.3601.37. ISSN 0036-8075.
- ^ Grenthe, I.; Wanner, H. «Guidelines for the extrapolation to zero ionic strength» (PDF). Archived from the original (PDF) on 2008-12-17. Retrieved 2007-07-23.
- ^ Ge, Xinlei; Wang, Xidong; Zhang, Mei; Seetharaman, Seshadri (2007). «Correlation and Prediction of Activity and Osmotic Coefficients of Aqueous Electrolytes at 298.15 K by the Modified TCPC Model». Journal of Chemical & Engineering Data. 52 (2): 538–547. doi:10.1021/je060451k. ISSN 0021-9568.
- ^ Ge, Xinlei; Zhang, Mei; Guo, Min; Wang, Xidong (2008). «Correlation and Prediction of Thermodynamic Properties of Nonaqueous Electrolytes by the Modified TCPC Model». Journal of Chemical & Engineering Data. 53 (1): 149–159. doi:10.1021/je700446q. ISSN 0021-9568.
- ^ Ge, Xinlei; Zhang, Mei; Guo, Min; Wang, Xidong (2008). «Correlation and Prediction of Thermodynamic Properties of Some Complex Aqueous Electrolytes by the Modified Three-Characteristic-Parameter Correlation Model». Journal of Chemical & Engineering Data. 53 (4): 950–958. doi:10.1021/je7006499. ISSN 0021-9568.
- ^ Ge, Xinlei; Wang, Xidong (2009). «A Simple Two-Parameter Correlation Model for Aqueous Electrolyte Solutions across a Wide Range of Temperatures». Journal of Chemical & Engineering Data. 54 (2): 179–186. doi:10.1021/je800483q. ISSN 0021-9568.
- ^ «Project: Ionic Strength Corrections for Stability Constants». IUPAC. Archived from the original on 29 October 2008. Retrieved 2008-11-15.
- ^ Klamt, Andreas (2005). COSMO-RS from quantum chemistry to fluid phase thermodynamics and drug design (1st ed.). Amsterdam: Elsevier. ISBN 978-0-444-51994-8.
- ^ a b N. Butler, James (1998). Ionic equilibrium: solubility and pH calculations. New York, NY [u.a.]: Wiley. ISBN 9780471585268.
- ^ Ellis, A. J.; Golding, R. M. (1963). «The solubility of carbon dioxide above 100 degrees C in water and in sodium chloride solutions». American Journal of Science. 261 (1): 47–60. Bibcode:1963AmJS..261…47E. doi:10.2475/ajs.261.1.47. ISSN 0002-9599.
External links[edit]
- AIOMFAC online-model An interactive group-contribution model for the calculation of activity coefficients in organic–inorganic mixtures.
- Electrochimica Acta Single-ion activity coefficients

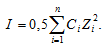
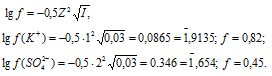
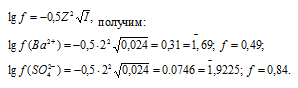
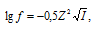
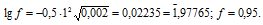

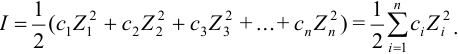
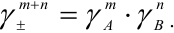
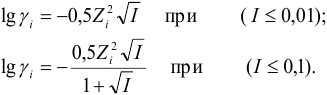
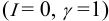 .
.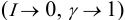 .
.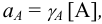
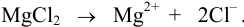
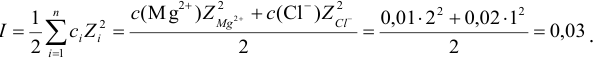
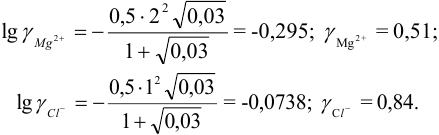
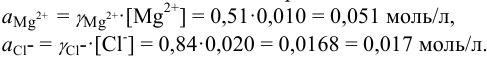
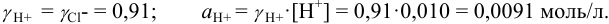
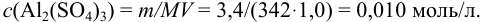
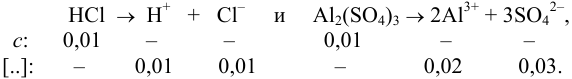
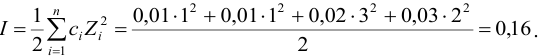
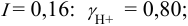
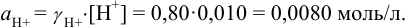
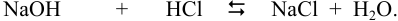
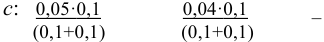
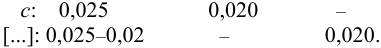
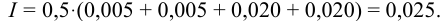
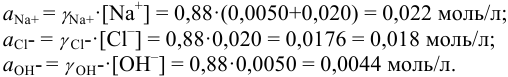
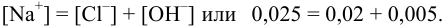







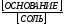












![{displaystyle gamma _{pm }={sqrt[{p+q}]{gamma _{mathrm {A} }^{p}gamma _{mathrm {B} }^{q}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c66f131bcf882828c4edbb068ee7800812be4e47)












![{displaystyle K={frac {[mathrm {S} ]^{sigma }[mathrm {T} ]^{tau }}{[mathrm {A} ]^{alpha }[mathrm {B} ]^{beta }}}times {frac {gamma _{mathrm {S} }^{sigma }gamma _{mathrm {T} }^{tau }}{gamma _{mathrm {A} }^{alpha }gamma _{mathrm {B} }^{beta }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95d7e43431f4648654306641285e434365d7af57)
![{displaystyle K={frac {[mathrm {S} ]^{sigma }[mathrm {T} ]^{tau }}{[mathrm {A} ]^{alpha }[mathrm {B} ]^{beta }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59e684b2a458ef9a608ef9a8d8f9e55473da1e86)