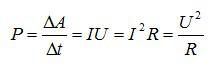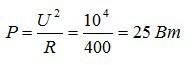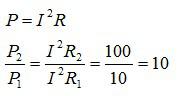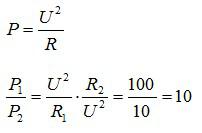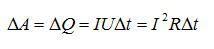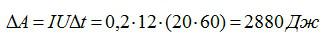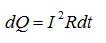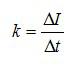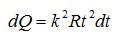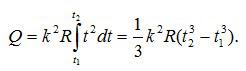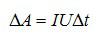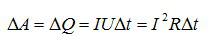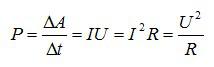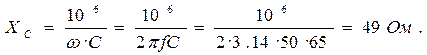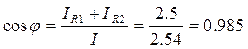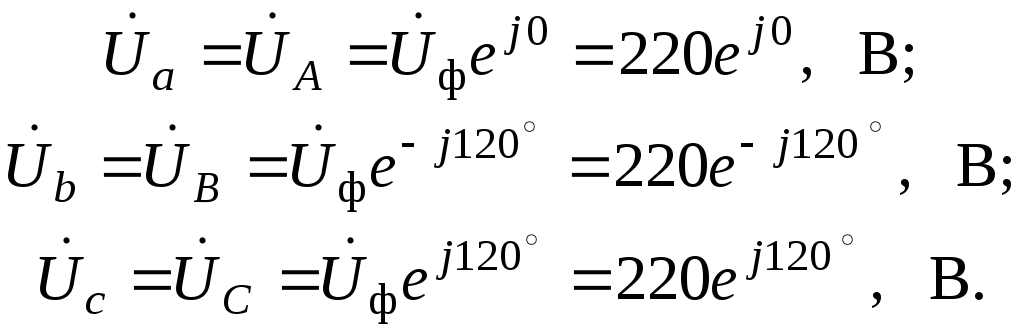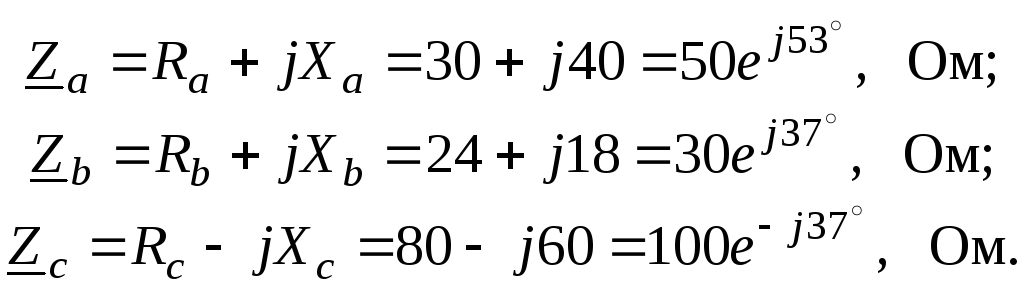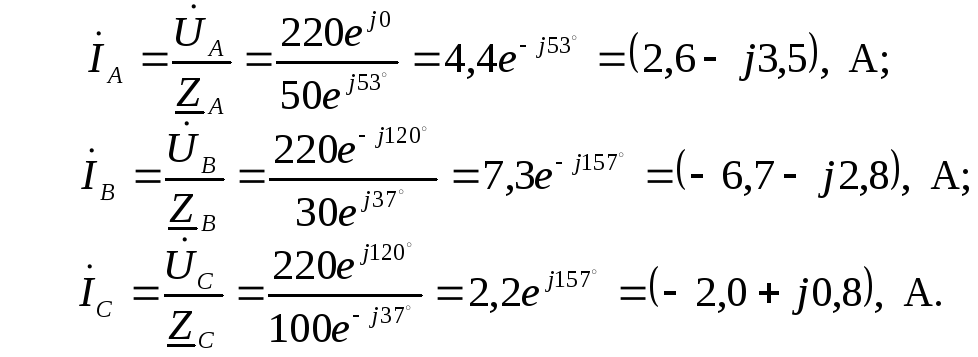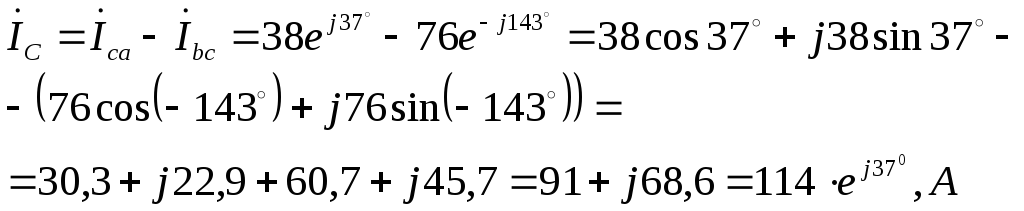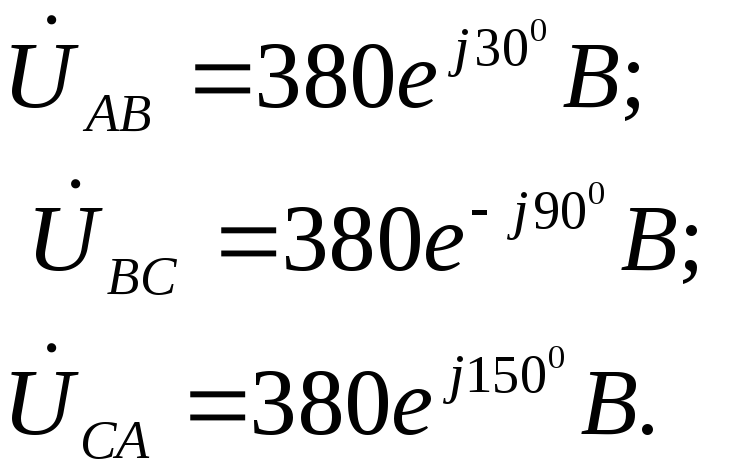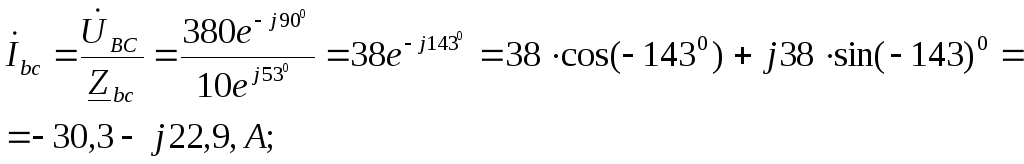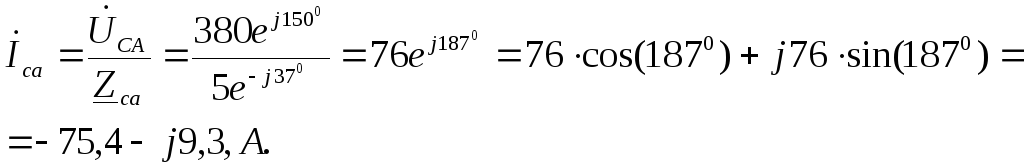Как найти активную мощность задачи

«Природа
так обо всём позаботилась,

что
повсюду ты находишь, чему учиться».

Леонардо
да Винчи

Задача
1.
В цепь переменного тока последовательно с лампочкой включен конденсатор с
переменной ёмкостью. Как изменится накал лампы, если: а) не меняя частоту,
уменьшить ёмкость конденсатора б) не меняя ёмкости, уменьшить частоту?

РЕШЕНИЕ:

Накал
лампы напрямую зависит от мощности, поэтому, чтобы понять, как изменится накал,
нам нужно узнать, как изменится мощность. Запишем формулу, по которой
вычисляется мощность в цепи переменного тока.

Сопротивление
лампочки никак не зависит от частоты. Установим, как зависит сила тока от
указанных параметров. Для этого, в первую очередь, вспомним связь между
амплитудными значениями заряда и напряжения, а затем – связь между амплитудными
значениями заряда и силы тока.

Исходя
из этих двух соотношений, выведем зависимость амплитудного значения силы тока
от амплитудного значения напряжения.

Запишем
теперь общее уравнение для гармонических колебаний силы тока и преобразуем это
уравнение в соответствии с выведенной зависимостью.

Амплитудное
напряжение остаётся неизменным, поскольку оно задано источником переменного
тока. Поэтому, исходя из полученного уравнения, накал лампы уменьшится и при
уменьшении ёмкости конденсатора, и при уменьшении частоты.

Ответ:
а) накал лампы уменьшится; б) накал лампы уменьшится.

Задача
2.
В цепи без активного сопротивления действующие значения силы тока и напряжения
равны 2 А и 50 В соответственно. Найдите разность фаз между колебаниями тока и
напряжения, если средняя мощность цепи равна 70,7 Вт.

ДАНО:	РЕШЕНИЕ Мощность в цепи переменного тока определяется по формуле Тогда

Ответ:
ток отстаёт от напряжения на   рад.

Задача
3.
В цепь переменного тока  последовательно включены резистор с сопротивлением 50
Ом, конденсатор с ёмкостью 50 мкФ и катушка с индуктивностью 2 мГн. Амплитудное
напряжение на зажимах равно 220 В, частота колебаний равна 100 Гц. Найдите
активную мощность цепи.

ДАНО:	СИ	РЕШЕНИЕ Запишем закон Ома для цепей переменного тока Полное сопротивление цепи определяется по формуле Тогда сила тока равна Активная мощность определяется по формуле Действующие значения напряжения и силы тока определяются по формулам Тогда активная мощность равна С учётом того, что активная мощность равна активная мощностьравна

Ответ:
352 Вт.

Задача
4.
В сеть переменного тока последовательно включен конденсатор ёмкостью 50 мкФ и
катушка с индуктивностью 20 мГн. Активное сопротивление цепи равно 80 Ом.
Известно, что за один период колебаний током совершается работа, равная 10 Дж.
Действующее значение напряжения равно 100 В. Найдите среднюю мощность цепи и
действующее значение силы тока. Частота колебаний равна 50 Гц.

ДАНО:	СИ	РЕШЕНИЕ Мощность – это работа в единицу времени Мощность в цепи переменного тока определяется по формуле Запишем формулу, с помощью которой можно вычислить разность фаз Индуктивное и ёмкостное сопротивления определяются по формуле Циклическую частоту можно найти по выражению Тогда разность фаз Действующее значение силы тока равно

В сегодняшней статье мы займемся решением задач на тему «Работа и мощность постоянного тока». Вдруг кому-нибудь пригодится.

Кстати, много полезной информации для студентов, а также приятные скидки, вы найдете на нашем телеграм-канале. Подписывайтесь!

Работа и мощность тока: задачи с решением

Перед непосредственным решением задач на работу и мощность электрического тока повторите теорию, ознакомьтесь с общей памяткой по решению задач. Также мы собрали для вас вместе более 40 формул по физике, держите их под рукой.

Задача №1. Мощность электрического тока

Условие

Сопротивление нити накала электрической лампы составляет 400 Ом, а напряжение на нити равно 100 В. Какова мощность тока в лампе?

Решение

По определению, мощность тока на участке цепи равна работе, деленной на время, за которое она была совершена:

Подставим значения, и найдем мощность:

Ответ: 25 Вт.

Задача №2. Расчет мощности электрического тока

Условие

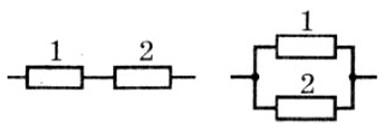
Два резистора соединены параллельно и последовательно. В каком из двух резисторов мощность тока больше (и во сколько раз) соответственно при параллельном и последовательном соединении?

Решение

1) При последовательном соединении сила тока в каждом резисторе одинакова, а мощность тока напрямую зависит от сопротивления резисторов:

Мощность тока во втором резисторе больше в 10 раз.

2) При параллельном соединении на резисторах будет разная сила тока, но одинаковое напряжение. Для мощности тока целесообразно использовать формулу:

Мощность тока в первом резисторе больше в 10 раз.

Ответ: В 10 раз больше во втором резисторе; в 10 раз больше в первом резисторе.

Задача №3. Работа электрического тока

Условие

Какова работа электрического тока в паяльнике, если сила тока в цепи равна 3 А, а сопротивление паяльника – 40 Ом? Время работы паяльника – 30 минут. Какое количество теплоты выделится в паяльнике за это время?

Решение

По закону Джоуля-Ленца, работа тока на наподвижном проводнике с сопротивлением R, преобразуется в тепло.

Вычислим работу:

При вычислениях не забывайте переводит все величины в систему СИ.

Работа тока равна выделившемуся количеству теплоты.

Ответ: 648 кДж.

Задача №4.  Расчет работы электрического тока

Условие

Какую работу ток совершает в электродвигателе за 20 минут, если сила тока в цепи равна 0,2 А, а напряжение составляет 12 В.

Решение

Применим формулу для работы тока:

Ответ: 2880 Дж.

Напоследок мы приберегли для вас задачу посложнее.

Задача №5 на закон Джоуля-Ленца

Условие

Сила тока в проводнике сопротивлением R=20 Ом нарастает в течение времени Δt=2 с по линейному закону от I0=0 до Imax=6 А. Определить количество теплоты Q1, выделившееся в этом проводнике за первую секунду, и Q2 — за вторую, а также найти отношение этих количеств теплоты Q2/Q1. 

Решение

Закон Джоуля – Ленца применим в случае постоянного тока (I =const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде:

Здесь сила тока I является некоторой функцией времени. В нашем случае I=kt, где k — коэффициент пропорциональности, равный отношению приращений силы тока к интервалу времени, за который произошло это приращение:

С учетом этого, формула для количества теплоты примет вид:

Для определения количества теплоты, выделившегося за конечный промежуток времени, выражение для бесконечно малого количества теплоты следует проинтегрировать в пределах от t1 до t2: 

При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t1 =О, t2= 1 с и, следовательно, Q1=60 Дж, а за вторую секунду — пределы интегрирования t1= 1 с, t2=2 с и тогда Q2=420 Дж.

Кстати, читайте в нашем блоге о том, как считать интегралы.

За вторую секунду выделится теплоты в 7 раз больше, чем за первую секунду.

Ответ: 60 Дж; 420 Дж; в 7 раз больше.

Вопросы на работу и мощность электрического тока

Вопрос 1. Что такое работа электрического тока?

Ответ. Работа электрического тока – это физическая величина, которая показывает, какая работа была совершена электрическим полем при перемещении зарядов по проводнику. Она равна произведению силы тока на участке цепи, напряжению на концах этого участка и времени, в течение которого протекает ток по проводнику.

Единица измерения работы – 1 Джоуль.

Вопрос 2. Сформулируйте закон Джоуля-Ленца.

Ответ. Это эмпирический закон преобразования работы тока в тепло. Он был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем. 

Работа электрического тока, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло, выделяющееся на проводнике.

При прохождении тока по проводнику положительные ионы в узлах кристаллических решеток проводника за счет энергии тока начинают сильнее колебаться, что сопровождается увеличением внутренней энергии проводника, т.е. его нагреванием.

Вопрос 3. Что такое мощность электрического тока?

Ответ. Мощность тока – физическая величина, характеризующая скорость совершения током работы. Мощность равна отношению работы к интервалу времени, за которые она была совершена:

Единицей измерения мощности является Ватт. 1 Ватт – это мощность, при которой за одну секунду совершается работа в 1 Джоуль.

Вопрос 4. Приведите пример внесистемной единицы измерения работы.

Ответ. На практике часто пользуются единицей, называемой ватт-час (втч). Так как в часе 3 600 секунд,  1 ватт-час равен 3 600 Дж.

Вопрос 5. Как измерить работу тока?

Ответ. В простейшем случае для измерения работы тока нужны амперметр, вольтметр и часы. На практике работу электрического тока измеряют с помощью счетчиков.

Нужна помощь в решении задач и выполнении других заданий? Профессиональный сервис для учащихся всегда к вашим услугам.

ОбразЦЫ РЕШЕНИЯ ЗАДАЧ НА РАСЧЕТ ОДНОФАЗНЫХ И ТРЕХФАЗНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА.

Пример решения задачи на расчет неразветленной цепи.

Задача:Последовательно с катушкой, активное сопротивление которой R₁=10 Ом и индуктив­ность L=0,0318 Гн, включен прием­ник, обладающий активным сопро­тивлением R₂=1 Ом и емкостью С=796 мкф (рис. I). К цепи при­ложено переменное напряжение, изменяющееся по закону u=169,8·sin(314·t).

Определить: полное сопротив­ление цепи, коэффициент мощно­сти цепи, ток в цепи, активную, реактивную и полную мощности, а также построить в масштабе векторную диаграмму.

Как нужно изменить величину емкости, чтобы в цепи наступил резонанс напряжений? Индуктивность катушки остается постоянной.

Решение:

1. Сравнивая закон изменения напряжения о цепи с общим выражением u=U_M·sin(ωt) , можно заключить, что амплиту­да напряжения U_M=169,8 B, а ω=2π·f=314 (1/сек).

Отсюда действующее значение напряжения

2. Индуктивное сопротивление катушки

3. Емкостное сопротивление конденсатора

4. Полное сопротивление цепи

5. Коэффициент мощности цепи

φ=28,35ْ

6. Сила тока в цепи

7. Активная мощность

8. Реактивная мощность

9. Полная мощность

S=I 2 z=9.6 2 ·12.5=1152 ВА

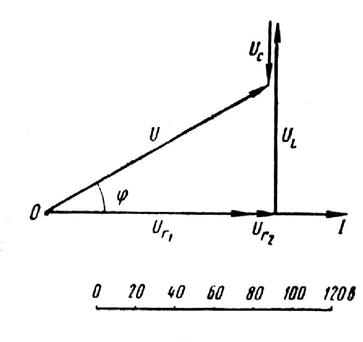
10. Построение векторной диаграммы начинаем с определения потерь напряжений на каждом сопротивлении:

Рис.2

Затем выбираем масштаб для напряжений (см. рис. 2). Построение диаграммы начинаем с вектора тока I, который от­кладываем по горизонтали вправо от точки О (рис. 2). Вдоль векто­ра тока откладываем в принятом масштабе напряжения U_R1 и U_R2 теряемые в активных сопротивлениях цепи. Эти напряжения совпа­дают по фазе с током. От конца вектора U_R2 откладываем в сторону опережения вектора тока под углом 90° вектор потери напряжения U_L в индуктивном сопро­тивлении. Из конца векто­ра U_L откладываем вектор U_C в сторону отставания от вектора тока на угол 90 ° . Геометрическая сумма че­тырех векторов равна пол­ному напряжению, прило­женному к цепи, т. е.

11. Для получения ре­зонанса напряжений необ­ходимо, чтобы Х_C=Х_L=10 Ом, тогда , откуда При этом ток в цепи станет , где .

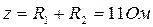
Пример решения задачи на расчет разветвленной цепи.

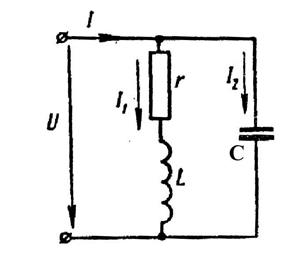
Задача: Катушка с активным сопротивлением R=20 Oм и ин­дуктивностью L=0,0637 Гн соединена параллельно с конденсатором емкостью С =65 мкФ (рис. 3).

Определить: токи в ветвях и в неразветвленной части цепи, ак­тивные мощности ветвей, углы сдвига фаз между током и напряже­нием первой и второй ветвей и всей цепи, если к цепи приложено напряжение U=100B, частота тока f=50 Гц. Как нужно изменить емкость во второй ветви, чтобы в цепи наступил резонанс токов?

Построить векторную диаграмму.

Решение:

1. Индуктивное сопротивление катушки

2. Емкостное сопротивление конденсатора

3. Токи в ветвях

4. Коэффициенты мощности ветвей

(отстающий)

(опережающий).

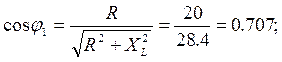
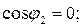
5. Активные и реактивные составляющие токов ветвей

;

6. Ток в неразвлетвленной части цепи

Реактивные токи ветвей должны вычитаться, так как реактивный ток ветви с емкостью принимается отрицательным.

7. Коэффициент мощности всей цепи

8. Активные мощности ветвей

P₂=0

Построение векторной диаграммы начинаем c вектора напряжения U (рис. 4). Под углом φ₁ к вектору напряжения (в сторону отста­вания) откладываем вектор тока I₁, под углом φ₂ (в сторону опере­жения) — вектор тока I₂. Геометрическая сумма этих векторов пред­ставляет ток I в неразветвленной части цепи. Проекции токов вет­вей на вектор напряжения являются активными составляющими I_R1 и I_R2; проекции этих токов на вектор, перпендикулярный вектору на­пряжения, — реактивными составляющими I_P1 и I_P2.

9. При резонансе токов ток I совпадает на фазе с напряжением, что возможно при равенстве реактивных токов ветвей I_P1=I_P2 (см. векторную диаграмму (рис.5)).

Расчет электрических цепей переменного синусоидального тока производится в комплексной форме. При этом величины синусоидальных ЭДС и токов представляются в виде комплексных амплитуд или комплексных действующих значений, а все элементы в схеме – в виде комплексных сопротивлений.

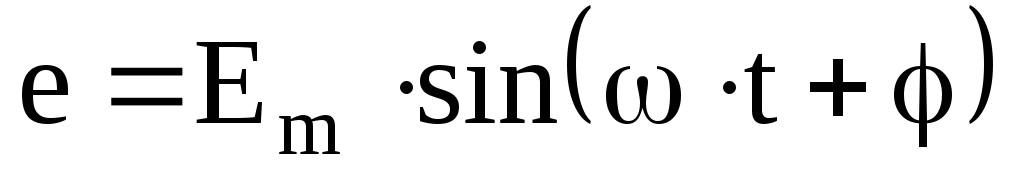
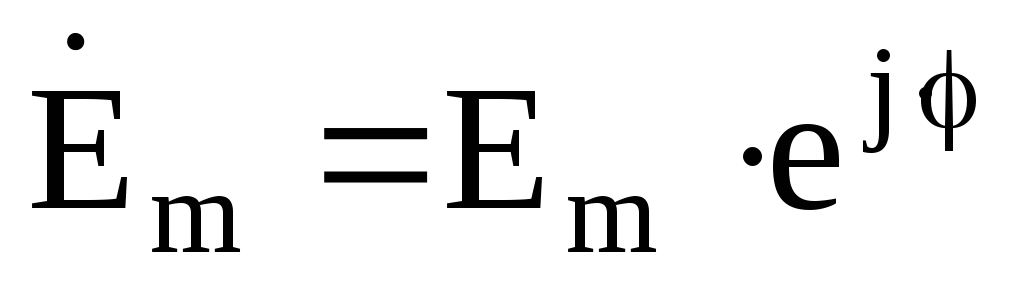
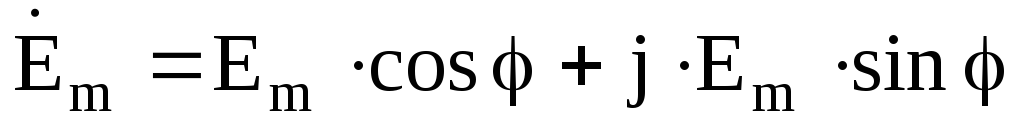
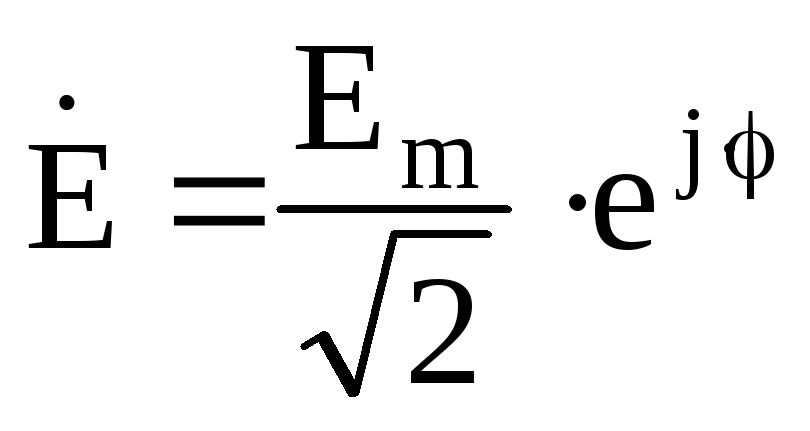
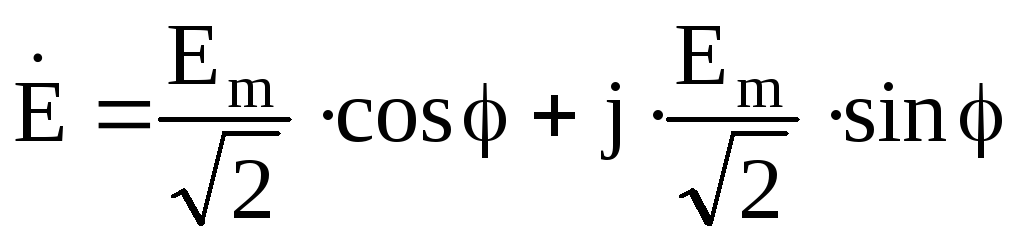
Например, если ЭДС источника равна , то комплексная амплитуда запишется в виде— в показательной форме записи, или— в алгебраической форме. Комплексное действующее значение синусоидальной ЭДС:— в показательной форме записи, или— в алгебраической форме.

Комплексные сопротивления элементов электрической цепи переменного тока:

— для идеального сопротивления,

— для идеальной индуктивности,

— для идеальной емкости.

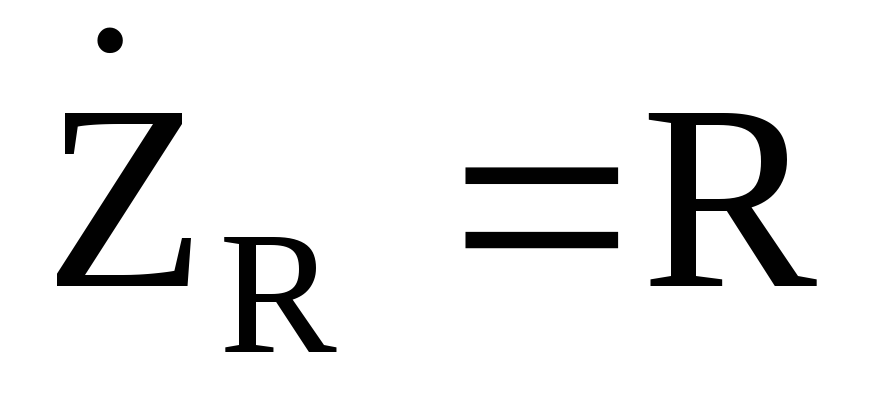
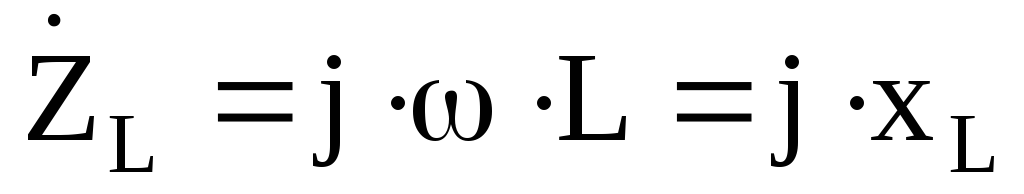
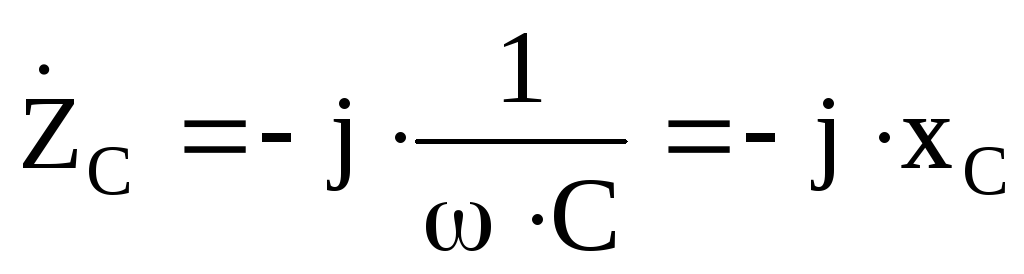
Далее расчет электрической цепи переменного тока можно вести любым методом, известным из раздела – «электрические цепи постоянного тока». При этом используется математический аппарат, разработанный для операций с комплексными числами.

Применяются три формы записи комплексного значения синусоидальной величины:

— показательная форма,

— алгебраическая форма,

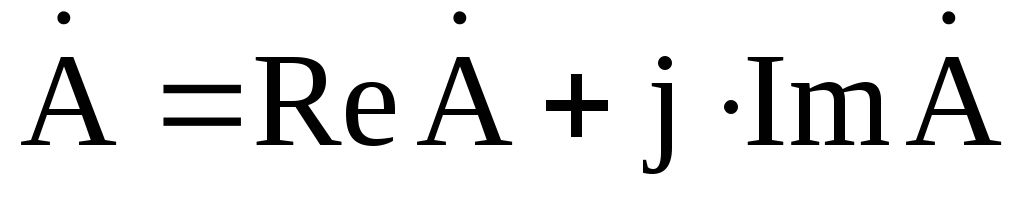
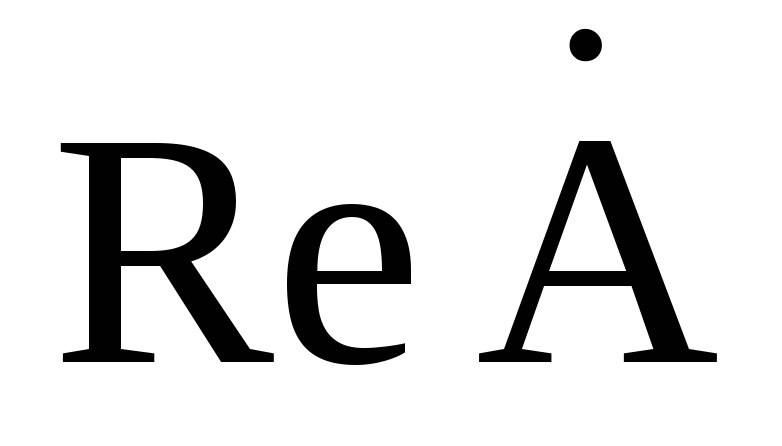
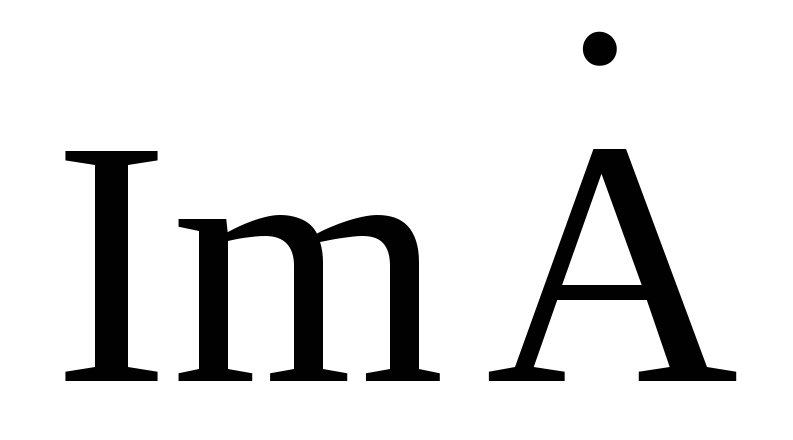
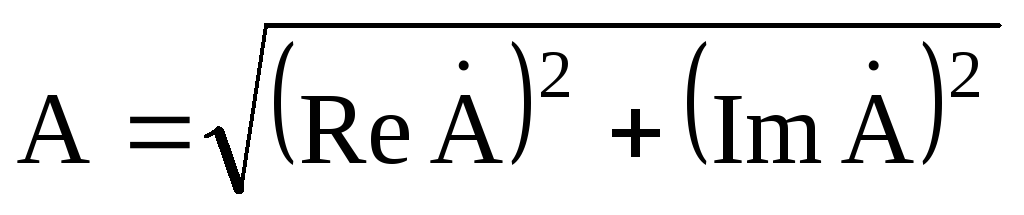
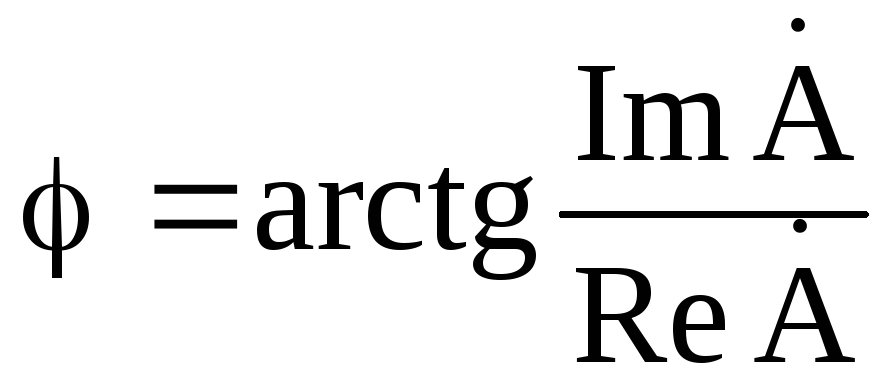
где и— действительная и мнимая часть комплексного значения синусоидальной величины. Переход от алгебраической формы к показательной осуществляется по формулам:

;.

Переход от показательной формы к тригонометрической осуществляется по формуле Эйлера:

.

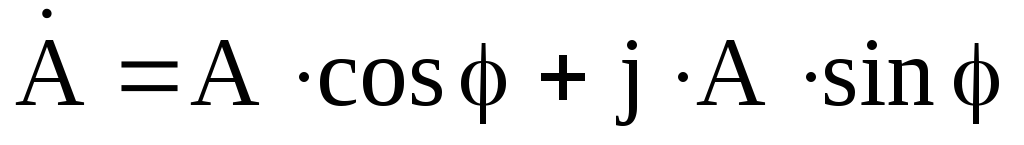
Сложение и вычитание комплексных величин производится в алгебраической форме, а умножение и деление в показательной.

При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных величин, сокращенно их называют комплексными значениями.

Расчет однофазных цепей

Р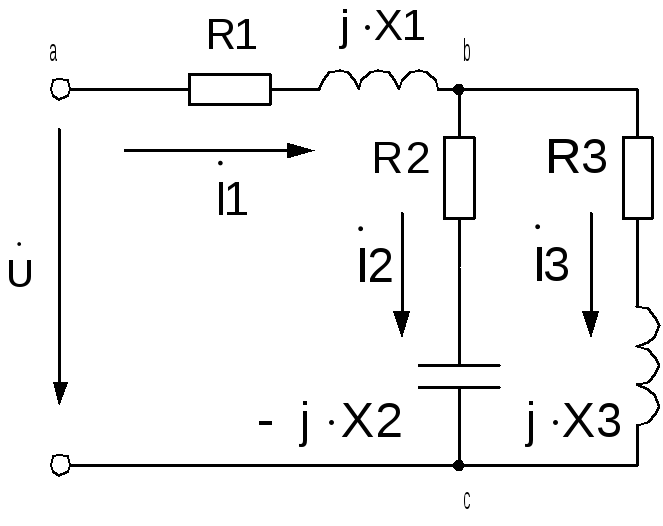асчет однофазных цепей переменного тока при наличии одного источника синусоидальной ЭДС производится методом эквивалентных преобразований. Рассмотрим пример расчета однофазной цепи приведенной на рис.

Рис. 2.4. Схема электрической цепи к примеру расчета

Пример расчета однофазной цепи

По заданным значениям активных и реактивных сопротивлений и напряжению источника определить токи во всех ветвях схемы и падения напряжения на ее участках. Определить комплекс полной мощности, активную и реактивную мощность. Расчет произвести комплексным методом. Выполнить проверку правильности расчета с использованием баланса активных мощностей схемы. Построить векторную диаграмму. Построить мгновенные значения синусоидальных токов ветвей. Исходные данные для расчета приведены в таблице.

В электротехнике большое количество задач посвящено цепям переменного тока . Рассмотрим примеры решения некоторых из них.

Задача 1

В сеть переменного тока включены последовательно катушка индуктивностью 3 мГн и активным сопротивлением 20 Ом и конденсатор емкостью 30 мкФ. Напряжение Uc на конденсаторе 50 В. Определите напряжение на зажимах цепи, ток в цепи, напряжение на катушке, активную и реактивную мощность.

Решение задачи начнём с определения тока в цепи, но для этого нужно сначала определить реактивное сопротивление конденсатора.

Как известно, реактивное сопротивление конденсатора зависит от частоты переменного тока (при её увеличении уменьшается, а при её уменьшении увеличивается), следовательно

Ток в цепи находим из соображения, что элементы в цепи соединены последовательно, а значит, ток на конденсаторе и катушке будет одним и тем же.

Следующим шагом мы определяем индуктивное сопротивление и напряжение катушки

Зная активное сопротивление обмотки катушки, можем определить падение напряжения на нем

Теперь, когда мы знаем напряжение на каждом из элементов, мы можем определить напряжение на зажимах цепи, которое будет равно

Активную мощность в данном случае можно определить как мощность, выделяемую на обмотке катушки

Для определения реактивной мощности необходимо для начала определить угол сдвига ϕ

Так как реактивная мощность имеет отрицательное значение, то цепь имеет емкостной характер.

Задача 2

В цепи как показано на схеме, подключены катушка, конденсатор и резисторы. Индуктивность катушки – 15 мГн, емкость конденсатора 20 мкФ, R1=10 Ом, R2=30 Ом. Напряжение источника 100 В, частота 100 Гц. Определить токи в цепи, активную, реактивную и полную мощность в цепи.

Данную задачу удобнее решать с помощью проводимостей, так как катушка и конденсатор соединены параллельно.

Тогда активная проводимость первой ветви равна

Реактивная проводимость первой ветви равна

Полная проводимость первой ветви

Аналогичный расчет произведем для второй ветви содержащей конденсатор

Полная проводимость цепи

Токи в цепи определим зная напряжение и проводимости

1. Примеры решения
   типовых задач

Задача 1.3.1
Трехфазный асинхронный двигатель
включен в сеть 380 В по схеме «звезда».
Параметры обмоток следующие: R_ф
= 2 Ом, Х_ф
= 8 Ом.

Требуется:
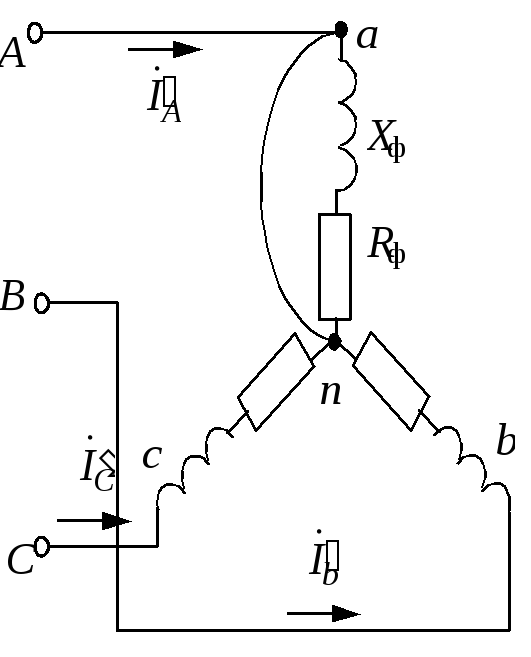
изобразить схему включения двигателя
в сеть; определить фазные и линейные
токи; определить потребляемую активную
мощность; построить векторную диаграмму
токов и напряжений; рассмотреть два
аварийных режима – обрыв и короткое
замыкание фазы А.

Решение:

Трехфазный
асинхронный двигатель является
симметричной
активно-индуктивной нагрузкой, поэтому
включается в сеть по схеме «звезда» без
нейтрального провода. Его схема замещения
представлена на рис. 1.3.8

Номинальное
напряжение сети является линейным
напряжением, т. е.
,
тогда фазное напряжение

Поскольку
нагрузка симметричная, то расчет можно
проводить для одной фазы.

Полное сопротивление
фазы

Ф

А(а)

азный ток

.

Для
схемы «звезда» линейный ток
.
Потребляемая активная мощность

г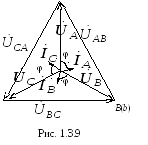де

— фазовый угол,

.

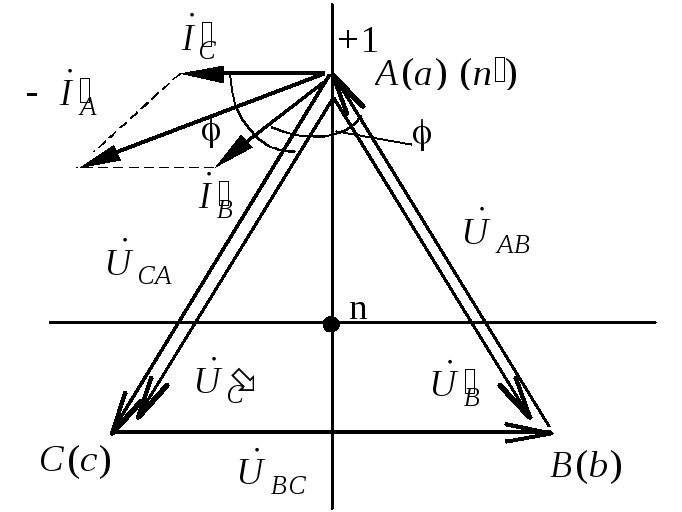
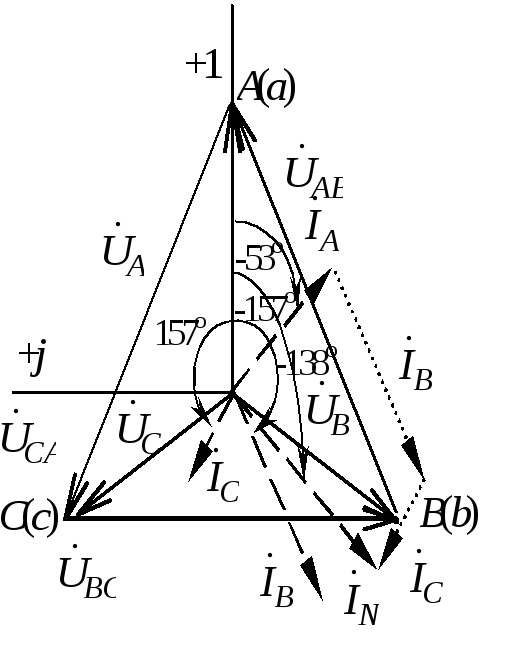
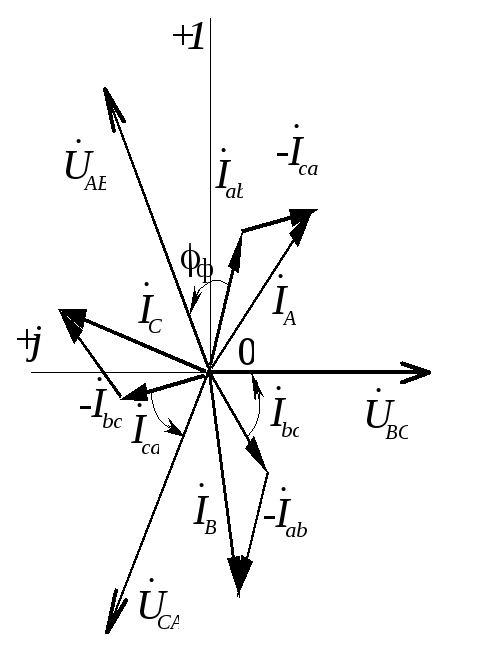
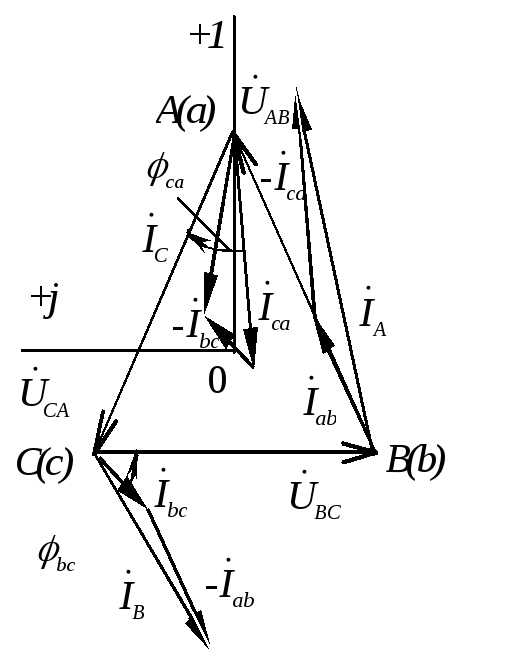
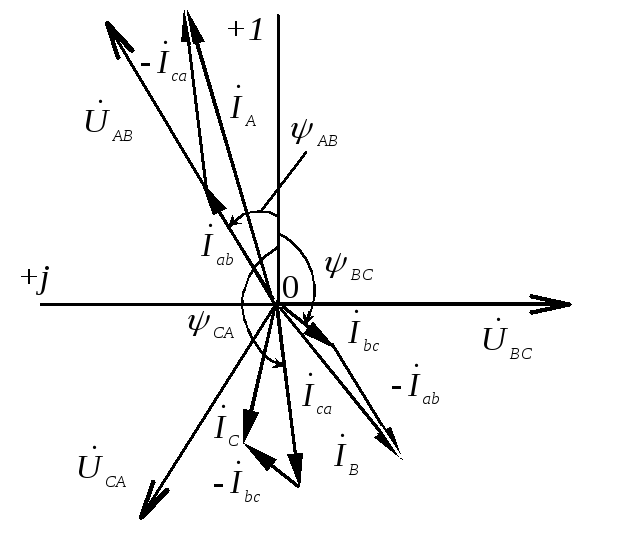
Векторная диаграмма
токов и напряжений показана на рис.
1.3.9. Для построения векторной диаграммы
необходимо выбрать масштабы напряжений

и токов
.

Рассмотрим аварийный
режим работы– обрыв фазы А (рис.1.3.10).

В этом случае
трехфазная цепь превращается в однофазную
,
причем фазы b
и с
оказываются включенными последовательно
на линейное напряжение
,
т. е. на каждую из этих фаз падает
напряжение

Фазные и линейные
токи

.

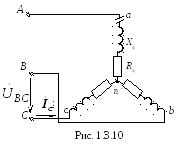
Потребляемая мощность Рис. 1.3.11 Как видно из расчета, потребляемая мощность снизилась почти в два раза. Если обрыв фазы произошел внутри самого двигателя (обрыв обмотки), то эта обмотка оказывается под повышенным напряжением , что видно из векторной диаграммы (рис.1.3.11). Неповрежденные обмотки находятся под пониженным напряжением, что не опасно для них.

Рассмотрим аварийный
режим работы – короткое замыкание фазы
«а» (рис.
1.3.12, а, б).

При коротком
замыкании фазы нейтральная точка
оказывается связана с питающей точкой
А,
значит, неповрежденные фазы b
и с
окажутся включенными на линейное
напряжение
,
что видно из векторной диаграммы.

Токи
в неповрежденных фазах

.

а

б

Рис. 1.3.12

Ток в фазе а
равен геометрической сумме токов

и

( по векторной диаграмме составляет
примерно 69 А).

Задача 1.3.2.
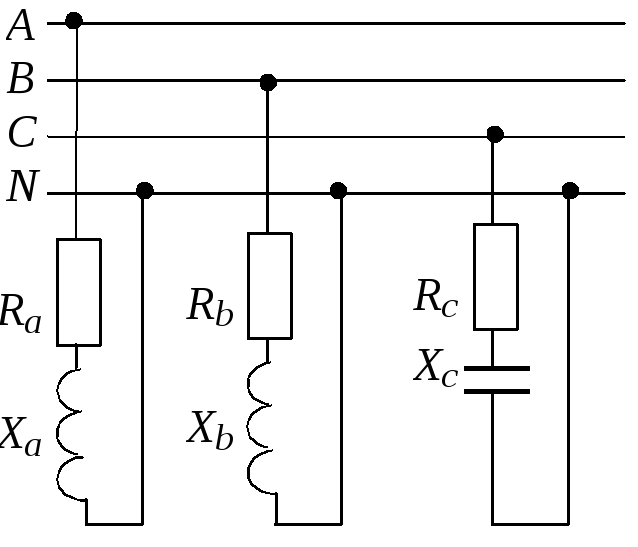
Три однофазных приемника включены в
трехфазную сеть с напряжением 380 В по
схеме “звезда с нейтральным проводом”.
Сопротивления приемников:

Ом;

Ом;

Ом.

Требуется
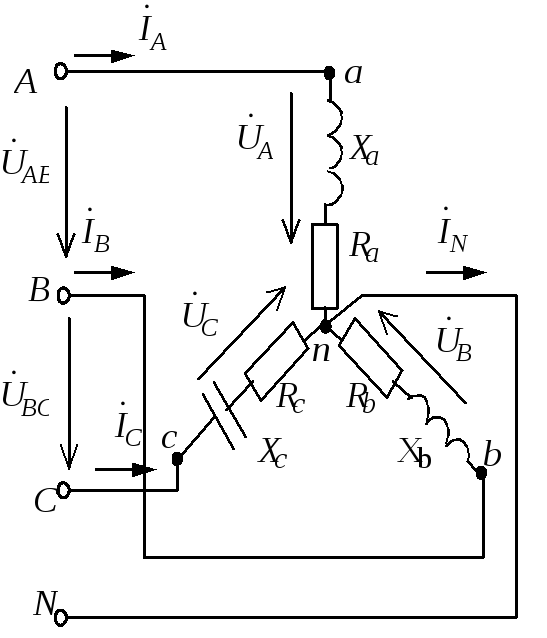
изобразить схему включения приемников;
определить токи в проводах сети; построить
векторную диаграмму токов и напряжений;
вычислить активную, реактивную и полную
(кажущуюся) мощности.

Решение:

Схема включения
приемников принципиальная и расчетная
представлены на рис. 1.3.13, а,б.

а	б
Рис. 1.3.13

Наличие
нейтрального провода обеспечивает
симметричную систему фазных напряжений
на приемниках. Напряжение сети – линейное
напряжение

В.

Система фазных
напряжений в комплексной форме

Сопротивления фаз

Для
схемы “звезда“ фазные и линейные токи
равны между собой и составляют

Ток в нейтральном
проводе

При построении векторных диаграмм фазные и линейные напряжения и токи строятся относительно комплексных осей откладываются с учетом начальных фаз. Ток в нейтральном проводе – это результат геометрического сложения векторов фазных токов, и его расположение и длина должны соответствовать расчетному значению (рис. 1.3.13).

Рис. 1.3.13

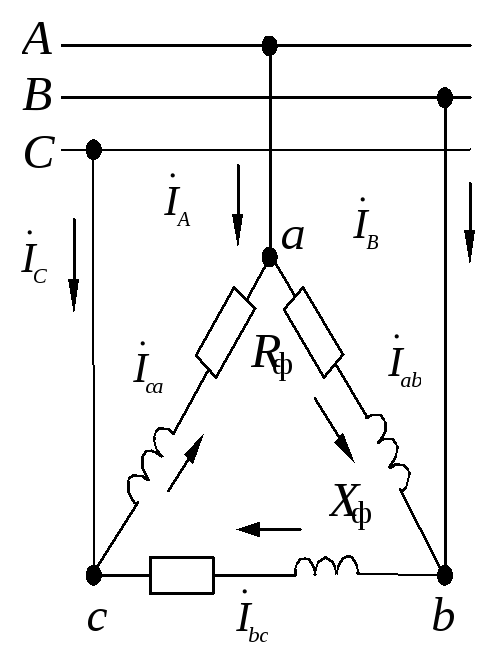
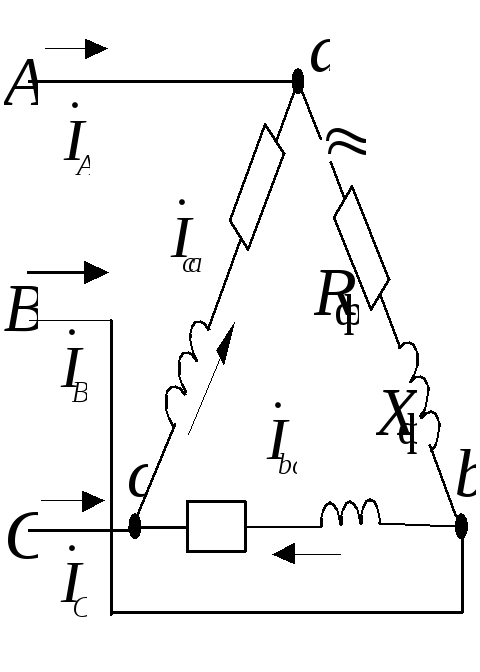
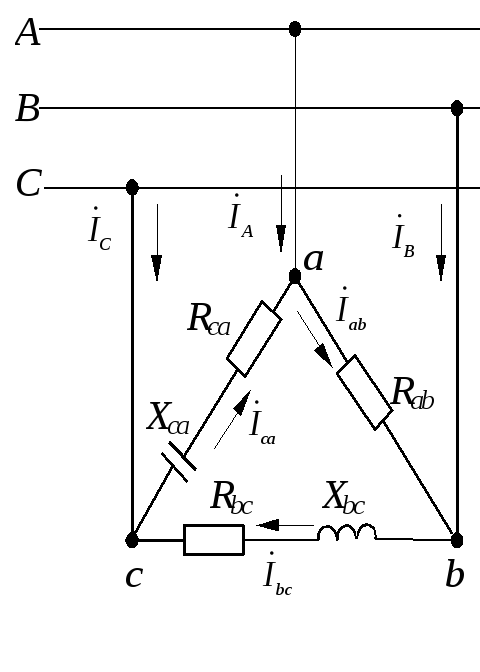
Задача 1.3.3.
К трехфазной системе напряжением 380 В
подключены три одинаковых приемника
(R_Ф =
3 Ом, X_LФ =
4 Ом), соединенные по схеме “треугольник“
(рис.1.3.14). Определить токи в фазных и
линейных проводах и потребляемую
мощность (активную, реактивную, полную).
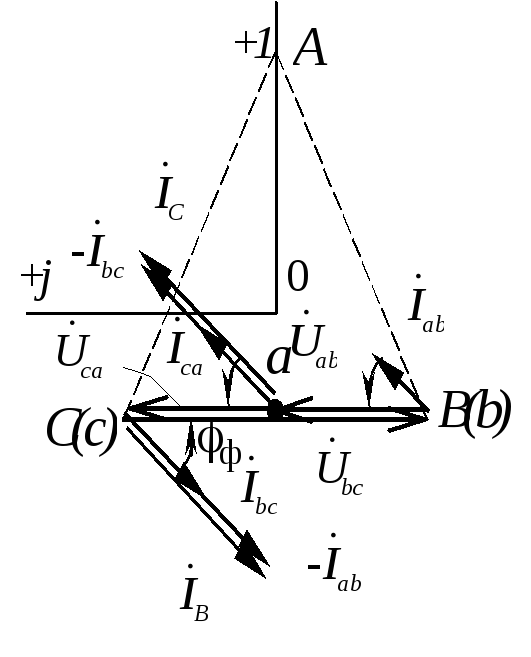
Построить векторную диаграмму токов и
напряжений.

Рассмотреть
аварийные режимы – обрывы фазного и
линейных проводов.

Решение:

Нагрузка фаз одинакова, поэтому расчет проводится для одной фазы. Напряжение сети — это линейное напряжение, в схеме “треугольник “ Uф = Uл = 380 В. Комплексное сопротивление фазы: где

Рис. 1.3.14

Фазные токи:

линейные токи
(только для симметричной нагрузки):

Активная мощность,
потребляемая нагрузкой:

реактивная мощность:

полная мощность:

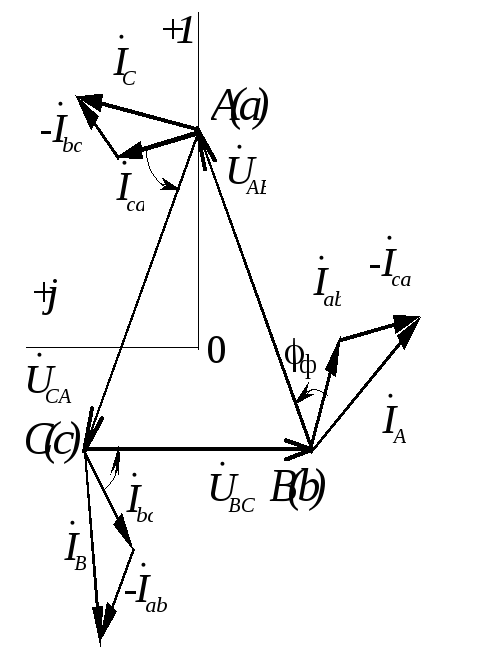
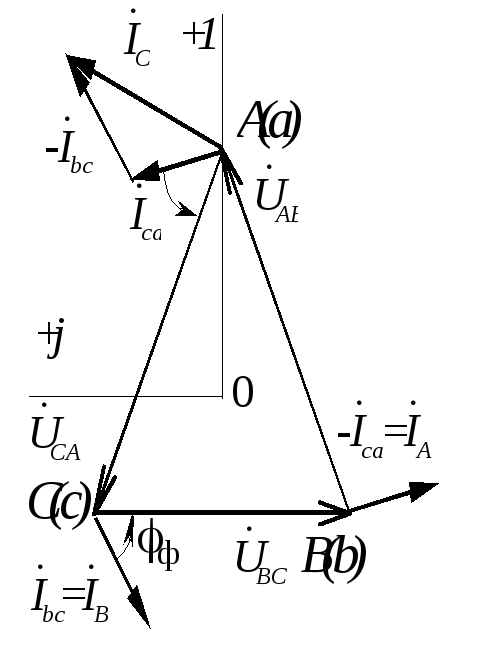
Векторная
диаграмма может быть построена в двух
вариантах в зависимости от изображения
системы напряжений (рис.1.3.15 ). Предварительно
выбирают масштабы тока и напряжения.

Рис. 1.3.15

Фазные токи отстают
от соответствующих напряжений на угол
_Ф
= 53.
Линейные токи находятся из соотношений:

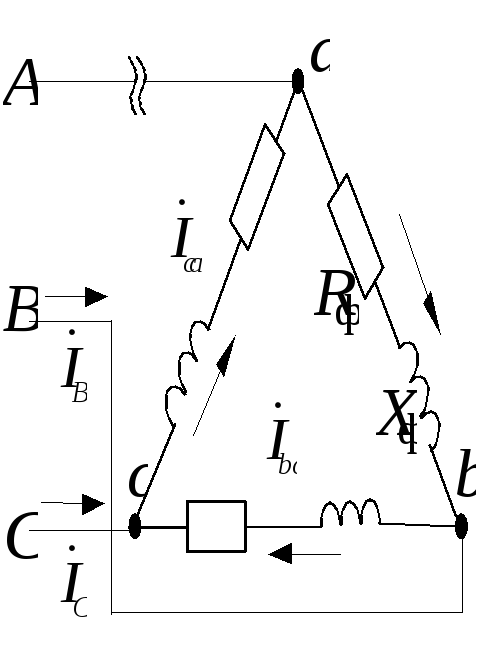
Рассмотрим обрыв
фазы “аb”
(рис.1.3.16,а). Определим токи в неповрежденных
фазах и в линии, построим векторную
диаграмму токов и напряжений.

а)	б)
Рис. 1.3.16

Токи
в неповрежденных фазах не изменяются,
так как не изменяются напряжения:

Линейные токи по
первому закону Кирхгофа (с учетом
):

.

Из этих уравнений
следует, что действующие значения
линейных токов

и

равны действующим значениям фазных
токов
,
а у линейного тока действующее значение
не изменяется

Векторная
диаграмма токов и напряжений строится
аналогично симметричному режиму и
приведена на рис.1.3.16,б.

Рассмотрим обрыв
линейного провода
А
(рис.1.3.17,а). Определим фазные и линейные
токи и построим векторную диаграмму
токов и напряжений.

К приемнику
подводится только напряжение

Сопротивление
фазы “bс”
включено на полное напряжение
,
а равные сопротивления фаз “аb”
и ”са”
включены последовательно друг с другом,
причем к каждому из них подведена
половина напряжения
.

а) б) Рис.1.3.17

Сеть становится
аналогичной однофазной с двумя
параллельными ветвями:

Ток фазы “bс” не
изменяется:

токи других фаз
:

линейные токи (
при
)
:

Векторная
диаграмма токов и напряжений представлена
на рис. 1.3.17,б.

Задача 1.3.4
В трехфазную сеть напряжением 380 В,
частотой f = 50 Гц включен трехфазный
асинхронный двигатель по схеме
“треугольник“. Потребляемая активная
мощность P = 1,44 кВт, коэффициент мощности
cos
= 0,85. Определить потребляемый двигателем
ток, токи в обмотках двигателя, активное
и индуктивное сопротивления, индуктивность
катушек, полную и реактивную потребляемые
мощности.

Решение:

Двигатель является
симметричной нагрузкой, поэтому расчет
ведем на фазу.

Сеть маркируется
линейным напряжением, поэтому U_Л
= 380 В.

При соединении по
схеме “треугольник“ U_Л
= U_Ф=
380 В.

Активная мощность,
потребляемая нагрузкой,

отсюда фазный ток,
протекающий в обмотках двигателя:

Потребляемые
двигателем токи — линейные токи:

Полное сопротивление
фазы обмотки двигателя:

Ом,

активное сопротивление

Ом,

индуктивное
сопротивление

Ом.

Индуктивность
обмотки определяется из выражения

,

Гн.

Полная потребляемая
мощность:

кВА;

реактивная мощность:

Задача 7.3
К трехпроводной
трехфазной линии с напряжением 380 В
подключены три однофазных приемника с
параметрами: R₁=
5 Ом, R₂=
6 Ом, X_L2=
8 Ом, R₃=4
Ом, X_C3=
3 Ом. Определить токи в фазах и линейных
проводах, активную, реактивную и полную
мощности и построить векторную диаграмму
токов и напряжений.

Решение:

	Однофазные приемники к трехпроводной сети подключаются по схеме “треугольник“ (рис.1.3.18). Нагрузка несимметричная, ток каждой фазы нужно считать отдельно. Исходная система напряжений: Комплексные сопротивления фаз: Ом;
Рис. 1.3.18

Ом;

Ом;

Фазные токи:

Линейные токи:

Сумма линейных
токов должна равняться нулю, и
действительно,

Активная мощность:

Реактивная
мощность:

здесь знак “минус”
показывает, что преобладает емкостная
нагрузка.

Полная мощность:

Векторные диаграммы
токов и напряжений в двух вариантах
(для разного представления исходной
системы напряжений) приведены на
рис.1.3.19.

Предварительно
выбирают масштабы тока и напряжения.
Векторы фазных токов

откладывают относительно векторов
соответствующих напряжений под углами

,

,

или в соответствии с полученными их
начальными фазами
;
;
.
Затем по первому закону Кирхгофа строят
векторы линейных токов
,
длина и направление которых должны
соответствовать расчетным данным.

Рис.1.3.19 Векторные диаграммы токов и напряжений несимметричной нагрузки

Соседние файлы в папке 2.2 Трехфазные цепи

• #
• #
• #
• #
• #

В блоге мы часто рассматриваем решение типовых задач по физике с конкретными примерами, чтобы у вас сложилось четкое представление о том, что делать с подобными заданиями и как их решать. В этой статье рассмотрим задачи на работу и мощность электрического тока.

Работа и мощность тока

Прежде чем перейти к решению задач, давайте разберемся с основными определениями данного раздела физики.

Работа электротока на участке цепи определяется произведением напряжения на концах этого участка, силы тока и времени, за которое эта работа была совершена. Физическая величина обозначается большой латинской буквой A и измеряется в Джоулях.

При прохождении электротока по однородному участку цепи, можно говорить о том, что электрическое поле на этом участке цепи совершает определенную работу.

Мощность электротока — это работа тока, совершенная за 1 единицу времени. Физическая величина обозначается символом P и измеряется в Ваттах.

Необходимые формулы

Чтобы рассчитать работу и мощность электротока, понадобятся следующие формулы:

1. Уравнение для вычисления работы тока:

(A=Utimes q)

где U — напряжение электрического поля, q — электрический заряд, проходящий по участку цепи.

Или так:

(A=Utimes Itimes t)

где U — напряжение поля, I — сила тока на этом участке цепи, t — время прохождения заряда.

2. Формула для нахождения мощности тока:

(P=frac At)

где A — работа электротока, t — время.

Или же:

(P=Utimes I)

где U — напряжение, I — сила тока.

3. Закон Джоуля-Ленца:

(Q=A=I^2times Rtimes t)

где R — сопротивление проводника.

Вопросы на работу и мощность электрического тока

Теоретические вопросы на работу и мощность электрического тока могут быть следующими:

1. Что за физическая величина работа электрического тока? (Ответ дан в нашей статье выше).
2. Что такое мощность электротока? (Ответ дан выше).
3. Дайте определение закону Джоуля-Ленца. Ответ: Работа электротока, который течет по неподвижному проводнику, имеющему сопротивление R, превращается в тепло в проводнике.
4. В чем измеряется работа тока? (Ответ выше).
5. В чем измеряется мощность? (Ответ выше).

Это примерный список вопросов. Суть теоретических вопросов по физике всегда одна: проверить понимание физических процессов, зависимости одной величины от другой, знание формул и единиц измерения, принятых в международной системе СИ.

Задачи с решением

Рассмотрим типовые задачи с решениями по этой теме.

Задача №1. Мощность электрического тока

В сеть напряжением 220 В включена электрическая лампа. Сила тока, проходящего через нее равна 0,45 А. Чему будет равна мощность электротока в лампе за 2 секунды?

Решение

1. Записываем вводные данные: U=220 В, I=0,45A, t=2с, P=?
2. Вспоминаем уравнение для определения мощности:( P=Utimes I)
3. Подставляем известные нам числовые значения в формулу и получаем ответ: P=99 Вт.

Задача №2. Расчет мощности электрического тока

В одной электролампе напряжение равно 24 В, а сила тока 0,7 А, во второй электролампе напряжение равно 120 В, а сила тока 0,5 А. У какой из этих двух электрических ламп мощность электротока больше?

Решение:

1. Фиксируем исходные данные: U₁=24 В, I₁=0,7 А, U₂=120 В, I₂=0,5 А, P₁=? P₂=?
2. По формуле (P=Utimes I) находим P₁ и P₂. P₁=16,8 Вт, P₂= 24 Вт.
3. Получаем ответ на задачу: мощность тока второй лампы больше мощности тока первой лампы.

Задача №3. Работа электрического тока

Какую работу совершает электроток в утюге с сопротивлением 80 Ом за 10 минут при условии, что утюг работает от сети 220 Вольт?

Решение

1. Записываем «Дано»: U=220 В, R=80 Ом, t=10 мин., A=?
2. Переводим минуты в секунды: 10 мин=600 с.
3. Записываем формулу для определения работы электротока: (A=frac{U^2}Rtimes t)
4. Подставляем известные нам из условий задачи числовые значения в формулу и получаем ответ: 363000 Дж или 363 кДж.

Задача №4. Расчет работы электрического тока

Два троллейбуса имеют одинаковые электродвигатели. В настоящий момент они находятся в движении. Первый троллейбус двигается с большей скоростью, второй — с меньшей. У какого троллейбуса работа электротока больше, при условии, что сопротивление и время движения одинаковы?

Решение

1. Данная задача не требует записи каких-либо формул. В ней проверяется понимание учащимися взаимозависимости двух физических величин.
2. Чем больше скорость движения, тем больше мощность электротока. Чем больше мощность, тем больше и работа, совершаемая электродвигателем. Следовательно, у первого троллейбуса она будет больше.

Задача №5 на закон Джоуля-Ленца

Аккумулятор с электродвижущей силой, равной 6 В и внутренним сопротивлением 0,1 Ом питает внешнюю цепь, у которой сопротивление равно 12,4 Ом. Какое количество теплоты выделится за 10 минут работы аккумулятора?

Решение:

1. Фиксируем имеющиеся данные: (epsilon)=6 В, r=0,1 Ом, R=12,4 Ом, Q=?
2. Переводим минуты в секунды, получаем 600 секунд.
3. Общее количество теплоты будет определяться по формуле: Q_внутр+Q_внеш. (Q_{внутр}=I^2times Rtimes t), (Q_{внеш}=I^2times rtimes t )
4. По формуле (I=frac epsilon{R+r}) находим силу тока.
5. Подставляем все известные нам данные в каждую формулу и получаем общее количество теплоты, выделенное за 10 минут работы, равное 1728 Дж.

Мы рассмотрели не слишком сложные задачи, большинство из которых можно решить при помощи одной формулы. Однако в школьных учебниках встречаются задания и посложнее. Если столкнулись со трудной для понимания темой по физике или любому другому предмету, не вешайте нос! Специалисты Феникс.Хелп с радостью придут вам на помощь. Любые письменные работы будут сделаны качественно и строго в обозначенные сроки.