From Wikipedia, the free encyclopedia
| Sound measurements | |
|---|---|
|
Characteristic |
Symbols |
| Sound pressure | p, SPL,LPA |
| Particle velocity | v, SVL |
| Particle displacement | δ |
| Sound intensity | I, SIL |
| Sound power | P, SWL, LWA |
| Sound energy | W |
| Sound energy density | w |
| Sound exposure | E, SEL |
| Acoustic impedance | Z |
| Audio frequency | AF |
| Transmission loss | TL |
|
|
|
|
Sound pressure or acoustic pressure is the local pressure deviation from the ambient (average or equilibrium) atmospheric pressure, caused by a sound wave. In air, sound pressure can be measured using a microphone, and in water with a hydrophone. The SI unit of sound pressure is the pascal (Pa).[1]
Mathematical definition[edit]
Sound pressure diagram:
- silence;
- audible sound;
- atmospheric pressure;
- sound pressure
A sound wave in a transmission medium causes a deviation (sound pressure, a dynamic pressure) in the local ambient pressure, a static pressure.
Sound pressure, denoted p, is defined by
where
- ptotal is the total pressure,
- pstat is the static pressure.
Sound measurements[edit]
Sound intensity[edit]
In a sound wave, the complementary variable to sound pressure is the particle velocity. Together, they determine the sound intensity of the wave.
Sound intensity, denoted I and measured in W·m−2 in SI units, is defined by
where
- p is the sound pressure,
- v is the particle velocity.
Acoustic impedance[edit]
Acoustic impedance, denoted Z and measured in Pa·m−3·s in SI units, is defined by[2]
where
Specific acoustic impedance, denoted z and measured in Pa·m−1·s in SI units, is defined by[2]
where
Particle displacement[edit]
The particle displacement of a progressive sine wave is given by
where
It follows that the particle velocity and the sound pressure along the direction of propagation of the sound wave x are given by
where
Taking the Laplace transforms of v and p with respect to time yields
Since 
Consequently, the amplitude of the particle displacement is related to that of the acoustic velocity and the sound pressure by
Inverse-proportional law[edit]
When measuring the sound pressure created by a sound source, it is important to measure the distance from the object as well, since the sound pressure of a spherical sound wave decreases as 1/r from the centre of the sphere (and not as 1/r2, like the sound intensity):[3]
This relationship is an inverse-proportional law.
If the sound pressure p1 is measured at a distance r1 from the centre of the sphere, the sound pressure p2 at another position r2 can be calculated:
The inverse-proportional law for sound pressure comes from the inverse-square law for sound intensity:
Indeed,
where
is the convolution operator,
- z−1 is the convolution inverse of the specific acoustic impedance,
hence the inverse-proportional law:
The sound pressure may vary in direction from the centre of the sphere as well, so measurements at different angles may be necessary, depending on the situation. An obvious example of a sound source whose spherical sound wave varies in level in different directions is a bullhorn.[citation needed]
Sound pressure level[edit]
Sound pressure level (SPL) or acoustic pressure level is a logarithmic measure of the effective pressure of a sound relative to a reference value.
Sound pressure level, denoted Lp and measured in dB,[4] is defined by:[5]
where
- p is the root mean square sound pressure,[6]
- p0 is a reference sound pressure,
- 1 Np is the neper,
- 1 B = (1/2 ln 10) Np is the bel,
- 1 dB = (1/20 ln 10) Np is the decibel.
The commonly used reference sound pressure in air is[7]
p0 = 20 μPa,
which is often considered as the threshold of human hearing (roughly the sound of a mosquito flying 3 m away). The proper notations for sound pressure level using this reference are Lp/(20 μPa) or Lp (re 20 μPa), but the suffix notations dB SPL, dB(SPL), dBSPL, or dBSPL are very common, even if they are not accepted by the SI.[8]
Most sound-level measurements will be made relative to this reference, meaning 1 Pa will equal an SPL of 94 dB. In other media, such as underwater, a reference level of 1 μPa is used.[9] These references are defined in ANSI S1.1-2013.[10]
The main instrument for measuring sound levels in the environment is the sound level meter. Most sound level meters provide readings in A, C, and Z-weighted decibels and must meet international standards such as IEC 61672-2013.
Examples[edit]
The lower limit of audibility is defined as SPL of 0 dB, but the upper limit is not as clearly defined. While 1 atm (194 dB peak or 191 dB SPL)[11][12] is the largest pressure variation an undistorted sound wave can have in Earth’s atmosphere (i.e. if the thermodynamic properties of the air are disregarded, in reality the sound waves become progressively non-linear starting over 150 dB), larger sound waves can be present in other atmospheres or other media, such as underwater or through the Earth.[13]
Ears detect changes in sound pressure. Human hearing does not have a flat spectral sensitivity (frequency response) relative to frequency versus amplitude. Humans do not perceive low- and high-frequency sounds as well as they perceive sounds between 3,000 and 4,000 Hz, as shown in the equal-loudness contour. Because the frequency response of human hearing changes with amplitude, three weightings have been established for measuring sound pressure: A, B and C.
In order to distinguish the different sound measures, a suffix is used: A-weighted sound pressure level is written either as dBA or LA. B-weighted sound pressure level is written either as dBB or LB, and C-weighted sound pressure level is written either as dBC or LC. Unweighted sound pressure level is called «linear sound pressure level» and is often written as dBL or just L. Some sound measuring instruments use the letter «Z» as an indication of linear SPL.[13]
Distance[edit]
The distance of the measuring microphone from a sound source is often omitted when SPL measurements are quoted, making the data useless, due to the inherent effect of the inverse proportional law. In the case of ambient environmental measurements of «background» noise, distance need not be quoted, as no single source is present, but when measuring the noise level of a specific piece of equipment, the distance should always be stated. A distance of one metre (1 m) from the source is a frequently used standard distance. Because of the effects of reflected noise within a closed room, the use of an anechoic chamber allows sound to be comparable to measurements made in a free field environment.[13]
According to the inverse proportional law, when sound level Lp1 is measured at a distance r1, the sound level Lp2 at the distance r2 is
Multiple sources[edit]
The formula for the sum of the sound pressure levels of n incoherent radiating sources is
Inserting the formulas
in the formula for the sum of the sound pressure levels yields
Examples of sound pressure[edit]
| Source of sound | Distance | Sound pressure level[a] | |
|---|---|---|---|
| (Pa) | (dBSPL) | ||
| Shock wave (distorted sound waves > 1 atm; waveform valleys are clipped at zero pressure)[11][12] | >1.01×105 | >191 | |
| Simple open-ended thermoacoustic device[14] | [clarification needed] | 1.26×104 | 176 |
| 1883 eruption of Krakatoa[15][16] | 165 km | 172 | |
| .30-06 rifle being fired | 1 m to shooter’s side |
7.09×103 | 171 |
| Firecracker[17] | 0.5 m | 7.09×103 | 171 |
| Stun grenade[18] | Ambient | 1.60×103 …8.00×103 |
158–172 |
| 9-inch (23 cm) party balloon inflated to rupture[19] | At ear | 4.92×103 | 168 |
| 9-inch (23 cm) diameter balloon crushed to rupture[19] | At ear | 1.79×103 | 159 |
| 9-inch (23 cm) party balloon inflated to rupture[19] | 0.5 m | 1.42×103 | 157 |
| 9-inch (23 cm) diameter balloon popped with a pin[19] | At ear | 1.13×103 | 155 |
| LRAD 1000Xi Long Range Acoustic Device[20] | 1 m | 8.93×102 | 153 |
| 9-inch (23 cm) party balloon inflated to rupture[19] | 1 m | 731 | 151 |
| Jet engine[13] | 1 m | 632 | 150 |
| 9-inch (23 cm) diameter balloon crushed to rupture[19] | 0.95 m | 448 | 147 |
| 9-inch (23 cm) diameter balloon popped with a pin[19] | 1 m | 282.5 | 143 |
| Loudest human voice[21] | 1 inch | 110 | 135 |
| Trumpet[22] | 0.5 m | 63.2 | 130 |
| Vuvuzela horn[23] | 1 m | 20.0 | 120 |
| Threshold of pain[24][25][21] | At ear | 20–200 | 120–140 |
| Risk of instantaneous noise-induced hearing loss | At ear | 20.0 | 120 |
| Jet engine | 100–30 m | 6.32–200 | 110–140 |
| Two-stroke chainsaw[26] | 1 m | 6.32 | 110 |
| Jackhammer | 1 m | 2.00 | 100 |
| Traffic on a busy roadway | 10 m | 0.20–0.63 | 80–90 |
| Hearing damage (over long-term exposure, need not be continuous)[27] | At ear | 0.36 | 85 |
| Passenger car | 10 m | 0.02–0.20 | 60–80 |
| EPA-identified maximum to protect against hearing loss and other disruptive effects from noise, such as sleep disturbance, stress, learning detriment, etc.[28] | Ambient | 0.06 | 70 |
| TV (set at home level) | 1 m | 0.02 | 60 |
| Normal conversation | 1 m | 2×10−3–0.02 | 40–60 |
| Very calm room | Ambient | 2.00×10−4 …6.32×10−4 |
20–30 |
| Light leaf rustling, calm breathing[13] | Ambient | 6.32×10−5 | 10 |
| Auditory threshold at 1 kHz[27] | At ear | 2.00×10−5 | 0 |
| Anechoic chamber, Orfield Labs, A-weighted[29][30] | Ambient | 6.80×10−6 | −9.4 |
| Anechoic chamber, University of Salford, A-weighted[31] | Ambient | 4.80×10−6 | −12.4 |
| Anechoic chamber, Microsoft, A-weighted[32][33] | Ambient | 1.90×10−6 | −20.35 |
- ^ All values listed are the effective sound pressure unless otherwise stated.
See also[edit]
- Acoustics
- Phon (unit)
- Loudness
- Sone (unit)
- Sound level meter
- Stevens’s power law
- Weber–Fechner law, especially The case of sound
References[edit]
- ^ «Sound Pressure is the force of sound on a surface area perpendicular to the direction of the sound». Retrieved 22 April 2015.
- ^ a b Wolfe, J. «What is acoustic impedance and why is it important?». University of New South Wales, Dept. of Physics, Music Acoustics. Retrieved 1 January 2014.
- ^ Longhurst, R. S. (1967). Geometrical and Physical Optics. Norwich: Longmans.
- ^ «Letter symbols to be used in electrical technology – Part 3: Logarithmic and related quantities, and their units», IEC 60027-3 Ed. 3.0, International Electrotechnical Commission, 19 July 2002.
- ^ Attenborough K, Postema M (2008). A pocket-sized introduction to acoustics. Kingston upon Hull: The University of Hull. doi:10.5281/zenodo.7504060. ISBN 978-90-812588-2-1.
- ^ Bies, David A., and Hansen, Colin. (2003). Engineering Noise Control.
- ^ Ross Roeser, Michael Valente, Audiology: Diagnosis (Thieme 2007), p. 240.
- ^ Thompson, A. and Taylor, B. N. Sec. 8.7: «Logarithmic quantities and units: level, neper, bel», Guide for the Use of the International System of Units (SI) 2008 Edition, NIST Special Publication 811, 2nd printing (November 2008), SP811 PDF.
- ^ Morfey, Christopher L. (2001). Dictionary of Acoustics. San Diego: Academic Press. ISBN 978-0125069403.
- ^ «Noise Terms Glossary». Retrieved 2012-10-14.
- ^ a b Self, Douglas (2020-04-17). Small Signal Audio Design. CRC Press. ISBN 978-1-000-05044-8.
this limit is reached when the rarefaction creates a vacuum, because you can’t have a lower pressure than that. This corresponds to about +194 dB SPL.
- ^ a b Guignard, J. C.; King, P. F.; North Atlantic Treaty Organization Advisory Group for Aerospace Research and Development Aerospace Medical Panel (1972). Aeromedical Aspects of Vibration and Noise. North Atlantic Treaty Organization, Advisory Group for Aerospace Research and Development.
In air at an assumed atmospheric pressure of 1 bar (100,000 N/m2) this occurs theoretically at approximately 191 dB SPL (working with rms values
- ^ a b c d e Winer, Ethan (2013). «1». The Audio Expert. New York and London: Focal Press. ISBN 978-0-240-82100-9.
- ^ HATAZAWA, Masayasu; SUGITA, Hiroshi; OGAWA, Takahiro; SEO, Yoshitoki (2004-01-01). «Performance of a Thermoacoustic Sound Wave Generator driven with Waste Heat of Automobile Gasoline Engine». Transactions of the Japan Society of Mechanical Engineers Series B. 70 (689): 292–299. doi:10.1299/kikaib.70.292. ISSN 0387-5016.
- ^ «Krakatoa Eruption — The Loudest Sound». Brüel & Kjær. Retrieved 2021-03-24.
160 km (99 miles) away from the source, registered a sound pressure level spike of more than 2½ inches of mercury (8.5 kPa), equivalent to 172 decibels.
- ^ Winchester, Simon (2003). Krakatoa: The Day the World Exploded, August 27, 1883. Penguin/Viking. p. 218. ISBN 978-0-670-91430-2.
- ^ Flamme, GregoryA; Liebe, Kevin; Wong, Adam (2009). «Estimates of the auditory risk from outdoor impulse noise I: Firecrackers». Noise and Health. 11 (45): 223–230. doi:10.4103/1463-1741.56216. ISSN 1463-1741. PMID 19805932.
- ^ Brueck S. E., Kardous C. A., Oza A., Murphy W. J (2014). «NIOSH HHE Report No. 2013-0124-3208. Health hazard evaluation report: measurement of exposure to impulsive noise at indoor and outdoor firing ranges during tactical training exercises» (PDF). Cincinnati, OH: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health.
{{cite web}}: CS1 maint: multiple names: authors list (link) - ^ a b c d e f g «Did You Know How Loud Balloons Can Be?». Retrieved 8 June 2018.
- ^ «LRAD Corporation Product Overview for LRAD 1000Xi». Retrieved 29 May 2014.
- ^ a b Realistic Maximum Sound Pressure Levels for Dynamic Microphones – Shure.
- ^ Recording Brass & Reeds.
- ^ Swanepoel, De Wet; Hall III, James W.; Koekemoer, Dirk (February 2010). «Vuvuzela – good for your team, bad for your ears» (PDF). South African Medical Journal. 100 (4): 99–100. doi:10.7196/samj.3697. PMID 20459912.
- ^ Nave, Carl R. (2006). «Threshold of Pain». HyperPhysics. SciLinks. Retrieved 2009-06-16.
- ^ Franks, John R.; Stephenson, Mark R.; Merry, Carol J., eds. (June 1996). Preventing Occupational Hearing Loss – A Practical Guide (PDF). National Institute for Occupational Safety and Health. p. 88. Retrieved 2009-07-15.
- ^ «Decibel Table – SPL – Loudness Comparison Chart». sengpielaudio. Retrieved 5 Mar 2012.
- ^ a b William Hamby. «Ultimate Sound Pressure Level Decibel Table». Archived from the original on 2005-10-19.
- ^ «EPA Identifies Noise Levels Affecting Health and Welfare» (Press release). Environmental Protection Agency. April 2, 1974. Retrieved March 27, 2017.
- ^ ««THE QUIETEST PLACE ON EARTH» – GUINNESS WORLD RECORDS CERTIFICATE, 2005″ (PDF). Orfield Labs.
- ^ Middlemiss, Neil (December 18, 2007). «The Quietest Place on Earth – Orfield Labs». Audio Junkies, Inc. Archived from the original on 2010-11-21.
- ^ Eustace, Dave. «Anechoic Chamber». University of Salford.
- ^ «Microsoft lab sets new record for the world’s quietest place». 2015-10-02. Retrieved 2016-09-20.
The computer company has built an anechoic chamber in which highly sensitive tests reported an average background noise reading of an unimaginably quiet −20.35 dBA (decibels A-weighted).
- ^ «Check out the world’s quietest room». Microsoft: Inside B87. Retrieved 2016-09-20.
- General
- Beranek, Leo L., Acoustics (1993), Acoustical Society of America, ISBN 0-88318-494-X.
- Daniel R. Raichel, The Science and Applications of Acoustics (2006), Springer New York, ISBN 1441920803.
External links[edit]
Media related to Sound pressure at Wikimedia Commons
- Sound Pressure and Sound Power, Effect and Cause
- Conversion of Sound Pressure to Sound Pressure Level and Vice Versa
- Table of Sound Levels, Corresponding Sound Pressure and Sound Intensity
- Ohm’s Law as Acoustic Equivalent, Calculations
- Relationships of Acoustic Quantities Associated with a Plane Progressive Acoustic Sound Wave
- Sound Pressure and Sound Power, Two Commonly Confused Characteristics of Sound
- How Many Decibels Is Twice as Loud? Sound Level Change and the Respective Factor of Sound Pressure or Sound Intensity
- Decibel (Loudness) Comparison Chart
Звуковое давление и уровень интенсивности звука
Звуковым полем называется пространство, в котором распространяется звуковая волна.
Основный характеристикой звукового поля является звуковое давление Р, интенсивность звука J (сила звука).
Интенсивность звука измеряется в (вт/м 2 ).
Связь между силой звука и звуковым давлением вычисляется по формуле:
Интенсивность звука находится по формуле:
Р — звуковое давление, Па;
с —скорость распространения звука в среде, м/с;
ρ0 — плотность среды распространения звука, кг/м 3 .
Уровень звукового давления вычисляется по формуле:
P — звуковое давление в точке измерения, Па;
P0 — звуковое давление на пороге слышимости и равна 2·10 -5 , Па;
Уровень интенсивности звука N в децибелах определяется по формуле (используется десятичный логарифм):
J — интенсивность звука в точке измерения (уровень вычисляется), Вт/м;
J0 — интенсивность звука при частоте 1000 Гц (порог слышимости), примерно равен 1·10 -12 вт/м.
Уровень интенсивности звука измеряется в децибелах (дц).
Логарифмическая шкала выражает частоты от 0 до 140 дц.
Как видно, выражение подчинено логарифмическому закону, то есть, если интенсивность звука увеличить в сто раз, то ощущение громкости увеличится всего лишь в 2 раза.
Уровень интенсивности звука в неперах вычисляется по формуле (используется натуральный логарифм):
Здесь, интенсивность звука измеряется в неперах, 1 непер равен 8,7 дб.
Уровни звукового давления и интенсивности.
Поскольку человеческий слух различает огромный диапазон изменения звукового давления (разница между самым тихим звуком 2∙10 -5 Па и самым громким звуком 20 Па составляет 10 6 ), то использовать при измерениях такую большую шкалу чрезвычайно неудобно, поэтому во всех измерительных приборах (шумомерах, измерительных компьютерных станциях и др.) используется логарифмическая шкала, которая позволяет сжать масштаб измерения звукового давления.
Для этого используется уровень звукового давления, который определяется как:
Уровень звукового давления измеряется в децибелах (дБ).
Например, если звуковое давление равно 2 Па, то уровень звукового давления равен:
Lp = 20 lg p/p0 = 20 lg (2 Па / (2∙10 -5 ) Па) = 20 lg (1 ∙ 10 +5 ) = 20∙5 = 100 дБ.
Обратный пример: если задан уровень звукового давления Lp = 80 дБ, то звуковое давление определяется следующим образом:
Lp = 20 lg p/p0, отсюда 80 дБ = 20 lg p / (2∙10 -5 ), значит, lg p/(2∙10 -5 ) = 4. Следовательно, 10 4 = p/(2∙10 -5 ), отсюда значение звукового давления будет равно p = 0,2 Па.
Увеличение звукового давления в два раза соответствует изменению уровня звукового давления на 6 дБ. Например, звуковое давление 2 Па соответствует уровню звукового давления 100 дБ, а звуковое давление 1 Па соответствует уровню 94 дБ, звуковое давление 4 Па – уровню 106 дБ и т.д.
Кроме того, следует обратить внимание на то, что уровни звукового давления нескольких одновременно работающих различных источников никогда не складываются. Для определения суммарного уровня необходимо рассчитать значения звукового давления, соответствующего каждому уровню: p1 и p2. Затем определить суммарное звуковое давление 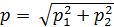
Например, если играют скрипка с уровнем 80 дБ и рояль с уровнем 86 дБ, то их суммарный уровень звукового давления определяется следующим образом. Уровню 80 дБ соответствует звуковое давление 0,2 дБ, уровню 86 дБ – звуковое давление 0,4 Па. Суммарное давление равно: p = 0,447 Па, отсюда скрипка и рояль вместе создают уровень звукового давления 86,98 дБ.
При оценке слухового восприятия звуковых колебаний, кроме звукового давления, часто используют и другую величину — интенсивность или силузвука. Громкость звука зависит от его интенсивности, которая, в свою очередь, зависит от звукового давления, создаваемого источником звука в точке прослушивания.
Интенсивность I и звуковое давление р связаны соотношением:
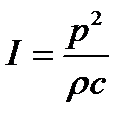
где ρ – плотность воздуха, равная 1,2 кГ/м 3 ;
с – скорость распространения звуковых колебаний в воздухе, равная при температуре 20°С 343 м/с.
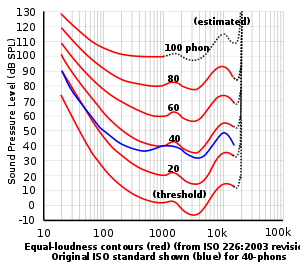
Из практики хорошо известно, что чем больший уровень звукового давления создаёт источник звука, тем громче он звучит. Однако одного только уровня звукового давления для характеристики громкости звучания недостаточно, поскольку чувствительность человеческого слуха различна для различных частот. По этой причине для его определения пользуются графиком, который наглядно показывает, как изменяется минимальное значение звукового давления, воспринимаемого человеческими органами слуха как звук, в зависимости от частоты акустических колебаний. Такой график называется кривой абсолютного порога слышимости (рис. 13.2). Определяется он в полосе частот от 20 до 20000 Гц – именно в этом диапазоне человеческий слух способен воспринимать акустические колебания как звук. Однако следует иметь в виду, что такая широкая полоса слышимых частот скорее физиологический предел возможностей человеческого слуха – в действительности подавляющее большинство людей даже в молодом возрасте (18-25 лет), когда острота слуха наивысшая, способно слышать звуки только в диапазоне 30-35…16000-18000 Гц. Тем не менее, есть данные, что отдельные люди способны слышать звуки даже с частотой 22000 Гц.
Порог слышимости – это минимальное значение звукового давления, при котором еще наблюдается слуховое ощущение. Он характеризует чувствительность слуха к интенсивности звуковой энергии.
Рис. 13.2. Кривая абсолютного порога слышимости, построенная по результатам измерений в условиях свободного поля
Абсолютный порог слышимости принято выражать в децибелах по отношению к некоторой стандартной величине звукового давления р1 = 2×10 -5 Па (10 -12 Вт/м 2 ), которая условно принята за точку отсчета (0 дБ) при таких оценках. Как видно из рис. 13.2, наибольшей чувствительностью человеческий слух обладает на средних частотах — в диапазоне от 2000 до 5000 Гц. Здесь абсолютный порог слышимости даже меньше 2×10 -5 Па (
Если создать три тональных звуковых сигнала с одним и тем же уровнем звукового давления p = 40 дБ – один с частотой 50 Гц, другой с частотой 100 Гц, третий с частотой 4 кГц и попытаться сравнить их громкости, то окажется, что сигнал с частотой 4 кГц будет звучать достаточно громко, сигнал с частотой 100 Гц – едва слышно, а вот сигнала с частотой 50 Гц не удастся услышать вовсе. Если обратиться к рис. 13.2, то причина будет ясна – сигнал с частотой 50 Гц при уровне звукового давления 40 дБ будет находиться ниже кривой абсолютного порога слышимости, сигнал с частотой 100 Гц лишь немного выше нее, и только сигнал с частотой 4 кГц будет более чем на 40 дБ превышать абсолютный порог слышимости. Этот эксперимент доказывает, что громкость зависит не только от интенсивности звука, но и от его частоты. На краях диапазона слышимых частот можно сформировать звуковые сигналы очень высокой интенсивности, но никакого ощущения громкости при этом не возникнет, хотя слуховая система при этом может быть даже повреждена.
Построение шкалы звуков по громкости и исследование влияния на нее основных параметров звукового сигнала было выполнено, прежде всего, на тональных сигналах различной интенсивности, частоты и длительности. Для того чтобы устранить зависимость субъективно воспринимаемой громкости звука от частоты и обеспечить возможность количественной ее оценки, используют метод сравнения громкости исследуемого звука с громкостью некоторого эталонного звука. Для того чтобы такие оценки можно было сравнивать между собой, на международном уровне договорились использовать в качестве эталона громкость звукового сигнала с частотой 1000 Гц.
Определяется громкость следующим образом. На эталонной частоте 1000 Гц устанавливается некоторый вполне определенный уровень звукового давления, например 40 дБ. После этого эксперту предлагается прослушать сигнал на какой-то другой частоте, например 63 Гц, и отрегулировать его уровень таким образом, чтобы он казался равногромким эталонному. Значение уровня звукового давления эталонного сигнала в децибелах при этом квалифицируется как уровень громкости исследуемого сигнала и оценивается в специальных единицах, которые называются фонами.
Звуковое давление и его уровни (spl)
В настоящее статье поговорим о том, что такое звуковое давление, рассмотрим понятие (импеданс) — удельное акустическое сопротивление среды. Также поговорим об уровнях звукового давления и интенсивности звука.
Чтобы лучше понимать о чём сегодня пойдёт речь, советую прочитать предыдущую статью по этой теме ( звуковые волны, виды, длина волны и скорость звука ).
Звуковое давление
Звуковая волна, как мы уже рассматривали в прошлой статье, распространяется в среде в виде волн сжатия и разряжения плотности.
В газах (в том числе и воздухе) плотность и давление связаны между собой:
p = RTp
А поскольку у волны имеются области сжатия и разряжения, то в первой области давление будут выше статического атмосферного. А в случае разряжения – ниже.
Вот как это выглядит:
Разность между мгновенным значением давления в данной точке среды и атмосферным давлением называется звуковым давлением.
Звуковое давление измеряется в паскалях (Па): 1 Па = 1 Н/м².
Наша слуховая система может определять очень большой диапазон разностей между мгновенным значением звукового давления и атмосферным.
На рисунке ниже представлено, различное звуковое давление от звуковых источников в децибелах (про децибелы подробнее читай далее):
Импеданс
Рассматривая звук, в прошлой статье ( читать ) мы выяснили, что звуковая волна зависит от частоты и амплитуды звукового давления. Если тело оказывает большое сопротивление приложенному звуковому давлению, то частицы приобретают малую скорость.
Поэтому импеданс – это удельное акустическое сопротивление среды. Представляет из себя отношение звукового давления к скорости колебаний частиц среды:
Z = p/v
Измеряется в (Па · с)/м или кг/(с · м²).
Удельное акустическое сопротивление для воздуха составляет (при температуре 20 С°) 413 кг/(с · м²). В металле, к примеру, оно составляет 47,7 × 10 кг/(с · м²). Так как в воздухе импеданс достаточно мал, то и излучаемая полезная энергия также мала.
Если рассматривать КПД (коэффициент полезного действия) музыкальных инструментов, голосового аппарата, громкоговорителей и т. п., то оно в воздухе находится в пределах 0,2-1%.
Энергетические параметры
Звуковая волна переносит энергию механических колебаний, значит она имеет энергетические параметры. Среди которых: акустическая энергия P (Дж); мощность W – энергия, переносимая в единицу времени (Вт); интенсивность I – количество энергии, проходящее в единицу времени через единицу площади, перпендикулярной к направлению распространения волны (Вт/м²); плотность – количество звуковой энергии в единице объёма (Дж/м²).
Уровни звукового давления (анг. SPL, sound pressure level)
Восприятие громкости человеком происходит не по линейному закону, пропорционально амплитуде колебаний, а по логарифмическому. Поэтому для определения параметров звука применяют логарифмические шкалы.
Человек различает огромный диапазон изменения звукового давления от тихого 2 × 10 ⁻⁵ Па до очень громкого 20 Па. Разница составляет 10⁶.
Использовать такую школу очень неудобно. Поэтому в измерительных приборах пользуются логарифмическими единицами – децибелами (дБ). Эта единица происходит от другой – бел, который равен десятикратному изменению интенсивности звука. Однако бел – единица крупная и неудобная для измерений. Поэтому применяется её десятая часть – децибел.
Уровень звукового давления определяется как:
L = 20 lg p/p₀
Например, если звуковое давление p = 2 Па, то уровень звукового давления равен: L = 20 lg (2 Па/(2 × 10 ⁻⁵) Па) = 20 lg (1 × 10⁺⁵) = 20 × 5 = 100 дБ.
Один децибел – примерно та наименьшая разница в громкости, которую человеческое ухо может почувствовать.
Полезно запомнить следующее. Изменение громкости в 3 дБ равно отношению 2:1. Поэтому если мы берем два одинаковых источника звука, т. е. удваиваем мощность, то громкость увеличиться на 3 дБ. Например, если к голосу присоединяется ещё один, равный по громкости, то уровень звука увеличится на 3 дБ. Если нужно ещё увеличить на 3 дБ, потребуется вдвое увеличить имеющийся состав.
Также можно обратиться к следующей таблице (в ней показано на сколько дБ нужно убавить, чтобы получить звучание в 2 раза тише, в 3 и т. д.):
| 1% | 10% | 25% | 33% | 50% | 100% |
| 1/100
(в 100 раз тише) |
1/10
(в 10 раз тише) |
1/4
(в 4 раза тише) |
1/3
(в 3 раза тише) |
1/2
(в 2 раза тише) |
1/1 |
| -40дБ | -20дБ | -12 дБ | -10 дБ | — 6 дБ | 0 дБ |
Для определения суммарного уровня давления нескольких инструментов их никогда не складывают. Вначале необходимо рассчитать значение звукового давления каждого инструмента. Допустим играют две скрипки. Одна с уровнем 80 дБ, другая 86 дБ. У первой звуковое давление равно — 0,2 Па, второй — 0,4 Па.
Рассчитывается так: L = 20 lg p/p₀, значит 80 дБ = 20 lg p / (2 × 10 ⁻⁵), далее lg p / (2 × 10 ⁻⁵) = 4. Следовательно 10⁴ = p / (2 × 10 ⁻⁵), отсюда значение звукового давления будет p = 0,2 Па.
После этого определяется суммарное звуковое давление
В нашем случае суммарное давление равно p = 0, 447 Па. Затем определяется суммарный уровень звукового давления. Который равен 86,98 дБ.
Уровень интенсивности звука
Уровень интенсивности звука также измеряется в децибелах по формуле:
L₁ = 10 lg I/I₀
I₀ – нулевой уровень, равный 10⁻¹² Вт/м².
Мощность, напряжение, ток
Перечисленные электрические характеристики также часто приводятся в децибелах и имеют свои специальные обозначения. Приведём несколько примеров:
L dBm = 10 lg WВт/ 1мВт – уровень мощности отнесённый к 1 мВт
L dBv = 20 lg UB/1B – уровень напряжения, отнесённый к 1 В (Америка)
L dBv = 20 lg UB/0,775 B – уровень напряжения, отнесённый к 0,775 В (Европа)
Спасибо, что читаете New Style Sound ( подписаться на новости )
http://lektsii.org/9-63226.html
http://nssound.ru/o-zvuke-i-zvukovykh-signalakh/zvukovoe-davlenie-i-ego-urovni-spl/
Уровень звукового давления
- Уровень звукового давления
-
- Звуковое давление не следует путать с давлением звука.
Звуково́е давле́ние — переменное избыточное давление, возникающее в упругой среде при прохождении через неё звуковой волны. Единица измерения — паскаль (Па).
Мгновенное значение звукового давления в точке среды изменяется как со временем, так и при переходе к другим точкам среды, поэтому практический интерес представляет среднеквадратичное значение данной величины, связанное с интенсивностью звука:
где
— интенсивность звука,
— звуковое давление,
— удельное акустическое сопротивление среды, < > t — усреднение по времени.
При рассмотрении периодических колебаний иногда используют амплитуду звукового давления; так, для синусоидальной волны
где
— амплитуда звукового давления.
Уровень звукового давления (англ. SPL, Sound Pressure Level) — измеренное по относительной шкале значение звукового давления, отнесённое к опорному давлению
= 20 мкПа, соответствующему порогу слышимости синусоидальной звуковой волны частотой 1 кГц:
дБ.
Уровни звукового давления от различных источников
- 10 дБ SPL — шёпот;
- 20 дБ SPL — норма шума в жилых помещениях;
- 40 дБ SPL — тихий разговор;
- 50 дБ SPL — разговор средней громкости;
- 70 дБ SPL — шум пишущей машинки;
- 80 дБ SPL — шум работающего двигателя грузового автомобиля;
- 100 дБ SPL — громкий автомобильный сигнал на расстоянии 5—7 м;
- 110 дБ SPL — шум работающего трактора на расстоянии 1 м;
- 120 дБ SPL — порог болевого ощущения;
- 150 дБ SPL — взлёт самолёта;
- 200 дБ SPL — взрыв атомной бомбы.
Давление свыше 140 дБ SPL может вызвать разрыв барабанной перепонки, баротравмы и даже смерть.
См. также
- Интенсивность звука
- Громкость звука
- Давление звука
- Давление звукового излучения
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Уровень звукового давления» в других словарях:
-
УРОВЕНЬ ЗВУКОВОГО ДАВЛЕНИЯ — логарифмический уровень эффективного звукового давления или среднеквадратического значения отклонений давления от атмосферного давления, вызванных прохождением звуковой волны … Российская энциклопедия по охране труда
-
уровень звукового давления — (МСЭ Т K.49). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN sound pressure levelSPL … Справочник технического переводчика
-
уровень звукового давления — 3.3 уровень звукового давления (sound pressure level) Lp, дБ: Величина, рассчитываемая как десять десятичных логарифмов отношения среднего квадрата данного звукового давления к квадрату опорного звукового давления. Примечание Опорное звуковое… … Словарь-справочник терминов нормативно-технической документации
-
уровень звукового давления Lp, дБ — 3.4 уровень звукового давления Lp, дБ (sound pressure level): Десятикратный десятичный логарифм отношения квадрата звукового давления к квадрату опорного звукового давления. Примечания 1 Обычно указывают частотную характеристику или полосу частот … Словарь-справочник терминов нормативно-технической документации
-
уровень звукового давления Lp — 3.2 уровень звукового давления Lp (sound pressure level), дБ: Величина, равная десяти десятичным логарифмам квадрата отношения данного среднеквадратического звукового давления к опорному звуковому давлению. Примечания 1 Опорное звуковое давление… … Словарь-справочник терминов нормативно-технической документации
-
Уровень звукового давления, — 3.1 Уровень звукового давления, Lр логарифм отношения данного звукового давления к опорному звуковому давлению. Уровень звукового давления в децибелах равен двадцати логарифмам этого отношения при основании, равном десяти. Опорное звуковое… … Словарь-справочник терминов нормативно-технической документации
-
уровень звукового давления L p , дБ — 3.1 уровень звукового давления L p , дБ (sound pressure level): Десять десятичных логарифмов отношения среднего квадрата звукового давления к квадрату опорного звукового давления. Примечание Опорное звуковое давление равно 20 мкПа. Источник … Словарь-справочник терминов нормативно-технической документации
-
уровень звукового давления Lp , дБ — 3.1 уровень звукового давления Lp , дБ (sound pressure level): Десять десятичных логарифмов отношения среднего квадрата звукового давления к квадрату опорного давления. Примечание Опорное звуковое давление равно 20 мкПа. Источник … Словарь-справочник терминов нормативно-технической документации
-
уровень звукового давления L, дБ — 3.2.1 уровень звукового давления L, дБ (sound pressure level): Величина, равная десяти десятичным логарифмам квадрата отношения среднеквадратичного звукового давления, измеренного при стандартных временной и частотной характеристиках… … Словарь-справочник терминов нормативно-технической документации
-
уровень звукового давления — garso slėgio lygis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. sound pressure level vok. Schalldruckpegel, m rus. уровень звукового давления, m pranc. niveau… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Что такое звуковое давление
Звуковые волны стоит понимать как колебания давления, которые распространяются в пространстве. Ухо человека способно распознавать это явление как звук. Единицей измерения такого давления является паскаль (Па).
Наименьшим звуковым давлением, которое может распознать орган слуха человека, является 5 Па. Эта граница принята за нижний порог слышимости. А вот верхним порогом принята отметка в 20 Па. Звук именно такой силы может быть воспринят человеком без болевого синдрома. Данная шкала не очень удобна, поэтому чаще всего используется шкала с единицей измерения — децибел (дБ). Здесь за 0 дБ принят порог слышимости, а 120 дБ – это уже показатель болевого порога.
Чем дальше человек находится от источника звука, тем меньше показатель звукового давления. Оказывает существенное влияние на данный показатель и характеристика помещения, способность стен отражать звук, расположение самого источника в пространстве и др. Осуществляя контроль производственных факторов мы позволяем обеспечить безопасность работающих.
Как измеряют уровень звукового давления
Для того, чтобы измерить уровень звукового давления, определяются контрольные точки. Чаще всего на предприятиях ими являются рабочие места сотрудников, а также те зоны, где пребывают работающие дольше всего. Измерение должно происходить на высоте 1,5 м от пола. Этот показатель взят для того, чтобы получить наиболее достоверные результаты.
Если измерение происходит в помещении, важно сделать два замера: один из них в зоне прямого звука, второй — в зоне отраженного звука. Если помещение имеет несколько источников шума тогда стоит проводить измерения в местах расположения самого интенсивного из них.
Определение понятия звуковая мощность
Звуковая мощность – это количество энергии, которая появляется из источника звука и передается за заданную единицу времени, измеряется в ваттах (Вт).
Если звуковое давление может быть измерено, то данная единица непосредственно не измеряется. Она может лишь вычисляться по формуле через полученные показатели звукового давления. Применяется специальная логарифмическая шкала мощности звука, которая аналогична шкале звукового давления.
Звуковая мощность – это понятие, которое никак не связано с местом расположения источника звука. На нее никак не влияют акустические характеристики помещения, а также понятие расстояния. Энергия из источника звука выходит вне зависимости от условий окружающей среды.
Показания звуковой мощности источника можно рассчитать на основании полученных результатов по измерению уровня шума в заданных точках. Стандартизированные измерения требуют получения данных из десяти точек измерения, произведенных специальным прибором – шумомером.
Влияние звуковой мощности и звукового давления на человека
Такие акустические явления негативно сказываются на организме человека. Наличие шума приводит к снижению внимания, концентрации, увеличению ошибок в процессе работы. Шум провоцирует замедленную реакцию у работника на сигналы, которые поступают от технических устройств. Он может привести к увеличению количества профессиональных заболеваний среди сотрудников, связанных с сердечно-сосудистой системой, с органами пищеварения, неврологией.
Уровень
давления звука Lp — это ощущаемая
интенсивность шума, измеряемая в дБ.
Lp
= P/P0
Здесь
P — давление звука в измеряемом месте,
мкПа, а P0 = 2 мкПа — контрольная величина.
Уровень
звукового давления зависит от внешних
факторов: расстояния до установки,
отражения звука и т.д. Наиболее простой
вид имеет зависимость уровня давления
от расстояния. Если известен уровень
мощности шума Lw, то уровень звукового
давления Lp в дБ на расстоянии r (в метрах)
от источника вычисляется так:
Lp
= Lw — lgr — 11
Пример:
мощность звука холодильного блока равна
78 дБ. Уровень звукового давления на
расстоянии 10 м от него равен: (78 — lg10 — 11)
дБ = 66 дБ.
Если
известен уровень звукового давления
Lp1 на расстоянии r1 от источника шума, то
уровень звукового давления Lp2 на
расстоянии r2 будет вычисляться так:
Lp2
= Lp1 — 20*lg(r2/r1)
Пример:
Уровень звукового давление на расстоянии
1 м от установки равно 65 дБ. Тогда уровень
звукового давления на расстоянии 10 м
от нее равен: (65 — 20*lg10) дБ = (65 — 20) дБ = 45
дБ..
Вообще,
в открытом пространстве уровень звукового
давления снижается на 6 дБ при увеличении
расстояния до источника шума в 2 раза.
В помещении зависимость будет сложнее
из-за поглощения звука поверхностью
пола, отражения звука и т.д.
5.Громкость шума
Чувствительность
человека к звукам разной частоты
неодинакова. Она максимальна к звукам
частотой около 4 кГц, стабильна в диапазоне
от 200 до 2000 Гц, и снижается при частоте
менее 200 Гц (низкочастотные звуки).
Громкость
шума зависит от силы звука и его частоты.
Громкость звука оценивают, сравнивая
ее с громкостью простого звукового
сигнала частотой 1000Гц. Уровень силы
звука частотой 1000Гц, столь же громкого,
как измеряемый шум, называется уровнем
громкости данного шума. На приведенной
ниже диаграмме показана зависимость
силы звука от частоты при постоянной
громкости.
При
малом уровне громкости человек менее
чувствителен к звукам очень низких и
высоких частот. При большом звуковом
давлении ощущение звука перерастает в
болевое ощущение. На частоте 1 кГц болевой
порог соответствует давлению 20 Па и
силе звука 10 Вт/кв.м.
Диаграмма
кривых равной громкости
6.Шумовые характеристики оборудования
Шумовые
характеристики оборудования представляют
в виде таблиц, где содержатся:
уровень
мощности шума в дБ с разбивкой по полосам
частот
общий
уровень звукового давления
Звуковое
давление в помещениях нормируется
санитарными нормативами, допустимые
значения различны для разных частот.
Шум, создаваемый системами вентиляции
и кондиционирования, принимают на 5 дБ
ниже допустимого уровня шума в помещении
(СНиП 11-12-77).
7.Суммирование источников шума
Шум
от нескольких источников не соответствует
сумме шумов от каждого источника в
отдельности. Для двух находящихся рядом
установок шум определяется следующим
образом:
Если
показатели уровня шума одинаковы, то
суммарный уровень шума на 3 дБ превышает
уровень шума каждой установки.
Если
разница уровней шума превышает 10 дБ,
суммарный уровень шума равен величине
большего из двух шумов.
Например,
общий шум от двух установок с уровнями
30 и 60 дБ, равен 60 дБ.
Если
разница уровней шума не более 10 дБ, нужно
воспользоваться приведенной ниже
таблицей. Вычисляем разность уровней
шума установок.
Например,
L1 = 52 дБ, а L2 = 48 дБ. Разность равна 4 дБ. В
верхней строке таблицы найдем 4 дБ, тогда
в нижней строке видим показатель 1.5 дБ.
Прибавим этот показатель к большему
уровню шума: 52 дБ + 1.5 дБ = 53.5 дБ. Это и
будет общий уровень шума от двух
установок.
|
Разница |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Показатель-добавка, |
2,6 |
2,1 |
1,8 |
1,5 |
1,2 |
1,0 |
0,8 |
0,6 |
0,5 |
0,4 |
Если
источников шума более двух, метод расчета
не меняется, и источники рассматриваются
парами, начиная с самых слабых.
Например,
есть четыре установки с уровнями шума
25 дБ, 38 дБ, 43 дБ и 50 дБ.
Сначала
делаем подсчет для двух слабейших
установок: 38 — 25 = 13 дБ. Разница больше 10
дБ, и эту установку вообще не учитываем.
Для
установок 38 и 43 дБ: 43 — 38 = 5 дБ, поправка
из таблицы равна 1.2 дБ. Суммарный шум
трех установок: 43 + 1.2 = 44.2 дБ.
Теперь
найдем полный шум всех установок. 50 —
44.2 = 5.8 дБ. Округляя разность уровней
шума до 6 дБ, по таблице находим поправку
1.0 дБ.
Итак,
общий уровень шума четырех установок
равен 50 + 1 = 51 дБ.
Таблица
уровней шума
|
Уровень |
Описание |
Аналогия |
|
160 |
невыносимый |
Самолет |
|
90 |
Крик |
|
|
70 |
Шум, |
Громкий |
|
60 |
||
|
50 |
Шум, |
Негромкий |
|
45 |
Практически |
|
|
40 |
Разговор |
|
|
35 |
очень |
|
|
30 |
Шепот, |
|
|
25 |
Неслышимый |
Тихий |
|
20 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

















propto p^{2}(r),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf101a3713c0641e63e2093d8d2c8f2bb424264d)



![{displaystyle L_{Sigma }=10log _{10}left({frac {p_{1}^{2}+p_{2}^{2}+dots +p_{n}^{2}}{p_{0}^{2}}}right)~{text{dB}}=10log _{10}left[left({frac {p_{1}}{p_{0}}}right)^{2}+left({frac {p_{2}}{p_{0}}}right)^{2}+dots +left({frac {p_{n}}{p_{0}}}right)^{2}right]~{text{dB}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c430352c5808ad08cb5bb81221d3058efd94d2d)


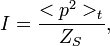
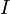 — интенсивность звука,
— интенсивность звука, 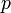 — звуковое давление,
— звуковое давление, 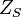 — удельное акустическое сопротивление среды,
— удельное акустическое сопротивление среды, 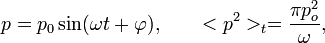
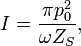
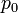 — амплитуда звукового давления.
— амплитуда звукового давления.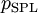 = 20 мкПа, соответствующему порогу слышимости синусоидальной звуковой волны частотой 1 кГц:
= 20 мкПа, соответствующему порогу слышимости синусоидальной звуковой волны частотой 1 кГц: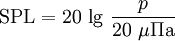 дБ.
дБ.