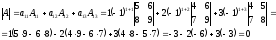Понятие минора и алгебраического дополнения было рассмотрено нами в теме «Как вычислить определитель матрицы третьего порядка». В данной статье разберем тему более подробно, а также научимся вычислять миноры и алгебраические дополнения матриц высших порядков.
Сначала рекомендуется повторить вычисление определителей второго, третьего и высших порядков.
Минор
Минором MijM_{ij} к элементу aija_{ij} определителя nn-го порядка называется определитель (n−1)(n-1)-го порядка, который получается из исходного определителя вычеркиванием ii-той строки и jj-того столбца.
Таким образом, минор — это определитель, который остается после вычеркивания определенной строки и определенного столбца. Например, M12M_{12} получается вычеркиванием 1-й строки и 2-го столбца, M34M_{34} — вычеркиванием 3-й строки и 4-го столбца.
Алгоритм нахождения миноров
- вычеркиваем i-ю строку;
- вычеркиваем j-й столбец;
- записываем определитель, который получили в результате действий 1 и 2.
Пример 1
Найти минор M34M_{34} к элементу a34a_{34} определителя ∣21−23−121213−1543−31∣begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
M34=∣21−23−121213−1543−31∣=∣21−2−12143−3∣=2⋅2⋅(−3)+1⋅1⋅4+(−2)⋅3⋅(−1)−(−2)⋅2⋅4−1⋅(−3)⋅(−1)−2⋅1⋅3=−12+4+6+16−3−6=5M_{34}=begin{vmatrix}2&1&-2&color{green}3\-1&2&1&color{green}2\color{green}1&color{green}3&color{green}-1&color{green}5\4&3&-3&color{green}1end{vmatrix}=begin{vmatrix}2&1&-2\-1&2&1\4&3&-3end{vmatrix}=2cdot2cdot(-3)+1cdot1cdot4+(-2)cdot3cdot(-1)-(-2)cdot2cdot4-1cdot(-3)cdot(-1)-2cdot1cdot3=-12+4+6+16-3-6=5.
Пример 2
Найти миноры матрицы K=(03−122100−2−102−5711)K= begin{pmatrix}0&3&-1&2\2&1&0&0\-2&-1&0&2\-5&7&1&1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
M11=(03−122100−2−102−5711)=∣100−102711∣=1⋅(−1)1+1∣0211∣=1⋅(−1)2∣0211∣=∣0211∣=1⋅(−1)2+1⋅2=1⋅(−1)3⋅2=−2M_{11}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\color{green}2&1&0&0\color{green}-2&-1&0&2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=1cdot(-1)^{1+1}begin{vmatrix}0&2\1&1end{vmatrix}=1cdot(-1)^{2}begin{vmatrix}0&2\1&1end{vmatrix}=begin{vmatrix}0&2\1&1end{vmatrix}=1cdot(-1)^{2+1}cdot2=1cdot(-1)^{3}cdot2=-2,
M12=(03−122100−2−102−5711)=∣200−202−511∣=2⋅(−1)1+1∣0211∣=2⋅(−1)2∣0211∣=2∣0211∣=2⋅(−1)2+1⋅2=2⋅(−1)3⋅2=−4M_{12}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&color{green}1&0&0\-2&color{green}-1&0&2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=2cdot(-1)^{1+1}begin{vmatrix}0&2\1&1end{vmatrix}=2cdot(-1)^{2}begin{vmatrix}0&2\1&1end{vmatrix}=2begin{vmatrix}0&2\1&1end{vmatrix}=2cdot(-1)^{2+1}cdot2=2cdot(-1)^{3}cdot2=-4,
M13=(03−122100−2−102−5711)=∣210−2−12−571∣=2⋅(−1)⋅1+0⋅7⋅(−2)+1⋅2⋅(−5)−0⋅(−1)⋅(−5)−2⋅2⋅7−1⋅1⋅(−2)=−2−10−28+2=−38M_{13}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&1&color{green}0&0\-2&-1&color{green}0&2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=2cdot(-1)cdot1+0cdot7cdot(-2)+1cdot2cdot(-5)-0cdot(-1)cdot(-5)-2cdot2cdot7-1cdot1cdot(-2)=-2-10-28+2=-38,
M14=(03−122100−2−102−5711)=∣210−2−10−571∣=1⋅(−1)3+3∣21−2−1∣=0M_{14}= begin{pmatrix}color{green}0&color{green}3&color{green}-1&color{green}2\2&1&0&color{green}0\-2&-1&0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=1cdot(-1)^{3+3}begin{vmatrix}2&1\-2&-1end{vmatrix}=0,
M21=(03−122100−2−102−5711)=∣3−12−102711∣=3⋅0⋅1+2⋅1⋅(−1)+(−1)⋅2⋅7−2⋅0⋅7−(−1)⋅1⋅(−1)−3⋅2⋅1=−2−14−1−6=−23M_{21}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&color{green}1&color{green}0&color{green}0\color{green}-2&-1&0&2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=3cdot0cdot1+2cdot1cdot(-1)+(-1)cdot2cdot7-2cdot0cdot7-(-1)cdot1cdot(-1)-3cdot2cdot1=-2-14-1-6=-23,
M22=(03−122100−2−102−5711)=∣0−12−202−511∣=0⋅0⋅1+(−1)⋅2⋅(−5)+2⋅1⋅(−2)−2⋅0⋅(−5)−(−1)⋅1⋅(−2)−0⋅2⋅1=10−4−2=4M_{22}= begin{pmatrix}0&color{green}3&-1&2\color{green}2&color{green}1&color{green}0&color{green}0\-2&color{green}-1&0&2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=0cdot0cdot1+(-1)cdot2cdot(-5)+2cdot1cdot(-2)-2cdot0cdot(-5)-(-1)cdot1cdot(-2)-0cdot2cdot1=10-4-2=4,
M23=(03−122100−2−102−5711)=∣032−2−12−571∣=0⋅(−1)⋅1+3⋅2⋅(−5)+2⋅7⋅(−2)−2⋅(−1)⋅(−5)−3⋅1⋅(−2)−0⋅2⋅7=−30−28−10+6=−62M_{23}= begin{pmatrix}0&3&color{green}-1&2\color{green}2&color{green}1&color{green}0&color{green}0\-2&-1&color{green}0&2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=0cdot(-1)cdot1+3cdot2cdot(-5)+2cdot7cdot(-2)-2cdot(-1)cdot(-5)-3cdot1cdot(-2)-0cdot2cdot7=-30-28-10+6=-62,
M24=(03−122100−2−102−5711)=∣03−1−2−10−571∣=0⋅(−1)⋅1+3⋅0⋅(−5)+(−1)⋅7⋅(−2)−(−1)⋅(−1)⋅(−5)−3⋅1⋅(−2)−0⋅0⋅7=14+5+6=25M_{24}= begin{pmatrix}0&3&-1&color{green}2\color{green}2&color{green}1&color{green}0&color{green}0\-2&-1&0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=0cdot(-1)cdot1+3cdot0cdot(-5)+(-1)cdot7cdot(-2)-(-1)cdot(-1)cdot(-5)-3cdot1cdot(-2)-0cdot0cdot7=14+5+6=25,
M31=(03−122100−2−102−5711)=∣3−12100711∣=1⋅(−1)2+1∣−1211∣=1⋅(−1)3∣−1211∣=−∣−1211∣=−(−1−2)=3M_{31}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&1&0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\color{green}-5&7&1&1end{pmatrix}=begin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=1cdot(-1)^{2+1}begin{vmatrix}-1&2\1&1end{vmatrix}=1cdot(-1)^{3}begin{vmatrix}-1&2\1&1end{vmatrix}=-begin{vmatrix}-1&2\1&1end{vmatrix}=-(-1-2)=3,
M32=(03−122100−2−102−5711)=∣0−12200−511∣=2⋅(−1)2+1∣−1211∣=2⋅(−1)3∣−1211∣=−2∣−1211∣=−2(−1−2)=6M_{32}= begin{pmatrix}0&color{green}3&-1&2\2&color{green}1&0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&color{green}7&1&1end{pmatrix}=begin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=2cdot(-1)^{2+1}begin{vmatrix}-1&2\1&1end{vmatrix}=2cdot(-1)^{3}begin{vmatrix}-1&2\1&1end{vmatrix}=-2begin{vmatrix}-1&2\1&1end{vmatrix}=-2(-1-2)=6,
M33=(03−122100−2−102−5711)=∣032210−571∣=0⋅1⋅1+3⋅0⋅(−5)+2⋅7⋅2−2⋅1⋅(−5)−0⋅0⋅7−3⋅1⋅2=28+10−6=32M_{33}= begin{pmatrix}0&3&color{green}-1&2\2&1&color{green}0&0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&7&color{green}1&1end{pmatrix}=begin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=0cdot1cdot1+3cdot0cdot(-5)+2cdot7cdot2-2cdot1cdot(-5)-0cdot0cdot7-3cdot1cdot2=28+10-6=32,
M34=(03−122100−2−102−5711)=∣03−1210−571∣=0⋅1⋅1+3⋅0⋅(−5)+(−1)⋅7⋅2−(−1)⋅1⋅(−5)−3⋅1⋅2−0⋅0⋅7=−14−5−6=−25M_{34}= begin{pmatrix}0&3&-1&color{green}2\2&1&0&color{green}0\color{green}-2&color{green}-1&color{green}0&color{green}2\-5&7&1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=0cdot1cdot1+3cdot0cdot(-5)+(-1)cdot7cdot2-(-1)cdot1cdot(-5)-3cdot1cdot2-0cdot0cdot7=-14-5-6=-25,
M41=(03−122100−2−102−5711)=∣3−12100−102∣=1⋅(−1)2+1∣−1202∣=1⋅(−1)3∣−1202∣=−∣−1202∣=−(−1)⋅(−1)1+1⋅2=1⋅(−1)2⋅2=2M_{41}= begin{pmatrix}color{green}0&3&-1&2\color{green}2&1&0&0\color{green}-2&-1&0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=1cdot(-1)^{2+1}begin{vmatrix}-1&2\0&2end{vmatrix}=1cdot(-1)^{3}begin{vmatrix}-1&2\0&2end{vmatrix}=-begin{vmatrix}-1&2\0&2end{vmatrix}=-(-1)cdot(-1)^{1+1}cdot2=1cdot(-1)^{2}cdot2=2,
M42=(03−122100−2−102−5711)=∣0−12200−202∣=2⋅(−1)2+1∣−1202∣=2⋅(−1)3∣−1202∣=−2∣−1202∣=−2⋅(−1)⋅(−1)1+1⋅2=2⋅(−1)2⋅2=4M_{42}= begin{pmatrix}0&color{green}3&-1&2\2&color{green}1&0&0\-2&color{green}-1&0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=2cdot(-1)^{2+1}begin{vmatrix}-1&2\0&2end{vmatrix}=2cdot(-1)^{3}begin{vmatrix}-1&2\0&2end{vmatrix}=-2begin{vmatrix}-1&2\0&2end{vmatrix}=-2cdot(-1)cdot(-1)^{1+1}cdot2=2cdot(-1)^{2}cdot2=4,
M43=(03−122100−2−102−5711)=∣032210−2−12∣=0⋅1⋅2+3⋅0⋅(−2)+2⋅(−1)⋅2−2⋅1⋅(−2)−3⋅2⋅2−0⋅0⋅(−1)=−4+4−12=−12M_{43}= begin{pmatrix}0&3&color{green}-1&2\2&1&color{green}0&0\-2&-1&color{green}0&2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=0cdot1cdot2+3cdot0cdot(-2)+2cdot(-1)cdot2-2cdot1cdot(-2)-3cdot2cdot2-0cdot0cdot(-1)=-4+4-12=-12,
M44=(03−122100−2−102−5711)=∣03−1210−2−10∣=0M_{44}= begin{pmatrix}0&3&-1&color{green}2\2&1&0&color{green}0\-2&-1&0&color{green}2\color{green}-5&color{green}7&color{green}1&color{green}1end{pmatrix}=begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0.
Алгебраическое дополнение
Алгебраическим дополнением AijA_{ij} к элементу aija_{ij} определителя n-го порядка называется число Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}, где i,ji, j — соответствующие строка и столбец, а MijM_{ij} — минор к элементу aija_{ij}.
Алгоритм нахождения алгебраических дополнений
- найти сумму номеров строки (i)(i) и столбца (j)(j);
- найти минор MijM_{ij} по алгоритму нахождения миноров, который представлен выше;
- подставить значения, полученные на шагах 1 и 2, в формулу Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}.
Пример 1
Найти алгебраическое дополнение A34A_{34} к элементу a34a_{34} определителя
∣21−23−121213−1543−31∣begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}.
A34=(−1)3+4⋅M34=(−1)7⋅∣21−23−121213−1543−31∣=−∣21−2−12143−3∣=−(2⋅2⋅(−3)+1⋅1⋅4+(−2)⋅3⋅(−1)−(−2)⋅2⋅4−1⋅(−3)⋅(−1)−2⋅1⋅3)=−(−12+4+6+16−3−6)=−5A_{34}=(-1)^{3+4}cdot M_{34}=(-1)^{7}cdot
begin{vmatrix}2&1&-2&color{green}3\-1&2&1&color{green}2\color{green}1&color{green}3&color{green}-1&color{green}5\4&3&-3&color{green}1end{vmatrix}=-begin{vmatrix}2&1&-2\-1&2&1\4&3&-3end{vmatrix}=-(2cdot2cdot(-3)+1cdot1cdot4+(-2)cdot3cdot(-1)-(-2)cdot2cdot4-1cdot(-3)cdot(-1)-2cdot1cdot3)=-(-12+4+6+16-3-6)=-5.
Пример 2
Найти алгебраические дополнения матрицы K=(03−122100−2−102−5711)K= begin{pmatrix}0&3&-1&2\2&1&0&0\-2&-1&0&2\-5&7&1&1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, выделим зеленым цветом.
A11=(−1)1+1⋅M11=(−1)1+1⋅∣100−102711∣=(−1)2∣100−102711∣=∣100−102711∣=−2A_{11}=(-1)^{1+1}cdot M_{11}=(-1)^{1+1}cdotbegin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=(-1)^{2}begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=begin{vmatrix}1&0&0\-1&0&2\7&1&1end{vmatrix}=-2,
A12=(−1)1+2⋅M12=(−1)1+2⋅∣200−202−511∣=(−1)3⋅∣200−202−511∣=−∣200−202−511∣=−(−4)=4A_{12}=(-1)^{1+2}cdot M_{12}=(-1)^{1+2}cdotbegin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=(-1)^{3}cdotbegin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=-begin{vmatrix}2&0&0\-2&0&2\-5&1&1end{vmatrix}=-(-4)=4,
A13=(−1)1+3⋅M13=(−1)1+3⋅∣210−2−12−571∣=(−1)4⋅∣210−2−12−571∣=∣210−2−12−571∣=−38A_{13}=(-1)^{1+3}cdot M_{13}=(-1)^{1+3}cdot begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=(-1)^{4}cdot begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=begin{vmatrix}2&1&0\-2&-1&2\-5&7&1end{vmatrix}=-38,
A14=(−1)1+4⋅M14=(−1)1+4⋅∣210−2−10−571∣=(−1)5⋅∣210−2−10−571∣=−∣210−2−10−571∣=0A_{14}=(-1)^{1+4}cdot M_{14}=(-1)^{1+4}cdotbegin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=(-1)^{5}cdot begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=-begin{vmatrix}2&1&0\-2&-1&0\-5&7&1end{vmatrix}=0,
A21=(−1)2+1⋅M21=(−1)2+1⋅∣3−12−102711∣=(−1)3⋅∣3−12−102711∣=−∣3−12−102711∣=−(−23)=23A_{21}=(-1)^{2+1}cdot M_{21}=(-1)^{2+1}cdotbegin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=(-1)^{3}cdotbegin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=-begin{vmatrix}3&-1&2\-1&0&2\7&1&1end{vmatrix}=-(-23)=23,
A22=(−1)2+2⋅M22=(−1)2+2⋅∣0−12−202−511∣=(−1)4⋅∣0−12−202−511∣=∣0−12−202−511∣=4A_{22}=(-1)^{2+2}cdot M_{22}=(-1)^{2+2}cdotbegin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=(-1)^{4}cdotbegin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=begin{vmatrix}0&-1&2\-2&0&2\-5&1&1end{vmatrix}=4,
A23=(−1)2+3⋅M23=(−1)2+3⋅∣032−2−12−571∣=(−1)5⋅∣032−2−12−571∣=−∣032−2−12−571∣=−(−62)=62A_{23}=(-1)^{2+3}cdot M_{23}=(-1)^{2+3}cdotbegin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=-begin{vmatrix}0&3&2\-2&-1&2\-5&7&1end{vmatrix}=-(-62)=62,
A24=(−1)2+4⋅M24=(−1)2+4⋅∣03−1−2−10−571∣=(−1)6⋅∣03−1−2−10−571∣=∣03−1−2−10−571∣=25A_{24}=(-1)^{2+4}cdot M_{24}=(-1)^{2+4}cdotbegin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=begin{vmatrix}0&3&-1\-2&-1&0\-5&7&1end{vmatrix}=25,
A31=(−1)3+1⋅M31=(−1)3+1⋅∣3−12100711∣=(−1)4⋅∣3−12100711∣=∣3−12100711∣=3A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{3+1}cdotbegin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=(-1)^{4}cdotbegin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=begin{vmatrix}3&-1&2\1&0&0\7&1&1end{vmatrix}=3,
A32=(−1)3+2⋅M32=(−1)3+2⋅∣0−12200−511∣=(−1)5⋅∣0−12200−511∣=−∣0−12200−511∣=−6A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{3+2}cdotbegin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=-begin{vmatrix}0&-1&2\2&0&0\-5&1&1end{vmatrix}=-6,
A33=(−1)3+3⋅M33=(−1)3+3⋅∣032210−571∣=(−1)6⋅∣032210−571∣=∣032210−571∣=32A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{3+3}cdotbegin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=begin{vmatrix}0&3&2\2&1&0\-5&7&1end{vmatrix}=32,
A34=(−1)3+4⋅M34=(−1)3+4⋅∣03−1210−571∣=(−1)7⋅∣03−1210−571∣=−∣03−1210−571∣=−(−25)=25A_{34}=(-1)^{3+4}cdot M_{34}=(-1)^{3+4}cdotbegin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=(-1)^{7}cdotbegin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=-begin{vmatrix}0&3&-1\2&1&0\-5&7&1end{vmatrix}=-(-25)=25,
A41=(−1)4+1⋅M41=(−1)4+1⋅∣3−12100−102∣=(−1)5⋅∣3−12100−102∣=−∣3−12100−102∣=−2A_{41}=(-1)^{4+1}cdot M_{41}=(-1)^{4+1}cdotbegin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=(-1)^{5}cdotbegin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=-begin{vmatrix}3&-1&2\1&0&0\-1&0&2end{vmatrix}=-2,
A42=(−1)4+2⋅M42=(−1)4+2⋅∣0−12200−202∣=(−1)6⋅∣0−12200−202∣=∣0−12200−202∣=4A_{42}=(-1)^{4+2}cdot M_{42}=(-1)^{4+2}cdotbegin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=(-1)^{6}cdotbegin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=begin{vmatrix}0&-1&2\2&0&0\-2&0&2end{vmatrix}=4,
A43=(−1)4+3⋅M43=(−1)4+3⋅∣032210−2−12∣=(−1)7⋅∣032210−2−12∣=−∣032210−2−12∣=−(−12)=12A_{43}=(-1)^{4+3}cdot M_{43}=(-1)^{4+3}cdotbegin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=(-1)^{7}cdotbegin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=-begin{vmatrix}0&3&2\2&1&0\-2&-1&2end{vmatrix}=-(-12)=12,
A44=(−1)4+4⋅M44=(−1)4+4⋅∣03−1210−2−10∣=(−1)8⋅∣03−1210−2−10∣=∣03−1210−2−10∣=0A_{44}=(-1)^{4+4}cdot M_{44}=(-1)^{4+4}cdotbegin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=(-1)^{8}cdotbegin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0.
Задачи на заказ недорого по любому предмету от наших экспертов!
Тест по теме «Минор матрицы и алгебраическое дополнение матрицы»
Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.
В данной теме рассмотрим понятия алгебраического дополнения и минора. Изложение материала опирается на термины, пояснённые в теме «Матрицы. Виды матриц. Основные термины». Также нам понадобятся некоторые формулы для вычисления определителей. Так как в данной теме немало терминов, относящихся к минорам и алгебраическим дополнениям, то я добавлю краткое содержание, чтобы ориентироваться в материале было проще.
Содержание темы:
- Минор $M_{ij}$ элемента $a_{ij}$.
- Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$.
- Минор k-го порядка матрицы $A_{mtimes n}$. Главный минор, базисный минор, окаймляющий минор.
- Минор k-го порядка матрицы $A_{ntimes n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Минор $M_{ij}$ элемента $a_{ij}$
Пусть задана квадратная матрица $A_{ntimes n}$ (т.е. квадратная матрица n-го порядка).
Минором $M_{ij}$ элемента $a_{ij}$ матрицы $A_{ntimes n}$ именуют определитель матрицы, полученной из матрицы $A$ вычёркиванием i-й строки и j-го столбца (т.е. строки и столбца, на пересечении которых находится элемент $a_{ij}$).
Для примера рассмотрим квадратную матрицу четвёртого порядка:
$A=left( begin{array} {cccc}
1 & 0 & -3 & 9\
2 & -7 & 11 & 5 \
-9 & 4 & 25 & 84\
3 & 12 & -5 & 58 end{array} right)$. Найдём минор элемента $a_{32}$, т.е. найдём $M_{32}$. Сперва запишем минор $M_{32}$, а потом вычислим его значение. Для того, чтобы составить $M_{32}$, вычеркнем из матрицы $A$ третью строку и второй столбец (именно на пересечении третьей строки и второго столбца расположен элемент $a_{32}$). Мы получим новую матрицу, определитель которой и есть искомый минор $M_{32}$:
Этот минор несложно вычислить, используя формулу №2 из темы вычисления определителей второго и третьего порядков:
$$
M_{32}=left| begin{array} {ccc}
1 & -3 & 9\
2 & 11 & 5 \
3 & -5 & 58 end{array} right|=
1cdot 11cdot 58+(-3)cdot 5cdot 3+2cdot (-5)cdot 9-9cdot 11cdot 3-(-3)cdot 2cdot 58-5cdot (-5)cdot 1=579.
$$
Итак, минор элемента $a_{32}$ равен 579, т.е. $M_{32}=579$.
Часто вместо словосочетания «минор элемента матрицы» в литературе встречается «минор элемента определителя». Суть остается неизменной: чтобы получить минор элемента $a_{ij}$ нужно вычеркнуть из исходного определителя i-ю строку и j-й столбец. Оставшиеся элементы записывают в новый определитель, который и является минором элемента $a_{ij}$. Например, найдём минор элемента $a_{12}$ определителя
$left| begin{array} {ccc}
-1 & 3 & 2\
9 & 0 & -5 \
4 & -3 & 7 end{array} right|$. Чтобы записать требуемый минор $M_{12}$ нам понадобится вычеркнуть из заданного определителя первую строку и второй столбец:
Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков:
$$
M_{12}=left| begin{array} {cc}
9 & -5\
4 & 7 end{array} right|=9cdot 7-(-5)cdot 4=83.
$$
Итак, минор элемента $a_{12}$ равен 83, т.е. $M_{12}=83$.
Алгебраическое дополнение $A_{ij}$ элемента $a_{ij}$
Пусть задана квадратная матрица $A_{ntimes n}$ (т.е. квадратная матрица n-го порядка).
Алгебраическое дополнением $A_{ij}$ элемента $a_{ij}$ матрицы $A_{ntimes n}$ находится по следующей формуле:
$$
A_{ij}=(-1)^{i+j}cdot M_{ij},
$$
где $M_{ij}$ – минор элемента $a_{ij}$.
Найдем алгебраическое дополнение элемента $a_{32}$ матрицы $A=left( begin{array} {cccc}
1 & 0 & -3 & 9\
2 & -7 & 11 & 5 \
-9 & 4 & 25 & 84\
3 & 12 & -5 & 58 end{array} right)$, т.е. найдём $A_{32}$. Ранее мы уже находили минор $M_{32}=579$, поэтому используем полученный результат:
Обычно при нахождении алгебраических дополнений не вычисляют отдельно минор, а уж потом само дополнение. Запись минора опускают. Например, найдем $A_{12}$, если $A=left( begin{array} {ccc}
-5 & 10 & 2\
6 & 9 & -4 \
4 & -3 & 1 end{array} right)$. Согласно формуле $A_{12}=(-1)^{1+2}cdot M_{12}=-M_{12}$. Однако чтобы получить $M_{12}$ достаточно вычеркнуть первую строку и второй столбец матрицы $A$, так зачем же вводить лишнее обозначение для минора? Сразу запишем выражение для алгебраического дополнения $A_{12}$:
Минор k-го порядка матрицы $A_{mtimes n}$
Если в предыдущих двух пунктах мы говорили лишь о квадратных матрицах, то здесь поведём речь также и о прямоугольных матрицах, у которых количество строк вовсе не обязательно равняется количеству столбцов. Итак, пусть задана матрица $A_{mtimes n}$, т.е. матрица, содержащая m строк и n столбцов.
Минором k-го порядка матрицы $A_{mtimes n}$ называется определитель, элементы которого расположены на пересечении k строк и k столбцов матрицы $A$ (при этом предполагается, что $k≤ m$ и $k≤ n$).
Например, рассмотрим такую матрицу:
$$A=left( begin{array} {cccc}
-1 & 0 & -3 & 9\
2 & 7 & 14 & 6 \
15 & -27 & 18 & 31\
0 & 1 & 19 & 8\
0 & -12 & 20 & 14\
5 & 3 & -21 & 9\
23 & -10 & -5 & 58 end{array} right)
$$
Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:
$$
left( begin{array} {cccc}
-1 & 0 & -3 & 9 \
boldblue{2} & boldblue{7} & 14 & boldblue{6} \
15 & -27 & 18 & 31\
boldblue{0} & boldblue{1} & 19 & boldblue{8}\
0 & -12 & 20 & 14\
boldblue{5} & boldblue{3} & -21 & boldblue{9}\
23 & -10 & -5 & 58 end{array} right);;
M=left|begin{array} {ccc}
2 & 7 & 6 \
0 & 1 & 8 \
5 & 3 & 9 end{array} right|.
$$
Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.
Минор k-го порядка матрицы $A_{mtimes n}=(a_{ij})$ называется главным, если на главной диагонали данного минора находятся только главные диагональные элементы матрицы $A$.
Напомню, что главными диагональными элементами именуют те элементы матрицы, у которых индексы равны: $a_{11}$, $a_{22}$, $a_{33}$ и так далее. Например, для рассмотренной выше матрицы $A$ такими элементами будут $a_{11}=-1$, $a_{22}=7$, $a_{33}=18$, $a_{44}=8$. На рисунке они выделены зелёным цветом:
$$left( begin{array} {cccc}
boldgreen{-1} & 0 & -3 & 9\
2 & boldgreen{7} & 14 & 6 \
15 & -27 & boldgreen{18} & 31\
0 & 1 & 19 & boldgreen{8}\
0 & -12 & 20 & 14\
5 & 3 & -21 & 9\
23 & -10 & -5 & 58 end{array} right)
$$
Например, если в матрице $A$ мы вычеркнем строки и столбцы с номерами 1 и 3, то на их пересечении будут расположены элементы минора второго порядка, на главной диагонали которого будут находиться только диагональные элементы матрицы $A$ (элементы $a_{11}=-1$ и $a_{33}=18$ матрицы $A$). Следовательно, мы получим главный минор второго порядка:
$$
M=left|begin{array} {cc}
boldgreen{-1} & -3 \
15 & boldgreen{18} end{array} right|
$$
Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.
Пусть некий минор $M$ k-го порядка матрицы $A_{mtimes n}$ не равен нулю, т.е. $Mneq 0$. При этом все миноры, порядок которых выше k, равны нулю. Тогда минор $M$ называют базисным, а строки и столбцы, на которых расположены элементы базисного минора, именуют базисными строками и базисными столбцами.
Для примера рассмотрим такую матрицу:
$$A=left( begin{array} {ccc}
-1 & 0 & 3 & 0 & 0 \
2 & 0 & 4 & 1 & 0\
1 & 0 & -2 & -1 & 0\
0 & 0 & 0 & 0 & 0 end{array} right)
$$
Запишем минор этой матрицы, элементы которого расположены на пересечении строк №1, №2, №3 и столбцов с №1, №3, №4. Мы получим минор третьего порядка (его элементы выделены в матрице $A$ фиолетовым цветом):
$$
left( begin{array} {ccc}
boldpurple{-1} & 0 & boldpurple{3} & boldpurple{0} & 0 \
boldpurple{2} & 0 & boldpurple{4} & boldpurple{1} & 0\
boldpurple{1} & 0 & boldpurple{-2} & boldpurple{-1} & 0\
0 & 0 & 0 & 0 & 0 end{array} right);;
M=left|begin{array} {ccc}
-1 & 3 & 0 \
2 & 4 & 1 \
1 & -2 & -1 end{array} right|.
$$
Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:
$$
M=left| begin{array} {ccc}
-1 & 3 & 0\
2 & 4 & 1 \
1 & -2 & -1 end{array} right|=4+3+6-2=11.
$$
Итак, $M=11neq 0$. Теперь попробуем составить любой минор, порядок которого выше трёх. Чтобы составить минор четвёртого порядка, нам придётся использовать четвёртую строку, однако все элементы этой строки равны нулю. Следовательно, в любом миноре четвёртого порядка будет нулевая строка, а это означает, что все миноры четвёртого порядка равны нулю. Миноры пятого и более высоких порядков составить мы не можем, так как матрица $A$ имеет всего 4 строки.
Мы нашли минор третьего порядка, не равный нулю. При этом все миноры высших порядков равны нулю, следовательно, рассмотренный нами минор – базисный. Строки матрицы $A$, на которых расположены элементы этого минора (первая, вторая и третья), – базисные строки, а первый, третий и четвёртый столбцы матрицы $A$ – базисные столбцы.
Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.
Введём ещё одно понятие – окаймляющий минор.
Пусть некий минор k-го порядка $M$ матрицы $A_{mtimes n}$ расположен на пересечении k строк и k столбцов. Добавим к набору этих строк и столбцов ещё одну строку и столбец. Полученный минор (k+1)-го порядка именуют окаймляющим минором для минора $M$.
Для примера обратимся к такой матрице:
$$A=left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & -17 & -3 & 19 & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & 12 & 20 & 21 & 54\
-7 & 10 & 14 & -36 & 79 end{array} right)
$$
Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:
$$
left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & boldred{-17} & -3 & boldred{19} & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & boldred{12} & 20 & boldred{21} & 54\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M=left|begin{array} {ccc}
-17 & 19 \
12 & 21 end{array} right|.
$$
Добавим к набору строк, на которых лежат элементы минора $M$, ещё строку №1, а к набору столбцов – столбец №5. Получим новый минор $M’$ (уже третьего порядка), элементы которого расположены на пересечении строк №1, №2, №5 и столбцов №2, №4, №5. Элементы минора $M$ на рисунке выделены красным цветом, а элементы, которые мы добавляем к минору $M$ – синим:
$$
left( begin{array} {ccccc}
-1 & boldblue{2} & 0 & boldblue{-2} & boldblue{-14}\
3 & boldred{-17} & -3 & boldred{19} & boldblue{29}\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 19 & -20 & -98\
6 & boldred{12} & 20 & boldred{21} & boldblue{54}\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M’=left|begin{array} {ccc}
2 & -2 & -14 \
-17 & 19 & 29 \
12 & 21 & 54 end{array} right|.
$$
Минор $M’$ является окаймляющим минором для минора $M$. Аналогично, добавляя к набору строк, на которых лежат элементы минора $M$, строку №4, а к набору столбцов – столбец №3, получим минор $M»$ (минор третьего порядка):
$$
left( begin{array} {ccccc}
-1 & 2 & 0 & -2 & -14\
3 & boldred{-17} & boldblue{-3} & boldred{19} & 29\
5 & -6 & 8 & -9 & 41\
-5 & boldblue{11} & boldblue{19} & boldblue{-20} & -98\
6 & boldred{12} & boldblue{20} & boldred{21} & 54\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M»=left|begin{array} {ccc}
-17 & -3 & 19 \
11 & 19 & -20 \
12 & 20 & 21 end{array} right|.
$$
Минор $M»$ также является окаймляющим минором для минора $M$.
Минор k-го порядка матрицы $A_{ntimes n}$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Вновь вернёмся к квадратным матрицам. Введём понятие дополнительного минора.
Пусть задан некий минор $M$ k-го порядка матрицы $A_{ntimes n}$. Определитель (n-k)-го порядка, элементы которого получены из матрицы $A$ после вычеркивания строк и столбцов, содержащих минор $M$, называется минором, дополнительным к минору $M$.
Для примера рассмотрим квадратную матрицу пятого порядка:
$$
A=left( begin{array}{ccccc}
-1 & 2 & 0 & -2 & -14\
3 & -17 & -3 & 19 & 29\
5 & -6 & 8 & -9 & 41\
-5 & 11 & 16 & -20 & -98\
-7 & 10 & 14 & -36 & 79 end{array} right)
$$
Выберем в ней строки №1 и №3, а также столбцы №2 и №5. На пересечении оных строк и столбцов будут элементы минора $M$ второго порядка. Эти элементы выделены в матрице $A$ зелёным цветом:
$$
left(begin{array}{ccccc}
-1 & boldgreen{2} & 0 & -2 & boldgreen{-14}\
3 & -17 & -3 & 19 & 29\
5 & boldgreen{-6} & 8 & -9 & boldgreen{41}\
-5 & 11 & 16 & -20 & -98\
-7 & 10 & 14 & -36 & 79 end{array} right);;
M=left|begin{array}{cc}
2 & -14 \
-6 & 41 end{array} right|.
$$
Теперь уберём из матрицы $A$ строки №1 и №3 и столбцы №2 и №5, на пересечении которых находятся элементы минора $M$ (элементы убираемых строк и столбцов показаны красным цветом на рисунке ниже). Оставшиеся элементы образуют минор $M’$:
$$
left( begin{array}{ccccc}
boldred{-1} & boldred{2} & boldred{0} & boldred{-2} & boldred{-14}\
3 & boldred{-17} & -3 & 19 & boldred{29}\
boldred{5} & boldred{-6} & boldred{8} & boldred{-9} & boldred{41}\
-5 & boldred{11} & 16 & -20 & boldred{-98}\
-7 & boldred{10} & 14 & -36 & boldred{79} end{array} right);;
M’=left|begin{array} {ccc}
3 & -3 & 19 \
-5 & 16 & -20 \
-7 & 14 & -36 end{array}right|.
$$
Минор $M’$, порядок которого равен $5-2=3$, является минором, дополнительным к минору $M$.
Алгебраическим дополнением к минору $M$ квадратной матрицы $A_{ntimes n}$ называется выражение $(-1)^{alpha}cdot M’$, где $alpha$ – сумма номеров строк и столбцов матрицы $A$, на которых расположены элементы минора $M$, а $M’$ – минор, дополнительный к минору $M$.
Словосочетание «алгебраическое дополнение к минору $M$» часто заменяют словосочетанием «алгебраическое дополнение минора $M$».
Для примера рассмотрим матрицу $A$, для которой мы находили минор второго порядка
$
M=left| begin{array} {ccc}
2 & -14 \
-6 & 41 end{array} right|
$ и дополнительный к нему минор третьего порядка:
$M’=left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|$. Обозначим алгебраическое дополнение минора $M$ как $M^*$. Тогда согласно определению:
$$
M^*=(-1)^alphacdot M’.
$$
Параметр $alpha$ равен сумме номеров строк и столбцов, на которых находится минор $M$. Этот минор расположен на пересечении строк №1, №3 и столбцов №2, №5. Следовательно, $alpha=1+3+2+5=11$. Итак:
$$
M^*=(-1)^{11}cdot M’=-left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|.
$$
В принципе, используя формулу №2 из темы вычисления определителей второго и третьего порядков, можно довести вычисления до конца, получив значение $M^*$:
$$
M^*=-left| begin{array} {ccc}
3 & -3 & 19\
-5 & 16 & -20 \
-7 & 14 & -36 end{array} right|=-30.
$$
Минор и алгебраическое дополнение матрицы.
Определение.
Минором Mij к элементу aij определителя n-го порядка называется определитель (n — 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца.
Пример 1.
Найти миноры матрицы A
Решение:
| M11 = |
|
= |
|
| M11 = |
|
= 1·3 — 0·0 = 3 — 0 = 3 |
| M12 = |
|
= -4·3 — 0·2 = -12 -0 = -12 |
| M13 = |
|
= -4·0 — 1·2 = 0 — 2 = -2 |
| M21 = |
|
= 7·3 — 1·0 = 21 — 0 = 21 |
| M22 = |
|
= 5·3 — 1·2 = 15 — 2 = 13 |
| M23 = |
|
= 5·0 — 7·2 = 0 — 14 = -14 |
| M31 = |
|
= 7·0 — 1·1 = 0 — 1 = -1 |
| M32 = |
|
= 5·0 — 1·(-4) = 0 + 4 = 4 |
| M33 = |
|
= 5·1 — 7·(-4) = 5 + 28 = 33 |
Определение.
Алгебраическим дополнением Aij к элементу aij определителя n-го порядка называется число
Aij = (-1)i + j · Mij
Свойства алгебраического дополнения матрицы
-
Сумма произведений элементов строки (столбца) определителя на алгебраические дополнения к элементам этой строки (столбца) равна определителю матрицы:
n Σ aij·Aij = det(A) j = 1 -
Сумма произведений элементов строки (столбца) определителя на алгебраические дополнения к элементам другой строки (столбца) равна нулю:
n Σ akj·Aij = 0 (i ≠ k) j = 1 -
Сумма произведений элементов «произвольной» строки на алгебраические дополнения к элементам i-той строки определителя равна определителю, в котором вместо i-той строки записана «произвольная» строка.
Пример 2.
Найти алгебраические дополнения матрицы A
Решение:
A11 = (-1)1 + 1·M11 = (-1)2·
10
03
= 1·3 — 0·0 = 3 — 0 = 3
A12 = (-1)1 + 2·M12 = (-1)3·
-40
23
= -(-4·3 — 0·2) = -(-12 -0) = 12
A13 = (-1)1 + 3·M13 = (-1)4·
-41
20
= -4·0 — 1·2 = 0 — 2 = -2
A21 = (-1)2 + 1·M21 = (-1)3·
71
03
= -(7·3 — 1·0) = -(21 — 0) = -21
A22 = (-1)2 + 2·M22 = (-1)4·
51
23
= 5·3 — 1·2 = 15 — 2 = 13
A23 = (-1)2 + 3·M23 = (-1)5·
57
20
= -(5·0 — 7·2) = -(0 — 14) = 14
A31 = (-1)3 + 1·M31 = (-1)4·
71
10
= 7·0 — 1·1 = 0 — 1 = -1
A32 = (-1)3 + 2·M32 = (-1)5·
51
-40
= -(5·0 — 1·(-4)) = -(0 + 4) = -4
A33 = (-1)3 + 3·M33 = (-1)6·
57
-41
= 5·1 — 7·(-4) = 5 + 28 = 33
определителя
по элементам строки или столбца
Дальнейшие свойства
связаны с понятиями минора и алгебраического
дополнения
Определение.
Минором
элемента
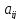
из элементов, оставшихся после вычеркиванияi-ой
стоки и j-го
столбца, на пересечении которых находится
этот элемент. Минор
элемента
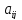
порядка имеет порядок (n—1).
Будем его обозначать через
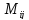
Пример 1.
Пусть

тогда
Этот минор получается
из A путём вычёркивания второй строки
и третьего столбца.
Определение.
Алгебраическим
дополнением
элемента
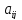
умноженный на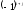

гдеi
–номер строки и j
-столбца, на пересечении которых находится
данный элемент.
VІІІ.
(Разложение определителя по элементам
некоторой строки). Определитель
равен сумме произведений элементов
некоторой строки на соответствующие
им алгебраические дополнения.
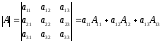
Пример 2. Пусть

тогда
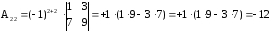
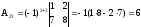
Пример 3. Найдём
определитель матрицы

разложив его по элементам первой строки.
Формально эта
теорема и другие свойства определителей
применимы пока только для определителей
матриц не выше третьего порядка, поскольку
другие определители мы не рассматривали.
Следующее определение позволит
распространить эти свойства на
определители любого порядка.
Определение.
Определителем
матрицы A
n-го порядка называется число, вычисленное
с помощью последовательного применения
теоремы о разложении и других свойств
определителей.
Можно проверить,
что результат вычислений не зависит от
того, в какой последовательности и для
каких строк и столбцов применяются
вышеуказанные свойства. Определитель
с помощью этого определения находится
однозначно.
Хотя данное
определение и не содержит явной формулы
для нахождения определителя, оно
позволяет находить его путём сведения
к определителям матриц меньшего порядка.
Такие определения называют рекуррентными.
Пример 4. Вычислить
определитель:
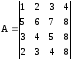
Хотя теорему о
разложении можно применять к любой
строке или столбцу данной матрицы,
меньше вычислений получится при
разложении по столбцу, содержащему как
можно больше нулей.
Поскольку у матрицы
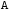
помощью свойства 7). Умножим первую
строку последовательно на числа (–5),
(–3) и (–2) и прибавим её ко 2-ой, 3-ей и 4-ой
строкам и получим:

Разложим получившийся
определитель по первому столбцу и
получим:
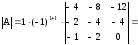
строки (–4), из 2-ой — (–2), из 3-ей — (–1)
согласно свойству 4)
(так как определитель
содержит два пропорциональных столбца).
§ 1.3. Некоторые виды матриц и их определители
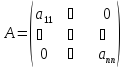
Определение.
Квадратная матрица,
у которой ниже или выше главной диагонали
стоят нулевые элементы (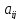
при
ij,
или
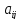
при
ij)
называется треугольной.
Их схематичное
строение соответственно имеет вид:
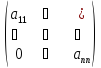
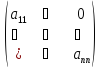
Здесь 0 – означает
нулевые элементы, а

произвольные элементы.
Теорема.
Определитель
квадратной треугольной матрицы равен
произведению её элементов, стоящих на
главной диагонали, т.е.

Например:
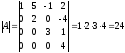
Определение.
Квадратная
матрица, у которой вне главной диагонали
стоят нулевые элементы, называется
диагональной.
Её схематический
вид:
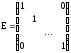
Диагональная
матрица, у которой на главной диагонали
стоят только единичные элементы
называется единичной
матрицей. Она обозначается через:
Определитель
единичной матрицы равен 1, т.е. E=1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Минор и алгебраическое дополнение матрицы
Содержание:
- Что такое минор и алгебраическое дополнение матрицы
- Общие понятия, основные формулы
- Решение миноров и алгебраических дополнений
Что такое минор и алгебраическое дополнение матрицы
Минор Mij к элементу aij определителя n-го порядка является определителем (n−1)-го порядка, получающимся из начального определителя после исключения i-той строки и j-того столбца.
Исходя из определения, минор представляет собой определитель, который остается после того, как вычеркнуть конкретную строку и конкретный столбец. К примеру, M12 будет получен в результате устранения первой строки и второго столбца. Для того чтобы получить M34 следует вычеркнуть третью строку и четвертый столбец.
Найти миноры с помощью вычерков можно, следуя алгоритму:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- устранение i-ой строки;
- вычерк j-ого столбца;
- запись определителя, который получился по итогам проделанных манипуляций.
Алгебраическое дополнение Aij к элементу aij определителя n-го порядка представляет собой число (A_{ij}=(-1)^{i+j}Mij), в котором i, j являются соответствующими строкой и столбцом, а Mij — минором к рассматриваемому элементу.
Порядок действия при определении алгебраического дополнения следующий:
- определение суммы номеров строки ( i ) и столбца ( j );
- поиск минора Mij, с помощью применения алгоритма вычисления миноров, который был рассмотрен выше;
- подстановка значений, которые были получены на первом и втором этапах расчета, в формулу (A_{ij}=(-1)^{i+j}Mij.)
Общие понятия, основные формулы
Предположим, что существует какая-то квадратная матрица или квадратная матрица n-го порядка:
(A_{ntimes n})
(Минор M_{ij} элемента a_{ij} матрицы A_{ntimes n}) будет являться определитель матрицы, которая получается из матрицы A в результате устранения i-й строки и j-го столбца, которые расположены таким образом, что их пересечение совпадает с элементом (a_{ij}.)
В качестве доказательства можно рассмотреть такую квадратную матрицу четвертого порядка:
(A=left( begin{array} {cccc} 1 & 0 & -3 & 9\ 2 & -7 & 11 & 5 \ -9 & 4 & 25 & 84\ 3 & 12 & -5 & 58 end{array} right))
Необходимо определить минор для элемента (a_{32}), то есть (M_{32}). В первую очередь следует записать минор (M_{32}), а затем рассчитать его. Порядок действий для составления (M_{32}) включает вычерк из матрицы A третьей строки и второго столбца. Данное действие обусловлено тем, что элемент (a_{32}) расположен там, где третья строка и второй столбец пересекаются. Таким образом, была получена новая матрица с определителем в виде искомого минора (M_{32}).
Данный минор достаточно просто рассчитать с помощью теоремы для вычисления определителей второго и третьего порядков. Расчет будет следующий:
(M_{32}=left| begin{array} {ccc} 1 & -3 & 9\ 2 & 11 & 5 \ 3 & -5 & 58 end{array} right|= 1cdot 11cdot 58+(-3)cdot 5cdot 3+2cdot (-5)cdot 9-9cdot 11cdot 3-(-3)cdot 2cdot 58-5cdot (-5)cdot 1=579)
Таким образом, минор элемента (a_{32}) равен 579, то есть (M_{32}=579)
Примечание
Нередко в тематической литературе вместо «минор элемента матрицы» употребляют понятие «минор элемента определителя». Смысл выражения сохраняется. Таким образом, для вычисления минора элемента (a_{ij}) требуется исключить из начального определителя i-ю строку и j-й столбец. Элементы, которые остались, следует записать в новый определитель, который представляет собой минор элемента (a_{ij}.)
В качестве примера можно рассчитать минор элемента (a_{12}) определителя:
(left| begin{array} {ccc} -1 & 3 & 2\ 9 & 0 & -5 \ 4 & -3 & 7 end{array} right|)
В первую очередь нужно записать искомый минор (M_{12}). Для этого можно исключить из заданного определителя первую строку и второй столбец:
Вычислить минор целесообразно с помощью формулы для расчета определителей второго и третьего порядков:
(M_{12}=left| begin{array} {cc} 9 & -5\ 4 & 7 end{array} right|=9cdot 7-(-5)cdot 4=83)
В результате минор элемента (a_{12}) составит 83, то есть (M_{12}=83)
Предположим, что существует какая-то квадратная матрица (A_{ntimes n}), то есть квадратная матрица n-го порядка. Алгебраическое дополнение (A_{ij}) элемента (a_{ij}) матрицы (A_{ntimes n}) можно определить, используя формулу:
(A_{ij}=(-1)^{i+j}cdot M_{ij},)
где (M_{ij}) является минором элемента (a_{ij}.)
В качестве примера можно рассчитать алгебраическое дополнение элемента (a_{32}) матрицы:
(A=left( begin{array} {cccc} 1 & 0 & -3 & 9\ 2 & -7 & 11 & 5 \ -9 & 4 & 25 & 84\ 3 & 12 & -5 & 58 end{array} right))
В результате необходимо получить значение для (A_{32}). В предыдущем примере уже был расчет для минора (M_{32}=579), поэтому целесообразно в данной задаче использовать имеющиеся данные:
Как правило, при определении алгебраических дополнений не требуется выполнять отдельный расчет минора перед вычислением непосредственно дополнения. К примеру, если требуется определить (A_{12}) при условии, что:
(A=left( begin{array} {ccc} -5 & 10 & 2\ 6 & 9 & -4 \ 4 & -3 & 1 end{array} right))
Необходимо записать справедливое равенство:
(A_{12}=(-1)^{1+2}cdot M_{12}=-M_{12})
Рассчитать (M_{12}) легко с помощью вычерка первой строки и второго столбца матрицы А. Поэтому нет необходимости вводить лишнее обозначение для минора. Достаточно сразу записать уравнение для алгебраического дополнения (A_{12}):
Решение миноров и алгебраических дополнений
Миноры и алгебраические дополнения встречаются в задачах не только с квадратными матрицами, но и прямоугольными. Во втором случае матрицы отличаются тем, что количество строк не обязательно совпадает с количеством столбцов. К примеру, записана матрица:
(A_{mtimes n})
В рассматриваемой матрице m строк и n столбцов. Минор k-го порядка матрицы (A_{mtimes n}) представляет собой определитель с элементами, расположенными на пересечении k строк и k столбцов матрицы A. Следует учитывать, что при этом k≤ m и k≤ n.
В качестве примера можно рассмотреть матрицу:
(A=left( begin{array} {cccc} -1 & 0 & -3 & 9\ 2 & 7 & 14 & 6 \ 15 & -27 & 18 & 31\ 0 & 1 & 19 & 8\ 0 & -12 & 20 & 14\ 5 & 3 & -21 & 9\ 23 & -10 & -5 & 58 end{array} right))
Можно записать для нее какой-то минор третьего порядка. Для этого следует отобрать какие-то три строки и три столбца рассматриваемой матрицы. Выберем для расчета строки №2, №4, №6 и столбцы №1, №2, №4. Данные строки и столбцы будут пересекаться в том месте, где расположены элементы искомого минора.
(M=left|begin{array} {ccc} 2 & 7 & 6 \ 0 & 1 & 8 \ 5 & 3 & 9 end{array} right|.)
Расположение миноров первого порядка будет совпадать с пересечением одной строки и одного столбца. Таким образом, выводим равенство миноров первого порядка элементам рассматриваемой матрицы.
Минор k-го порядка матрицы (A_{mtimes n}=(a_{ij})) является ключевым в том случае, когда главная диагональ рассматриваемого минора включает исключительно ключевые диагональные элементы матрицы A.
Примечание
Главные диагональные элементы представляют собой такие элементы матрицы, которые содержат индексы, равные( a_{11}, a_{22}, a_{33}) и так далее. К примеру, матрица А, которая рассматривается в примере, содержит элементы (a_{11}=-1, a_{22}=7, a_{33}=18, a_{44}=8.)
(left( begin{array} {cccc} {-1} & 0 & -3 & 9\ 2 &{7} & 14 & 6 \ 15 & -27 & {18} & 31\ 0 & 1 & 19 & {8}\ 0 & -12 & 20 & 14\ 5 & 3 & -21 & 9\ 23 & -10 & -5 & 58 end{array} right))
В том случае, когда в матрице А исключены строки и столбцы, которые соответствуют номерам 1 и 3, их пересечение будет совпадать с элементами минора второго порядка. Главная диагональ этого минора будет содержать лишь диагональные элементы матрицы А. К примеру, такими элементами являются элементы ( a_{11}=-1) и (a_{33}=18) матрицы A. Таким образом, главный минор второго порядка будет равен:
(M=left|begin{array} {cc} {-1} & -3 \ 15 & {18} end{array} right|)
В том случае, если выбрать строки и столбцы с другими номерами, получится другой главный минор второго порядка.
Можно предположить, что какой-то минор M k-го порядка матрицы A_{mtimes n} обладает ненулевым значением, то есть Mneq 0. В данном случае, для всех миноров с порядками выше, чем k, справедливо равенство нулю. Тогда минор M является базисным, а строки и столбцы, содержащие элементы базисного минора, носят названием базисных строк и базисных столбцов.
В качестве примера можно рассмотреть следующую матрицу:
(A=left( begin{array} {ccc} -1 & 0 & 3 & 0 & 0 \ 2 & 0 & 4 & 1 & 0\ 1 & 0 & -2 & -1 & 0\ 0 & 0 & 0 & 0 & 0 end{array} right))
Запись минора рассматриваемой матрицы с элементами, распложенными на месте, где пересекаются строки №1, №2, №3 и столбцы №1, №3, №4, представляет собой минор третьего порядка и имеет следующий вид:
(; M=left|begin{array} {ccc} -1 & 3 & 0 \ 2 & 4 & 1 \ 1 & -2 & -1 end{array} right|)
Рассчитать значение искомого минора можно, используя правило для расчета определителей второго и третьего порядков:
(M=left| begin{array} {ccc} -1 & 3 & 0\ 2 & 4 & 1 \ 1 & -2 & -1 end{array} right|=4+3+6-2=11)
В результате:
(M=11neq 0)
Далее можно попытаться записать какой-либо минор с порядком выше, чем 3. Для составления минора четвертого порядка необходимо воспользоваться четвертой строкой, элементы которой имеют нулевые значения. Исходя из этого, можно заключить, что любой минор четвертого порядка обладает нулевой строкой. Таким образом, значение каждого из миноров четвертого порядка равно нулю. Записать миноры пятого порядка и выше не представляется возможным по причине наличия в матрице А всего четырех строк.
По результатам вычислений удалось определить минор третьего порядка с ненулевым значением. Одновременно с этим, миноры более высоких порядков равны нулю, из чего можно сделать вывод: рассматриваемый минор является базисным. Строки №1, №2, №3 матрицы А, которые содержат элементы данного минора, являются базисными строками, а столбцы №1, №3, №4 матрицы А — базисными столбцами.
Пример, который был рассмотрен, является тривиальным. Однако с его помощью удобно продемонстрировать смысл базисного минора. В реальных условиях базисных миноров может быть более одного, а решение подобных задач на нахождение подобного минора существенно сложнее и объемнее.
Еще одним важным термином является окаймляющий минор. Для раскрытия понятия можно предположить, что какой-то минор k-го порядка M матрицы (A_{mtimes n}) находится в месте, где пересекаются k строки и k столбцы. Если прибавить к совокупности данных строк и столбцов дополнительные строку и столбец, то минор (k+1)-го порядка, который получился в результате, представляет собой окаймляющий минор для минора M.
В качестве примера можно рассмотреть матрицу:
(A=left( begin{array} {ccccc} -1 & 2 & 0 & -2 & -14\ 3 & -17 & -3 & 19 & 29\ 5 & -6 & 8 & -9 & 41\ -5 & 11 & 19 & -20 & -98\ 6 & 12 & 20 & 21 & 54\ -7 & 10 & 14 & -36 & 79 end{array} right))
В первую очередь нужно записать минор второго порядка с элементами, расположенными в месте, где пересекаются строки №2 и №5, а также столбцы №2 и №4.
(M=left|begin{array} {ccc} -17 & 19 \ 12 & 21 end{array} right|)
К комплекту строк с элементами минора М требуется прибавить одну строку №1, а к столбцам — столбец №5. В результате манипуляций получится новый минор M’ третьего порядка с элементами, расположенными там, где пересекаются строки №1, №2, №5 и столбцы №2, №4, №5.
(M’=left|begin{array} {ccc} 2 & -2 & -14 \ -17 & 19 & 29 \ 12 & 21 & 54 end{array} right|)
Минор M’ представляет собой окаймляющий минор для минора M. Таким же образом, путем добавления к комплекту строк с элементами минора М строки №4, а к совокупности столбцов — столбца №3, можно записать минор M», то есть минор третьего порядка.
( M»=left|begin{array} {ccc} -17 & -3 & 19 \ 11 & 19 & -20 \ 12 & 20 & 21 end{array} right|.)
Минор M», аналогично предыдущему, представляет собой окаймляющий минор для минора M.
Предположим, что существует какой-то минор M k-го порядка матрицы (A_{ntimes n}.)
Определитель (n-k)-го порядка с элементами, полученными из матрицы A путем исключения строк и столбцов, которые содержали минор M, называется минором, дополнительным к минору M.
В качестве примера можно рассмотреть квадратную матрицу пятого порядка:
(A=left( begin{array}{ccccc} -1 & 2 & 0 & -2 & -14\ 3 & -17 & -3 & 19 & 29\ 5 & -6 & 8 & -9 & 41\ -5 & 11 & 16 & -20 & -98\ -7 & 10 & 14 & -36 & 79 end{array} right))
В рассматриваемой матрице можно выбрать строки №1 и №3, столбцы №2 и №5. Пересечение данных строк и столбцов будет совпадать с элементами минора М второго порядка.
( M=left|begin{array}{cc} 2 & -14 \ -6 & 41 end{array} right|)
Далее следует исключить из матрицы А строки №1 и №3, а также столбцы №2 и №5. На пересечении данных компонентов расположены элементы минора М. Элементы, которые остались нетронутыми, сформируют минор M’.
(M’=left|begin{array} {ccc} 3 & -3 & 19 \ -5 & 16 & -20 \ -7 & 14 & -36 end{array}right|)
Минор M’ с порядком, соответствующим 5-2=3, представляет собой минор, являющийся дополнительным к минору M.
Запись алгебраического дополнения к минору M квадратной матрицы (A_{ntimes n}) имеет следующий вид:
((-1)^{alpha}cdot M’)
В данном случае alpha является суммой номеров строк и столбцов матрицы A, содержащих элементы минора M, а M’ является дополнительным к минору M. Термин «алгебраическое дополнение к минору M», как правило, формулируют таким образом: «алгебраическое дополнение минора M».
В качестве примера можно рассмотреть матрицу А. Ранее для рассматриваемой матрицы был определен в ходе расчетов минор второго порядка:
(M=left| begin{array} {ccc} 2 & -14 \ -6 & 41 end{array} right|)
Дополнительным к данному минору является такой минор третьего порядка:
(M’=left| begin{array} {ccc} 3 & -3 & 19\ -5 & 16 & -20 \ -7 & 14 & -36 end{array} right|)
В качестве обозначения алгебраического дополнения минора M целесообразно использовать: M^*
Исходя из определения, получим:
(M^*=(-1)^alphacdot M’)
Параметр alpha представляет собой сумму номеров строк и столбцов, которым соответствует минор М. Расположение данного минора соответствует пересечению строк №1, №3 и столбцов №2, №5. Таким образом:
(alpha=1+3+2+5=11)
В результате можно записать:
(M^*=(-1)^{11}cdot M’=-left| begin{array} {ccc} 3 & -3 & 19\ -5 & 16 & -20 \ -7 & 14 & -36 end{array} right|)
Благодаря формуле для расчета определителей второго и третьего порядков, представляется возможным вычислить алгебраическое дополнение:
(M^*=-left| begin{array} {ccc} 3 & -3 & 19\ -5 & 16 & -20 \ -7 & 14 & -36 end{array} right|=-30)