В данной публикации мы рассмотрим, что такое алгебраическая сумма, а также приведем примеры для лучшего понимания теоретического материала.
Алгебраическая сумма – это математическое выражение, которое можно представить в виде суммы положительных и отрицательных слагаемых.
a – b = a + (-b)
Из данного определения следует, что любую разность можно заменить суммой, изменив знак вычитаемого на противоположный. Это применимо к любому количеству уменьшаемых и вычитаемых.
a – b + c – d = a + (-b) + c + (-d)
Примеры:
- 15 – 6 = 15 + (-6)
- 27 – 13 – 19 + 5 + 40 = 27 + (-13) + (-19) + 5 + 40
Рассмотренное правило работает и в обратную сторону:
a + (-b) = a – b
Примеры:
- 301 + (-89) + (-76) = 301 – 89 – 76
- (-35) + 57 + 62 + (-16) = 57 – 35 + 62 – 16
В последнем примере после знака “равно” мы поменяли слагаемые местами, чтобы выражение выглядело более красиво. Согласно свойствам сложения, на результат этот никак не повлияет (переместительный закон).
Содержание:
- § 1 Правило нахождения модуля суммы слагаемых с одинаковыми знаками
- § 2 Правило нахождения модуля суммы слагаемых с разными знаками
§ 1 Правило нахождения модуля суммы слагаемых с одинаковыми знаками
В этом уроке рассмотрим правило вычисления алгебраической суммы двух чисел.
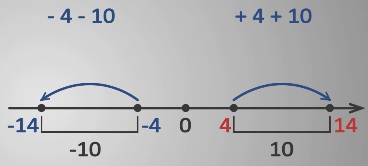
Найдем значения выражений: -4 – 10 и +4+10 с помощью координатной прямой.
Вспомним, что вычитание – это движение влево, а сложение – движение вправо по координатной прямой.
На координатной прямой отметим точки -4 и +4. От точки -4 отложим влево 10 единичных отрезков, получим координату -14. От точки +4 отложим вправо 10 единичных отрезков, получим координату +14.
По рисунку видно, что -4-10 = -14; +4+10 = +14.
Проанализируем выражения. В каждом выражении слагаемые имеют одинаковые знаки: в первом знак минус, во втором знак плюс, значения суммы имеют тот же знак, что и слагаемые.
Найдем сумму модулей l-4l + l-10l = l-14l.
l -4l = 4
l-10l = 10
4+10 = 14, а 14 – модуль числа -14.
Аналогично l4l + l10l = l14l
l4l = 4
l10l = 10
4+10=14, а 14 – модуль и +14 тоже.
Можно сделать вывод:
Если слагаемые имеют одинаковые знаки, то значение суммы имеет тот же знак, что и слагаемые, а модуль суммы равен сумме модулей слагаемых.
Например:
В сумме -14-23 оба слагаемых имеют знак минус, значит, значение суммы тоже будет иметь знак минус, складываем модули 14+23=37, в итоге значение суммы -37.
§ 2 Правило нахождения модуля суммы слагаемых с разными знаками
Найдем значения выражений, в которых слагаемые имеют разные знаки.
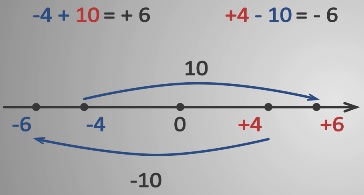
Например, -4+10 и +4-10.
Отметим на координатной прямой точки -4 и +4. От координаты -4 отложим вправо 10 единичных отрезков, получим число +6. От координаты +4 отложим влево 10 единичных отрезков, получим точку -6. Таким образом, -4+10= +6 и +4-10 = -6.
Сделаем анализ выражений.
Сравним модули слагаемых l-4l < l10l; l+4l < l-10l,обратим внимание, результат суммы имеет знак слагаемого с большим модулем. Из большего модуля вычтем меньший:
l+10l – l-4l = 6 и l-10l – l+4l = 6, значит
-4+10= 6, а +4-10= -6.
Вывод:
Если слагаемые имеют разные знаки, то значение суммы имеет тот же знак, что и слагаемое с большим модулем, а модуль суммы равен разности модулей слагаемых при условии, что из большего модуля вычитается меньший модуль.
Например, найдем значение выражения 9 – 25, слагаемые имеют разные знаки +9 и -25, найдем модули слагаемых l+9l = 9, l-25l = 25.
Больший модуль 25, значит, знаком результата суммы будет знак минус. Найдем разность модулей 25 – 9 = 16. Значит значение суммы равно минус 16.
Вспомним, противоположные числа – это числа, которые отличаются знаками, их модули одинаковые. Следовательно, сумма противоположных чисел равна 0, так как разность одинаковых модулей равна 0.
Вывод:
Сумма противоположных чисел равна 0. Также можно утверждать, что если сумма двух чисел равна 0, то данные числа будут противоположными.
Если одно из слагаемых равно 0, то значение суммы равно другому слагаемому.
Например, -8,3 + 0, слагаемые с разными знаками, модуль -8,3 больше чем модуль 0, значит знак суммы — минус, найдем разность модулей l-8.3l – l0l = 8, 3, следовательно сумма равна -8,3.
Итак, на этом уроке Вы познакомились с правилом вычисления алгебраической суммы двух чисел.
Список использованной литературы:
- Математика.6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича //автор-составитель Л.А. Топилина. Мнемозина 2009.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И. Зубарева, А.Г. Мордкович.- М.: Мнемозина, 2013.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. /Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013.
- Справочник по математике — http://lyudmilanik.com.ua
- Справочник для учащихся в средней школе http://shkolo.ru
Алгебраическая сумма — это выражение, которое можно представить в виде суммы положительных и отрицательных чисел.
Рассмотрим примеры алгебраических сумм.
Пример 1.
Запиши выражения без скобок:
а)
−56++15+−7=−56+15−7
;
б)
+17+−13+−5=17−13−5
;
в)
23++73−−54=23+73+54
;
г)
−−6+−12−4=6−12−4
.
Обрати внимание!
;
+−a=−a
;
−+a=−a
;
−−a=a
.
Пример 2.
Назови слагаемые алгебраической суммы:
а)
17+−13+51
.
Слагаемыми данной алгебраической суммы являются числа (17), (-13) и (51).
б)
−27+13−6−37
.
Выражение перепишем в виде:
.
Оно состоит из слагаемых: (-27), (13), (-6) и (-37).
Цели урока:
- Образовательные:
- вывод правила вычисления значения алгебраической суммы двух чисел;
- формирование умений применения данного правила при вычислении значений
алгебраической суммы
- Развивающие: развивать наблюдательность, внимание, память,
логическую и математическую речь - Воспитательные: воспитывать аккуратность, взаимоуважение,
активизация познавательной и творческой активности учащихся
Дидактические приемы: использование поискового метода, метода
самостоятельной работы с учебником
Учитель: Здравствуйте, ребята! Я рада вас видеть, и, надеюсь, что наше
сотрудничество на уроке будет успешным.
- Какую главную тему мы начали изучать в 6-м классе? (“+” и “ — ”
числа) - Что мы изучали на прошлых уроках? (Выражения, содержащие “+” и “ — ”
, алгебраическую сумму и ее свойства). - Какие приемы вычисления алгебраической суммы вы знаете? (Координатная
прямая, изменение t — ры, “доход” — “расход”, “долг” — “прибыль”)
А сегодня на уроке нам предстоит установить закономерность, в которую входят
эти приемы вычисления алгебраической суммы – это правило вычисления значения
алгебраической суммы.
Запишите в тетради число и тему урока. А для начала поработаем устно, сделаем
разминку:
- Назовите наименьшее натуральное число
- Можно количество цветов в спектре радуги разделить на 2 без остатка? А
на 7? - Если t — ра воздуха была -6º, затем потеплело на 4º. Какой стала t – ра?
- Периметр прямоугольника из проволоки равен 20 см. Его разогнули и
сделали квадрат. Чему равна S квадрата?
На доске показываются числа (2-3 сек.), затем закрываются:
1814; — 0,25; 0; ¼,: 1841
- Сколько было всего чисел?
- Какие по счету натуральные числа?
- На каком месте отрицательное число?
- На каком месте обыкновенная дробь?
- Найдите сумму второго и четвертого чисел
- Какому историческому событию соответствует 1 – е число? 5-е число?
- Какие целые числа заключены между числами
- – 2,09 и 2,09
- – 5,6 и – 0,8
- Какая из 2-х точек правее?
- А (а) или В ( — а) ?
- Д (с) или К (с+2) ?
- С (х) или Е (х – а) ?
- Решите уравнение:
- │х│ = ½
- 1/2
- -1/2
- 0,5 и ½
- │х│ — 2 = 0
- х = 2
- х = -2
- х = 2 и х = -2
Учитель: Ну что ж, разминку сделали, а сейчас займемся выводом Правила вычисления
алгебраической суммы двух чисел. Девизом нашей работы будут слова великого
персидского поэта и ученого XY века Джами: “Используй в деле знания что припас!
Чтобы зажженный факел не погас!”
Работать будем самостоятельно и вы, выполняя упражнения, сможете
сформулировать Правило вычисления значения алгебраической суммы двух чисел.
Выполняем самостоятельно № 258
Учащиеся читают задания, записывают ответы и делают выводы в заранее
заготовленных карточках
| 1 | – 6 – 8 = — 14 | — 6 + 8 = 2 |
| 6 + 8 = 14 | + 6 – 8 = -2 | |
| — 2 – 11 = -13 | — 2 + 11 = 9 | |
| 11 + 2 = 13 | — 11 + 2 = -9 | |
| 2 | – 6 – 8 = (– 6) + ( –  = — 14 = — 14 |
— 6 + 8 = (-6) + (+8) = 2 |
| 6 + 8 = (+6) + (8) = 14 | + 6 – 8 = (+6) + (-8) = -2 | |
| — 2 – 11 = (-2) + (-11) = -13 | — 2 + 11 = (-2) + (+11) = 9 | |
| 11 + 2 = (+11) + (+2) = 13 | — 11 + 2 = (-11) + (+2) = -9 | |
| 3 | Знаки слагаемых — одинаковые | Знаки слагаемых — разные |
| 4 | Знак суммы совпадает со знаками слагаемых | Знак суммы имеет знак слагаемого с большим модулем |
| 5 | │(- 6) + (-8)│ = │-14 │ = 14
│– 6│ +│ – 8│= 6+8 = 14 |
|
| │ 6 + 8│ = │14│ = 14
│6│ + |
||
| │ (-2) + (-11) │ = │-13│ = 13
│- 2│+│ – 11│ = 2 + 11 = 13 |
||
| │11 + 2│ = │13I│ = 13
│11│ + |
||
| Вывод: модуль сумы равен сумме модулей | ||
| 6 | │(-6) + (+8)│ = │2│ = 2
│8│ |
|
| │(-8) + (+6) │ = │-2│ = 2
│-8│ – │6│ = 8 |
||
| │(-2) + (+11)│ = I9I = 9
│11│ – │2│ = 11 — 2 = 9 |
||
| │ (+2) + (-11) │ = │-9│ = 9
│-11│ – │2│ = |
||
| Вывод: модуль суммы равен разности модулей | ||
| 7 | Если слагаемые имеют одинаковые знаки, то сумма имеет тот же знак, что и слагаемые, а модуль суммы равен сумме модулей слагаемых |
Если слагаемые имеют разные знаки, то сумма имеет тот же знак, что и слагаемое с большим модулем, а модуль суммы равен разности слагаемых при условии, что из большего модуля вычитается меньший. |
На доске вывешивается плакат:
| М | Р | Б | А | У | П | Г | А | Т | А |
| -12 | 12 | 20 | -20 | -6 | 6 | -10 | 10 | 19 | -5 |
Используя правило, найдем значения выражений, рядом с ответом ставим
соответствующую букву:
- (+16) + (+4) =
- (+8) + (+2) =
- 7 + 12 =
- (+16) + (-4) =
- (-8) + (-2) =
- 7 – 12 =
- (-16) + (-4) =
- (-8) + (+2) =
- (-16)+ (+4) =
- (+8) + (-2 = )
Учащиеся проговаривают правило в каждом примере:
- (+16) + (+4). Оба слагаемых имеют один и тот же знак — “+”, значит сумма имеет
тот же знак “+”, далее складываем модули 16 + 4 = 20, в итоге получаем +20,
буква Б; - (+16) +(-4) Слагаемые имеют разные знаки, причем слагаемое с большим модулем
имеет знак “+”, поэтому и сумма имеет знак “+”, далее, вычитаем из большего
модуля меньший (или находим разность модулей) 16 – 4 = 12, получаем +12, буква Р
и т.д.
Какое получилось слово? БРАМАГУПТА – индийский математик, живший в YII веке,
пользовался отрицательными числами. Положительные представлял как “имущества”,
отрицательные числа как “долги”. Правила сложения “+” и “-” чисел выражал так:
- “Сумма двух имуществ есть имущество” “+” + “+” = “+”
- “Сумма двух долгов есть долг” “ — ” + “ — ” = “ — ”
А теперь вы попробуйте с помощью знаков и символов изобразить правило
сложения алгебраической суммы с разными знаками. Какой знак имеет в этом случае
и почему?
- “+” + “-” = “+” , если │ + │ > │ — │
- “+” + “-” = “ — ”, если │ — │ < │ + │
- Домашнее задание: стр. 62 -правило
- № 275 (а, б) (“3”)
- № 275 (а, б) № 288 (“ 4 ”)
- № 275 (а, б) № 288 №286 (“ 5 ”)
- Итог урока.: Какова была цель нашего урока?
- Мы достигли поставленной цели?
- Сформулируйте алгоритм сложения положительных чисел, алгоритм сложения
отрицательных чисел, алгоритм сложения чисел с разными знаками: - Проанализируйте свою работу на уроке.
| Алгоритм сложения положительных чисел:
1) В результате поставить знак “+”. |
| Алгоритм сложения отрицательных чисел:
1) В результате поставить знак “-”. |
| Алгоритм сложения чисел с разными знаками:
1) В результате поставить знак числа с большим модулем. |
- Выставление оценок
Заранее заготовленные алгоритмы раздаются каждому учащемуся
Скачать материал

Скачать материал




- Сейчас обучается 267 человек из 65 регионов


- Сейчас обучается 387 человек из 62 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
+
–
+
–
и
и
складываем
ставим общий знак
вычитаем
ставим знак большего
+
–
и -
2 слайд
Проверка
домашнего
задания -
3 слайд
№ 262
Найдите значение выражения:
а) 5,3 + (– 5,3) =
б) 3 + (– 1) =
а + (– а) = 0
0
2
в) 3,2 + (– 3,2) =
г) (– 2,5) + 2,5 =
д) 0 + (– 1,8) =
е) (– 5) + (–=
0
0
– 1,8
– 13 -
4 слайд
№ 263
Найдите значение выражения:
а) 0 + (– 2,1) =
б) 0 + (– 3,8) =
г) (–+ 3,1 =
д) (– 4,1) + 4,1 =
в) – 3 + (– 5) =
– 2,1
– 3,8
– 8
– 4,9
0
е) (– 10) + (– 12) =
– 22 -
5 слайд
№ 277
Длина одной из сторон треугольника х см.
а) Что могут означать выражения х – 6, 1,25х?
длины двух других сторон
б) Что означает математическая модель
х + (х – 6) + 1,25х = 33?
периметр треугольника -
6 слайд
РТ № 8.3
Заполните пропуски.
–
25,49 – 17,8 =
7,69
= – 7,69
–
34,7 + 129,3 =
164
= – 164
+
101,9 – 54,31 =
47,59
= 47,59
–
4,08 – 0,546 =
3,534
= – 3,534 -
-
8 слайд
Название этого исторического места в Крыму вы узнаете, если укажете правильный ответ.
– 18 – 32 -
9 слайд
Название этого исторического места в Крыму вы узнаете, если укажете правильный ответ.
– 16 + 32
-
10 слайд
Название этого исторического места в Крыму вы узнаете, если укажете правильный ответ.
+ 33 – 44
-
11 слайд
Название этого исторического места в Крыму вы узнаете, если укажете правильный ответ.
– 37 – 17
-
12 слайд
Название этого исторического места в Крыму вы узнаете, если укажете правильный ответ.
+ 45 – 15
-
13 слайд
Название этого исторического места в Крыму вы узнаете, если укажете правильный ответ.
– 24 + 48
-
14 слайд
Название этого исторического места в Крыму вы узнаете, если укажете правильный ответ.
– 37 – 23
-
15 слайд
Название этого исторического места в Крыму вы узнаете, если укажете правильный ответ.
-
-
17 слайд
29.12.2020
К л а с с н а я р а б о т а.
-
18 слайд
№ 265
а) – 78 + 20 + 26 – 46 – 100 – 22 =
– 200
б) – 51 – 37 – 22 + 59 + 24 + 27 =
0
Найдите значение выражения: -
19 слайд
№ 267
Вычислите:
а) (– 4,49) – (– 0,57) + 2,44 – 8,101 – 0,57 –
– (– 4,49) =
= – 4,49 + 0,57 + 2,44 – 8,101 – 0,57 + 4,49 =
= – 5,661
б) – 4,36 + 4,306 + (– 8,8) – (– 9,854)
– (+4,306) + 8,8 =
– 4,36 + 4,306 – 8,8 + 9,854 – 4,306 + 8,8 =
= 5,494 -
20 слайд
№ 269
Найдите значение выражения: -
21 слайд
№ 269
Найдите значение выражения:
0
5 -
22 слайд
В четырёхугольнике АВСD АВ = х см. Выразите остальные стороны этого четырёхугольника, если: ВС на 1 см меньше АВ; СD в 1,52 раза больше АВ; АD на 1 см больше СD.
№ 278
х
х – 1
1,52х
х + х – 1 + 1,52х + 1,52х + 1 = 12,6
А
В
С
D
1,52х + 1
Составьте уравнение, зная, что периметр АВСD ра- вен 12,6 см. -
23 слайд
Решите полученное уравнение.
№ 278
х + х – 1 + 1,52х + 1,52х + 1 = 12,6
5,04х = 12,6
х = 12,6 : 5,04
х = 2,5
Найдите длины всех сторон четырёхугольника АВСD.
х
х – 1
1,52х
А
В
С
D
1,52х + 1
АВ = 2,5 см
ВС = 1,5 см
СD = 3,8 см
АD = 4,8 см -
24 слайд
Дома:
У: № 264; 266; 268
РТ: № 8.5 -
25 слайд
Самостоятельная работа
стр. 34
С – 8.2 -
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 266 046 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 12.12.2020
- 172
- 0
- 07.12.2020
- 645
- 3
- 11.11.2020
- 679
- 0
- 05.10.2020
- 143
- 0
- 24.09.2020
- 538
- 0
- 15.08.2020
- 530
- 1
- 02.08.2020
- 274
- 4
- 17.07.2020
- 3475
- 37
Вам будут интересны эти курсы:
-
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
-
Курс повышения квалификации «Введение в сетевые технологии»
-
Курс повышения квалификации «Экономика: инструменты контроллинга»
-
Курс повышения квалификации «Правовое регулирование рекламной и PR-деятельности»
-
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
-
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
-
Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
-
Курс профессиональной переподготовки «Техническая диагностика и контроль технического состояния автотранспортных средств»