Как найти алгоритм от наименьшего числа - Исправление недочетов и поиск решений вместе с Examum.ru

Идея
метода состоит в том, что определяется
место наименьшего числа при сортировке
ряда по возрастанию (наибольшего числа
при сортировке по убыванию), которое
затем меняется местами с первым числом
ряда. После этого ряд чисел рассматривается
уже без первого числа. Найденное
наименьшее (наибольшее) число выставляется
аналогичным образом на второе место и
в дальнейшем ряд чисел рассматривается
уже без двух первых чисел, которые
выставлены в нужном порядке. Это
повторяется многократно до тех пор,
пока останется одно число, после чего
процесс сортировки прекращается.

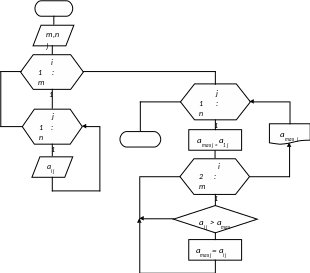
На
рис.9.2 приведен алгоритм сортировки

чисел по возрастанию. Блок – схема
представлена двумя вложенными циклами.
Внешний цикл с параметром цикла k
осуществляет назначение каждый раз
числа на роль минимального a_min
в
рассматриваемом ряде чисел и одновременно
отсекает уже выставленное вперед число
после предыдущего цикла.

Вложенный
цикл с параметром цикла i
представляет собой типовой алгоритм
определения наименьшего числа из ряда
чисел. Здесь роль наименьшего числа

играет число

,
которое изменяется последовательно от
a₁
до a_n_-1.
Вложенный цикл рассматривает ряд чисел,
начиная с соседнего с

,
то есть с числа

.
За пределами вложенного цикла производится
обмен числами, наименьшего и первого в
рассматриваемом ряде. Здесь роль
переменной

,
используемой в методе смежных пар,
играет переменная

Если
в роли минимального числа ряда осталось
первое число a_k,
то обмен не нужен. Этот факт устанавливается
проверкой условия

.

Рис.
9.2 Блок – схема сортировки чисел по
возрастанию
методом определения наименьшего числа

В
отличие от предыдущего метода, этот
алгоритм осуществляет сортировку чисел
по «жесткой» программе. То есть, независимо
от того, сортирован ли исходный ряд или
нет, тело внешнего цикла будет выполнено

раз. В этом случае непроизводительно
расходуется машинное время, что определяет
недостаток метода. Но, тем не менее, этот
метод имеет свою область применения.
Таким методом удобно решать задачи по
определению нескольких (больше одного)
минимальных чисел ряда. В этом случае
достаточно установить правую границу
параметра внешнего цикла k

не n-1,
а то число, которое определяет количество
искомых минимальных элементов ряда.

Сортировка
по убыванию осуществляется аналогично.
При этом в рассмотренной блок-схеме
идентификатор

необходимо заменить идентификатором

,
что вызывает правильные ассоциации,
а операцию сравнения » < » – на
операцию » > «.

9.2. Типовые алгоритмы решения задач с использованием матриц

Отличительной
особенностью алгоритмов решения задач
с использованием матриц (двухмерных
массивов) от алгоритмов, ориентированных
на работу с рядами чисел (векторами),
является наличие двух вложенных циклов.

На
рис.9.3 приведен алгоритм вычисления
суммы элементов матрицы a(m×n).
Внешний цикл предназначен для установления
текущего адреса i
строки
матрицы, а внутренний (вложенный) –
текущего адреса j
ее
столбца.

Вычисление
произведения Р
элементов
матрицы осуществляется по аналогичной
блок – схеме, в которой следует заменить
символ S

на P,
операцию S
= 0
на операцию P
= 1,
а операцию S
= S
+ a_i_j

– на операцию P
=P*a_i_j.

Рис.
9.3 Блок – схема вычисления суммы
элементов матрицы

В
некоторых случаях возникает вопрос,
какой цикл должен быть внешним, а какой
– внутренним. Ответ на него следующий.

Если
условием задачи предусматриваются
какие-либо операции
в строках,
то внешний
цикл должен определять текущий адрес
строки,
если же предусматриваются операции
в столбцах,
то внешний
цикл должен определять текущий адрес
столбца.
Если же операции над элементами матрицы
не акцентируются на строках или на
столбцах, как в случае вычисления суммы
или произведения элементов матрицы, то
взаимное расположение циклов может
быть любым.

Пример
1.
В
заданной матрице a(m×n)
определить наибольшие элементы строк.

Алгоритм
решения этой задачи представлен на
рис.9.4.
Здесь
внешний цикл определяет текущий адрес
строки. Получив адрес строки

,
первый элемент ее

(элемент первого столбца) берется в в
качестве начального значения переменной

.
Вложенный цикл предусматривает
определение текущего порядкового номера
элемента в данной строке (номер столбца).
В дальнейшем используется типовой
алгоритм определения наибольшего числа
в ряде чисел (в строке матрицы).

Рис.9.4.
Блок-схема определения максимального
элемента
в
строке матрицы

Следует
подчеркнуть, что в задаче требуется
определить максимальные элементы в
строках,
поэтому внешний цикл алгоритма
устанавливает текущий адрес строки.

Пример
2.
В
заданной матрице a(m×n)
определить наибольший элемент в каждом
столбце.

Алгоритм
решения этой задачи приведен на рис.9.5.
В отличие от предыдущего примера в этом
алгоритме внешний цикл определяет
текущий адрес столбца.

В
случае примера с вычислением суммы всех
элементов матрицы (Рис.9.3) внешний цикл
может определять как текущий адрес
строки, так и текущий адрес столбца,
поскольку здесь не акцентируется место
операций (строки или столбцы). Областью
операций являются все элементы матрицы
без уточнения, в каких строках или
столбцах они расположены.

Приведенные
алгоритмы составляют далеко не полный
перечень алгоритмов с операциями над
элементами матриц. Однако они могут
быть использованы как фрагменты при
разработке более сложных алгоритмов.

Следует
хорошо понимать логику типовых алгоритмов,
хорошо запомнить
их и умело применять при решении различных
задач. Это позволит экономить время на
разработку алгоритмов других задач, в
которых используются типовые алгоритмы.

Рис.
9.5 Блок-схема определения максимального
элемента

в
каждом столбце матрицы

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Автор материалов — Лада Борисовна Есакова.

Алгоритм – это точно сформулированное исполнителю предписание совершить определенную последовательность действий для решения задачи за конечное число шагов.

Алгоритм может быть задан одним из следующих способов:

— Словесное описание последовательности действий на естественном языке;

— Графическое изображение в виде блок-схемы;

— Запись при помощи псевдокода (алгоритмического языка);

— Запись на языке программирования.

В этом типе задач рассматривается, в основном, словесное описание алгоритмов на естественном языке, а потому никаких специальных знаний для решения задачи не требуется.

Проверка буквенной последовательности на соответствие алгоритму

Пример 1.

Из букв А, И, 3, У, Т, М, К, С формируется слово. Известно, что слово сформировано по следующим правилам:

а) в слове нет подряд идущих двух гласных или двух согласных;

б) первая буква слова в русском алфавите стоит до буквы «К».

Какое из следующих слов удовлетворяет всем перечисленным условиям?

1) АЗИМУТ

2) ТУЗИК

3) МУЗА

4) АИСТ

Решение:

Поочередно проанализируем каждое слово:

1) а) выполняется б) выполняется (буква «А» в русском алфавите стоит до буквы «К»)

2) а) выполняется б) не выполняется (буква «Т» в русском алфавите стоит после буквы «К»)

3) а) выполняется б) не выполняется (буква «М» в русском алфавите стоит после буквы «К»)

4) а) не выполняется (две подряд идущие гласные).

Ответ: 1

Поиск числа, соответствующего алгоритму

Пример 2.

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. К этой записи дописываются справа ещё два разряда по следующему правилу:

а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите такое наименьшее число N, для которого результат работы алгоритма больше 125. В ответе это число запишите в десятичной системе счисления.

Решение:

Алгоритм приписывает в конце числа 10, если в двоичной записи числа было нечетное количество единиц, или 00 если четное. Наименьшее число N найдем, если возьмем наименьший результат, больший 125. Это число 126.

126₁₀ = 1111110₂ может получиться в результате работы алгоритма из числа 11111₂.

11111₂ = 31₁₀.

Ответ: 31

Пример 3.

Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.

1. Складываются первая и вторая, а также вторая и третья цифры исходного числа.

2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходное число: 348. Суммы: 3 + 4 = 7; 4 + 8 = 12. Результат: 127. Укажите наименьшее число, в результате обработки которого автомат выдаст число 1412.

Решение:

Наименьшим число будет тогда, когда на первом месте стоит наименьшая возможная цифра. Поскольку сумма первой и второй цифр равна 14 или 12, то наименьшая первая цифра – это 3 (в сумме с 9 даст 12), тогда вторая цифра – это 9. А третья цифра в сумме со второй дает 14, т.е. равна 14-9 = 5.

Получилось число 395.

Ответ: 395

Пример 4.

Автомат получает на вход четырёхзначное десятичное число. По этому числу строится новое число по следующим правилам.

1. Складываются первая и вторая, а также третья и четвёртая цифры.

2. Полученные два числа записываются друг за другом в порядке возрастания (без разделителей).

Пример. Исходное число: 8754. Суммы: 8+7 = 15; 5+4 = 9. Результат: 915. Определите, сколько из приведённых ниже чисел могут быть получены, как результат работы автомата.

1419 1518 406 911

1) 1 2) 2 3) 3 4)4

Решение:

Проанализируем поочередно все числа на соответствие алгоритму:

1419 – не соответствует, т.к. сумма двух цифр не может дать число 19;

1518 – соответствует, например, на вход могло подаваться число 9699;

406 – не соответствует, т.к. 40 < 6 (не соблюдается порядок возрастания);

911 – соответствует, например, на вход могло подаваться число 3656;

Итого, может быть получено два числа из списка.

Ответ: 2

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задача №6. Анализ алгоритма.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Алгоритмы поиска простых чисел

Время на прочтение
6 мин

Количество просмотров 134K

«Самое большое простое число 2^32582657-1. И я с гордостью утверждаю, что запомнил все его цифры… в двоичной форме».
Карл Померанс

Натуральное число называется простым, если оно имеет только два различных делителя: единицу и само себя. Задача поиска простых чисел не дает покоя математикам уже очень давно. Долгое время прямого практического применения эта проблема не имела, но все изменилось с появлением криптографии с открытым ключом. В этой заметке рассматривается несколько способов поиска простых чисел, как представляющих исключительно академический интерес, так и применяемых сегодня в криптографии.

Решето Эратосфена

Решето Эратосфена — алгоритм, предложенный древнегреческим математиком Эратосфеном. Этот метод позволяет найти все простые числа меньше заданного числа n. Суть метода заключается в следующем. Возьмем набор чисел от 2 до n. Вычеркнем из набора (отсеим) все числа делящиеся на 2, кроме 2. Перейдем к следующему «не отсеянному» числу — 3, снова вычеркиваем все что делится на 3. Переходим к следующему оставшемуся числу — 5 и так далее до тех пор пока мы не дойдем до n. После выполнения вышеописанных действий, в изначальном списке останутся только простые числа.

Алгоритм можно несколько оптимизировать. Так как один из делителей составного числа n обязательно

, алгоритм можно останавливать, после вычеркивания чисел делящихся на

Иллюстрация работы алгоритма из Википедии:

Сложность алгоритма составляет

, при этом, для хранения информации о том, какие числа были вычеркнуты требуется

$O(n)$ памяти.

Существует ряд оптимизаций, позволяющих снизить эти показатели. Прием под названием wheel factorization состоит в том, чтобы включать в изначальный список только числа взаимно простые с несколькими первыми простыми числами (например меньше 30). В теории предлагается брать первые простые примерно до

. Это позволяет снизить сложность алгоритма в

раз. Помимо этого для уменьшения потребляемой памяти используется так называемое сегментирование. Изначальный набор чисел делится на сегменты размером

и для каждого сегмента решето Эратосфена применяется по отдельности. Потребление памяти снижается до

Решето Аткина

Более совершенный алгоритм отсеивания составных чисел был предложен Аткином и Берштайном и получил название Решето Аткина. Этот способ основан на следующих трех свойствах простых чисел.

Свойство 1

Если n — положительное число, не кратное квадрату простого числа и такое, что

. То n — простое, тогда и только тогда, когда число корней уравнения

нечетно.

Свойство 2

Если n — положительное число, не кратное квадрату простого числа и такое, что

. То n — простое, тогда и только тогда, когда число корней уравнения

нечетно.

Свойство 3

Если n — положительное число, не кратное квадрату простого числа и такое, что

. То n — простое, тогда и только тогда, когда число корней уравнения

нечетно.

Доказательства этих свойств приводятся в этой статье.

На начальном этапе алгоритма решето Аткина представляет собой массив A размером n, заполненный нулями. Для определения простых чисел перебираются все

. Для каждой такой пары вычисляется

и значение элементов массива

увеличивается на единицу. В конце работы алгоритма индексы всех элементов массива, которые имеют нечетные значения либо простые числа, либо квадраты простого числа. На последнем шаге алгоритма производится вычеркивание квадратов оставшихся в наборе чисел.

Из описания алгоритма следует, что вычислительная сложность решета Аткина и потребление памяти составляют

$O(n)$ . При использовании wheel factorization и сегментирования оценка сложности алгоритма снижается до

, а потребление памяти до

Числа Мерсенна и тест Люка-Лемера

Конечно при таких показателях сложности, даже оптимизированное решето Аткина невозможно использовать для поиска по-настоящему больших простых чисел. К счастью, существуют быстрые тесты, позволяющие проверить является ли заданное число простым. В отличие от алгоритмов решета, такие тесты не предназначены для поиска всех простых чисел, они лишь способны сказать с некоторой вероятностью, является ли определенное число простым.

Один из таких методов проверки — тест Люка-Лемера. Это детерминированный и безусловный тест простоты. Это означает, что прохождение теста гарантирует простоту числа. К сожалению, тест предназначен только для чисел особого вида

$2^p-1$ , где p — натуральное число. Такие числа называются числами Мерсенна.

Тест Люка-Лемера утверждает, что число Мерсенна

простое тогда и только тогда, когда p — простое и

$M_p$ делит нацело

$(p-1)$ -й член последовательности

$S_k$ задаваемой рекуррентно:

$S_1=4, S_k=S_{k-1}^2-2$ для

$k > 1$ .

Для числа

$M_p$ длиной p бит вычислительная сложность алгоритма составляет

${displaystyle O(p^{3})}$ .

Благодаря простоте и детерминированности теста, самые большие известные простые числа — числа Мерсенна. Самое большое известное простое число на сегодня —

$2^{82,589,933}-1$ , его десятичная запись состоит из 24,862,048 цифр. Полюбоваться на эту красоту можно здесь.

Теорема Ферма и тест Миллера-Рабина

Простых чисел Мерсенна известно не очень много, поэтому для криптографии с открытым ключом необходим другой способ поиска простых чисел. Одним из таким способов является тест простоты Ферма. Он основан на малой теореме Ферма, которая гласит, что если n — простое число, то для любого a, которое не делится на n, выполняется равенство

$a^{n-1}equiv 1{pmod {n}}$ . Доказательство теоремы можно найти на Википедии.

Тест простоты Ферма — вероятностный тест, который заключается в переборе нескольких значений a, если хотя бы для одного из них выполняется неравенство

$a^{n-1} notequiv 1 pmod n$ , то число n — составное. В противном случае, n — вероятно простое. Чем больше значений a использовано в тесте, тем выше вероятность того, что n — простое.

К сожалению, существуют такие составные числа n, для которых сравнение

$a^{n-1}equiv 1{pmod {n}}$ выполняется для всех a взаимно простых с n. Такие числа называются числам Кармайкла. Составные числа, которые успешно проходят тест Ферма, называются псевдопростыми Ферма. Количество псевдопростых Ферма бесконечно, поэтому тест Ферма — не самый надежный способ определения простых чисел.

Тест Миллера-Рабина

Более надежных результатов можно добиться комбинируя малую теорему Ферма и тот факт, что для простого числа p не существует других корней уравнения

, кроме 1 и -1. Тест Миллера-Рабина перебирает несколько значений a и проверяет выполнение следующих условий.

Пусть p — простое число и

, тогда для любого a справедливо хотя бы одно из условий:

$a^{d}equiv pm1{pmod {p}}$
Существует целое число r < s такое, что $a^{2^{r}d}equiv -1{pmod {p}}$

По теореме Ферма

$a^{p-1}equiv1pmod p$ , а так как

из свойства о корнях уравнения

следует что если мы найдем такое a, для которого одно из условий не выполняется, значит p — составное число. Если одно из условий выполняется, число a называют свидетелем простоты числа n по Миллеру, а само число n — вероятно простым.

Чем больше свидетелей простоты найдено, тем выше вероятность того, что n — простое. Согласно теореме Рабина вероятность того, что случайно выбранное число a окажется свидетелем простоты составного числа составляет приблизительно

$1/4$ .

Следовательно, если проверить k случайных чисел a, то вероятность принять составное число за простое

Сложность работы алгоритма

, где k — количество проверок.

Благодаря быстроте и высокой точности тест Миллера-Рабина широко используется при поиске простых чисел. Многие современные криптографические библиотеки при проверке больших чисел на простоту используют только этот тест и, как показал Мартин Альбрехт в своей работе , этого не всегда оказывается достаточно.

Он смог сгенерировать такие составные числа, которые успершно прошли тест на простоту в библиотеках OpenSSL, CryptLib, JavaScript Big Number и многих других.

Тест Люка и Тест Baillie–PSW

Чтобы избежать уязвимости, связанные с ситуациями, когда сгенерированное злоумышленником составное число, выдается за простое, Мартин Альбрехт предлагает использовать тест Baillie–PSW. Несмотря на то, что тест Baillie–PSW является вероятностным, на сегодняшний день не найдено ни одно составное число, которое успешно проходит этот тест. За нахождение подобного числа в 1980 году авторы алгоритма пообещали вознаграждение в размере $30. Приз пока так и не был востребован.

Ряд исследователей проверили все числа до

$2^{64}$ и не обнаружили ни одного составного числа, прошедшего тест Baillie–PSW. Поэтому, для чисел меньше

$2^{64}$ тест считается детерминированным.

Суть теста сводится к последовательной проверке числа на простоу двумя различными методами. Один из этих методов уже описанный выше тест Миллера-Рабина. Второй — тест Люка на сильную псевдопростоту.

Тест Люка на сильную псевдопростоту

Последовательности Люка — пары рекуррентных последовательностей

${U_{n}(P,Q)}, {V_{n}(P,Q)}$ , описываемые выражениями:

${displaystyle U_{0}(P,Q)=0,quad U_{1}(P,Q)=1,quad U_{n+2}(P,Q)=Pcdot U_{n+1}(P,Q)-Qcdot U_{n}(P,Q),,ngeq 0}$

${displaystyle V_{0}(P,Q)=2,quad V_{1}(P,Q)=P,quad V_{n+2}(P,Q)=Pcdot V_{n+1}(P,Q)-Qcdot V_{n}(P,Q),,ngeq 0}$

Пусть

— последовательности Люка, где целые числа P и Q удовлетворяют условию

${displaystyle D=P^{2}-4Qneq 0}$

Вычислим символ Якоби:

$left({frac {D}{p}}right)=varepsilon$ .

Найдем такие r, s для которых выполняется равенство

Для простого числа n выполняется одно из следующих условий:

n делит
n делит $V_{2^js}$ для некоторого j < r

В противном случае n — составное.

Вероятность того, что составное число n успешно пройдет тест Люка для заданной пары параметров P, Q не превышает 4/15. Следовательно, после применения теста k раз, эта вероятность составляет

Тесты Миллера-Рабина и Люка производят не пересекающиеся множества псевдопростых чисел, соответственно если число p прошло оба теста, оно простое. Именно на этом свойстве основывается тест Baillie–PSW.

Заключение

В зависимости от поставленной задачи, могут использоваться различные методы поиска простых чисел. К примеру, при поиске больших простых чисел Мерсенна, сперва, при помощи решета Эратосфена или Аткина определяется список простых чисел до некоторой границы, предположим, до

$10^8$ . Затем для каждого числа p из списка, с помощью теста Люка-Лемера, на простоту проверяется

Чтобы сгенерировать большое простое число в криптографических целях, выбирается случайное число a и проверяется тестом Миллера-Рабина или более надежным Baillie–PSW. Согласно теореме о распределении простых чисел, у случайно выбранного числа от 1 до n шанс оказаться простым примерно равен

${frac {1}{ln n}}$ . Следовательно, чтобы найти простое число размером 1024 бита, достаточно перебрать около тысячи вариантов.

P.S. Исходники

Реализацию всех описанных алгоритмов на Go можно посмотреть на GitHub.

Источник

Алгоритмы вычисления наименьшего общего кратного (НОК) и наибольшего общего делителя (НОД) описаны в одной теме, т.к. для эффективного вычисления НОК нужно вычислить НОД.

1 Алгоритм расчета наибольшего общего делителя

Даны два целых числа A и B, их наибольший общий делитель — такое число C, что на него делится без остатка и A, и B

В школе нас учили искать НОД разложением на простые множители, однако такая задача крайне тяжело решается на компьютере, зато мы можем заставить его перебрать все числа от min(a, b) до единицы и проверить условие делимости, однако и это не самый эффективный способ.

Люди, интересующиеся алгоритмами, сразу вспомнять алгоритм Евклида, однако, на мой взгляд, нет смысла зубрить алгоритмы — наиболее ценно их понимание и способность разработать нечто аналогичное. Для этого я предлагаю пытаться визуализировать задачу.

Целое число — это количество чего-либо неделимого. На следующей картинке два числа показаны в виде прямоугольников, под значением числа можно понимать количество «блоков в прямоугольнике». Показано схематично (я не пытался рисовать точно).

В физической интерпретации — замените блоки на кирпичи. НОД — размер кузова грузовика, такой что им можно перевезти все кирпичи, наполняя каждый раз кузов доверху.

Эффективный алгоритм расчета НОД строится на следующих наблюдениях (постарайтесь их «почувствовать»):

если A делится на B без остатка — то НОД(A, B) = B;
любое число, которое делит оба числа A и B, делит также и A-B, поэтому
НОД(A, B) <= НОД (A — B, B);. То есть уменьшение числа A на значение B не повлияет на результат вычисления НОД;
мы можем воспользоваться предыдущим пунктом несколько (t) раз — если A = B*t + r для целых чисел t и r — то НОД(A, B) = НОД(r, B).

Из второго пункта следует идея следующего алгоритма поиска НОД: Отнимать от большего меньшее, пока числа не станут равны. Полученное число и является наибольшим общим делителем. Такой алгоритм будет работать значительно быстрее чем полный перебор, но и его можно улучшить — посмотрим визуализацию (исходное состояние показано выше):

В какой-то момент числа окажутся равны и мы получим результат. Этот момент обязательно настанет — в крайнем случае когда оба числа станут равны единице (потому что это ей кратны любые целые числа).

Из последней иллюстрации видно, что многократное вычитание можно заменить на получение остатка от деления (об этом же говорит третье «наблюдение»). Тогда алгоритм можно записать на псевдокоде следующим образом:

наибольший_общий_делитель(a, b) {
  если a делится на b без остатка то - верни b;
  если b делится на a без остатка то - верни a;
  
  если a > b - то верни наибольший_общий_делитель(a mod b, b);
  иначе верни наибольший_общий_делитель(a, b mod a);
}

Тут mod — операция получения остатка от деления.

2 Алгоритм расчета наименьшего общего кратного

Наименьшее общее кратное двух целых чисел A и B есть наименьшее натуральное число, которое делится на A и B без остатка.

Чтобы лучше понять о чем речь — предлагаю такую геометрическую интерпретацию: значения A и B задают длины отрезков. НОК — это длина другого отрезка, который можно составить как из целого количества отрезков A, так и отрезков B:

Для любых чисел мы можем найти общее кратное C = A*B, однако, оно не всегда будет наименьшим. Примитивный алгоритм вычисления НОК мог бы заключаться в переборе всех чисел от max(A, B) до A*B. Однако, это не самое эффективное решение. На самом деле, если длина отрезка A = 4, а B = 3, то перебирать надо все отрезки, кратные 4, т.е. max(A, B).

Обратите снимание, что если A и B взаимнопростые (иными словами НОД(A, B) = 1) — то НОК(A, B) = A*B. Если же у этих чисел есть делители d0, d1, ..., dn, то их общими кратными будут числа: (A*B)/d0, (A*B)/d1, … (A*B)/dn. Значит, чтобы найти наименьшее общее кратное, нужно найти наибольший из делителей:

наименьшее_общее_кратное(a, b) {
  верни (A*B)/наибольший_общий_делитель(a, b);
}

Источник

Алгоритмы над целыми числами. Проверка на простоту, разложение на множители. Наибольший общий
делитель и наименьшее общее кратное: алгоритм Евклида. Признак Паскаля. Расширенный алгоритм Евклида

Алгоритмы над целыми числами применяются при решении множества задач: для сокращения дробей, разложения на
множители.

Алгоритм Евклида для нахождения НОД

Свой алгоритм Евклид (древнегреческий математик, живший примерно в 300 г. до
н.э.) придумал для решения задачи о соизмеримости двух отрезков. Общей мерой
(единицей измерения) отрезков с длинами $L_1$ и $L_2$ является отрезок
с наибольшей возможной длиной $L$, который можно уложить без остатка как в
первом отрезке, так и во втором. Например, для отрезков 10 и 15 такой общей мерой будет отрезок с длиной 5 (им
можно
пользоваться как единицей измерения для обоих отрезков). При этом 5 будет наибольшим общим
делителем
10 и 15.

В общем случае, алгоритм Евклида — это метод нахождения
наибольшего общего делителя (НОД) нескольких чисел.

Целое число $a$ делится на целое число $b$ ($b ne 0$), если
существует целое число $k$, такое что $a=kb$. В таком случае $b$ называют делителем
числа $a$; число $a$ называют кратным числа $b$.

Если $a$ и $b$ делятся на $c$,
то их сумма $a+b$ и их разность $a-b$ делятся на $c$.

Если $a$ делится на $c$, а $b$ делится на $d$, то их
произведение $a*b$ делится на $c*d$.

$a$ и $b$ – положительные целые числа, $c$ — является общим делителем
чисел $a$ и $b$, если $a$ делится на $c$ и $b$ делится на $c$.

Среди общих делителей чисел $a$ и $b$ (не равных одновременно нулю) есть наибольший общий
делитель
(по-английски Greatest common divisor — GCD), обозначаемый НОД($a,b$) или $GCD(a,b)$.

Если $a$ делится на $b$, то $GCD(a,b) = b$. Например: $GCD(50,10)=10$.

$GCD(a,a)=a$. Например: $GCD(32,32)=32$.

Если $a gt b$, то $GCD(a,b)=GCD(a-b,b)$.

Если $GCD(a,b)=1$, то числа $a$ и $b$ — взаимно простые.

Алгоритм Евклида с вычитаниями

Последовательно вычитая из большего числа меньшее до тех пор, пока они не станут равными, придем к НОД этих
чисел.

Пример: Найти НОД двух чисел 264 и 192.

Решение:
НОД(264, 192) = НОД(72, 192) = НОД(72, 120) = НОД(72, 48) =
НОД(24, 48) = НОД(24, 24) = 24

Задача. Найти НОД двух натуральных чисел $a$ и $b$.

Используем для решения задачи алгоритм Евклида с вычитаниями.

Реализация на Pascal:

function GCD( a,b:integer ):integer; { определение НОД двух чисел }
begin
  while a <> b do
    if a > b then a:=a-b else b:=b-a;
  GCD := b;
end;

begin { Пример использования }
  writeln(GCD(10,15)); { Выведет 5 }
end.

Реализация на С/C++:

#include <stdio.h>

int GCD( int a, int b ){ // определение НОД двух чисел
  while(a != b)
    if (a > b) a-=b; else b-=a;
  return b;
}

int main(){ // Пример использования
  printf("%d",GCD(10,15)); // Выведет 5
  return 0;
}

Алгоритм Евклида с делением

Если применить алгоритм Евклида с вычитаниями к паре чисел $(1,10^{20})$, то будет выполнено около $10^{20}$
вычитаний, это слишком долго!

Можно за один раз вычитать из $a$ $b$ столько раз, сколько можно. Алгоритм Евклида с делением основан на том, что
если $a=bq+r$, где $r$ — остаток от деления $a$ на $b$ ($0 le r < b$), то $GCD(a,b) = GCD(r,b)$.

Последовательно
применяя это утверждение можно понять, что НОД двух чисел – это последний не
равный нулю остаток от деления большего числа на меньшее.

Пример: найти НОД двух чисел 6069 и 663.

Решение:

6069 = 663*9+102 НОД(6069, 663) = НОД
(663, 102)
663 = 102*6+51 НОД(663, 102) = НОД
(102, 51)
102 = 51*2+0 НОД(102, 51) = 51
(согласно утверждению 3)

Следовательно, 51 = НОД(102, 51) = НОД(663, 102) = НОД(6069, 663)

Демонстрационная Flash-программа показывает вычисление НОД любых 2 чисел:

Рассмотрим алгоритм и процедуру-функцию к решению задачи 1.1, используя для нахождения НОД двух
чисел алгоритм Евклида с делением.

Алгоритм:

Функция Вычисление_НОД(целое a, целое b)
  Пока (b <> 0)
    r := a по модулю b  (остаток от деления a на b), r - временная переменная (буфер)
    a := b
    b := r
  конец цикла
  Вывод результата - a
Конец функции

Реализация на Pascal:

function GCD( a,b:int64 ):int64; { Функция для вычисления НОД при помощи деления }
begin
  if b = 0 then { Если b = 0 }
    GCD := a {  следовательно a=НОД }
  else { Пока b <> 0 }
    GCD := GCD(b,a mod b); { Вычисляем остаток от деления a на b, а заменяем на b, b заменяем на r }
end;

begin
  writeln(GCD(264, 192)); { Выведет: 24 }
end.

Реализация на Python:

def GCD(a,b): # Функция для вычисления НОД при помощи деления
  return a if b == 0 else GCD(b,a%b) # Вычисляем остаток от деления a на b, а заменяем на b, b заменяем на r=a mod b
  # НОД = a если b = 0 иначе НОД=НОД(b,r), r - остаток от деления a на b

print GCD(264, 192) # Выведет: 24

Вычислить НОД трех натуральных чисел $a$, $b$ и $c$ можно так:

$GCD(a,b,c)=GCD(GCD(a,b),c)$

В общем случае, справедлива следующая рекуррентная формула:

$GCD(a_1,a_2,…,a_n) = GCD(GCD(a_1,a_2,…,a_{n-1}), a_n)$.

Ниже приведена функция нахождения НОД для массива натуральных чисел $a(1..n)$ с использованием цикла.

function GCD( ... )...
    ....

function GCDM( a : array of int64 ):int64;
var d : int64; i : integer;
begin
  d := a[0];
  for i:= 1 to length(a)-1 do
    d := GCD(d, a[i]);
  GCDM := d;
end;

begin { Пример вызова }
  writeln(GCDM([15,10,25]));
end.

Диофантовы уравнения, расширенный алгоритм Евклида

С помощью алгоритма Евклида можно доказать одно важное свойство НОД.

Если $GCD(a,b)=d$, то можно найти такие целые числа $x$ и $y$, что $ax+by=d$.

Важным частным случаем этого утверждения является:

Если числа $a$ и $b$ взаимно просты ($GCD(a,b) = 1$), то найдутся такие целые числа $x$ и $y$,
что $ax + by = 1$.

Решение в целых числах уравнения $ax + by = c$ для любого
целого $c$ получается из решения предыдущего уравнения умножением на $c$.

Уравнение вида $ax+by=c$, разрешимое в целых числах, называется диофантовым уравнением (по имени
древнегреческого математика Диофанта).

Существует несколько типов задач, которые сводятся к решению диофантовых уравнений. К таким, например, относятся:

задачи по размену суммы денег купюрами определенного достоинства;
задачи на переливание.

Критерий разрешимости диофантова уравнения:

Чтобы уравнение $ax+by=c$ имело решение в целых числах $(x,y)$, необходимо и достаточно, чтобы $c$
делилось на $d=GCD(a,b)$.

Если это условие выполнено и $(x_0,y_0)$ – одно из решений этого уравнения, то все целочисленные
решения выглядят так:

$x = x_0 + {b_1}{t}$

$y = y_0 — {a_1}{t}$, где $t$ — целое число;

$a_1=a/d$, $b_1=b/d$.

Способ решения уравнения $ax + by = d$ основан на алгоритме Евклида: определяя $GCD(a,b)$
методом последовательного деления, на каждом шаге выражаем остаток от деления через исходные числа $a$, $b$ до тех
пор, пока остаток не станет нулем. Следовательно, на предыдущем шаге остаток равен $GCD(a,b)$, и мы одновременно
получаем одно из решений уравнения.

$a = {b}{q_1}+{r_1}$; $r_1=a-{b}{q_1} = {a}{x_1}+{b}{y_1}$

$b = {r_1}{q_2}+{r_2}$; ${r_2}=b-{r_1}{q_2}=a(-{x_1}{q_2})+b(1-{y_1}{q_2}) = a{x_2}+ b{y_2}$;

$r_1={r_2}{q_3}+{r_3}$; ${r_3}={r_1}-{r_2}{q_3}=a({x_1}-{x_2}{q_3})+b(y_1-{y_2}{q_3})= a{x_3}+b{y_3}$

…

$r_{n-2}=r_{n-1}{q_n}+{r_n}$; ${r_n}=a(x_{n-2}-{x_{n-1}}{q_n})+b(y_{n-2}-y_{n-1}{q_n})= a{x_n}+b{y_n}$

$r_{n-1}$ делится на $r_n$ без остатка

Следовательно, $r_n=GCD(a,b)$, а $(x_n,y_n)$ – искомое решение уравнения $ax + by = d$;

Рекуррентные формулы определения решения, как видно из выкладок, имеют следующий вид:
(для запоминания: начальная “1” — для первого параметра в функции НОД)

$x_{-1}=1$; $y_{-1}=0$; ($a = {a}cdot{1} + {b}cdot{0}$ — представление числа $a$)

$x_0=0$; $y_0=1$; ($b = {a}cdot{0} + {b}cdot{1}$ — представление числа $b$)

…..

$x_n=x_{n-2}-x_{n-1}{q_n}$; $y_n=y_{n-2}-y_{n-1}{q_n}$; $n ge 1$

Замечание.
Достаточно рассмотреть одно рекуррентное соотношение, например, для вычисления
$x$, так как можно использовать исходное уравнение для определения $y=(d–ax)/b$.

Пример 1.3:
Найти целочисленное решение уравнения $258x + 114y = 6$

Рис.1.1

Решение:

258 = 114 · 2
+ 30; $q_1 = 2$;

114 = 30 · 3
+ 24; $q_2 = 3$;

30 = 24 · 1
+ 6; $q_3 = 1$;

24 = 6 · 4; НОД(258,114) = 6

x₃= 4; y₃= -9 (таблица вычислений на рис.1.1);

Проверка: ${258}*{4} – {114}*{9} = 6$

Алгоритм для решения в целых числах уравнения $ax+by=c$.

1. Найдем по алгоритму Евклида с делениями $d=GCD(a,b)$.
Одновременно определяем решение уравнения $ax_0+by_0=d$ по вышеизложенным рекуррентным формулам.

2. Проверим, делится ли число $c$ на $GCD(a,b)$. Если нет, то решений в целых числах не существует.

3. Если делится, то делим на $d$ коэффициенты в правой и левой части уравнения $ax+by=c$.
Получим эквивалентное уравнение ${a_1}{x}+{b_1}{y}={c_1}$,
где $a_1=a/d$, $b_1=b/d$, $c_1=c/d$.

4. Найденная пара чисел $(x_0,y_0)$ – частное решение уравнения ${a_1}x+{b_1}y=1$, общее
решение этого уравнения находится по формулам:
$x = x_0+{b_1}t$ и
$у = y_0-{a_1}t$,
где $x_h={b_1}t$,
$y_h=-{a_1}t$ ($t$ – любое целое число) являются общим решением однородного
уравнения ${a_1}x+{b_1}y=0$.

5. Частное решение исходного уравнения $ax+by=c$ получается
умножением пары $(x_0,y_0)$ на $c_1$. Общее решение уравнения $ax+by=c$
получается сложением частного решения и общего решения однородного уравнения
$ax+by=0$ (или эквивалентного ${a_1}x+{b_1}y=0$).

Достоинство данного алгоритма в том, что решение уравнения определяется одновременно с нахождением
$GCD(a,b)$ без дополнительных массивов. Алгоритм справедлив также при $a lt b$.

Целочисленное решение уравнения $ax_0+by_0=GCD(a,b)$

function dioph2( a,b:int64; var x0,y0:int64 ):int64;
var x1,y1,q,r,x,y:int64;
begin
  x0 := 1; y0 := 0;
  x1 := 0; y1 := 1;
  while b <> 0 do begin
    q := a div b; { Частное }
    r := a mod b; { Остаток }
    a := b;
    b := r;
    x := x0 - x1 * q; y := y0 - y1 * q;
    x0 := x1; y0 := y1;
    x1 := x; y1 := y;
  end;
  dioph2 := a; { НОД(a,b) }
end;

var a,b,x0,y0,GCD : int64;
  test : integer;
begin
  for test := 1 to 1000000 do begin { Прогоняем тесты }
    a := random(2000)+1; { Генерируем 2 случайных числа }
    b := random(2000)+1;
    GCD := dioph2(a,b,x0,y0);
    assert( a*x0+b*y0 = GCD ); { Проверка что ответ верный! }
  end;
end.

Решение общего линейного диофантова уравнения.

Диофантово уравнение общего вида:
${a_1}{x_1} + {a_2} {x_2} + … + {a_n} {x_n} = c$,
где $a_1, a_2, …, a_n, c$ — целые числа, а $GCD(a_1,…,a_n)$ — наибольший общий делитель чисел $a_i$, где
$1 le i le n$ и не все числа $a_i$ равны нулю.

С помощью алгоритма Евклида можно доказать, что диофантово
уравнение ${a_1}{x_1}+{a_2}{x_2}+…+{a_n}{x_n} = GCD(a_1,a_2,…,a_n)$
всегда разрешимо, следовательно, критерий разрешимости:
для существования решения в целых числах этого уравнения необходимо и достаточно,
чтобы число $с$ делилось на $GCD(a_1,a_2,…,a_n)$.

Рассмотрим алгоритм решения на частном примере.

Пример: найти решение уравнения $18x+42y+10z=14$ в целых числах.

Решение:

Для принятых выше обозначений $a_1=18$, $a_2=42$, $a_3=10$, $c=14$.

Легко угадывается решение: $(x = 0; y = 2; z = -7)$.

Если любому целому числу, представимому левой частью уравнения, сопоставить конкретный набор $(x,y,z)$, то действия с
такими числами
(сложение, вычитание, умножение на любое целое число) эквивалентны аналогичным
действиям с соответствующими наборами (поэлементно). В частности, для
коэффициентов уравнения числу 18 можно сопоставить набор $(1,0,0)$, т.к. 18 · 1 +
42 · 0 +10
· 0 = 18, для
числа 42 — набор (0,1,0),
а для числа 10 — набор (0,0,1).

Найдем число $d=GCD(18,42,10)$ и целочисленное решение уравнения $18x+42y+10z=d$

Используем свойства:

$GCD(a_1,a_2,a_3)=GCD(GCD(a_1,a_2),a_3))$
для последовательного определения НОД чисел;

$GCD(a,b)=GCD(b,r)$, где $r$ — остаток
целочисленного деления $a$ на $b$, причем $0 ≤ r < |b |$.

Представим обобщенный алгоритм Евклида для решения
диофантова уравнения в табличном виде (рис.1.2).

Знак ↑ пределяет выражение, как в ячейке выше и для
наглядности таблицы используется в пассивных столбцах, не участвующих в
текущих вычислениях. В каждой строке подчеркивается текущий найденный набор.

$a_1$	набор	$a_2$	набор	$a_3$	набор	примечание
18	(1,0,0)	42	(0,1,0)	10	(0,0,1)	$GCD(a,b)=GCD(b,r)$ $r=a-bq$; $0 le r < \|b\|$
6	(-2,1,0)	18	(1,0,0)	↑	↑	6 = 42 – 18 · 2 (-2,1,0) = (0,1,0) — (1,0,0) · 2
6	(-2,1,0)	0	(7,-3,0)	↑	↑	0 = 18 – 6 · 3 (7,-3,0) = (1,0,0) — (-2,1,0) · 3
4	(2,-1,1)	↑	↑	6	(-2,1,0)	4 = 10 – 6 · 1 (2,-1,1) = (0,0,1) — (-2,1,0)
2	(-4,2,-1)	↑	↑	4	(2,-1,1)	2 = 6 – 4 · 1 (-4,2,-1) = (-2,1,0) — (2,-1,1)
2	(-4,2,- 1)	↑	↑	0	(10,- 5,3)	0 = 4 – 2 · 2 (10,-5,3) = (2,-1,1) — (-4,2,-1) · 2
2	(-4,2,-1)	0	(7,- 3,0)	0	(10,-5,3)	итоговая строка результатов

Последняя строка таблицы определяет результаты решения диофантова
уравнения.

Ненулевое
значение в первом столбце определяет $GCD(18,42,10)=2$. Соответствующий
набор $(x = -4, y = 2, z = -1)$ определяет частное решение уравнения $18x + 42y +
10z=GCD(18, 42,10)$. Правая часть исходного уравнения делится на GCD
коэффициентов, следовательно, частное решение исходного уравнения существует и
определяется умножением на целочисленный коэффициент $c/d=7$, т.е. набор $(x=-28, y=14, z=-7)$ является частным
решение исходного уравнения. Наборы при нулевых результирующих коэффициентах
определяют независимые решения однородного уравнения $18x+42y+10z=0$. Независимость
наборов означает, что нельзя получить соответствующие компоненты одного набора
из другого умножением на какое-либо целое число (это следует из сравнения
третьих компонент в наборах). Очевидно, что решение однородного уравнения можно
умножать на любую целочисленную константу, получая вновь решение.
Следовательно, общее решение уравнения можно записать следующим образом.

$begin{cases}
x = -28 + 7 t_1 + 10 t_2 \
y = 14 — 3 t_1 — 5 t_2 \
z = -7 + 0 t_1 + 3 t_2 end{cases}$
где $t_1$, $t_2$ — любые целые числа

Легко проверить, что для любых целых $t_1$ и $t_2$ тройки $(x,y,z)$
являются решениями уравнения $18x+42y+10z=14$.

Например, для $t_1=4$ и $t_2=0$ имеем $(x=0; y=2; z=-7)$,
$18 cdot 0 + 42 cdot 2 — 10 cdot 7=14$.

Алгоритм решения диофантова уравнения

Ниже приводится алгоритм решения уравнения ${a_1}{x_1}+{a_2}{x_2}+…+{a_n}{x_n}=GCD(a_1,a_2,…,a_n)$

Функция GCD(n, a(), x())

Задать набор N а_1{1,0,…,0}

Цикл i от 2 до n

Задать набор N а$_i $ {0,…0,1$_i $,0,…,0}

Пока a(i ) ≠ 0

q = a(1)a(i)

t = a(i); Nt
=_ Na$_i $_ { набор
временный }

a(i) = a(1) — q*a(i); Na$_i $_
= Na_1 — q*Na$_i $ { покомпонентно}

a (1) = t
Na _1 = Nt

Конец пока

{набор Na$_i $
содержит решение однородного уравнения}

Конец цикла i

GCD = a(1)
{НОД коэффициентов}

x () = Na _1

{набор Na _1 содержит
частное решение уравнения}

конец функции

Реализация на Pascal:

type
  TVector = array [1..100] of Integer;

var
  n, i, a1, ai, tmp: Integer;
  a, x1, xi: TVector;

procedure SetUnitVector(var v: TVector; index: Integer);
begin
  FillChar(v, SizeOf(TVector), 0);
  v[index] := 1;
end;

procedure CalculateVector(var v1, v2: TVector; q: Integer);
var i, tmp: Integer;
begin
  for i := 1 to n do begin
    tmp := v2[i];
    v2[i] := v1[i] - q * v2[i];
    v1[i] := tmp;
  end;
end;

begin
  { Ввод исходных данных }
  Write('Введите количество компонент n: '); ReadLn(n);
  Write('Введите компоненты Ai через пробел: ');
  for i := 1 to n do Read(a[i]);
  ReadLn;
  { Вычисления }
  SetUnitVector(x1, 1);
  a1 := a[1];
  for i := 2 to n do begin
    SetUnitVector(xi, i);
    ai := a[i];
    while ai <> 0 do begin
      CalculateVector(x1, xi, a1 div ai);
      tmp := ai;
      ai := a1 mod ai;
      a1 := tmp;
    end;
  end;
  { Вывод ответа }
  WriteLn('НОД = ', a1);
  for i := 1 to n do Write(x1[i], ' ');
  WriteLn;
end.

Задача:
Разменять 14 рублей “трешками” и “пятерками”.

Задачи переливания

Задача. В ведре 12 литров молока. Как разлить молоко на две
равные части, используя только бидоны 5 и 7 литров?

Покажем, как
эта задача сводится к решению в целых числах уравнения
$7x+5y=6$.

Следующий алгоритм
переливания (рисунок 4) всегда приводит к решению подобных задач:

1) В
первый сосуд, если он пуст, наливаем (+1 для x)

2) Из
первого сосуда доливаем второй (если возможно)

3) Из второго сосуда, если он полон, выливаем (-1для
y)

Последующий
пункт алгоритма выполняется, если невозможно выполнить предыдущий пункт.
Каждое действие по отдельному пункту алгоритма составляет шаг переливания с
дальнейшим циклическим возвратом к анализу п.1.

Согласно
диофантовому уравнению, процесс заканчиваем, когда суммарный объем
жидкости в обоих сосудах станет равным искомому объему.

Как видно из рисунка 4,
достижение нужного объема может произойти раньше (в некоторых случаях, даже
значительно раньше).

Рис.1.4

Подсчитывая
количество «наливаний» ($x$ со знаком
«+») для одного сосуда и «выливаний» ($y$
со знаком «-«) для другого, находим решение соответствующего
диофантова уравнения.

7 * 3 + 5
*(-3) = 6; $x$ = 3, $y$ = -3

Решений у такого уравнения бесконечно много. Если выберем сосуд 5 л в качестве
первого – получим решение:

5 * 4 + 7 * (-2) = 6.

Количество шагов переливаний может зависеть от того, какой вместительности сосуд считать
за “первым” (например, если в задаче заменить 5-литровый сосуд 3-литровым).

Для закрепления алгоритма при решении тренировочных задач 1.3 и 1.4 воспользуйтесь
программой «Переливай-ка».

Задача 1.3: Разлить поровну 16 ведер кваса, находящегося в 16-ведерном
бочонке, имея два пустых бочонка по 11 и 6 ведер.

Задача 1.4: Имеются три бочонка вместимостью 6, 3 и 7 ведер. В первом и
третьем содержится 4 и 6 ведер кваса соответственно. Требуется разделить квас
поровну между первым и третьим бочонком (по 5 вёдер).

Простые числа

Натуральное
число называется простым, если оно не имеет делителей кроме единицы и
самого себя.

Основная
теорема арифметики. Любое целое положительное число разлагается на простые
множители и притом единственным образом (докажите самостоятельно).

Задача 1.5.
Определить простые делители натурального числа $n$.

Basic:

INPUT n
PRINT n; "=";
WHILE (n mod 2 = 0)
  n = n  2
  IF n <> 1 THEN
    PRINT " 2 * ";
  ELSE
    PRINT " 2 ": END
  END IF
WEND
i = 3
WHILE i <= n
  IF n mod i = 0 THEN
    PRINT i;
    n = n  i
    IF n<>1 THEN PRINT "*";
  ELSE
    i = i + 2
  END IF
WEND

Алгоритм:

Ввести n
Вывести n " ="
Пока n делится на 2:
  n разделить на 2
  Если n ≠ 1 то
    Вывести " 2 * "
  иначе
    Вывести " 2"
    Закончить программу
i = 3
Пока i ≤ n
  Если n делится на i то
    Вывести i
    n разделить на i
    Если n ≠ 1 то вывести "*"
  иначе
    i = i + 2

Delphi:

{$APPTYPE CONSOLE}
var
  N : int64;
  i : longint;
begin
  Reset(Input,'factor.in');
  Rewrite(Output,'factor.out');
  Read(N);
  Write(N,' =');
  for i:=2 to trunc(sqrt(N)) do { Перебираем все числа до корня из N }
    while N mod i = 0 do begin { Пока N делится на i }
      write(' ',i); { Выводим множитель i }
      N := N div i; { Делим на i }
      if N <> 1 then write(' *'); { Если ещё будут множители, то выводим знак умножения }
    end;
  if N<>1 then write(' ',N); { Оставшийся множитель }
end.

Решето Эратосфена для нахождения простых чисел

Задача.
Найти и вывести на экран простые числа, не превосходящие заданного числа N.

Древнегреческий
математик Эратосфен (250 – 194 годы до н.э.) записывал все подряд числа на
папирусе, а затем выкалывал составные числа по следующему правилу: сначала
числа, делящиеся на 2, затем на 3, на 5 и т.д., то есть просеивал их как сквозь
решето. В результате чего на папирусе оставались лишь простые числа. Этот
алгоритм нахождения простых чисел носит название решета Эратосфена.

Basic:

INPUT "Введите N "; N
DIM a(1 TO N)
FOR i = 2 TO N
  IF a(i) = 0 THEN
    h = i
    FOR j = i + h TO N STEP h
      a(j) = 1
    NEXT j
  END IF
NEXT i
FOR i = 2 TO N
  IF a(i) = 0 THEN PRINT i;
NEXT i

Алгоритм:

Ввести $N$
Массив ${a_i}$, $i=1,…,N$ (элементы массива нулевые)
Цикл $i = 2 .. n$
Если $a_i = 0$ то
Шаг=i

Для j = j + h до n с шагом h

a(j) = 1

конец цикла

конец если

конец цикла

Для от i = 2 до n

Если a(i) = 0 то вывести
i;

конец цикла

Основная идея этой реализации алгоритма заключается в том, что индексы элементов массива представляют собой числа, а
элементы массива – признаки того, являются ли эти числа простыми (значение 0) или составными (значение 1).

{ Решето Эратосфена }
var
  { Индексы элементов массива simple - числа, а элементы массива simple – признаки того, являются ли эти числа простыми }
  simple : array [2..30000000] of Boolean; { Является ли число простым? }
  N,i,j : Integer;
begin
  { Ввод исходных данных: число N до которого искать простые числа }
  Write('Введите N: '); ReadLn(N);
  { Сначала "выписываем" все числа от 2 до N }
  for i := 2 to N do
    simple[i] := true;
  { Проходим в цикле все числа от 2 до N и выводим из них только простые }
  for i := 2 to N do
    if simple[i] then begin
      { Вывод результата - очередного простого числа }
      Write(i,' ');
      { Для простого числа i вычёркиваем все кратные ему }
      j := 2*i; { Первое кратное - удвоенное число i }
      while j <= N do begin { Если оно попадает в допустимый диапазон }
        simple[j] := false; { то мы его вычёркиваем }
        j := j + i; { и переходим к следующему кратному i числу }
      end;
    end;
end.

Цепные дроби

Цепная дробь (или непрерывная дробь) — это математическое выражение вида:

$[a_0; a_1, a_2, a_3,cdots] = a_0+frac{1}{a_1+frac{1}{a_2+frac{1}{a_3+ldots}}}$

где a0 где a0 есть целое число и все остальные an
натуральные числа (то есть неотрицательные целые). Любое вещественное число можно представить в виде цепной дроби
(конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально.
Число представляется периодической цепной дробью тогда и только тогда, когда оно является квадратичной
иррациональностью.

Источник