Как найти алгоритм шифрования

Классический криптоанализ

На протяжении многих веков люди придумывали хитроумные способы сокрытия информации — шифры, в то время как другие люди придумывали еще более хитроумные способы вскрытия информации — методы взлома.

В этом топике я хочу кратко пройтись по наиболее известным классическим методам шифрования и описать технику взлома каждого из них.

Шифр Цезаря

Самый легкий и один из самых известных классических шифров — шифр Цезаря отлично подойдет на роль аперитива.
Шифр Цезаря относится к группе так называемых одноалфавитных шифров подстановки. При использовании шифров этой группы «каждый символ открытого текста заменяется на некоторый, фиксированный при данном ключе символ того же алфавита» wiki.

Способы выбора ключей могут быть различны. В шифре Цезаря ключом служит произвольное число k, выбранное в интервале от 1 до 25. Каждая буква открытого текста заменяется буквой, стоящей на k знаков дальше нее в алфавите. К примеру, пусть ключом будет число 3. Тогда буква A английского алфавита будет заменена буквой D, буква B — буквой E и так далее.

Для наглядности зашифруем слово HABRAHABR шифром Цезаря с ключом k=7. Построим таблицу подстановок:

a

b

c

d

e

f

g

h

i

j

k

l

m

n

o

p

q

r

s

t

u

v

w

x

y

z

h

i

j

k

l

m

n

o

p

q

r

s

t

u

v

w

x

y

z

a

b

c

d

e

f

g

И заменив каждую букву в тексте получим: C(‘HABRAHABR’, 7) = ‘OHIYHOHIY’.

При расшифровке каждая буква заменяется буквой, стоящей в алфавите на k знаков раньше: D(‘OHIYHOHIY’, 7) = ‘HABRAHABR’.

Криптоанализ шифра Цезаря

Малое пространство ключей (всего 25 вариантов) делает брут-форс самым эффективным и простым вариантом атаки.
Для вскрытия необходимо каждую букву шифртекста заменить буквой, стоящей на один знак левее в алфавите. Если в результате этого не удалось получить читаемое сообщение, то необходимо повторить действие, но уже сместив буквы на два знака левее. И так далее, пока в результате не получится читаемый текст.

Аффиный шифр

Рассмотрим немного более интересный одноалфавитный шифр подстановки под названием аффиный шифр. Он тоже реализует простую подстановку, но обеспечивает немного большее пространство ключей по сравнению с шифром Цезаря. В аффинном шифре каждой букве алфавита размера m ставится в соответствие число из диапазона 0… m-1. Затем при помощи специальной формулы, вычисляется новое число, которое заменит старое в шифртексте.

Процесс шифрования можно описать следующей формулой:

,

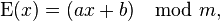
где x — номер шифруемой буквы в алфавите; m — размер алфавита; a, b — ключ шифрования.

Для расшифровки вычисляется другая функция:

,

где a^-1 — число обратное a по модулю m. Это значит, что для корректной расшифровки число a должно быть взаимно простым с m.

С учетом этого ограничения вычислим пространство ключей аффиного шифра на примере английского алфавита. Так как английский алфавит содержит 26 букв, то в качестве a может быть выбрано только взаимно простое с 26 число. Таких чисел всего двенадцать: 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23 и 25. Число b в свою очередь может принимать любое значение в интервале от 0 до 25, что в итоге дает нам 12*26 = 312 вариантов возможных ключей.

Криптоанализ аффиного шифра

Очевидно, что и в случае аффиного шифра простейшим способом взлома оказывается перебор всех возможных ключей. Но в результате перебора получится 312 различных текстов. Проанализировать такое количество сообщений можно и в ручную, но лучше автоматизировать этот процесс, используя такую характеристику как частота появления букв.

Давно известно, что буквы в естественных языках распределены не равномерно. К примеру, частоты появления букв английского языка в текстах имеют следующие значения:

Т.е. в английском тексте наиболее встречающимися буквами будут E, T, A. В то время как самыми редкими буквами являются J, Q, Z. Следовательно, посчитав частоту появления каждой буквы в тексте мы можем определить насколько частотная характеристика текста соответствует английскому языку.

Для этого необходимо вычислить значение:

,

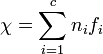
где n_i — частота i-й буквы алфавита в естественном языке. И f_i — частота i-й буквы в шифртексте.

Чем больше значение χ, тем больше вероятность того, что текст написан на естественном языке.

Таким образом, для взлома аффиного шифра достаточно перебрать 312 возможных ключей и вычислить значение χ для полученного в результате расшифровки текста. Текст, для которого значение χ окажется максимальным, с большой долей вероятности и является зашифрованным сообщением.

Разумеется следует учитывать, что метод не всегда работает с короткими сообщениями, в которых частотные характеристики могут сильно отличатся от характеристик естественного языка.

Шифр простой замены

Очередной шифр, относящийся к группе одноалфавитных шифров подстановки. Ключом шифра служит перемешанный произвольным образом алфавит. Например, ключом может быть следующая последовательность букв: XFQABOLYWJGPMRVIHUSDZKNTEC.

При шифровании каждая буква в тексте заменяется по следующему правилу. Первая буква алфавита замещается первой буквой ключа, вторая буква алфавита — второй буквой ключа и так далее. В нашем примере буква A будет заменена на X, буква B на F.

При расшифровке буква сперва ищется в ключе и затем заменяется буквой стоящей в алфавите на той же позиции.

Криптоанализ шифра простой замены

Пространство ключей шифра простой замены огромно и равно количеству перестановок используемого алфавита. Так для английского языка это число составляет 26! = 2⁸⁸. Разумеется наивный перебор всех возможных ключей дело безнадежное и для взлома потребуется более утонченная техника, такая как поиск восхождением к вершине:

1. Выбирается случайная последовательность букв — основной ключ. Шифртекст расшифровывается с помощью основного ключа. Для получившегося текста вычисляется коэффициент, характеризующий вероятность принадлежности к естественному языку.
2. Основной ключ подвергается небольшим изменениям (перестановка двух произвольно выбранных букв). Производится расшифровка и вычисляется коэффициент полученного текста.
3. Если коэффициент выше сохраненного значения, то основной ключ заменяется на модифицированный вариант.
4. Шаги 2-3 повторяются пока коэффициент не станет постоянным.

Для вычисления коэффициента используется еще одна характеристика естественного языка — частота встречаемости триграмм.
Чем ближе текст к английскому языку тем чаще в нем будут встречаться такие триграммы как THE, AND, ING. Суммируя частоты появления в естественном языке всех триграмм, встреченных в тексте получим коэффициент, который с большой долей вероятности определит текст, написанный на естественном языке.

Шифр Полибия

Еще один шифр подстановки. Ключом шифра является квадрат размером 5*5 (для английского языка), содержащий все буквы алфавита, кроме J.

При шифровании каждая буква исходного текста замещается парой символов, представляющих номер строки и номер столбца, в которых расположена замещаемая буква. Буква a будет замещена в шифртексте парой BB, буква b — парой EB и так далее. Так как ключ не содержит букву J, перед шифрованием в исходном тексте J следует заменить на I.

Например, зашифруем слово HABRAHABR. C(‘HABRAHABR’) = ‘AB BB EB DA BB AB BB EB DA’.

Криптоанализ шифра Полибия

Шифр имеет большое пространство ключей (25! = 2⁸³ для английского языка). Однако единственное отличие квадрата Полибия от предыдущего шифра заключается в том, что буква исходного текста замещается двумя символами.

Поэтому для атаки можно использовать методику, применяемую при взломе шифра простой замены — поиск восхождением к вершине.
В качестве основного ключа выбирается случайный квадрат размером 5*5. В ходе каждой итерации ключ подвергается незначительным изменениям и проверяется насколько распределение триграмм в тексте, полученном в результате расшифровки, соответствует распределению в естественном языке.

Перестановочный шифр

Помимо шифров подстановки, широкое распространение также получили перестановочные шифры. В качестве примера опишем Шифр вертикальной перестановки.

В процессе шифрования сообщение записывается в виде таблицы. Количество колонок таблицы определяется размером ключа. Например, зашифруем сообщение WE ARE DISCOVERED. FLEE AT ONCE с помощью ключа 632415.

Так как ключ содержит 6 цифр дополним сообщение до длины кратной 6 произвольно выбранными буквами QKJEU и запишем сообщение в таблицу, содержащую 6 колонок, слева направо:

Для получения шифртекста выпишем каждую колонку из таблицы в порядке, определяемом ключом: EVLNE ACDTK ESEAQ ROFOJ DEECU WIREE.

При расшифровке текст записывается в таблицу по колонкам сверху вниз в порядке, определяемом ключом.

Криптоанализ перестановочного шифра

Лучшим способом атаки шифра вертикальной перестановки будет полный перебор всех возможных ключей малой длины (до 9 включительно — около 400 000 вариантов). В случае, если перебор не дал желаемых результатов, можно воспользоваться поиском восхождением к вершине.

Для каждого возможного значения длины осуществляется поиск наиболее правдоподобного ключа. Для оценки правдоподобности лучше использовать частоту появления триграмм. В результате возвращается ключ, обеспечивающий наиболее близкий к естественному языку текст расшифрованного сообщения.

Шифр Плейфера

Шифр Плейфера — подстановочный шифр, реализующий замену биграмм. Для шифрования необходим ключ, представляющий собой таблицу букв размером 5*5 (без буквы J).

Процесс шифрования сводится к поиску биграммы в таблице и замене ее на пару букв, образующих с исходной биграммой прямоугольник.
Рассмотрим, в качестве примера следующую таблицу, образующую ключ шифра Плейфера:

Зашифруем пару ‘WN’. Буква W расположена в первой строке и первой колонке. А буква N находится во второй строке и третьей колонке. Эти буквы образуют прямоугольник с углами W-E-S-N. Следовательно, при шифровании биграмма WN преобразовывается в биграмму ES.
В случае, если буквы расположены в одной строке или колонке, результатом шифрования является биграмма расположенная на одну позицию правее/ниже. Например, биграмма NG преобразовывается в биграмму GP.

Криптоанализ шифра Плейфера

Так как ключ шифра Плейфера представляет собой таблицу, содержащую 25 букв английского алфавита, можно ошибочно предположить, что метод поиска восхождением к вершине — лучший способ взлома данного шифра. К сожалению, этот метод не будет работать. Достигнув определенного уровня соответствия текста, алгоритм застрянет в точке локального максимума и не сможет продолжить поиск.
Чтобы успешно взломать шифр Плейфера лучше воспользоваться алгоритмом имитации отжига.

Отличие алгоритма имитации отжига от поиска восхождением к вершине заключается в том, что последний на пути к правильному решению никогда не принимает в качестве возможного решения более слабые варианты. В то время как алгоритм имитации отжига периодически откатывается назад к менее вероятным решениям, что увеличивает шансы на конечный успех.

Суть алгоритма сводится к следующим действиям:

1. Выбирается случайная последовательность букв — основной-ключ. Шифртекст расшифровывается с помощью основного ключа. Для получившегося текста вычисляется коэффициент, характеризующий вероятность принадлежности к естественному языку.
2. Основной ключ подвергается небольшим изменениям (перестановка двух произвольно выбранных букв, перестановка столбцов или строк). Производится расшифровка и вычисляется коэффициент полученного текста.
3. Если коэффициент выше сохраненного значения, то основной ключ заменяется на модифицированный вариант.
4. В противном случае замена основного ключа на модифицированный происходит с вероятностью, напрямую зависящей от разницы коэффициентов основного и модифицированного ключей.
5. Шаги 2-4 повторяются около 50 000 раз.

Алгоритм периодически замещает основной ключ, ключом с худшими характеристиками. При этом вероятность замены зависит от разницы характеристик, что не позволяет алгоритму принимать плохие варианты слишком часто.

Для расчета коэффициентов, определяющих принадлежность текста к естественному языку лучше всего использовать частоты появления триграмм.

Шифр Виженера

Шифр Виженера относится к группе полиалфавитных шифров подстановки. Это значит, что в зависимости от ключа одна и та же буква открытого текста может быть зашифрована в разные символы. Такая техника шифрования скрывает все частотные характеристики текста и затрудняет криптоанализ.

Шифр Виженера представляет собой последовательность нескольких шифров Цезаря с различными ключами.

Продемонстрируем, в качестве примера, шифрование слова HABRAHABR с помощью ключа 123. Запишем ключ под исходным текстом, повторив его требуемое количество раз:

Цифры ключа определяют на сколько позиций необходимо сдвинуть букву в алфавите для получения шифртекста. Букву H необходимо сместить на одну позицию — в результате получается буква I, букву A на 2 позиции — буква C, и так далее. Осуществив все подстановки, получим в результате шифртекст: ICESCKBDU.

Криптоанализ шифра Виженера

Первая задача, стоящая при криптоанализе шифра Виженера заключается в нахождении длины, использованного при шифровании, ключа.

Для этого можно воспользоваться индексом совпадений.

Индекс совпадений — число, характеризующее вероятность того, что две произвольно выбранные из текста буквы окажутся одинаковы.
Для любого текста индекс совпадений вычисляется по формуле:

,

где f_i — количество появлений i-й буквы алфавита в тексте, а n — количество букв в тексте.

Для английского языка индекс совпадений имеет значение 0.0667, в то время как для случайного набора букв этот показатель равен 0.038.
Более того, для текста зашифрованного с помощью одноалфавитной подстановки, индекс совпадений также равен 0.0667. Это объясняется тем, что количество различных букв в тексте остается неизменным.

Это свойство используется для нахождения длины ключа шифра Виженера. Из шифртекста по очереди выбираются каждая вторая буквы и для полученного текста считается индекс совпадений. Если результат примерно соответствует индексу совпадений естественного языка, значит длина ключа равна двум. В противном случае из шифртекста выбирается каждая третья буква и опять считается индекс совпадений. Процесс повторяется пока высокое значение индекса совпадений не укажет на длину ключа.

Успешность метода объясняется тем, что если длина ключа угадана верно, то выбранные буквы образуют шифртекст, зашифрованный простым шифром Цезаря. И индекс совпадений должен быть приблизительно соответствовать индексу совпадений естественного языка.
После того как длина ключа будет найдена взлом сводится к вскрытию нескольких шифров Цезаря. Для этого можно использовать способ, описанный в первом разделе данного топика.

P.S.

Исходники всех вышеописанных шифров и атак на них можно посмотреть на GitHub.

Ссылки

1. Криптоанализ классических шифров на сайте practicalcryptography.com.
2. Частотные характеристики английского языка на сайте practicalcryptography.com
3. Описание алгоритма имитации отжига на wikipedia
4. Описание поиска восхождением к вершине на wikipedia

§ Предисловие

Это алгоритм для шифрования сообщений. Он сложный, трудоемкий и напрямую не используется из-за своей очень невысокой скорости работы. А скорость работы у него невероятно медленная по той причине, что такой алгоритм оперирует гигантскими числами.

§ Открытый и закрытый ключи

Этот алгоритм основан на ключах, один из них открытый, другой — закрытый. Это называется пара ключей (публичный — то есть открытый, и приватный — закрытый). Ключи представляют собой просто очень большое число, то есть реально, просто число, и ничего более, кроме того, что оно гигантское. Для простоты и наглядности ключи у меня будут далее крайне простыми, не превышающие тысячи, поскольку чем больше ключ, тем сложнее его считать.

Теперь представим следующую ситуацию. Есть Алиса, и есть Боб. Они сверхсекретные агенты, и они не могут выдать то, о чем они болтают между собой, и какие сверхсекретные данные передают. Алиса сидит на телефоне, Боб сидит на другом конце телефона а посередине сидит их общий заклятый враг и внимательно слушает, о чем они говорят. Алисе надо передать Бобу очень секретное число, но просто сказать по телефону она ему не может — враг не дремлет.

• Алиса спрашивает у Боба открытый ключ, он ей говорит его по телефону. Ключ становится известен всем, в том числе не только Алисе, но и еще тому, кто сидит и слушает их
• Алиса берет это число (открытый ключ), производит определенные действия над тем числом, что хочет закодировать и отсылает Бобу. Человек посередине эту информацию тоже перехватил.
• Боб же берет закрытый ключ, который он создал вместе с открытым и производя математические действия, расшифровывает число Алисы
• Человек посередине не знает закрытого ключа Боба, а по открытому ключу он не может ничего сделать, потому что расшифровать сообщение можно только с помощью закрытого. Человек с досады кусает свои локти.

Вкратце:

• Боб создает открытый и закрытый ключи (они взаимосвязаны, как Том и Джерри)
• Алиса получает открытый ключ Боба
• Кодирует с его помощью свое число
• Отсылает число по небезопасному каналу связи
• Боб расшифровывает число с помощью закрытого ключа

Более абстрактно:

• Создать открытый и закрытый ключи
• Передать открытый ключ тому, кто будет шифровать
• Зашифровать сообщение с помощью открытого ключа
• Передать зашифрованное сообщение по каналу связи
• Расшифровать сообщение с помощью закрытого ключа

§ Открытый ключ

Задача создать открытый и закрытый ключи — очень сложна, если речь заходит о колоссальных цифрах. Сложность именно в том, как их быстро вычислить. Дело в том, что если взять два гигантских простых числа, и умножить, обратно потом найти эти простые числа уже весьма проблематично. Алгоритм RSA устройчив к взлому исключительно потому, что:

Невозможно быстро и эффективно разложить на множители огромные числа

Вот так вот. Если бы это было реально, то алгоритм RSA утратил бы свою криптостойкость и пришлось бы искать еще какой-нибудь метод. Сейчас рулят эллиптические кривые, но я без понятия как они работают, поэтому расскажу только про RSA.

Шаг 1. Взять два простых числа p и q

Кстати говоря, это далеко не так просто, как кажется. Если речь идет о небольших простых числах, не превышающих к примеру миллиарда, то их нахождение для взломщика не составляет вообще никакого труда. На любом процессоре разложить подобные числа можно за несколько миллисекунд. Однако, как только речь заходит о числах порядка аж 800-1000 десятичных знаков, то тогда никакой сверхмощной видеокарты, да и вообще вычислительной мощности всей планеты не хватит, чтобы даже за 1 год взломать такой код. Единственный, кто может справиться с этой задачей — это алгоритм Шора для квантовых компьютеров, которые сейчас находятся пока что в довольно неразвитой стадии на 2020 год.

Да, простые то числа взять можно, только вот надо чтобы они реально простые были, потому что составные числа работать не будут в RSA вообще. Они будут просто ломать всё. Это значит, что надо бы еще найти простые числа, а это сложная задача. Существуют разные тесты простоты, но в этой статье я их рассматривать не буду.

Получив простые числа p, q, надо их перемножить:

n = pq

И получим n, который будет играть важную роль дальше.

Шаг 2. Вычислить открытую экспоненту e

Перед тем, как вычислить открытую экспоненту, надо рассчитать функцию Эйлера, которая считается для двух простых чисел невероятно простым способом:

phi (n) = (p-1)(q-1)

То есть нужно лишь просто вычесть из p и q по единице и умножить их. Для чего это все? Здесь есть строгое математическое доказательство, приводить которое я тут не буду, потому что сложно и много. Просто надо поверить на слово. А если хочется проверить, то надо смотреть специальную литературу.

Теперь самый ответственный момент. Надо взять наобум число

e

такое, которое бы попало в следующий диапазон:

1 lt e lt phi(n)

И при этом его наибольший общий делитель (НОД) был равен 1, или, другими словами, чтобы ни одно целое число, кроме 1, не смогло поделить

e

и

phi (n)

, то есть, чтобы у этих двух чисел не было наибольшего общего делителя, больше чем 1.

Примеры:

• Числа 5 и 15 имеют НОД(5,15) = 5 — число 15 делится на 5, и 5 делится на 5 без остатка
• НОД(7, 14) = 7 — число 7 делится на 7, и 14 делится на 7 тоже
• НОД(12, 15) = 3 — число 12 делится на 3, число 15 делится на 3
• НОД(9, 11) = 1 — вот это в самый раз, ни одно число не делится, кроме как на 1

Шаг 3. Открытый ключ

Теперь появились все данные, чтобы найти открытый ключ, который представлен как пара {e, n}. Теперь перейду к практической части вычисления открытого ключа.

• Берется (для примера) p=47, q=31, оба числа простые
• Получается n = pq = 47*31 = 1457 — это число часть как открытого, так и закрытого ключа
• Вычисляем
  phi (n) = (p-1)(q-1)

  = (47-1)(31-1) = 1380

• Теперь, надо взять такое
  e

  , чтобы НОД(
  e

  ,
  phi (n)

  ) = 1, берем число e=257 (для примера), проверятся НОД(257, 1380) = 1, все верно

Открытый ключ {e, n} равен {257, 1457}.

§ Закрытый ключ

Теперь задача в том, чтобы сформировать закрытый ключ на числах p, q. Как я и говорил ранее, закрытый ключ нужен, чтобы расшифровать то сообщение, которое было зашифровано с помощью открытого ключа. Закрытый ключ базируется на тех же самых p,q, и потому у него будет точно та же компонента n, что и у открытого ключа. Закрытый же ключ будет представлен как пара {d, n}, где d — закрытая компонента, n = pq.

Существует формула для поиска закрытого ключа:

d = e^{-1} mod phi (n)

Но, ее понять сложно без подготовки. Лучше ее переписать в следующем виде:

(de) mod phi(n) = 1

И что это значит? Это значит, что надо найти

d

такое, что при умножении на

e

и потом после деления на

phi(n)

получился остаток 1.

Вот возьмем простой пример, допустим

e

= 7,

phi(n)

= 60:

7d mod 60 = 1

Теперь надо подобрать такое d, при котором остаток от деления на 60 был бы 1. Пробуем:

• d = 1 — 7*1 mod 60 = 7, не подходит
• d = 9 — 7*9 mod 60 = 63 mod 60 = 3, не подходит
• d = 23 — 23*7 mod 60 = 161 mod 60 = 41, не подходит
• d = 43 — 43*7 mod 60 = 301 mod 60 = 1, подошло

Получается, что для числа

e

= 7 число

d

= 43. Таким образом, мы смогли найти закрытый ключ {43, 77}, при этом открытый ключ был {7, 77}.

Поиск закрытого ключа происходит с помощью расширенного алгоритма Евклида, объяснение которого здесь тоже не приводится.

§ Пример шифрования и дешифрования

А теперь самое главное: как шифровать и дешифровать сообщение.

Шифрование числа происходит по следующей формуле:

b = a^e mod n

Дешифрование происходит так:

a = b^d mod n

И это весь алгоритм. Стоит только учесть, что так как числа

d

и

e

огромны, то не так просто будет возвести такие числа в такую вот степень.

Для начала, составим открытый и закрытый ключи. Генерация открытого ключа происходит по такому алгоритму:

• Возьмем p=11, q=23, n = pq = 253
• Число Эйлера
  phi(n) = (11-1)(13-1) = 220

• Выберем открытую экспоненту
  e

  = 17, ибо НОД(17, 220) = 1

Итак, открытый ключ будет равен {17, 253}. Теперь надо найти закрытый ключ, используя вот это уравнение:

17d mod 253 = 1

Пока что находим перебором, но можно искать с помощью расширенного алгоритма НОД. Но в данном случае просто перебором, про НОД позже расскажу.

Путем подбора (я просто программой перебрал числа d=1..253),

d

оказалось равным 134. Проверим, 134*17 mod 253 = 1, все подошло. Закрытый ключ равен {134, 253}.

Теперь надо попробовать что-нибудь зашифровать и расшифровать. Поскольку число n у нас 253, то зашифровать можно сообщение только от 0 до 252 включительно, ибо если попытаться использовать 253, то такое сообщение просто превратится в 0 при расшифровке. Это не проблема, но надо учитывать, что шифровать число более чем n нельзя.

Выбираем a=110, теперь шифруем с помощью открытого ключа.

b = 110^{17} mod 253 = 77

У нас получился b=77. Даже зная n=253, нельзя получить обратно 110, потому что нужен для этого закрытый ключ. Однако, если разложить 253 на простые множители p, q, то тогда можно найти и закрытый ключ d. Однако, при большом значении n это сделать невозможно. Расшифровка с помощью закрытого ключа делается так:

a = 77^{134} mod 253 = 110

Что и требовалось сделать. Все работает корректно. Процедура для быстрого возведения в степень приведена в этой статье.

§ Нахождение закрытого ключа с помощью расширенного НОД

Существуют способы, при которых можно найти d, зная e, не используя при этом перебор, и этот способ — расширенный алгоритм Евклида, о котором я уже писал ранее в другой статье. То есть как находить коэффициенты к расширенному алгоритму, об этом здесь я говорить не стану, а только опишу самую суть того, почему надо использовать именно этот НОД.

Поскольку числа

e

и

phi(n)

взаимно простые, но их НОД будет равен 1:

НОД(

e

,

phi(n)

) =

xe + yphi(n)

= 1

Здесь значения x, y получаются из решения расширенного алгоритма НОД. Теперь применим модуль к левой и правой части:

xe mod phi(n) + yphi(n) mod phi(n) = 1 mod phi(n)

Поскольку любой модуль от 1 будет 1, а модуль самого от себя,

yphi(n) mod phi(n)

будет равняться 0, то уравнение сокращается:

xe mod phi(n) = 1

Тут сразу же видно, что x — это как раз тот самый искомый d. В общем-то и всё.

§ Программный код

Получение значений расширенного НОД:

int NOD(int a, int b, int & x, int & y) {

    int x1, y1, d;
    if (a == 0) { x = 0; y = 1; return b; }
    d = NOD(b % a, a, x1, y1);
    x = y1 - (int)(b / a) * x1;
    y = x1;
    return d;
}

Быстрое возведение в степень:

unsigned long fpow(unsigned long a, unsigned long b, unsigned long m) {

    int id;
    unsigned long r = 1;
    for (id = 31; id >= 0; id--) {
        if (b & (1 << id)) r = (r * a) % m;
        if (id) r = (r * r) % m;
    }
    return r;
}

22 ноя, 2020

© 2007-2023 Все мелочи классно колючие

Понятие шифрования

Как только в мире зародилось понятие секретной информации, которая должна была оставаться доступной лишь узкому кругу людей, так сразу же стало использоваться и шифрование. Происходило это в очень давние времена. В частности, есть шифровальный метод, названный в честь Цезаря. Возможно, он сам его придумал, или просто любил использовать.

Суть криптографии состоит в том, чтобы сделать недоступным смысл сообщения и иметь возможность расшифровать его, задействовав определенные алгоритмы и ключи. Здесь ключ алгоритма шифрования – это некое скрытое состояние шифровальных и дешифровальных параметров. Тот, кто знает ключ, прочтет и засекреченное послание. Впрочем, не факт, что посторонние его не смогут прочитать, даже если ключа у них нет.

Криптоанализ – это и есть распознание шифра без наличия ключа. А криптостойкость шифра определяется по количеству времени, необходимому для его взлома. Высокая криптостойкость говорит о том, что перед вами «сильный» алгоритм шифрования. А если изначально невозможно понять, получится ли взломать – это вообще отлично.

Требования к алгоритмам шифрования

Алгоритм шифрования данных может быть программным либо аппаратным. Последний вариант обходится дороже, но он же и производительнее, проще в использовании и дает более высокую защиту. Программное криптографическое закрытие данных практичнее и гибче.

Скачать
файл

Обычно требования к криптографическим системам выдвигаются такие:

• нельзя, чтобы зашифрованное сообщение читалось без ключа;
• чтобы определить по фрагменту зашифрованного сообщения и куску этого же открытого текста, какой именно использовался ключ, необходимо провести столько же операций (не меньше), сколько вообще тут могло быть применено ключей;
• когда речь идет о расшифровке данных путем подбора, то количество операций должно быть четко ограничено снизу и превышать возможности (в том числе и связанные с сетевыми вычислениями) современных компьютеров;
• даже если алгоритм шифрования известен, защита все равно должна оставаться надежной;
• необходимо, чтобы даже небольшое изменение ключа давало сильное изменение вида закодированного послания;
• структуру алгоритма шифрования менять нельзя;
• если в ходе шифрования в текст вносятся дополнительные биты, то в зашифрованном послании они должны быть абсолютно незаметны;
• исходник и зашифрованное сообщение должны быть одинаковыми по длине;
• если в ходе шифрования последовательно задействовалось несколько ключей, то нельзя допускать, чтобы зависимость между ними легко отслеживалась;
• какой бы ключ из всех существующих ни был выбран, он должен гарантировать полную защиту данных;
• требуется наличие возможности для реализации алгоритма, как аппаратным, так и программным способом. Если ключ становится длиннее, это не должно отражаться на качественных параметрах алгоритма шифрования.

Виды алгоритмов шифрования

Современных алгоритмов шифрования с высокой криптографической стойкостью (то есть, таких, которым «не страшен» криптоанализ) сейчас очень много. Обычно их разделяют на три группы:

Симметричные алгоритмы шифрования

Под симметричностью здесь понимается применение для расшифровки того же самого ключа, которым было зашифровано послание. Основные требования (их два) к симметричным алгоритмам такие: статистических закономерностей в шифруемом сообщении оставаться не должно, линейности – тоже. Симметричные системы в свою очередь делят на блочные и поточные.

В блочных системах шифрование выполняется так: исходное сообщение делится на блоки, а затем каждый из них кодируется с использованием определенного ключа.

В поточных алгоритмах формируется так называемая выходная гамма (определенная последовательность), и в процессе ее генерирования осуществляется шифрование послания. То есть, она потоком накладывается на исходник.

В ходе симметричного шифрования для подстановки и перестановки исходных данных задействуются сложные, многоуровневые алгоритмы. Этих уровней (их еще называет проходами) может быть очень много и каждый – со своим ключом (ключ прохода).

В ходе подстановки сначала выполняется первое требование, которому должен отвечать симметричный шифр: биты сообщения перемешиваются (по заданному алгоритму), тем самым убираются все статистические данные. А путем перестановок достигается соответствие второму требованию: алгоритм становится нелинейным. Для этого часть сообщения (объём этой части задается) меняется на стандартное значение, взятое из исходного массива.

Если сравнивать симметричные алгоритмы шифрования с асимметричными, то и там, и там будут свои плюсы и минусы. Преимущество симметричных систем в том, что они больше изучены, проще в применении, шифруют быстро, и при меньшей допустимой длине ключа дают ту же стойкость.

А недостатки здесь такие: обмен ключами усложняется из-за того, что в ходе этого обмена может нарушиться их секретность (а без обмена тут не обойтись). И еще, если сеть довольно объёмна, то управлять ключами тоже становится сложно.

Вот несколько симметричных шифров:

• ГОСТ 28147-89 — стандартный отечественный образец;
• 3DES — тройной DES или Triple-DES;
• RC6 —Шифр Ривеста;
• Twofish;
• SEED — шифровальный алгоритм корейского происхождения;
• Camellia – японский шифр;
• CAST — название составлено из инициалов разработчиков (Carlisle Adams и Stafford Tavares);
• IDEA;
• XTEA —самый простой алгоритм шифрования;
• AES – стандартный американский образец;
• DES – шифр применялся в Соединенных Штатах до появления AES.

Асимметричные алгоритмы шифрования

Другое название асимметричных шрифтов – криптосистемы с открытым ключом. Суть здесь в том, что ключ в открытом виде передается по открытому каналу и применяется для того, чтобы проверить подлинность электронной подписи и зашифровать послание. А вот создание электронной подписи и дешифровка осуществляется с помощью уже другого, засекреченного ключа.

В основе асимметричных алгоритмов шифрования – идея односторонних функций ƒ(х), в которых найти х совершенно просто, однако даже когда х известен, значение ƒ(х) определить практически невозможно. В качестве примера подобной функции можно привести справочник телефонных номеров крупного города. Если вы знаете фамилию и инициалы человека, то запросто отыщете тут его номер телефона, но обратное действие (по номеру найти человека) намного сложнее.

Пусть, например абонент В хочет переслать для абонента А закодированное послание. Тогда он, используя открытый ключ, шифрует текст и пересылает его по открытому каналу связи, но уже в зашифрованном виде. А расшифровку получатель (то есть, абонент А), делает уже другим, секретным ключом.

Важно: тут обязательна аутентификация личности абонента А перед В в момент получения сообщения, чтобы исключить возможность подмены открытого ключа абонента А на какой-то другой (принадлежащий мошенникам).

Вот несколько существующих асимметричных шрифтов:

• RSA — по инициалам Rivest-Shamir-Adleman (Ривест — Шамир — Адлеман);
• DSA — Digital Signature Algorithm;
• Elgamal — шифросистема Эль-Гамаля;
• Diffie-Hellman — обмен ключами Диффи — Хелмана;
• ECC — Elliptic Curve Cryptography (криптография эллиптической кривой);
• ГОСТ Р 34.10-2001;
• Rabin;
• Luc;
• McEliece.

Хеш-функции как алгоритмы шифрования информации

Название термина хеширование взято от английского слова hash. Хеширование — это когда некий массив информации любой длины преобразуют в битовый файл, длина которого уже фиксирована.

Хеш-функций существует сейчас много, разных по разрядности, криптостойкости, сложности вычисления и т.п.

Наибольший интерес представляют именно криптостойкие, и основных требований к ним обычно два:

• К имеющемуся сообщению С невозможно подобрать сообщение С’, которое будет обладать аналогичным хешем.
• Задача подбора пар сообщений (СС’) с одинаковым хешем должна быть практически невыполнимой.

Описанные требования – это так называемые коллизии первого и второго рода. Но есть и еще одно важное требование для хеш-функций: если аргумент меняется, то должна меняться и сама функция, причем существенно. То есть, важно, чтобы по значению хеша нельзя было ничего узнать об аргументе (даже частично, об отдельных битах).

Вот несколько примеров хеш-алгоритмов шифрования:

• SHA-2 (SHA-224, SHA-256, SHA-384, SHA-512);
• MD2;
• MD4;
• MD5;
• Adler-32;
• N-Hash;
• Skein;
• Snefru;
• IP Internet Checksum (RFC 1071);
• CRC;
• SHA-1;
• RIPEMD-160;
• RIPEMD-256;
• RIPEMD-320;
• HAVAL;
• Tiger (TTH);
• ГОСТ Р34.11-94 (ГОСТ 34.311-95);
• Whirlpool.

Сферы применения алгоритмов шифрования

Любые пользовательские и архивные данные непременно должны быть защищены, и это забота цифровых сервисов. Последствия утечек бывают плачевными. К примеру, чужими электронными материалами с целью мошенничества могут воспользоваться хакеры.

Сейчас жизнь современного человека тесно связана с самыми разными гаджетами и IT-технологиями. Через мобильные приложения проводятся платежи, финансовые сделки, рабочие операции и т.п. Это отнюдь не безопасные каналы передачи данных, поэтому обязательно нужно заботиться об их защите.

Вот в каких сферах задействуются алгоритмы шифрования информации:

• банковские операции;
• сфера IT;
• компьютерные технологии;
• телевидение;
• радио;
• иные коммуникационные каналы;
• программирование.

Криптография есть всюду, где используются IT и цифровизация. Конечно, это довольно сложное, однако и перспективное направление деятельности в науке.

Алгоритмы шифрования и криптовалюты

Росту всемирной популярности криптовалют не в последнюю очередь поспособствовало стремительное развитие алгоритмов шифрования. Перспективы активного применения технологии блокчейн очевидны уже сейчас, а она опирается как раз на алгоритмы шифрования.

Майнинг (выработка криптовалют) осуществляется за счет разных компьютерных технологий, которыми вполне можно взламывать алгоритмы шифрования. Это одна из уязвимостей, которую в криптовалютах второго и последующих поколений стараются устранять. К примеру, биткоин (криптовалюта первого поколения) майнится с помощью брутфорс SHA-256.

А взломать этот алгоритм можно через майнинг-ферму (нужно лишь слегка перенастроить). Собственный алгоритм шифрования есть у эфириума, но там свои нюансы. В случае с биткоином применяются асики (интегральные микросхемы узкой направленности), которые «умеют» делать лишь одну операцию – перебирать хеши в SHA-256. А вот для майнинга эфириума применяются уже универсальные процессоры на CUDA-ядрах.

Конечно же, в обозримом будущем эти проблемы будут закрыты, ведь по сути криптовалюты еще только начинают развиваться.

Тем, кто хочет стать профессиональным криптографом, нужно сначала освоить IT, программирование, информатику, работу алгоритмов. По всем перечисленным направлениям существует много самых разных специальных курсов.

Нередко люди воспринимают блокчейн как что-то сложное для понимания. На самом деле основная идея технологии проста. Чтобы разобраться с принципом работы блокчейна, следует начать с криптографии. 

В материале мы на примерах покажем как с помощью криптографических алгоритмов шифруются данные. После прочтения вы станете лучше понимать как устроен блокчейн, в чем его уникальность и почему он считается анонимным.

1. P2P: где используются одноранговые сети
2. Шифрование в блокчейне: на пальцах
3. Блокчейн — цепочка блоков транзакций. Разбираем определение по словам
4. Шифрование в блокчейне: зачем нужна цифровая подпись
5. Принцип работы блокчейна: кто создает блоки
6. Для каких целей и задач подходит блокчейн

Зачем шифровать данные в блокчейне

Благодаря алгоритмам шифрования, технология блокчейн считается наиболее безопасной разновидностью одноранговых сетей. Для начала разберемся, зачем в блокчейне что-то шифровать. 

В традиционной архитектуре «клиент-сервер» за безопасность отвечает сервер. Он выполняет следующие функции:

1. Обеспечивает доступ пользователей к данным. Сервер хранит логины и пароли своих клиентов. Он должен проверить пользователя, прежде чем дать ему доступ к сети. Данный процесс называется аутентификация.
2. Следит за сохранностью данных. Сервер не дает злоумышленникам получить доступ к личным данным пользователей. Другими словами, сервер гарантирует конфиденциальность.
3. Контролирует изменение данных. Сервер не дает пользователям удалять данные друг друга. Прежде чем вступить в силу, любое изменение согласуется с сервером. Таким образом поддерживается целостность данных. 

Так как в блокчейне сервера отсутствуют, то для этих целей применяют криптографию. Криптографические алгоритмы шифрования позволяют выполнять описанные функции без постороннего вмешательства.

Криптография — совокупность алгоритмов шифрования информации для обеспечения аутентификации, конфиденциальности и целостности данных.

Криптография была известна задолго до появления блокчейна. Чтобы понять, как алгоритмы шифрования выполняют функции сервера, рассмотрим реальный исторический пример.

В середине 1650-х голландский ученый Христиан Гюйгенс обнаружил кольца Сатурна. Он не был уверен в правильности своих наблюдений, поэтому решил все перепроверить. Пока он занимался проверкой, его могли опередить другие ученые. Поэтому в одной из своих работ ученый написал сообщение:

aaaaaaacccccdeeeeeghiiiiiiillllmmnnnnnnnnnooooppqrrstttttuuuuu

Позже Христиан Гюйгенс перепроверил все данные и был готов рассказать об открытии. Он раскрыл, что в шифре содержались буквы исходной фразы, расставленные по алфавиту. Сама фраза была следующей:

Annulo cingitur, tenui plano, nusquam cohaerente, ad eclipticam inclinato

«Окружен кольцом тонким, плоским, нигде не подвешенным, наклоненным к эклиптике»

Расстановка букв по алфавиту — один из алгоритмов шифрования. Гюйгенсу удалось зафиксировать свое открытие и не выдавать его конкурентам. Другими словами, алгоритм заменил сервер: сохранил данные в конфиденциальности без сторонней помощи.

В приведенном примере важно выбрать правильный алгоритм шифрования. Криптография отвечает на вопрос, какой использовать алгоритм шифрования для той или иной цели.

Почему выбрали алгоритм с хеш-функциями

Давайте представим себя на месте разработчиков блокчейна. Нам нужно найти идеальный алгоритм шифрования для того, чтобы осуществлять функции сервера в блокчейне. Сформулируем критерии:

1. Нужен такой тип математических функций, который легко шифрует информацию без возможности расшифровки.

Это односторонние функции. Самый простой пример такой функции — умножение. Если мы знаем только ответ, то не можем однозначно сказать какие два числа были умножены. Например, число 6 может быть произведением разных чисел: 6 и 1, 2 и 3, 12 и 0,5 или даже 47,2440945 и 0,127.

1. Нужен такой тип односторонних функций, который превращает информацию произвольного размера в шифр определенной длины.

Это хеш-функции. Они преобразуют сообщения в хеши. Информацию в таком виде можно удобно и безопасно использовать в программировании.

Сообщение может быть любого типа: текст, изображение, видео или звук. Чтобы с сообщением можно было проводить математические операции, его записывают в виде двоичного кода.

Хеш может состоять как из букв, так и из цифр. Какие цифры и буквы будут в хеше, а также сколько их будет, зависит от конкретной хеш-функции. Рассмотрим подробнее наиболее известную — SHA-256. 

Как работает хеш-функция SHA-256

Она известна тем, что используется в блокчейне биткоина. SHA означает «безопасный алгоритм хеширования»‎, а число 256 — объем кэша в битах.

Работа хеш-функции SHA-256 напоминает создание отпечатков пальцев. Чтобы идентифицировать человека, не надо знать всю информацию о нем. Достаточно знать отпечаток его пальца. SHA-256 вычисляет такой «отпечаток» у текстов, видео, картинок, музыки и любого вида информации. 

Если не углубляться в технические детали, алгоритм работы можно описать следующим образом:

1. На вход поступает сообщение — файл размером до 2 млн терабайт.
2. Выполняются математические преобразования.
3. На выходе получается хеш — 64-значное число.

Попробовать закодировать текст и посмотреть как работает хеш-функция можно онлайн. Для примера закодируем два сообщения: «Maff.io» и «maff.io». SHA-256 популярна, в том числе потому, что кодирует сообщения моментально.

Первое, что бросается в глаза, то как сильно отличаются хеши. Даже небольшое изменение в сообщении меняет хеш настолько сильно, что невозможно заметить сходства между новым и старым значением. Хеш-функция SHA-256 гарантирует, что невозможно изменить сообщение, не меняя хеша. 

Второе, на что следует обратить внимание — набор из букв и цифр в хеше. На самом деле это одно 64-значное число, просто записанное в шестнадцатеричной системе счисления. Чтобы найти два разных сообщения с одинаковым хешем, придется перебирать их миллионы лет.

Таким образом, если два сообщения имеют одинаковый хеш, то можно быть уверенным, что они одинаковые. Вот почему алгоритмы с хеш-функциями считаются таким надежным.

Пример работы: транзакции в блокчейне

Без хеш-функций существование блокчейна было бы невозможно. Блокчейн уникален тем, что гарантирует неизменность и анонимность хранимых данных. Это означает, что любые данные проверяются на подлинность, но при этом их никто не может увидеть. То есть, это если ломбард проверял золото, которое лежит в закрытом сейфе. Теперь покажем как в этом помогают хеш-функции.

Блокчейн регулярно обновляет данные, добавляя записи об изменениях — «транзакции». Именно при обновлении транзакционной информации любая система уязвима для атаки. Банки сглаживают этот риск с помощью строгого контроля за правами доступа пользователей. У блокчейна нет централизованного органа контроля, поэтому в работу вступают криптографические хеш-функции.

Транзакции и их хеши помещаются в блоки. Хеш в каждом новом блоке зависит от хеша в предыдущем. Таким образом, все когда-либо выполненные транзакции можно выразить одним числом — хешем последнего блока. Изменив даже одну транзакцию, изменятся все последующие хеши по цепочке и такая версия блокчейна будет считаться недействительной.

На использовании хеш-функций базируется весь принцип работы блокчейна. Хеши делают каждый блок похожим на деталь пазла. Изменить деталь незаметно не получится — целостность всего пазла нарушится. Аналогично и в блокчейне. Если изменится один блок, то придется методом перебора восстанавливать все последующие блоки. Чтобы осуществить такой перебор, не хватит никаких вычислительных мощностей.

Заключение

В статье мы рассказали о том, что криптографические алгоритмы шифрования применяются для обеспечения безопасности в блокчейне. Подробно рассмотрели использование хеш-функций и показали, что они являются основой технологии блокчейн.