Как найти алгоритм в игре

Часть 1. Общий алгоритм поиска

Введение

Поиск пути — это одна из тех тем, которые обычно представляют самые большие сложности для разработчиков игр. Особенно плохо люди понимают алгоритм A*, и многим кажется, что это какая-то непостижимая магия.

Цель данной статьи — объяснить поиск пути в целом и A* в частности очень понятным и доступным образом, положив таким образом конец распространённому заблуждению о том, что эта тема сложна. При правильном объяснении всё достаточно просто.

Учтите, что в статье мы будем рассматривать поиск пути для игр; в отличие от более академических статей, мы опустим такие алгоритмы поиска, как поиск в глубину (Depth-First) или поиск в ширину (Breadth-First). Вместо этого мы постараемся как можно быстрее дойти от нуля до A*.

В первой части мы объясним простейшие концепции поиска пути. Разобравшись с этими базовыми концепциями, вы поймёте, что A* на удивление очевиден.

Простая схема

Хотя вы сможете применять эти концепции и к произвольным сложным 3D-средам, давайте всё-таки начнём с чрезвычайно простой схемы: квадратной сетки размером 5 x 5. Для удобства я пометил каждую ячейку заглавной буквой.

Простая сетка.

Самое первое, что мы сделаем — это представим эту среду в виде графа. Я не буду подробно объяснять, что такое граф; если говорить просто, то это набор кружков, соединённых стрелками. Кружки называются «узлами», а стрелки — «рёбрами».

Каждый узел представляет собой «состояние», в котором может находиться персонаж. В нашем случае состояние персонажа — это его позиция, поэтому мы создаём по одному узлу для каждой ячейки сетки:

Узлы, обозначающие ячейки сетки.

Теперь добавим рёбра. Они обозначают состояния, которых можно «достичь» из каждого заданного состояния; в нашем случае мы можем пройти из любой ячейки в соседнюю, за исключением заблокированных:

Дуги обозначают допустимые перемещения между ячейками сетки.

Если мы можем добраться из A в B, то говорим, что B является «соседним» с A узлом.

Стоит заметить, что рёбра имеют направление; нам нужны рёбра и из A в B, и из B в A. Это может показаться излишним, но не тогда, когда могут возникать более сложные «состояния». Например, персонаж может упасть с крыши на пол, но не способен допрыгнуть с пола на крышу. Можно перейти из состояния «жив» в состояние «мёртв», но не наоборот. И так далее.

Пример

Допустим, мы хотим переместиться из A в T. Мы начинаем с A. Можно сделать ровно два действия: пройти в B или пройти в F.

Допустим, мы переместились в B. Теперь мы можем сделать два действия: вернуться в A или перейти в C. Мы помним, что уже были в A и рассматривали варианты выбора там, так что нет смысла делать это снова (иначе мы можем потратить весь день на перемещения A → B → A → B…). Поэтому мы пойдём в C.

Находясь в C, двигаться нам некуда. Возвращаться в B бессмысленно, то есть это тупик. Выбор перехода в B, когда мы находились в A, был плохой идеей; возможно, стоит попробовать вместо него F?

Мы просто продолжаем повторять этот процесс, пока не окажемся в T. В этот момент мы просто воссоздадим путь из A, вернувшись по своим шагам. Мы находимся в T; как мы туда добрались? Из O? То есть конец пути имеет вид O → T. Как мы добрались в O? И так далее.

Учтите, что на самом деле мы не движемся; всё это было лишь мысленным процессом. Мы продолжаем стоять в A, и не сдвинемся из неё, пока не найдём путь целиком. Когда я говорю «переместились в B», то имею в виду «представьте, что мы переместились в B».

Общий алгоритм

Этот раздел — самая важная часть всей статьи. Вам абсолютно необходимо понять его, чтобы уметь реализовывать поиск пути; остальное (в том числе и A*) — это просто детали. В этом разделе вы будете разбираться, пока не поймёте смысл.

К тому же этот раздел невероятно прост.

Давайте попробуем формализовать наш пример, превратив его в псевдокод.

Нам нужно отслеживать узлы, которых мы знаем как достичь из начального узла. В начале это только начальный узел, но в процессе «исследования» сетки мы будем узнавать, как добираться до других узлов. Давайте назовём этот список узлов reachable:

reachable = [start_node]

Также нам нужно отслеживать уже рассмотренные узлы, чтобы не рассматривать их снова. Назовём их explored:

explored = []

Дальше я изложу ядро алгоритма: на каждом шаге поиска мы выбираем один из узлов, который мы знаем, как достичь, и смотрим, до каких новых узлов можем добраться из него. Если мы определим, как достичь конечного (целевого) узла, то задача решена! В противном случае мы продолжаем поиск.

Так просто, что даже разочаровывает? И это верно. Но из этого и состоит весь алгоритм. Давайте запишем его пошагово псевдокодом.

Мы продолжаем искать, пока или не доберёмся до конечного узла (в этом случае мы нашли путь из начального в конечный узел), или пока у нас не закончатся узлы, в которых можно выполнять поиск (в таком случае между начальным и конечным узлами пути нет).

while reachable is not empty:

Мы выбираем один из узлов, до которого знаем, как добраться, и который пока не исследован:

    node = choose_node(reachable)

Если мы только что узнали, как добраться до конечного узла, то задача выполнена! Нам просто нужно построить путь, следуя по ссылкам previous обратно к начальному узлу:

    if node == goal_node:
       path = []
       while node != None:
            path.add(node)
            node = node.previous
        
        return path

Нет смысла рассматривать узел больше одного раза, поэтому мы будем это отслеживать:

    reachable.remove(node)
    explored.add(node)

Мы определяем узлы, до которых не можем добраться отсюда. Начинаем со списка узлов, соседних с текущим, и удаляем те, которые мы уже исследовали:

    new_reachable = get_adjacent_nodes(node) - explored

Мы берём каждый из них:

    for adjacent in new_reachable:

Если мы уже знаем, как достичь узла, то игнорируем его. В противном случае добавляем его в список reachable, отслеживая, как в него попали:

        if adjacent not in reachable:
            adjacent.previous = node  # Remember how we got there.
            reachable.add(adjacent)

Нахождение конечного узла — это один из способов выхода из цикла. Второй — это когда reachable становится пустым: у нас закончились узлы, которые можно исследовать, и мы не достигли конечного узла, то есть из начального в конечный узел пути нет:

return None

И… на этом всё. Это весь алгоритм, а код построения пути выделен в отдельный метод:

function find_path (start_node, end_node):
    reachable = [start_node]
    explored = []

    while reachable is not empty:
        # Choose some node we know how to reach.
        node = choose_node(reachable)

        # If we just got to the goal node, build and return the path.
        if node == goal_node:
            return build_path(goal_node)

        # Don't repeat ourselves.
        reachable.remove(node)
        explored.add(node)

        # Where can we get from here?
        new_reachable = get_adjacent_nodes(node) - explored
        for adjacent in new_reachable:
            if adjacent not in reachable
                adjacent.previous = node  # Remember how we got there.
                reachable.add(adjacent)

    # If we get here, no path was found :(
    return None

Вот функция, которая строит путь, следуя по ссылкам previous обратно к начальному узлу:

function build_path (to_node):
    path = []
    while to_node != None:
        path.add(to_node)
        to_node = to_node.previous
    return path

Вот и всё. Это псевдокод каждого алгоритма поиска пути, в том числе и A*.

Перечитывайте этот раздел, пока не поймёте, как всё работает, и, что более важно, почему всё работает. Идеально будет нарисовать пример вручную на бумаге, но можете и посмотреть интерактивное демо:

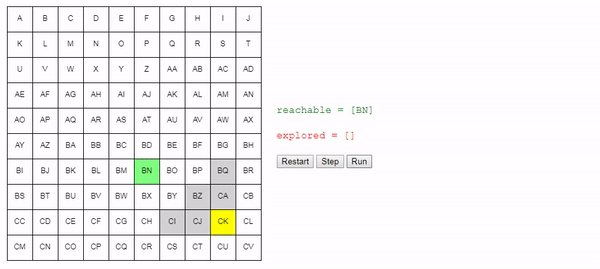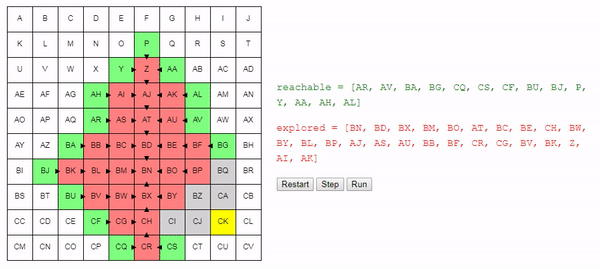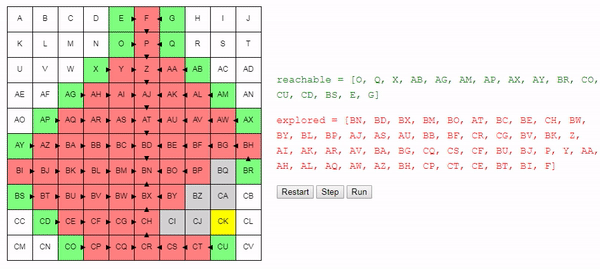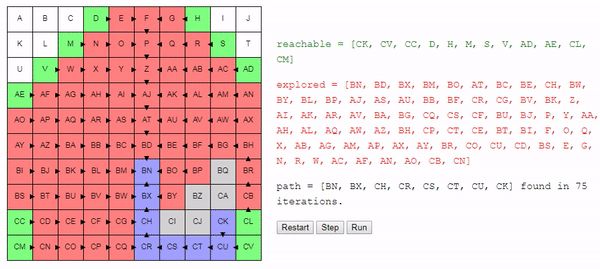
Интерактивное демо

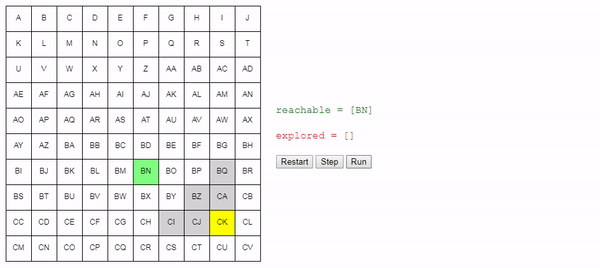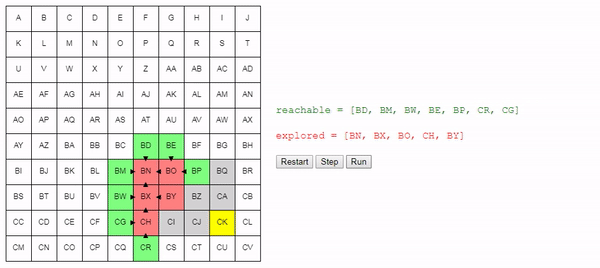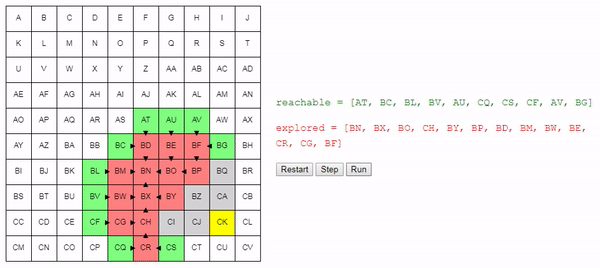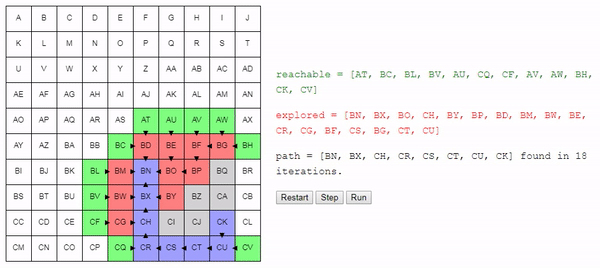
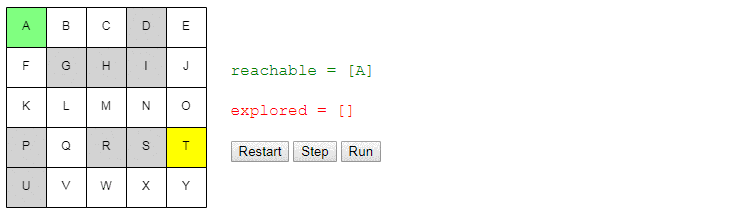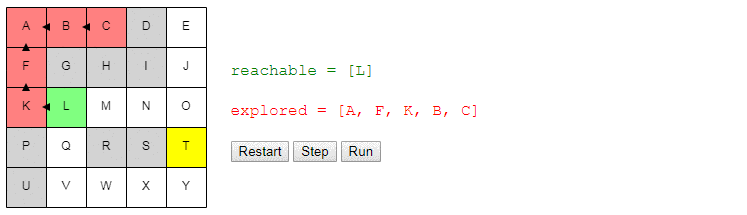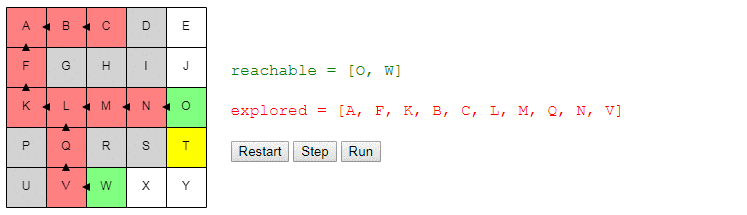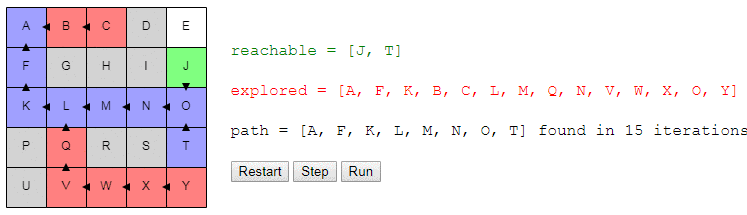
Вот демо и пример реализации показанного выше алгоритма (запустить его можно на странице оригинала статьи). choose_node просто выбирает случайный узел. Можете запустить алгоритм пошагово и посмотреть на список узлов reachable и explored, а также на то, куда указывают ссылки previous.

Заметьте, что поиск завершается, как только обнаруживается путь; может случиться так, что некоторые узлы даже не будут рассмотрены.

Заключение

Представленный здесь алгоритм — это общий алгоритм для любого алгоритма поиска пути.

Но что же отличает каждый алгоритм от другого, почему A* — это A*?

Вот подсказка: если запустить поиск в демо несколько раз, то вы увидите, что алгоритм на самом деле не всегда находит один и тот же путь. Он находит какой-то путь, и этот путь необязательно является кратчайшим. Почему?

Часть 2. Стратегии поиска

Если вы не полностью поняли описанный в предыдущем разделе алгоритм, то вернитесь к нему и прочтите заново, потому что он необходим для понимания дальнейшей информации. Когда вы в нём разберётесь, A* покажется вам совершенно естественным и логичным.

Секретный ингредиент

В конце предыдущей части я оставил открытыми два вопроса: если каждый алгоритм поиска использует один и тот же код, почему A* ведёт себя как A*? И почему демо иногда находит разные пути?

Ответы на оба вопроса связаны друг с другом. Хоть алгоритм и хорошо задан, я оставил нераскрытым один аспект, и как оказывается, он является ключевым для объяснения поведения алгоритмов поиска:

node = choose_node(reachable)

Именно эта невинно выглядящая строка отличает все алгоритмы поиска друг от друга. От способа реализации choose_node зависит всё.

Так почему же демо находит разные пути? Потому что его метод choose_node выбирает узел случайным образом.

Длина имеет значение

Прежде чем погружаться в различия поведений функции choose_node, нам нужно исправить в описанном выше алгоритме небольшой недосмотр.

Когда мы рассматривали узлы, соседние с текущим, то игнорировали те, которые уже знаем, как достичь:

if adjacent not in reachable:
    adjacent.previous = node  # Remember how we got there.
    reachable.add(adjacent)

Это ошибка: что если мы только что обнаружили лучший способ добраться до него? В таком случае необходимо изменить ссылку previous узла, чтобы отразить этот более короткий путь.

Чтобы это сделать, нам нужно знать длину пути от начального узла до любого достижимого узла. Мы назовём это стоимостью (cost) пути. Пока примем, что перемещение из узла в один из соседних узлов имеет постоянную стоимость, равную 1.

Прежде чем начинать поиск, мы присвоим значению cost каждого узла значение infinity; благодаря этому любой путь будет короче этого. Также мы присвоим cost узла start_node значение 0.

Тогда вот как будет выглядеть код:

if adjacent not in reachable:
    reachable.add(adjacent)

# If this is a new path, or a shorter path than what we have, keep it.
if node.cost + 1 < adjacent.cost:
    adjacent.previous = node
    adjacent.cost = node.cost + 1

Одинаковая стоимость поиска

Давайте теперь рассмотрим метод choose_node. Если мы стремимся найти кратчайший возможный путь, то выбирать узел случайным образом — не самая лучшая идея.

Лучше выбирать узел, которого мы можем достичь из начального узла по кратчайшему пути; благодаря этому мы в общем случае будем предпочитать длинным путям более короткие. Это не значит, что более длинные пути не будут рассматриваться вовсе, это значит, что более короткие пути будут рассматриваться первыми. Так как алгоритм завершает работу сразу после нахождения подходящего пути, это должно позволить нам находить короткие пути.

Вот возможный пример функции choose_node:

function choose_node (reachable):
    best_node = None

    for node in reachable:
        if best_node == None or best_node.cost > node.cost:
            best_node = node
    
    return best_node

Интуитивно понятно, что поиск этого алгоритма расширяется «радиально» от начального узла, пока не достигнет конечного. Вот интерактивное демо такого поведения:

Заключение

Простое изменение в способе выбора рассматриваемого следующим узла позволило нам получить достаточно хороший алгоритм: он находит кратчайший путь от начального до конечного узла.

Но этот алгоритм всё равно в какой-то степени остаётся «глупым». Он продолжает искать повсюду, пока не наткнётся на конечный узел. Например, какой смысл в показанном выше примере выполнять поиск в направлении A, если очевидно, что мы отдаляемся от конечного узла?

Можно ли сделать choose_node умнее? Можем ли мы сделать так, чтобы он направлял поиск в сторону конечного узла, даже не зная заранее правильного пути?

Оказывается, что можем — в следующей части мы наконец-то дойдём до choose_node, позволяющей превратить общий алгоритм поиска пути в A*.

Часть 3. Снимаем завесу тайны с A*

Полученный в предыдущей части алгоритм достаточно хорош: он находит кратчайший путь от начального узла до конечного. Однако, он тратит силы впустую: рассматривает пути, которые человек очевидно назовёт ошибочными — они обычно удаляются от цели. Как же этого можно избежать?

Волшебный алгоритм

Представьте, что мы запускаем алгоритм поиска на особом компьютере с чипом, который может творить магию. Благодаря этому потрясающему чипу мы можем выразить choose_node очень простым способом, который гарантированно создаст кратчайший путь, не теряя времени на исследование частичных путей, которые никуда не ведут:

function choose_node (reachable):
    return magic(reachable, "любой узел, являющийся следующим на кратчайшем пути")

Звучит соблазнительно, но магическим чипам всё равно требуется какой-то низкоуровневый код. Вот какой может быть хорошая аппроксимация:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = magic(node, "кратчайший путь к цели")
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Это отличный способ выбора следующего узла: вы выбираем узел, дающий нам кратчайший путь от начального до конечного узла, что нам и нужно.

Также мы минимизировали количество используемой магии: мы точно знаем, какова стоимость перемещения от начального узла к каждому узлу (это node.cost), и используем магию только для предсказания стоимости перемещения от узла к конечному узлу.

Не магический, но довольно потрясающий A*

К сожалению, магические чипы — это новинка, а нам нужна поддержка и устаревшего оборудования. БОльшая часть кода нас устраивает, за исключением этой строки:

# Throws MuggleProcessorException
cost_node_to_goal = magic(node, "кратчайший путь к цели")

То есть мы не можем использовать магию, чтобы узнать стоимость ещё не исследованного пути. Ну ладно, тогда давайте сделаем прогноз. Будем оптимистичными и предположим, что между текущим и конечным узлами нет ничего, и мы можем просто двигаться напрямик:

cost_node_to_goal = distance(node, goal_node)

Заметьте, что кратчайший путь и минимальное расстояние разные: минимальное расстояние подразумевает, что между текущим и конечным узлами нет совершенно никаких препятствий.

Эту оценку получить достаточно просто. В наших примерах с сетками это расстояние городских кварталов между двумя узлами (то есть abs(Ax - Bx) + abs(Ay - By)). Если бы мы могли двигаться по диагонали, то значение было бы равно sqrt( (Ax - Bx)^2 + (Ay - By)^2 ), и так далее. Самое важное то, что мы никогда не получаем слишком высокую оценку стоимости.

Итак, вот немагическая версия choose_node:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = estimate_distance(node, goal_node)
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Функция, оценивающая расстояние от текущего до конечного узла, называется эвристикой, и этот алгоритм поиска, леди и джентльмены, называется … A*.

Интерактивное демо

Пока вы оправляетесь от шока, вызванного осознанием того, что загадочный A* на самом деле настолько прост, можете посмотреть на демо (или запустить его в оригинале статьи). Вы заметите, что в отличие от предыдущего примера, поиск тратит очень мало времени на движение в неверном направлении.

Заключение

Наконец-то мы дошли до алгоритма A*, который является не чем иным, как описанным в первой части статьи общим алгоритмом поиска с некоторыми усовершенствованиями, описанными во второй части, и использующим функцию choose_node, которая выбирает узел, который по нашей оценке приближает нас к конечному узлу. Вот и всё.

Вот вам для справки полный псевдокод основного метода:

function find_path (start_node, end_node):
    reachable = [start_node]
    explored = []

    while reachable is not empty:
        # Choose some node we know how to reach.
        node = choose_node(reachable)

        # If we just got to the goal node, build and return the path.
        if node == goal_node:
            return build_path(goal_node)

        # Don't repeat ourselves.
        reachable.remove(node)
        explored.add(node)

        # Where can we get from here that we haven't explored before?
        new_reachable = get_adjacent_nodes(node) - explored
        for adjacent in new_reachable:
            # First time we see this node?
            if adjacent not in reachable:
                reachable.add(adjacent)
        
            # If this is a new path, or a shorter path than what we have, keep it.
            if node.cost + 1 < adjacent.cost:
                adjacent.previous = node
                adjacent.cost = node.cost + 1

    # If we get here, no path was found :(
    return None

Метод build_path:

function build_path (to_node):
    path = []
    while to_node != None:
        path.add(to_node)
        to_node = to_node.previous
    return path

А вот метод choose_node, который превращает его в A*:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = estimate_distance(node, goal_node)
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Вот и всё.

А зачем же нужна часть 4?

Теперь, когда вы поняли, как работает A*, я хочу рассказать о некоторых потрясающих областях его применения, которые далеко не ограничиваются поиском путей в сетке ячеек.

Часть 4. A* на практике

Первые три части статьи начинаются с самых основ алгоритмов поиска путей и заканчиваются чётким описанием алгоритма A*. Всё это здорово в теории, но понимание того, как это применимо на практике — совершенно другая тема.

Например, что будет, если наш мир не является сеткой?

Что если персонаж не может мгновенно поворачиваться на 90 градусов?

Как построить граф, если мир бесконечен?

Что если нас не волнует длина пути, но мы зависим от солнечной энергии и нам как можно больше нужно находиться под солнечным светом?

Как найти кратчайший путь к любому из двух конечных узлов?

Функция стоимости

В первых примерах мы искали кратчайший путь между начальным и конечным узлами. Однако вместо того, чтобы хранить частичные длины путей в переменной length, мы назвали её cost. Почему?

Мы можем заставить A* искать не только кратчайший, но и лучший путь, причём определение «лучшего» можно выбирать, исходя из наших целей. Когда нам нужен кратчайший путь, стоимостью является длина пути, но если мы хотим минимизировать, например, потребление топлива, то нужно использовать в качестве стоимости именно его. Если мы хотим по максимуму увеличить «время, проводимое под солнцем», то затраты — это время, проведённое без солнца. И так далее.

В общем случае это означает, что с каждым ребром графа связаны соответствующие затраты. В показанных выше примерах стоимость задавалась неявно и считалась всегда равной 1, потому что мы считали шаги на пути. Но мы можем изменить стоимость ребра в соответствии с тем, что мы хотим минимизировать.

Функция критерия

Допустим, наш объект — это автомобиль, и ему нужно добраться до заправки. Нас устроит любая заправка. Требуется кратчайший путь до ближайшей АЗС.

Наивный подход будет заключаться в вычислении кратчайшего пути до каждой заправки по очереди и выборе самого короткого. Это сработает, но будет довольно затратным процессом.

Что если бы мы могли заменить один goal_node на метод, который по заданному узлу может сообщить, является ли тот конечным или нет. Благодаря этому мы сможем искать несколько целей одновременно. Также нам нужно изменить эвристику, чтобы она возвращала минимальную оцениваемую стоимость всех возможных конечных узлов.

В зависимости от специфики ситуации мы можем и не иметь возможности достичь цели идеально, или это будет слишком много стоить (если мы отправляем персонажа через половину огромной карты, так ли важна разница в один дюйм?), поэтому метод is_goal_node может возвращать true, когда мы находимся «достаточно близко».

Полная определённость не обязательна

Представление мира в виде дискретной сетки может быть недостаточным для многих игр. Возьмём, например, шутер от первого лица или гоночную игру. Мир дискретен, но его нельзя представить в виде сетки.

Но есть проблема и посерьёзней: что если мир бесконечен? В таком случае, даже если мы сможем представить его в виде сетки, то у нас просто не будет возможности построить соответствующий сетке граф, потому что он должен быть бесконечным.

Однако не всё потеряно. Разумеется, для алгоритма поиска по графам нам определённо нужен граф. Но никто не говорил, что граф должен быть исчерпывающим!

Если внимательно посмотреть на алгоритм, то можно заметить, что мы ничего не делаем с графом, как целым; мы исследуем граф локально, получая узлы, которых можем достичь из рассматриваемого узла. Как видно из демо A*, некоторые узлы графа вообще не исследуются.

Так почему бы нам просто не строить граф в процессе исследования?

Мы делаем текущую позицию персонажа начальным узлом. При вызове get_adjacent_nodes она может определять возможные способы, которыми персонаж способен переместиться из данного узла, и создавать соседние узлы на лету.

За пределами трёх измерений

Даже если ваш мир действительно является 2D-сеткой, нужно учитывать и другие аспекты. Например, что если персонаж не может мгновенно поворачиваться на 90 или 180 градусов, как это обычно и бывает?

Состояние, представляемое каждым узлом поиска, не обязательно должно быть только позицией; напротив, оно может включать в себя произвольно сложное множество значений. Например, если повороты на 90 градусов занимают столько же времени, сколько переход из одной ячейки в другую, то состояние персонажа может задаваться как [position, heading]. Каждый узел может представлять не только позицию персонажа, но и направление его взгляда; и новые рёбра графа (явные или косвенные) отражают это.

Если вернуться к исходной сетке 5×5, то начальной позицией поиска теперь может быть [A, East]. Соседними узлами теперь являются [B, East] и [A, South] — если мы хотим достичь F, то сначала нужно скорректировать направление, чтобы путь обрёл вид [A, East], [A, South], [F, South].

Шутер от первого лица? Как минимум четыре измерения: [X, Y, Z, Heading]. Возможно, даже [X, Y, Z, Heading, Health, Ammo].

Учтите, что чем сложнее состояние, тем более сложной должна быть эвристическая функция. Сам по себе A* прост; искусство часто возникает благодаря хорошей эвристике.

Заключение

Цель этой статьи — раз и навсегда развеять миф о том, что A* — это некий мистический, не поддающийся расшифровке алгоритм. Напротив, я показал, что в нём нет ничего загадочного, и на самом деле его можно довольно просто вывести, начав с самого нуля.

Дальнейшее чтение

У Амита Патела есть превосходное «Введение в алгоритм A*» [перевод на Хабре] (и другие его статьи на разные темы тоже великолепны!).

Зачем нужен pathfinder и как его внедрить в игру так, чтобы игроки не считали врагов идиотами?

Поиск пути или pathfinder — определение компьютером самого оптимального маршрута между двумя точками. С ним часто можно столкнуться при разработке игр, например, если в них есть свободно передвигающиеся враги. В этой статье мы разберёмся, где и зачем поиск пути может пригодиться, и как подступиться к этой проблеме.

Почему возникает проблема поиска пути?

Компьютерным болванчикам нельзя просто сказать: «Эй ты, иди к башне!», — как людям. Им нужно прописать чёткий набор команд (иди один метр влево, потом метр вперёд и т.д.) или указать путь из промежуточных точек, чтобы они успешно добрались от точки A до точки B. Как раз нахождением этих промежуточных точек и занимается алгоритм поиска пути. Но этим его задачи не ограничиваются. Дополнительно он может определять расстояние до цели и то, возможно ли вообще добраться до какой-то точки.

Есть такой вид игр-головоломок — лабиринт Минотавра. Игрока помещают на сетчатое поле со стенками. Одна из клеток поля является выходом, а на другой стоит монстр. Задача игрока — добраться до выхода раньше, чем монстр доберётся до него. Игрок и монстр ходят по очереди на сколько-то клеток, но монстр всегда перемещается быстрее игрока.

Игрок бы постоянно проигрывал, но у монстра есть минус: он хоть и быстр, но туп. Он всегда пытается добраться до игрока кратчайшим способом и не обращает внимание на то, что в лабиринте есть стены. Если монстру на пути встречается стена, он просто стоит и грустно вздыхает перед ней, не пытаясь обойти.

В таких играх глупость врага оправдана, так как она является частью геймплея головоломки. В остальных играх пользователь ожидает, что враг начнёт искать пути обхода, а не будет застревать в камнях и деревьях.

Как найти путь?

Задача поиска пути состоит из двух этапов: адаптирование игрового мира в математическую модель и поиск в этой модели пути между двумя точками.

Адаптирование игрового мира

Компьютер не может просто посмотреть на камень и сказать, что это камень. Поэтому ему надо описать игровой мир в виде чисел и выбрать набор признаков, по которым будет определяться, что между двумя точками можно пройти.

Большая часть алгоритмов строится на графах — в математике так называется фигура, которая состоит из точек и соединяющих их линий (рёбер). Поэтому пути прохода по игровому миру превращают в графы. В качестве точек-кружочков обычно берут минимальную площадь мира, в которой передвижение от одного края до второго происходит мгновенно (или же за достаточно маленькое время, чтобы считать его мгновенным). Иначе говоря, в играх эти кружочки — это позиции персонажа. Рёбра же обозначают тот факт, что ты с первого куска мира можешь перейти на второй.

Одна из простых вариаций графа — игровая сетка, где кружочками являются клетки, а рёбра проводятся между любыми соседними клетками, свободными от препятствий. Проще всего разобраться в этом на примере пошаговых игр, у которых сетку видно невооружённым глазом, вроде Sneaky-Sneaky или Return of the Necrodancer.

Клетки, на которых стоят непреодолимые препятствия, обозначаются крестиком, а проходимые места — пустотой. Или, если говорить на языке программирования, клетки обозначаются 0 или 1, где 0 означает, что пройти нельзя, а 1 — что пройти можно. Более сложные игры вроде Heroes of Might and Magic III отличаются только тем, что их сетка рисуется более произвольно, а клетки, которые расположены на разных типах земли, отнимают разное количество шагов.

При работе с трёхмерными мирами можно использовать двухмерную карту проекции ландшафта с указанием высот в точках. В этом случае на каждой ячейке написана её высота, а проходимость определяется через разницу высот соседних клеток.

В Death Stranding упрощённую карту для поиска пути можно увидеть при сканировании местности. Крестиками показываются непроходимые места, жёлтым — проходимые с трудом, голубым — легко проходимые.

Зачастую адаптация игрового мира — это самая сложная часть, потому что алгоритмы поиска оптимальных маршрутов изобретены давно, можно даже найти готовый код для них. Поэтому разработчики внедряют один из алгоритмов и потом экспериментируют с разными моделями и вариациями сравнений двух путей, или комбинируют разные алгоритмы в попытках добиться наилучшего и наименее затратного результата.

Алгоритмы поиска пути

Как бы человек искал выход, если бы его внезапно высадили посреди лабиринта? Например, он мог бы воспользоваться правилом «одной руки», отмечать обследованные пути верёвкой или мелом, пока не найдёт выход. Большинство алгоритмов действуют по схожей схеме, за исключением того, что компьютер может размножаться и «ощупывать» одновременно несколько путей. Различаются же алгоритмы точностью и скоростью получения результата.

Поиск в ширину

Поиск в ширину начинает исследовать пути от начальной точки сразу во все стороны. Сначала ощупывает соседние со стартом точки, потом соседние с ними и так далее, пока не найдёт конечную точку или поле не закончится.

Работу алгоритма можно представить в виде монстра с щупальцами, которые могут раздваиваться. Это монстр сидит на стартовой клетке, тянет щупальца во все стороны и проверяет, можно ли здесь пройти. Если щупалец не хватает, он раздваивает одно из них, чтобы охватить все возможные дороги. Эта эпопея продолжается, пока одно из щупалец не нащупает конечную точку. Тогда путь щупальца от старта до конца и становится кратчайшим путём.

Если же описывать работу в виде алгоритма, то получатся такие шаги:

Такой алгоритм на каждом N цикле находит все точки, к которым можно дойти за N шагов. Чтобы получить путь, нужно запоминать не только проверенные точки, а ещё и последовательность точек до них. Или хотя бы предыдущую точку, с которой мы пришли на эту, чтобы по шагам восстановить маршрут.

Поиск в ширину хорошо работает, если переход между соседними точками всегда занимает одинаковое количество времени (или другого параметра, по которому мы стараемся минимизировать путь). Но если это не так, то он превращается в алгоритм Дейкстры.

Алгоритм Дейкстры

Алгоритм Дейкстры работает с моделями, в которых расстояния между точками могут быть разными. Например, в Heroes of Might and Magic III проход по снегу тратит на 50% больше очков перемещения, так что условно можно посчитать, что проход по снегу занимает 1.5 шага вместо 1 по обычной земле. В этом случае обход снега может быть быстрее, чем проход напрямую по нему, хоть визуально и будет пройдено большее расстояние.

От поиска в ширину алгоритм Дейкстры отличает пара моментов. Кроме сохранения уже проверенных точек, сохраняется ещё и количество шагов, потраченных на то, чтобы добраться до них. Точки исключаются из последующей проверки не тогда, когда были уже проверены, а только в случае, если предыдущий найденный путь до неё занимал меньшее количество «шагов». Точки в списке рассматриваются не по порядку, сначала выбираются те, до которых меньше идти.

Алгоритм:

Эвристический алгоритм

Минусом как поиска в ширину, так и алгоритма Дейкстры является то, что компьютер ищет путь во все стороны сразу и тратит время на очевидно бесперспективные пути, которые отдаляют от цели, а не приближают к ней.

Эвристический алгоритм помогает это исправить. Он работает точно так же, как и алгоритм Дейкстры, но с одним изменением. При выборе следующей точки на рассмотрение первой выбирается не та точка, которая ближе к началу пути, а та, что ближе к концу. Расстояние до конца рассчитывается приблизительно, например, просто как расстояние между двумя точками на карте.

Минус алгоритма в том, что найденный путь необязательно будет самым кратким. Зато его нахождение потребует меньше времени.

Алгоритм A*

Алгоритм А* пытается усидеть на обоих стульях сразу: найти кратчайшее расстояние, но сделать это за меньшее время, чем алгоритм Дейкстры. Поэтому следующая точка на рассмотрение выбирается по минимальной сумме расстояний до начала и до конца пути. Это единственное отличие от предыдущих алгоритмов.

Есть и другие алгоритмы, которые дают преимущества при разных условиях. Сами алгоритмы по поиску пути довольно просты, но они работают для сферических идеальных условий в вакууме. В реальных играх существует много нюансов, которые могут усложнить алгоритм. Например, может быть несколько вариантов перемещений, повороты, препятствия могут двигаться, могут быть узкие места, в которых врагам желательно не толпиться. Каждое такое условие делает движение более интересным, но и замедляет работу алгоритма. Из-за этого приходится что-то упрощать или выкручиваться по-другому для оптимизации работы игры.

Несколько интересных примеров можно прочитать в статьях про новый алгоритм поиска пути в Factorio и про устройство поведения полчищ крыс в A Plague Tale: Innocence.

Дополнительные материалы

Бонус: на этом сайте можно наглядно визуализировать работу разных алгоритмов, самостоятельно выстроив для них преграды.

Текст написала Алёна Киселёва, автор в Smirnov School. Мы готовим концепт-художников, левел-артистов и 3D-моделеров для игр и анимации. Если придёте к нам на курс, не забудьте спросить о скидке для читателей с DTF.

Оптимальная игра в 2048 с помощью марковского процесса принятия решений +30

Математика, Математика

---

Рекомендация: подборка платных и бесплатных курсов монтажа видео — https://katalog-kursov.ru/

В предыдущей статье про 2048 мы использовали цепи Маркова, чтобы выяснить, что в среднем для победы нужно не менее 938,8 ходов, а также исследовали с помощью комбинаторики и полного перебора количество возможных конфигураций поля игры.

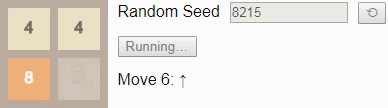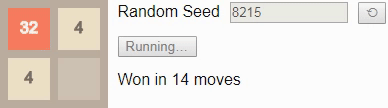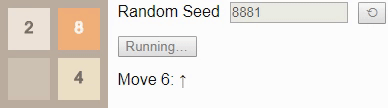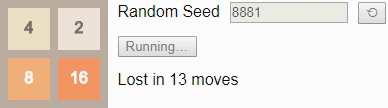
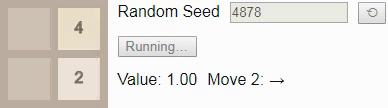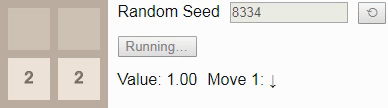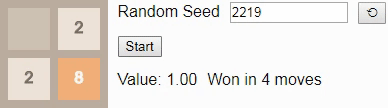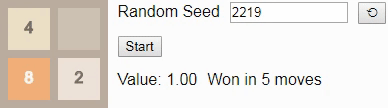
В этом посте мы используем математический аппарат под названием «марковский процесс принятия решений» для нахождения доказуемо оптимальных стратегий игры 2048 для полей размером 2×2 и 3×3, а также на доске 4×4 вплоть до тайла 64. Например, вот оптимальный игрок в игру 2×2 до тайла 32:

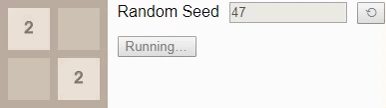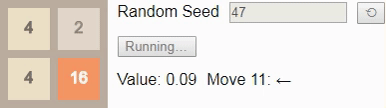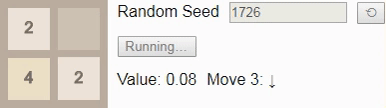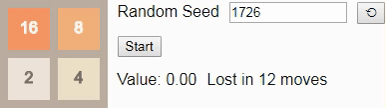
Случайное начальное число (random seed) определяет случайную последовательность тайлов, добавляемых игрой на поле. «Стратегия» игрока задаётся таблицей, называемой алгоритмом (policy). Она сообщает нам, в каком направлении нужно сдвигать тайлы в любой возможной конфигурации поля. В этом посте мы рассмотрим способ создания алгоритма, оптимального в том смысле, что он максимизирует шансы игрока на получение тайла 32.

Оказывается, что в игре 2×2 до тайла 32 очень сложно выиграть — даже если играть оптимально, игрок выигрывает только примерно в 8% случаев, то есть игра оказывается не особо интересной. Качественно игры 2×2 сильно отличаются от игр 4×4, но они всё равно полезны для знакомства с основными принципами.

В идеале мы хотим найти оптимальный алгоритм для полной игры на поле 4×4 до тайла 2048, но как мы убедились из предыдущего поста, количество возможных конфигураций поля очень велико. Поэтому невозможно создать оптимальный алгоритм для полной игры, по крайней мере, с помощью используемых здесь методов.

Однако мы можем найти оптимальный алгоритм для укороченной игры 4×4 до тайла 64, и, к счастью, мы увидим, что оптимальная игра на полях 3×3 качественно выглядит похожей на некоторые успешные стратегии полной игры.

Код (исследовательского качества), на котором основана эта статья, выложен в открытый доступ.

Марковские процессы принятия решений (MDP) — это математическая основа моделирования и решения задач, в которой нам необходимо предпринять последовательность взаимосвязанных решений в условиях неопределённости. Таких задач полно в реальном мире, и MDP находят активное применение в экономике, финансовом деле и в искусственном интеллекте. В случае 2048 последовательность решений — это направление перемещения тайлов в каждом ходе, а неопределённость возникает потому, что игра добавляет тайлы на поле случайным образом.

Чтобы представить игру 2048 в виде MDP, нам нужно записать её определённым образом. В него входят шесть основных концепций: состояния, действия и вероятности перехода кодируют динамику игры; вознаграждения, значения и алгоритмы используются для фиксации целей игрока и способов их достижения. Чтобы развить эти шесть концепций, мы возьмём в качестве примера наименьшую нетривиальную игру, похожую на 2048, которая играется на поле 2×2 только до тайла 8. Давайте начнём с первых трёх концепций.

Состояния, действия и вероятности перехода

Состояние фиксирует конфигурацию поля в заданный момент игры, указывая значение тайла в каждой из клеток поля. Например, — это возможное состояние в игре на поле 2×2. Действие — это перемещение влево, вправо, вверх или вниз. Каждый раз, когда игрок совершает действие, процесс переходит в новое состояние.

Вероятности перехода кодируют динамику игры, определяя состояния, которые с большей вероятностью будут следующими, с учётом текущего состояния и действия игрока. К счастью, мы можем точно узнать, как работает 2048, прочитав её исходный код. Самым важным¹ является процесс, который использует игра для размещения на поле случайного тайла. Этот процесс всегда одинаков: выбираем свободную клетку с одинаковой вероятностью и добавляем новый тайл или со значением 2 с вероятностью 0,9, или со значением 4 с вероятностью 0,1.

В начале каждой игры с помощью этого процесса на поле добавляются два тайла. Например, одним из таких возможных начальных состояний является такое: . Для каждого возможного в этом состоянии действия, а именно Left, Right, Up и Down, возможные следующие состояния и соответствующие вероятности перехода имеют следующий вид:

На этой схема стрелки обозначают каждый возможный переход в последующее состояние справа. Вес стрелки и метка обозначают соответствующую вероятность перехода. Например, если игрок сдвигает тайлы вправо (R), то оба тайла 2 сдвигаются к правому краю, оставляя слева две свободные клетки. Новый тайл будет с вероятностью 0,1 тайлом 4, и может появиться или в верхней левой, или в нижней левой клетке, то есть вероятность состояния равна

.

Из каждого из этих последующих состояний мы можем рекурсивно продолжать этот процесс перебора возможных действий и каждого из их последующих состояний. Для возможными последующими состояниями являются такие:

Здесь сдвиг вправо невозможен, поскольку ни один из тайлов не может сдвинуться вправо. Более того, если игрок достигнет последующего состояния , выделенного красным, то он проиграет, поскольку из этого состояния невозможно выполнить допустимых действий. Это произойдёт, если игрок выполнит сдвиг влево, а игра разместит тайл 4, что произойдёт с вероятностью 0,1; из этого можно предположить, что сдвиг влево не является наилучшим действием в этом состоянии.

Ещё один последний пример: если игрок сдвинется вверх, а не влево, то одним из возможных последующих состояний будет , и если мы переберём все допустимые действия и последующие состояния из этого состояния, то мы сможем увидеть, что сдвиг влево или вправо приведёт тогда к тайлу 8, что означает нашу победу (выделенную зелёным):

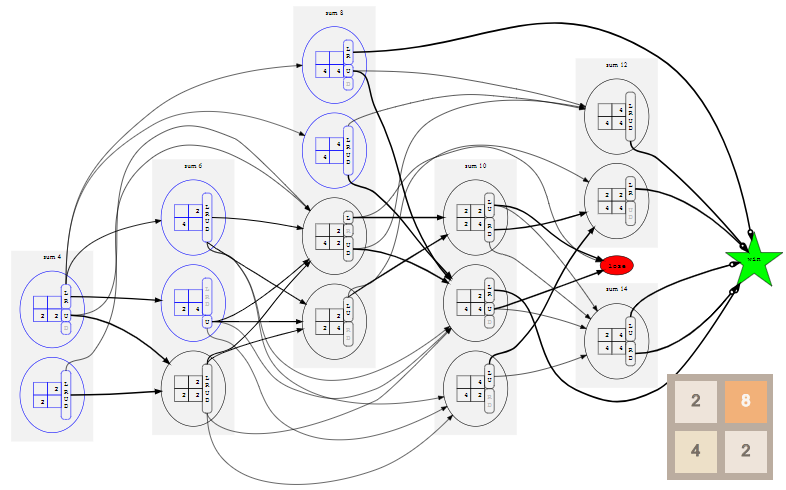
Если мы повторим этот процесс для всех возможных начальных состояний и всех их возможных последующих состояний, и так далее рекурсивно, пока не достигнем состояния выигрыша или проигрыша, то сможем построить полную модель со всеми возможными состояниями, действиями и их вероятностями перехода. Для игры 2×2 до тайла 8 эта модель выглядит так (нажмите для увеличения; возможно придётся прокрутить страницу вниз):

Чтобы сделать схему поменьше, все состояния проигрыша нужно свести к единому состоянию lose, показанному красным овалом, а все выигрышные состояния аналогичным образом свести к единому состоянию win, показанному зелёной звездой. Это возможно, потому что на самом деле нас не интересует, как именно выиграл или проиграл игрок, а важен сам результат.

Игра приближённо протекает на схеме слева направо, потому что состояния упорядочены в «слои» по сумме своих тайлов. Полезное свойство игры заключается в том, что после каждого действия сумма тайлов на поле увеличивается на 2 или на 4. Так получается потому, что слияние тайлов не изменяет сумму тайлов на поле, а игра всегда добавляет или 2, или 4. Возможные начальные состояния, которые являются слоями с суммой 4, 6 и 8, показаны синим.

Даже в модели такого минимального примере 70 состояний и 530 переходов. Однако, можно значительно снизить эти значения, заметив, что многие из перечисленных нами состояний тривиально связаны поворотами и отражениями, как описано в Приложении А. На практике это наблюдение очень важно для уменьшения размера модели и её эффективного решения. Кроме того, оно позволяет создавать более удобные схемы, но для перехода ко второму набору концепций марковского процесса принятия решений это не обязательно.

Вознаграждения, значения и алгоритмы

Чтобы завершить спецификацию модели, нам нужно закодировать каким-то образом тот факт, что цель игрока заключается в достижении состояния win². Мы сделаем это, определив вознаграждения. В общем случае при каждом переходе MDP в состояние игрок получает вознаграждение, зависящее от состояния. Мы присвоим вознаграждению за переход в состояние win значение 1, а за переход в другие состояния — значение 0. То есть единственный способ получить вознаграждение — достичь состояния выигрыша³.

Теперь, когда у нас есть модель MDP игры, описанная относительно состояний, действий, вероятностей перехода и вознаграждений, мы готовы к её решению. Решение MDP называется алгоритмом. По сути, это таблица, в которой для каждого возможного состояния указано действие, которое нужно совершить в этом состоянии. Решить MDP — значит найти оптимальный алгоритм, то есть такой, который позволяет игроку со временем получить как можно большее вознаграждение.

Чтобы сделать её точной, нам нужна последняя концепция MDP: значение состояния в соответствии с заданным алгоритмом — это ожидаемое вознаграждение, которое получит игрок, если начнёт с этого состояния и затем будет следовать алгоритму. Для объяснения этого необходимы некоторые записи.

Пусть

— это множество состояний, и для каждого состояния

будет множеством действий, допустимых в состоянии

. Пусть

обозначает вероятность перехода в каждое последующее состояние

, учитывая, что процесс находится в состоянии

и игрок совершает действие

. Пусть

обозначает вознаграждение за переход в состояние

. Наконец, пусть

означает алгоритм, а

обозначает действие, которое нужно совершить в состоянии

, чтобы следовать алгоритму

.

Для заданного алгоритма

и состояния

значение состояния

согласно

равно

где первый член — это мгновенное вознаграждение, а суммирование даёт ожидаемое значение последующих состояний при условии, что игрок будет продолжать следовать алгоритму.

Коэффициент

— это коэффициент обесценивания, который замещает значение мгновенного вознаграждения на значение ожидаемого в будущем вознаграждения. Другими словами, он учитывает стоимость денег с учётом фактора времени: вознаграждение сейчас обычно стоит больше, чем то же вознаграждение позже. Если

близок к 1, то это означает, что игрок очень терпелив: он не против подождать будущего вознаграждения; аналогично, меньшие значения

означают, что игрок менее терпелив. Пока мы присвоим коэффициенту обесценивания

значение 1, что соответствует нашему предположению о том, что игрока волнует только победа, а не время, которое для неё потребуется ⁴.

Так как же нам найти алгоритм? В каждом из состояний мы хотим выбирать действие, максимизирующее ожидаемое будущее вознаграждение:

Это даёт нам два связанных уравнения, которые мы можем решить итеративно. То есть выбрать исходный алгоритм, который может быть очень простым, вычислить значение каждого состояния в соответствии с этим простым алгоритмом, а затем найти новый алгоритм на основании этой функции значений, и так далее. Примечательно, что в очень ограниченных технических условиях такой итеративный процесс гарантированно сойдётся к оптимальному алгоритму

и оптимальной функции значений

относительно этого оптимального алгоритма.

Такой стандартный итеративный подход хорошо срабатывает для моделей MDP игр на поле 2×2, но не подходит для моделей игр 3×3 и 4×4, которые имеют гораздо больше состояний, а потому потребляют гораздо больше памяти и вычислительных мощностей. К счастью, оказывается, что мы можем воспользоваться структурой наших моделей 2048 для гораздо более эффективного решения этих уравнений (см. Приложение Б).

Оптимальная игра на поле 2×2

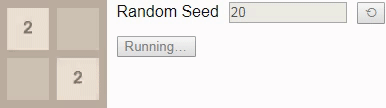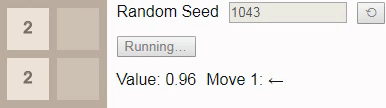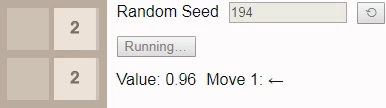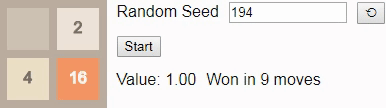
Теперь мы готовы увидеть оптимальные алгоритмы в действии! Если ввести начальное число 42 и нажмёте на кнопку Start в оригинале статьи, то достигнете тайла 8 за 5 ходов. Начальное число определяет последовательность новых тайлов, размещаемых игрой; если выбрать другое начальное число, нажав на кнопку ?, то (обычно) игра будет развиваться иначе.

В игре 2×2 до тайла 8 смотреть особо не на что. Если игрок следует оптимальному алгоритму, то всегда будет выигрывать. (Как мы видели выше при построении вероятностей перехода, если игрок играет неоптимально, то есть возможность проигрыша.) Это отражается в том, что значение состояния на протяжении всей игры остаётся равным 1.00 — при оптимальной игре есть хотя бы одно действие в каждом достижимом состоянии, которое ведёт к победе.

Если мы вместо этого попросим игрока сыграть до тайла 16, то даже при оптимальной игре победа уже не будет гарантирована. В этом случае при игре до тайла 16 выбор нового начального числа должно приводить к победе в 96% случаев, поэтому мы в качестве начального числа выбрали одно из тех немногих, что ведут к проигрышу.

В результате присвоения коэффициенту обесценивания

значения 1 значение каждого состояния сообщает нам вероятность победы из этого состояния. Здесь значение начинается с 0.96, а затем постепенно снижается до 0.90, потому что исход зависит от того, будет ли следующий тайл иметь значение 2. К сожалению, игра выставляет тайл 4, поэтому игрок проигрывает, несмотря на оптимальную игру.

Наконец, мы ранее установили, наибольшим достижимым тайлом на поле 2×2 является тайл 32, поэтому давайте посмотрим на оптимальный алгоритм. Здесь вероятность выигрыша падает всего до 8%. (Это та же игра и тот же алгоритм, использованный во введении, но теперь интерактивные.)

Стоит заметить, что каждый из показанных выше алгоритмов является оптимальным алгоритмом соответствующей игры, но гарантий его уникальности нет. Может быть множество аналогичных оптимальных алгоритмов, но мы с определённостью можем сказать, что ни один из них не является строго лучшим.

Если вы хотите более подробно исследовать эти модели для игры 2×2, то в Приложении А есть схемы, показывающие все возможные пути прохождения игры.

Оптимальная игра на поле 3×3

На поле 3×3 можно играть до тайла 1024, и у такой игры 25 миллионов состояний. Поэтому начертить схему MDP, которую мы делали для игр 2×2, совершенно невозможно, но мы всё равно можем понаблюдать за оптимальным алгоритмом в действии⁵:

Так же, как и в игре 2×2 до тайла 32, в игре 3×3 до тайла 1024 очень сложно выиграть — при оптимальной игре вероятность выигрыша всего около 1%. В качестве менее бесполезного развлечения можно выбрать игру до тайла 512, в которой вероятность выигрыша при оптимальной игре гораздо выше, примерно 74%:

Рискуя антропоморфировать большую таблицу состояний и действий, которой и является алгоритм, я вижу здесь элементы стратегий, которые я использую при игре в 2048 на поле 4×4⁶. Мы видим, что алгоритм засовывает тайлы с высокими значениями на края и обычно в углы (хотя в игре до 1024 он часто ставит тайл 512 посередине границы поля). Также можно заметить, что он «ленив» — даже когда есть два тайла с высокими значениями, которые можно объединить, он продолжает объединять значения с меньшими значениями. Логично, что особенно в стеснённых условиях поля 3×3, стоит пользоваться возможностью увеличения суммы своих тайлов без риска (мгновенного) проигрыша — если ему не удаётся объединить меньшие тайлы, он всегда может объединить большие, что освобождает поле.

Важно заметить, что не обучали алгоритм этим стратегиям и не давали ему никаких подсказок
о том, как играть. Все его поведения и кажущийся интеллект возникают исключительно из решения задачи оптимизации с учётом переданными нами вероятностей перехода и функции вознаграждения.

Оптимальная игра на поле 4×4

Как выяснилось в предыдущем посте, игра до тайла 2048 на поле 4×4 имееет не менее триллионов состояний, поэтому пока невозможно даже перечислить все состояния, не говоря уж о решении MDP для получения оптимального алгоритма.

Однако мы можем выполнить перебор и выполнить решение для игры 4×4 до тайла 64 — в этой модели будет «всего» 40 миллиардов состояний. Как и в игре 2×2 до тайла 8, при оптимальной игре проиграть невозможно. Поэтому наблюдать за ней не очень интересно, так как во многих случаях существует несколько хороших состояний, и выбор между ними выполняется произвольным образом.

Однако если мы уменьшим коэффициент обесценивания

, что сделает игрока немного нетерпеливым, то он будет предпочитать выигрывать быстрее, а не позже. Тогда игра будет выглядеть немного более нацеленной. Вот оптимальный игрок при

:

Изначально значение равно примерно 0.72; точное начальное значение отражает ожидаемое количество шагов, которые потребуются для победы из случайно выбранного начального состояния. Оно постепенно увеличивается с каждым ходом, потому что вознаграждение за достижение состояния победы становится ближе. Алгоритм снова хорошо использует границы и углы поля для построения последовательностей тайлов в удобном для объединения порядке.

Заключение

Мы разобрались, как представить игру 2048 в виде марковского процесса принятия решений и получили доказуемо оптимальные алгоритмы для игр на полях 2×2 и 3×3, а также для ограниченной игры на поле 4×4.

Использованные здесь методы требуют для решения перечисления всех состояний модели. Применение эффективных стратегий перечисления состояний и эффективных стратегий решения этой модели (см. Приложение Б) делает их пригодными для моделей, у которых до 40 миллиардов состояний, то есть для игры 4×4 до 64. Вычисления для этой модели потребовали примерно одной недели работы экземпляра OVH HG-120 с 32 ядрами, 3,1ГГц и 120ГБ ОЗУ. Следующая ближайшая игра 4×4 до тайла 128 скорее всего будет содержать во много раз больше состояний и потребует гораздо больше вычислительных мощностей. Вычисление доказуемо оптимального алгоритма для полной игры до 2048, вероятно, потребует других методов решения.

Часто выясняется, что MDP на практике слишком велики для решения, поэтому существуют проверенные техники нахождения приближенных решений. В них обычно используется хранение приблизительных функции значений и/или алгоритма, например, с помощью обучения (возможно, глубокого) нейросети. Также вместо перечисления всего пространства состояний их можно обучать на данных симуляций, используя методы обучения с подкреплением. Существование доказуемо оптимальных алгоритмов для игр меньшего размера могут сделать 2048 полезным испытательным стендом для таких методов — это может стать интересной темой для исследований в будущем.

---

Приложение А: канонизация

Как мы видели на примере полной модели для игры 2×2 до тайла 8, количество состояний и переходов очень быстро растёт, и становится сложно графически представить даже игры на поле 2×2.

Чтобы сохранять контроль над размером модели, мы можем снова воспользоваться наблюдением из предыдущего поста о перечислении состояний: многие из последующих состояний являются просто поворотами и отражениями друг друга. Например, состояния

и

являются просто зеркальными копиями — это просто отражения по вертикальной оси. Если лучшим действием в первом состоянии будет сдвиг влево, то лучшим действием во втором состоянии обязательно будет сдвиг вправо. То есть с точки зрения принятия решений о выборе действия достаточно выбрать одно из состояний в качестве канонического и определять наилучшее действие, которое нужно сделать из канонического состояния. Каноническое состояние заданного состояния получается нахождением всех его возможных поворотов и отражений, записью каждого как числа по основанию 12 и подбором состояния по наименьшему числу — подробности см. в предыдущем посте. Важно здесь то, что каждое каноническое состояние заменяет класс эквивалентных состояний, связанных с ним поворотом или отражением, поэтому нам не придётся иметь с ними дело по отдельности. Заменив представленные выше последующие состояния их каноническими состояниями, мы получим более компактную схему:

К сожалению, из схемы следует, что сдвиг вверх (U) из каким-то образом приведёт к . Однако парадокс разрешается, если читать стрелки и добавлять при необходимости поворот или отражение, чтобы найти действительное каноническое состояние последующего состояния.

Эквивалентные действия

Также мы можем заметить, что на показанной выше схеме на самом деле не важно, в каком направлении игрок выполнит сдвиг из состояния — канонические последующие состояния и их вероятности переходов одинаковы для всех действий. Чтобы понять, почему, стоит посмотреть на «промежуточное состояние» после того, как игрок выполнил сдвиг для перемещения тайлов, но когда игра ещё не добавила новый случайный тайл:

Промежуточные состояния отмечены пунктирными линиями. Важнее всего здесь заметить то, что все они связаны поворотом на 90°. Эти повороты не важны, если мы в результате канонизируем последующие состояния.

В более общем смысле, если два или более действий имеют одинаковое каноническое «промежуточное состояние», то у этих действий должны быть одинаковые канонические последующие состояния, а потому они эквивалентны. В показанном выше примере каноническим промежуточным состоянием оказывается последнее: .

Следовательно, мы можем ещё больше упростить схему для , если просто объединим все эквивалентные действия:

Разумеется, состояния, для которых все действия эквивалентны в таком смысле, встречаются относительно редко. Рассмотрев ещё одно потенциальное начальное состояние , мы увидим, что сдвиги влево и вправо эквивалентны, но сдвиг вверх отличается; сдвиг вниз недопустим, потому что тайлы уже находятся внизу.

Схемы моделей MDP для игр 2×2

Благодаря канонизации мы можем уменьшить модели до масштаба, при котором можно отрисовать полные MDP для некоторых небольших игр. Давайте снова начнём с наименьшей нетривиальной модели: игры 2×2 до тайла 8:

По сравнению со схемой без канонизации, эта оказалась гораздо более компактной. Мы видим, что кратчайшая возможная игра состоит всего из единственного хода: если нам повезёт начать из состояния с двумя соседними тайлами 4, что бывает только в одной игре на 150, нам достаточно всего лишь соединить их, чтобы получить тайл 8 и состояние win. С другой стороны, мы видим, что проиграть всё равно возможно: если из состояния игрок выполнит сдвиг вверх, то с вероятностью 0,9 получит , а если снова сделает сдвиг вверх, то с вероятностью 0,9 получит , и в этот момент игра будет проиграна.

Мы можем ещё сильнее упростить схему, если будем знать оптимальный алгоритм. Определение алгоритма порождает из модели MDP цепь Маркова, потому что каждое состояние имеет единственное действие или группу эквивалентных действий, определяемых алгоритмом. Порождённая цепь для игры 2×2 до 8 имеет такой вид:

Мы видим, что к состоянию lose больше не ведёт ни одно ребро, потому что при оптимальной игре в 2×2 до тайла 8 проиграть невозможно. Кроме того, каждое состояние теперь помечено своим значением, которое в этом случае всегда равно 1,000. Поскольку мы присвоили коэффициенту обесценивания

значение 1, то значение состояния на самом деле является вероятностью выигрыша из этого состояния при оптимальной игре.

Схемы становятся немного хаотичнее, но мы можем построить похожие модели для игры 2×2 до тайла 16:

Если мы посмотрим на оптимальный алгоритм для игры до тайла 16, то увидим, что начальные состояния (синие) имеют значения меньше единицы, и что существуют пути к состоянию lose, в частности, из двух состояний, в которых сумма тайлов равна 14:

То есть если мы будем играть в эту игру до тайла 16 оптимальным образом, то всё равно сможем проиграть, и это будет зависеть от конкретной последовательности выдаваемых нам игрой тайлов 2 и 4. Однако в большинстве случаев мы выиграем — значения в начальных состояния примерно равны 0,96, поэтому мы ожидаем выигрыша примерно в 96 играх из сотни.

Однако наши перспективы при игре до тайла 32 на поле 2×2 гораздо хуже. Вот полная модель:

Мы видим, что множество рёбер ведёт к состоянию lose, и это плохой признак. Это подтверждается, если посмотреть на схему, ограниченную оптимальной игрой:

Среднее значение для начальных состояний приблизительно равно 0.08, поэтому стоит ожидать победы примерно в 8 играх из ста. Основная причина этого становится очевидной, когда мы посмотрим на правую часть схемы: достигнув состояния с суммой 28, единственный способ победить — получить тайл 4, чтобы достичь состояния . Если мы получим тайл 2, что происходит в 90% случаев, то проиграем. Наверно, такая игра будет не очень интересной.

Приложение Б: методы решения

Для эффективного решения моделей MDP, похожих на те, что мы построили здесь для 2048, мы можем использовать важные свойства их структуры:

1. Модель перехода является направленным ациклическим графом (НАГ). С каждым ходом сумма тайлов должна увеличиваться, а конкретно — на 2 или на 4, то есть возврат к уже посещённому состоянию невозможен.
2. Более того, состояния можно упорядочить в «слои» по суммам их тайлов, как мы делали это в рисунке первой модели MDP, и все переходы будут выполняться из текущего слоя с суммой или в следующий слой с суммой , или в слой после него, с суммой .
3. Все состояния в слое с наибольшей суммой будут переходить в состояние проигрыша или выигрыша, которые имеют известные значения, а именно 0 или 1.

Свойство (3) означает, что мы можем пройти в цикле по всем состояниям в последнем слое, в котором известны все последующие значения, и сгенерировать функцию значений для этого последнего слоя. Далее, благодаря свойству (2), мы знаем, что состояния во втором с конца слое должны переходить или в состояния в последнем слое, для которого мы только что вычислили значения, или в состояние победы или проигрыша, которые имеют известные значения. Таким образом мы можем проделать путь назад, слой за слоем, всегда зная значения состояний в следующих двух слоях; это позволяет нам построить и функцию значений, и оптимальный алгоритм для текущего слоя.

В предыдущем посте мы выполняли работу в прямом порядке, с начальных состояний и перечисляли все состояния, слой за слоем, используя отображение-свёртку для распараллеливания работы внутри каждого слоя. Для решения мы можем использовать выходные данные этого перечисления, которые являются огромным списком состояний, чтобы выполнить работу в обратном порядке, снова применяя отображение-свёртку для параллельной работы в каждом слое. Как и в прошлый раз, мы разобьём слои на «части» по их максимальным значениям тайлов с отслеживанием дополнительной информации.

Основная реализация решателя по-прежнему довольно требовательна к памяти, потому что для обработки текущей части за один проход ей ей нужно хранить в памяти функции значений нескольких (до четырёх) частей. Можно снизить это требование до одновременного хранения в памяти всего одной части с помощью того, что обычно называется

— значения для каждой возможной пары состояние-действие согласно алгоритму

, а не

, но эта реализация решателя оказалась гораздо более медленной, поэтому все результаты получены с помощью основного решателя

на машине с большим количеством ОЗУ.

В случае обоих решателей слоистая структура модели позволяет нам построить и решить модель всего одним проходом вперёд и одним проходом назад, что является значительным улучшением по сравнению с обычным методом итеративного решения. Это одна из причин, по которой мы способны решать такие достаточно большие модели MDP с миллиардами состояний. Также важными причинами являются методы канонизации из Приложения А, позволяющие снизить количество учитываемых состояний, и низкоуровневые оптимизации эффективности из предыдущего поста.

---

Я благодарю Хоуп Томас за редактуру черновиков этой статьи.

Если вы дочитали до этого места, то вам, возможно, стоит подписаться на мой twitter, или даже выслать резюме на работу в Overleaf.

Примечания

1. Здесь также присутствуют определённые нюансы объединения тайлов: например, если у нас есть четыре тайла 2 в ряд, и мы выполняем сдвиг, чтобы соединить их, то результатом будет два тайла 4, а не один тайл 8. То есть мы не можем объединить только что соединённые тайлы за один сдвиг. Оригинал кода объединения тайлов находится здесь, а упрощённый, но аналогичный код, который я использовал для объединения линии (столбца или строки) тайлов — здесь; его тесты выложены тут.
2. Схемы графов взяты из потрясающего инструмента dot в graphviz.
3. Существуют и некоторые другие возможные цели. Например, в первом посте этой серии я пытался достичь целевого тайла 2048 за наименьшее возможное количество ходов; а многие люди стремятся достичь максимально возможного тайла, к чему стимулирует и система очков игры. Эти разные цели можно достичь, соответствующим образом настраивая модель и её вознаграждения. Например, простая награда в 1 за ход до проигрыша игрока будет соответствовать цели как можно более долгой игры, что, как мне кажется, аналогично стремлению к получению наибольшего возможного тайла.
4. С технической точки зрения, чтобы система вознаграждений работала в соответствии с описанием, в дополнение к состояниям win и lose нам нужно ещё одно особое состояние. Уравнения, которые мы выводим для и , подразумевают, что все состояния имеют хотя бы одно допустимое действие и последующее состояние, поэтому мы не можем просто остановить процесс в состояниях lose и win. Поэтому мы можем ввести поглощающее состояние end с тривиальным действием, которое просто возвращает процесс обратно к состоянию end с вероятностью 1. Тогда мы можем добавить тривиальное действие к состояниям lose и win, чтобы выполнялся переход к поглощающему состоянию end с вероятностью 1. Поскольку состояние end привлекает нулевое вознаграждение, оно не будет изменять результаты. Стоит также упомянуть, что существуют более общие способы определения MDP, которые предоставят другие способы обхода этой технической сложности, например, можно сделать вознаграждения зависящими от всего перехода, а не только от состояния, или сделать алгоритмы стохастическими (здесь проявляется побочный эффект: мы сможем обрабатывать состояния с недопустимыми действиями, но они потребуют дополнительных обозначений.
5. Кроме того, что коэффициент обесценивания хорошо обоснован в экономической теории, он часто требуется для обеспечения сходимости функции значений. Если процесс выполняется бесконечно и продолжает накапливать аддитивные вознаграждения, то он может накапливать бесконечное значение. Геометрическое обесценивание гарантирует, что бесконечная сумма всё равно будет сходящейся, даже если такое произойдёт. Для процессов со структурой вознаграждений, которые мы здесь рассматриваем, мы можем без проблем присвоить коэффициенту обесценивания значение 1, потому что процесс организован таким образом, что в нём не существует циклов с ненулевыми вознаграждениями, а потому все вознаграждения ограничены.
6. У алгоритмов 3×3 и 4×4 есть изъян: полностью оптимальные алгоритмы для каждого состояния слишком велики для загрузки в браузере(не говоря уже о том, что так мы злоупотребим великодушием GitHub, хостящего этот сайт). Поэтому игрок имеет доступ только к алгоритмам состояний, имеющих вероятность не менее от на самом деле возникающих во время игры согласно оптимальному алгоритму. Это означает, что, к сожалению, примерно одна сотая часть читателей выберет случайное начальное число, которое приведёт процесс к состоянию, не входящему в доступные клиенту данные, и в таком случае он завершится ошибкой. Эти состояния выбираются вычислением вероятностей перехода для поглощающей цепи Маркова, порождённой оптимальным алгоритмом. Математика здесь по сути такая же, как и в первом посте о цепях Маркова для игры 2048.
7. Разумеется, я не утверждаю, что великолепно играю в 2048. Данные из моего первого поста говорят об обратном!

Выигрышные стратегии в играх

На предыдущем уроке мы рассмотрели различные игры и примеры выигрышных стратегий в этих играх.

На этом уроке мы на практике научимся составлять алгоритмы выигрышных стратегий в различных играх. Кроме того, мы научимся записывать эти алгоритмы в виде блок-схем.

Рассмотрим следующую игру.

Пример 1.

Двое играют в шашки на доске 8 х 8. При этом запрещается бить шашки соперника или превращать шашки в дамки. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

Решение.

Давайте рассуждать логически: на доске изначально16 шашек, вариантов походить у обоих игроков более чем достаточно (рис. 1).

Рис. 1. Шашки

Из этого следует такая подсказка: выигрышная стратегия должна быть простой и не сильно привязанной к правилам самих шашек.

Вспоминаем про один из основных способов построения стратеги: симметрия.

Докажем, что при правильной игре всегда выигрывает второй игрок. Для этого ему достаточно ходить симметрично первому относительно центра доски (рис. 2).

Рис. 2. Симметрия хода

Очевидно, что при таком подходе у второго игрока всегда будет ход (это достигается благодаря тому, что центр доски расположен не в какой-то из клеток, а на стыке 4 клеток). Таким образом, поскольку ходы рано или поздно закончатся (напомним, что в шашках нельзя ходить назад – только бить или ходить дамкой, но бить и менять шашки на дамки в наших шашках запрещено условием задачи), то они закончатся у первого игрока (так как у второго всегда будет ход).

Ответ: выигрышная стратегия есть у второго игрока.

Рассмотрим еще один пример выигрышной стратегии, в которой используется симметрия. Однако в этом примере мы попытаемся составить четкий алгоритм игры (похожий на тот, который может реализовать компьютер). Этот алгоритм мы попытаемся записать в виде блок-схемы.

Пример 2. Дана полоска размерами 1 х 99. Двое учеников по очереди делают свои ходы. За один ход разрешается зачеркнуть одну произвольную клетку полоски или какие-то две соседние клетки полоски. Проигрывает тот, кто не сможет сделать ход. Кто выиграет при правильной игре?

Решение.

Мы уже намекнули, что необходимо использовать симметрию. Однако клеток в полоске – нечетное число. Это подсказка к тому, что симметрию будет использовать первый игрок.

Вырисовывается следующая выигрышная стратегия: первый игрок закрашивает 50-ю клетку полоски. После его хода полоска разбивается на две одинаковые полоски (рис. 3).

Рис. 3. Полоса игры

Теперь задача первого игрока – ходить симметрично тому, как ходит второй игрок. Как видим, у первого игрока всегда будет ход после хода второго игрока (рис. 4).

Рис. 4. Полоса игры

Значит, выигрышная стратегия существует у первого игрока.

Составим четкий алгоритм выигрышной стратегии:

1. Закрасить клетку с номером 50.

2. Если второй игрок закрасил клетку с номером k, то закрасить клетку с номером 100-k.

3. Если второй игрок закрасил клетки с номерами k и k+1, то закрасить клетки с номерами 100-k и 99-k.

Этот алгоритма принесет первому игроку победу.

Составим блок-схему для описания этого алгоритма (рис. 5):

Рис. 5. Блок-схема алгоритма выигрышной стратегии игры

Рассмотрим еще один пример на нахождение выигрышной стратегии.

Пример 3.

Двое по очереди ставят крестики и нолики в клетки таблицы 9 х 9. Первый игрок ставит крестики, второй – нолики. В конце игры надо посчитать, сколько строк и столбцов, в которых крестиков больше, чем ноликов. Это количество очков первого игрока. Соответственно, количество строк и столбцов, в которых ноликов больше – это очки второго игрока. Выигрывает тот, у кого больше очков. Кто выиграет при правильной игре?

Решение.

И снова воспользуемся симметрией. У нас опять есть подсказка – нечетное количество клеток доски. Поэтому напрашивается такая стратегия: первый игрок своим первым ходом ставит крестик в центр. А дальше ходит симметрично второму игроку относительно центра (рис. 6).

Рис. 6. Крестики-нолики

Мы получаем, что если в каком-то столбце или строке ноликов больше, то в симметричном ему столбце или строке их, соответственно, меньше. А вот центральные строка и столбец остаются за первым игроком, так как в них в центре стоит крестик, а остальные клетки разбиты на симметричные пары. Значит, при такой игре выиграет первый игрок.

Ответ: выиграет первый игрок.

На этом уроке мы рассмотрели на практике составление выигрышных стратегий.

На следующем уроке мы начнем изучение новой темы – Среда программирования Лого.

---

Шашки

Шашки – одна из самых древних игр (рис. 7).

Рис. 7. Шашки (Источник)

У Платона встречается миф о том, как бог Гермес, придумавший эту игру, предложил богине Луне играть с ним в шашки с тем условием, что в случае проигрыша он получит от Луны пять дней. Одержав победу, Гермес прибавил эти пять дней к тем 360 дням, которые до этого составляли год.

По одной из исторических версий шашки изобрел греческий воин Паламед, известный как участник осады Трои. Осада города продолжалась 10 лет и, чтобы убить скуку, Паламед придумал эту увлекательную игру, возможно, рисуя клетки на земле.

Увлекались шашками и египетские фараоны. Во время раскопок в Египте обнаружили гробницу вельможи, который был приближенным фараона. На стенах гробницы есть росписи, отражающие три страсти древнего египтянина – охоту, рыбную ловлю и игру в шашки. В Лувре хранятся две шашечные доски, принадлежащие фараонам. Из гробницы Тутанхамона была извлечена доска для игры в шашки, состоявшая из тридцати клеток.

За несколько веков до нашей эры уже играли на 64-клеточной доске. Шашки были двух цветов – белые и черные. И представляли собой как бы две армии, которым предстояло сражение. Отступление не предусматривалось, поэтому шашки могли ходить только вперед. Если шашка прорывалась в тыл к противнику, то повышалась ее боевая способность и она становилась дамкой. Взятие происходило с помощью перескакивания одной шашки через другую. Точно так же в бою победивший воин перешагивает через побежденного, чтобы дальше продолжить сражение.

Играют в шашки в «Декамероне» Боккаччо, играют в «Дон Кихоте» Сервантеса.

На Руси появление шашек связывают с именем киевского князя Владимира Мономаха (1053–1125). Однако археологические раскопки показали, что еще в III–IV веках нашей эры уже играли в шашки. Во многих былинах рассказывается о том, что шашки были одной из любимых игр русских богатырей.

Петр I всячески поощрял игру в шашки и в шахматы. На учрежденных им «ассамблеях» тот петербургский сановник, которому подошел черед устраивать у себя «ассамблею», должен был, помимо всего прочего, выделить особую комнату для шахмат и шашек.

Примерно в 1535 году в правила шашек добавляют условие: если шашку соперника можно бить, то игрок обязан это делать. Это правило игры используется до сих пор в неизменном виде.

Любителями шашек были Державин, Пушкин. Л.Н. Толстой в «Войне и мире» сравнивает стратегию военного искусства со стратегией шашечной игры. Шашками увлекались Александр Суворов и Антон Чехов, Александр Грин и Фридрих Шопен и многие другие известные личности. Наполеон шахматам предпочитал шашки, черпая в этой игре идеи для тактики ведения боя.

---

Морской бой

Мы уже обсуждали игру «Морской бой» (рис. 8), когда говорили о методе координат в 5 классе. Теперь же может возникнуть вопрос: а есть ли алгоритм выигрышной стратегии для этой игры?

Рис. 8. Морской бой (Источник)

Ответить на этот вопрос однозначно нельзя, но, с большой долей вероятности, такого алгоритма нет. Дело в том, что во многих логических играх начальные положения игроков оговорены правилами. «Морской бой» относится к тому типу игр, в которых сама игра во многом определяется начальным положением (в данном случае – кораблей соперников). А свои корабли игроки располагают произвольным образом.

Кроме того, важно помнить, что в большинстве логических игр игроки знают позиции друг друга, а весь смысл морского боя состоит в том, что соперники не видят расположения кораблей друг друга.

Однако есть несколько тактик ведения игры. Одна из них состоит в поиске четырехпалубника. Такой большой корабль тяжело спрятать. Для того чтобы гарантировать себе нахождение четырехпалубника, достаточно «простреливать» одну клетку в любом четырехугольнике 1 х 4. Даже в случае редкого невезения для этого понадобится максимум 24 выстрела. Однако такое невезение бывает редко – чаще всего «по пути» вы убьете еще несколько кораблей противника, уменьшите количество «проверяемых» клеточек с учетом того, что рядом с кораблем встык другой корабль стоять не может, и с успехом найдете четырехпалубник.

Еще одна достаточно популярная стратегия – простреливать диагонали. Расположение кораблей, при котором ни на одной из главных диагоналей не стоит корабль – большая редкость.

Однако это не более чем рекомендации: на самом деле, гораздо больше зависит от удачного расположения кораблей и везения с элементами логики.

---

Игры без алгоритма

На прошлом уроке мы уже рассматривали одну игру, в которой не нужно было придумывать алгоритм для победы. Победитель определялся автоматически, независимо от игры обоих соперников.

Сейчас мы рассмотрим еще одну задачу, которая является примером игры без алгоритма. Точнее, игры, в которой надо не найти алгоритм, а доказать его отсутствие.

Задача.

Существует одна из разновидностей шахмат (рис. 9) – когда каждый из игроков делает по два хода. Доказать, что в такой игре у второго игрока не может существовать выигрышная стратегия.

Рис. 9. Шахматы (Источник)

Доказательство.

Для доказательства воспользуемся так называемым «методом от противного». Пусть такая стратегия у второго игрока существует.

Тогда первый игрок может своим ходом сделать следующий «маневр»: походит любым конем первым своим ходом, а вторым ходом вернет коня обратно.

Что произойдет в этом случае: получается, что второй игрок как бы станет первым, так как перед его ходом на доске снова начальная позиция. Тогда, если бы существовала выигрышная стратегия для второго игрока, то после такой «передачи хода», она стала бы выигрышной для первого игрока – и партию выиграл бы он. Значит, она не была бы выигрышной для второго игрока – получили противоречие.

Можно возразить, что второй игрок тоже может повторить аналогичные манипуляции с конем. В ответ на это первый также будет повторять эти манипуляции до тех пор, пока либо партию не признают ничейной, либо второй игрок не перестанет повторять движения конем. Но если партию признают ничейной, то стратегия для второго игрока оказалась невыигрышной – противоречие. А случай, когда второй игрок становится как бы «первым», мы уже разобрали выше.

Доказано.

Таким образом, не найдя алгоритма и даже не попытавшись это сделать, мы доказали, что у второго игрока не может быть выигрышной стратегии.

Умение доказывать подобные вещи может пригодиться для сохранения массы времени – ведь можно было потратить годы на поиски выигрышной стратегии, не зная, что ее не существует.

Список литературы

1. Босова Л.Л. Информатика и ИКТ: учебник для 6 класса. – М.: БИНОМ. Лаборатория знаний, 2012.

2. Босова Л.Л. Информатика: рабочая тетрадь для 6 класса. – М.: БИНОМ. Лаборатория знаний, 2010.

3. Босова Л.Л., Босова А.Ю. Уроки информатики в 5–6 классах: методическое пособие. – М.: БИНОМ. Лаборатория знаний, 2010.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт iv-k.ltd.ua (Источник)

2. Интернет-сайт primwiki.ru (Источник)

3. Интернет-сайт taina-chess.narod.ru (Источник)

Домашнее задание

1. §3.1., 3.4 (Босова Л.Л. Информатика и ИКТ: учебник для 6 класса).

2. Попытайтесь самостоятельно составить выигрышную стратегию какой-либо игры.

3. Запишите составленный алгоритм в виде блок-схемы.

Ⅰ Предисловие

Возможно, вы играли в игры MMRPG, такие как World of Warcraft, Fairy Sword и League of Legends. В этих играх есть очень важная особенность, которую персонаж автоматически найден. Когда персонаж находится в определенной позиции на игровой карте, мы используем мышь, чтобы щелкнуть другое относительно дальнее место, и персонаж автоматически обходится на препятствия и пройдет. Так как реализована эта функция? Давайте рассмотрим эту функцию в этой статье.

Анализ алгоритма II

На самом деле, это очень типичная проблема поиска. Отчамая точка персонажа — это то, где он сейчас находится, и конечная точка — позиция щелчка мыши. Нам нужно найти путь от начальной точки до конца на карте. Этот путь должен обойти все препятствия на карте, и он выглядит очень умным способом. Сак -наземная умство и общее объяснение заключается в том, что способ ходить не должен быть слишком рядом. Теоретически, самый короткий путь, очевидно, является самым умным способом, и это оптимальное решение этой проблемы.

Однако в объяснении кратчайшего пути на предыдущей диаграмме я сказал, что, если график очень большой, выполнение самого короткого алгоритма пути Дейкстры займет много. В реальной разработке программного обеспечения мы сталкиваемся с супер большими картами и массивными способами поиска. Эффективность выполнения алгоритма слишком низкая, что, очевидно, неприемлемо.

[Структура данных и алгоритм]-> Алгоритм-> Как рассчитывается оптимальный маршрут программного обеспечения MAP?

Фактически, такие как планирование маршрута путешествия и поиск игрового пути, эти реальные проблемы разработки программного обеспечения, в целом, нам не нужно иметь оптимальное решение (то есть самый короткий путь). В случае взвешивания качества и эффективности внедрения маршрута нам нужно только искать подраздел. Так как же быстро найти второй лучший маршрут рядом с самым коротким маршрутом?

Этот алгоритм планирования быстрого пути — это то, о чем мы должны поговорить в этой статьеA алгоритм*. Фактически, алгоритм A — это оптимизация и преобразование алгоритма Dijkstra. Как превратить алгоритм Dijkstra в алгоритм A*? Давайте взглянем. Если вы не знакомы с алгоритмом Dijkstra, вы можете перейти к статье в моей ссылке выше.

Алгоритм Dijkstra на самом деле немного похожАлгоритм BFS , Он находит ближайшую точку к отправной точке, чтобы расширить наружу. Эта идея расширения на самом деле немного слепа. Почему это слепо? Я использую пример на рисунке ниже, чтобы объяснить. Предполагая, что рисунок ниже соответствует реальной карте. Каждая вершина находится в положении рисунка. Мы используем двухмерную координату (x, y), чтобы указать, где x и y соответственно представляют горизонтальные координаты и вертикальные координаты, соответственно.

В реализации алгоритма Dijkstra мы используем очередь приоритетов для записи вершин, которые перенесены к вершинам и длине пути этой вершины и отправной точки. Чем меньше длина вершины и отправной точки, тем больше она избирается из очереди приоритета и расширяется. Из примера на рисунке можно видеть, что, хотя мы ищем маршрут от S до T, Сначала был найден поиск в первый раз. Наблюдение за невооруженным глазом, это направление поиска полностью изменено с направлением маршрута, который мы ожидали (с t на восток на восток), а направление, поиск по маршруту, очевидно, смещено.

Причина работы в том, что мы организуем заказ в соответствии с размером длины пути вершины и отправной точкой. Чем ближе к отправной точке, тем раньше будет выпущена очередь. Мы не приняли во внимание расстояние от этой вершины до конца. Поэтому на карте, хотя три вершины 1, 2 и 3 наиболее близки к отправной точке, он становится дальше и дальше от конечной точки Анкет

Итак, если мы все всесторонне сделаем больше факторов, как далеко мы можем пойти до конечной точки, и рассмотреть его, чтобы судить, какая вершина должна быть вне очереди, можно сначала избежать бега?

Когда мы пересекаем определенную вершину, длина пути от отправной точки к этой вершине определена, и мы записываем ее как g (i) (я представляю номер вершины). Однако мы неизвестны из этой вершины до конечной точки. Хотя точное значение не может быть известно заранее, мы можем заменить его другими оценками.

Здесь мы можем использовать эту вершину и конечную точкуПрямое расстояние, То есть расстояние от Оу джи Ли, приходится на приблизительно оценку этой вершины и конечной точки.Длина пути(Прямое расстояние и длина пути не являются концепцией). Мы записываем это расстояние h (i) (i), и профессиональное название называетсяВдохновение (эвристическая функция)Сущность Поскольку формула расчета OU Ji LILI будет включать расчеты, требующий времени, требующий времени, поэтому мы обычно используем другую формулу более простой расстояния расчета, называемогоМанхэттенское расстояние (Манхэттенское расстояние)Сущность Расстояние между Манхэттеном — это сумма расстояния между горизонтальными и вертикальными координатами между двумя точками. Процесс расчета включает только метод добавления и вычитания и символические биты, поэтому расстояние более эффективно, чем эудзи.

	private int hManhattan(Vertex v1, Vertex v2) {
		return Math.abs(v1.x - v2.x) + Math.abs(v1.y - v2.y);
	}

Оказалось, что длина пути между вершиной и отправной точкой была просто оценена, которая сначала вышла из очереди. Теперь существует значение оценки длины пути пути от вершины до конца. I) + H ( i) определить, какая вершина должна быть сначала вне очереди. Интегрированным мы можем эффективно избежать предвзятости, упомянутого ранее. Здесь f (i) майор называетсяФункция оценки。

После приведенного выше описания мы можем обнаружить, что алгоритм A* представляет собой простое преобразование алгоритма Dijkstra. Фактически, с точки зрения реализации кода, нам нужно только изменить несколько мест.

In the implementation of the code of the A* algorithm, the definition of the vertex vertex class, which is slightly different from the definition in the Dijkstra algorithm, is slightly different, more x, y coordinates, and the f (i) value just упомянул. Graph Dijkstra 。 ， Dijkstra —— Dijkstra 。

Vertex

package com.tyz.astar.core;

/**
   * Построение вершины
 * @author Tong
 */
public class Vertex {
	int id; // Венчурный номер
	int distance; // от начальной точки до расстояния от этой вершины
	int f; //f(i) = g(i) + h(i)
	int x; // горизонтальные координаты вершины на карте
	int y; // вертикальные координаты вершины на карте

	Vertex(int id, int x, int y) {
		this.id = id;
		this.x = x;
		this.y = y;
		this.f = Integer.MAX_VALUE;
		this.distance = Integer.MAX_VALUE;
	}

}

package com.tyz.astar.core;

/**
   * Построение края
 * @author Tong
 */
public class Edge {
	private int start; 	// start -Up vertex number
	private int end;	// настройки на краю
	private int weight;	// Вес края

	public Edge() {
	}

	public Edge(int start, int end, int weight) {
		this.start = start;
		this.end = end;
		this.weight = weight;
	}

	public int getStart() {
		return start;
	}

	public void setStart(int start) {
		this.start = start;
	}

	public int getEnd() {
		return end;
	}

	public void setEnd(int end) {
		this.end = end;
	}

	public int getWeight() {
		return weight;
	}

	public void setWeight(int weight) {
		this.weight = weight;
	}
	
	
}

（ ）

package com.tyz.astar.core;

/**
   * Реализуйте приоритетную очередь (маленький верхний дамп)
 * @author Tong
 */
class PriorityQueue {
	private Vertex[] nodes;
	private int count;
	
	public PriorityQueue(int vertex) {
		this.nodes = new Vertex[vertex+1];
		this.count = 0;
	}
	
	/**
	  * Первый элемент команды из очереди
	  * @Return Team First Element
	 */
	Vertex poll() {
		Vertex vertex = this.nodes[1];
		this.nodes[1] = this.nodes[this.count--];
		heapifyUpToDown(1);
		
		return vertex;
	}
	
	/**
	  * Добавьте элементы и сложите их в приоритет
	 * @param vertex
	 */
	void add(Vertex vertex) {
		this.nodes[++this.count] = vertex;
		vertex.id = this.count;
		heapifyDownToUp(count);
	}
	
	/**
	  * Обновите значение распределения элемента в очереди
	 * @param vertex
	 */
	void update(Vertex vertex) {
		this.nodes[vertex.id].distance = vertex.distance;
		heapifyDownToUp(vertex.id);
	}
	
	boolean isEmpty() {
		return this.count == 0;
	}
	
	void clear() {
		this.count = 0;
	}
	
	/**
	  * Сверху донизу
	 * @param index
	 */
	private void heapifyUpToDown(int index) {
		while (index <= this.count) {
			int maxPos = index;
			
			if (index * 2 <= this.count && 
						this.nodes[maxPos].distance > this.nodes[index*2].distance) {
				maxPos = 2 * index;
			} else if ((index * 2 + 1) <= count &&
						this.nodes[maxPos].distance > this.nodes[index*2+1].distance) {
				maxPos = index * 2 + 1;
			} else if (maxPos == index) {
				break;
			}
			swap(index, maxPos);
			index = maxPos;
		}
	}
	
	/**
	  * Фантастика снизу вверх
	 * @param index
	 */
	private void heapifyDownToUp(int index) {
		while (index / 2 > 0 && 
					this.nodes[index].distance < this.nodes[index / 2].distance) {
			swap(index, index / 2);
			index /= 2;
		}
	}
	
	/**
	  * Обмен значением подписки, соответствующей двум элементам
	 * @param index
	 * @param maxPos
	 */
	private void swap(int index, int maxPos) {
		this.nodes[index].id = maxPos; // Loving обменная запись
		this.nodes[maxPos].id = index;
		
		Vertex temp = this.nodes[index];
		this.nodes[index] = this.nodes[maxPos];
		this.nodes[maxPos] = temp;
	}
}

A* Dijkstra ， ：

• 。A* f （ f(i) = g(i) + h(i) ）， ， Dijkstra distance （ g(i) ） ；
• A* distance ， f ；
• ， Dijkstra ，A* 。

👇

package com.tyz.astar.core;

import java.util.LinkedList;

/**
 * Алгоритм* понимает две точки, чтобы найти право на карту
 * @author Tong
 */
public class Graph {
	private LinkedList<Edge>[] adj; // административная таблица
	private int vertex; // номер стихи
	private Vertex[] vertexs;

	@SuppressWarnings("unchecked")
	public Graph(int vertex) {
		this.vertex = vertex;
		this.vertexs = new Vertex[this.vertex];
		this.adj = new LinkedList[vertex];
		for (int i = 0; i < vertex; i++) {
			this.adj[i] = new LinkedList<Edge>();
		}
	}
	
	/**
	  * Добавить вершину
	 * @param id
	 * @param x
	 * @param y
	 */
	public void addVetex(int id, int x, int y) {
		this.vertexs[id] = new Vertex(id, x, y);
	}
	
	public void addEdge(int start, int end, int weight) {
		this.adj[start].add(new Edge(start, end, weight));
	}
	
	/**
	  * Используйте алгоритм A *, чтобы найти кратчайшее расстояние между вершиной Strat до конечной вершины
	  * @param Start Purpert Point
	  * @param end termid termid
	 */
	public void astar(int start, int end) {
		int[] predecessor = new int[this.vertex]; // используется для восстановления кратчайшего пути
		// построить небольшую верхнюю кучу в соответствии со значением F вершины
		PriorityQueue queue = new PriorityQueue(this.vertex); // маленькая верхняя куча
		boolean[] inqueue = new boolean[this.vertex];
		inqueue[start] = true;
		this.vertexs[start].distance = 0;
		this.vertexs[start].f = 0;
		queue.add(this.vertexs[start]);
		inqueue[start] = true;
		
		while (!queue.isEmpty()) {
			Vertex minVertex = queue.poll(); // возьмите верхний элемент и удалите его из очереди
			for (int i = 0; i < this.adj[minVertex.id].size(); i++) {
				Edge edge = this.adj[minVertex.id].get(i);
				Vertex nextVertex = this.vertexs[edge.getEnd()];
				if (nextVertex.distance > minVertex.distance + edge.getWeight()) {
					nextVertex.distance = minVertex.distance + edge.getWeight();
					nextVertex.f = nextVertex.distance + 
									hManhattan(nextVertex, this.vertexs[end]);
					predecessor[nextVertex.id] = minVertex.id;
					if (inqueue[nextVertex.id] == true) {
						queue.update(nextVertex); 
					} else {
						queue.add(nextVertex);
						inqueue[nextVertex.id] = true;
					}
				}
				if (nextVertex.id == end) { // Пока вы приедете к концу, вы можете остановиться
					queue.clear(); // повернуть состояние очереди, чтобы опустить, чтобы выпрыгнуть из цикла
					break;
				}
			}
		}
		// выходной путь
		System.out.print(start);
		print(start, end, predecessor);
	}
	
	private int hManhattan(Vertex v1, Vertex v2) {
		return Math.abs(v1.x - v2.x) + Math.abs(v1.y - v2.y);
	}
	
	/**
	  * Путь рекурсивной печати
	 * @param start
	 * @param end
	 * @param predecessor
	 */
	private void print(int start, int end, int[] predecessor) {
		if (start == end) {
			return;
		}
		print(start, predecessor[end], predecessor);
		System.out.println("->" + end);
	}
	
}

A* ， Dijkstra ， ， ？

s t ， ， s t ， 。 ， ， 。

Dijkstra ， ， ， ， 。 ， ， ， 。

A* Dijkstra ， ， while ， ，Dijkstra ，A* 。 For the Dijkstra algorithm, when the end point is out of the queue, the distance value of the end point is the minimum value of all vertices in the priority queue. Even if it runs, the distance value of the end point will not be updated очередной раз. A* ， ， while ， ， dist 。

A* ， f ， 。 ， ， 。

Как реализовать проблему поиска в игровой дороге

A* ， 。 ， ， ， ， 、 。 ， ， ， 。

， ， 。 ， 。 。 ， ， ， 1。 ， ， ， 。 1 ， A* ， 。

IV Резюме

A* （Heuristically Search Algorithm）Сущность ， A* ， ， IDA* ， ， ， ， 。

， ， 。 ， ， ， ， 。 ， ， 。