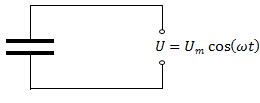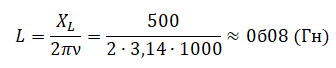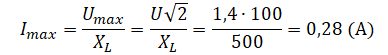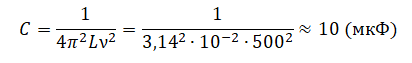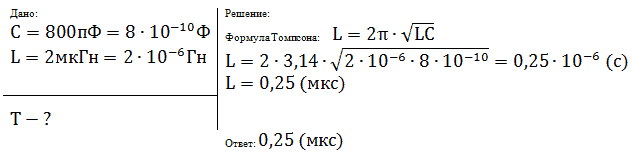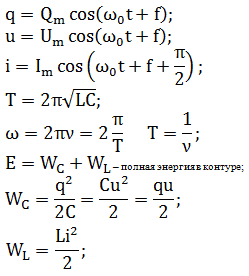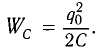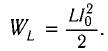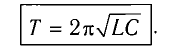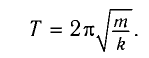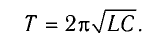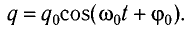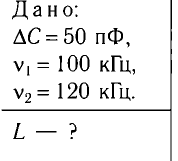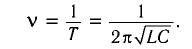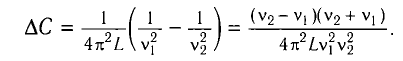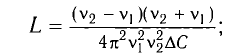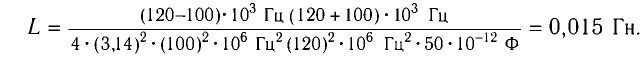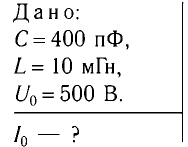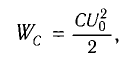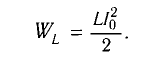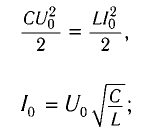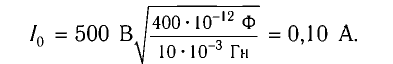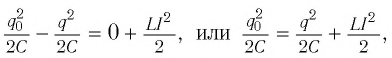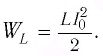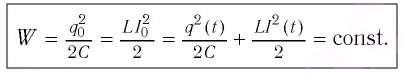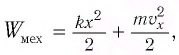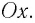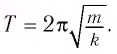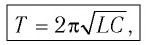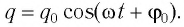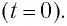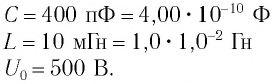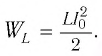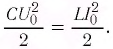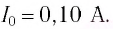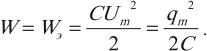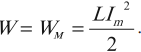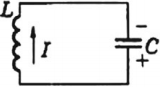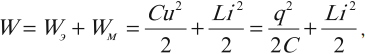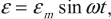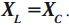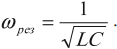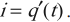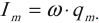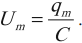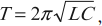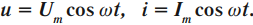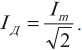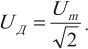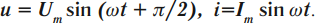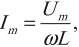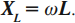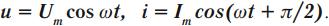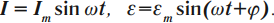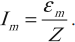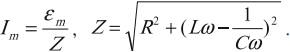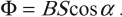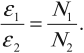Опишем колебания, которые происходят в цепи переменного тока при включении в нее конденсатора и катушки индуктивности. А также рассмотрим условия, при выполнении которых в цепи переменного тока наступает резонанс. Получим формулы для вычисления амплитуд напряжений, введем понятия емкостного и индуктивного сопротивления и выясним, какую роль играют эти величины.
Конденсатор в цепи переменного тока
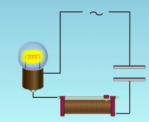
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
u=φ1−φ2=qC
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
qC=Umaxcosωt
Следовательно, заряд конденсатора меняется по гармоническому закону:
q=CUmaxcosωt
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i=q´=−CUmaxsinωt=CUmaxcos(ωt+π2)
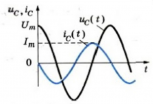
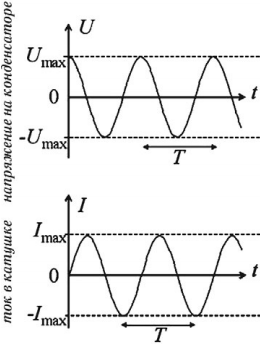
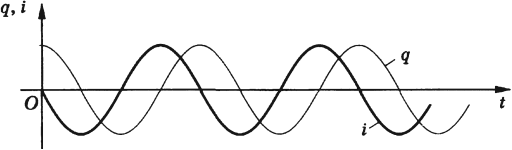
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π2 (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
Амплитуда силы тока равна:
Imax=UmaxCω
Примем, что:
1Cω=XC
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Определение
I=UXC
Величина XC, равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура qmax=10−6 Кл. Амплитудное значение силы тока в контуре Imax=10−3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q2max2C=LI2max2
Отсюда:
LC=q2maxI2max
√LC=qmaxImax
T=2π√LC=2πqmaxImax=2·3,1410−610−3≈6,3·10−3 (с)
Катушка индуктивности в цепи переменного тока
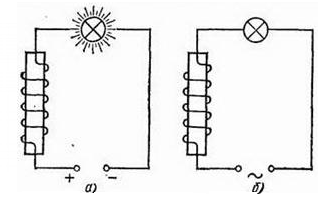
Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).
Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока.
Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока.
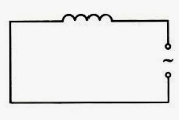
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля →Ei, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля →Eк, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства →Ei=−→Eк следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции ei) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать:
ei=−u
Напомним, что сила переменного тока изменяется по гармоническому закону:
i=Imaxsinωt
Тогда ЭДС самоиндукции равна:
ei=−Li´=−LωImaxcosωt
Так как u=−ei, то напряжение на концах катушки оказывается равным:
u= LωImaxcosωt=LωImaxsin(ωt+π2)=Umax(ωt+π2)
Амплитуда напряжения равна:
Umax=LωImax
Следовательно, колебания напряжения на катушке опережают колебания силы тока на π2, или колебания силы тока отстают от колебаний напряжения на π2, что одно и то же.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).
Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна:
Imax=UmaxLω
Введем обозначение:
Lω=XL
Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим:
Определение
I=UXL
Величина XL, равная произведению циклической частоты на индуктивность, называется индуктивным сопротивлением. Индуктивное сопротивление зависит от частоты. Поэтому в цепи постоянного тока, в котором отсутствует частота, индуктивное сопротивление катушки равно нулю.
Пример №2. Катушка с индуктивным сопротивлениемXL=500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока Imax в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.
Индуктивное сопротивление катушки выражается формулой:
XL=Lω=2πνL
Отсюда:
Так как амплитуда напряжения связана с его действующим значением соотношением Umax=U√2, то для амплитуды силы тока получаем:
Резонанс в электрической цепи
Механические и электромагнитные колебания имеют разную природу, но процессы, происходящие при этом, идентичны. Поэтому можно предположить, что резонанс в электрической цепи так же реален, как резонанс в колебательной системе, на которую действует периодическая сила.
Напомним, что в механической системе резонанс тем более заметен, чем меньше в колебательной системе трение между ее элементами. Роль трения в электрической цепи играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника, который при этом нагревается. Следовательно, резонанс в электрической цепи будет отчетливо наблюдаться при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная частота колебаний в колебательном контуре определяется формулой:
ω0=1√LC
Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру равна собственной частоте колебательного контура:
ω=ω0=1√LC
Определение
Резонанс в электрическом колебательном контуре — явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
После включения внешнего переменного напряжения резонансное значение силы тока в цепи устанавливается не моментально, а постепенно. Амплитуда колебаний силы тока возрастает до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
I2maxR2=UmaxImax2
Упростив это уравнение, получим:
ImaxR=Umax
Следовательно, амплитуда установившихся колебаний силы тока при резонансе определяется уравнением:
Imax=UmaxR
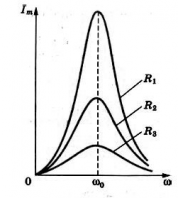
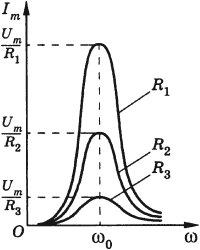
При сопротивлении, стремящемся к нулю, сила тока возрастает до бесконечно больших значений. При большом сопротивлении сила тока возрастает незначительно. Это хорошо видно на графике ниже.
Пример №3. В цепь переменного тока с частотой ν = 500 Гц включена катушка индуктивностью L = 10 мГн. Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?
Электрическая цепь, описываемая в условии, представляет собой колебательный контур. Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (ν = ν0).
Но:
ν0=12π√LC
Тогда:
ν=12π√LC
Отсюда:
Задание EF22579
К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой ν.
Индуктивность L катушки колебательного контура можно плавно менять от максимального значения Lmax до минимального Lmin, а ёмкость его конденсатора постоянна.
Ученик постепенно уменьшал индуктивность катушки от максимального значения до минимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.
Алгоритм решения
1.Установить, что вызывает увеличение амплитуды силы тока.
2.Объяснить, какие изменения вызвало уменьшение индуктивности.
3.Объяснить, при каком условии в течение всего эксперимента амплитуда силы тока может только расти.
Решение
В колебательном контуре источником тока возбуждаются вынужденные колебания. Частота этих колебаний равна частоте источника — ν. Амплитуда колебаний зависит от того, как соотносятся между собой внешняя частота и частота собственных электромагнитных колебаний, которая определяется формулой:
ν0=12π√LC
По мере увеличения внешней частоты от нуля до ν0 амплитуда растет. Она достигает максимума тогда, когда происходит резонанс. При этом внешняя частота равна частоте собственных электромагнитных колебаний: ν = ν0. Затем амплитуда начинает убывать.
В данном случае, ученик меняет не внешнюю частоту, а частоту собственных электромагнитных колебаний. При плавном уменьшении индуктивности контура от максимального значения Lmax до минимального Lmin частота возрастает от ν0min до ν0max. Причем:
ν0min=12π√LminC
ν0max=12π√LmaxC
Из того факта, что амплитуда всё время увеличивалась, можем сделать вывод, что частота ν0 всё время приближалась к частоте источника тока, при этом ν > ν0max. В противном случае наблюдалось бы уменьшений амплитуды силы тока.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22785
В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.
Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях.
Ответ:
а) период колебаний силы тока в контуре
б) фаза колебаний напряжения на конденсаторе
в) заряд конденсатора
г) энергия магнитного поля катушки
д) амплитуда колебаний напряжения на катушке
Алгоритм решения
- Определить, от чего зависит каждая из перечисленных величин.
- Установить, какие величины меняются, а какие нет.
Решение
В колебательном контуре происходят гармонические колебания. Поэтому период колебаний силы тока в контуре — величина постоянная.
Фаза — это величина, которая определяет положение колебательной системы в любой момент времени. Поскольку в системе происходят колебания, фаза меняется.
Заряд конденсатора — колебания происходят за счет постоянной перезарядки конденсатора. Следовательно, эта величина тоже меняется.
Энергия магнитного поля катушки — в колебательном контуре происходят взаимные превращения энергии магнитного поля катушки в энергию электрического поля конденсатора, и обратно. Поэтому энергия магнитного поля катушки постоянно меняется.
В условии задачи сказано, что колебания незатухающие. Это значит, что полная механическая энергия колебательной системы сохраняется. Поскольку именно от нее зависит амплитуда колебаний напряжения на катушке, то эта величина также остается постоянной.
Ответ: ад
pазбирался: Алиса Никитина | обсудить разбор
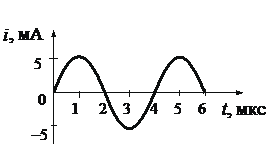
Задание EF18656
Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10k
Слайд 1
Цели урока:
- Образовательные: обобщение и
систематизация знаний по теме, проверка знаний,
умений, навыков. В целях повышения интереса к
теме работу вести с помощью опорных конспектов. - Воспитательные: воспитание
мировоззренческого понятия
(причинно-следственных связей в окружающем мире),
развитие у школьников коммуникативной культуры. - Развивающие: развитие самостоятельности
мышления и интеллекта, умение формулировать
выводы по изученному материалу, развитие
логического мышления, развитие грамотной устной
речи, содержащей физическую терминологию.
Тип урока:систематизация и обобщение
знаний.
Слайд 2
Техническая поддержка урока:
- Демонстрации:
- Плакаты.
- Показ слайдов с помощью информационно –
компьютерных технологий. - Дидактический материал:
- Опорные конспекты с подробными записями на
столах. - Оформление доски:
- Плакат с кратким содержанием опорных
конспектов (ОК); - Плакат – рисунок с изображением колебательного
контура; - Плакат – график зависимости колебаний заряда
конденсатора, напряжения между обкладками
конденсатора, силы тока в катушке от времени,
электрической энергии конденсатора, магнитной
энергии катушки от времени.
Слайд 3
План урока:
1. Этап повторения пройденного материала.
Проверка домашнего задания.
Четыре группы задач по теме:
- Электромагнитные колебания.
- Колебательный контур.
- Свободные колебания. Свободные колебания –
затухающие колебания - Характеристика колебаний.
2. Этап применения теории к решению задач.
3. Закрепление. Самостоятельная работа.
4. Подведение итогов.
ХОД УРОКА
Учитель: Темой урока является
«Решение задач по теме: «Электромагнитные
колебания и волны» на примере разбора задач ЕГЭ»
К доске вызываются 3 ученика для проверки
домашнего задания.
– Задания по этой теме можно разделить на
четыре группы.
Слайд 4
Четыре группы задач по теме:
1. Задачи с использованием общих законов
гармонических колебаний.
2. Задачи о свободных колебаниях конкретных
колебательных систем.
3. Задачи о вынужденных колебаниях.
4. Задачи о волнах различной природы.
– Мы остановимся на решении задач 1 и 2 групп.
Урок начнем с повторения необходимых понятий
для данной группы задач.
Слайд 5
Электромагнитные колебания – это
периодические и почти периодические изменения
заряда, силы тока и напряжения.
Колебательный контур – цепь,
состоящая из соединительных проводов, катушки
индуктивности и конденсатора.
Свободные колебания – это колебания,
происходящие в системе благодаря начальному
запасу энергии с частотой, определяемой
параметрами самой системы: L, C.
Скорость распространения электромагнитных
колебаний равна скорости света: С = 3 . 108(м/с)
Основные характеристики колебаний
Амплитуда (силы тока, заряда, напряжения) –
максимальное значение (силы тока, заряда,
напряжения): Im, Qm, Um
Мгновенные значения (силы тока, заряда,
напряжения) – i, q, u
Слайд 6
Схема колебательного контура
Учитель: Что представляют
электромагнитные колебания в контуре?
Слайд 7
Электромагнитные колебания представляют
периодический переход электрической энергии
конденсатора в магнитную энергию катушки и
наоборот согласно закону сохранения энергии.
Слайд 8
Задача №1 (д/з)
Колебательный контур содержит конденсатор
емкостью 800 пФ и катушку индуктивности
индуктивностью 2 мкГн. Каков период собственных
колебаний контура?
Слайд 9
Задача № 2 (д/з)
Колебательный контур состоит из конденсатора
емкостью С и катушки индуктивности
индуктивностью L. Как изменится период свободных
электромагнитных колебаний в этом контуре, если
электроемкость конденсатора и индуктивность
катушки увеличить в 3р.
Слайд 10
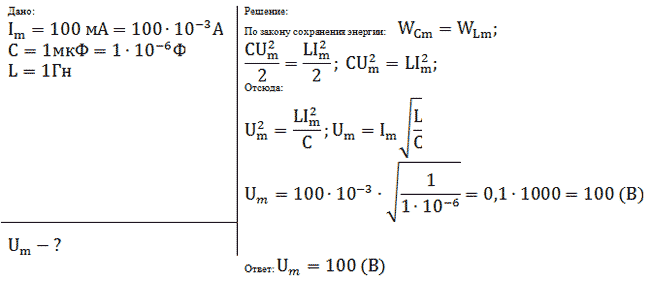
Задача № 3 (д/з)
Амплитуда силы тока при свободных колебаниях в
колебательном контуре 100 мА. Какова амплитуда
напряжения на конденсаторе колебательного
контура, если емкость этого конденсатора 1 мкФ, а
индуктивность катушки 1 Гн? Активным
сопротивлением пренебречь.
Слайд 11
Схема электромагнитных колебаний
Ученик 1 наглядно описывает процессы в
колебательном контуре.
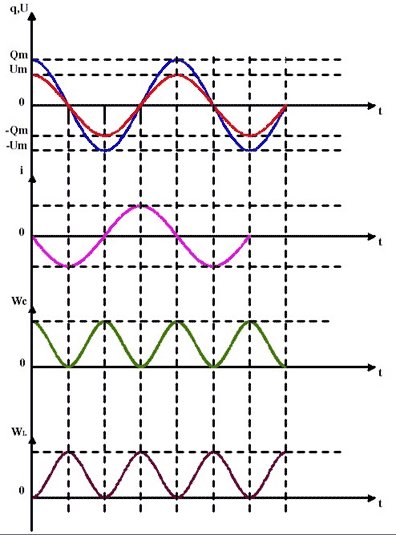
Слайд 12
Ученик 2 комментирует электромагнитные
колебания в контуре, используя графическую
зависимость заряда, напряжения. Силы тока,
электрической энергии конденсатора, магнитной
энергии катушки индуктивности от времени.
Слайд 13
Уравнения, описывающие колебательные процессы
в контуре:
Обращаем внимание, что колебания силы тока в
цепи опережают колебания напряжения между
обкладками конденсатора на π/2.
Описывая изменения заряда, напряжения и силы
тока по гармоническому закону, необходимо
учитывать связь между функциями синуса и
косинуса.
Слайд 14
Задача № 1.
По графику зависимости силы тока от времени в
колебательном контуре определите, какие
преобразования энергии происходят в
колебательном контуре в интервале времени от
1мкс до 2мкс?
1. Энергия магнитного поля катушки
увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется
в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора
уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора
преобразуется в энергию магнитного поля катушки.
Слайд 15
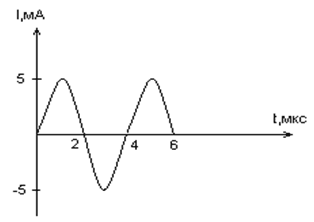
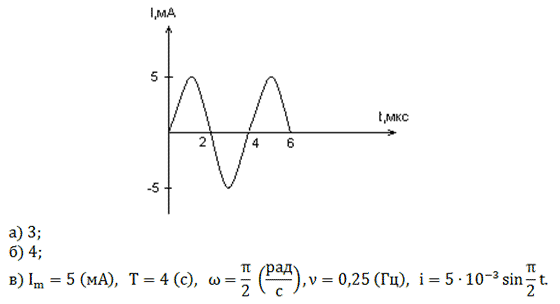
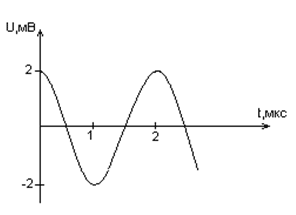
Задача № 2.
По графику зависимости силы тока от времени в
колебательном контуре определите:
а) Сколько раз энергия катушки достигает
максимального значения в течение первых 6 мкс
после начала отсчета?
б) Сколько раз энергия конденсатора достигает
максимального значения в течение первых 6 мкс
после начала отсчета?
в) Определите по графику амплитудное значение
силы тока, период, циклическую частоту, линейную
частоту и напишите уравнение зависимости силы
тока от времени.
Слайд 16
Задача № 3 (д/з)
Дана графическая зависимость напряжения между
обкладками конденсатора от времени. По графику
определите, какое преобразование энергии
происходит в интервале времени от 0 до 2 мкс?
1. Энергия магнитного поля катушки
увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется
в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора
уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора
преобразуется в энергию магнитного поля катушки.
Слайд 17
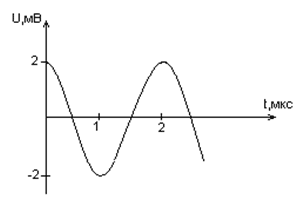
Задача № 4 (д/з)
Дана графическая зависимость напряжения между
обкладками конденсатора от времени. По графику
определите: сколько раз энергия конденсатора
достигает максимального значения в период от
нуля до 2мкс? Сколько раз энергия катушки
достигает наибольшего значения от нуля до 2 мкс?
По графику определите амплитуду колебаний
напряжений, период колебаний, циклическую
частоту, линейную частоту. Напишите уравнение
зависимости напряжения от времени.
Слайд № 18
К доске вызываются 2 ученика
Задача № 5, 6
Слайд 19
Слайд 20
Задача № 7
Заряд на обкладках конденсатора
колебательного контура изменяется по закону
q = 3·10–7cos800πt. Индуктивность контура 2Гн.
Пренебрегая активным сопротивлением, найдите
электроемкость конденсатора и максимальное
значение энергии электрического поля
конденсатора и магнитного поля катушки
индуктивности.
Слайд 21
Слайд 22
Задача № 8
В идеальном колебательном контуре происходят
свободные электромагнитные колебания. В таблице
показано, как изменяется заряд конденсатора в
колебательном контуре с течением времени.
| t, 10–6(C) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| q, 10–9(Кл) | 2 | 1,5 | 0 | –1,5 | –2 | –1,5 | 0 | 1,5 | 2 | 1,5 |
1. Напишите уравнение зависимости заряда от
времени. Найдите амплитуду колебаний заряда,
период, циклическую частоту, линейную частоту.
2. Какова энергия магнитного поля катушки в
момент времени t = 5 мкс, если емкость конденсатора
50 пФ.
Домашнее задание. Напишите уравнение
зависимости силы тока от времени. Найдите
амплитуду колебаний силы тока. Постройте
графическую зависимость силы тока от времени.
Слайд 23
Слайд 24
Самостоятельная работа:
Приложение 1
Колебательный контур в физике — формулы и определения с примерами
Колебательный контур:
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
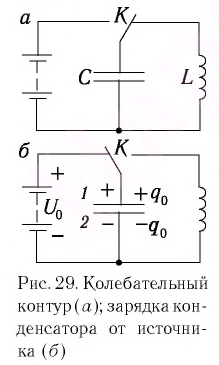
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.
В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R
Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +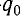

С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.
Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения 
После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.
Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения 
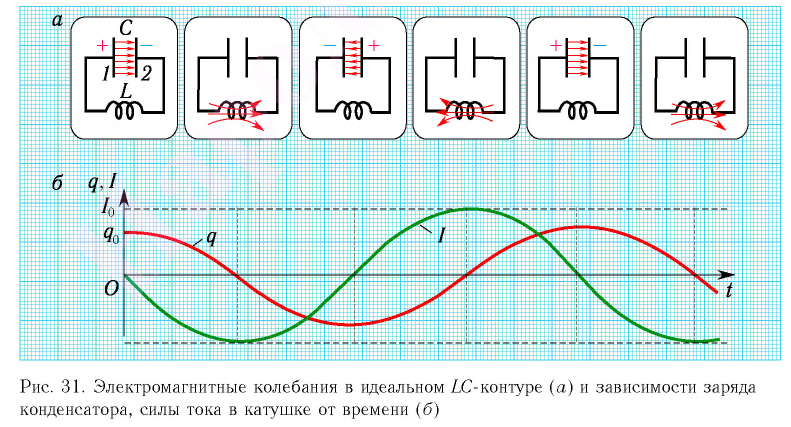
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений 

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:
Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
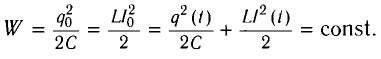
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.
Для пружинного маятника полная механическая энергия в любой момент времени 2 ,
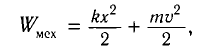
и период его колебаний
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора 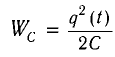
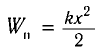
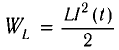
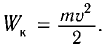
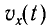
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на 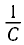
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Таблица 4
Сопоставление физических величин, характеризующих электромагнитные и механические колебания
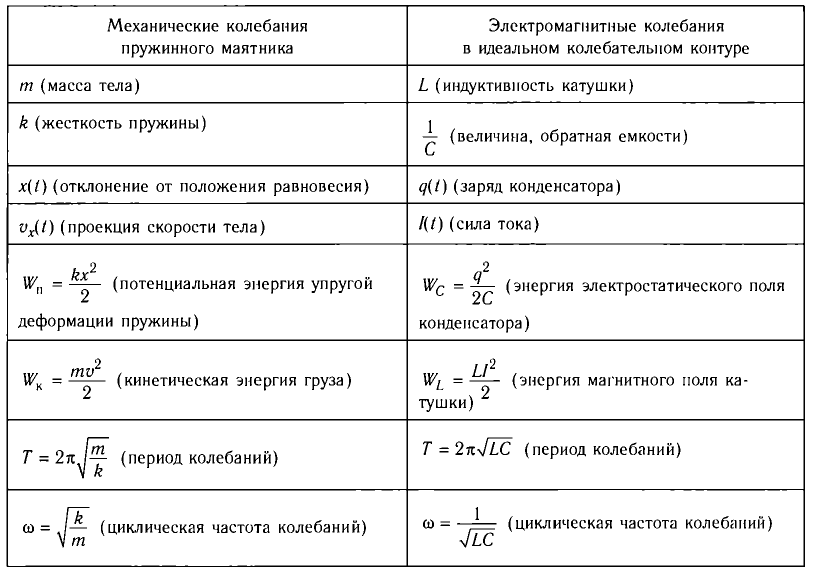
Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.
Для определения начальной фазы 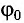
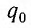
Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.
Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.
Пример №1
При изменении емкости конденсатора идеального LC-контура на 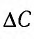
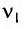
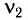
Решение
Частота колебаний в контуре
Поскольку частота колебаний в контуре увеличилась (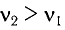
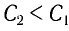
Из условия задачи получаем систему уравнений
Откуда 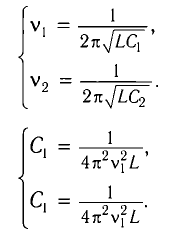
Вычитая из первого уравнения второе, получаем
Ответ: L = 0,015 Гн.
Пример №2
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока 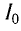
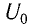
Решение
Максимальная энергия электростатического поля конденсатора
а максимальная энергия магнитного поля катушки
Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 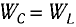
откуда
Ответ: 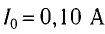
Колебательный контур и свободные электромагнитные колебания в контуре
Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью 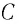
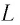
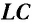
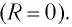
Подключив (при помощи ключа 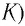
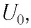
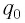
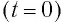
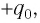
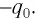
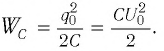
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 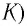
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 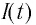
Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 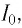
При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):
где 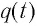
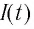
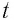
В момент полной разрядки конденсатора 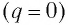
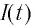
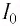
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения 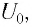
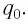
Таким образом, в идеальном 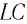
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд 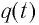
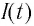
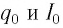
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального 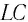
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
где 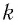
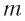
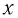
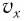
Период его колебаний:
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора 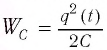
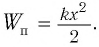
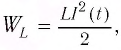
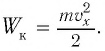
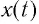
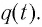
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу 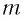
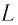
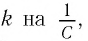
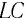
которая называется формулой Томсона.
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Для определения начальной фазы 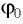
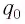
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура 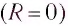
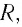
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Пример решения задачи:
Идеальный колебательный контур состоит из конденсатора емкостью 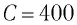
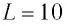
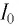
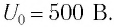
Дано:

Решение
Максимальная энергия электростатического поля конденсатора:
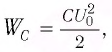
а максимальная энергия магнитного поля катушки:
Так как контур идеальный 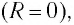
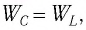
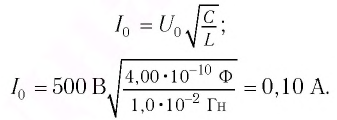
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Исследовательские методы в физике
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Распространение механических волн в средах
- Электромагнитное поле
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Последовательный колебательный контур
Последовательный колебательный контур обозначение на схеме
Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно.
Идеальный последовательный колебательный контур
На схемах идеальный последовательный колебательный контур обозначается вот так:

Реальный последовательный колебательный контур
Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:
С — собственно сама емкость конденсатора
Принцип работы последовательного колебательного контура
Генератор частоты и последовательный колебательный контур
Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:
Генератор (Ген)у нас будет выдавать синус.
Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.
А вот и сама схема в реальности:
Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R — это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно «прячется» внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.
Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта Uш , а также снимая осциллограмму с самого генератора UГЕН .
С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.
Влияние частоты генератора на сопротивление колебательного контура
В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.
Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.
Частота 200 Герц с копейками:
Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый
Добавляем частоту. 600 Герц с копейками
Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.
Добавляем частоту. 2 Килогерца
Сила тока стала еще больше.
Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.
Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.
И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.
Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.
Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.
Увеличиваем частоту еще больше
Сила тока начинает падать, а сдвиг фаз увеличивается.
Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.
Резонанс последовательного колебательного контура
Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:
Это явление носит название резонанса.
Не будем углубляться в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.
Как вы помните, если у нас сопротивление становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.
Формула Томсона (резонанса) для последовательного колебательного контура
Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора XL=XC , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:
Реактивное сопротивление конденсатора вычисляется по формуле:
Приравниваем обе части и вычисляем отсюда F:
В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.
Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.
Замеряем индуктивность катушки:
И замеряем нашу емкость:
Высчитываем по формуле нашу резонансную частоту:
У меня получилось 5, 09 Килогерц.
С помощью регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)
Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:
и конденсатор в 1000 пФ
Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.
Теперь небольшой прикол 
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!
Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:


Народ! Халява. Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:
Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Объяснение резонанса напряжения
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.
Добротность последовательного колебательного контура
Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:
Давайте посчитаем добротность в нашем случае.
Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала генератора частоты 2 Вольта.
А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.
Считаем по формуле добротности:
Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.
Есть также вторая формула для вычисления добротности.
R — сопротивление потерь в контуре, Ом
L — индуктивность, Генри
С — емкость, Фарад
Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.
Также хочу добавить пару слов о добротности. Добротность контура — это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.
Видео на тему «Как работает колебательный контур. Резонанс»:
Резюме
Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.
Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.
На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.
При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.
При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.
При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.
Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.
На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса — индуктивную составляющую тока.
Конденсатор, катушка и резонанс в цепи переменного тока
теория по физике 🧲 колебания и волны
Опишем колебания, которые происходят в цепи переменного тока при включении в нее конденсатора и катушки индуктивности. А также рассмотрим условия, при выполнении которых в цепи переменного тока наступает резонанс. Получим формулы для вычисления амплитуд напряжений, введем понятия емкостного и индуктивного сопротивления и выясним, какую роль играют эти величины.
Конденсатор в цепи переменного тока
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
u = φ 1 − φ 2 = q C . .
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
q C . . = U m a x cos . ω t
Следовательно, заряд конденсатора меняется по гармоническому закону:
q = C U m a x cos . ω t
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i = q ´ = − C U m a x sin . ω t = C U m a x cos . ( ω t + π 2 . . )
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π 2 . . (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
Амплитуда силы тока равна:
I m a x = U m a x C ω
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Величина X C , равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура q m a x = 10 − 6 Кл. Амплитудное значение силы тока в контуре I m a x = 10 − 3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q 2 m a x 2 C . . = L I 2 m a x 2 . .
L C = q 2 m a x I 2 m a x . .
√ L C = q m a x I m a x . .
T = 2 π √ L C = 2 π q m a x I m a x . . = 2 · 3 , 14 10 − 6 10 − 3 . . ≈ 6 , 3 · 10 − 3 ( с )
Катушка индуктивности в цепи переменного тока
Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).
Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока.
Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля → E i , порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля → E к , создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства → E i = − → E к следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции e i ) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать:
Напомним, что сила переменного тока изменяется по гармоническому закону:
i = I m a x sin . ω t
Тогда ЭДС самоиндукции равна:
e i = − L i ´ = − L ω I m a x cos . ω t
Так как u = − e i , то напряжение на концах катушки оказывается равным:
u = L ω I m a x cos . ω t = L ω I m a x sin . ( ω t + π 2 . . ) = U m a x ( ω t + π 2 . . )
Амплитуда напряжения равна:
U m a x = L ω I m a x
Следовательно, колебания напряжения на катушке опережают колебания силы тока на π 2 . . , или колебания силы тока отстают от колебаний напряжения на π 2 . . , что одно и то же.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).
Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна:
I m a x = U m a x L ω . .
Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим:
Величина X L , равная произведению циклической частоты на индуктивность, называется индуктивным сопротивлением. Индуктивное сопротивление зависит от частоты. Поэтому в цепи постоянного тока, в котором отсутствует частота, индуктивное сопротивление катушки равно нулю.
Пример №2. Катушка с индуктивным сопротивлением X L = 500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока I m a x в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.
Индуктивное сопротивление катушки выражается формулой:
X L = L ω = 2 π ν L
Так как амплитуда напряжения связана с его действующим значением соотношением U m a x = U √ 2 , то для амплитуды силы тока получаем:
Резонанс в электрической цепи
Механические и электромагнитные колебания имеют разную природу, но процессы, происходящие при этом, идентичны. Поэтому можно предположить, что резонанс в электрической цепи так же реален, как резонанс в колебательной системе, на которую действует периодическая сила.
Напомним, что в механической системе резонанс тем более заметен, чем меньше в колебательной системе трение между ее элементами. Роль трения в электрической цепи играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника, который при этом нагревается. Следовательно, резонанс в электрической цепи будет отчетливо наблюдаться при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная частота колебаний в колебательном контуре определяется формулой:
Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру равна собственной частоте колебательного контура:
Резонанс в электрическом колебательном контуре — явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
После включения внешнего переменного напряжения резонансное значение силы тока в цепи устанавливается не моментально, а постепенно. Амплитуда колебаний силы тока возрастает до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
I 2 m a x R 2 . . = U m a x I m a x 2 . .
Упростив это уравнение, получим:
I m a x R = U m a x
Следовательно, амплитуда установившихся колебаний силы тока при резонансе определяется уравнением:
I m a x = U m a x R . .
При сопротивлении, стремящемся к нулю, сила тока возрастает до бесконечно больших значений. При большом сопротивлении сила тока возрастает незначительно. Это хорошо видно на графике ниже.
Пример №3. В цепь переменного тока с частотой ν = 500 Гц включена катушка индуктивностью L = 10 мГн. Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?
Электрическая цепь, описываемая в условии, представляет собой колебательный контур. Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (ν = ν0).
ν 0 = 1 2 π √ L C . .
К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой ν.
Индуктивность L катушки колебательного контура можно плавно менять от максимального значения Lmax до минимального Lmin, а ёмкость его конденсатора постоянна.
Ученик постепенно уменьшал индуктивность катушки от максимального значения до минимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.
Алгоритм решения
Решение
В колебательном контуре источником тока возбуждаются вынужденные колебания. Частота этих колебаний равна частоте источника — ν. Амплитуда колебаний зависит от того, как соотносятся между собой внешняя частота и частота собственных электромагнитных колебаний, которая определяется формулой:
ν 0 = 1 2 π √ L C . .
По мере увеличения внешней частоты от нуля до ν0 амплитуда растет. Она достигает максимума тогда, когда происходит резонанс. При этом внешняя частота равна частоте собственных электромагнитных колебаний: ν = ν0. Затем амплитуда начинает убывать.
В данном случае, ученик меняет не внешнюю частоту, а частоту собственных электромагнитных колебаний. При плавном уменьшении индуктивности контура от максимального значения Lmax до минимального Lmin частота возрастает от ν0min до ν0max. Причем:
ν 0 m i n = 1 2 π √ L m i n C . .
ν 0 m a x = 1 2 π √ L m a x C . .
Из того факта, что амплитуда всё время увеличивалась, можем сделать вывод, что частота ν0 всё время приближалась к частоте источника тока, при этом ν > ν0max. В противном случае наблюдалось бы уменьшений амплитуды силы тока.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.
Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях.
а) период колебаний силы тока в контуре
б) фаза колебаний напряжения на конденсаторе
в) заряд конденсатора
г) энергия магнитного поля катушки
д) амплитуда колебаний напряжения на катушке
Алгоритм решения
- Определить, от чего зависит каждая из перечисленных величин.
- Установить, какие величины меняются, а какие нет.
Решение
В колебательном контуре происходят гармонические колебания. Поэтому период колебаний силы тока в контуре — величина постоянная.
Фаза — это величина, которая определяет положение колебательной системы в любой момент времени. Поскольку в системе происходят колебания, фаза меняется.
Заряд конденсатора — колебания происходят за счет постоянной перезарядки конденсатора. Следовательно, эта величина тоже меняется.
Энергия магнитного поля катушки — в колебательном контуре происходят взаимные превращения энергии магнитного поля катушки в энергию электрического поля конденсатора, и обратно. Поэтому энергия магнитного поля катушки постоянно меняется.
В условии задачи сказано, что колебания незатухающие. Это значит, что полная механическая энергия колебательной системы сохраняется. Поскольку именно от нее зависит амплитуда колебаний напряжения на катушке, то эта величина также остается постоянной.
pазбирался: Алиса Никитина | обсудить разбор | оценить

http://www.ruselectronic.com/posledovatelnyj-kolebatelnyj-kontur/
Электромагнитные колебания и волны
Содержание
- Свободные электромагнитные колебания. Колебательный контур
- Вынужденные электромагнитные колебания. Резонанс
- Гармонические электромагнитные колебания
- Переменный ток. Производство, передача и потребление электрической энергии
- Емкостное сопротивление
- Электромагнитное поле
- Свойства электромагнитных волн
- Различные виды электромагнитных излучений и их применение
- Основные формулы раздела «Электромагнитные колебания и волны»
Свободные электромагнитные колебания. Колебательный контур
Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
Колебательный контур — это замкнутый контур, образованный последовательно соединенными конденсатором и катушкой.
Сопротивление катушки ( R ) равно нулю.
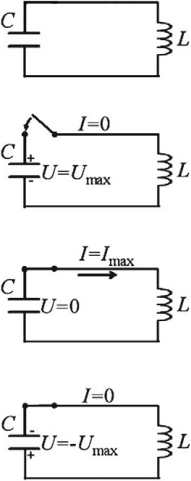
Если зарядить конденсатор до напряжения ( U_m ), то в начальный момент времени ( t_1=0 ), напряжение на конденсаторе будет равно ( U_m ). Заряд конденсатора в этот момент времени будет равен ( q_m=CU_m ). Сила тока равна нулю.
Полная энергия системы будет равна энергии электрического поля:
Конденсатор начинает разряжаться, по катушке начинает течь ток. Вследствие самоиндукции в катушке конденсатор разряжается постепенно.
Ток достигает своего максимального значения ( I_m ) в момент времени ( t_2=T/4 ). Заряд конденсатора в этот момент равен нулю, напряжение на конденсаторе равно нулю.
Полная энергия системы в этот момент времени равна энергии магнитного поля:
В следующий момент времени ток течет в том же направлении, постепенно (вследствие явления самоиндукции) уменьшаясь до нуля. Конденсатор перезаряжается. Заряды обкладок имеют заряды, по знаку противоположные первоначальным.
В момент времени ( t_3=T/2 ) заряд конденсатора равен ( q_m ), напряжение равно ( U_m ), сила тока равна нулю.
Полная энергия системы равна энергии электрического поля конденсатора.
Затем конденсатор снова разряжается, но ток через катушку течет в обратном направлении.
В момент времени ( t_4=3T/4 ) сила тока в катушке достигает максимального значения, напряжение на конденсаторе и его заряд равны нулю. С этого момента ток в катушке начинает убывать, но не сразу (явление самоиндукции). Энергия магнитного поля переходит в энергию электрического поля. Конденсатор начинает заряжаться, и через некоторое время его заряд равен первоначальному, а сила тока станет равной нулю.
Через время, равное периоду ( T ), система возвращается в начальное состояние. Совершилось одно полное колебание, дальше процесс повторяется.
Важно!
Колебания, происходящие в колебательном контуре, – свободные. Они совершаются без какого-либо внешнего воздействия — только за счет энергии, запасенной в контуре.
В контуре происходят превращения энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. В любой произвольный момент времени полная энергия в контуре равна:
где ( i, u, q ) – мгновенные значения силы тока, напряжения, заряда в любой момент времени.
Эти колебания являются затухающими. Амплитуда колебаний постепенно уменьшается из-за электрического сопротивления проводников.
Вынужденные электромагнитные колебания. Резонанс
Вынужденными электромагнитными колебаниями называют периодические изменения заряда, силы тока и напряжения в колебательном контуре, происходящие под действием периодически изменяющейся синусоидальной (переменной) ЭДС от внешнего источника:
где ( varepsilon ) – мгновенное значение ЭДС, ( varepsilon_m ) – амплитудное значение ЭДС.
При этом к контуру подводится энергия, необходимая для компенсации потерь энергии в контуре из-за наличия сопротивления.
Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением при совпадении частоты вынужденных колебаний внешней ЭДС с частотой собственных колебаний в контуре.
Емкостное и индуктивное сопротивления по-разному изменяются в зависимости от частоты. С увеличением частоты растет индуктивное сопротивление, а емкостное уменьшается. С уменьшением частоты растет емкостное сопротивление и уменьшается индуктивное сопротивление. Кроме того, колебания напряжения на конденсаторе и катушке имеют разный сдвиг фаз по отношению к колебаниям силы тока: для катушки колебания напряжения и силы тока имеют сдвиг фаз ( varphi_L=-pi/2 ), а на конденсаторе ( varphi_C=pi/2 ). Это означает, что когда растет энергия магнитного поля катушки, то энергия электрического поля конденсатора убывает, и наоборот. При резонансной частоте индуктивное и емкостное сопротивления компенсируют друг друга и цепь обладает только активным сопротивлением. При резонансе выполняется условие:
Резонансная частота вычисляется по формуле:
Важно!
Резонансная частота не зависит от активного сопротивления ( R ). Но чем меньше активное сопротивление цепи, тем ярче выражен резонанс.
Чем меньше потери энергии в цепи, тем сильнее выражен резонанс. Если активное сопротивление очень мало ( (Rto0) ), то резонансное значение силы тока неограниченно возрастает. С увеличением сопротивления максимальное значение силы тока уменьшается, и при больших значениях сопротивления резонанс не наблюдается.
График зависимости амплитуды силы тока от частоты называется резонансной кривой. Резонансная кривая имеет больший максимум в цепи с меньшим активным сопротивлением.
Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке. Эти напряжения становятся одинаковыми и во много раз больше внешнего напряжения. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. При резонансе амплитуды этих напряжений одинаковы и они компенсируют друг друга. Падение напряжения происходит только на активном сопротивлении.
При резонансе возникают наилучшие условия для поступления энергии от источника напряжения в цепь: при резонансе колебания напряжения в цепи совпадают по фазе с колебаниями силы тока. Установление колебаний происходит постепенно. Чем меньше сопротивление, тем больше времени требуется для достижения максимального значения силы тока за счет энергии, поступающей от источника.
Явление резонанса используется в радиосвязи. Каждая передающая станция работает на определенной частоте. С приемной антенной индуктивно связан колебательный контур. При приеме сигнала в катушке возникают переменные ЭДС. С помощью конденсатора переменной емкости добиваются совпадения частоты контура с частотой принимаемых колебаний. Из колебаний всевозможных частот, возбужденных в антенне, контур выделяет колебания, равные его собственной частоте.
Резонанс может привести к перегреву проводов и аварии, если цепь не рассчитана на работу в условиях резонанса.
Гармонические электромагнитные колебания
Гармоническими электромагнитными колебаниями называются периодические изменения заряда, силы тока и напряжения, происходящие по гармоническому – синусоидальному или косинусоидальному – закону.
В электрических цепях это могут быть колебания:
- силы тока – ( i=I_mcos(omega t+varphi+frac{pi}{2}); )
- напряжения – ( u=U_mcos(omega t+varphi); )
- заряда – ( q=q_mcos(omega t+varphi); )
- ЭДС – ( varepsilon=varepsilon_msinomega t. )
В этих уравнениях ( omega ) –циклическая частота, ( varphi ) – начальная фаза колебаний, амплитудные значения: силы тока – ( I_m ), напряжения – ( U_m ) и заряда – ( q_m ).
Важно!
Если в начальный момент времени заряд имеет максимальное значение, а сила тока равна нулю, то колебания заряда совершаются по закону косинуса с начальной фазой, равной нулю. Если в начальный момент времени заряд равен нулю, а сила тока максимальна, то колебания заряда совершаются по закону синуса.
Сила тока равна первой производной заряда от времени:
Амплитуда колебаний силы тока равна:
Колебания заряда и напряжения в колебательном контуре происходят в одинаковых фазах. Амплитуда напряжения равна:
Колебания силы тока смещены по фазе относительно колебаний заряда на ( pi/2 ).
Период свободных электромагнитных колебаний
Период свободных электромагнитных колебаний находится по формуле Томсона:
где ( L ) – индуктивность катушки, ( C ) – электроемкость конденсатора.
Циклическая частота: ( omega=frac{2pi}{T}=frac{1}{sqrt{LC}} )
Важно!
Период и циклическая частота не зависят от начальных условий, а определяются только индуктивностью катушки и электроемкостью конденсатора. Амплитуда колебаний заряда и силы тока определяются начальным запасом энергии в контуре.
При свободных гармонических колебаниях происходит периодическое преобразование энергии. Период колебаний энергии в два раза меньше, чем период колебаний заряда, силы тока и напряжения. Частота колебаний энергии в два раза больше частоты колебаний заряда, силы тока и напряжения.
Переменный ток. Производство, передача и потребление электрической энергии
Переменным называется ток, изменяющийся по величине и направлению по гармоническому закону.
Переменный ток представляет пример вынужденных электромагнитных колебаний. Для описания переменного электрического тока используют следующие величины:
• мгновенное значение силы тока – i;
• мгновенное значение напряжения – u;
• амплитудное значение силы тока – Im;
• амплитудное значение напряжения –Um.
Цепь переменного тока представляет собой колебательный контур, к которому приложена внешняя синусоидальная ЭДС. В цепь переменного тока могут включаться различные нагрузки: резистор, катушка, конденсатор.
Активное сопротивление
Проводник, преобразующий всю энергию электрического тока во внутреннюю, называется активным сопротивлением ( R ). (Эту величину мы раньше называли сопротивлением.) Активное сопротивление зависит от материала проводника, его длины и площади поперечного сечения и не зависит от частоты переменного тока.
В проводнике с активным сопротивлением колебания силы тока и напряжения совпадают по фазе:
Мгновенное значение мощности: ( p=i^2R, )
среднее значение мощности за период: ( overline{p}=frac{I_m^2R}{2}. )
Действующим значением силы переменного тока ( I_Д ) называют значение силы постоянного тока, который в том же проводнике выделяет то же количество теплоты , что и переменный ток за то же время:
Действующим значением напряжения переменного тока ( U_Д ) называют значение напряжения постоянного тока, который в том же проводнике выделяет то же количество теплоты, что и переменный ток за то же время:
Для цепи с активным сопротивлением выполняется закон Ома для мгновенных, амплитудных и действующих значений.
Индуктивное сопротивление
Катушка в цепи переменного тока имеет большее сопротивление, чем в цепи постоянного тока. В такой цепи колебания напряжения опережают колебания силы тока по фазе на ( pi/2 ). Колебания силы тока и напряжения происходят по закону:
Амплитуда силы тока в катушке:
где ( L ) – индуктивность катушки.
Индуктивным сопротивлением ( X_L ) называют физическую величину, равную произведению циклической частоты на индуктивность катушки:
Индуктивное сопротивление прямо пропорционально частоте. Физический смысл индуктивного сопротивления: ЭДС самоиндукции препятствует изменению в ней силы тока. Это приводит к существованию индуктивного сопротивления, уменьшающего силу тока.
Для цепи с индуктивным сопротивлением выполняется закон Ома.
Емкостное сопротивление
В цепи постоянного тока через конденсатор ток не идет. Для переменного тока конденсатор обладает конечным сопротивлением, обратно пропорциональным его емкости. В цепи переменного тока сопротивление конденсатора меньше, чем в цепи постоянного тока.
В такой цепи колебания напряжения отстают от колебаний силы тока по фазе на ( pi/2 ). Колебания силы тока и напряжения происходят по закону:
Амплитуда силы тока в катушке: ( I_m=Comega U_m. ).
Если ввести обозначение ( X_C=frac{1}{omega C} ), то получим соотношение между амплитудными значениями силы тока и напряжения, аналогичное закону Ома: ( I_m=frac{U_m}{X_C}. )
Емкостным сопротивлением ( X_C ) называют величину, обратную произведению циклической частоты на электроемкость конденсатора. Емкостное сопротивление обратно пропорционально частоте.
Физический смысл емкостного сопротивления: изменению переменного тока в любой момент времени противодействует электрическое поле между обкладками конденсатора.
В цепи переменного тока колебания силы тока и ЭДС происходят по синусоидальному закону с одинаковой циклической частотой ( omega ) и разностью фаз ( varphi ):
Соотношения амплитудных значений силы тока ( I_m ) и ЭДС ( varepsilon_m ) в цепи переменного тока связаны между собой законом Ома для цепи переменного тока:
Он гласит: амплитуда силы переменного тока прямо пропорциональна амплитуде ЭДС и обратно пропорциональна полному сопротивлению цепи:
Величина ( Z ) называется полным сопротивлением цепи переменного тока.
Электрическая энергия имеет перед другими видами энергии следующие преимущества:
- можно передавать на большие расстояния с малыми потерями;
- удобно распределять между потребителями;
- легко превращать в другие виды энергии.
В настоящее время производится и используется энергия переменного тока. Это связано с возможностью преобразовывать его напряжение и силу тока с малыми потерями энергии, что особенно важно при передаче электроэнергии на большие расстояния.
Различают следующие типы электростанций:
- тепловые;
- гидроэлектростанции;
- атомные.
Получение переменного тока
Переменный ток получают с помощью генератора переменного тока.
Генератор переменного тока (электромеханический генератор переменного тока) – это устройство, преобразующее механическую энергию в электрическую. В основе работы генератора переменного тока лежит явление электромагнитной индукции.
Процесс получения переменного тока можно рассмотреть на примере вращения витка провода в однородном магнитном поле. Магнитный поток через площадь витка равен:
Если период вращения витка ( T ), то угол ( alpha=frac{2pi t}{T}=omega t ).
Тогда ( Phi=BScosomega t. )
ЭДС индукции изменяется по закону ( e=-Phi’=BSomegasinomega t=varepsilon_msinomega t. )
Амплитуда ЭДС ( varepsilon_m=BSomega. )
Если рамка содержит ( N ) витков, то ( varepsilon_m=NBSomega. )
Основные части генератора переменного тока:
- обмотка статора с большим числом витков, в ней индуцируется ЭДС. Статор состоит из отдельных пластин из электротехнической стали для уменьшения нагрева от вихревых токов;
- ротор (вращающаяся часть генератора) создает магнитное поле. Для получения нужной частоты переменного тока может иметь несколько пар полюсов. На гидроэлектростанциях в генераторе число пар полюсов равно 40–50, на тепловых электростанциях – 10-16;
- клеммы для снятия напряжения.
Промышленные генераторы вырабатывают напряжение порядка 104 В. Промышленная частота переменного тока в нашей стране 50 Гц.
Передача электроэнергии
Электроэнергия производится в основном вдалеке от основных потребителей энергии, там, где есть топливные ресурсы.
С электростанции переменный ток по проводам линии электропередач (ЛЭП) поступает к различным потребителям электрической энергии. Для уменьшения потерь при передаче переменного тока необходимо использовать высокое напряжение. Чем длиннее линия, тем выше должно быть напряжение. В высоковольтных ЛЭП оно может достигать 500 кВ. Генераторы на электростанциях вырабатывают напряжение 16–20 кВ. Потребителям не нужно высокое напряжение. Возникает необходимость преобразования напряжения. С электростанции электрический ток поступает на повышающую подстанцию, затем передается по линии электропередач на понижающую подстанцию, где напряжение понижается до 6–10 кВ, а затем до 220–380 В. Для преобразования напряжения используют трансформатор.
Трансформатор – устройство, преобразующее переменное напряжение без изменения его частоты.
На схемах трансформатор обозначается:
Основные части трансформатора:
- замкнутый сердечник из электротехнической стали;
- две катушки-обмотки.
Катушка, подключаемая к источнику переменного напряжения, называется первичной обмоткой; катушка, к которой подключается нагрузка, – вторичной обмоткой.
Сердечник набирается из отдельных пластин для уменьшения потерь на нагревание вихревыми токами.
Принцип действия основан на явлении электромагнитной индукции. При подключении первичной обмотки к полюсам источника напряжения в ней возникает переменный ток. Напряжение изменяется с течением времени по гармоническому закону. С такой же частотой будут изменяться сила тока в катушке и магнитный поток, создаваемый этим током.
При изменении магнитного потока в каждом витке провода первичной обмотки возникает переменная ЭДС самоиндукции. Этот магнитный поток будет пронизывать и вторую катушку. В каждом ее витке возникает ЭДС индукции, изменяющаяся по гармоническому закону с той же частотой. Число витков в обмотках различно. Отношение ЭДС самоиндукции ( varepsilon_1 ) в первичной обмотке к ЭДС индукции во вторичной обмотке ( varepsilon_2 ) равно отношению числа витков в первичной обмотке ( N_1 ) к числу витков во вторичной обмотке ( N_2 ):
Режим работы
- Режим холостого хода – разомкнута цепь вторичной обмотки. Напряжение ( U_2 ) на ее концах в любой момент времени равно ЭДС индукции ( varepsilon_2 ), взятой с противоположным знаком. Поэтому можно записать:
где ( k ) – коэффициент трансформации.
Если ( k>1 ), то трансформатор понижающий, если ( k<1 ), то повышающий.
- Режим нагрузки. При подключении нагрузки к концам вторичной обмотки в ней возникает переменный ток. Напряжение ( U_2 ) на ее концах в любой момент времени отличается от ЭДС индукции ( varepsilon_2 ) на величину падения напряжения на внутреннем сопротивлении вторичной обмотки ( r ): ( U_2=varepsilon_2-I_2r ) или ( U_2=I_2R ).
Мощность тока в обмотках одинакова. Поэтому увеличение напряжения на входе повышающего трансформатора в ( k ) раз сопровождается уменьшением силы тока во вторичной катушке во столько же раз.
В трансформаторе нет потерь на трение, так как нет вращающихся частей. Потери в сердечнике состоят из потерь на нагревание и на перемагничивание.
Отношение мощности ( P_2 ), потребляемой нагрузкой, к мощности ( P_1 ), потребляемой первичной обмоткой трансформатора, называется коэффициентом полезного действия трансформатора:
КПД трансформатора – 98%.
Потребление электрической энергии: промышленность – около 70%; сельское хозяйство; транспорт; строительство; средства связи; в быту.
Электромагнитное поле
Электромагнитное поле – это особый вид материи, с помощью которого осуществляется электромагнитное взаимодействие заряженных тел или частиц.
Это понятие было введено Д. Максвеллом, развившим идеи Фарадея о том, что переменное магнитное поле порождает вихревое электрическое поле.
Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Вихревое электрическое поле порождает появление вихревого магнитного поля и так далее. Эти переменные электрическое и магнитное поля, существующие одновременно, и образуют единое электромагнитное поле.
Характеристиками этого поля являются вектор напряженности и вектор магнитной индукции.
Если электрический заряд покоится, то вокруг него существует только электрическое поле.
Если напряженность электрического поля равна нулю, а магнитная индукция отлична от нуля, то обнаруживается только магнитное поле.
Если электрический заряд двигается с постоянной скоростью, то вокруг него существует электромагнитное поле.
Максвелл предположил, что при ускоренном движении зарядов в пространстве будет возникать возмущение, которое будет распространяться в вакууме с конечной скоростью. Когда это возмущение достигнет второго заряда, то изменится сила, с которой электромагнитное поле действует на этот заряд.
При ускоренном движении заряда происходит излучение электромагнитной волны. Электромагнитное поле материально. Оно распространяется в пространстве в виде электромагнитной волны.
Свойства электромагнитных волн
Электромагнитная волна – это изменяющееся во времени и распространяющееся в пространстве электромагнитное поле.
Существование электромагнитных волн было теоретически предсказано английским физиком Дж. Максвеллом в 1864 году. Электромагнитные волны были открыты Г. Герцем.
Источник электромагнитной волны – ускоренно движущаяся заряженная частица – колеблющийся заряд.
Важно!
Наличие ускорения – главное условие излучения электромагнитной волны. Интенсивность излученной волны тем больше, чем больше ускорение, с которым движется заряд.
Источниками электромагнитных волн служат антенны различных конструкций, в которых возбуждаются высокочастотные колебания.
Электромагнитная волна называется монохроматической, если векторы ( vec{E} ) и ( vec{B} ) совершают гармонические колебания с одинаковой частотой (частотой волны).
Длина электромагнитной волны: ( lambda=cT=frac{c}{nu}, )
где ( c ) – скорость электромагнитной волны, ( T ) – период, ( nu ) – частота электромагнитной волны.
Свойства электромагнитных волн
- В вакууме электромагнитная волна распространяется с конечной скоростью, равной скорости света 3·108 м/с.
- Электромагнитная волна поперечная. Колебания векторов напряженности переменного электрического поля и магнитной индукции переменного магнитного поля взаимно перпендикулярны и лежат в плоскости, перпендикулярной к вектору скорости волны.
- Электромагнитная волна переносит энергию в направлении распространения волны.
Важно!
Электромагнитная волна в отличие от механической волны может распространяться в вакууме.
Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени.
Обозначение – ( I ), единица измерения в СИ – ватт на квадратный метр (Вт/м2).
Важно!
Плотность потока излучения электромагнитной волны от точечного источника убывает обратно пропорционально квадрату расстояния от источника и пропорциональна четвертой степени частоты.
Электромагнитная волна обладает общими для любых волн свойствами, это:
- отражение,
- преломление,
- интерференция,
- дифракция,
- поляризация.
Электромагнитная волна производит давление на вещество. Это означает, что у электромагнитной волны есть импульс.
Различные виды электромагнитных излучений и их применение
Электромагнитные излучения имеют длины волн от 10-12 до 104 м или частоты от 3·104 до 3·1020.
Различают следующие виды электромагнитных излучений:
- радиоволны;
- инфракрасное излучение;
- видимое излучение (свет);
- ультрафиолетовое излучение;
- рентгеновское излучение;
- гамма-излучение.
Границы между диапазонами условны, но излучения имеют качественные различия в свойствах. При переходе от излучений с малой частотой к излучениям с большей частотой волновые свойства проявляются слабее, а корпускулярные (квантовые) – сильнее.
Радиоволны
( lambda ) = 103–10-3 м, ( nu ) = 105–1011 Гц. Источники радиоволн – колебательный контур, вибратор.
Радиоволны делятся на:
- длинные (длина больше 1 км);
- средние (от 100 м до 1 км);
- короткие (от 10 до 100 м);
- ультракороткие (меньше 10 м).
Свойства: отражение, поглощение, интерференция, дифракция. Применение: радиосвязь, телевидение, радиолокация.
Радиосвязью называется передача информации с помощью радиоволн. Радиосвязь осуществляется с помощью модулированных радиоволн. Модуляцией радиоволны называется изменение ее параметров (амплитуды, частоты, начальной фазы) с частотой, меньшей частоты передаваемой волны.
Схема радиосвязи показана на рисунке:
Передача радиоволн. Генератор высокой частоты вырабатывает высокочастотные колебания несущей частоты. Звуковые колебания поступают в микрофон, где преобразуются в электромагнитные колебания. В модуляторе эти колебания преобразуются в модулированные колебания. После усиления модулированные колебания поступают в передающую антенну, которая излучает электромагнитные волны. На рисунке показан звуковой сигнал низкой частоты и модулированный высокочастотный сигнал.
Прием радиоволн. Электромагнитные колебания поступают в приемную антенну и вызывают электромагнитные колебания в приемном контуре. Эти колебания поступают в усилитель, а затем в детектор. В качестве детектора используют устройство с односторонней проводимостью. Это может быть полупроводниковый диод. В детекторе сигнал демодулируют (детектируют). Процесс детектирования заключается в выделении из высокочастотных модулированных колебаний колебаний низкой (звуковой) частоты. После сглаживания и усиления сигнал поступает в динамик. На рисунке показаны процессы детектирования (демодуляции) и сглаживания.
Радиолокацией называют обнаружение и определение местоположения объектов с помощью радиоволн. Излучение осуществляется короткими импульсами. В интервале времени между излучением двух последовательных импульсов осуществляется прием отраженного от объекта сигнала. Для радиолокации используют ультракороткие радиоволны.
Инфракрасное (тепловое) излучение
( lambda ) = 10-3 – 10-7 м, ( nu ) = 1011 – 1014 Гц. Источники – атомы и молекулы вещества.
Это излучение испускают все тела при температуре, отличной от 0 К. Свойства: нагревает вещество при поглощении; интерференция; дифракция; проходит через дождь, снег, дымку; невидимо; преломление, отражение. Применение: в приборах ночного видения, в физиотерапии, промышленности (для сушки). Регистрируют с помощью термопары, болометра, фотографическим методом.
Видимое излучение
( lambda ) = 8·10-7 – 4·10-7 м, ( nu ) = 4·1011 – 8·1014 Гц.
Это излучение воспринимается глазом. Свойства: отражение, преломление, поглощение, интерференция, дифракция.
Ультрафиолетовое излучение
( lambda ) = 10-8 – 4·10-7 м, ( nu ) = 8·1014 – 3·1015 Гц. Источники – кварцевые лампы.
Ультрафиолетовое излучение дают светящиеся пары ртути и твердые тела, у которых температура выше 1000°С. Свойства: химическое действие; большая проникающая способность; биологическое действие; невидимо. Применение: в медицине, промышленности. Регистрируют фотографическими методами.
Рентгеновское излучение
( lambda ) = 10-8 – 10-11 м, ( nu ) = 3·1016 – 3·1019 Гц. Источник – рентгеновские трубки.
Возникает при торможении быстрых электронов. Свойства: высокая химическая активность; биологическое действие; интерференция; дифракция на кристаллической решетке; высокая проникающая способность. Применение: в медицине, промышленности, науке.
Гамма-излучение
Длина волны меньше 10-11 м, частота от 1020 Гц и выше. Источник – ядерные реакции.
Свойства: высокая проникающая способность, сильное биологическое действие. Применение: в медицине, промышленности (дефектоскопия), науке.
Шкала электромагнитных излучений позволяет сделать вывод: все электромагнитные излучения обладают одновременно волновыми и квантовыми свойствами, которые дополняют друг друга.
Важно!
Волновые свойства сильнее выражены при малых частотах и больших длинах волн, а квантовые – при больших частотах и малых длинах волн.
Решение задач по теме «Электромагнитные колебания и волны»
По этой теме можно выделить четыре группы задач:
- на определение параметров колебательного контура;
- на уравнения гармонических электромагнитных колебаний;
- на применение закона Ома;
- на расчет мощности и КПД трансформатора.
Решение первой группы задач на определение параметров колебательного контура основано на использовании формулы Томсона (формулы периода свободных электромагнитных колебаний) и закона сохранения и превращения энергии в колебательном контуре. Поэтому необходимо записать уравнения для мгновенных значений заряда и напряжения на конденсаторе и силы тока в катушке; записать уравнение для полной энергии колебательного контура в произвольный момент времени. В качестве дополнительных формул могут понадобиться формулы электроемкости плоского конденсатора, индуктивности катушки и длины электромагнитной волны. Помните, что скорость распространения электромагнитной волны в вакууме равна скорости света – 3·108 м/с. В среде с показателем преломления ( n ) скорость света можно рассчитать по формуле: ( v=frac{c}{n}. )
Важно!
Амплитудное значение напряжения – ( U_m=frac{q_m}{C} ), амплитудное значение силы тока – ( I_m=q_momega ).
При решении второй группы задач на уравнения гармонических электромагнитных колебаний рекомендуется записать заданное в задаче уравнение и уравнение гармонических колебаний в общем виде. Сравнить эти уравнения и определить основные характеристики: амплитуду, частоту, фазу.
При решении задач на закон Ома нужно помнить, что электроизмерительные приборы показывают действующие значения напряжения и силы тока. Действующие значения величин пропорциональны амплитудным значениям. Важно помнить, что резонанс возникает при равенстве индуктивного и емкостного сопротивлений.
Решение четвертой группы задач на расчет мощности и КПД трансформатора опирается на знание формул КПД и мощности в цепи.
Основные формулы раздела «Электромагнитные колебания и волны»
Электромагнитные колебания и волны
3.2 (63.87%) 62 votes
google.com/+ВикторЦекунов
Репетитор по математике, физике (Минск): Виктор Иванович.
Высшая математика и физика для студентов.
Профессиональный репетитор окажет помощь в решении задач, подготовит к экзаменам. Занятия в Серебрянке, индивидуально. (90 мин)
= 20 $.
Тел: +375(29) 127 61 86.
___________________________________________________________________________________
Оказываю
платные услуги: решение задач по физике. Оплата WebMoney.
Заказы направляйте сюда: Платные услуги
___________________________________________________________________________________
4.1.
Механические колебания.
4.1.1. Гармонические колебания.
4.1.2. Свободные затухающие колебания.
4.1.3. Вынужденные колебания. Резонанс.
4.2. Электрические колебания.
4.3. Упругие волны. Акустика.
4.4. Электромагнитные волны. Излучение.
_______________________________________________________________________________________________
4.1. Механические колебания. 4.1.1. Гармонические колебания.
4.1.1-1.
Частица совершает гармоническое колебание с амплитудой А и периодом Т = 12 с.
Найти время t₁ , за
которое смещение частицы изменяется от 0 до А/2.
Решение:
Т = 12 с
х(0) = 0
х(t₁) =
А/2 (1)
t₁ – ?
Так как начальное положение частицы х(0) = 0, то частица колеблется по закону
синуса с начальной фазой ϕ₀ = 0:
x = Asin(ωt + ϕ₀) или
x = Asinωt, (2)
где ω = 2π/T –
круговая частота.
С учётом условия (1), запишем (2) в виде:
х(t₁) = Asin(ωt₁);
А/2 = Asin( (2π/T)t₁ );
1/2 = sin(2πt₁/T); 2πt₁/T = π/6. Отсюда
t₁ = T/12.
t₁
= 12/12 = 1 с.
Ответ: t₁ = T/12 = 1 c.
4.1.1-2.
Определить период Т простых гармонических колебаний диска радиусом R = 40
см около горизонтальной оси, проходящей через образующую диска.
Решение:
R = 0,4
м
T − ?
В данном случае диск − это физический маятник, период колебаний которого
определим по формуле:
, (1)
где −
I
момент инерции диска относительно оси вращения, проходящей через точку подвеса
А (см. рис.); x = AO = R −
расстояние от точки подвеса до центра тяжести О диска; m −
масса диска; g = 9,8
м/с² − ускорение свободного падения.
Момент инерции I₀ диска относительно оси симметрии диска:
I₀ = mR²/2.
По
теореме Штейнера:
I = I₀ + mR². Имеем
I = mR²/2 + mR² = 3mR²/2. Тогда по (1)
4.1.1-3.
Материальная точка движется согласно уравнению r(t) = A(icosωt + jsinωt), где
A = 0,5
м, ω = 5
с⁻¹. Изобразите на рисунке траекторию движения. Определите модуль скорости и
модуль нормального ускорения.
Решение:
r(t) = A(icosωt + jsinωt) (1)
A = 0,5
м
ω = 5
с⁻¹
v − ?
an − ?
Представим (1) в виде:
r(t) = iAcosωt + jAsinωt (1*)
Радиус вектор r(t)
точки: r(t) = ix + jy, где x, y −
проекции радиус вектора соответственно на оси OX и OY; i, j −
единичные векторы (орты), направленные соответственно по оси OX и OY.
Тогда (1*) примет вид
ix + jy = iAcosωt + jAsinωt,
отсюда получим два уравнения
x = Acosωt, (*)
y = Asinωt. (**)
Возведём их в квадрат
x² = A²cos²ωt,
y² = A²sin²ωt.
Сложим эти уравнения
x² + y² = A²cos²ωt + A²sin²ωt или x² + y² = A²(cos²ωt + sin²ωt).
Отсюда, т.к. cos²ωt + sin²ωt = 1,
получим уравнение траектории движения точки
x² + y² = A². (2)
Уравнение (2) − это уравнение окружности радиусом R = A = 0,5
м с центром в начале координат (см. рис.).
Найдём проекции скорости vx и vy. Для этого продифференцируем x и y из
(*) и (**) по времени t:
vx = xtʹ = (Acosωt)tʹ = — Aωsinωt;
vy = ytʹ = (Asinωt)tʹ = Aωcosωt.
Тогда квадрат скорости
v² = vx² + vy² или v² = (-
Aωsinωt)² + (Aωcosωt)² или
v² = A²ω²(sin²ωt + cos²ωt) или v² = A²ω².
Отсюда модуль скорости v:
v = Aω. (3)
v =
0,5·5 = 2,5 м/с².
Модуль нормального ускорения an: an = v²/R или, с учётом (3) и R = A, получим an = A²ω²/A или
an = Aω².
an =
0,5·5² = 12,5 м/с².
Ответ: траектория − окружность радиусом R = A = 0,5
м с центром в начале координат, v = Aω = 2,5 м/с², an = Aω² = 12,5 м/с².
_______________________________________________________________________________________________
4.1.2. Свободные затухающие колебания.
4.1.2-1.
Амплитуда затухающих колебаний уменьшилась в n = 100
за 15 с. Чему равен коэффициент затухания β?
Решение:
t = 15 c
n = 100
A = A₀/n (*)
β – ?
Зависимость амплитуды А затухающих колебаний от времени t:
A = A₀e—βt, (1)
где A₀ –
начальная амплитуда; β – коэффициент затухания.
Имеем из (1) и (*):
A₀/n = A₀e—βt; 1/n = e—βt; eβt = n; βt = ln(n)
отсюда
β = ln(n)/t.
β =
ln(100)/15 = 0,307 1/c.
Ответ: β = ln(n)/t = 0,307 1/c.
4.1.2-2. Найти
логарифмический декремент затухания тонкого стержня, подвешенного за один из
его концов, если за промежуток времени t = 5
мин его полная механическая энергия уменьшилась в n = 4·10² раз. Длина
стержня L = 50 см.Решение:
t = 5 мин = 300 с
n = 400
L = 0,5
м
λ − ?
В данном случае стержень − это физический маятник.
Логарифмический декремент затухания λ
λ = βT, (1)
где β –
коэффициент затухания, T− период колебаний стержня.
1. Найдём коэффициент затухания
β.
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
ω –
частота затухающих колебаний; ω₀ – собственная частота колебаний.
Зависимость от времени t полной механической энергии Е физического маятника:
Е = E₀e-2βt,
где E₀ – начальная (при t = 0) полная механическая энергия.
Отсюда имеем
n = Е₀/Е = Е₀/(E₀e-2βt) = 1/(e-2βt) =
e2βt.
Получили n = e2βt.
Прологарифмируем это равенство Ln(n) = 2βt. Отсюда
β = Ln(n)/(2t). (3)
2. Найдём период Т затухающих колебаний.
Оценим коэффициент
β2 по (3).
β = Ln(400)/(2·300)
= 0,009986, отсюда
β² = (0,009986)² ≈ 0,0000997.
Собственная частота колебаний физического маятника:

где J = mL²/3 –
момент инерции стержня относительно оси вращения, m –
масса стержня, g – ускорение свободного падения, d = L/2 –
расстояние от точки подвеса до центра тяжести стержня.
Подставим всё в (4) и, после упрощения, получим

По (4*) оценим ω₀2:
ω₀2 = 3·9,8/(2·0,5) = 29,9.
Так как β² << ω₀2,
то, пренебрегая β², из (2) следует ω ≈ ω₀ , поэтому период затухающих колебаний T
T = 2π/ω = 2π/ω₀ или
. (4**)
Подставим в (1) найденные β из (3) и Т из (4**) и, после упрощения, получим
.
= 0,01157.
4.1.2-3. Логарифмический
декремент затухания тела, колеблющегося с частотой 50 Гц, равен 0,02.
Определите: время, за которое амплитуда колебаний тела уменьшится в 20
раз; число колебаний тела, чтобы произошло подобное уменьшение амплитуды.Решение:
ν = 50 Гц
λ =
0,02
n = 20
t − ?
N − ?
1. Пусть β –
коэффициент затухания; T = 1/ν – период, ν – частота колебаний. Логарифмический декремент
затухания λ:
λ = βT или λ = β/ν,
отсюда
β = λν. (1)
Амплитуда А затухающих колебаний
A = A₀·e—βt,
где A₀ −
начальная амплитуда (при t = 0).
Подставим сюда из условия задачи A = A₀/n:
A₀/n = A₀·e—βt,
отсюда eβt = n и,
после логарифмирования, βt = Ln(n), отсюда
t = ( Ln(n) )/β и, с
учётом (1),
t = ( Ln(n) )/(λν). (2)
2. Число колебаний N за время t:
N = t/T = tν = (
и, с учётом (2), ) = ν( Ln(n) )/(λν) или
N = ( Ln(n) )/λ. (3)
3. Вычисления по формулам (2) и (3):
t = ( Ln(20)
)/(0,02·50) ≈ 3 с.
N = ( Ln(20)
)/0,02 ≈ 150.
Ответ: t = ( Ln(n) )/(λν) ≈ 3
с; N =( Ln(n) )/λ ≈
150.
4.1.2-4. Составьте
дифференциальное уравнение гармонических свободных затухающих крутильных
колебаний механической системы.Решение:
Пусть
система (например, тонкий однородный диск, подвешенный в горизонтальном
положении к упругой нити) совершает крутильные колебания относительно
закреплённой оси Z (ось нити). Пусть на диск действует упругая сила,
проекция момента которой на ось Z равна
Mz = — kϕ, (1)
где k −
постоянная, ϕ −
угол поворота из положения равновесия. Знак “минус” указывает на то, что при
отклонении системы на угол ϕ, момент упругой силы возвращает систему к положению
равновесия. Поместим диск в вязкую среду ( например, жидкость ). Момент силы
сопротивления Mc,
действующий на диск, пропорционален угловой скорости ϕʹ:
Mc = — ηϕʹ,
(2)
где η −
постоянная.
Уравнение динамики вращательного движения диска имеет вид
Iϕʹʹ = Mz + Mc,
(3)
где I –
момент инерции диска относительно оси вращения.
С учётом (1) и (2), уравнение (3) примет вид Iϕʹʹ = —
kϕ — ηϕʹ,
отсюда
ϕʹʹ + (η/I)ϕʹ + (k/I)ϕ = 0.
Применив обозначения 2β = η/I, ω₀² = k/I, перепишем последнее уравнение:
ϕʹʹ + 2βϕʹ + ω₀²ϕ = 0.
Это дифференциальное уравнение описывает затухающие крутильные колебания
механической системы.
Ответ: ϕʹʹ + 2βϕʹ + ω₀²ϕ = 0.
4.1.2-5.
Найти добротность Q осциллятора, у которого отношение резонансной частоты ωрез
к частоте затухающих колебаний ω равно η.
Решение:
ωрез/ω = η (*)
Q − ?
Пусть β − коэффициент затухания, ω₀ − собственная частота колебаний, T = 2π/ω −
период затухающих колебаний, λ = βT = 2πβ/ω − логарифмический декремент
затухания. Тогда добротность Q:
Q = π/λ = π/(2πβ/ω), или
Q = ω/(2β). (1)
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
Формула для резонансной частоты ωрез:
ωрез² = ω₀² — 2β². (3)
Из (2) вычтем (3)
ω² — ωрез² = (ω₀² — β²) — (ω₀² — 2β²), или
ω² — ωрез² = ω₀² — β² — ω₀² + 2β², или
ω² — ωрез² = β². (**)
С учётом условия (*) имеем ωрез = ωη. Тогда (**) примет вид
ω² — ω²η² = β², или
ω²(1 — η²) = β², отсюда
Подставляя полученное выражение ω в (1), окончательно получим:
___________________________________________________________________________________
4.1.3. Вынужденные колебания. Резонанс.
4.1.3-1.
Осциллятор массы m движется по закону x = Asinωt под действием вынуждающей силы
Fₓ = F₀cosωt. Найти коэффициент затухания β осциллятора.
Решение:
m,
x = Asinωt,
Fₓ = F₀cosωt,
β − ?
Установившееся смещение х(t) осциллятора при вынужденных колебаниях:
x = Acos(ωt — ϕ), (1)
где амплитуда А колебаний
(2)

ω₀ − собственная частота колебаний осциллятора,
f₀ = F₀/m. (*)
Так как по условию смещение х(t) осциллятора x = Asinωt, то из (1) следует: ϕ =
π/2
(т. к. cos(ωt — π/2) = sinωt). Тогда из (3) имеем:



4.1.3-2.
При неизменной амплитуде вынуждающей силы амплитуда вынужденных колебаний при
частотах ω₁ = 100 с⁻¹ и ω₂ = 300 с⁻¹ оказывается одинаковой. Найти резонансную
частоту ωрез.
Решение:
F₀ = const (амплитуда
вынуждающей
силы)
ω₁ = 100 с⁻¹
ω₂ = 300 с⁻¹
А₁ = А₂
ωрез − ?
Амплитуда А вынужденных колебаний:
(*)
где f₀ =
F₀/m, m − масса
осциллятора, β − коэффициент затухания, ω₀ −
собственная частота колебаний, ω − частота вынужденных колебаний.
При постоянной
амплитуде вынуждающей силы F₀ (и,
следовательно, постоянной f₀) из (*) при двух разных частотах ω₁
и ω₂ получаем две амплитуды А₁ и А₂ вынужденных колебаний:
С учётом условия А₁ = А₂ , получим
Отсюда, приравнивая знаменатели и, возводя полученное равенство в квадрат,
получим
(ω₀² — ω₁²)² + 4β²ω₁² = (ω₀² — ω₂²)² + 4β²ω₂² или
ω₀⁴ — 2ω₀²ω₁²+ ω₁⁴ + 4β²ω₁² = ω₀⁴ — 2ω₀²ω₂² + ω₂⁴ + 4β²ω₂² или
— 2ω₀²ω₁²+ ω₁⁴ + 4β²ω₁² = — 2ω₀²ω₂² + ω₂⁴ + 4β²ω₂² или
2ω₀²(ω₂² — ω₁²) + (ω₁⁴ — ω₂⁴) + 4β²(ω₁² — ω₂²) = 0 или
— 2ω₀²(ω₁² — ω₂²) + (ω₁² — ω₂²)(ω₁² + ω₂²) + 4β²(ω₁² — ω₂²) = 0 и, после
деления на (ω₁² — ω₂²) ≠ 0:
— 2ω₀² + ω₁² + ω₂² + 4β² = 0. (1)
Формула для резонансной частоты ωрез:
отсюда ω₀² = ωрез² + 2β² и подставим в (1)
— 2(ωрез² + 2β²) + ω₁² + ω₂² + 4β² = 0 или
— 2ωрез² + ω₁² + ω₂² = 0, отсюда
_______________________________________________________________________________________________ 4.2. Электрические колебания.4.2-1.
Небольшая магнитная стрелка совершает малые колебания вокруг оси,
перпендикулярной направлению внешнего магнитного поля. При изменении индукции
этого поля период колебаний стрелки уменьшился в η = 5
раз. Во сколько раз и как изменилась индукция поля? Затухание колебаний
пренебрежимо мало.
Решение:
T₁/T₂ = η = 5
B₂/B₁ − ?
Момент сил М, действующий на стрелку со стороны магнитного
поля
М = [B·Pm],
где Pm −
вектор магнитного момента стрелки.
Модуль момента сил
М = B·Pm·sinϕ, где ϕ –
угол между векторами B и Pm.
При малых колебаниях угол ϕ очень мал и sinϕ ≈ ϕ. Тогда
М = B·Pm·ϕ.
При повороте стрелки на угол ϕ возникает момент сил М, стремящийся вернуть стрелку в
положение равновесия, т.е. М = — B·Pm·ϕ. Если J – момент инерции стрелки относительно оси вращения,
то основное уравнение динамики вращательного движения примет вид
Jϕ’’ = M или Jϕ’’ = —
B·Pm·ϕ отсюда
ϕ’’ + (B·Pm/J)·ϕ = 0. (1)
Если ω – циклическая
частота колебаний, то сравнивая (1) с уравнением гармонических колебаний
ϕ’’ + ω²ϕ = 0,
получим
ω² = B·Pm/J,
отсюда
ω = √(B·Pm/J).
Тогда период T
колебаний
T = 2π/ω или
T = 2π√( J/(B·Pm) ). (2)
На основе (2) для разных B₁ и B₂ получим соответствующие T₁ и T₂
T₁ = 2π√( J/(B₁·Pm) )
T₂ = 2π√( J/(B₂·Pm) ).
Отсюда
T₁/T₂ = √(B₂/B₁) и
отсюда
B₂/B₁ = (T₁/T₂)² = η² =
25. Итак
B₂/B₁ = η² =
25.
Ответ: индукция магнитного поля увеличится в η² = 25
раз.
4.2-2. Индуктивность
катушки равна 0,125 Гн. Уравнение колебаний силы ток в ней имеет вид:
i = 0,4cos(1000t), где
все величины выражены в системе СИ. Определить амплитуду напряжения на катушке.
Решение:
L = 0,125 Гн
i = 0,4cos(1000t). (1)
Um − ?
Уравнение колебаний силы тока в катушке имеет вид:
i = Imcos(ωt). (2)
Из (1) и (2) имеем
Im = 0,4
А − амплитуда силы тока в катушке; ω = 1000 с⁻¹− частота.
Индуктивное сопротивление катушки: XL = ωL .
По закону Ома
Im = Um/XL,
отсюда
Um= XL·Im или
Um = ωL·Im.
Um
= 1000·0,125·0,4 = 50 В.
Ответ: Um = 50 В.4.2-3. Электрический
колебательный контур состоял из последовательно соединенных катушки с
индуктивностью L = 0,8
Гн и конденсатора емкостью С. Сопротивление катушки и соединительных проводов
было равно R =
2000 Ом. После того, как часть витков в катушке замкнулась накоротко,
индуктивность ее уменьшилась в n = 7 раз, частота собственных колебаний в контуре
возросла в k = 3
раза, а коэффициент затухания этих колебаний не изменился. Определить емкость
конденсатора.Решение:
L = 0,8 Гн
R =
2000 Ом
L₂ = L/n
n = 7
ω₂ = kω
k = 3
β = const
C − ?
Коэффициент затуханий β = R/(2L).
ω и ω₂ −
начальная и конечная частоты собственных колебаний в контуре, где
ω = √(
1/(LC) — β² ) =
√( 1/(LC) — R²/(4L²) );
ω₂ = √(
1/(L₂C) — β² ) =
√( n/(LC) — R²/(4L²) ).
Возведём в квадрат равенство ω₂ = kω, получим ω₂² = k²ω² или
n/(LC) — R²/(4L²) = k²( 1/(LC) — R²/(4L²) ),
отсюда
C = 4L(k² — n)/( R²(k² — 1)
).
C =
4·0,8·(3² — 7)/( 2000²·(3² — 1) ) = 2·10⁻⁷ Ф.
Ответ: C = 4L(k² — n)/( R²(k² — 1) ) = 2·10⁻⁷ Ф.
4.2-4.
Ток в колебательном контуре зависит от времени как I = Imsinω₀t, где Im = 9,0
мА, ω₀ = 4,5·10⁴ с⁻¹. Ёмкость конденсатора С = 0,50 мкФ. Найти индуктивность
контура и напряжение на конденсаторе в момент t = 0.
Решение:
I = Imsinω₀t (*)
Im = 9·10⁻³ А
ω₀ = 4,5·10⁴ с⁻¹
С = 0,5·10⁻⁶ Ф
L − ?
U(0) − ?
1). Собственная частота ω₀ колебательного контура
, отсюда
1
L = ––––– . (1)
ω₀²C
2). Закон сохранения энергии в колебательном контуре:
LI²/2 + CU²/2 = LIm²/2
или, с учётом (*),
L(Imsinω₀t)²/2 + CU²/2 = LIm²/2.
Отсюда при t = 0 (т.к. sinω₀0 = 0) получим напряжение U(0) = Um на конденсаторе
в момент времени t = 0 (
Um − максимальное напряжение):
CU²(0) = LIm²
и, подставляя сюда L из (1), получим
Im²
CU²(0) = ––––– или
ω₀²C
Im
U(0) = Um = –––– . (2)
ω₀C
Вычисления по формулам (1) и (2 ):
1
L = –––––––––––––––– = 0,001 Гн = 1 мГн.
(4,5·10⁴)²·0,5·10⁻⁶
9·10⁻³
U(0) = Um = –––––––––––––– = 0,4 В.
4,5·10⁴·0,5·10⁻⁶
_______________________________________________________________________________________________
4.3. Упругие волны. Акустика.
4.3-1.
По шнуру слева направо бежит со скоростью v
незатухающая гармоническая волна. При этом поперечное смещение точки О шнура
изменяется по закону y = Acos(ωt). Как зависит от времени смещение точки шнура,
находящейся правее точки О на расстоянии x от
нее?
Решение:
y = Acos( ω(t — x/v) ).
Ответ: y = Acos( ω(t – x/v) ).
4.3-2.
Уравнение плоской звуковой волны имеет вид ξ = 60cos(1800t — 5,3x). где ξ – в мкм, t – в секундах, х – в метрах.
Найти:
а) отношение амплитуды смещения частиц среды к длине волны;
б) амплитуду
колебаний скорости частиц среды и ее отношение к скорости распространения
волны;
в) амплитуду колебаний относительной деформации среды и её связь с амплитудой колебаний скорости частиц среды.
Решение:
ξ = 60·10⁻⁶cos(1800t – 5,3x)
(1)
a) A/λ – ?
б) Vm – ? Vm/v – ?
в) (∂ξ/∂x)m – ? (∂ξ/∂x)m = f(Vm) – ?
а) Уравнение плоской синусоидальной волны
ξ = Acos(ωt – kx).
(2)
Из (1) и (2) следует
A = 60·10⁻⁶ м – амплитуда колебаний частиц среды,
ω = 1800 1/с – циклическая частота,
k = 5,3 1/м – волновое число.
k = 2π/λ, отсюда λ = 2π/k. Тогда
A/λ = A/(2π/k) или
A/λ = Ak/(2π).
A/λ =
60·10⁻⁶·5,3/(2·3,14) = 5,1·10⁻⁵.
б)
Амплитуда
колебаний скорости частиц среды
Vm = Aω. (*)
Vm =
60·10⁻⁶·1800 = 0,11 м/с. = 11 см/с.
Скорость
распространения волны
v = ω/k. (3)
Тогда ( см. (*) )
Vm/v = Aω/(ω/k) = Ak.
Vm/v = Ak.
Vm/v = 60·10⁻⁶·5,3 = 3,2·10⁻⁴.в) Относительную деформацию среды найдём дифференцируя (2) по х:
∂ξ/∂x = ( Acos(ωt – kx) )xʹ = — Aksin(ωt – kx).
Отсюда амплитуда колебаний относительной деформации среды:
(∂ξ/∂x)m = Ak. (**)
(∂ξ/∂x)m = 60·10⁻⁶·5,3 = 3,2·10⁻⁴.
Связь между амплитудой колебаний относительной деформации среды (dξ/dx)m и амплитудой колебаний скорости частиц среды Vm найдем по (*) и (**). Имеем
(dξ/dx)m = Ak = (Vm/ω)k = Vmk/ω = ( с учётом (3) ) = Vm/v. Получили
(dξ/dx)m = Vm/v или
Vm = v·(dξ/dx)m ,
где v = ω/k = 1800/5,3 = 340 м/с – скорость волны.
Ответ: a) A/λ = 5,1·10⁻⁵;
б) Vm = 0,11 м/с, Vm/v = 3,2·10⁻⁴;
в) (∂ξ/∂x)m = 3,2·10⁻⁴, Vm = v·(dξ/dx)m , где v = 340 м/с – скорость волны.
4.3-3.
Что такое амплитуда колебаний скорости частиц среды?
Решение:
Объясню
на простом примере. В озере на воде поплавок. Бросьте в воду камешек,
от него во все стороны пойдут волны. Поплавок колеблется на волнах.
Скорость колебаний поплавка − это скорость колебаний частиц среды (воды). Максимальная скорость колебаний поплавка − это амплитуда колебаний скорости частиц среды.
Амплитуда
колебаний скорости частиц среды
Vm = Aω (A —
амплитуда, ω —
циклическая частота).
Скорость распространения волны
v = ω/k (k —
волновое число).
A, ω, k
определяют из общего вида уравнения бегущей плоской синусоидальной волны
ξ = Acos(ωt – kx).
4.3-4.
Точечный изотропный источник испускает звуковые колебания с частотой ν = 1,45
кГц. На расстоянии r₁ = 5 м от источника амплитуда смещения частиц среды А₁ =
50 мкм, а в точке А, находящейся на расстоянии r₂ = 10 м от источника,
амплитуда смещения в η = 3 раза меньше А₁. Найти:
а) коэффициент затухания волны γ;
б) амплитуду колебаний скорости частиц среды в точке А.
Решение:
ν = 1450 Гц
r₁ = 5 м
А₁ = 50·10⁻⁶ м
r₂ = 10 м
А₂ = А₁/η (η = 3) (*)
а) γ − ?
б) Vm − ? (в точке А)
От данного точечного источника распространяются сферические волны. Для
однородной поглощающей среды уравнение сферической волны:
(1)
где ξ − смещение частиц среды; ω = 2πν − циклическая частота; k − волновое
число.
а). Из (1) выпишем амплитуду A смещения частиц среды (множитель перед
косинусом):
A =
(A₀/r)·e⁻ᵞʳ.
Отсюда для r = r₁ и r = r₂ получаем амплитуды смещения частиц среды A₁ и A₂
соответственно
A₁ = (A₀/r₁)·e⁻ᵞr₁ , (**)
A₂ = (A₀/r₂)·e⁻ᵞr₂ . (***)
Делим (**) на (***) и, с учётом (*), получаем:
·η = (r₂/r₁)·eᵞ⁽r₂⁻r₁⁾ отсюда ηr₁/r₂ = eᵞ⁽r₂⁻r₁⁾ , отсюда, по определению логарифма, имеем
ln(ηr₁/r₂) = γ(r₂ — r₁), отсюда
γ = ln(3·5/10)/(10 — 5) ≈
0,08 м⁻¹.
б). Для нахождения скорости смещения частиц среды V найдём частную производную
по времени t от (1):
V = ∂ξ/∂t = (A₀/r)·e⁻ᵞʳ·( — ωsin(ωt—kr) ).
С учётом ω = 2πν, имеем
V =
— (2πνA₀/r)·e⁻ᵞʳ·sin(ωt-kr).
Отсюда амплитуда колебаний скорости частиц среды Vm (множитель перед синусом):
Отсюда в точке А (r = r₂) амплитуда колебаний скорости частиц среды
Vm = (2πνA₀/r₂)·e⁻ᵞr₂
и, с учётом (***), получим Vm = 2πνA₂. Тогда, учтя (*), окончательно получим:
Vm = 2πνA₁/η.
Vm = 2·3,14·1450·50·10⁻⁶/3 ≈ 0,15 м.
4.3-5. Плоская
звуковая волна, частота которой 100 Гц и амплитуда 5 мкм, распространяется со
скоростью 300 мс в воздухе, плотность которого равна 1,2 кгм³.
Определить интенсивность волны.Решение:
ν = 100 Гц
а = 5·10⁻⁶ м
V = 300
мс
ρ = 1,2
кгм³
I − ?
Интенсивность I
звуковой волны
I = ρа²ω²V/2 и
т.к. ω = 2πν, то
I = ρа²(2πν)²V/2.
I =
1,2·(5·10⁻⁶)²·(2·3,14·100)²·300/2 = 1,77·10⁻³ Вт/м².
Ответ: I = 1,77·10⁻³ Вт/м².
4.3-6.
Стальная струна длины l = 100 см и диаметра d = 0,50 мм даёт основной тон
частоты ν = 256 Гц. Найти силу её натяжения.
Решение:
l = 1 м
d = 0,5·10⁻³ м
ν = 256 Гц
ρ = 7800 кг/м³ (плотность стали)
F − ?
В закреплённой с обоих концов натянутой струне при возбуждении поперечных
колебаний устанавливаются стоячие волны. Основной тон частоты ν колебаний
струны:
ν = V/2l, отсюда
V = 2lν, (1)
где
− фазовая скорость поперечных волн в струне.
Отсюда
F = V²ρ₁ , (2)
где ρ₁ = m/l − линейная плотность струны, m = ρV₀ − масса струны, V₀ = (πd²/4)l
= πd²l/4 − объём струны.
Имеем: ρ₁ = ρV₀/l = ρ(πd²l/4)/l = ρπd²/4. Получили
ρ₁ = ρπd²/4. (3)
Подставляя в (2) V из (1) и ρ₁ из (3), получим силу натяжения F струны
F = (2lν)²ρπd²/4, или
F = πρ(lνd)².
F = 3,14·7800· (1·256·0,5·10⁻³)² ≈ 401,3 Н.
Ответ: F = πρ(lνd)² ≈ 401,3 Н.
_______________________________________________________________________________________________
4.4. Электромагнитные волны. Излучение.
4.4-1.
Электромагнитная волна с частотой 6·10¹⁴ Гц распространяется в
стекле, показатель преломления которого 1,5. Какова скорость волны в стекле и
значение волнового числа?
Решение:
ν = 6·10¹⁴
Гц
n = 1,5
c = 3·10⁸
м/с (скорость света в вакууме)
V – ? k – ?
Скорость V волны
в стекле:
V = c/n . (1)
Длина волны в стекле:
λ = V/ν = c/(nν). (*)
Волновое число k:
k = 2π/λ или с
учётом (*)
k = 2πnν/с.
(2)
Вычисления по (1), (2)
V = 3·10⁸/1,5
= 2·10⁸ м/с.
k = 2·3,14·1,5·6·10¹⁴/(3·10⁸) =
1,88·10⁷ (1/м).
Ответ: V = 2·10⁸
м/с; k =
1,88·10⁷ (1/м).
4.4-2. Определить
показатель преломления призмы из парафина , если его диэлектрическая
проницаемость Ԑ = 2 и магнитная проницаемость μ = 1.
Решение:
Ԑ = 2
μ = 1
n – ?
Показатель преломления среды
n = C/V. (1)
С – скорость света в вакууме.
Скорость света в среде
V = C/√(Ԑμ). (2)
Из (1) и (2) имеем
n = √(Ԑμ).
n =
√(2·1) = 1,41.
Ответ: n = 1,41.
___________________________________________________________________________________