Как найти амплитуду колебаний при резонансе - Исправление недочетов и поиск решений вместе с Examum.ru

Резонанс

При заданных возмущающей силе F_max.возм
и коэффициенте трения β амплитуда Y_m является функцией только угловой частоты возмущающей силы.

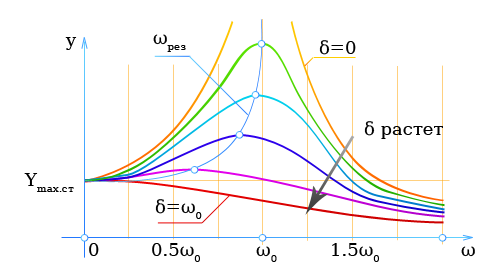
На рисунке показана зависимость Y_m от ω (резонансная кривая).
Параметром служит коэффициент затухания δ.

При ω ≈ ω₀ она достигает особенно большого значения (резонанс).

При самых малых значениях δ величина Y_m резко возрастает.

Если δ > 0, то в случае резонанса ω < ω₀; величина Y_max.ст представляет собой статическое отклонение системы под действием постоянной силы Y_max.возм (ω = 0).

Для определения резонансной частоты необходимо найти максимум функции Ym = Ym(ω) и приравнять первую производную нулю; тогда, если

ω_рез	резонансная частота, при которой амплитуда максимальна,	радиан/сек
ω₀	частота собственных незатухающих колебаний системы,	радиан/сек
m	масса колебательной системы,	кг
β	коэффициентом вязкого трения,	кг/сек
δ	коэффициентом затухания,	радиан/сек

Частота резонанса

[
ω_{рез} = sqrt{ω_{0}^2 — frac{β^2}{2m^2}} = sqrt{ω_{0}^2 — 2δ^2}
]

Условие отсутствия резонанса

[
δ geqslant frac{ω_{0}}{sqrt{2}}
]

Амплитуда резонанса

Чтобы найти величину амплитуды в резонансном случае, нужно подставить формулу (1) в формулу отклонения при вынужденных колебаниях.

Если

Y_max.рез	резонансная амплитуда колебаний системы,	метр
F_max.возм	максимальное значение возмущающей силы,	Ньютон
m	масса колебательной системы,	кг
ω_рез	резонансная частота, при которой амплитуда максимальна,	радиан/сек
ω₀	частота собственных незатухающих колебаний системы,	радиан/сек
ω	частота колебаний системы с затуханием,	радиан/сек
β	коэффициентом вязкого трения,	кг/сек
δ	коэффициентом затухания,	радиан/сек

то имеем

[

Y_m = frac
{
F_{max.возм}
}
{
β sqrt{ ω_{0}^2 — frac{β^2}{4m^2} }
}

]

[

Y_m = frac{F_{max.возм}}{βω}

]

[

Y_m = frac{F_{max.возм}}{2δmω}

]

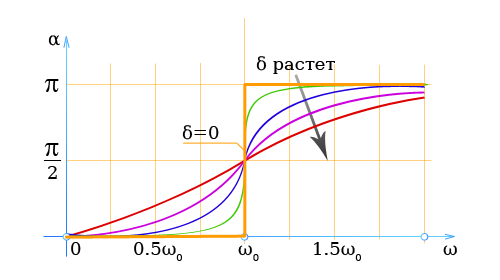
Согласно формуле, разность фаз α также зависит от частоты возмущающей силы.
Параметром служит коэффициент δ.

На рисунке представлена зависимость α от частоты.

Независимо от величины затухания при ω = ω₀ разность фаз составляет

[

α = 90°

]

Резонанс играет большую роль в технике и в повседневной жизни. В большинстве механических устройств под действием внешних периодических сил могут возникать колебания. При резонансе происходит нарастание амплитуды колебаний, и это может привести к разрушениям («резонансная катастрофа»). В случае вращательного движения резонансную частоту называют критическим числом оборотов.

Резонанс	стр. 558

Источник

Механические колебания.

Гармонические колебания.
Уравнение гармонических колебаний.
Пружинный маятник.
Математический маятник.
Свободные и вынужденные колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: nu =1/T . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

к оглавлению ▴

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение x=0 . Основная задача механики в данном случае состоит в нахождении функции x(t) , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на pi /2 , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

(1)

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина alpha , равная значению фазы при t=0 , называется начальной фазой. Начальная фаза отвечает начальной координате тела: $x_{0}=Acos alpha$ .

Величина называется omega циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное 2 pi радиан: , откуда

$omega = frac{displaystyle 2pi }{displaystyle T}$ (2)

(3)

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):

$x=Acos(frac{displaystyle 2pi t }{displaystyle T}+ alpha), x=Acos(2 pi nu t + alpha)$ .

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину $x_{0}$ и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае $x_{0}=A$ , поэтому можно положить alpha=0 . Мы получаем закон косинуса:

График гармонических колебаний в этом случае представлен на рис. 2.

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае $x_{0}=0$ , так что можно положить . Получаем закон синуса:

График колебаний представлен на рис. 3.

Рис. 3. Закон синуса

к оглавлению ▴

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:

$v_{x}=dot{x}=-Aomega sin(omega t+alpha )$ . (4)

Теперь дифференцируем полученное равенство (4):

$a_{x}=ddot{x}=-Aomega^{2} cos(omega t+alpha )$ . (5)

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем $-omega^{2}$ :

$a_{x}=-omega^{2}x$ . (6)

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

$ddot{x}+omega^{2}x=0$ . (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой omega и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

к оглавлению ▴

Пружинный маятник.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате x=0 отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости vec F со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

$ma_{x}=F_{x}$ . (8)

Если x>0 (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и $F_{x}<0$ . Наоборот, если x<0 , то $F_{x}>0$ . Знаки и $F_{x}$ всё время противоположны, поэтому закон Гука можно записать так:

$F_{x}=-kx$

Тогда соотношение (8) принимает вид:

$ma_{x}=-kx$

или

$a_{x}=-frac{displaystyle k}{displaystyle m}x$ .

Мы получили уравнение гармонических колебаний вида (6), в котором

$omega ^{2}=frac{displaystyle k}{displaystyle m}$ .

Циклическая частота колебаний пружинного маятника, таким образом, равна:

$omega =sqrt{frac{displaystyle k}{displaystyle m}}$ . (9)

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

$T=2 pi sqrt{frac{displaystyle m}{displaystyle k}}$ . (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

к оглавлению ▴

Математический маятник.

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

и спроектируем его на ось :

$ma_{x}=T_{x}$ .

Если маятник занимает положение как на рисунке (т. е. x>0 ), то:

$T_{x}=-Tsinvarphi =-Tfrac{displaystyle x}{displaystyle l}$ .

Если же маятник находится по другую сторону от положения равновесия (т. е. x<0 ), то:

$T_{x}=Tsinvarphi =-Tfrac{displaystyle x}{displaystyle l}$ .

Итак, при любом положении маятника имеем:

$ma_{x}=-Tfrac{displaystyle x}{displaystyle l}$ . (11)

Когда маятник покоится в положении равновесия, выполнено равенство T=mg . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):

$ma_{x}=-mgfrac{displaystyle x}{displaystyle l}$ ,

или

$a_{x}=-frac{displaystyle g}{displaystyle l}x$ .

Это — уравнение гармонических колебаний вида (6), в котором

$omega ^{2}=frac{displaystyle g}{displaystyle l}$ .

Следовательно, циклическая частота колебаний математического маятника равна:

$omega =sqrt{frac{displaystyle g}{displaystyle l}}$ . (12)

Отсюда период колебаний математического маятника:

$T=2pi sqrt{frac{displaystyle l}{displaystyle g}}$ . (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

к оглавлению ▴

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы F(t) , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна $omega_{0}$ , а вынуждающая сила зависит от времени по гармоническому закону:

$F(t)=F_{0}cos omega t$ .

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
omega вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

Рис. 7. Резонанс

Мы видим, что вблизи частоты $omega=omega_{r}$ наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: $omega_{r} approx omega_{0}$ , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, $omega_{r} = omega_{0}$ , а амплитуда колебаний возрастает до бесконечности при $omega Rightarrow omega_{0}$ .

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Диаграмма Айнса-Стретта приведена на рисунке 7, область устойчивости заштрихована.

О 0.5 1 1.5 2

Рисунок 7 — Диаграмма Айнса-Стретта

Анализ устойчивости параметрических колебаний производится по расположению функции И = ад рассматриваемой системы. На диаграмме линия 1 соответствует параметрам левого привода (у л = 7°29′ , с = 7780 Нм/рад. Линия И = ад пересекает чередующиеся области устойчивости и неустойчивости. Параметрические резонансы возможны в области неустойчивости. Из расположения на диаграмме графика 1 видно, что линия пересекает широкую область неустойчивости. Это означает большую вероятность потери динамической устойчивости практически при любом технически возможном значении частот возмущения. Приведенный резонанс (а = 1) является основным и наиболее опасным. В этом случае соотношение частот возмущений и собственной равно р = 2ю0.

Приведенное относится к условиям, когда диссипация энергии отсутствует Это имеет место при работе приводов водометов на суше — перед входом в воду и выходом из нее. При движении на плаву работа водометов сопровождается существенной диссипацией энергии. В этом случае амплитуда параметрических колебаний наиболее существенна на режиме первого основного резонанса (а = 1,р = 2га0), наиболее опасного и слабо чувствительного к действию диссипативных сил. Критическое значение частоты равно

,=^оД п)2 — п)2+)2,

V 2 п п 4 п

2пв

где Д — декремент затуханий, Д = , в — коэффи-

®о

циент затуханий. Устойчивость системы может быть повышена введением гасителя колебаний, т.е. дополнительной податливости одного из элементов привода, например шестерни трансмиссии. Настройка гасителя позволяет отстраиваться от резонанса, исключая при определенном значении параметра глубины модуляции попадание в область динамической неустойчивости.

Другим эффективным путем исключения параметрических колебаний является сокращение параметра модуляции. Это достигается ограничением угла установки карданных валов с асинхронными шарнирами. Когда по условиям компоновки это невыполнимо, то необходимо

введение в конструкцию шарниров равных угловых скоростей (ШРУС), у которых параметр модуляции угловой скорости на порядок ниже, чем у асинхронных. На рисунке 7 линия 2 соответствует параметрам левого привода с шарниром равных угловых скоростей. Из анализа расположения этой линии на диаграмме Айнса-Стретта следует, что привод с ШРУС практически исключает вероятность возбуждения параметрических колебаний.

ВЫВОДЫ

Снижение динамической нагруженности, формируемой параметрическими резонансами, может быть достигнуто введением в конструкцию привода гасителя, а также шарниров равных угловых скоростей, что создает предпосылки повышения долговечности элементов привода.

Сокращение амплитуд колебаний динамического момента, действующего в приводе водомета, содержащем пространственно расположенные карданные передачи, повышение долговечности его элементов также достигается взаимным расположением элементов карданной передачи при монтаже.

Список литературы

1 Альгин В. Б. Систематизация и расчёт мобильной машины как

многомассовой системы. Динамика машинного агрегата. Механика машин, механизмов и материалов //Международный научно-технический журнал. 2013. №2(23). С. 5-18.

2 Черных И. В. Моделирование электротехнических устройств в

МА^АВ, SimPowerSystems и Simulink. 1-е издание. СПб.: Питер, 2007. 288 с.

3 Пановко Я. Г. Введение в теорию механических колебаний : учебное

пособие. 2-е изд. М. : Наука. Главная редакция физико-математической литературы, 1980. 272 с.

УДК 629.11.01:62-23;534.1 Б.М. Тверсков

Курганский государственный университет

АМПЛИТУДЫ КОЛЕБАНИЙ ПРИ РЕЗОНАНСЕ

Аннотация. Рассмотрен способ расчета амплитуд крутильных колебаний при резонансе, и приведены значения амплитуд колебаний при испытаниях дотрансфор-маторной зоны трансмиссии колесных тягачей. Выявлены частоты вращения коленчатого вала, при которых возникают резонансные колебания.

Ключевые слова: амплитуда, резонанс, жесткость, момент трения.

B.M. Tverskov Kurgan State University

VIBRATION AMPLITUDE AT RESONANCE

Abstract. This paper shows the method of calculation of the torsional vibrations amplitudes at resonance and the values of the oscillations amplitudes cotransformation transmission zone of wheel tractors on trials. Frequency of crankshaft rotation at which resonant vibrations occur is identified.

Keywords: amplitude, resonance, stiffness of the damper, friction torque.

Резонанс колебаний возникает при совпадении частоты одного из периодических возбуждающих крутящих моментов с собственной частотой крутильных форм сис-

темы. Упругие и инерционные моменты системы при этом уравновешиваются, и работа возмущающих сил идет на преодоление сил сопротивления.

Возбуждающие крутящие моменты, действующие на каждую массу системы, периодичны, и их можно рассматривать состоящими из гармонических составляющих.

Форма вынужденных колебаний при резонансе близка одной из форм свободных колебаний. Это может быть лишь при равенстве возбуждающих моментов и моментов сопротивления, действующих одновременно на отдельные массы системы. Моменты сопротивления и возбуждающие могут не полностью взаимно уравновешиваться из-за различной величины их амплитуд или сдвига по фазе. Вследствие этого форма вынужденных колебаний может не совпадать с формой свободных колебаний. Внутреннее трение обычно невелико, потому форма вынужденных резонансных колебаний близка форме свободных колебаний. Установившиеся вынужденные колебания могут быть, если за период одного колебания имеется равенство суммы работ всех возбуждающих моментов сумме работ моментов сопротивления. В противном случае амплитуды колебаний нарастают или уменьшаются.

Амплитуды колебаний при резонансе определяются из условия равенства работ возмущающих сил и сил сопротивлений за каждый цикл колебаний. Расчет выполняется в основном для резонансных режимов, так как они наиболее опасны. Приравнивая работу возбуждающих крутящих моментов работе моментов сопротивлений за период одного колебания, находят резонансные амплитуды всех масс системы. Работу возбуждающих моментов считают из условия отставания максимального углового перемещения массы от максимального значения возбуждающего момента на фазовый угол.

При действии в многомассовой крутильной системе на каждую массу периодического крутящего момента возникают резонансные колебания всей системы, колебания всех масс происходят синхронно (с одинаковыми или противоположными фазами): все массы одновременно проходят нейтральное положение и одновременно проходят положения максимальных отклонений. При этом гармонические составляющие возбуждающих моментов, действующих на различные массы системы, имеют максимальные значения в разное время, так как вспышки в различных цилиндрах чередуются через определенный угол поворота коленчатого вала двигателя — возбудителя колебаний.

Возбуждающий момент не влияет на резонансные колебания системы, и она колеблется по закону свободных колебаний. В условиях резонанса вектор крутящего момента опережает вектор углового перемещения массы на фазовый угол, т.к. возбуждающий момент уравновешивается моментом сопротивления.

Для двигателя, например, работу возбуждения резонансных колебаний совершают не полные крутящие моменты, действующие на отдельные массы системы, а моменты, равные по величине проекции их векторов на перпендикуляры к направлению, соответствующему максимальному угловому отклонению. Проекции векторов моментов равны произведению полного значения момента на синус угла между вектором возбуждающего момента и угловым перемещением масс.

Расчет вынужденных колебаний ведется по числу масс, на которые действуют возбуждающие моменты и моменты сопротивления. Для поршневого двигателя внутреннего сгорания, например, такими массами являются моторные, эквивалентные коленам вала с приведенными к ним массами.

Общая работа сил, возбуждающих резонансные колебания всей многомассовой системы, может быть определена суммированием элементарных работ масс системы.

Максимумы гармоник возбуждающих моментов, действующих на отдельные массы, имеют относительные угловые смещения (фазовые углы), определяемые выражением и фазовыми диаграммами. Поэтому все фазовые углы между возбуждающими моментами и угловыми перемещениями отдельных масс можно выразить через угол между рассматриваемой гармоникой возбуждающего момента, действующего на первую массу, направлением перемещения этой массы и фазовые углы.

В связи с большим поглощением энергии на создание резонанса (10% и более от передаваемой мощности) прохождение резонансной частоты вызывает трудности. Но наличие в реальных трансмиссионных системах демпфирования амплитуды колебаний при резонансе ограничены по величине.

Для оценки нагружений имеют значение первые три-пять форм колебаний. Если при этом число возбуждающих гармоник выше, то общее число резонансов может быть очень большое. Но далеко не каждый из этих резонансов сопровождается колебаниями, опасными для прочности крутильной системы.

Известно, что форма вынужденных колебаний при резонансе лишь немного отличается от формы собственных колебаний. Из-за отсутствия равенства между моментами возбуждающих сил и сил сопротивления полного совпадения форм нет: чем больше потери на трение, тем больше разница между моментами этих сил. Часто потери на трение невелики, и потому отличие форм вынужденных и свободных колебаний при резонансе небольшое.

Работа возмущающего момента, приложенного к одному валу поршневого двигателя, может быть представлена как [1]

2п

= MMdak

i=0

где Mki — амплитуда гармонического момента k-го порядка, приложенного к i-му колену; ан — угол отклонения от гармонического момента k-го порядка, приложенного к i-му колену; ю — частота собственных колебаний.

Работа возмущающего момента k-го порядка по всем коленам вала за один цикл колебаний:

2п

п km п

Wbi = X f Mkida = Mki n(cos s X aki cos kSi +

i=1 „ i=1

sin s

X aki sin kSi

где в — фазовый угол; §1 — угол поворота коленчатого вала между вспышками в первом и 1-м цилиндрах двигателя; ак- амплитуда колебаний 1-той массы от момента к-го порядка; к — порядок гармоники возбуждающего момента; Ми — амплитуда гармонического момента к-го порядка.

Максимальные колебания устанавливаются при таком значении фазового угла 8, когда выражение, стоящее в скобках, принимает максимальное значение. Для этого надо первую производную этого выражения по в принять равной нулю.

В окончательном виде будем иметь:

| 11 11 = жМк Д (Уак1С08к51)2 + Уак1С08к51)2

п п п

где , (Уак1 С0йк51)2 + Уак1 С0эк51)2 = у ак1,

V 1=1 1=1 и

где у аи — геометрическая сумма относительных

1=1

амплитуд (равнодействующий вектор амплитуд перемещений).

Из допущения о совпадении форм собственных и резонансных колебаний следует:

А а к1 к1

Мк У

Хк У ак

Ак =

У ^ + ^и®са2 + ^21 ®са2+1 + … + £п:]+п «Са]п где £,£2- коэффициенты демпфирования,

тельные амплитуды колебаний масс.

Амплитуды колебания масс системы при резонансе под действием гармонического момента Мк можно определить в таком порядке:

— рассчитать амплитуды колебаний для собственной частоты (дс той формы, которая возбуждается в резонансе гармоникой Мк;

— построить фазовую диаграмму для порядка момента М ;

— по амплитудам моторных масс построить в некотором масштабе геометрическую сумму ак , направляя векторы параллельно векторам фазовой диаграммы гармоники М;

— подставить сумму У а^ (измеренную в милли-

1 =1

метрах и умноженную на масштаб) и остальные величины в формулу (5), % ;

к1 _ к1

■ определив масштабы форм

, умножить

Следовательно, WbI = П Мк Акг У ак1

1=1

где Ак.- амплитуда колебаний первой массы от гармонического момента к-го порядка.

Равнодействующий вектор амплитуд перемещений ак строится с помощью относительных амплитуд форм собственных колебаний, вычисленных для частоты (с , при этом а1 = 1.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Работа сил сопротивления за одно колебания может быть выражена:

п п

ШС! = Ул□ЮcAki2 = л□ЮcAki2 У а1 ,

1=1 1=1

где £ — коэффициент демпфирования для одного колена вала; Ак- амплитуда колебаний 1-й массы вала от гармонического момента 6-го порядка.

При резонансе работа возмущающих сил равна работе сил сопротивления. Приравняв выражения для них, получим:

^Уа^ Ак = —гт

У ак

1=1

Амплитуды формы колебаний берутся из таблицы для частоты (с, где первой массой может быть немоторная масса и амплитуда первой моторной массы не равна единице.

Найдя одну действительную амплитуду по формуле, все остальные можно определить по форме колебаний.

Если учесть отдельно силы сопротивления, приложенные к немоторным массам системы, то в уравнении работ появляются добавочные члены. Тогда формула принимает вид:

приведенные к массам j2

; а): :а]+1…а]+п — относи-

A а 1 1

на него все амплитуды а для частоты (с.

Гармонические моменты, которые дают фазовую диаграмму с совпадающими по направлению лучами, т.е. совпадают по фазе во всех цилиндрах, называют главными. Порядок главных гармоник кратен числу вспышек. В

этом случае геометрическая сумма У ак превращает-

1 =1

ся в алгебраическую. По фазовыем диаграммам строятся геометрические суммы относительных амплитуд. При определенном расположении колен вала и заданном че-

редовании вспышек в двигателе величина У ак1 зави-

1=1

сит только от формы колебаний.

Одной лишь формы собственных колебаний для расчета напряжений в деталях крутильной системы при резонансе недостаточно. Необходимы и другие гармоники. Амплитуды касательных напряжений при резонансах определяют по тем же формулам, что и при отсутствии резонансов. При этом значения напряжений всегда уменьшаются. Полученные напряжения нужно проверять экспериментом.

Результат расчета резонансных колебаний зависит от правильности определения моментов возбуждающих сил и сил сопротивления. Моменты возбуждающих сил определяются обычно с погрешностью 20-30%, погрешность расчета сил сопротивления может составлять 50100%.

Резонансы колебаний крутильных систем могут быть на частотах вращения более низких, чем рабочие. Тогда при пуске и остановке, а также при переходе с одного режима работы на другой система будет проходить через резонансные зоны. При этом возможно, что увеличение оборотов протекает медленно и в каждый небольшой отрезок времени колебания системы можно рассматривать как установившиеся, а напряжения в ее элементах при резонансах будут соответствовать расчетным; второй случай: набор оборотов происходит быстро, при этом амплитуды достигают максимальных величин не в момент совпадения частот возмущающих моментов с частотами собственных колебаний, а несколько позже.

При повышении оборотов максимум амплитуд смещается в сторону больших частот колебаний (рисунок 1 а), а при понижении — в сторону меньших частот колебаний

(рисунок 1 б).

Рисунок 1 — Смещение максимума амплитуд колебаний при повышении оборотов (а) и при понижении оборотов (б)

Максимальные значения амплитуд при быстрых проходах через резонанс значительно меньше в сравнении с амплитудами при установившихся резонансных колебаниях. Это связано с тем, что при быстром прохождении число циклов вблизи резонанса явно недостаточно для внесения в систему необходимого запаса энергии для увеличения амплитуды. В системах с относительно небольшим трением при быстром прохождении через резонанс амплитуда колебаний после первого максимума убывает скачкообразно и имеет несколько максимумов с меньшими значениями. При этом колебания носят характер затухающих биений. Последнее объясняется тем, что при быстром прохождении через резонанс возникают сильные колебания с частотой, равной собственной частоте системы, которые на успевают затухнуть к моменту когда частота возмущающего момента гармоники уже несколько изменилась.

Смещение уменьшенного максимума амплитуд с увеличением скорости прохождения через резонанс составляет несколько процентов. Эта закономерность постоянная: быстрое прохождение резонансной частоты -меньше максимальная амплитуда и больше её смещение. Объяснить это явление можно меньшим количеством энергии, получаемой системой при быстром прохождении через резонансную частоту, что годится, если резонансная частота находится в нерабочей зоне оборотов. В этом случае не требуется принимать меры для устранения резонанса. Известно, например, что трансмиссия автомобиля ГАЗ-21 входила в резонанс при частоте около 1500 об/мин. Но т.к. работа совершается в основном при частоте значительно большей, заметного отрицательного влияния резонанса не отмечалось.

Неравномерные появления возмущающих моментов

в системе и неравномерное вращения валов влияют на резонансные колебания. В поршневых двигателях это может быть из-за неравномерной загрузки цилиндров, а также из-за неравномерного изменения возмущающего момента при вращении крутильной системы. Сильный резонанс может наступить при неуравновешенности двигателя, например после отключении цилиндров. С этим столкнулись потребители ^образного дизеля ЯМЗ-8401, когда на холостых оборотах один из блоков автоматически отключался. Амплитуда колебания момента при этом достигала 2-2,5 максимальных моментов (рисунок 2). Работа двигателя и трансмиссии сопровождалась сильными стуками и поломками деталей трансмиссии. Достаточно было нажать на педаль подачи топлива, и стуки прекращались.

Рисунок 2 — Осциллограмма с записью крутящих моментов на торсионе (М1) и карданном валу (М2) между согласующим редуктором и гидротрансформатором тягача КЗКТ-7428 при резонансных колебаниях. Диаметр торсиона 33 мм, на карданном валу резиновая муфта

Наблюдается четкая синхронность появления амплитуд колебаний на валах до и после согласующего редуктора. Трансмиссионная цепь при её реальной короткой длине нагружается по всей длине практически одновременно.

Устранить резонанс удалось только значительным увеличением угловой жесткости торсиона, соединяющего двигатель и согласующий редуктор, когда резонанс был смещен за пределы рабочих оборотов.

Резонансы в крутильной системе могут появиться при частотах вращения более низких, чем рабочие. Тогда при пуске и остановке двигателя, а также при переходе с одного режима работы на другой система будет проходить через резонансную частоту. Возможны два случая: первый — набор оборотов происходит медленно, колебания системы можно рассматривать как установившиеся. Напряжения в деталях системы будут соответствовать рас-

¡иг

Рисунок 3 — Осциллограмма с записью крутящего момента на входе ГМТ тягача КЗКТ-545 при запуске двигателя

стартером на нейтрали; обороты входного вала

четам. Второй случай — набор оборотов быстрый, амплитуды колебаний достигают максимальных величин не в момент совпадения частот возмущающих моментов с частотами собственных колебаний, а несколько позже.

Так как далеко не каждый резонанс сопровождается колебаниями, опасными для прочности системы, необходимо анализировать каждый из появившихся резо-нансов.

Изменение частоты собственных колебаний путем изменения жесткости и моментов инерции деталей крутильной системы дает возможность сместить резонансные режимы в нерабочую зону оборотов, исключив таким способом повышенные нагружения деталей.

В некоторых трансмиссионных системах возникающие в валах напряжения от крутильных колебаний можно уменьшить, изменяя величину работы, вносимой возбуждающими моментами, например, подбором порядка зажигания по цилиндрам двигателей.

В трансмиссионных системах большие нагрузки могут появиться также при остановке двигателя. На рисунке 5 приведена запись моментов при остановке двигателя на торсионе, соединяющем согласующий редуктор, и на карданном валу, соединяющем согласующий редуктор ГМТ тягача МАЗ-537.

Размахи моментов в дотрансформаторной зоне при пуске двигателя, как правило, самые большие. Положительные значения размахов могут в несколько раз пре-

вышать максимальный момент двигателя.

С упругофрикционным демпфером размахи колебаний крутящего момента при пуске составляли 3300 Нм, положительное значение их было 2400 Нм. Таким образом, величина отрицательного значения размаха составляет половину его положительного значения. Пуск совершается в течение 0,5…1 с. За это время происходит от трех до десяти вспышек, после чего частота повышается до 500…800 об/мин, а величина размахов уменьшается до пределов, характерных для рабочего диапазона частоты вращения коленчатого вала (рисунок). Частота колебаний момента равна 10… 15 Гц. С увеличением частоты вращения коленчатого вала до 1500… 1800 об/мин возникают колебания резонансного характера с частотой 130 Гц от возмущающего момента 4,5 порядка. Размахи колебаний составляют 1350 Нм. Второй резонанс появляется при частоте вращения 2100 об/мин от возмущающего момента третьего порядка. Размахи здесь достигают 175 Нм при частоте колебаний 110 Гц. Аналогичная картина наблюдается и в стоповом режиме. При 1500…1300 об/мин также отмечается появление резонанса 4.5 порядка с размахами колебаний 850… Э00 Н.м, с частотой колебаний момента 130 Гц. При 2100 об/мин возмущающий момент третьего порядка, размахи 1700 Нм, частота 110 Гц.

Для разгона автопоезда на первой, второй и третьей передачах также характерно появление резонансов ко-

Рисунок 4 — Осциллограмма с записью нагрузок на торсионе и карданной валу между повышающей передачей и гидротрансмиссией тягача МА3-537 при запуске двигателя стартером с выключенной передачей. Демпфер опытной

конструкции с торсионом. Диаметр торсиона 32 мм

Рисунок 5 — Осциллограмма с записью крутящего момента в дотрансформаторной зоне трансмиссии при остановке

двигателя тягача МАЗ-537

лебаний момента с теми же параметрами (при 1500…1800 об/мин и 2100 об/мин), как и в стоповом режиме. Включение блокировочного фрикциона ГМТ приводит к резкому нагружению трансмиссии до величин, указанных в таблице 1.

Остановка двигателя вызывает динамическое нагру-жение с размахами до 2000 Нм, причем 2/3 размаха имеет отрицательное значение. Порядок резонирующей гармоники при остановке двигателя — 4,5. Влияние предна-тяга пружин демпфера на величину размаха обнаружено не было: размахи оставались практически одинаковыми как с преднатягом, так и без него.

Максимальные размахи при пуске двигателя с резиновым демпфером, жесткость которого может быть определена с помощью графика, составляют 2800 Нм. Положительная величина момента при этом — 1950 Нм. Резонанс при частоте 1500…1800 ‘ об/мин не наблюдался, а при частоте 2100 об/мин отмечен резонанс колебаний с размахом 1400 Нм и частотой 110 гц, вызванный третьей гармоникой момента двигателя.

В стоповом режиме и разгоне на различных передачах характер нагружения трансмиссии с резиновым демпфером практически одинаков.

При остановке двигателя размах достигает 2500 Нм, из которого отрицательное значение — 1700 Нм.

Снижение жесткости торсионного демпфера путем уменьшения диаметра торсиона с 35 мм до 28 мм приводило к снижению размахов колебаний на 30…50%.

Для установки на тягачах МАЗ-537 был принят резиновый демпфер. Влияние на нагруженность трансмиссии тягача резиновой муфты, устанавливаемой на карданном валу, соединяющем повышающую передачу и ГМТ тягача, показано в таблице 1.

ЗАКЛЮЧЕНИЕ

Амплитуды колебаний деталей при резонансе теоретически могут возрастать до бесконечности. Однако из-за действия сопротивления в колебательной системе амплитуды при резонансе редко увеличиваются более чем в 2-3 раза. Для гашения резонансных колебаний трансмиссии автомобилей и тракторов за их двигателями устанавливаются демпферы крутильных колебаний, содержащие фрикционные элементы. Другой способ исключить последствия резонанса — вывести частоту появления резонанса автомобилей и тракторов за пределы рабочих частот. Заметно в этом случае влияет на величину амплитуды установка дополнительной резиновой муфты.

Как следует из таблицы 1, во всех исследованных вариантах размахи колебаний крутящего момента на кар-

данном валу, соединяющем ГМТ и согласующий редуктор тягача МАЗ-537 (дотрансформаторная зона), без резиновой муфты были на 15…30% больше, чем с резиновой муфтой. При этом с резиновым демпфером размахи были на 9…12% меньше, чем с упругофрикционным демпфером.

В стоповом режиме увеличение размахов из-за отсутствия резиновой муфты на карданном валу было до 28%. Такие же результаты получены при трогании и разгоне тягача на различных передачах в ГМТ.

Частота колебаний момента с резиновым демпфером, но без резиновой муфты на карданном валу по сравнению с упруго-фрикционным демпфером снизилась с 80…100 Гц до 25…30 Гц. Резонанс колебаний с 1-й, 2-й и 3-й гармониками при этом отмечен на режиме максимальной мощности. При наличии резиновой муфты на карданном валу резонансы колебаний появляются также при максимальной мощности. Они вызваны 3-й гармоникой крутящего момента двигателя.

Список литературы

1 Бабаков И. М. Теория колебаний. М. : Наука, 1968. 560 с.

2 Рихерт М. М, Доброгаев Р. П., Ляхов М. И. и др. Конструкция и

расчет автотракторных двигателей. М.: Машиностроение, 1964. 552 с.

3 Маслов Г. С. Расчеты колебаний валов. Справочник. М. :

Машиностроение, 1980. 151 с.

4 Тверсков Б. М. Нагруженность трансмиссии автомобилей

крутильными колебаниями: учебное пособие. Курган: Изд-во КГУ, 1997. 122 с.

УДК 629.113.585

Б.М. Тверсков, С.С. Гулезов

Курганский государственный университет

РАЗМЕЩЕНИЕ ДВИГАТЕЛЯ НА АВТОМОБИЛЕ

Аннотация. В статье рассмотрены преимущества и недостатки бокового расположения двигателя на грузовом автомобиле большой грузоподъемности при его использовании в различных дорожных условиях. Во внимание принимаются размеры грузовой платформы и возможность охлаждения двигателя при различных расположениях двигателя, размеры и число мест в кабине.

Ключевые слова: двигатель, система охлаждения, вентилятор, воздушный поток.

Режим исследования Демпфер

Уп руго-фрикционный Резиновый

С резиновой муфтой Без резиновой муфты С резиновой муфтой Без резиновой муфты

Пуск двигателя 3300 4750 2800 3600

Увеличение частоты вращения коленчатого вала 1550 1750 1400 1800

Стоповый режим 1500 1750 1400 1800

Интенсивный разгон автопоезда 1400 1700 1400 1850

Таблица 1 — Размахи колебаний крутящего момента на карданном валу, соединяющем ГМТ и согласующий редуктор МАЗ-537, Нм

Источник

Колебательный контур является типичным представителем резонансных колебательных систем, играющих важную роль в большинстве разделов физики — в механике это различного типа маятники и звуковые резонаторы (струны, мембраны, трубы, свистки, органы), в электродинамике — колебательные контуры, закрытые и открытые резонаторы с распределенными параметрами, в оптике — лазерные резонаторы, эталоны Фабри — Перо и т.д. Принципы описания всех колебательных систем настолько общи, что теория колебаний стала самостоятельным разделом физики. Поэтому изучение параметров, свойств и характеристик колебательного контура полезно рассматривать как общее введение в мир резонансных колебательных систем.

В теории колебаний выделяются два класса явлений — явления в линейных и нелинейных колебательных системах. Линейными называются такие системы, параметры которых не зависят от амплитуды колебаний. Например, для маятников это означает такие малые колебания, при которых упругость пружин и стержней не зависит от амплитуды колебания, а натяжение нити подвеса определяется только гравитационными силами. Для электрических колебательных контуров независимыми от амплитуды токов и напряжений должны оставаться такие величины, как индуктивность $L$, емкость $C$ и сопротивление $R$.

Резонансные системы имеют два важных свойства.

Свойство избирательно реагировать на внешние источники сигналов, выделяя только те из них, частоты которых совпадают с собственной частотой колебательной системы.
Свойство запасать энергию колебаний, возбужденных внешним источником, поддерживая колебания в течение определенного времени после выключения внешнего источника.

Колебательный контур характеризуется двумя основными параметрами: частотой собственных (резонансных) колебаний $omega _{0} $ и добротностью $Q$, характеризующей отношение мощности энергии собственного колебания к мощности потерь за период.

На рис. 18 приведены примеры «параллелей» электрических и механических колебательных систем. В электрических резонаторах происходит периодический переход электрической энергии, запасенной в конденсаторе $(W_Э =frac 12 CU^2),$ в магнитную энергию катушки индуктивности $(W_M =frac 12 LI^2)$ и обратно. В маятниках происходит аналогичный циклический переход энергии из потенциальной (поднятого груза или сжатой пружины) в кинетическую и обратно.

Свободные колебания происходят в замкнутой цепи без вынуждающей силы (рис. 19,а).

Согласно второму закону Кирхгофа для такой цепи можно написать:
$$
Rcdot I+U_{C} =-Lcdot frac{dI}{dt}.
$$
Выражая $U_{C} $ через заряд $q$, получим уравнение

$$
Rcdot I+Lcdot frac{dI}{dt} +frac{q}{C} =0 mbox{ (СИ). }
$$
Дифференцируя по времени и учитывая равенство $I=frac{dq}{dt} $, получаем
$$
Lfrac{d^{2} I}{dt^{2} } +Rfrac{dI}{dt} +frac{I}{C} =0 mbox{ (СИ). }
$$
Разделив на $L$ и вводя обозначения
$delta =frac{R}{2cdot L} $ и $omega _{0}^{2} =frac{1}{LC} $,
получим общее уравнение для свободных колебаний линейной резонансной системы:
$$
I»+2delta , I’+omega _{0}^{2} I=0,
$$
где параметр $delta $ называется затухание, а параметр $omega _{0} $ — собственная частота, или частота свободных колебаний. Оно решается подстановкой $I=Acdot e^{iomega , t} $, которая приводит к характеристическому уравнению
$$
-omega ^{2} +2iomega , delta +omega _{0}^{2} =0,
$$
с решением
$$
lambda , _{1,2} =i, delta pm sqrt{omega _{0}^{2} -delta ^{2} } .
$$
Общее решение имеет две составляющие
$$
I=Acdot e^{iomega _{1} , t} +Bcdot e^{iomega _{2} , t} .
$$
Константы $A$ и $B$ определяются начальными данными задачи, например, зарядом $q_{0} $ или напряжением на конденсаторе $U_{0} $. Характер начальных данных определяется конкретной физической системой.

Частный пример схемы для возбуждения свободных колебаний в колебательном контуре приведен на рис. 19,б. Конденсатор $C$ заряжается от батареи до напряжения $U_{0} $ (положение «а» переключателя), а затем переключается в точку «б». Свободные колебания будут представлять собой циклический переход энергии электрического поля (в конденсаторе) в энергию магнитного поля (в индуктивности) и обратно.

Подставив найденные значения $A$ и $B$, получим общее решение для свободных колебаний в контуре
$$
I=ifrac{U_{0} }{Lsqrt{omega _{0}^{2} -delta ^{2} } } e^{-delta , t} frac{e^{isqrt{omega _{0}^{2} -delta ^{2} } , t} -e^{-isqrt{omega _{0}^{2} -delta ^{2} } , t} }{2} .
$$

Если бы колебательный контур состоял только из идеальных (без потерь) реактивных элементов (индуктивности $L$ и емкости $C$), то переход энергии из электрической в магнитную и обратно совершался бы без потерь, а в контуре существовали бы незатухающие свободные колебания с собственной частотой $omega _{0} =2pi , f=sqrt{frac{1}{LC}}.$

Наличие в схеме активного элемента $R$ приводит к тому, что часть энергии за каждый период переходит в тепло и колебания затухают с некоторой постоянной времени $tau $. Роль частоты в уравнении теперь играет величина $omega _{p} =sqrt{omega _{0}^{2} -delta ^{2} } $, зависящая от отношения реактивной мощности к потерям на активном сопротивлении $R$. При этом вовсе не обязательно в схему должен быть включен отдельный резистор. В его качестве может выступать, например, омическое сопротивление провода, которым намотана катушка индуктивности, а также сопротивление утечки изоляторов конденсатора. Кроме того, часть энергии колебаний может излучаться контуром в окружающее пространство в виде электромагнитной волны. На этом основано действие так называемых связанных контуров: если вблизи данного колебательного контура расположен другой, то в нем «наводятся» (возникают) колебания за счет того, что часть энергии трансформируется из первого контура во второй. Передача энергии совершается переменным электромагнитным полем, возникающим вокруг первого контура.

Если затухание мало, т. е. $delta <omega _{0} $, то мы получаем уравнение слабо затухающих колебаний в виде
$$
I=-frac{U_{0} }{Lomega _{p} } e^{-delta , t} sin omega _{p} t=-I_{0} e^{-delta , t} sin omega _{p} t.
$$
При этом резонансная частота приближается к частоте собственных колебаний:
$$
omega _{p} =sqrt{omega _{0}^{2} -delta ^{2} } approx omega _{0} left(1-frac{1}{2} frac{delta ^{2} }{omega _{0}^{2} } right).
$$
Таким образом, при малом затухании резонансная частота практически совпадает с собственной, однако колебания при этом не являются гармоническими. Для гармонических колебаний должно соблюдаться условие $Ileft(tright)=Ileft(t+Tright)$, где $T$ — период колебания. В нашем случае $Ileft(tright)ne Ileft(t+Tright)$, и о периоде можно говорить лишь как о времени, через которое повторяются нули функции (рис. 20). Именно в этом смысле мы будем ниже использовать термин «период колебаний».

Введем понятия добротности $Q$ и логарифмического декремента затухания $gamma $ контура. Из отношение амплитуд $n$–того и $(n + k)$–го колебаний равно
$I_{n} I_{n+k}^{-1} = e^{kdelta T}$, где $T=2, pi omega ^{-1} $ — период колебания («повторения нулей»). Логарифмическим декрементом затухания $gamma $ называется величина
$$
gamma =delta , T=frac{1}{k} ln frac{I_{n} }{I_{n+k} } =ln frac{I_{n} }{I_{n+1} } .
$$
Из уравнения для тока видно, что величина $delta $ обратно пропорциональна времени, за которое амплитуда колебаний уменьшается в $e$ раз. Из последнего уравнения следует, что декремент затухания $gamma $ показывает уменьшение амплитуды за период колебания:
$$
gamma =delta , T=frac{2; pi , delta }{omega } .
$$
С логарифмическим коэффициентом затухания однозначно связан другой, более распространенный параметр, характеризующий колебательную систему, добротность $Q$.

Добротность контура $Q$ определяется соотношением
$$
Q=frac{omega _{0} L}{R} =frac{1}{omega _{0} CR} =frac{rho }{R},
$$
где $rho =sqrt{frac LC} $ (СИ).
Физический смысл добротности заключается в отношении запасенной в контуре энергии к энергии потерь за период колебания
$$
Q=omega cdot frac{W_0}{Delta W},
$$
откуда можно найти связь добротности с другими параметрами контура
$$
Q=frac{pi }{gamma } =frac{pi }{delta , T} =frac{omega }{2, delta } =omega frac{L}{R} mbox{ (СИ).}
$$

Экспериментально добротность определяется по резонансной кривой как отношение резонансной частоты $omega _{p} $ к полосе частот $2cdot Delta omega $, определяемой на уровне $U_{1,2} =pm frac{U_p}{sqrt{2}}$:
$$
Q=frac{omega _{з}}{2cdot Delta omega } =frac{f_{з}}{2cdot Delta f} ,
$$
где $U_{p} $ — амплитуда колебания на резонансной частоте контура. Величина $rho =sqrt{frac LC}$ называется характеристическим (волновым) сопротивлением контура.

При большом затухании, т.е. при $delta >omega _{0} $, величина $omega _{0}^{2} -delta ^{2} $ отрицательна, корень из нее мнимый. Такой случай называется апериодическим процессом. Общее решение, аналогичное, полученному ранее, будет иметь вид
$$
I=-frac{U_{0} }{Lsqrt{(delta ^{2} -omega _{0}^{2} )} } e^{-delta , , t} mbox{sh}sqrt{(delta ^{2} -omega _{0}^{2} )} , t.
$$
График этой функции приведен на рис. 21.

Критическим условием, при котором затухающие колебания переходят в апериодический процесс, является условие $delta =omega _{0} $. В этом случае решение общего уравнения имеет вид
$$
I=-frac{U_{0} }{omega L} (omega t)e^{-delta , t} , =-frac{U_{0} }{L} t, e^{-delta , t} .
$$
Остается добавить, что аналогичные параметры могут быть введены для любой резонансной колебательной системы независимо от ее физической природы (механические, термодинамические, электромагнитные, оптические, аэро– и гидродинамические системы).

Колебательный контур, рассмотренный в предыдущем разделе, представлял собой замкнутую электрическую цепь, в которой совершаются свободные колебания.

В случае вынужденных колебаний мы должны подводить к контуру электрическую энергию от внешнего источника (генератора). Есть много способов для подключения источника внешней энергии к контуру, которые сводятся к той или иной комбинации двух основных: в разрыв цепи контура (рис. 22, а) или параллельно емкостной и индуктивной ветвям контура (рис. 22,б).

В зависимости от способа включения различают соответственно последовательный (рис. 22,а) и параллельный (рис. 22,б) колебательные контуры. Они предъявляют разные требования к согласованию с генератором и нагрузкой. Поэтому нужно отличать собственные параметры контура от параметров нагруженного контура, получаемые с учетом влияния генератора и «нагрузки» (входного сопротивления той цепи, в которую включен контур). В параллельном контуре (рис. 22,б) возникает резонанс токов. Для его поддержания в качестве вынуждающей силы необходимо применение генератора стабильного тока. В последовательном контуре (рис. 22,а) имеет место резонанс напряжений, и для его поддержания должен применяться внешний генератор стабильного напряжения.

Закон Кирхгофа, позволяющий исследовать процессы в контуре (рис. 22,а) в зависимости от частоты, записывается в виде
$$
U=U_{R} +U_{L} +U_{C} =IR+iI(omega L-frac{1}{omega C} )=Icdot Z.
$$
Контур представляет для генератора некоторое комплексное сопротивление
$$
Z=R_L +icdot (omega L-frac{1}{omega C} ),
$$
$$
left|Zright| = sqrt{R_L^2 +(omega L-frac{1}{omega C})^2}, mbox{tg}varphi =frac{omega L-frac{1}{omega C} }{R_L}
$$
где $left|Zright|$ — модуль комплексного сопротивления; $R_{L}$ — омическое сопротивление катушки индуктивности; $varphi $ — сдвиг фазы между активным и реактивным сопротивлениями, равный сдвигу фазы между током $I$ в цепи и входным напряжением $U$.

Из последнего выражения видно, что сопротивление цепи будет минимально и равно активному сопротивлению $R_{L} $ на некоторой частоте $omega _{0} $, определяемой условием
$$
omega _0 L=frac{1}{omega _0 C} , mbox{ где } omega _{0} =frac{1}{sqrt{LC}} mbox{ (СИ).}
$$
Таким образом, на резонансной частоте сопротивление контура минимально, чисто активно, а ток в цепи совпадает по фазе с входным напряжением (напряжением генератора). Фактически это и есть определение резонанса в последовательном колебательном контуре.

Для практических целей представляет интерес исследовать поведение напряжений на реактивных элементах контура в зависимости от частоты генератора и определить его добротность $Q$.

Поскольку фазы $U_{L} $ и $U_{C} $ независимо от частоты всегда сдвинуты относительно тока $I$ на $+$ и $-90^{circ}$ соответственно, то достаточно исследовать зависимость от частоты их модулей. Это можно сделать исходя из уравнений
$$
U_{R} =IR, U_{L} =Iomega L, U_{C} =frac{I}{omega C}, I=frac{U}{Z} .
$$

Для примера раскроем уравнения для $I$ и $U_{L} $. Используя введенное для свободных колебаний понятие добротности $Q=left(omega _{0} RCright)^{-1}$, получим следующее выражение для тока в последовательном контуре:
$$
I=frac{U}{sqrt{R^{2} +(omega L-frac{1}{omega C} )^{2} } } =frac{U}{R} frac{1}{sqrt{1+Q^{2} (frac{omega }{omega _{0} } -frac{omega _{0} }{omega } )^{2} } } .
$$
Тогда напряжение на индуктивности будет равно
$$
U_{L} =omega LI=Ufrac{Qfrac{omega }{omega _{0} } }{sqrt{1+Q^{2} (frac{omega }{omega _{0} } -frac{omega _{0} }{omega } )^{2} } } .
$$

Аналогичное уравнение можно получить для напряжения на $C$. При $omega =omega _{0} $ напряжения на $L$ и $C$ будут равны $U_{L0} =U_{C0} =Qcdot U$, т.е. в $Q$ раз больше напряжения вынуждающей эдс.

На самом деле максимумы напряжения на элементах $L$ и $C$ несколько выше и смещены от резонансной частоты и выражаются следующими соотношениями:
$$
omega _{Lmax } =omega _{0} sqrt{frac{2}{2-frac{R^{2} C}{L} } } =omega _{0} sqrt{frac{2}{2-left(frac{1}{Q} right)^{2} } } , omega _{Cmax } =frac{omega _{0}^{2} }{omega _{L} } .
$$

При добротности контура $Q ge 10$ сдвиг частот максимумов $U_{L} $ и $U_{C} $ относительно резонансной частоты $omega _{0} $ не превышает 1% и экспериментально резонансную частоту и добротность можно определять по резонансной кривой любого из напряжений $U_{L} $ и $U_{C} $. Напряжение на реактивных элементах $U_{L} $ и $U_{C} $ при $omega =omega _{0} $ в $Q$ раз больше, чем входное напряжение $U$, поэтому резонанс в последовательном контуре называется резонансом напряжений.

Важно отметить, что для нашего анализа существенно, что само входное напряжение $U$ от частоты не зависит. В противном случае все параметры зависели бы не только от самого контура, но и от параметров источника сигнала. Как было показано в предыдущем параграфе, для этого выходное сопротивление генератора должно быть много меньше $R$.

Схема подключения параллельного контура представлена на рис. 21,б. Из–за комплексного характера нагрузки ток генератора является комплексной величиной. Поэтому модуль тока $I$ может оказаться меньше не только суммы модулей токов индуктивной и емкостной ветвей контура, но и каждого из них в отдельности. Именно это и происходит при резонансе в параллельном контуре: токи в индуктивной и емкостной ветвях контура в $Q$ раз больше, чем ток, потребляемый от генератора тока. Поэтому резонанс в параллельном контуре называется резонансом токов.

Комплексное сопротивление параллельного контура равно
$$
Z=frac{Z_{1} Z_{2} }{Z_{1} +Z_{2} } =
frac{(R_{L} +iomega L)(iomega C)^{-1}}{R_{L} +i(omega L-(omega C)^{-1} )} approx
frac{LC^{-1}}{R_{L} +i(omega L-(omega C)^{-1})} .
$$

Мы пренебрегли величиной $R_{L} $ в числителе, поскольку она в $Q$ раз меньше индуктивного сопротивления, но этого нельзя делать в знаменателе, поскольку при резонансе величина в скобках стремится к нулю.

Условие резонанса для параллельного контура то же, что и для последовательного — равенство реактивных сопротивлений ветвей с $L$ и $C$:
$$
omega _{0} L=frac{1}{omega _{0} C}, mbox{ где } omega _{0} =frac{1}{sqrt{LC} } mbox{ (СИ). }
$$
Таким образом, при резонансе сопротивление контура становится чисто активным и равным
$$
R_{э} =frac{L}{ C R_{L} } =frac{rho ^{2} }{R_{L} } ,
$$
где — $rho =sqrt{frac LC} $ волновое сопротивление контура.

Сопротивление $R_{э} $ отдельного физического эквивалента в контуре не имеет, а является комбинацией волнового сопротивления $rho $ и сопротивления потерь $R_{L} $. Поэтому оно не составляет отдельной ветви параллельного контура и не ответвляет в себя ток. Следовательно, «переносить» его куда–либо или к чему–нибудь «подсоединять» (например, к внутреннему сопротивлению источника тока) бессмысленно. На схеме это просто условное обозначение того факта, что на резонансной частоте параллельный колебательный контур представляет для внешнего генератора некоторое чисто активное сопротивление величиной $R_{э} $, а в формулах символическая запись определенной комбинации $rho $ и $R_{L} $, даваемой последней формулой.

Добротность параллельного контура
$$
Q=frac{omega _{0} L}{R_{L} } =frac{1}{R_{L} omega _{0} C} =frac{R_{э} }{rho } =R_{э} sqrt{frac{C}{L} } .
$$

Собственные параметры параллельного контура, т.е. резонансная частота $omega _{0} $ и добротность $Q$ будут такими же, как и в последовательном контуре при тех же $C$, $L$ и $R_{L}.$

Источник