Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания, колебательный контур, резонанс.
Давайте начнём с одного математического приёма, чтобы не отвлекаться потом на его объяснение. Это — тригонометрический метод введения вспомогательного угла. Он наверняка вам известен, но всё же повторить его не помешает.
Речь идёт о преобразовании выражения . Вынесем за скобки «амплитудный множитель»
:
Зачем нужно такое вынесение за скобки? Оказывается, в скобках при синусе и косинусе образовались замечательные множители! Сумма квадратов этих множителей равна единице:
Значит, эти множители являются соответственно косинусом и синусом некоторого угла :
(1)
В результате получаем:
Остаётся заметить, что в скобках стоит синус суммы, так что мы приходим к окончательному выражению:
(2)
При этом для «начальной фазы» имеем из (1) простую формулу:
(3)
Теперь мы готовы рассмотреть вынужденные колебания, происходящие в колебательном контуре с активным сопротивлением. К источнику переменного напряжения последовательно подключены: резистор сопротивлением
, катушка индуктивности
и конденсатор ёмкости
(рис. 1).
Рис. 1. Колебательный контур с резистором
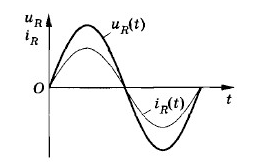
Так как элементы соединены последовательно, сила тока в них одинакова в любой момент времени (вспомните условие квазистационарности!). Поэтому нам будет удобно начать не с напряжения источника, как раньше, а с силы тока, и считать, что ток в цепи колеблется по закону синуса: .
А теперь вспоминаем материал предыдущего листка.
1. Пусть — мгновенное значение напряжения на резисторе. Оно связано с силой тока обычным законом Ома:
(4)
2. Напряжение на конденсаторе отстаёт по фазе от тока на
; это значит, что фаза напряжения
равна
. Амплитуда напряжения
равна:
Таким образом,
(5)
3. Напряжение на катушке , наоборот, опережает по фазе силу тока на
. Амплитуда:
В результате получаем:
(6)
Напряжение источника равно сумме напряжений на резисторе, катушке и конденсаторе:
Подставляя сюда выражения (4)–(6), получим:
(7)
Вот теперь нам и понадобится метод вспомогательного угла. Выражение во внешних скобках имеет для этого подходящий вид: . Пользуясь выражениями (2) и (3), получим:
(8)
где
(9)
Угол является сдвигом фаз между напряжением источника и силой тока в цепи: фаза напряжения больше фазы тока на величину
. Амплитуда напряжения:
(10)
Получив все эти результаты, мы их несколько переиначим и приведём в соответствие с тем, что было в предыдущем листке.
Начнём с напряжения источника. Предположим, как и ранее, что оно меняется по закону синуса:
Как мы сейчас выяснили, фаза тока меньше фазы напряжения на величину :
При этом амплитуда силы тока находится из формулы (10):
(11)
Выражение (11) имеет вид закона Ома:
где
(12)
Величина — это полное сопротивление цепи. Такое сопротивление оказывает наш колебательный контур переменному току.
Закон Ома в данном случае выполнен лишь для амплитудных значений тока и напряжения. Мгновенные значения и
уже не будут пропорциональны друг другу — ведь между ними имеется сдвиг фаз, равный
.
Резонанс в колебательном контуре
Как видно из выражения (11), амплитуда силы тока в контуре зависит от частоты колебаний. Построим график этой зависимости — так называемую резонансную кривую (рис. 2).
Рис. 2. Резонансная кривая
При имеем
. Математическая причина стремления тока к нулю — неограниченное возрастание ёмкостного сопротивления
, в результате чего полное сопротивление
также стремится к бесконечности.
Физическая причина очевидна: ток малой частоты — это почти постоянный ток, а для постоянного тока конденсатор является разрывом цепи.
При опять-таки имеем
: график асимптотически приближается к оси
.
Теперь это происходит за счёт неограниченного роста индуктивного сопротивления . Физическая причина также ясна: при быстром изменении тока в катушке возникает большая ЭДС самоиндукции, препятствующая его увеличению.
При некоторой частоте амплитуда силы тока достигает максимума: наступает резонанс. Из (11) нетрудно видеть, что величина
принимает максимальное значение
(13)
и происходит это при выполнении равенства
Отсюда находим :
Это хорошо знакомая нам частота собственных колебаний в контуре с нулевым активным сопротивлением. Она же, как видим, является резонансной частотой нашего контура.
Из (13) мы видим, что резонансное значение амплитуды тока тем больше, чем меньше активное сопротивление
. На рис. 3 представлены три резонансные кривые. Верхняя кривая отвечает достаточно малому сопротивлению
, средняя кривая — большему сопротивлению, нижняя кривая — ещё большему сопротивлению.
Рис. 3. Резонансные кривые при различных
Таким образом, резонансный пик тем острее, чем меньше активное сопротивление контура. При весьма большом активном сопротивлении (как это видно из нижней резонансной кривой) понятие резонанса фактически утрачивает смысл.
При резонансе в контуре происходят любопытные вещи.
1. Амплитуды напряжений на конденсаторе и катушке равны друг другу. Действительно:
При малых значениях эти амплитуды могут значительно превосходить амплитуду
напряжения источника! Это, кстати, является наглядной демонстрацией одного важного факта:
Хотя сумма мгновенных значений напряжения на элементах контура равна мгновенному значению напряжению источника, сумма амплитуд напряжений на отдельных элементах может и не быть равной амплитуде напряжения источника.
2. Равен нулю сдвиг фаз между током в контуре и напряжением источника: . Математически мы это видим из соотношения (9): при
получается
.
Физическую причину синфазности тока и напряжения понять также не сложно. Дело в том, что напряжения и
на конденсаторе и катушке колеблются в противофазе (т. е. разность фаз между ними равна
), а их амплитуды при резонансе равны. Стало быть, они отличаются только знаком:
, и в сумме дают нуль. Получается, что
(словно бы в цепи имелся один только резистор), а колебания напряжения и тока на резисторе происходят синфазно.
Резонанс играет важнейшую роль в радиосвязи. Когда осуществляется приём радиосигнала, радиоволны различных частот возбуждают в контуре колебания. Но амплитуды колебаний будут малы для сигналов тех радиостанций, частоты которых отличаются от собственной частоты контура. Контур выделяет лишь ту радиоволну, частота которой равна его собственной частоте; именно эти колебания будут иметь значительную амплитуду.
Поэтому, когда мы настраиваем приёмник на какую-то радиостанцию, мы меняем собственную частоту контура (как правило, путём изменения ёмкости конденсатора), пока не наступит резонанс с искомой радиоволной.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Переменный ток. 2» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10-3сек.
1 мкс=0,001 мс = 0,000001сек =10-6сек.
1000 мкс = 1 мс.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 103 Гц = 1 кГц;
1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.
Рисунок 2. Радиан.
Тогда,
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.
Итак,
?= 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Определение
Переменный ток — вынужденные электромагнитные колебания.
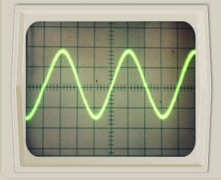
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Определение
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
Внимание!
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙108 м/с).
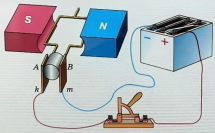
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
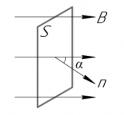
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
Численно магнитный поток определяется формулой:
Φ=BScosα
При равномерном вращении рамки угол α увеличивается пропорционально времени:
α=2πnt
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Φ=BScos2πnt
Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:
ω=2πn
Следовательно:
Φ=BScosωt
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
e=−Φ´=−BS(cosωt)´=BSωsinωt=εmaxsinωt
εmax — амплитуда ЭДС индукции, равная:
εmax=BSω
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
u=Umaxsinωt
u=Umaxcosωt
где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).
Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:
i=Imaxsin(ωt+φс)
где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
u=Umaxcosωt=12cos300,25π=12√22≈8,5 (В).
Активное сопротивление в цепи переменного тока
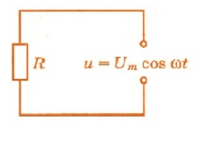
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
u=Umaxcosωt
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
i=uR=UmaxcosωtR=Imaxcosωt
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Imax=UmaxR
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Определение
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
P=I2R
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
p=i2R
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p=(Imaxcosωt)2R
Вспомним из курса математики:
cos2α=1+cos2α2
Отсюда:
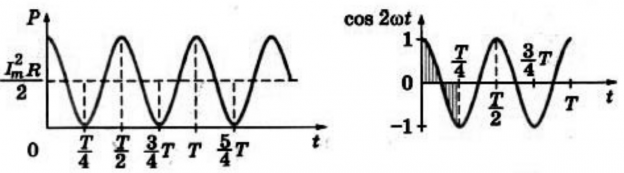
p=I2max2R(1+cos2ωt)=I2maxR2+I2maxR2cos2ωt
График зависимости мгновенной мощности от времени:
На протяжении первой четверти периода, когда cos2ωt>0, мощность в любой момент времени больше величины I2maxR2. На протяжении второй четверти периода, когда cos2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos2ωt=0, следовательно, средняя за период мощность равна I2maxR2.
Средняя мощность −p равна:
−p=I2maxR2=−i2R
Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcosωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p=(Imaxcosωt)2R=10(1·cos(100π·1)2=10 (Дж)
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
−i2=I2max2
Определение
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I=√−i2=Imax√2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U=√−u2=Umax√2
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
P=I2R=UI
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P=I2R
I=Imax√2
P=(Imax√2)2R=I2max2R=222·5=10 ⎛⎝Дж⎞⎠
Задание EF22720
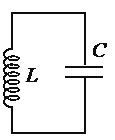
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу Томсона.
3.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.
• Амплитуда напряжения: U0=5 В.
• Циклическая частота колебаний: ω = 1000π с–1.
Запишем формулу Томсона:
T=2πω=2π1000π=21000=0,002 (с)
Ответ: 0,002
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18735
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Описать, что происходит в момент замыкания и размыкания цепи.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
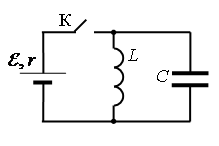
• ЭДС источника тока: ε=5 В.
• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.
• Сопротивление ЭДС источника тока: r = 2 Ом.
• Индуктивность катушки: L = 1 мГн.
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18116
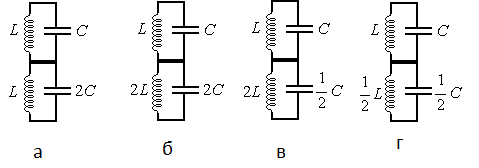
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?
Алгоритм решения
- Выделить цель эксперимента.
- Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
- Выбрать верную пару контуров
Решение
Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18656
Алгоритм решения
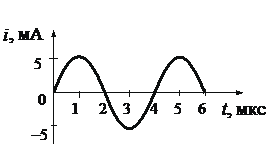
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.6k
Переменный электрический ток
Переменный ток (AC — Alternating Current) — электрический ток, меняющий свою величину и направление с течением времени.
Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC.
Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
DC — Direct Current — постоянный ток, не меняющий своей величины и направления.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.
Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.
Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.
Термины AC и DC применимы как для тока, так и для напряжения.
Параметры переменного тока и напряжения
Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:
Период T — время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частота f — величина, обратная периоду, равная количеству периодов за одну секунду.
Один период в секунду это один герц (1 Hz). Частота f = 1/T
Циклическая частота ω — угловая частота, равная количеству периодов за 2π секунд.
ω = 2πf = 2π/T
Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фаза ψ — величина угла от нуля (ωt = 0) до начала периода.
Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение — величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.
i = i(t); u = u(t)
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:
i = Iampsin(ωt); u = Uampsin(ωt)
С учётом начальной фазы:
i = Iampsin(ωt + ψ); u = Uampsin(ωt + ψ)
Здесь Iamp и Uamp — амплитудные значения тока и напряжения.
Амплитудное значение — максимальное по модулю мгновенное значение за период.
Iamp = max|i(t)|; Uamp = max|u(t)|
Может быть положительным и отрицательным в зависимости от положения относительно нуля.
Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) — максимальное отклонение от нулевого значения.
Среднее значение (avg) — определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение — среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) — определяется как квадратный корень из среднеарифметического квадратов всех
мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой Iamp (Uamp)
среднеквадратичное значение определится из расчёта:

Среднеквадратичное — это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов.
Является объективным количественным показателем для любой формы тока.
В активной нагрузке переменный ток совершает такую же работу за время периода,
что и равный по величине его среднеквадратичному значению постоянный ток.
Коэффициент амплитуды и коэффициент формы
Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой
амплитудное, среднеквадратичное и средневыпрямленное значения.
Коэффициент амплитуды — отношение амплитудного значения к среднеквадратичному.
Для синусоидального тока и напряжения коэффициент амплитуды KA = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды KA = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды KA = 1
Коэффициент формы — отношение среднеквадратичного значения к средневыпрямленному.
Для переменного синусоидального тока или напряжения коэффициент формы KФ 
Для тока и напряжения треугольной или пилообразной формы KФ 
Для переменного тока и напряжения прямоугольной формы KФ = 1
Замечания и предложения принимаются и приветствуются!
Как найти амплитуду силы тока
Обычный амперметр показывает среднеквадратическое значение силы тока. Определить же ее амплитудное значение поможет осциллограф. Для этого к нему придется добавить специальный мощный низкоомный резистор — шунт.

Инструкция
Убедитесь в том, что цепь, в которой необходимо определить амплитудное значение силы тока, не имеет гальванической связи с электросетью. Если такая связь имеется, описанный далее способ измерения использовать нельзя.
Обесточьте цепь, включите в ее разрыв шунт с таким сопротивлением, чтобы его влияние на силу тока было минимальным (если цепь состоит из нескольких последовательно соединенных частей, место ее разрыва выберите как можно ближе к точке с нулевым потенциалом).
Параллельно шунту подключите электронно-лучевой осциллограф, переключенный в режим работы с открытым входом. Не соединяйте корпус осциллографа ни с чем, а чтобы не получить электрический удар из-за разности потенциалов между общими проводами осциллографа и испытуемого устройства, работайте в резиновых перчатках.
Пока цепь выключена, рукояткой перемещения луча по вертикали точно совместите горизонтальную линию на экране осциллографа с нулевой линией накладки с сеткой.
Включите ток в цепи, после чего регулировкой усиления осциллографа добейтесь, чтобы амплитудное значение напряжения помещалось на экране по высоте. Сосчитайте и запишите количество делений на экране (относительно нулевой линии), соответствующее этому значению.
Обесточьте цепь. Отключите шунт от проверяемой цепи, но не от осциллографа, а в проверяемой цепи восстановите соединение. Включите шунт в разрыв другой цепи, состоящей из нагрузки, потребляющей примерно такой же ток, амперметра постоянного тока и источника регулируемого постоянного напряжения.
Регулируя источник, добейтесь, чтобы линия на экране отклонилась от нулевой линии сетки на то же количество делений. Прочитайте показания амперметра — они будут соответствовать амплитуде тока в ходе предыдущего измерения.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.