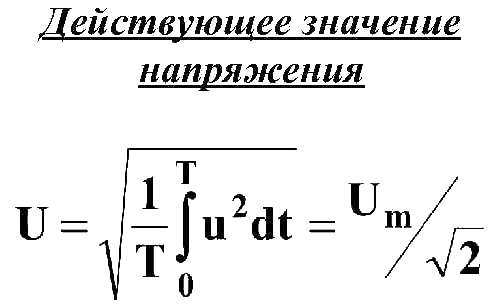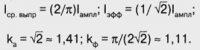Как найти амплитуду напряжения на входе - Исправление недочетов и поиск решений вместе с Examum.ru

Действующее напряжение и амплитудное напряжение — что это, и в чем отличие

Все знают, что действующее напряжение в розетке 220 Вольт (230 по новым нормам, но для данной темы это не имеет особого значения). Это легко проверить при помощи мультиметра, который измерит разность потенциалов между фазой и рабочим нулевым проводником. То есть, при идеальных условиях, потенциал на нулевом проводе 0, а на фазном 220 Вольт. На самом деле все немного не так — переменный ток имеет синусоидальную форму с потенциалом на пиках 310 и -310 Вольт (амплитудное напряжение). Для того чтобы это увидеть, необходимо воспользоваться осциллографом.

Синусоида действующего и амплитудного напряжения

Понятно, что данный материал в большей степени ориентирован на простую аудиторию, у которой не то, что осциллографа нет, даже мультиметр наверняка не у каждого есть. Поэтому все примеры будут браться из среды программы Electronics Workbench, доступной каждому.

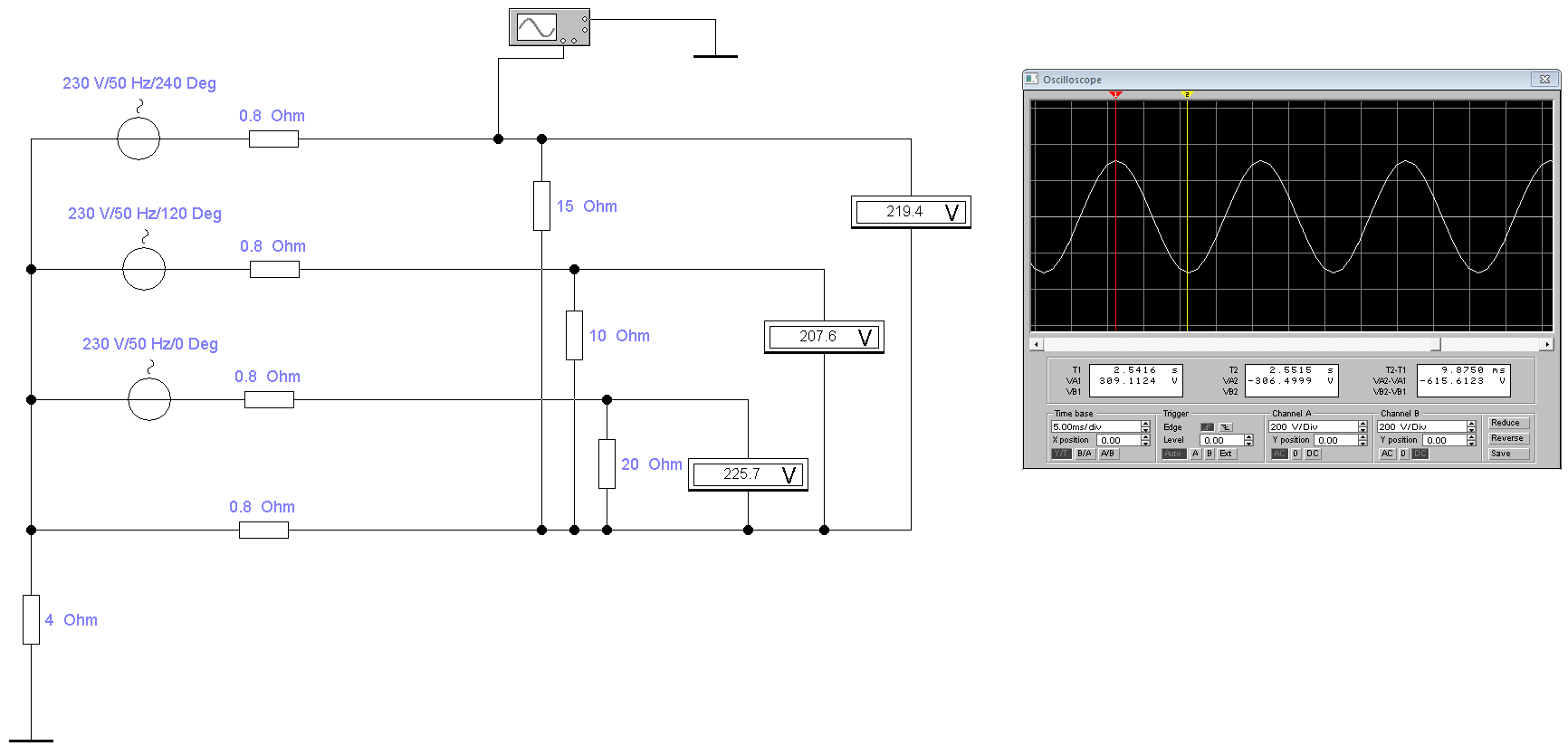
И первое, что нам нужно посмотреть — это синусоиду напряжения фазы из розетки. Для этого в программе отрисуем трехфазную сеть и подключим осциллограф к одной из фаз:

Как видно при показании вольтметра 219,4 Вольт между одной из фаз и PEN проводником, осциллограф показал синусоиду с амплитудой 309,1 Вольт. Это значение напряжения называется максимальным (амплитудным). А 219,4 Вольт, которые показывает вольтметр — это действующее напряжение. Его также называют среднеквадратичным или эффективным. И прежде чем перейти к рассмотрению данной особенности, кратко, простыми словами пройдемся по отрисованной схеме трехфазной сети и разберемся в природе синусоиды.

Начнем со схемы:

Слева на право — три источника переменного напряжения с фазовыми углами 0, 120, 240 градусов и соединенными звездой.
Резистор 4 Ом — это заземление нейтрали трансформатора.
Резисторы по 0,8 Ом — условное сопротивление проводов, зависящее от сечения провода и длины линии.
Резисторы 15, 10 и 20 Ом — нагрузка потребителей по трем фазам.
К одной из фаз подключен осциллограф, показывающий амплитуду 309,1 Вольт.

Теперь рассмотрим синусоиду. Переменное напряжение в отличие от постоянного, график которого прямая на осциллографе, непрерывно изменяется как по величине, так и по направлению. Причем изменения эти происходят периодически, то есть точно повторяются через равные промежутки времени.

Переменное напряжение генерируется на электростанциях и посредством повышающих и понижающих распределительных трансформаторов попадает к конечному потребителю. При этом трансформация по пути никак не сказывается на синусоиде напряжения.

Видео — действующее напряжение и амплитудное

С полным и наглядным изложением рассматриваемого вопроса вы можете ознакомиться в следующем видео:

Работа генератора трехфазного переменного тока

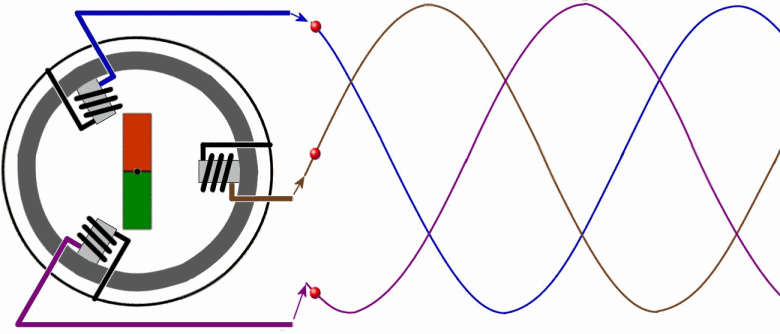
Рассмотрим упрощенно работу генератора трехфазного переменного тока. Обмотки статора (фазы А, В и С) генератора расположены под углом 120 градусов относительно друг друга. Ротор с магнитом вращаясь индуцирует в обмотках статора периодически изменяющиеся ЭДС. Выглядит это следующим образом:

Такое вращение происходит с частотой 50 оборотов в секунду, то есть с частотой 50 Герц. Это значит, что электроны движутся в течение 1 секунды 50 раз в одном направлении (положительный полупериод синусоиды), и 50 — в обратном (отрицательный полупериод), 100 раз проходя чрез нулевое значение. Получается, что к примеру обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.

Определение действующего напряжения

Теперь непосредственно о том, почему произошел переход от максимального, амплитудного значения напряжения 310 Вольт к действующему 220 Вольт. Ответ можно найти в самом определении.

Действующее (эффективное или среднеквадратичное) значение напряжения — это такое напряжение постоянного тока, которое на такой же резистивной нагрузке выделит такую же мощность, как измеряемое переменное напряжение. Соответственно, действующее значение силы тока — такое значение силы постоянного тока, при прохождении которого через резистивную нагрузку выделится такая же мощность, что и при прохождении измеряемого тока.

Можно сформулировать и немного иначе. Действующее значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведет такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.

Общая формула расчета действующего напряжения произвольной формы следующая:

Объяснение действующего напряжения

Определение и формула — это хорошо. Но лучше все понять на наглядном примере. Объяснить все можно через мощность. Причем есть сложный для восприятия способ и более простой, который мы и рассмотрим далее.

Нам нужно взять один период синусоиды переменного напряжения, на этом промежутке построить синусоиду переменного тока и проанализировать мощность. Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.

Точные значения в конкретный момент при данном объяснении не принципиальны, поэтому все построения приблизительные. Естественно нужно понимать, что деля напряжение на сопротивление, мы получим синусоиду переменного тока с амплитудой в R раз меньшей, чем у напряжения. R – это значение сопротивления.

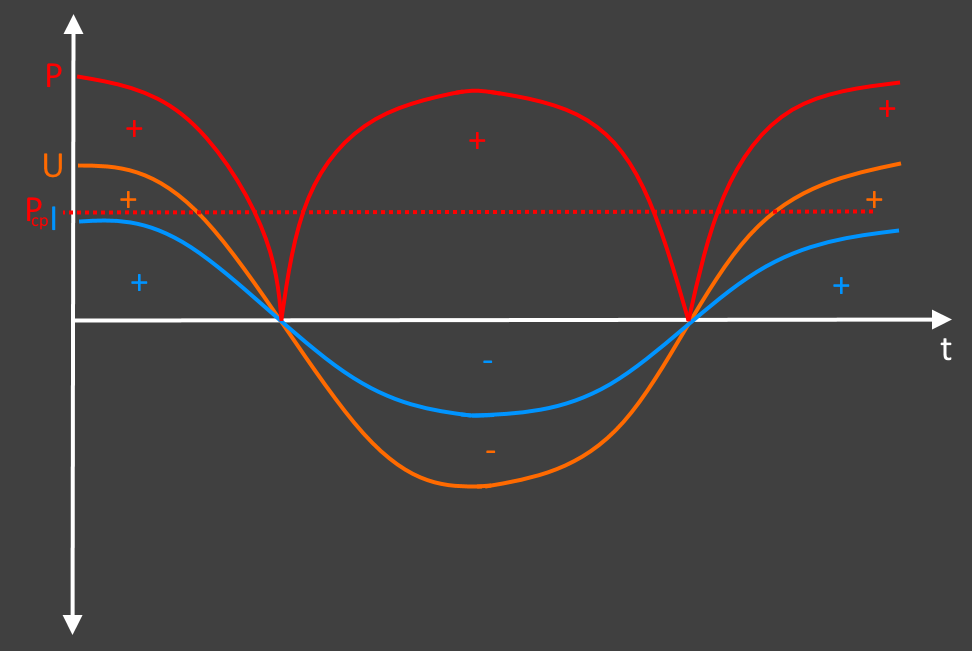
Теперь по двум синусоидам строим график мощности по формуле мощность равна силе тока умноженной на напряжение (P = I × U). Так как напряжение и ток имеют общие нулевые точки, то график мощности не будет заходить в отрицательную область. То есть сила тока со знаком «+» и напряжение со знаком «+» дадут мощность со знаком «+», так же как и сила тока со знаком «-» и напряжение со знаком «-» дадут мощность со знаком «+».

Анализируя полученный график можно отметить, что мощность пульсирующая. Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:

Pд = (Imax × Umax) / 2, где Pд — мощность действующая, Imax — сила тока максимальная, Umax — напряжение максимальное.

Двойку можно представить в виде корень из двух умножить на корень из двух. Получаем Действующее значение мощности = сила тока максимальная деленная на корень из двух умноженная на напряжение максимальное деленное на корень из двух (Pд = (Imax/√2) × (Umax/√2)).

Соответственно сила тока максимальная деленная на корень из двух — это действующее значение силы переменного тока, а напряжение максимальное деленное на корень из двух – это действующее значение переменного напряжения.

И действительно, если мы возьмем максимальное напряжение из предыдущего примера 309,1 Вольт и разделим на корень из двух, то получим действующее напряжение (то, которое показывает вольтметр) 219,4 Вольт.

Источник

Переменный ток

(AC — Alternating Current) — электрический ток, меняющий свою величину и направление с течением времени.

с постоянной составляющей
DC
. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.

— Direct Current — постоянный ток, не меняющий своей величины и направления.

) для периодически меняющегося электрического тока любой формы. Тогда величина
DC
будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей
AC
.

При синусоидальной форме тока, например в электросети, постоянная составляющая DC

равна нулю.

Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка. Запись AC+DC

в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности. Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей
DC
и среднеквадратичного значения переменной составляющей
AC
.

Термины AC

и
DC
применимы как для тока, так и для напряжения.

Что такое переменное напряжение?

Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.

Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид

где Т – период.

Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда

Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже

Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.

Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением

где Um – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла),

φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.

Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.

Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.

Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда

В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.

Параметры переменного тока и напряжения

Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:

Период
T
— время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.

Частота
f
— величина, обратная периоду, равная количеству периодов за одну секунду. Один период в секунду это один герц (1 Hz)

Циклическая частота
ω
— угловая частота, равная количеству периодов за
2π
секунд.

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°

Начальная фаза
ψ
— величина угла от нуля (
ωt
= 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.

Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.

Мгновенное значение

— величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени
t
.

Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени. Например, синусоидальный ток или напряжение можно выразить функцией:

i = I ampsin(ωt); u = U ampsin(ωt)

С учётом начальной фазы:

i = I ampsin(ωt + ψ); u = U ampsin(ωt + ψ)

Здесь I amp

и
U amp
— амплитудные значения тока и напряжения.

Что такое действующее напряжение переменного тока?

Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?

Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения

Для переменного напряжения мгновенное значение выделяемой энергии составит

где u – мгновенное значение напряжения

Тогда количество энергии за полный период от t0 = 0 до t1 = T составит

Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения

Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.

Вычислим действующее значение синусоидального напряжения

Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.

Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение

Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения

Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.

С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.

Всё о напряжении

Напряжение — разность потенциалов между двумя точками пространства. Измеряется в вольтах. Так напряжение между плюсовым и минусовым контактом батарейки составляет 1,5 вольта, а между поверхностью земли и грозовым облаком — миллионы вольт!

Всем известно, что в нашей розетке напряжение переменного тока составляет 220 — 230 вольт. А вот, в трёхфазной розетке — 380 вольт. Разница заключается в том, что в первом случае мы получаем фазное, а во втором — линейное напряжение. Так что же такое линейное напряжение и что такое фазное напряжение , и каково соотношение между ними? И по какой причине соотношения именно таковы.

Как в квартиру, так и на предприятие электроэнергия передаётся от генерирующих электростанций по высоковольтным линиям электропередач (в нашей стране — частотой 50 Гц). На трансформаторных подстанциях высокое напряжение понижается, и распределяется по потребителям . Но если у вас в квартире сеть однофазная (надо заметить, что в последнее время у бытовых потребителей имеется возможность подключения к трёхфазной сети), то на производстве — трехфазная, давайте разберёмся, в чём же разница.

Действующее значение и амплитудное значение напряжения

Говоря — 220 или 380 вольт, мы имеем ввиду действующие значения напряжений, другими словами — среднеквадратичные значения напряжений. Фактически амплитудное значение переменного напряжения всегда выше фазного Umф или линейного Umл. Для синусоидального напряжения его амплитуда больше действующего значения в квадратный корень из 2 раз,(1,414 раза).

Отсюда выходит, что фазное напряжение в 220 соответствует амплитудному — 310 вольт, а для линейного напряжения в 380 вольт амплитуда окажется равной 537 вольт. Разумеется, на практике напряжение в розетке часто не соответствует именно 220 вольтам, оно может быть больше или меньше этой величины, но должно укладываться в допустимые параметры.

Что такое фазное напряжение в сети переменного тока?

На электростанции обмотки генератора соединены по схеме «звезда», то есть объединены концами X, Y и Z в одной точке, которая называется нейтралью или нулевой точкой генератора. Такая схема называется четырехпроводной трехфазной схемой. К выводам обмоток A, B и C присоединяются линейные провода, а к нулевой точке — нейтральный или нулевой провод.

Напряжения между выводом A и нулевой точкой, B и нулевой точкой, С и нулевой точкой, — называются фазными напряжениями, их обозначают Ua, Ub и Uc, ну а поскольку сеть симметрична, то можно просто написать Uф — фазное напряжение.

Линейное напряжение трехфазной сети

Действующее напряжение между выводом A и B, между выводом B и C, между выводом C и A, — называются линейными напряжениями, то есть это напряжения между линейными проводами трехфазной сети. Их обозначают Uab, Ubc, Uca, или можно просто написать Uл.

Линейное напряжение в наших электросетях составляет приблизительно 380 вольт. Соотношение фазного и линейного напряжения в любой трёхфазной сети с заземлённой нейтралью составляет 1,732, или квадратный корень из 3. Не смотря на то что фактическое напряжение в сети может изменяться в определённых пределах, в зависимости от загруженности, соотношение между фазным и линейным напряжением остаётся неизменным.

Что такое среднее значение переменного напряжения?

Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением

где Т – период переменного напряжения,

fu(t) – функциональная зависимость напряжения от времени.

Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.

В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.

Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно

где Um – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла).

Источник

Журнал «Радио», номер 6, 1999г.
Автор: С. Бирюков, г. Москва

В редакцию поступают заметки и статьи, в которых авторы предлагают использовать однополупериодное выпрямление для снижения напряжения вдвое, например, для питания паяльника на 120 В от сети 220 В, или для уменьшения мощности, выделяемой нагревателем кипятильника, в четыре раза. Напряжение и мощность действительно снижаются, но не в такой степени, как нередко предполагают авторы.
Данная статья посвящена влиянию формы электрического тока на его действие. В ней также рассказывается об измерении напряжения и тока электрических сигналов различной формы.

Прежде всего следует напомнить, что переменный электрический ток независимо от его формы характеризуется амплитудным I_ампл (синоним — максимальное), средним I_ср и эффективным I_эфф (среднеквадратичным, действующим) значениями. Действие тока на различные нагрузки при изменении его формы изменяется по-разному.

К примеру, зарядный ток аккумулятора при переходе от двухполупериодного выпрямления к однополупериодному уменьшается вдвое. Если же нагрузкой выпрямителя является нагреватель, при таком изменении формы вдвое уменьшается не ток, а мощность. Поскольку, как известно, мощность Р пропорциональна квадрату тока (P=I₂R), то для однополупериодного выпрямления ток уменьшается не вдвое, а в корень из двух раз! Чтобы избежать подобных противоречий и введены перечисленные понятия.

Первая из трех величин, характеризующих переменный ток, — его амплитудное значение I_ампл. Оно равно максимальному мгновенному значению тока за период его изменения. Как ни странно, с точки зрения воздействия тока разной формы на различные нагрузки, амплитуда тока наименее информативна. Вот почему значение переменного тока определяют сравнением его действия с действием постоянного тока.

Среднее значение переменного тока — это значение такого постоянного тока, который переносит такой же заряд электричества за тот же промежуток времени, что и переменный ток. Для переменного тока, форма которого симметрична относительно оси времени (например, синусоидальный сигнал) среднее значение тока равно нулю. Поэтому обычно под средним значением понимают средневыпрямленное, т. е. среднее значение тока после его выпрямления. Среднее значение тока характеризует его действие, например, при зарядке аккумулятора.

Эффективное значение переменного тока — это значение постоянного тока, который, проходя через активную линейную нагрузку (скажем, резистор), выделяет за тот же промежуток времени такое же количество тепла, какое выделит в этой нагрузке переменный ток. Именно эффективное значение тока важно применительно к нагревательным приборам.

Для характеристики формы периодических сигналов введены два параметра: коэффициент амплитуды k_а=I_ампл/I_эфф и коэффициент формы k_ф=I_эфф/I_{ср.выпр.}

При наиболее распространенной форме сигнала — синусоидальной — рассмотренные значения составляют:

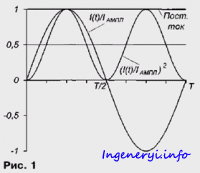
Графически среднее значение переменного тока — это площадь под кривой, характеризующей зависимость тока от времени. Эффективное значение соответствует квадратному корню из площади под кривой, описывающей зависимость квадрата тока от времени. На рис. 1 приведены графики для обычного синусоидального сигнала I(t)/I_ампл и его квадрата (I(t)/I_ампл)² . Из сопоставления графиков видно, что квадрат тока (а ему пропорциональна мгновенная мощность) пульсирует с удвоенной частотой по сравнению с током. Кроме того, отклонение кривой квадрата тока относительно линии на уровне 0,5 вверх и вниз одинаковы. При расчете площади под этой кривой отклонения компенсируются, а значит, она вдвое меньше, чем площадь под прямой, характеризующей постоянный ток. Поскольку эффективное значение тока пропорционально квадратному корню из площади, очевидно, что оно в корень из двух меньше, чем амплитудное значение тока.

К сожалению, площадь под синусоидой I(t)/I_ампл без знания интегрального исчисления не определить, придется поверить приведенным выше соотношениям.

Для напряжения переменного электрического сигнала существуют те же характеризующие значения, что и для тока, — амплитудное U_ампл , среднее U_ср и эффективное U_эфф. Связь между ними такая же. При эффективном напряжении сети 220 В амплитудное напряжение составляет 311 В, средневыпрямленное — 198 В.

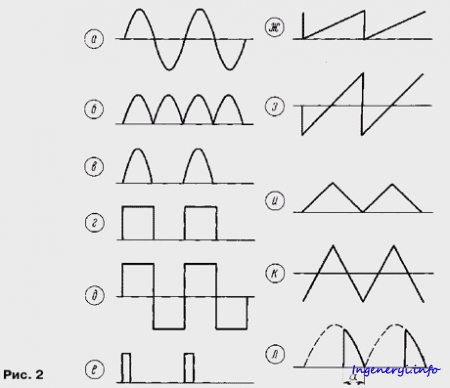
На практике радиолюбителю приходится встречаться с электрическими сигналами разнообразной формы. Рассмотрим некоторые из них.

Синусоидальное напряжение (рис. 2,а) при двухполупериодном выпрямлении (рис. 2,б) сохраняет свои характеристики, причем среднее напряжение становится строго равным средневыпрямленному.

Выше было сказано, что при однополупериодном выпрямлении (рис. 2,в) среднее значение напряжения уменьшается в два раза по сравнению с двухполупериодным, а эффективное — в корень из двух раз. Нетрудно понять, что если в каком-либо регуляторе мощности из N полупериодов на нагрузку пропускается один, среднее напряжение уменьшается в N раз (во столько же раз уменьшается и мощность в нагрузке), а эффективное — в корень из N раз.

Меандр (рис. 2,г). Так называют сигнал, который одну половину периода равен своему максимальному значению, а другую — нулю (рис. 2,г). Для него среднее значение равно половине амплитудного. Мощность, выделяемая током такой формы в нагрузке, вдвое меньше, чем мощность от постоянного тока, поэтому эффективное значение сигнала в корень из двух раз меньше амплитудного. В случае двуполярного меандра (рис. 2,д) напряжения U_ампл , U_{ср.выпр} и U_эфф совпадают между собой.

Последовательность прямоугольных импульсов (рис. 2,е) длительностью t с периодом повторения T. Для такого сигнала существует понятие «скважность», которая обычно обозначается буквой Q и определяется как отношение периода к длительности импульсов: Q = T/t. Поскольку ток сигнала такой формы действует в Q раз меньшее время, чем постоянный ток, среднее значение сигнала в Q раз меньше амплитудного, а эффективное в корень из Q раз.

Пилообразный сигнал (рис. 2,ж,з). Для него среднее значение (средневыпрямленное для двуполярного) равно половине амплитудного (площадь треугольника равна половине произведения основания на высоту). Для расчета эффективного значения следует определить площадь под параболой, описывающей зависимость квадрата сигнала от времени. Так просто эту площадь не посчитать, при математическом расчете эффективное значение получается в корень из трех раз меньше амплитудного.

То же соотношение справедливо и для сигнала треугольной формы (рис. 2,и), в том числе и двуполярного (рис. 2,к).

Напряжение на выходе фазоимпульсного регулятора (рис. 2,л). Его форму характеризует угол проводимости a, который может в общем случае меняться в пределах от 0 до числа пи . Амплитудное значение напряжения такой формы составляет

среднее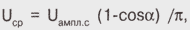
эффективное

где U_ампл.с — амплитудное напряжение сети на входе регулятора, а угол a в последнюю формулу должен подставляться в радианах.

На рис. 3 приведены зависимости, описываемые этими формулами.

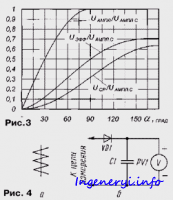
Как измерительные приборы реагируют на сигналы различной формы? Отметим, прежде всего, что практически все стрелочные и цифровые мультиметры в режиме измерения постоянного напряжения и тока определяют среднее значение исследуемого сигнала.

Для измерения эффективного напряжения и тока подходят приборы электромагнитной системы — на их шкале нанесено изображение соответствующего знака (рис. 4,а). Эти приборы обычно используются в различных щитках для контроля сетевого напряжения. Они относительно просты и дешевы, но потребляют заметную мощность, работают в узком частотном диапазоне и имеют нелинейную шкалу.

Специальные приборы для точного измерения эффективного напряжения в широком частотном диапазоне сложны и дороги.

Чтобы определить амплитудное значение напряжения, обычно используют диодный выпрямитель, нагруженный на вольтметр постоянного тока и конденсатор большой емкости (рис. 4,б). Точность такого измерения достаточна для напряжения, значительно превышающего падение на диоде (около 0,6 В).

Стрелочные и цифровые мультиметры при контроле переменного напряжения и тока определяют средневыпрямленное значение и умножают его на коэффициент формы синусоидального сигнала. В результате при измерении напряжения синусоидальной формы на индикаторе прибора мы видим его эффективное значение. При любой другой форме сигналов интерпретация результатов измерения вольтметром переменного тока затруднена.

Например, при подключении вольтметра переменного тока, в котором использован однополупериодный выпрямитель и нет разделительного конденсатора на входе, к выходу двухполупериодного выпрямителя он покажет или ноль или значение, вдвое выше эффективного в зависимости от полярности подключения. Если же его подключить к выходу однополупериодного выпрямителя, то он покажет или ноль или эффективное напряжение невыпрямленного сигнала. И в том и в другом случае результаты измерений недостоверны. При наличии разделительного конденсатора интерпретация показаний еще более затруднительна.

Поэтому для измерения переменного однополярного напряжения при отсутствии специализированных приборов следует применять вольтметр постоянного тока. Такой вольтметр измеряет, как уже указывалось, среднее напряжение, и для получения эффективного значения его показания следует умножить на коэффициент формы. А чтобы получить амплитудное значение, достаточно эффективное умножить на коэффициент амплитуды.

Зная амплитудное значение напряжения последовательности прямоугольных импульсов, по результату измерений среднего значения нетрудно определить скважность импульсов, что иногда очень удобно.

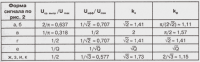
В таблице приведены отношения среднего и эффективного значений к амплитудному, а также коэффициенты формы и амплитуды для рассмотренных сигналов.

Обсудить на форуме

Источник

Что показывает вольтметр, или математика розетки

Время на прочтение
7 мин

Количество просмотров 106K

О чем эта статья

Сегодня я ненадолго отступлю от своей обычной темы о визуальном программировании контроллеров и обращусь к теме измерений напряжения прямо в ней, в розетке!

Родилась эта статья из дискуссий за чаем, когда разразился спор среди «всезнающих и всеведающих» программистов о том, чего многие из них не понимают, а именно: как измеряется напряжение в розетке, что показывает вольтметр переменного напряжения, чем отличается пиковое и действующие значения напряжений.

Скорее всего, это статья будет интересна тем, кто начинает творить свои устройства. Но, возможно, поможет и кому-то опытному освежить память.

В статье рассказано о том, какие напряжения есть в сети переменного тока, как их измеряют и о том, что следует помнить при проектировании электронных схем.
Всему дано краткое и упрощённое математическое обоснование, чтобы было ясно не только «как», но и «почему».

Кому не интересно читать про интегралы, ГОСТы и фазы — могут сразу переходить к заключению.

Вступление

Когда люди начинают говорить о напряжении в розетке, очень часто стереотип «в розетке 220В» скрывает от их взора реальное положение дел.

Начнем с того, что согласно ГОСТ 29322-2014, сетевое напряжение должно составлять 230В±10% при частоте 50±0,2Гц (межфазное напряжение 400В, напряжение фаза-нейтраль 230В). Но в том же ГОСТ имеется примечание: «Однако системы 220/380 В и 240/415 В до сих пор продолжают применять».

Согласитесь, что это уже совсем не то однозначное «в розетке 220В», к которому мы привыкли. А когда речь начинает идти о «фазном», «линейном», «действующем» и «пиковом» напряжениях — вообще каша получается знатная. Так сколько же вольт в розетке?

Чтобы ответить на этот вопрос начнем с того, как измеряется напряжение в сети переменного тока.

Как измерять переменное напряжение?

Прежде, чем углубиться в дебри цепей переменного тока и напряжения, вспомним школьную физику цепей тока постоянного.

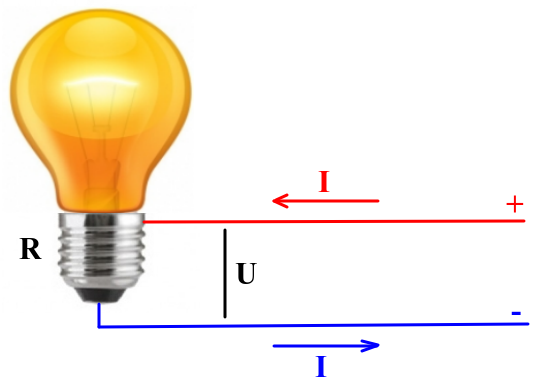
Цепи постоянного тока — вещь простая. Если мы возьмем некоторую активную нагрузку (пусть это будет обычная лампа накаливания, как на рисунке) и воткнем ее в цепь постоянного тока, то все, что происходит в нашей цепи будет характеризоваться всего двумя величинами: напряжением на нагрузке U и током, протекающим через нагрузку I. Мощность, которая потребляется нагрузкой однозначно вычисляется по формуле, известной со школы:

Или, если учесть, что по закону Ома

, то мощность P, потребляемую нагрузкой-лампочкой, можно вычислить по формуле

$P={U^2 over R}$ .

С переменным напряжением все куда сложнее: в каждый момент времени — оно может иметь разное мгновенное значение. Следовательно, в разные моменты времени, на нагрузке, подключенной к источнику переменного напряжения (например, на лампе накаливания, воткнутой в розетку) будет выделяться разная мощность. Это очень неудобно с точки зрения описания электрической цепи.

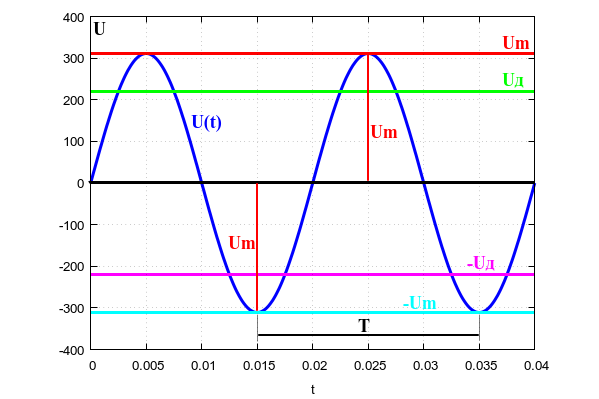
Но нам повезло: форма напряжения в розетке синусоидальная. А синусоида, как известно, полностью описывается тремя параметрами: амплитудой, периодом и фазой. В однофазных сетях (а обычная розетка с двумя дырочками именно и есть однофазная сеть) про фазу можно забыть. На рисунке подробно показаны два периода сетевого однофазного напряжения. Того самого, что в розетке.

Рассмотрим, что означают все эти буковки на рисунке.

Период T — это время между двумя соседними минимумами или соседними максимумами синусоиды. Для осветительной сети РФ этот период составляет 20 миллисекунд, что соответствует частоте 50Гц. Частота колебаний напряжения электрической сети выдерживается очень точно, до долей процента.

Очевидно, что в любых двух точках синусоиды, отстоящих друг от друга на целое число периодов, напряжения всегда равны между собой.

Амплитуда Um — это максимальное напряжение, пик синусоиды. Про действующее напряжение Uд поговорим чуть ниже.

Напряжение в розетке (или однофазной сети) описывается формулой

$U(t)=U_m cdot sin( 2 cdot pi cdot {t over T} );$

где t — текущий момент времени, Um — амплитуда (или пиковое значение) напряжения, T — период сетевого напряжения.

Если с однофазным переменным напряжением более или менее все ясно, то попробуем посчитать мощность, которая выделяется на нашей любимой лампе накаливания, при втыкании ее прямо в розетку.

Так как лампа накаливания является активной нагрузкой (а это значит, что ее сопротивление не зависит от частоты напряжения и тока), то мгновенная мощность, выделяемая на лампе накаливания, воткнутой в розетку, будет вычисляться по формуле

$P(t)=U(t) cdot I(t) = {U^2(t) over R};$

где t — текущий момент времени, а R — сопротивление лампы накаливания при нагретой спирали. Зная амплитуду переменного напряжения Um, можно записать:

$P(t) = {{( U_m cdot sin( 2 cdot pi cdot {t over T} ) )^2} over R}$

Понятно, что мгновенная мощность — неудобный параметр, да и на практике не особо нужный. Поэтому практически обычно применяется мощность, усредненная за период.
Именно усредненная мощность указана на лампочках, нагревателях и прочих бытовых утюгах.

Рассчитывается усредненная мощность в общем случае по формуле:

$P_{ср} = {1 over {R cdot T} } cdot int_0^T { U^2(t) } dt$

А для нашей синусоиды — по гораздо более простой формуле:

$P_{ср} = {{U_m^2} over {2 cdot R}}$

Можете сами подставить вместо

$U(t)$ функцию

$U_m cdot sin( 2 cdot pi cdot {t over T} )$ и взять интеграл, если не верите.

Не думайте, что про мощность я вспомнил просто так, из вредности. Сейчас поймете, зачем она нам была нужна. Переходим к следующему вопросу.

Что же показывает вольтметр?

Для цепей постоянного тока, тут все однозначно — вольтметр показывает единственное напряжение между двумя контактами.

С цепями переменного тока все опять сложнее. Некоторые (и этих некоторых не так мало, как я убедился) считают, что вольтметр показывает пиковое значение напряжения Um, но это не так!

На самом деле, вольтметры обычно показывают действующее или эффективное, оно же среднеквадратичное, напряжение в сети Uд.

Разумеется, речь идет о вольтметрах переменного напряжения! Поэтому, если будете измерять вольтметром напряжение сети, обязательно убедитесь, что он находится в режиме измерения переменного напряжения.

Оговорюсь, что «пиковые вольтметры», показывающие амплитудные значения напряжения, тоже существуют, но на практике при измерении напряжения питающей сети в быту обычно не применяются.

Разберемся, почему такие сложности. Почему бы не измерять просто амплитуду? Зачем выдумали какое-то «действующее значение» напряжения?

А все дело в потребляемой мощности. Я ведь не просто так писал о ней. Дело в том, что действующее (эффективное) значение переменного напряжения равно величине такого постоянного напряжения, которое за время, равное одному периоду этого переменного напряжения, произведет такую же работу, что и рассматриваемое переменное напряжение.

Или, по-простому, лампочка накаливания будет светить одинаково ярко, воткнем ли мы ее в сеть постоянного напряжения 220В или в цепь переменного тока с действующим значением напряжения 220В.

Для тех, кто уже знаком с интегралами или еще не забыл математику, приведу общую формулу расчета действующего напряжения произвольной формы:

$U_д = sqrt { {1 over T} cdot int_0^T { U^2(t) }dt }$

Из этой формулы также становится ясно, почему действующее (эффективное) значение переменного напряжения также называют «среднеквадратичным».

Заметим, что подкоренное выражение и есть та самая «усредненная за период мощность», стоит только поделить это выражение на сопротивление нагрузки R.

Применительно к синусоидальной форме напряжения, страшный интеграл после несложных преобразований превратится в простую формулу:

$U_д = {U_m over sqrt 2}$

где Uд — действующее или среднеквадратичное значение напряжение (то самое, которое обычно показывает вольтметр), а Um — амплитудное значение.

Действующее напряжение хорошо тем, что для активной нагрузки, расчет усредненной мощности полностью совпадает с расчетом мощности на постоянном токе:

$P_{ср} = {U_m^2 over {2 cdot R}} = {U_д^2 over R}$

Это и не удивительно, если вспомнить определение действующего значения напряжения, которое было дано чуть выше.

Ну и, наконец, посчитаем, чему же равна амплитуда напряжения в розетке «на 220В«:

В худшем случае, если у вас сеть на 240В, да еще и с допуском +10%, амплитуда будет аж

Поэтому, если хотите, чтобы ваши устройства, питающиеся от сети, работали стабильно и не сгорали, выбирайте элементы, которые выдерживают пиковые напряжения не менее 400В. Разумеется, речь идет об элементах, на которые непосредственно подаётся сетевое напряжение.

Отмечу, что для не-синусоидальной формы сигнала действующее значение напряжения рассчитывается по иным формулам. Кому интересно — могут сами взять интегралы или обратиться к справочникам. Нас же интересует питающая сеть, а там всегда должна быть синусоида.

Фазы, фазы, фазы…

Помимо обычной однофазной осветительной сети ~220В все слышали и о трехфазной сети ~380В. Что такое 380В? А это межфазное эффективное напряжение.

Помните, я сказал, что в однофазной сети про фазу синусоиды можно забыть? Так вот, в трехфазной сети этого делать нельзя!

Если говорить по простому, то фаза — это сдвиг во времени одной синусоиды относительно другой. В однофазной сети мы всегда могли принять за начало отсчета любой момент времени — на расчеты это не влияло. В трехфазной сети необходимо учитывать насколько одна синусоида отстоит от другой. В трехфазных сетях переменного тока каждая из фаз отстоит от другой на треть периода или на 120 градусов. Напомню, что период измеряется также в градусах и полный период равен 360 градусов.

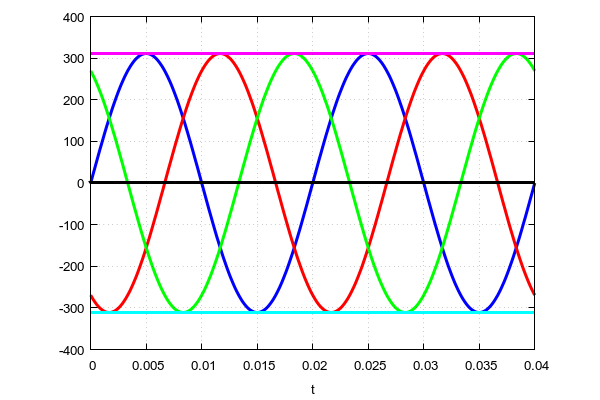
Если мы возьмем осциллограф с тремя лучами и прицепимся к трем фазам и одному нулю, то увидим такую картину.

«Синяя» фаза — начинается от нуля отсчета. «Красная» фаза — на треть периода (120 градусов) позже. И, наконец «зеленая» фаза начинается на две трети периода (240 градусов) позже «синей». Все фазы абсолютно симметричны друг относительно друга.

Какую именно фазу брать за точку отсчета — не важно. Картина будет одинаковой.

Математически можно записать уравнения всех трех фаз:

«Синяя» фаза:

$P(t)=U_m cdot sin( 2 cdot pi cdot {t over T} - 0 )$

«Красная» фаза:

$P(t)=U_m cdot sin( 2 cdot pi cdot {t over T} - { {2 over 3} cdot pi} )$

«Зеленая» фаза:

$P(t)=U_m cdot sin( 2 cdot pi cdot {t over T} - { {4 over 3} cdot pi} )$

Если измерить напряжение между любой из фаз и нулем в трехфазной сети — то получим обычные 220В (или 230В или 240В — как повезет, см. ГОСТ).

А если измерить напряжение между двумя фазами — то получим 380В (или 400В или 415В — не забываем об этом).

То есть трехфазная сеть — многолика. Ее можно использовать как три однофазные сети с напряжением 220В или как одну трехфазную сеть с напряжением 380В.

Откуда взялось 380В? А вот откуда.

Если мы подставим в формулу расчета действующего напряжения наши данные о двух любых фазах, то получим:

$U_{дф} = sqrt { {U_m^2 over T} cdot int_0^T ({{ sin(2 cdot pi cdot {t over T} - 0) - sin(2 cdot pi cdot {t over T} - {2 over 3} cdot pi) }})^2 dt }$

или, упрощая:

$U_{дф} = U_m cdot { sqrt 3 over sqrt 2 } = U_д cdot sqrt 3$

Uдф — действующее межфазное, оно же линейное напряжение.

Учитывая, что амплитуда каждой фазы

получим, что

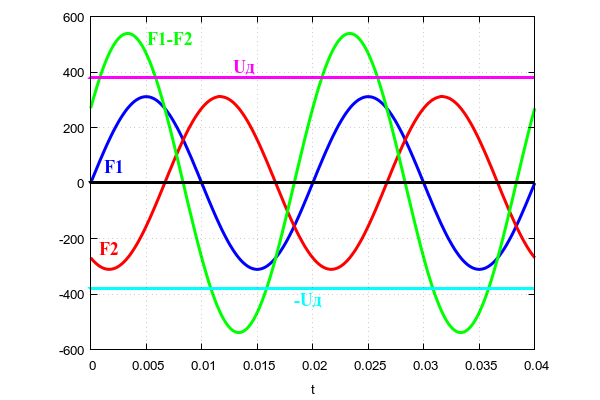
$U_{дф} approx 380B$ для межфазного напряжения. На рисунке наглядно показано, как образуется межфазное напряжение, которое обозначено F1-F2 из двух фазных напряжений фаз F1 и F2. Напряжение фаз F1 и F2 измеряется относительно нулевого провода. Линейное напряжение F1-F2 измеряется между двумя разными фазными проводами.

Как видим, что действующее межфазное напряжение больше амплитуды синусоидального напряжения одной фазы.

Амплитуда межфазного напряжения составляет:

$U_{mф} = U_{дф} cdot sqrt 2 =380B cdot sqrt 2 approx 538B$

Для наихудшего случая (сеть 240В и межфазное напряжение 415В, да еще 10% сверху) амплитуда межфазного напряжения составит:

$U_{mф} = U_{дф} cdot sqrt 2 =(415B + 10%) cdot sqrt 2 approx 645B$

Учтите это при работе в трехфазных сетях и выбирайте элементы, рассчитанные не менее, чем на 650В, если им предстоит работать между двумя фазами!

Надеюсь, теперь понятно что показывает вольтметр переменного тока?

Заключение

Итак, очень кратко, почти на пальцах, мы ознакомились с тем какие напряжения действуют в бытовых сетях переменного тока. Подведем краткие итоги всего, изложенного выше.

Фазное напряжение — это напряжение между фазой и нулевым проводом.
Линейное или межфазное напряжение — это напряжение между двумя разными фазными проводами одной трехфазной сети.
В сетях переменного тока РФ действуют три, хоть и близких, но разных стандарта (фазное/линейное): 220В/380В, 230В/400В и 240В/415В переменного тока с частотой 50Гц.
Вольтметр переменного тока обычно показывает действующее (оно же среднеквадратичное, оно же эффективное) напряжение, которое в раза меньше, чем пиковое (амплитудное) напряжение в сети.
В наихудшем с точки зрения стандартов случае пиковое фазное напряжение составляет примерно 373В, а пиковое линейное напряжение — 645B. Это следует учитывать при разработке электронных схем.

Надеюсь эта статья помогла кому-то разобраться в теме и ответить для себя на некоторые вопросы.

Отправлять предложения и пожелания, замеченные опечатки и просто мнения можно в комментарии или на почту: shiotiny@yandex.ru.

Источник

Переменный электрический ток

Переменный ток (AC — Alternating Current) — электрический ток, меняющий свою величину и направление с течением времени.

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC.
Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.

DC — Direct Current — постоянный ток, не меняющий своей величины и направления.

В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.

При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.

Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.

Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.

Термины AC и DC применимы как для тока, так и для напряжения.

Параметры переменного тока и напряжения

Период T — время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.

Частота f — величина, обратная периоду, равная количеству периодов за одну секунду.

Один период в секунду это один герц (1 Hz). Частота f = 1/T

Циклическая частота ω — угловая частота, равная количеству периодов за 2π секунд.

ω = 2πf = 2π/T

Начальная фаза ψ — величина угла от нуля (ωt = 0) до начала периода.
Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.

Мгновенное значение — величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.

i = i(t); u = u(t)

Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:

i = I_ampsin(ωt); u = U_ampsin(ωt)

С учётом начальной фазы:

i = I_ampsin(ωt + ψ); u = U_ampsin(ωt + ψ)

Здесь I_amp и U_amp — амплитудные значения тока и напряжения.

Амплитудное значение — максимальное по модулю мгновенное значение за период.

I_amp = max|i(t)|; U_amp = max|u(t)|

Может быть положительным и отрицательным в зависимости от положения относительно нуля.

Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) — максимальное отклонение от нулевого значения.

Среднее значение (avg) — определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.

Средневыпрямленное значение — среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) — определяется как квадратный корень из среднеарифметического квадратов всех
мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой I_amp (U_amp)
среднеквадратичное значение определится из расчёта:

Среднеквадратичное — это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов.
Является объективным количественным показателем для любой формы тока.

В активной нагрузке переменный ток совершает такую же работу за время периода,
что и равный по величине его среднеквадратичному значению постоянный ток.

Коэффициент амплитуды и коэффициент формы

Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой
амплитудное, среднеквадратичное и средневыпрямленное значения.

Коэффициент амплитуды — отношение амплитудного значения к среднеквадратичному.

Для синусоидального тока и напряжения коэффициент амплитуды K_A = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды K_A = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды K_A = 1

Коэффициент формы — отношение среднеквадратичного значения к средневыпрямленному.

Для переменного синусоидального тока или напряжения коэффициент формы K_Ф ≈ 1.111
Для тока и напряжения треугольной или пилообразной формы K_Ф ≈ 1.155
Для переменного тока и напряжения прямоугольной формы K_Ф = 1

Замечания и предложения принимаются и приветствуются!

Источник