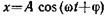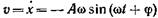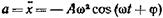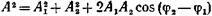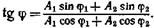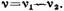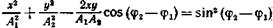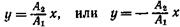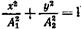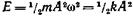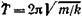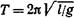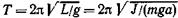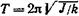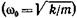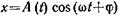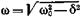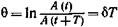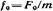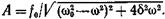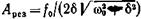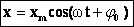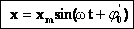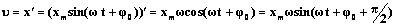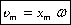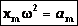Амплитуда скорости груза, теория и онлайн калькуляторы
Амплитуда скорости груза
Скорость груза пружинного маятника
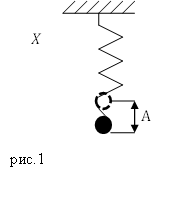
Рассмотрим пружинный маятник, который представляет собой груз массой $m$, подвешенный на пружине, которую считают абсолютно упругой (ее коэффициент упругости равен $k$). Пусть груз движется вертикально, движения происходят под воздействием силы упругости пружины и силы тяжести, если система выведена из состояния равновесия и предоставлена самой себе. Массу пружины считаем малой в сравнении с массой груза. Начало отсчета поместим на оси X (ось направлена вниз) в точке равновесия груза.
Пружинный маятник является примером гармонического осциллятора. Колебания гармонического осциллятора служат важным примером периодического движения и являются моделью во многих задачах физики. Колебания такого груза можно считать гармоническими и описывать при помощи уравнения:
[xleft(tright)=A{cos left({omega }_0t+alpha right)left(1right), }]
где $xleft(tright)$ — смещение груза от положения равновесия в момент времени ($t$); ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$- амплитуда колебаний; ${(omega }_0t+alpha )$ — фаза колебаний; $alpha $ — начальная фаза колебаний.
Скорость колебаний груза при этом найдем как:
[frac{dx}{dt}=-A{omega }_0{sin left({omega }_0t+alpha right)left(2right). }]
Амплитудой скорости колебаний груза при этом является величина равная:
[{left(frac{dx}{dt}right)}_{max}=A{omega }_0left(3right).]
Для пружинного маятника амплитуда колебаний скорости груза равна:
[{left(frac{dx}{dt}right)}_{max}=Asqrt{frac{k}{m}}left(4right).]
Амплитуда скорости колебаний математического и физического маятников
Будем считать математический маятник шариком (грузом), подвешенным на длинной невесомой и нерастяжимой нити. Математический маятник является примером гармонического осциллятора, совершающим колебания, которые описывает уравнение:
[ddot{varphi }+{omega }^2_0varphi =0 left(5right).]
Решением уравнения (5) является выражение:
[varphi ={varphi }_0{cos left({omega }_0t+alpha right)left(6right), }]
где $varphi $ — угол отклонения нити от положения равновесия, $alpha $ — начальная фаза колебаний; ${varphi }_0$ — амплитуда колебаний; ${omega }_0=sqrt{frac{g}{l}}$ — циклическая частота колебаний.
Амплитудой скорости колебаний груза на нити в данном случае является величина равная:
[{left(frac{dvarphi }{dt}right)}_{max}={varphi }_0{omega }_0left(7right).]
Для математического маятника амплитуда скорости колебаний груза равна:
[{left(frac{dvarphi }{dt}right)}_{max}={varphi }_0sqrt{frac{g}{l}}left(8right).]
Примеры задач на амплитуду скорости груза
Пример 1
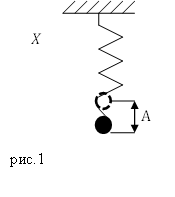
Задание. Колебательная система представляет собой груз, массы $m, $подвешенный на упругой пружине (рис.1). Смещение груза вдоль оси X изменяется по закону: $x(t)=2{cos (10 t)(м) }.$ Чему равно максимальное значение кинетической энергии груза ($E_{k max}$)?
Решение. Кинетическую энергию груза можно найти и определения:
[E_{k }=frac{m{(frac{dx}{dt})}^2}{2} left(1.1right).]
Из уравнения колебаний груза найдем уравнение изменения его скорости:
[frac{dx}{dt}=frac{d}{dt}left(2{cos left(10 tright) }right)=-20{sin left(10 tright)left(frac{м}{с}right)(1.2). }]
Используя выражение (1.2) получим уравнение изменения кинетической энергии в виде:
[E_{k }=frac{m}{2}{(20{sin (10t) })}^2=frac{400m}{2}{sin}^2left(10tright)left(1.3right).]
Из выражения (1.3) следует, что максимальное значение кинетической энергии (ее амплитуда), учитывая, что ${sin}^2left(10tright)le 1$ равно:
[E_{k max}=200cdot mleft(Джright).]
Ответ. $E_{k max}=200cdot m$ Дж
Пример 2
Задание. Скорость колебаний груза на нити (математический маятник) изменяется в соответствии с гармоническим законом: $frac{dvarphi }{dt}(t)=5{sin left(2pi tright) }$. Чему равны амплитуда скорости амплитуда угла отклонения ${varphi }_0$? Запишите уравнение $varphi (t)$ для этих колебаний.textit{}
Решение. Амплитуду скорости изменения угла отклонения мы видим непосредственно в уравнении:
[frac{dvarphi }{dt}(t)=5{sin left(2pi tright)left(2.1right). }]
Она равна:
[{left(frac{dvarphi }{dt}right)}_{max}=5 .]
Амплитуду угла отклонения найдем, используя соотношение:
[{left(frac{dvarphi }{dt}right)}_{max}={varphi }_0{omega }_0left(2.2right),]
где ${omega }_0=2pi $ исходя из уравнения (2.1). Получаем:
[{varphi }_0=frac{{left(frac{dvarphi }{dt}right)}_{max}}{{omega }_0}=frac{5}{2pi } left(2.3right).]
Уравнение $varphi (t)$, учитывая (2.3) будет иметь вид:
[varphi left(tright)=-frac{5}{2pi }{cos left(2pi tright) }.]
Ответ. 1) ${left(frac{dvarphi }{dt}right)}_{max}=5. 2) {varphi }_0=frac{5}{2pi }$. 3) $varphi left(tright)=-frac{5}{2pi }{cos left(2pi tright) }$
Читать дальше: виды равновесия.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Как обозначается амплитуда колебаний? Как найти амплитуду?
Начиная с седьмого класса в школах начинают преподавать такую тему, как «Механические колебания». Начиная с ОГЭ и заканчивая ЕГЭ, эта тема прослеживается во многих экзаменах и вступительных испытаниях. Важной частью ее является изучение понятия амплитуды колебаний. Поэтому для начала ознакомимся с тем, что такое амплитуда колебаний и как обозначается амплитуда колебаний в физике, ведь со временем многое забывается, а именно данной переменной почему-то во многих школах уделяют меньше всего внимания.
Что такое амплитуда колебаний?
Амплитуда колебаний — это максимально возможное отклонение или смещение величины в большую или меньшую сторону от положения равновесия или от среднего значения. К примеру, для пружинного маятника положение равновесия — это покоящийся на пружине груз, а когда он начинает двигаться, то обретает определенную амплитуду, которая определяется растяжением или сжатием пружины.
Для математического же маятника немного проще — максимальное отклонения груза от положения покоя — это и есть амплитуда колебаний.
В то время как амплитуда колебаний радиоволн считается именно по отклонению от среднего значения.
Теперь перейдем к тому, какой буквой обозначается амплитуда колебаний.
Обозначение
В седьмом классе детей приучают обозначать амплитуду колебаний простой буквой «А». Например: А=4 см, то есть амплитуда равна четырем сантиметрам.
Но уже в восьмом классе ученики изучают такое понятие, как механическая работа, и именно она в физике обозначается буквой «А». Ученики начинают путаться в этих значениях, и к 10-11-у классу не имеют четкого представления о том, как обозначается амплитуда колебаний в физике.
В случае с пружинными и математическими маятниками лучше всего записывать амплитуду через максимальные значения. То есть Хмакс. означает максимальное отклонения от положения равновесия. Например Хмакс.=10 см, то есть пружина, как вариант, растянется максимум на 10 см. Это и будет амплитудой колебаний.
В 11-м классе выпускники изучают электромагнитные колебания. И там встречаются колебания заряда, напряжения и силы тока. Для того чтобы записать амплитуду напряжения, принято обозначать ее как максимальное значение. Для заряда и прочих величин соответственно.
Как найти амплитуду колебаний?
Обычно в задачах на нахождение амплитуды представлен график, подобный тому, что нарисован на картинке выше. В таком случае амплитудой будет являться максимальное значение по вертикальной оси Y. Амплитуда показано красной чертой.
Например, на данном рисунке изображен график колебаний математического маятника.
Зная, что амплитуда колебаний математического маятника — это максимальное удаление от положение равновесия, можем определить, что максимальное значение Х=0,3 см.
Найти амплитуду с помощью вычислений можно следующими способами:
1. Если груз совершает гармонические колебания и в задаче известны путь, который проходит тело, и количество колебаний, то амплитуда находится как отношение пути к количеству колебаний, умноженному на 4.
2. Если в задаче дан математический маятник, то при известных максимальной скорости и длине нити можно найти амплитуду, которая будет равна произведению максимальной скорости на квадратный корень из отношения длины к ускорению свободного падения. Эта формула похожа на формулу периода математического маятника.
Только вместо 2п используется максимальная скорость.
В уравнениях же амплитудой является все то, что записано до косинуса, синуса или переменной омеги.
Заключение
В этой статье было сказано о том, как обозначается амплитуда колебаний и как она находится. Данная тема является лишь малой долей большого раздела колебательных процессов, но это не снижает ее важности. Ведь не понимая, что такое амплитуда, невозможно работать с графиками правильно и решать уравнения.
Гармонические колебания
О чем эта статья:
9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.
Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.
Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.
Формула периода колебаний
T = t/N
N — количество колебаний [—]
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты
ν = N/t = 1/T
N — количество колебаний [—]
Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .
Она используется в уравнении гармонических колебаний:
Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
Уравнение гармонических колебаний
x — координата в момент времени t [м]
t — момент времени [с]
(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ
Фаза колебаний
t — момент времени [с]
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
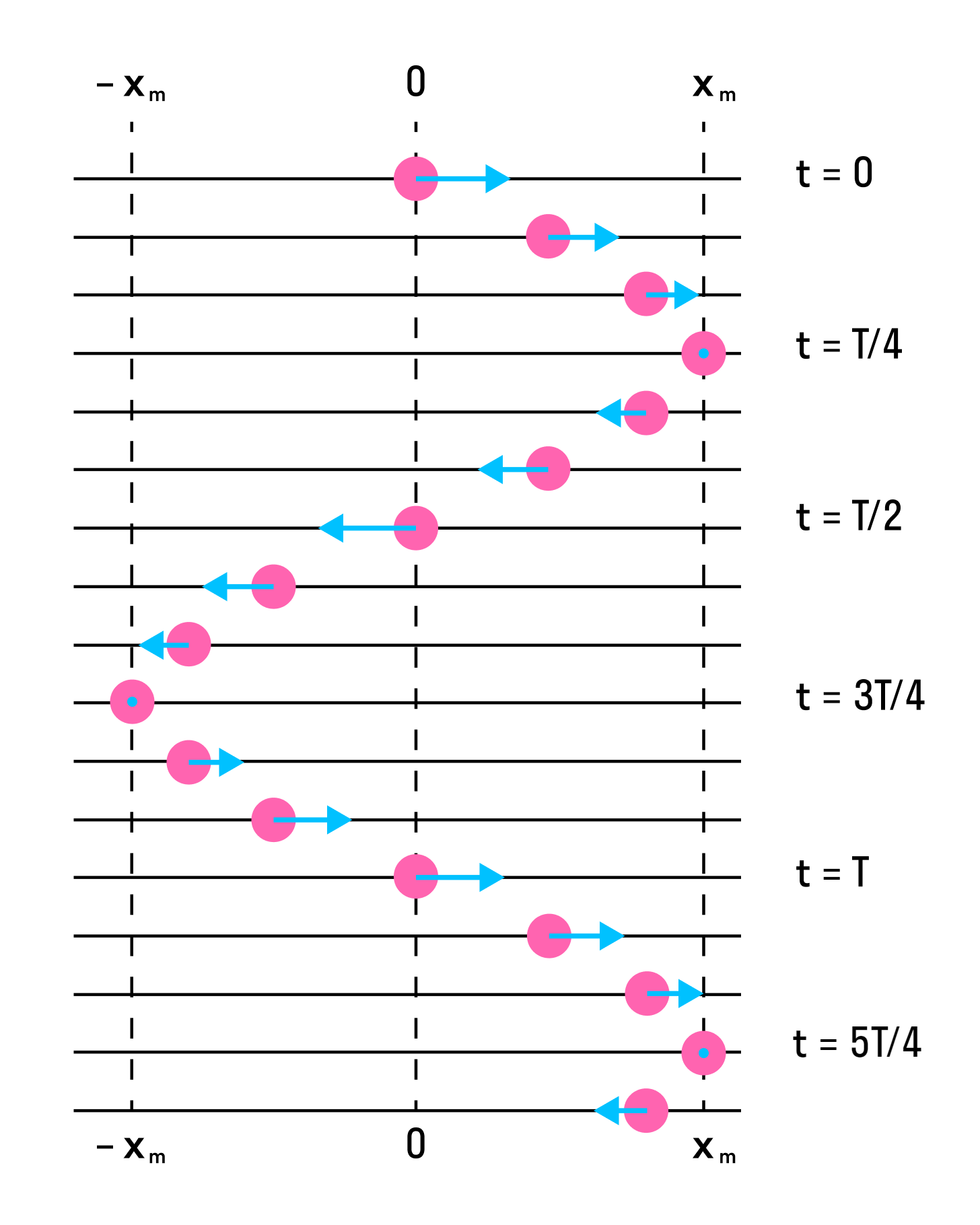
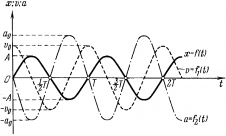
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
Формула периода колебания математического маятника
l — длина нити [м]
g — ускорение свободного падения [м/с 2 ]
На планете Земля g = 9,8 м/с 2
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.
Формула периода колебания пружинного маятника
m — масса маятника [кг]
k — жесткость пружины [Н/м]
Закон сохранения энергии для гармонических колебаний
Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.
Рассмотрим его на примере математического маятника.
- Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
- Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
Если колебание описывать по закону синуса
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
http://skysmart.ru/articles/physics/garmonicheskie-kolebaniya
http://fizmat.by/kursy/kolebanija_volny/garmonicheskoe
• Уравнение гармонических колебаний
где х — смещение колеблющейся точки от положения равновесия;
t — время; А, ω, φ— соответственно амплитуда, угловая частота,
начальная фаза колебаний; 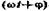
• Угловая частота колебаний
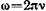
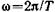
где ν и Т — частота и период колебаний.
• Скорость точки, совершающей гармонические колебания,
• Ускорение при гармоническом колебании
• Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле
где a1и А2— амплитуды составляющих колебаний; φ1 и φ2— их начальные фазы.
• Начальная фаза φ результирующего колебания может быть найдена из формулы
• Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами ν1 и ν2,
• Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами A1 и A2 и начальными фазами φ1 и φ2,
Если начальные фазы φ1 и φ2 составляющих колебаний одинаковы, то уравнение траектории принимает вид
т. е. точка движется по прямой.
В том случае, если разность фаз 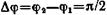
принимает вид
т. е. точка движется по эллипсу.
• Дифференциальное уравнение гармонических колебаний материальной точки

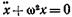
где m — масса точки; k — коэффициент квазиупругой силы (k=тω 2 ).
• Полная энергия материальной точки, совершающей гармонические колебания,
• Период колебаний тела, подвешенного на пружине (пружинный маятник),
где m — масса тела; k — жесткость пружины. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).
Период колебаний математического маятника
где l — длина маятника; g — ускорение свободного падения. Период колебаний физического маятника
где J — момент инерции колеблющегося тела относительно оси
колебаний; а — расстояние центра масс маятника от оси колебаний;
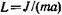
Приведенные формулы являются точными для случая бесконечно малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах не более 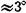
Период крутильных колебаний тела, подвешенного на упругой нити,
где J — момент инерции тела относительно оси, совпадающей с упругой нитью; k — жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.
• Дифференциальное уравнение затухающих колебаний
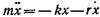
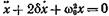
где r — коэффициент сопротивления; δ — коэффициент затухания: 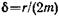
• Уравнение затухающих колебаний
где A (t) — амплитуда затухающих колебаний в момент t; ω — их угловая частота.
• Угловая частота затухающих колебаний
О Зависимость амплитуды затухающих колебаний от времени
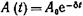
где А — амплитуда колебаний в момент t=0.
• Логарифмический декремент колебаний
где A (t) и A (t+T) — амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.
• Дифференциальное уравнение вынужденных колебаний
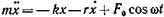
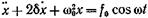
где 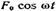
колеблющуюся материальную точку и вызывающая вынужденные
колебания; F — ее амплитудное значение;
• Амплитуда вынужденных колебаний
• Резонансная частота и резонансная амплитуда 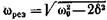
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10297 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.
Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.
1) амплитуда колебаний скорости
2) циклическая частота колебаний
3) максимальная кинетическая энергия груза
4) период колебаний
А) Формула 
Б) Данная формула показывает амплитуду колебаний скорости. Ее можно выразить как 


Скорость груза пружинного маятника
Рассмотрим пружинный маятник, который представляет собой груз массой $m$, подвешенный на пружине, которую считают абсолютно упругой (ее коэффициент упругости равен $k$). Пусть груз движется вертикально, движения происходят под воздействием силы упругости пружины и силы тяжести, если система выведена из состояния равновесия и предоставлена самой себе. Массу пружины считаем малой в сравнении с массой груза. Начало отсчета поместим на оси X (ось направлена вниз) в точке равновесия груза.
Пружинный маятник является примером гармонического осциллятора. Колебания гармонического осциллятора служат важным примером периодического движения и являются моделью во многих задачах физики. Колебания такого груза можно считать гармоническими и описывать при помощи уравнения:
где $xleft(t
ight)$ – смещение груза от положения равновесия в момент времени ($t$); $<omega >_0=sqrt<frac>>0$- циклическая частота колебаний маятника, $A$- амплитуда колебаний; $<(omega >_0t+alpha )$ – фаза колебаний; $alpha $ – начальная фаза колебаний.
Скорость колебаний груза при этом найдем как:
Амплитудой скорости колебаний груза при этом является величина равная:
Для пружинного маятника амплитуда колебаний скорости груза равна:
Амплитуда скорости колебаний математического и физического маятников
Будем считать математический маятник шариком (грузом), подвешенным на длинной невесомой и нерастяжимой нити. Математический маятник является примером гармонического осциллятора, совершающим колебания, которые описывает уравнение:
Решением уравнения (5) является выражение:
где $varphi $ – угол отклонения нити от положения равновесия, $alpha $ – начальная фаза колебаний; $<varphi >_0$ – амплитуда колебаний; $<omega >_0=sqrt<frac>$ – циклическая частота колебаний.
Амплитудой скорости колебаний груза на нити в данном случае является величина равная:
Для математического маятника амплитуда скорости колебаний груза равна:
Примеры задач на амплитуду скорости груза
Задание. Колебательная система представляет собой груз, массы $m, $подвешенный на упругой пружине (рис.1). Смещение груза вдоль оси X изменяется по закону: $x(t)=2<cos (10 t)(м) >.$ Чему равно максимальное значение кинетической энергии груза ($E_$)?
Решение. Кинетическую энергию груза можно найти и определения:
Из уравнения колебаний груза найдем уравнение изменения его скорости:
Используя выражение (1.2) получим уравнение изменения кинетической энергии в виде:
Из выражения (1.3) следует, что максимальное значение кинетической энергии (ее амплитуда), учитывая, что $^2left(10t
ight)le 1$ равно:
Ответ. $E_=200cdot m$ Дж
Задание. Скорость колебаний груза на нити (математический маятник) изменяется в соответствии с гармоническим законом: $frac
ight) >$. Чему равны амплитуда скорости амплитуда угла отклонения $<varphi >_0$? Запишите уравнение $varphi (t)$ для этих колебаний. extit<>
Решение. Амплитуду скорости изменения угла отклонения мы видим непосредственно в уравнении:
Амплитуду угла отклонения найдем, используя соотношение:
где $<omega >_0=2pi $ исходя из уравнения (2.1). Получаем:
Уравнение $varphi (t)$, учитывая (2.3) будет иметь вид:
Начиная с седьмого класса в школах начинают преподавать такую тему, как «Механические колебания». Начиная с ОГЭ и заканчивая ЕГЭ, эта тема прослеживается во многих экзаменах и вступительных испытаниях. Важной частью ее является изучение понятия амплитуды колебаний. Поэтому для начала ознакомимся с тем, что такое амплитуда колебаний и как обозначается амплитуда колебаний в физике, ведь со временем многое забывается, а именно данной переменной почему-то во многих школах уделяют меньше всего внимания.
Что такое амплитуда колебаний?
Амплитуда колебаний — это максимально возможное отклонение или смещение величины в большую или меньшую сторону от положения равновесия или от среднего значения. К примеру, для пружинного маятника положение равновесия — это покоящийся на пружине груз, а когда он начинает двигаться, то обретает определенную амплитуду, которая определяется растяжением или сжатием пружины.
Для математического же маятника немного проще — максимальное отклонения груза от положения покоя — это и есть амплитуда колебаний.
В то время как амплитуда колебаний радиоволн считается именно по отклонению от среднего значения.
Теперь перейдем к тому, какой буквой обозначается амплитуда колебаний.
Обозначение
В седьмом классе детей приучают обозначать амплитуду колебаний простой буквой «А». Например: А=4 см, то есть амплитуда равна четырем сантиметрам.
Но уже в восьмом классе ученики изучают такое понятие, как механическая работа, и именно она в физике обозначается буквой «А». Ученики начинают путаться в этих значениях, и к 10-11-у классу не имеют четкого представления о том, как обозначается амплитуда колебаний в физике.
В случае с пружинными и математическими маятниками лучше всего записывать амплитуду через максимальные значения. То есть Хмакс. означает максимальное отклонения от положения равновесия. Например Хмакс.=10 см, то есть пружина, как вариант, растянется максимум на 10 см. Это и будет амплитудой колебаний.
В 11-м классе выпускники изучают электромагнитные колебания. И там встречаются колебания заряда, напряжения и силы тока. Для того чтобы записать амплитуду напряжения, принято обозначать ее как максимальное значение. Для заряда и прочих величин соответственно.
Как найти амплитуду колебаний?
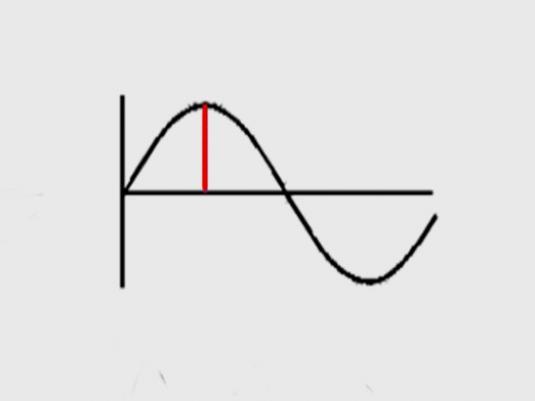
Обычно в задачах на нахождение амплитуды представлен график, подобный тому, что нарисован на картинке выше. В таком случае амплитудой будет являться максимальное значение по вертикальной оси Y. Амплитуда показано красной чертой.
Например, на данном рисунке изображен график колебаний математического маятника.
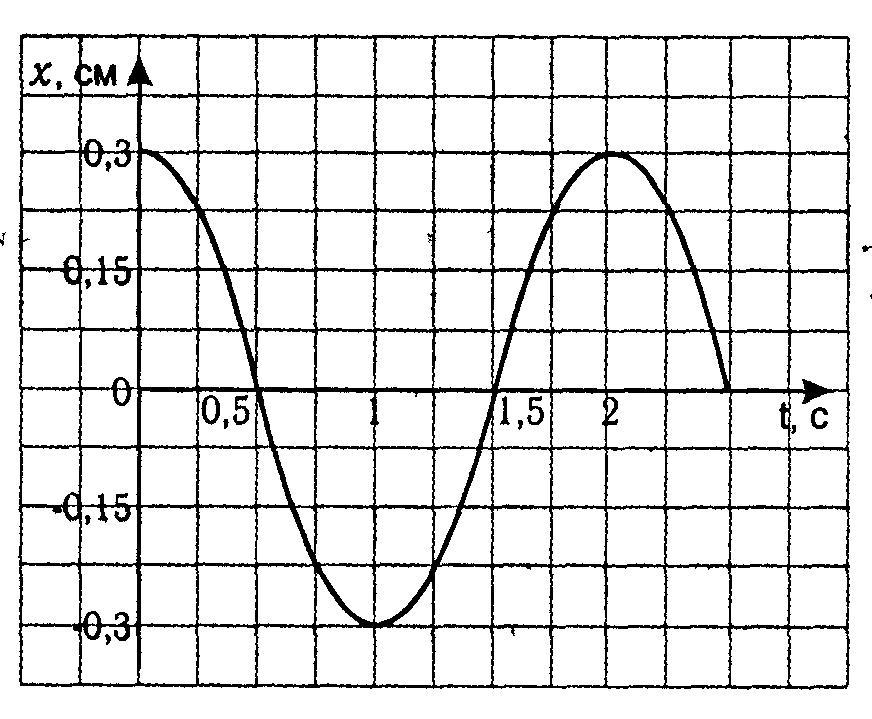
Зная, что амплитуда колебаний математического маятника — это максимальное удаление от положение равновесия, можем определить, что максимальное значение Х=0,3 см.
Найти амплитуду с помощью вычислений можно следующими способами:
1. Если груз совершает гармонические колебания и в задаче известны путь, который проходит тело, и количество колебаний, то амплитуда находится как отношение пути к количеству колебаний, умноженному на 4.
2. Если в задаче дан математический маятник, то при известных максимальной скорости и длине нити можно найти амплитуду, которая будет равна произведению максимальной скорости на квадратный корень из отношения длины к ускорению свободного падения. Эта формула похожа на формулу периода математического маятника.
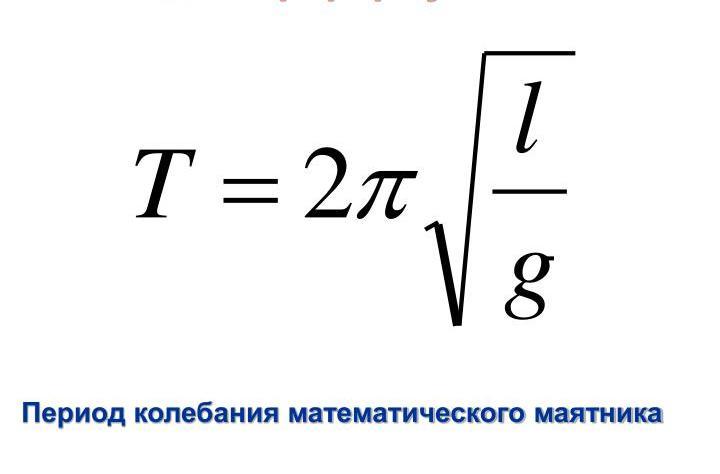
Только вместо 2п используется максимальная скорость.
В уравнениях же амплитудой является все то, что записано до косинуса, синуса или переменной омеги.
Заключение
В этой статье было сказано о том, как обозначается амплитуда колебаний и как она находится. Данная тема является лишь малой долей большого раздела колебательных процессов, но это не снижает ее важности. Ведь не понимая, что такое амплитуда, невозможно работать с графиками правильно и решать уравнения.
Автор:
05-02-2019 22:50
Жду ваши вопросы и мнения в комментариях
Уравнение амплитуды скорости и амплитуды ускорения
• Т — период колебаний — минимальный промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание
• ω0 — циклическая (круговая) частота — число полных колебаний за 2π секунд:
Частота и период гармонических колебаний не зависят от амплитуды. Изменяя амплитуду колебаний груза на пружине, мы не изменяем частоту колебаний этой системы.
Колебания характеризуются не только смещением, но и скоростью vx, и ускорением ax. Если смещение описывается уравнением x = A cos(ω0t + φ), то, по определению, .
В этих уравнениях vm =ω0A — амплитуда скорости; am =ω0 2 A — амплитуда ускорения.
Из уравнений (2.1.5) и (2.1.6) видно, что скорость и ускорение также являются гармоническими колебаниями.
2.1.3. Графики смещения скорости и ускорения
Параметры колебаний запишем в виде системы уравнений:
Из этой системы уравнений можно сделать следующие выводы:
• скорость колебаний тела максимальна и по абсолютной величине равна амплитуде скорости в момент прохождения через положение
Гармонические колебания.
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями.
Например, в случае механических гармонических колебаний:.
В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают.
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0.
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: 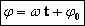
Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
Скорость и ускорение при гармонических колебаниях.
Согласно определению скорости, скорость – это производная от координаты по времени
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2.
Величина 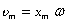
Следовательно, для скорости при гармоническом колебании имеем: 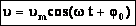

Согласно определению ускорения, ускорение – это производная от скорости по времени:
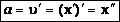
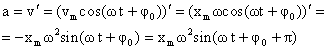
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе).
Величина
— максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: 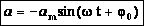
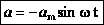
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).
Сравним выражения для смещения и ускорения при гармонических колебаниях:
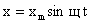
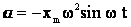
Можно записать: 
т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.
Часто бывает удобно записывать уравнения для колебаний в виде: 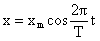
где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: 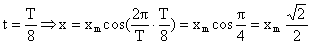
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
источники:
http://www.eduspb.com/node/1780
http://fizmat.by/kursy/kolebanija_volny/garmonicheskoe