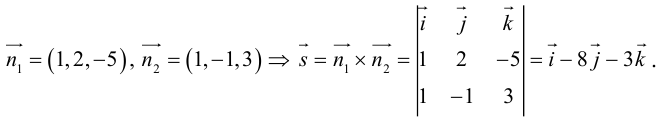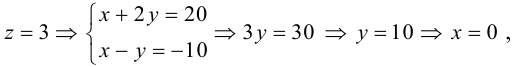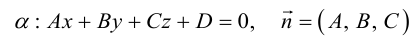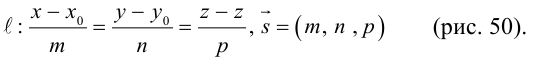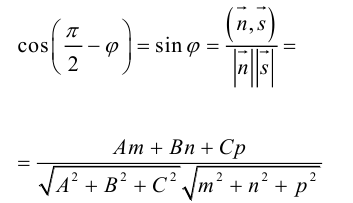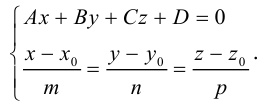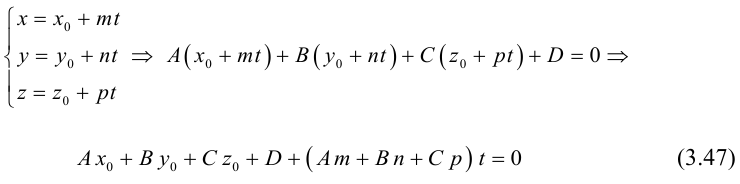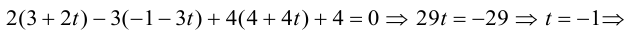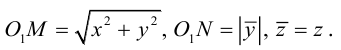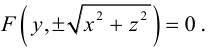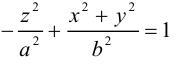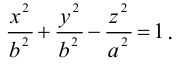1. Типовые задачи с решениями
Задача 1.1.
Найти координаты образа
и прообраза
точки
при повороте вокруг начала координат
на угол
.
Решение.
Найдем аналитическое выражение поворота,
данного в задаче:
Чтобы найти
координаты образа
точки
,
надо подставить в эти формулы вместо
и
данные координаты точки
,
т.е.
.
Тогда
;
,
т.е.
.
Чтобы найти
координаты прообраза
точки
,
т.е. координаты точки, для которой
теперь является образом, надо положить
и найти
и
:
Умножив второе
уравнение системы на
и сложив с первым, найдем
:
Подставляя найденное
значение
в одно из уравнений системы, найдем
:
Таким образом,
.
Ответ:
,
.
Задача 1.2.
Найти уравнение образа
и прообраза
прямой
при осевой симметрии с осью
.
Решение.
Аналитическое выражение осевой симметрии
имеет вид:
Чтобы найти
уравнение образа
прямой
,
нужно выразить из этой системы
и
и подставить их в уравнение прямой
:
.
Опуская штрихи, получаем:
.
Чтобы найти
уравнение прообраза
прямой
,
запишем уравнение прямой
(образа прямой
)
в виде
и подставим в него
и
из аналитического выражения
:
.
Получили для прямых
и
одно и то же уравнение. Это не случайно,
т.к. при осевой симметрии (так же как и
при центральной) образ и прообраз любой
фигуры всегда совпадают.
Ответ:
,
.
Задача 1.3.
Даны прямые
и
.
Найти такие точки
и
,
что
и
,
где
.
Решение.
,
т.е.
.
Тогда учитывая, что
,
получаем:
(рис. 18).
С
ледовательно,
чтобы найти координаты точки
,
надо сначала найти уравнение образа
прямой
при параллельном переносе на вектор
,
а затем решить систему уравнений прямых
и
.
Найдем аналитическое
выражение параллельного переноса на
вектор
:
Найдем уравнение
образа
:
,
т.е.
.
Решаем систему
Сложив почленно
уравнения системы, получим:
.
Итак,
.
Так как
,
то
,
т.е.
−
прообраз точки
.
Найдем координаты прообраза
точки
:
откуда
,
т.е.
.
Ответ:
,
.
2. Задачи для решения на практическом занятии
2.1.
Вывести аналитическое выражение
центральной симметрии с центром
.
2.2. Найти
координаты образа
и прообраза
точки
в центральной симметрии с центром
.
2.3.
Найти уравнение образа
и прообраза
прямой
при повороте на угол
вокруг начала координат.
2.4.
В ортонормированном репере дано
аналитическое выражение преобразований
и
:
Доказать, что
и
− движения. Определить их род. Найти их
инвариантные точки.
2.5.
Даны прямые
и
.
Найти координаты таких точек
и
,
что
,
и
.
2.6.
Найти уравнение оси симметрии точек
и
.
3. Задачи для самостоятельного решения
3.1.
Найти координаты образа
и прообраза
точки
при параллельном переносе на вектор
.
3.2.
Найти уравнение образа
и прообраза
прямой
при
центральной симметрии с центром
.
3.3.
Даны прямые
и
.
Найти координаты таких точек
и
,
что
,
и
.
3.4.
Найти инвариантные точки преобразования,
заданного формулами:
а)
б)
3.5.
Найти аналитическое выражение композиции
осевых симметрий
и определить вид этого движения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Отображения и преобразования множеств. Аналитическое выражение преобразований, группа преобразований. Движения плоскости. Простейшие виды движений
Лекция 9. Отображения и преобразования множеств. Аналитическое выражение преобразований, группа преобразований. Движения плоскости. Простейшие виды движений
Литература. [1] § 39, 40.
Пусть дано отображение . Если для любого элемента y из существует только один прообраз, то отображение называется инъективным или однозначным. В этом случае нельзя найти два элемента и множества X, для которых . Если при отображении f выполнено условие: , т.е. для любого элемента из Y существует по крайней мере один прообраз, то отображение называется сюръективным или отображением X на Y. Отображение, которое одновременно является сюръективным и инъективным, носит название биективного или взаимно однозначного отображения. Таким образом, отображение тогда и только тогда является биективным, когда для любого элемента y из множества Y существует один и только один элемент x из X, для которого .
Пусть взаимно однозначное отображение множества X на множество Y. Поставим в соответствие каждому элементу y из Y его прообраз x из множества X. Мы построили отображение , которое носит название обратного к отображению . Оно обычно обозначается через . Легко показать, что также биективное отображение. Действительно, в силу того, что взаимно однозначное отображение, для любого элемента y из Y существует один и только один прообраз x в множестве X. Таким образом, каждому элементу y из Y ставится в соответствие один и только один элемент из X.
Определение 1. Взаимно однозначное отображение множества X на себя называется преобразованием этого множества.
Если дана некоторая плоскость, то её отображение в себя можно задать в координатной форме. Выберем на плоскости некоторую аффинную систему координат. Рассмотрим отображение . Будем считать, что точке ставится в соответствие точка . Координаты точки зависят от , координат точки :
(1)
Обратно, если заданы функции (1), то можно считать что они определяют некоторое отображение плоскости в себя: каждой точке ставится в соответствие точка . Соотношения (1) называются аналитическим выражением или формулами отображения f.
Пример 1. Отображение f задано своими аналитическим выражением Выяснить, является ли оно преобразованием плоскости.
Решение. Проверим условия инъективности и сюръективности. Пусть и — точки, удовлетворяющие условию . Тогда: Отсюда: Мы получили систему уравнений относительно и . Легко видеть, она совместна и имеет единственное решение . Таким образом, из условия следует, что точки и совпадают. Отображение f является инъективным.
Пусть произвольная точка плоскости. Для того чтобы существовала такая точка A, для которой , достаточно, чтобы её координаты удовлетворяли системе уравнений: Так как определитель этой системы отличен от нуля, то она всегда имеет единственное решение. Нетрудно выразить x и y через x’ и y’. Для этого сложим уравнения системы и вычтем из первого удвоенное второе. После преобразований получим: Сюръективность отображения f доказана. Таким образом, f преобразование плоскости.
Пример 2. Дано аналитическое представление преобразования f плоскости:
Найти формулы обратного преобразования.
Решение. Отображение каждой точке плоскости ставит в соответствие точку , для которой . Обозначим координаты точек и через x, y и x’, y’. Из данного аналитического представления следует: Выразим отсюда x’, y’ через x, y: , . Таким образом, формулы обратного преобразования имеют вид:
Рассмотрим примеры необходимых нам преобразований плоскости и выведем их аналитические выражения.
Определение 2. Пусть дан вектор . Отображение плоскости на себя, которое каждой точке M ставит в соответствие такую точку M’, для которой называется параллельным переносом плоскости на вектор .
Легко видеть, параллельный перенос является преобразованием плоскости, его будем обозначать через . Найдем аналитическое выражение параллельного переноса. Пусть в выбранной системе координаты вектор равны . Предположим, что точка M имеет координаты x и y, a её образ x’ и y’. Так как , то . Отсюда получим формулы параллельного переноса:
(2)
Рассмотрим еще одно преобразование вращение плоскости.
Определение 3. Пусть на ориентированной плоскости даны точка O и ориентированный угол . Преобразование, которое точке O ставит в соответствие ту же точку O, а любой точке A, отличной от O, — точку A’, удовлетворяющую условиям: . называется вращением плоскости с центром в точке O на угол .
Преобразование вращения будем обозначать через . Найдем его аналитическое выражение, при условии, что на плоскости дана прямоугольная декартова система координат, а центр вращения совпадает с ее началом.
Решение. Пусть точка A имеет координаты x и y, а её образ — x’ и y’. Обозначим через ориентированный угол между положительным направлением оси абсцисс и вектором (рис. 125). Тогда ориентированный угол между векторами и равен . Как было показано, , и , . Так как OA=OA’, то
==,==
Таким образом:
(3)
Соотношения (3) представляют собой аналитическое выражение вращения.
При формулы вращения имеют вид: В этом случае преобразование представляет собой центральную симметрию относительно центра вращения.
Определение 4. Пусть дана прямая l. Отображение, которое каждой точке прямой l ставит в соответствие ту же точку, a точке A, не принадлежащей l, — точку A’, удовлетворяющую условиям: прямая AA’ перпендикулярна l и середина отрезка AA’ принадлежит l, называется осевой симметрией плоскости с осью l.
Осевую симметрию будем обозначать через . Докажите самостоятельно, что осевая симметрия – преобразование плоскости. Пусть на плоскости выбрана прямоугольная декартовая система координат. Найдем аналитическое выражение осевой симметрии, при условии, что ее ось совпадает с осью абсцисс. Обозначим координаты точки A через x и y, а её образа A’ при указанной симметрии x’ и y’ (рис. 126). Тогда вектор параллелен оси ординат, a середина M отрезка AA’ лежит на оси абсцисс. Координаты вектора и точки M соответственно равны , . Используя условие параллельности вектора оси Оу, получим: или . Так как точка M лежит на оси Ох, то . Таким образом:
(4)
Формулы (4) являются искомым аналитическим выражением осевой симметрии.
Определение 5. Пусть f и g – два преобразования множества Х. Под произведением преобразования f на преобразование g будем понимать отображение, определяемое формулой , где х – произвольный элемент множества Х.
Покажем, что произведение преобразований также является преобразованием множества Х. Пусть . Так как f и g биективные отображения множества X на себя, то из следует и . Поэтому h инъективное отображение. Докажем его сюръективность. Пусть y — произвольный элемент из X. Тогда существует такой элемент z, что . Аналогично, существует такой элемент x из множества X, для которого . Отсюда вытекает, что . Таким образом, h сюръективное отображение. Биективность h доказана.
Пример 3. Найти формулы произведения , если даны аналитические выражения преобразований f и g:
Решение. Возьмем произвольную точку . Пусть , тогда координаты M’ равны . Обозначим через M» образ точки M’ при преобразовании g: . Используя формулы преобразования g, найдем координаты этой точки: , или . Таким образом, аналитическое выражение преобразования имеет вид:
Замечание. Если мы определим формулы произведения , то получим: (проведите вычисления самостоятельно). Отсюда видно, что произведение преобразований, вообще говоря, не обладает свойством коммутативности.
Определение 6. Преобразование, которое каждому элементу множества X ставит в соответствие тот же самый элемент, называется тождественным.
Тождественное преобразование обычно обозначается через e. Легко видеть, что аналитическое выражение тождественного преобразования плоскости имеет вид: Тождественное преобразование является нейтральным элементом относительно операции произведения преобразований, что означает, что для любого преобразования :. Действительно, возьмем произвольный элемент x множества X: .
Выберем произвольное преобразование и найдем произведение . Пусть y произвольный элемент множества X. Согласно определению обратного преобразования, элемент удовлетворяет условию: . Поэтому . Отсюда следует, что . Возьмем произвольный элемент х множества Х. Пусть , тогда . Таким образом, . Или: . Мы показали, что преобразование — обратное к преобразованию относительно операции произведения преобразований. И так, операция произведения преобразований обладает свойством обратимости. Она же, как отмечалось выше, не удовлетворяет свойству коммутативности. Докажем ее ассоциативность.
Теорема 1. Для любых трех преобразований f, g и h множества X справедливо равенство: .
Доказательство. Пусть x произвольный элемент множества X. Тогда из определения произведения преобразований получим: С другой стороны, Таким образом, для любого элемент x справедливо равенство: . Теорема доказана.
Из курса алгебры известно, что множество G называется группой, если на нем определена ассоциативная и обратимая алгебраическая операция. Если эта операция коммутативна, то G называется абелевой группой. Пусть F совокупность всех преобразований множества X. Произведение преобразований является ассоциативной и обратимой алгебраической операцией на F. Поэтому F группа относительно операции произведения преобразований. Она, вообще говоря, не является абелевой.
Определение 7. Любая подгруппа группы F называется группой преобразований множества X.
Пусть G — подмножество F. В силу теоремы 1, G тогда и только тогда группа преобразований, когда операция произведения преобразований алгебраически замкнута и обратима на G. Поэтому G группа преобразований в том и только в том случае, когда для любых двух элементов f и g из G их произведение принадлежит G, и для любого элемента f этому же множеству принадлежит и обратное преобразование .
Пример 4. Доказать, что множество, состоящее из четырех преобразований f, g, h и e образуют группу преобразований плоскости.
f: g: h: e:
Решение. Составим таблицу произведений элементов из G:
|
I II |
e |
f |
g |
h |
|
e |
e |
f |
g |
h |
|
f |
f |
e |
h |
g |
|
g |
g |
h |
e |
f |
|
h |
h |
g |
f |
e |
В таблице на пересечении соответствующей строки и столбца помещен результат произведения , те произведение элемента строки, умноженной слева на элемент столбца. Проверим, например, что. Пусть точка M имеет координаты x и y, . Точка M’ имеет координаты . Поэтому координаты точки равны . Отсюда следует, что . Результаты остальных произведений проверьте самостоятельно. Из таблицы следует, операция произведения преобразований алгебраически замкнута на G. Легко видеть, что e тождественное преобразование в G. Каждый элемент из G имеет обратный, причем он совпадает с самим элементом: . Нами проверено, что G группа преобразований.
Определение 1. Преобразование плоскости называется движением, если расстояние между образами любых двух точек совпадает с расстоянием между самими точками.
Таким образом, f движение плоскости в том и только в том случае, когда для любых двух её точек A и В выполнено равенство: .
Покажем, что параллельный перенос, вращение и осевая симметрия, введенные нами в предыдущем параграфе, движения плоскости.
Рассмотрим параллельный перенос плоскости на вектор . Пусть A и В две произвольные точки, , их образы при рассматриваемом параллельном переносе. Следует доказать, что . Из определения параллельного переноса (см. § 28) получим: . Представим вектор в виде: (рис. 127). Отсюда следует, что . Так как векторы равны, то их длины совпадают. Параллельный перенос является движением.
Рассмотрим осевую симметрию с осью l. Пусть A и В — две произвольные точки, — их образы при данной осевой симметрии. Докажем, что . Выберем прямоугольную декартову систему координат так, чтобы ось абсцисс содержала прямую l (рис. 128). Если в этой системе точки А и В имеют координаты: , то из формулы осевой симметрии (см § 28) следует, что координаты точек A, и B равны: ). Найдем расстояния между этими точками: . Осевая симметрия – движение плоскости.
Наконец, рассмотрим вращение плоскости и покажем, что оно также является движением плоскости. Пусть A и B — две произвольные точки, их образы при вращении вокруг точки О на ориентированный угол (рис. 129). Воспользуемся аналитическими выражением вращения (см. § 28). Выберем прямоугольную декартовую систему координат так, чтобы её начало совпадало с центром О вращения. Пусть точки A, B, A’, B’ в этой системе имеют координаты: . Из формул вращения следует: Вычислим расстояние между точками A’ и B’:
Таким образом, при вращении сохраняется расстояние между точками. Утверждение доказано.
Отображения и преобразования множеств. Аналитическое выражение преобразований, группа преобразований. Движения плоскости. Простейшие виды движений
Объемы тел вращения
Краткая теория
Объемы тел, образованных вращением
криволинейной трапеции, ограниченной кривой
, осью
и двумя
вертикалями
и
, вокруг осей
и
, выражаются соответственно формулами:
Объем тела, образованного вращением
около оси
фигуры,
ограниченной кривой
, осью
и двумя
параллелями
и
, можно определять по формуле:
Если кривая задана в иной форме
(параметрически, в полярных координатах и т.д.), то в приведенных формулах
нужно сделать соответствующую замену переменной интегрирования.
В более общем случае объемы тел,
образованных вращением фигуры, ограниченной кривыми
и
(причем
) и прямыми
,
, вокруг координатных осей
и
, соответственно равны:
Объем тела, полученного при вращении
сектора, ограниченного дугой кривой
и двумя
полярными радиусами
,
, вокруг полярной оси, может быть вычислен по формуле:
Этой же формулой удобно пользоваться
при отыскании объема тела, полученного вращением вокруг полярной оси фигуры,
ограниченной некоторой замкнутой кривой, заданной в полярных координатах.
Если
– площадь
сечения тела плоскостью, перпендикулярной к некоторой прямой (которую принимаем
за ось
), в точке с абсциссой
, то объем этого тела равен:
где
и
– абсциссы
крайних сечений тела.
Примеры решения задач
Задача 1
С помощью
определенного интеграла вычислить объем тела, полученного вращением фигуры
вокруг указанной оси координат.
вокруг
оси
Решение
Сделаем
чертеж:
Объем
тела, образованного вращением вокруг оси
фигуры можно найти по формуле:
В нашем
случае получаем
Ответ:
Задача 2
Найдите
объем тела, полученного вращением вокруг оси абсцисс криволинейной трапеции,
ограниченной линиями:
и
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Сделаем
чертеж:
Объем
тела можно найти по формуле:
Ответ:
Задача 3
Определить
объем, образованный вращением кривой
вокруг
полярной оси.
Решение
Ответ:
Задача 4
Вычислить
объем тела, ограниченного однополосным гиперболоидом
и
плоскостями
.
Решение
Здесь
удобнее рассмотреть сечения данного тела плоскостями, перпендикулярными к оси
. Тогда объем выразится
формулой:
где
– площадь получаемого сечения, зависящая от
точки с аппликатой
, через которую проходит
секущая плоскость. При пересечении однополосного гиперболоида плоскостью
получается эллипс, который можно определить
уравнениями:
откуда
следует, что полуоси эллипса:
Учитывая, что площадь эллипса с
полуосями
и
равна
, воспользовавшись параметрическим заданием эллипса:
мы можем записать аналитическое
выражение функции
:
Тогда искомый объем:
Ответ:
Содержание:
- Сферическое движение твёрдого тела
- Исследование сферического движения твердого тела методом мгновенных осей
- Мгновенная ось вращения. Аксоиды
- Угловая скорость и угловое ускорение твердого тела во время сферического движения
- Вычисление углового ускорения тела
- Скорость и ускорение точек твердого тела во время сферического движения
- Исследование сферического движения твердого тела методом углов Эйлера
- Углы Эйлера. Уравнения сферического движения твердого тела
- Определение угловой скорости и углового ускорения тела по уравнениям его движения
- Аналитическое нахождения скоростей точек тела при сферическом движении. Уравнения мгновенной оси вращения
- Аналитическое нахождения ускоренний точек тела при сферическом движении
- Примеры решения задач на нахождение кинематических характеристик сферического движения тела
Сферическое движение (движение твёрдого тела вокруг неподвижной точки) — это движение абсолютно твёрдого тела, при котором оно имеет одну неподвижную точку.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Сферическое движение твёрдого тела
Если твердое тело движется так, что одна его точка остается все время неподвижной, то такое движение называется вращательным движением твердого тела вокруг неподвижной точки или сферическим движением. Название «сферический движение »следует из того, что траектории всех точек тела при таком движении размещены на поверхностях сфер, с центром в неподвижной точке.
Примером сферического движения тела может быть движение гироскопа в карданном подвесе или движение волчка, заостренный конец которой опирается на подставку и остается неподвижным.
При изучении кинематики сферического движения тела нужно установить основные характеристики этого движения, то есть уравнения движения, угловую скорость и угловое ускорение тела, и вывести формулы для вычисления скоростей и ускоренний точек тела. Ниже рассмотрим два основных метода исследования кинематики сферического движения: метод мгновенных осей и метод углов Эйлера.
Исследование сферического движения твердого тела методом мгновенных осей
Теорема Эйлера-Даламбера о конечном перемещении твердого тела во время сферического движения
Теорема. Твердое тело, имеющее одну неподвижную точку, можно переместить с одного положения в любое другое одним поворотом этого тела вокруг оси, проходящей через неподвижную точку.
Сформулированная теорема Эйлера-Даламбера является обобщением теоремы 2, доказанной в разделе 4 (см. § 4.2).
Доказательство. Положение свободного твердого тела в пространстве определяется
тремя его точками, которые не лежат на одной прямой. Во время сферического движения тела, когда одна точка является неподвижной, для определения его положения в пространстве достаточно знать положение двух его точек.
Для доказательства теоремы проведем сферическую поверхность произвольного радиуса с центром в неподвижной точке О. Будем считать, что эта сфера неизменно связана с телом S, что осуществляет сферическое движение, и поэтому положения сферы будет определять положение тела S в пространстве (Рис. 5.1).
Пусть положение 

(Теорема 2 § 4.2), найдем точку Р на сфере в случае конечного перемещения тела с неподвижной точкой. Для этого соединим точки 





С и D соответственно касательным к дугам







Аналогично доказывается, что точки 






который нужно вернуть дугу ВР до совпадения с дугой 


Мгновенная ось вращения. Аксоиды
Очевидно, что перемещение твердого тела, имеющего неподвижную точку, с положения, которое оно занимает в момент времени t, в положение, соответствующее моменту времени 



При приближении 

Иначе говоря: ось, вокруг которой нужно вращать тело, имеющее одну неподвижную точку, при перемещении его с одного положения в другое, бесконечно близкое к первому, называется мгновенной осью вращения для конкретного момента времени.
Мгновенная ось вращения — это геометрическое место точек тела, скорости которых в конкретный момент равны нулю. Положение мгновенной оси вращения не остается неизменным за сферического движения тела, а со временем меняет свое положение в пространстве. Геометрическое место мгновенных осей относительно неподвижной системы отсчета, относительно которой рассматривается движение тела, называется недвижимым аксоидом (поверхность и на рис. 5.2).
Неподвижный аксоид является конической поверхностью с вершиной в неподвижной
точке О, поскольку все мгновенные оси вращения проходят через эту неподвижную точку.
Геометрическое место мгновенных осей в самом подвижном теле называется подвижным аксоидом (поверхность ИИ на рис. 5.2).
Движимый аксоид есть также конической поверхностью с вершиной в неподвижной точке О.Во время сферического движения тела движимый аксоид 

Практически понятие аксоидов используется для классификации видов
прецессионного движения гироскопов.
Угловая скорость и угловое ускорение твердого тела во время сферического движения
Из теоремы Эйлера-Даламбера следует, что сферическое движение твердого тела в каждый момент времени является вращательным вокруг мгновенной оси, а потому
величинами, которые характеризуют сферическое движение тела в каждый момент
времени, будут мгновенная угловая скорость и мгновенное угловое ускорение тела.
Если за промежуток времени 



При этом нужно иметь в виду, что величина 


Вектор мгновенной угловой скорости 

Угловое ускорение тела во время сферического движения характеризует скорость изменения со временем вектора угловой скорости по величине и направлению. Вектор углового ускорения равен первой производной за временем от вектора угловой скорости
Вектор углового ускорения 

Договоримся вектор углового ускорения 
Вычисление углового ускорения тела
Существует два основных способа нахождения вектора углового ускорения тела во время сферического движения. Один из них — аналитический, который рассмотрим в § 5.2, базируется на углах Эйлера. В этом параграфе рассмотрим второй способ, который использует расписание вектора углового ускорения 
Пусть тело совершает сферический движение и в заданный момент времени имеет угловую скорость 
Если ввести единичный вектор
Тогда
Составляющая 



Составляющая 

Производная 



Составляющая углового ускорения 
Вектор 




В частном случае, когда угловая скорость тела при сферическом движении постоянная по величине 
Скорость и ускорение точек твердого тела во время сферического движения
Поскольку в каждый момент времени тело, которое движется вокруг неподвижной точки, имеет мгновенную ось вращения 

где 


Размер 


или с учетом, что
ускорения точек тела в случае сферического движения:
Тут 

Итак,
Равенство (5.8) выражает теорему Ривальса об ускорении точки тела, осуществляет сферический движение, которая формулируется так: ускорение любой точки твердого тела в случае сферического движения равна векторной сумме вращательного и доосевого ускоренния.
Вектор вращательного ускорения




где 

Вектор доосевого ускорения 



Модуль доосевого ускорения
Модуль полного ускорения 
Исследование сферического движения твердого тела методом углов Эйлера
В предыдущем параграфе исследованы движение твердого тела с неподвижной точкой геометрическим методом (методом мгновенной оси). Ниже рассмотрим аналитический метод исследования кинематики сферического движения тела, основанный на углах Эйлера.
Углы Эйлера. Уравнения сферического движения твердого тела
Как уже отмечалось в 5.1.1, положения твердого тела в пространстве определяется тремя точками, не лежащих на одной прямой, то есть девятью координатами этих точек. Положение всех остальных точек тела можно найти через заданные три точки. В твердом теле расстояние между отдельными точками тела не меняется, а потому координаты этих трех заданных точек должны удовлетворять трем уравнениям, которые выражают неизменность расстояний между отдельными точками тела. В случае свободного твердого тела остается шесть независимых координат, то есть свободное тело имеет шесть
степеней свободы.
В случае сферического движения тела одна точка закреплена, а следовательно, число независимых величин уменьшается до трех, то есть тело при таком движении имеет три степени свободы.
Три степени свободы, которыми тело в случае сферического движения, требуют для определения положения тела относительно произвольной системы координат трех независимых величин. Эти величины можно задать разными способами. В теоретической механике наибольшее применение получили углы Эйлера.
Через неподвижную точку О твердого тела проведем оси неподвижной декартовой системы координат
Подвижную декартову систему координат


Взаимное положение этих систем определяется углами Эйлера. Дадим определение углов
Эйлера.
Линия пересечения ON неподвижной плоскости 



Для изменения этого угла тело должно вращаться вокруг оси 
Следующим углом Эйлера является угол между координатными плоскостями 






Для полного определения положения подвижной системы координат относительно неподвижной нужно задать угол между линией узлов и подвижной осью 


Углы Эйлера положительные, когда они отложены по осям


Во время движения тела с одной закрепленной точкой углы 
Эти уравнения называются уравнениями сферического движения тела.
Заметим, что описанный вариант выбора углов 
Существуют их модификации. Так при исследовании динамики кораблей и самолетов
используют углы Эйлера-Крылова.
Определение угловой скорости и углового ускорения тела по уравнениям его движения
Пусть сферическое движение тела описывается уравнениями (5.12). вычислим величину и направление угловой скорости тела в произвольный момент времени, как функцию углов Эйлера и их производных.
В случае изменения угла







Как будет показано в разделе 8, при вращении тела вокруг нескольких осей, пересекающихся результирующее движение будет мгновенно-вращательным с угловой скоростью, равной геометрической сумме составляющих угловых скоростей. В случае сферического движения тела вектор результирующей мгновенной угловой скорости равен
Для нахождения величины и направления вектора мгновенной угловой скорости
Проектируя обе части равенства (5.13) на оси 
Проекции векторов 

а для нахождения проекций вектора 








Подставим полученные величины проекций в правые части равенств (5.14):
Аналогично, проектируя равенство (5.13) на оси неподвижной системы координат 

Равенства (5.15) и (5.16) называются кинематическими уравнениями Эйлера. Эти уравнения дают возможность найти модуль мгновенной угловой скорости и направляющие косинусы вектора 
Модуль и направляющие косинусы вектора углового ускорения также определим по его проекциями на неподвижные и подвижные оси координат.
Найдем проекции вектора углового ускорения на неподвижные оси координат 


Дифференцируя первое равенство (5.18) с учетом, что векторы
Сравнивая (5.19) с другим равенством (5.18), находим
то есть проекция углового ускорения на неподвижную ось декартовой системы координат равна производной по времени от проекции угловой скорости на соответствующую ось.
Определим проекции углового ускорения на движущиеся оси координат 
Единичные векторы подвижной системы координат обозначим через


Разложим векторы угловой скорости 

Вектор углового ускорения, как производная по времени от вектора угловой скорости, равна
Второе слагаемое полученной зависимости с учетом (5.21) преобразуется
Угловое ускорение 
Сравнивая выражения (5.22) и (5.23), находим проекции вектора углового ускорения на оси подвижной системы координат
то есть, проекции углового ускорения на движущиеся оси декартовой системы координат равны производным по времени от проекций угловой скорости на соответствующие подвижные оси. Модуль мгновенного углового ускорения и направляющие косинусы вектора 
Аналитическое нахождения скоростей точек тела при сферическом движении. Уравнения мгновенной оси вращения
Пусть движение тела, имеющего одну неподвижную точку, задано уравнениями (5.12).
Найдем скорость произвольной точки М (рис. 5.8). если координаты точки 

С другой стороны вектор скорости точки можно представить через его проекции на неподвижные оси координат
Приравнивая соответствующие компоненты в различных представлениях вектора
скорости 
Каждую из формул (5.26) можно получить из предыдущей циклической перестановкой букв 
Если координаты точки 


Модуль и направляющие косинусы вектора скорости произвольной точки тела во время сферического движения найдем по формулам:
По найденным проекциям скоростей точек тела во время его сферического движения можно найти уравнения мгновенной оси вращения.
Скорость каждой точки на мгновенной оси вращения в данный момент времени равна нулю, то есть 
Откуда 
Уравнение (5.29) является уравнением мгновенной оси вращения тела, имеющего одну
неподвижную точку, в неподвижной системе координат, то есть уравнением мгновенной
оси вращения тела во время сферического движения.
Аналогичным методом выводится уравнение мгновенной оси вращения в подвижной системе координат, которое будет иметь вид
Аналитическое нахождения ускоренний точек тела при сферическом движении
Согласно теореме Ривальса, ускорения произвольной точки тела в случае сферического движения определяется по формуле (5.8), то есть
Раскрывая второе слагаемое последнего равенства как двойное векторное произведение, то есть
Найдем проекции вектора ускорения 



Приравнивая соответствующие компоненты при 
Формулы (5.32) определяют проекции вектора ускорения точки тела на оси неподвижной системы координат
Аналогично находят проекции вектора ускорения 
Модуль вектора ускорения точки и его направляющие косинусы с соответствующими осями координат вычисляются по формулам:
Примеры решения задач на нахождение кинематических характеристик сферического движения тела
Задача 5.1. Конус с углом при вершине


Решение. Конус находится в сферическом движении, поскольку точка О остается неподвижной. Для решения этой задачи можно использовать оба предложены методы исследования кинематики сферического движения тела. Проиллюстрируем их на этой задачи.
а) Метод мгновенных осей
По условию задачи конус катится без скольжения, поэтому мгновенной осью вращения 
Скорость точки С можно найти по формуле (5.6)
С треугольника АСК
Тогда
Вектор угловой скорости 

Определим скорость точки В:
Поскольку центр конуса движется с постоянной линейной скоростью, то величина угловой скорости конуса 

Найдем предварительно угловую скорость 
В случае качения конуса без скольжения мгновенная ось вращения 


откуда
Вектор 
Тогда
Вектор 


Переходим к определению ускоренний точек А и В, воспользовавшись зависимостями (5.8), (5.9) и (5.10):
Векторы вращательного 

б) Метод углов Эйлера
Для решения задачи этим методом нужно выбрать оси подвижной и неподвижной систем координат и вывести уравнение движения конуса. оси неподвижной системы координат 
Исходное положение конуса выбираем так, чтобы диаметр АВ лежал в вертикальной плоскости 
Подвижную ось 
В начальный момент времени ось 




При выводе уравнений движения тела, вращающегося вокруг неподвижной точки, нужно иметь в виду, что Эйлеру углы независимые между собой тогда, когда тело имеет единую вязь в виде неподвижной точки О.
Если, кроме точечной связи, на тело наложены другие связи, то Эйлеру углы становятся зависимыми между собой.
В данной задачи конус катится по плоскости без скольжения. Поэтому дополнительными связями является плоскость, по которой катится конус, и условие движения без скольжения. При таком движения конуса угол нутации





Точка С движется по кругу, а потому
Поскольку 

Скорость точки А, лежащей в данный момент времени в плоскости контакта, равна нулю. С другой стороны,

Направление 

Покажем тело в произвольный момент времени и установим закон его движения.
Из построения углов Эйлера следует, что линия узлов ON лежит в горизонтальной
плоскости и перпендикулярна осям 


плоскостями 



Направления изменения углов φ и ψ показаны на рис. 5.12 дуговыми стрелками.
По правилу выбора положительных направлений углов Эйлера (§ 5.2, 5.2.1) имеем
Как было отмечено выше, прецессионного движение и собственное вращение происходят с постоянными угловыми скоростями, поэтому:
Поскольку при

По известным формулам (5.16), (5.17), (5.20), (5.25) находим проекции векторов угловой скорости и углового ускорения на оси неподвижной системы координат, а также их модули:
Векторы


При
тогда
Из результатов вычислений (г) видно, что вектор 



перпендикулярно к осям 


Для определения скоростей точек А и В используем формулы (5.26) и (5.27). Находим координаты точек А и В при 

Тогда:
Следовательно, скорость точки А равна нулю.
Аналогично находим скорость точки В:
Скорость точки В равна 


Для нахождения ускоренний точек А и В используем формулы (5.32), (5.33), (5.34) и известные величины (в) и (г).
Получим:
Ускорение точки А равно 
Аналогично находим ускорение точки В:
Вектор ускорения 



Результаты расчетов, полученные двумя методами, совпадают.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Содержание:
Аналитическая геометрия
В этой главе все геометрические объекты мы будем определять и изучать с помощью соответствующих уравнений этих объектов и, следовательно, в принципе геометрия может быть изложена без единого чертежа. И, действительно, все чертежи, которые мы будем использовать, будут служить лишь для визуальной иллюстрации наших рассуждений.
Уравнение поверхности в выбранной декартовой системе координат
т. е. в виде связи или зависимости между координатами х, у, z произвольной точки поверхно-аналогично, уравнение
определяет некоторую линию (кривую) в системе координат 
Кривая в пространстве может быть задана как пересечение двух поверхностей и, следовательно, она определяется системой из уравнений этих поверхностей:
Кроме того, кривую на плоскости или в пространстве можно также задать с помощью зависимостей координат произвольной то’жи этой кривой от некоторого параметра, т. е. с помощью параметрических уравнений:
где t — действительный параметр.
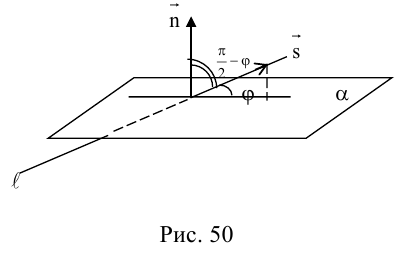
Плоскость в пространстве. Различные виды уравнения плоскости
Найдем уравнение плоскости в пространстве с выбранной в нем декартовой системой координат 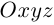
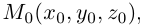
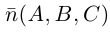
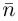
Пусть 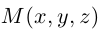
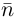
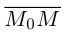
или, учитывая, что 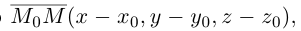
Преобразовав полученное уравнение к виду
мы получим тем самым общее уравнение плоскости.
Рассмотрим теперь некоторые частные случаи общего уравнения плоскости. Если в общем уравнении плоскости отсутствует, одна из координат, то нормальный вектор 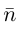
Аналогично, если в общем уравнении плоскости отсутствуют две координаты, то нормальный вектор данной плоскости перпендикулярен соответствующей координатной плоскости и, значит, плоскость расположена параллельно этой координатной плоскости.
Научимся теперь находить уравнение плоскости по трем элементам.
1) Плоскость, проходящая через точку, параллельно двум векторам.
Пусть плоскость 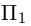
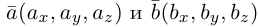
Обозначим через 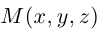
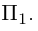
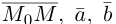
Раскрыв определитель (проще всего, разлагая его по первой строке), получим общее уравнение плоскости
2)Плоскость, проходящая через две точки, параллельно вектору.
Найдем уравнение плоскости 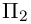
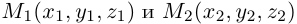
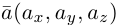
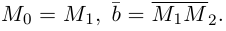
— искомое уравнение плоскости
3)Плоскость, проходящая через три точки.
Если плоскость 
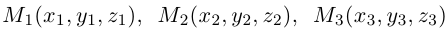
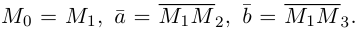
Замечание. Во всех трех случаях уравнение плоскости можно найти, вычислив предварительно ее нормальный вектор. Например, в первом случае в качестве нормального вектора можно взять векторное произведение 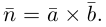
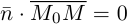
Пример №1
Найти уравнение плоскости 11 ^ — перпендикулярной плоскости
параллельной вектору 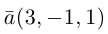
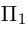
Решение. Из уравнения плоскости 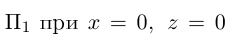
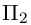
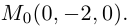
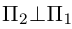
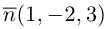
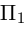
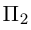
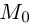
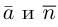
Таким образом, общее уравнение плоскости 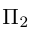
Пусть плоскость 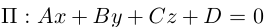
Разделив обе части уравнения плоскости на число D. мы можем записать его в виде:
Числа а, b, с представляют собой величины отрезков, которые плоскость П отсекает на координатных осях. Полученное уравнение называется уравнением плоскости в отрезках.
Найдем теперь формулу для вычисления расстояния от точки 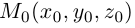
Обозначим искомое расстояние через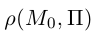
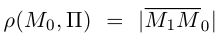
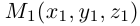
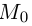
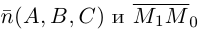
С другой,
так как 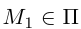
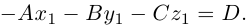
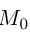
В заключение этого параграфа выясним характер взаимного расположения двух плоскостей. Пусть плоскости заданы своими общими уравнениями:
Очевидно, что угол 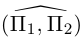
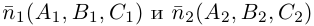
В частности,
Пример №2
Убедиться в том, что плоскость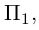
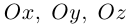
параллельны и найти расстояние между ними.
Решение. Запишем уравнение плоскости II| в отрезках:
Преобразовав его к общему виду, получим:
Так как нормальные векторы 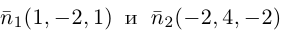
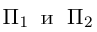
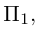
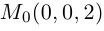
Уравнения прямой в пространстве
Пусть прямая L в пространстве с декартовой системой координат 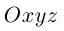
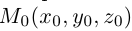
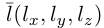
Обозначим через 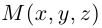
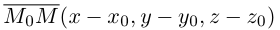
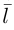
Эта двойная пропорция представляет собой канонические уравнения прямой в пространстве.
Заметим, что в канонических уравнениях прямой формально допускается запись нулей в знаменателях, это означает лишь то, что прямая перпендикулярна соответствующей координатной оси или координатной плоскости.
Если прямая проходит через две точки 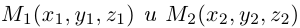
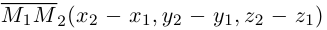
Коллинеарные векторы 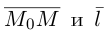
Если точка М перемещается вдоль прямой, параметр t изменяется в пределах от 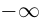
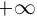
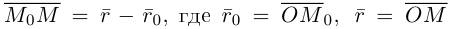
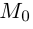
Это уравнение называется векторным уравнением прямой.
Переходя в полученном векторном уравнении к координатам, запишем параметрические уравнения прямой:
Прямую в пространстве можно задать также как пересечение двух плоскостей.
Система
составленная из уравнений этих плоскостей, дает нам общие уравнения прямой в пространстве. Для перехода от общих к каноническим уравнениям прямой, достаточно найти какую-нибудь точку на ней, решив при фиксированном значении одной из координат систему уравнений плоскостей, а также определить направляющий вектор прямой, которым может служить векторное произведение нормальных векторов 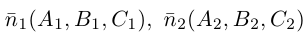
Пример №3
Найти канонические уравнения прямой
Решение. Полагая в данной системе z = 0, получим
Решив эту систему, найдем х = 1, у = —2. Таким образом, мы получили точку 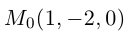
Осталось записать канонические уравнения данной прямой:
Научимся теперь вычислять расстояние от точки до прямой в пространстве. Пусть задана точка 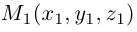
Искомое расстояние 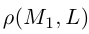
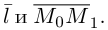
Пусть нам известны канонические уравнения двух прямых в пространстве:
Очевидно,
Один из углов между этими прямыми равен углу между их направляющими векторами 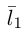
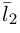
Изучим взаимное расположение прямых 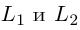
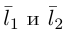
В случае, когда 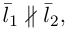
Прямые пересекаются, очевидно, тогда и только тогда, когда векторы 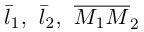
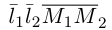
Расстояние 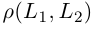
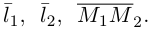
Пример №4
Убедиться в том, что прямые
являются скрещивающимися. Найти расстояние между ними и уравнение общего перпендикуляра к ним.
Решение. Первая прямая проходит через точку 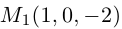
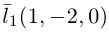
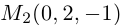
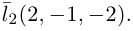
следовательно, прямые 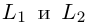
Осталось найти уравнение общего перпендикуляра к данным прямым. Заметим, прежде всего, что его направляющим вектором является уже вычисленный нами вектор 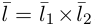
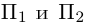
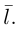
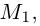
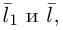
Таким образом, плоскость 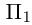
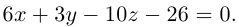
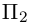
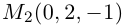
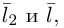
и, стало быть, 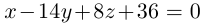
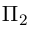
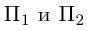
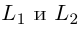
В заключение этого параграфа вычислим угол между прямой L, заданной каноническими уравнениями
и плоскостью П, для которой известно ее общее уравнение
Очевидно, искомый угол 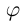
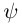
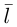
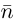
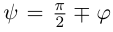
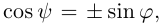
В частности, если
Прямая на плоскости
Для прямой на плоскости наблюдается большее разнообразие ее уравнений, так как на плоскости прямая фиксируется точкой, через которую она проходит и, либо вектором ей перпендикулярным (нормальным вектором), либо вектором ей параллельным (направляющим вектором) и, следовательно, для прямой на плоскости можно записывать как уравнения, характерные для плоскости в пространстве (§1), так и аналоги уравнений прямой в пространстве (§2). Перечислим, не повторяя деталей, изложенных в предыдущих двух параграфах, основные уравнения прямой на плоскости и связанные с ними формулы.
Пусть прямая L на плоскости с выбранной в ней системой координат 
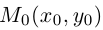
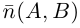
Уравнение такой прямой имеет вид:
откуда после очевидных преобразований получим уравнение
которое представляет собой общее уравнение прямой на плоскости.
Пусть прямая L отсекает на координатных осях 
Тогда, как и для плоскости, мы можем записать уравнение прямой в отрезках:
Если прямая L содержит точку 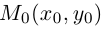
то ее каноническое уравнение имеет вид:
По аналогии с прямой в пространстве, прямая на плоскости может быть задана также векторным уравнением
и параметрическими уравнениями
Расстояние от точки 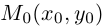
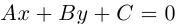
Найдем еще одно уравнение прямой на плоскости, характерное для этого геометрического объекта. Пусть прямая L, заданная своим каноническим уравнением 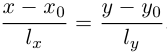
Тогда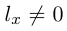
где 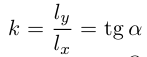
представляет собой уравнение прямой с угловым коэффициентом, которая проходит через точку
Если две прямые на плоскости заданы общими или каноническими уравнениями, то их взаимное расположение исследуется по аналогии с плоскостями или прямыми, заданными такими же уравнениями (§1 или §2). Изучим поэтому взаимное расположение двух прямых, которые заданы уравнениями с угловым коэффициентом. Итак, рассмотрим две прямые
Предположим сначала, что прямые не являются перпендикулярными, обозначим через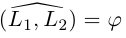
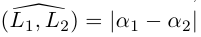
Если же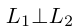
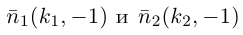
Таким образом, для перпендикулярности прямых 
Очевидно. прямые 
Пример №5
Даны прямая 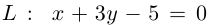
Решение. Прямые
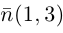
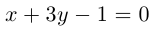
Так как 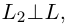
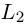
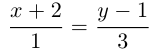
Из уравнения прямой L находим 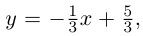
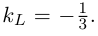
откуда, 
Кривые второго порядка на плоскости
В предыдущих трех параграфах нами были изучены линейные геометрические объекты -плоскость и прямая в пространстве и на плоскости. Мы показали, что в декартовой системе координат они определяются алгебраическими уравнениями первой степени, т. е. линейными уравнениями. Предметом нашего исследования в этом параграфе будут являться кривые второго порядка, т. е. линии на плоскости, уравнения которых в декартовой системе координат Оху имеют вид:
где А, В, С, D, Е, F — действительные числа. Мы убедимся в том, что, за исключением случаев вырождения данное уравнение определяет одну из трех замечательных линий — эллипс, гиперболу или параболу. Приведем сначала геометрическое определение каждой из этих линий и найдем их канонические уравнения.
Эллипс
Определение: Эллипсом называется множество точек на плоскости, для каждой из которых сумма расстояний до двух фиксированных точек (фокусов эллипса) есть величина постоянная.
Найдем каноническое уравнение эллипса. Обозначим через 2с фокусное расстояние, т. е. расстояние между фокусами, а через 2а — постоянную сумму расстояний от точек эллипса до фокусов. Из неравенства треугольника следует, что 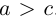
Пусть М(х, у) — произвольная точка эллипса. По определению этой линии,
Упростим последнее уравнение:
откуда, использовав обозначение 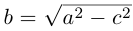
Построим эту линию. Для этого прежде всего заметим, что она симметрична относительно координатных осей и начала координат, так как переменные x и у входят в каноническое уравнение в квадратах. Отсюда следует, что эллипс достаточно построить в первой координатной четверти и затем отразить его относительно координатных осей. Из канонического уравнения эллипса находим:
Очевидно, эта функция определена и убывает при 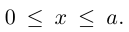
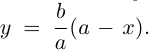
Числа а и b называются соответственно большой и малой полуосями эллипса. Точка O(0,0) -центр эллипса, точки 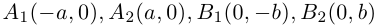
Форму эллипса характеризует величина 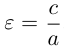
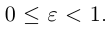
то при 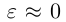
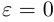
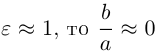
Замечание. В уравнении эллипса может оказаться, что 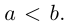
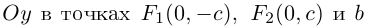
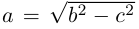
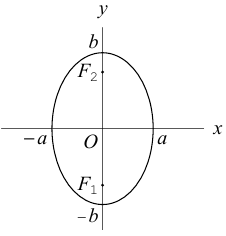
Гипербола
Определение: Гипербола представляет собой линию на плоскости, для каждой точки которой абсолютная величина разности расстояний до двух фиксированных точек (фокусов гиперболы) есть величина постоянная.
Обозначим и здесь фокусное расстояние через 2с. а через 2а — постоянную абсолютную величину разности расстояний от точек гиперболы до фокусов. Для гиперболы а < с, что следует из неравенства треугольника. Выберем декартову систему координат на плоскости точно также, как и при выводе канонического уравнения эллипса.
По определению гиперболы для произвольной точки М(х, у) этой линии
Избавляясь от корней в этом уравнении, получим:
Обозначая здесь 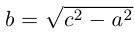
Как видно из ее уравнения, гипербола симметрична относительно координатных осей и начала координат. Из канонического уравнения гиперболы следует, что в первой четверти
Эта функция возрастает, 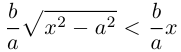
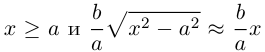
а а а а
Это означает, что в первой четверти гипербола, выходя из точки (а, 0) на оси Ох, приближается
затем при больших значениях х к прямой 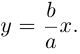
Прямые 
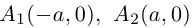
Как и для эллипса, определим эксцентриситет гиперболы как отношение половины фокусного расстояния к действительной полуоси:
Так как
то эксцентриситет гиперболы характеризует величину угла, в котором она располагается. При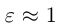
Замечание. В каноническом уравнении гиперболы знаки перед квадратами могут располагаться и в обратном порядке:
В этом случае фокусы и вершины находятся на оси
Парабола
Определение: Параболой называется множество точек плоскости, равноудаленных от. фиксированной точки (фокуса параболы) и фиксированной прямой (директрисы параболы).
Обозначим расстояние от фокуса до директрисы через р. Число р > 0 называется параметром параболы. Выберем удобную систему координат на плоскости: ось Ох направим через фокус F перпендикулярно директрисе D, а начало координат возьмем посередине между директрисой и фокусом.
Если М(х,у) — произвольная точка параболы, то по определению этой кривой
После возведения в квадрат и очевидных преобразований, получим каноническое уравнение параболы:
Очевидно, парабола проходит через начало координат и симметрична относительно оси Ох. Точка O(0,0) называется вершиной параболы, ось Ох — осью параболы.
Замечание. Если бы при выборе системы координат мы направили ее оси в противоположные стороны, то каноническое уравнение параболы приняло бы вид:
Аналогично, уравнения
также определяют параболы, фокусы которых расположены на оси Оу. а директрисы параллельны оси Ох.
Приведение уравнения кривой второго порядка к каноническому виду
Покажем, что общее уравнение кривой второго порядка на плоскости, кроме случаев вырождения, определяет одну из линий — эллипс, гиперболу или параболу.
Выясним сначала, как преобразуются координаты точки на плоскости при параллельном переносе системы координат. Предположим, что осуществлен параллельный перенос системы координат Оху в точку 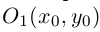
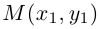
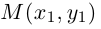
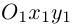
Так как 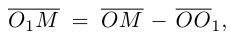
Рассмотрим теперь уравнение второго порядка на плоскости в частном случае, когда оно не содержит произведения координат ху :
причем коэффициенты А и С не равны одновременно нулю. Здесь возможны три случая.
а) АС > 0. Очевидно, всегда можно считать, тгго А > 0, С > 0. Выделяя в уравнении второго порядка полные квадраты по переменным х и у, получим:
где 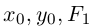
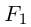
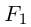
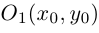
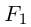
и, следовательно, в смещенной с помощью параллельного переноса в точку 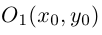
b) АС < 0. Будем считать для определенности, что А > 0. С < 0.
В этом случае исходное уравнение второго порядка также приводится к виду (1). При F = 0 оно определяет пару прямых, проходящих, через точку 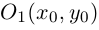
Если же 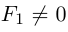
и, стало быть, после параллельного переноса системы координат в точку 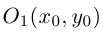
c) АС = 0. Предположим, например, что
Выделяя в данном уравнении второго порядка полный квадрат по переменной у, получим:
С {у ~ Уо)2 + Dx + F1=0.
Если в этом уравнении D = 0, то при 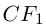
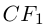
Если же 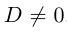
т.е. после параллельного переноса системы координат в точку 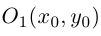
Аналогично. если в исходном уравнении второго порядка 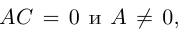
Пример №6
Привести уравнение второго порядка к каноническому виду, назвать и построить кривую:
Решение. Выделяя полные квадраты по обеим переменным, получим:
что представляет собой каноническое уравнение эллипса в смещенной в точку 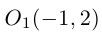
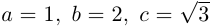
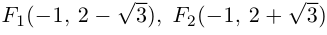
Пример №7
Найти каноническое уравнение параболы с вершиной в точке 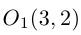
Решение. Фокус параболы находится в точке F(0 , 2), следовательно, уравнение параболы с учетом смещения имеет вид:
Здесь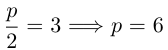
каноническое уравнение параболы.
Замечание. Для приведения к каноническому виду уравнения второго порядка, содержащего произведение координат ху, необходимо кроме параллельного переноса выполнить еще и поворот системы координат на определенный угол. Например, для равносторонней гиперболы ху = 1 следует повернуть систему координат Оху вокруг ее начала на угол 45° против часовой стрелки. Поскольку вершины гиперболы находятся на расстоянии 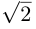
Поверхности второго порядка в пространстве
В заключение этой главы мы изучим поверхности в пространстве, которые в декартовой системе координат задаются алгебраическими уравнениями второй степени. Существуют пять видов таких поверхностей: эллипсоид, гиперболоиды, параболоиды, цилиндры второго порядка и конус второго порядка.
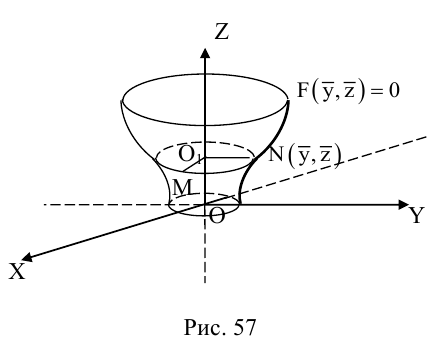
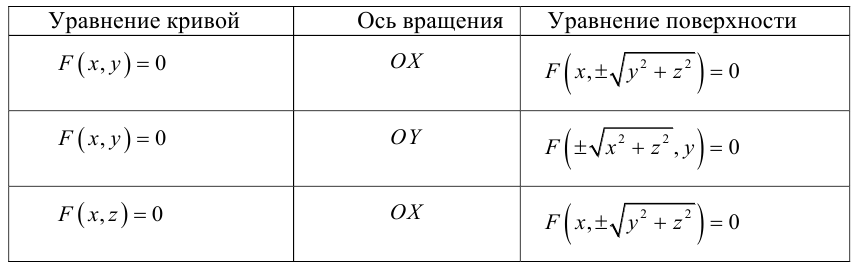
Поверхность вращения
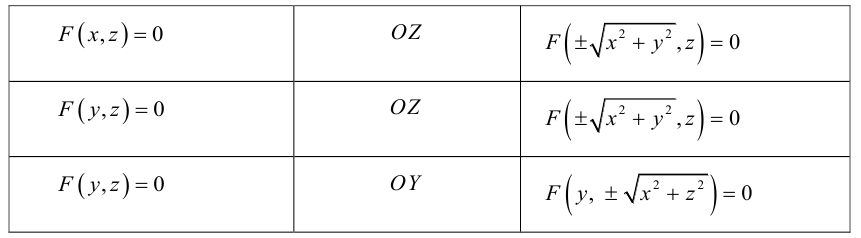
Найдем уравнение поверхности, которая получается вращением некоторой линии вокруг одной из координатных осей. Пусть линия L, которая в координатной плоскости Oyz задается уравнением F(y, z) = 0. вращается вокруг оси Oz.
Пусть M(x,y,z) — произвольная точка на поверхности вращения. Перегоним ее по окружности, расположенной в сечении поверхности плоскостью, проходящей через данную точку перпендикулярно оси Oz, в точку N на линии L. Поскольку расстояние от точки М до оси Oz равно 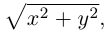
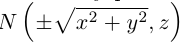
Найдем теперь уравнения поверхностей, которые получаются вращением кривых второго порядка с последующей линейной деформацией этих поверхностей.
Эллипсоид
Возьмем в плоскости Oyz эллипс
и будем вращать его вокруг оси Oz. В результате, как следует из предыдущего пункта, мы получим поверхность с уравнением
которая называется эллипсоидом вращения. Заменив в найденном уравнении координату х на —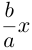
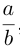
Положительные числа а, b, с называются полуосями эллипсоида.
Очевидно, сечениями эллипсоида плоскостями параллельными координатным, являются эллипсы.
Замечание. В частном случае, когда а = b = с = R эллипсоид превращается в сферу
радиуса R с центром в начале координат.
Гиперболоиды
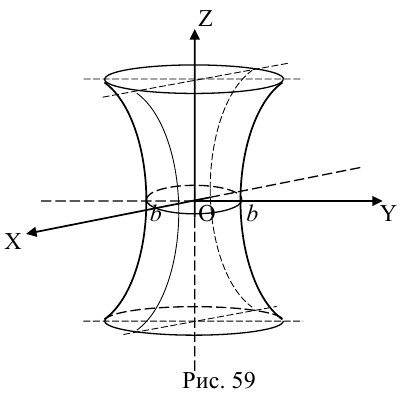
а) Однополостный гиперболоид.
Вращая гиперболу
вокруг оси Oz, получим однополостный гиперболоид вращения с уравнением
После линейной деформации вдоль оси Ох эта поверхность превращается в однополостный гиперболоид общего вида с осью Oz :
Аналогично, уравнения однополостных гиперболоидов с осями Ох и Оу имеют, соответственно, вид:
Сечениями однополостного гиперболоида плоскостями, перпендикулярными его оси, являются эллипсы, а в сечениях плоскостями, перпендикулярными другим координатным осям, располагаются гиперболы.
Двухполостный гиперболоид
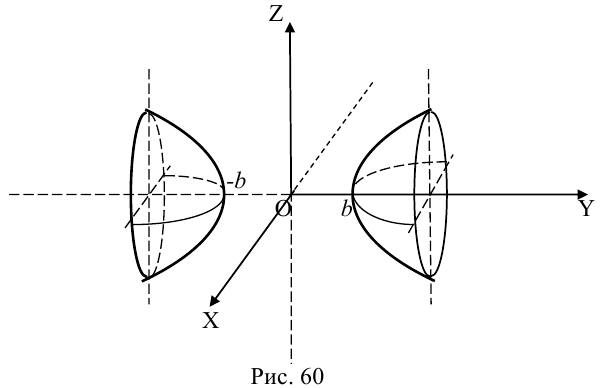
Поверхность, полученная вращением вокруг оси Оz гиперболы
вершины которой расположены на оси вращения, называется двухполостным гиперболоидом вращения. Запишем уравнение двухполостного гиперболоида:
Линейная деформация двухполостного гиперболоида вращения вдоль оси Ох прообразует его в двухполостный гиперболоид общего вида с осью Oz. Уравнение этой поверхности имеет вид:
Двухполостные гиперболоиды с осями Ох и Оу имеют, соответственно, уравнения:
Как и в случае однополостного гиперболоида, сечениями двухполостного гиперболоида плоскостями, параллельными координатным, являются эллипсы и гиперболы.
Параболоиды
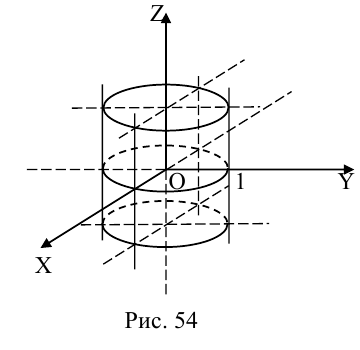
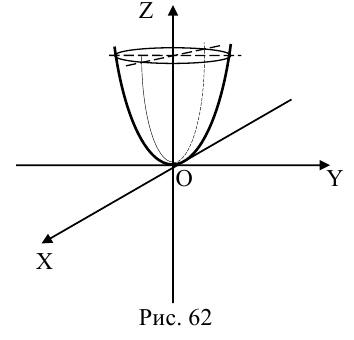
а) Эллиптический параболоид
Вращение параболы вокруг ее оси приводит к поверхности, которая называется параболоидом вращения. В частности, если параболу с каноническим уравнением 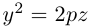
Линейная деформация параболоида вращения вдоль оси Оу превращает его в эллиптический параболоид с уравнением:
Положительные числа p, q называются параметрами параболоида, точка O(0,0) — вершина, ось Oz — ось эллиптического параболоида.
Уравнения эллиптических параболоидов с осями Ох и Оу имеют, соответственно, вид:
Как следует из уравнения эллиптического параболоида, плоскости, перпендикулярные его оси, пересекают эту поверхность по эллипсам, а в сечениях плоскостями, параллельными другим координатным, находятся параболы.
Замечание. Изменение знака в правой части уравнения эллиптического параболоида приводит к отражению этой поверхности относительно координатной плоскости, перпендикулярной оси параболоида.
b) Гиперболический параболоид.
Будем поступательно перемещать образующую параболу
расположенную в плоскости Oyz, параллельно самой себе вдоль направляющей параболы
находящейся в плоскости Oxz. Полученная таким образом поверхность называется гиперболическим параболоидом или седловидной поверхностью.
Найдем уравнение этой поверхности. Пусть М(х. у, z) — произвольная точка гиперболического параболоида. По его построению точка М принадлежит параболе с вершиной в точке 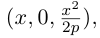
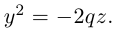
то, подставив в него координаты точки М, мы и получим после несложных преобразований уравнение гиперболического параболоида:
Здесь, как и для эллиптического параболоида, числа р, q — параметры гиперболического параболоида, точка O(0,0) и ось Oz — соответственно вершина и ось гиперболического параболоида.
Замечание 1. Седловидная поверхность может быть также получена перемещением параболы 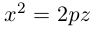
Судя по уравнению гиперболического параболоида, в сечениях этой поверхности плоскостями z = h > 0 находятся гиперболы, действительные оси которых параллельны координатной оси Ох. Аналогично, плоскости z = h < 0 пересекают данную поверхность по гиперболам с действительными осями, параллельными оси Оу. Наконец, плоскость Оху пересекает гиперболический параболоид по двум прямым
Гиперболические параболоиды, осями которых служат координатные оси Ох и Оу, имеют, соответственно, уравнения:
Замечание 2. Отразив седловидную поверхность относительно координатной плоскости, перпендикулярной ее оси, получим гиперболический параболоид, уравнение которого отличается знаком правой части от уравнения исходной поверхности.
Цилиндры второго порядка
Цилиндром второго порядка называется поверхность, полученная перемещением некоторой прямой (образующей) вдоль кривой второго порядка (направляющей), расположенной в плоскости, не содержащей образующую, параллельно фиксированному ненулевому вектору в пространстве.
Ограничимся случаем, когда направляющая расположена в одной из координатных плоскостей, а образующая перпендикулярна этой плоскости. Возьмем для определенности в плоскости Оху кривую второго порядка и будем перемещать прямую, параллельную оси Oz, вдоль этой кривой. Так как проекцией любой точки M(x,y,z) полученного таким образом цилиндра на плоскость Оху является точка N(x,y), принадлежащая кривой второго порядка, то координаты точки М удовлетворяют уравнению этой кривой. Следовательно, уравнением построенного цилиндра является уравнение его направляющей.
Перечислим теперь цилиндры второго порядка.
1) 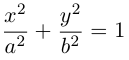
В частности, при а = b мы получим круговой цилиндр.
2 2 X у
2) 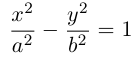
3) 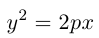
Аналогичные уравнения имеют цилиндры второго порядка, образующие которых параллельны осям Ох и Оу, а направляющие расположены в координатных плоскостях Oyz и Oxz, соответственно.
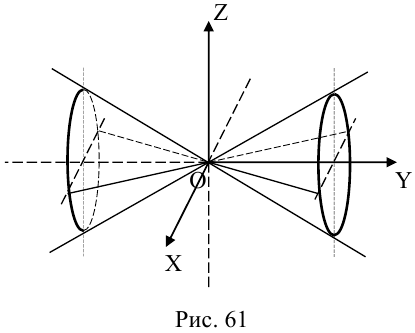
Конус второго порядка
Конус второго порядка представляет собой поверхность, которая может быть получена перемещением прямой (образующей), имеющей неподвижную точку, которая называется вершиной конуса, вдоль кривой второго порядка (направляющей), расположенной в плоскости, не содержащей вершину.
Найдем уравнение конуса, вершина которого совпадает с началом координат, а направляющей служит эллипс с уравнением
расположенный в плоскости z = с, с > 0.
Пусть M(x,y,z) — произвольная точка конуса. Обозначим через 
а точки M — уравнениям
Из последних уравнений мы находим:
Подставив найденные выражения для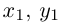
Координатная ось Oz называется осью конуса. Если а = b, то конус является круговым.
Конусы второго порядка с осями Ох и Оу имеют, соответственно, уравнения:
Покажем, что вид конуса второго порядка не зависит от выбора направляющей. Действительно, если в качестве направляющей взять гиперболу
находящегося в плоскости 2 = с, то после рассуждений, аналогичных предыдущим, получим поверхность с уравнением
т. е. конус с осью Ох. Если же за направляющую мы выберем в плоскости z = с параболу с уравнением
то построенный таким образом конус имеет уравнение
Наблюдая со стороны положительной полуоси Оу, повернем систему координат Oxz вокруг оси Оу на угол 45° против часовой стрелки. Тогда произведение xz в системе координат
запишется как 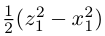
и, стало быть, эта поверхность является конусом с осью
Как следует из уравнения конуса и его построения, плоскости, перпендикулярные его оси, пересекают эту поверхность по эллипсам, сечениями конуса плоскостями, параллельными его оси, являются гиперболы, и, наконец, в сечениях конуса плоскостями, параллельными образующей, располагаются параболы.
Приведение уравнения поверхности второго порядка к каноническому виду
По аналогии с уравнением кривой второго порядка (§4, пункт 4), уравнение поверхности второго порядка, не содержащее произведений координат, мы можем за счет выделения полных квадратов привести к уравнению одной из рассмотренных в пунктах 1—5 поверхностей. Следовательно, мы получим одну из поверхностей второго порядка в смещенной с помощью параллельного переноса системе координат. Исключение, правда, составляет случай, когда уравнение поверхности содержит полный квадрат и два линейных слагаемых относительно других координат. Такая поверхность представляет собой параболический цилиндр в смещенной с помощью параллельного переноса и повернутой затем вокруг одной из координатных осей системе координат.
Пример №8
Привести уравнение второго порядка
к каноническому виду, назвать и построить поверхность.
Решение. После выделения полных квадратов по переменным у, z получим:
Переписав это уравнение в виде
мы замечаем, что в смещенной с помощью параллельного переноса в точку 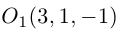
Прямая на плоскости. Общее уравнение прямой на плоскости
Докажем, что всякая прямая на плоскости задается в любой пдск уравнением первой степени относительно двух переменных.
Если A – некоторая точка на прямой 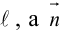
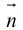
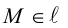
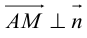
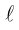
Чтобы вывести уравнение прямой, зададим на плоскости пдск XOY .
В этой системе координат
Пусть M (x, y) – произвольная точка
на 
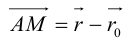
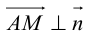
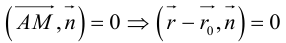

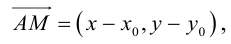
Координаты точек, лежащих на прямой
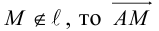
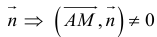
Определение: Любой ненулевой вектор 

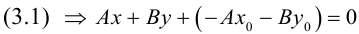
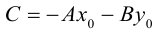
(3.2) – общее уравнение прямой на плоскости,
Уравнение прямой с направляющим вектором
Определение: Любой ненулевой вектор 
Если A – некоторая точка на прямой 
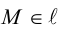
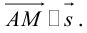

Чтобы вывести уравнение прямой, зададим на плоскости пдск XOY . В этой системе координат
Пусть M (x, y) – произвольная точка на . Тогда 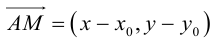
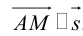
(3.3) – уравнение прямой на плоскости с направляющим вектором.
Если 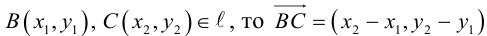
Уравнение прямой с угловым коэффициентом
Пусть 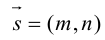
Определение: Угловым коэффициентом прямой 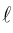
Очевидно, что если 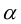
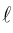
Рассмотрим уравнение (3.3) прямой с направляющим вектором
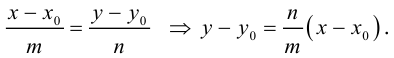
Отсюда следует (3.5) – уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку
Из (3.5) получим 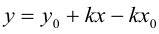
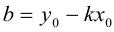
(3.6) – уравнение прямой с угловым коэффициентом.
Угол между прямыми на плоскости
Определение: Углом между двумя прямыми на плоскости называется любой из двух смежных углов, образованных ими при пересечении. Если прямые параллельны, то угол между ними равен 0 или
Пусть прямые заданы общими уравнениями.
Условие параллельности прямых:
Условие перпендикулярности прямых:
Рассмотрим случай, когда прямые заданы уравнениями с угловым коэффициентом.
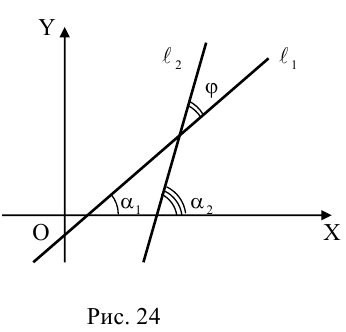
Так как 
Условие параллельности прямых:
Условие перпендикулярности:
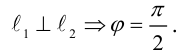
не существует, то
Пример №9
Даны вершины треугольника:
Написать:
а) уравнение медианы AM , б) высоты AH , в) найти угол между AM и AH
(рис. 25).

Перепишем уравнение медианы в общем виде:
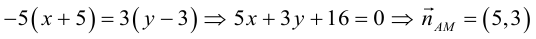
б)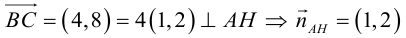
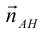
в)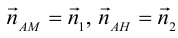
Расстояние от точки до прямой на плоскости
Пусть в некоторой пдск XOY задана прямая 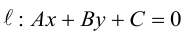
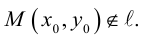
Пусть 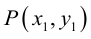
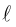
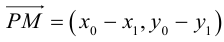
Нормаль
где d – искомое расстояние, 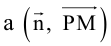
Следовательно,
Так как 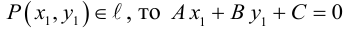
Отсюда
(3.8) – формула для вычисления расстояния от точки до прямой на плоскости.
Пример №10
Найти длину высоты
Уравнение 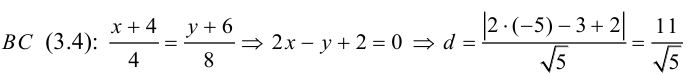
искомая длина высоты АН.
Кривые второго порядка
Окружность
Определение: Кривые второго порядка – плоские линии, которые в пдск XOY задаются уравнениями второй степени относительно двух переменных x,y.
Определение: Окружностью называется совокупность точек плоскости, равноудаленных от фиксированной точки, называемой ее центром.
Выведем уравнение окружности. Зададим пдск XOY . Пусть 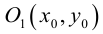
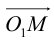
Если точка M (x, y) не лежит на окружности, то 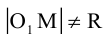
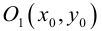
Если 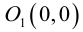
(3.10) – каноническое уравнение окружности.
Пример №11
Показать, что уравнение 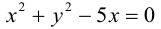
Приведем данное уравнение к виду (3.9), выделив полный квадрат по переменной x :
Пример №12
Написать уравнение линии центров окружностей
Найдем центр второй окружности:
Уравнение прямой (3.4), проходящей через две точки:
Эллипс
Определение: Эллипс – совокупность точек плоскости, сумма расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
Чтобы вывести уравнение эллипса, выберем пдск следующим образом: ось абсцисс проведем через фокусы 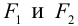
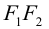
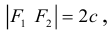
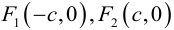
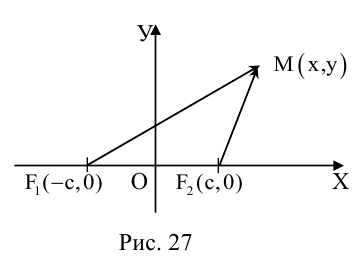
2a>2c определению эллипса.
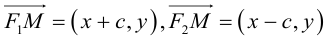
Запишем в виде уравнения свойство точек, принадлежащих эллипсу, сформулированное в определении:
(3.11) – уравнение эллипса в выбранной системе координат. Преобразуем его к
более простому (каноническому) виду. Для этого умножим (3.11) на сопряженное выражение:
Сложим (3.11) и (3.12) и результат возведем в квадрат:
Так как по определению a>c, то есть 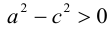
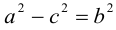
Тогда из (3.13) получим:
(3.14) – каноническое уравнение эллипса.
Исследуем форму эллипса по его каноническому уравнению. Найдем точки пересечения с осями координат:
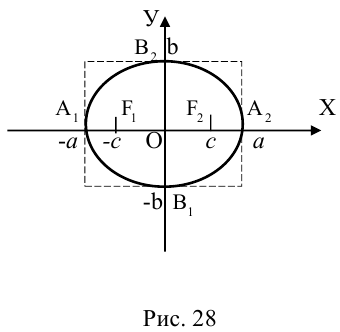
Из (3.14) следует, что
Значит, эллипс расположен в прямоугольнике со сторонами 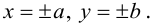
Кроме того, из уравнения следует, что он симметричен относительно OX и OY . O(0,0) – точка пересечения осей симметрии – центр симметрии эллипса.
Ось, на которой лежат фокусы, называется фокальной осью эллипса. Точки пересечения эллипса с осями симметрии называются его вершинами.
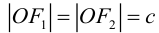
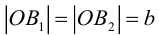
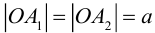
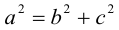
Отношение полуфокусного расстояния к длине большой полуоси 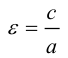
Так как 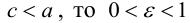
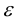
ЗАМЕЧАНИЕ 1. Уравнение эллипса, центр которого 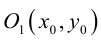
ЗАМЕЧАНИЕ 2. К кривым второго порядка эллиптического типа относятся также мнимый эллипс
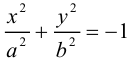
Пример №13
Найти эксцентриситет эллипса 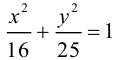
Так как 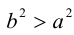
Гипербола
Определение: Гипербола – совокупность точек плоскости, модуль разности расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
Чтобы вывести уравнение гиперболы, выберем пдск следующим образом:
ось абсцисс проведем через фокусы 
ка 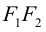
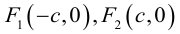
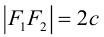
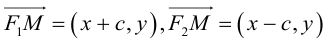
Запишем свойство точек, принадлежащих гиперболе, сформулированное в определении:
(3.16) – уравнение гиперболы в выбранной системе координат ( «+» – если разность расстояний положительна, и «–» – если отрицательна). Чтобы привести это уравнение к более простому виду, умножим (3.16) на сопряженное выражение и выполним такие же действия, как при упрощении уравнения эллипса, после чего получим:
По определению 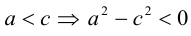
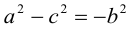
(3.18) – каноническое уравнение гиперболы.
Исследуем форму гиперболы по ее каноническому уравнению.
Из (3.18) следует, что гипербола симметрична относительно осей координат. Если x=0, 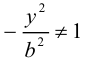
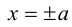
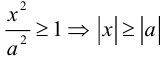
c – полуфокусное расстояние, a – действительная полуось, b – мнимая полуось. Отношение полуфокусного расстояния к длине действительной полуоси называется эксцентриситетом гиперболы: 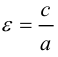
Считая, что 
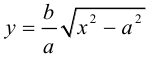
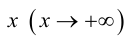
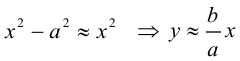
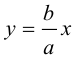
причем ординаты точек на ней меньше соответствующих ординат точек на этой
прямой: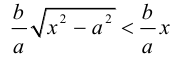
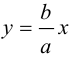
Из симметрии гиперболы следует, что то же самое происходит во второй, третьей и четвертой четвертях. Поэтому 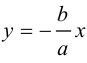
Итак, прямые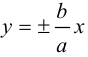
Если фокусы гиперболы лежат на OY , то ее уравнение имеет вид:
Гиперболы (3.18) и (3.19) называются сопряженными (рис. 31). Уравнения асимптот (3.19) такие же, как и для (3.18), но действительной является ось OY .
Если a = b, то гипербола называется равносторонней: 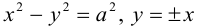
Очевидно, в этом случае асимптоты перпендикулярны. После поворота осей координат на 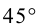
ЗАМЕЧАНИЕ 1. Если центр гиперболы в точке 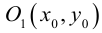
ЗАМЕЧАНИЕ 2. К кривым второго порядка гиперболического типа относится также пара пересекающихся прямых:
Пример №14
Найти координаты центра и написать уравнения асимптот гиперболы
Приведем данное уравнение к виду (3.20):
Таким образом, 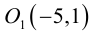
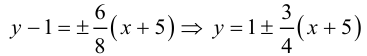
Парабола
Определение: Парабола – совокупность точек плоскости, равноудаленных от фиксированной точки этой плоскости, называемой фокусом, и фиксированной прямой, не проходящей через эту точку, называемой директрисой. Чтобы вывести уравнение параболы, выберем пдск следующим образом: ось абсцисс проведем через фокус перпендикулярно директрисе, а ось ординат посередине между фокусом и директрисой (рис. 33).
Пусть расстояние между фокусом F и директрисой DK равно p . Тогда 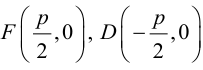
(3.21) – уравнение параболы в выбранной системе координат.
Упростим его:
(3.22) – каноническое уравнение параболы; p называется ее параметром.
Из уравнения следует, что парабола симметрична относительно OX и проходит через начало координат. Кроме того, если 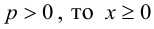
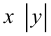
Если фокус параболы на оси ОУ (рис. 35), то ее каноническое уравнение имеет вид
ЗАМЕЧАНИЕ 1. Если вершина параболы в точке 
ЗАМЕЧАНИЕ 2. К кривым второго порядка параболического типа относятся также 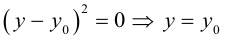
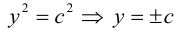
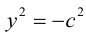
Пример №15
Написать уравнение геометрического места точек, равноудаленных от прямой x + y — 1 = 0 и точки F(-3,2).
По определению множество точек, равноудаленных от данных точки и прямой, является параболой. Пусть M (x, y) – произвольная точка искомой параболы, тогда 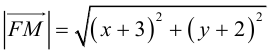
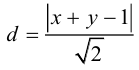
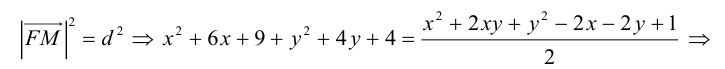
Если оси координат системы XOY повернуть на угол 
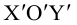
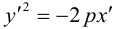
ЗАМЕЧАНИЕ. Можно показать, что, кроме окружности, эллипса, гиперболы, параболы и вырожденных случаев, указанных в замечаниях, других кривых второго порядка не существует.
Преобразования координат на плоскости
Преобразование координат — замена системы координат на плоскости, в пространстве или, в самом общем случае, на заданном n-мерном многообразии.
Параллельный перенос координатных осей
Пусть на плоскости задана пдск ХОУ. Будем называть ее “старой”. “Новая” система координат 
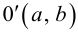
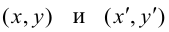
Пусть 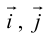
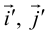
Тогда
так как 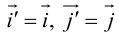
Так как 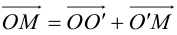
или
(3.23) – формулы параллельного переноса осей пдск.
Поворот координатных осей на угол α
Поворот координатных осей на угол 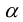
Пусть “новая” пдск 
Из рис. 38 очевидно, что
Так как 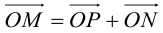
(3.24) – формулы поворота координатных осей на угол , выражающие старые координаты точки через новые.
Если обозначить 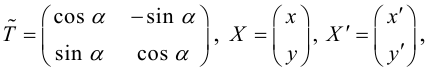
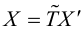
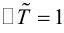
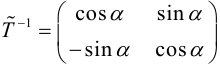
(3.25) – формулы поворота координатных осей на угол 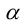
Пример №16
Каким будет уравнение прямой x + y — 1 = 0 после поворота координатных осей на угол
новое уравнение прямой (рис. 39).
Линейные преобразования на плоскости
Рассмотрим систему линейных уравнений:
Каждой точке плоскости M(x, y) по формулам (3.26) можно поставить в соответствие единственную точку 
Преобразование (3.26) определяется матрицей 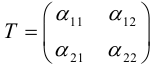
(3.26) можно переписать в виде 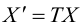
Пример №17
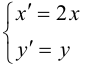
оси OX в 2 раза.
Пример №18
при этом направление обхода 
Определение: Линейное преобразование (3.26) называется невырожденным, если
В этом случае существует обратная матрица 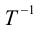
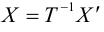
Можно показать, что невырожденное линейное преобразование переводит прямую в прямую, а кривую второго порядка – в кривую второго порядка.
Пример №19
Пусть 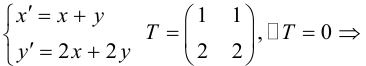
Какими будут образы точек, лежащих, например, на прямой x + y — 1 = 0
(рис. 42)?
Очевидно, что если 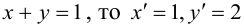
Пример №20
Рассмотрим формулы (3.25):
Очевидно, что поворот осей пдск на угол 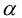
Так как это линейное преобразование невырожденное, то существует
Заметим, что в этом случае
Определение: Матрица A называется ортогональной, если 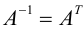
Линейное преобразование, матрица которого ортогональна, называется ортогональным.
Таким образом, поворот координатных осей – ортогональное линейное преобразование.
Можно показать, что если A – ортогональная матрица, то 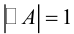
Произведение линейных преобразований
Рассмотрим матрицы 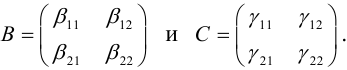
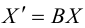
В свою очередь точка N под действием линейного преобразования 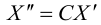
Такое последовательное выполнение линейных преобразований называется их произведением:
Покажем, что произведение линейных преобразований также линейное преобразование, и найдем его матрицу. Подставим (3.27) в (3.28):
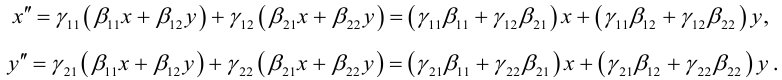
То есть
(3.29) – система линейных уравнений, а потому произведение линейных преобразований линейно. Матрица (3.29) имеет вид:
Таким образом, матрица произведения линейных преобразований равна произведению их матриц. Само же правило умножения матриц, сформулированное в гл.1, находит объяснение в этом выводе.
Приведение квадратичной формы к каноническому виду
Определение: Квадратичной формой относительно двух переменных x и y называется однородный многочлен второй степени:
Уравнение 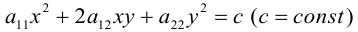
начала координат, то есть является центральной кривой (эллиптического или гиперболического типа).
Предположим, что уравнение 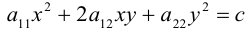
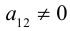
угол 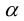
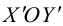
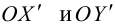
Матрица 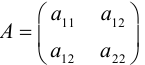
Пусть
Вычислим
Таким образом, квадратичная форма может быть записана в матричном виде:
Пусть x, y – координаты точек плоскости в системе XOY , а 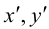
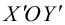
(3.32) – ортогональное линейное преобразование с матрицей
По определению ортогональной матрицы
(В результате ортогонального преобразования не происходит изменение площадей фигур, то есть фигуры не деформируются.)
Чтобы узнать, как изменится матрица квадратичной формы в результате линейного преобразования (3.32), подставим (3.32) в (3.31): 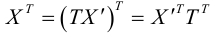
(свойство 2 умножения матриц и равенство (3.33)) – матрица новой квадратичной формы.
Так как в “новой” системе координат кривая должна задаваться каноническим уравнением, то есть в нем должно отсутствовать произведение координат xy, то 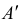
, где 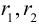
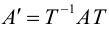
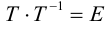
По определению равных матриц имеем:
Системы уравнений (3.34), (3.35) – линейные и однородные. Они имеют нетривиальное решение, если их определители равны 0.
Это означает, что 
Уравнение (3.36) называется характеристическим уравнением матрицы A (характеристическим уравнением квадратичной формы). Его решения 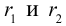
Покажем, что дискриминант квадратного уравнения (3.36) положителен, то есть любая квадратичная форма двух переменных имеет 2 различных собственных значения.
Вычислим определитель (3.36):
Дискриминант
так как 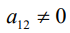
Таким образом, коэффициентами при 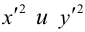
Решим (3.36) и подставим 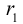
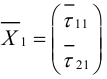
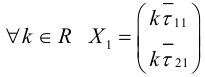
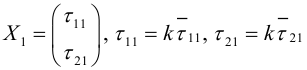
Векторы 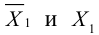
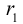
Аналогично подставим 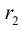
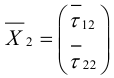
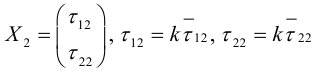
Можно показать, что 
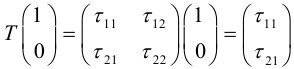
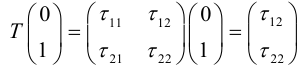
вектор, поэтому ортами “новой” системы координат 
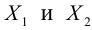
ВЫВОД.
Чтобы привести квадратичную форму к каноническому виду, надо:
- Составить и решить характеристическое уравнение (3.36); его решения – собственные значения – являются коэффициентами при
в каноническом виде квадратичной формы.
- Найти единичные собственные векторы, решив (3.34) и (3.35); они будут ортами новой системы координат
.При этом если ось
сонаправлена с
– канонический вид, который квадратичная форма имеет в системе
.
Приведение общего уравнения кривой второго порядка к каноническому виду
Общее уравнение кривой второго порядка имеет вид:
В результате невырожденного линейного преобразования с матрицей T квадратичная форма перейдет в квадратичную форму, линейная – в линейную, а свободный член 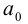
После поворота осей подберем параллельный перенос новой системы 
Пример №21
Привести к каноническому виду ранее полученное уравнение параболы (стр. 58) и построить ее:
1) Составим матрицу квадратичной формы:
2) Составим и решим характеристическое уравнение (3.36):
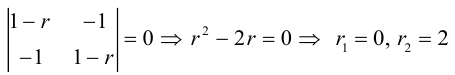
3) Найдем первый единичный собственный вектор, то есть решим систему (3.34):
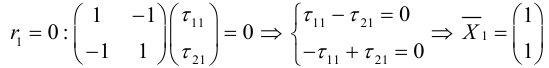
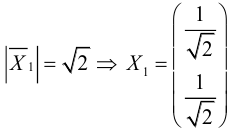
4) Найдем второй единичный собственный вектор, то есть решим (3.35):
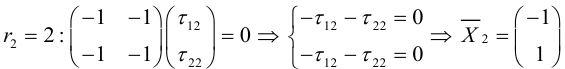
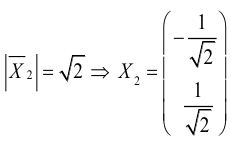
Заметим, что 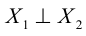
В полученной таким образом системе координат 
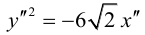
Сравните эскиз (рис. 36) и данный рисунок, являющийся результатом точных расчетов.
Плоскость
Покажем, что плоскость в пространстве задается в любой пдск линейным уравнением относительно трех переменных x, y, z.
Если A – некоторая точка на плоскости 
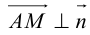
Чтобы вывести уравнение плоскости, зададим в пространстве пдск OXYZ . В этой системе координат
Пусть M(x,y,z) – произвольная точка на плоскости 
Тогда 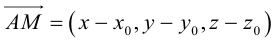
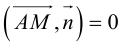
Вычислив скалярное произведение, получим:
Координаты точек, лежащих в плоскости 
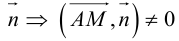
Раскрыв скобки в (3.38), получим 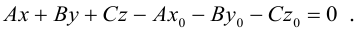
Обозначим 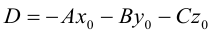
(3.39) – общее уравнение плоскости в пространстве,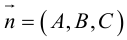
Определение: Любой ненулевой вектор 
Особые случаи расположения плоскости
Выясним, какие особенности в расположении плоскости влечет за собой равенство нулю одного или нескольких коэффициентов в уравнении (3.39).
координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат.
, так как
, значит, плоскость
.
, так как
.Значит, плоскость
.
так как
. Значит, плоскость
.
проходит через OX .
проходит через OY .
проходит через OZ .
-
или
.
или
.
-
или
.
– плоскость YOZ .
– плоскость XOZ .
– плоскость XOY .
Уравнение плоскости в отрезках
Пусть плоскость 
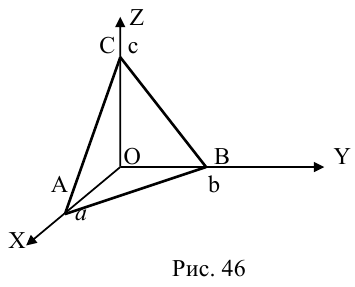
Рассмотрим 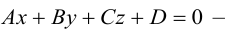
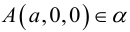
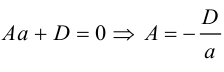
Аналогично 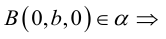
Подставив А, В, С в общее уравнение, получим
(3.40) – уравнение плоскости в отрезках.
Пример №22
Вычислить объем тетраэдра, образованного плоскостями
Перепишем уравнение плоскости в виде (3.40):
уравнение данной плоскости в отрезках. Поэтому (рис. 47)
Уравнение плоскости, проходящей через три точки
Пусть в некоторой пдск заданы три точки, не лежащие на одной прямой:
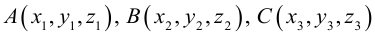
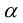
Чтобы вывести ее уравнение, рассмотрим произвольную точку этой плоскости M(x,y,z) . Тогда 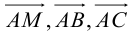
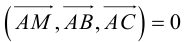
(3.41) – уравнение плоскости, проходящей через три точки.
ЗАМЕЧАНИЕ. Если точки лежат на одной прямой, то векторы 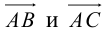
Пример №23
Написать уравнение плоскости, проходящей через точки
Угол между плоскостями
Определение: Углом между плоскостями называется любой из двух смежных двугранных углов, образованных плоскостями при их пересечении.
Если плоскости параллельны, то угол между ними равен 0 или 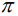
Рассмотрим плоскости 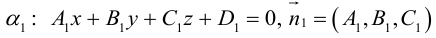
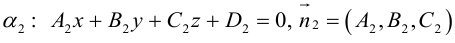
Очевидно,
или
Если 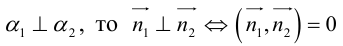
Если 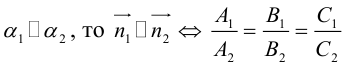
Пример №24
Найти угол между плоскостями
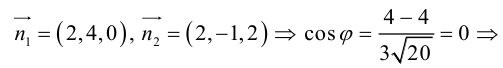
Прямая линия в пространстве
Всякая линия в пространстве есть результат пересечения двух поверхностей. В частности прямую линию можно рассматривать как результат пересечения двух плоскостей
и
Если 
определяет прямую линию в пространстве.
Уравнения (3.42) называются общими уравнениями прямой в пространстве.
Очевидно, одна и та же прямая может быть результатом пересечения разных пар плоскостей (рис. 48), поэтому прямую в пространстве можно задать различными способами.
Уравнения (3.42) неудобны в использовании, так как не дают представления о расположении прямой относительно выбранной системы координат.
Поэтому выведем более удобные уравнения, эквивалентные (3.42), то есть из бесконечного множества плоскостей, проходящих через данную прямую, выберем в некотором смысле более заметную пару.
Канонические уравнения прямой в пространстве
Пусть в некоторой пдск задана прямая 
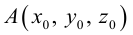
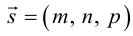
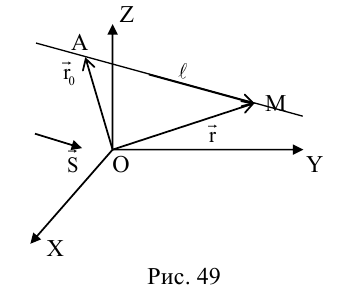
Для произвольной точки 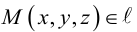
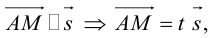
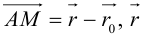
(рис. 49).
Отсюда 
(3.43) – векторное уравнение прямой в пространстве. Из (3.43) получаем:
(3.44) – параметрические уравнения прямой в пространстве, 
Выразим из каждого уравнения (3.44) параметр:
Тогда
(3.45) – канонические уравнения прямой в пространстве, то есть уравнения прямой, проходящей через точку 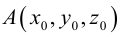
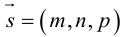
Заметим, что уравнения (3.45) задают прямую как результат пересечения плоскостей
одна из которых параллельна OZ , а вторая – OY или как
где первая плоскость параллельна OZ , а вторая – OX .
Если прямая 
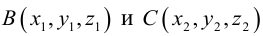
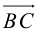
(3.46) – уравнения пространственной прямой, проходящей через две заданные точки.
Угол между прямыми в пространстве
Рассмотрим прямые, заданные в некоторой пдск каноническими уравнениями:
и
Определение: Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.
Из определения следует, что 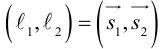
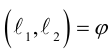
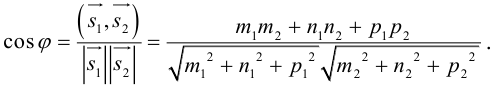
1)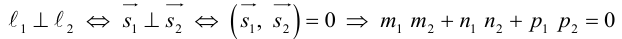
2)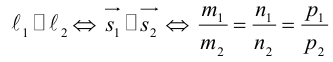
Пример №25
Найти угол между прямой 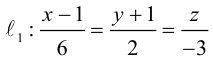
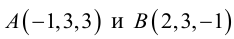
Заметим, что уравнение прямой 
Приведение общих уравнений прямой в пространстве к каноническому виду
Рассмотрим прямую 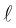
Привести эти уравнения к каноническому виду можно двумя способами:
- найти координаты какой-либо точки
, лежащей на
, ее направляющий вектор s и написать уравнения (3.45);
- найти координаты двух точек, лежащих на
, и воспользоваться уравнениями (3.46).
1 способ.
Координаты точки A – любое частное решение системы линейных уравнений (3.42). Эта система имеет бесконечное множество решений, так как ранги основной и расширенной матриц 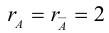
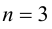
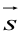
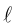
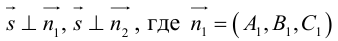
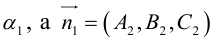
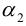
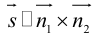
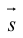
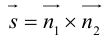
Пример №26
Привести уравнения прямой 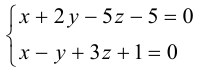
Найдем какое-нибудь частное решение этой системы: пусть, например,
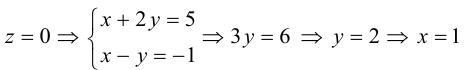
Таким образом, 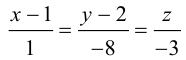
2 способ.
Найдем два произвольных частных решения системы уравнений, задающей прямую.
В рассмотренном примере 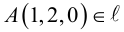
тогда 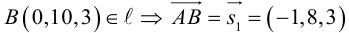
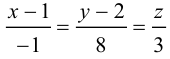
Угол между прямой и плоскостью
Определение: Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.
Пусть в некоторой пдск заданы плоскость
и прямая
Определение общих точек прямой и плоскости
Чтобы найти общие точки прямой : 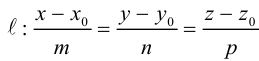
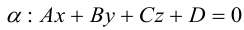
Решение этой системы будет наименее трудоемким, если перейти к параметрическим уравнениям прямой (3.44):
1) Пусть 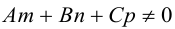
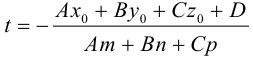
и по формулам (3.44) M(x,y,z) – их точку пересечения.
2) Пусть 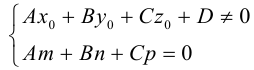
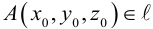
3) Пусть 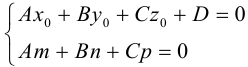
Пример №27
Найти проекцию точки 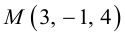
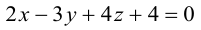
Пусть прямая 
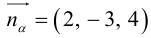
Напишем канонические уравнения прямой (3.45):
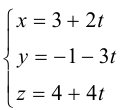
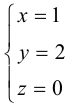
Цилиндрические поверхности
Уравнение F(x, y, z)=0 задает в пространстве некоторую поверхность.
Пусть уравнение содержит только две переменные, например, F(x,y)=0.Рассмотренное в плоскости XOY , оно задает некоторую кривую. Но ему будут удовлетворять и все точки пространства, которые проецируются в точки этой кривой, так как в уравнении отсутствует z , то есть все точки M(x,y,z) у которых х и у связаны соотношением 
Пример №28
Построить поверхность 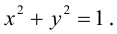
На плоскости это уравнение задает окружность с центром О(0, 0) и R=1.
В пространстве ему удовлетворяют координаты всех точек, проекция которых на плоскость ХОУ лежит на этой окружности. Очевидно, что эта поверхность – круговой цилиндр
(рис. 54).
Цилиндрические поверхности бывают не только круговыми.
Определение: Цилиндрической называется поверхность, полученная движением прямой, параллельной некоторому вектору, и пересекающей при движении некоторую кривую. При этом движущаяся прямая называется образующей, а кривая, которую она пересекает, называется направляющей цилиндрической поверхности.
Для поверхности 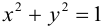
ВЫВОД. Если уравнение поверхности содержит только две переменные, то оно задает цилиндрическую поверхность. У поверхности F(y,z) ,образующая параллельна OX , а направляющая лежит в плоскости YOZ . Для поверхности F(x,z) ,образующая параллельна OY , направляющая в плоскости XOZ .
Пример №29
Построить и назвать поверхности 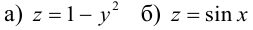
Поверхности вращения
Определение: Поверхностью вращения называется поверхность, полученная в результате вращения плоской кривой вокруг оси, лежащей в ее
плоскости.
Из определения следует, что сечением такой поверхности любой плоскостью, перпендикулярной оси вращения, является окружность.
Пусть в плоскости YOZ задана кривая 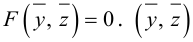
Пусть M(x,y,z) – произвольная точка на поверхности, 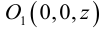
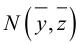
Тогда 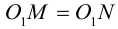
Но
Таким образом, уравнение поверхности вращения получим, если в уравнении кривой 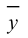
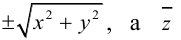
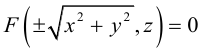
Очевидно, что если кривая F(y,z)=0 вращается вокруг OY , то уравнение
поверхности вращения имеет вид:
Некоторые поверхности второго порядка
1. Пусть эллипс 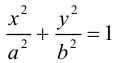
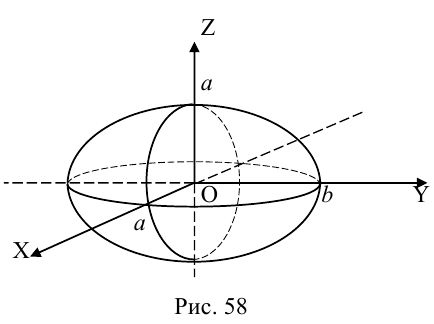
Полученная поверхность является поверхностью второго порядка, так ее уравнение 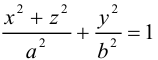
Поверхность, задаваемая уравнением 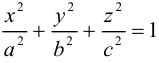
2. Если гипербола 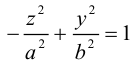
поверхности вращения имеет вид
или
Такая поверхность называется однополостным гиперболоидом вращения (рис. 59).
3. Если гипербола 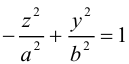
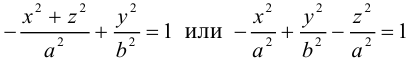
4. Если пара пересекающихся прямых 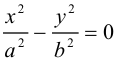
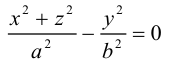
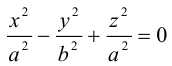
5. При вращении параболы 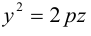
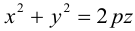
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Векторная алгебра
- Геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика


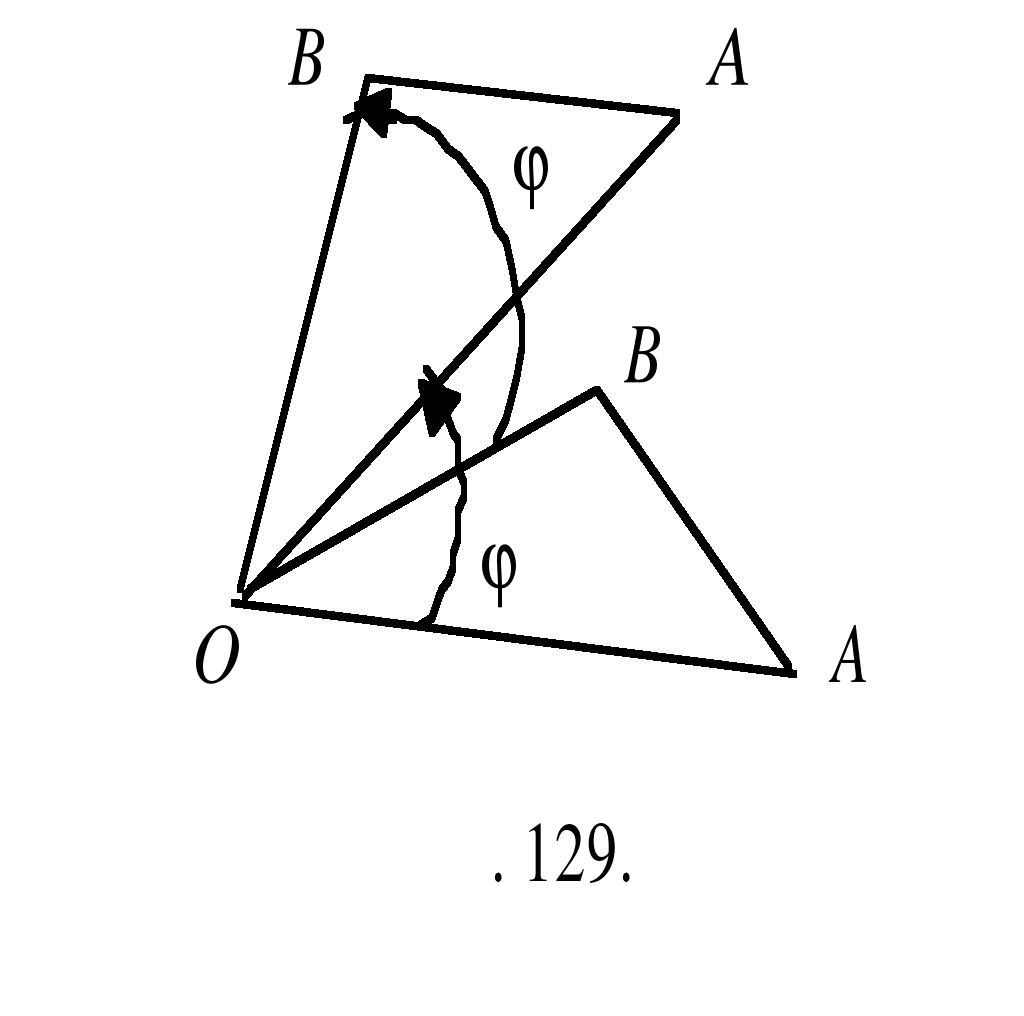







































































































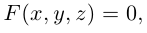
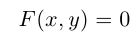
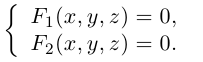

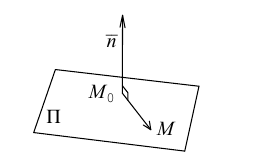
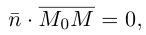
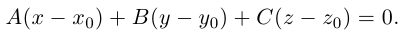
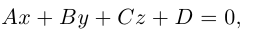
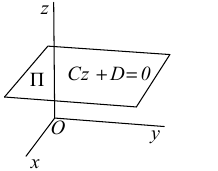
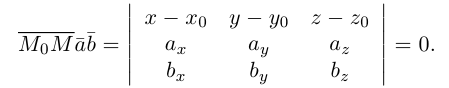
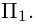
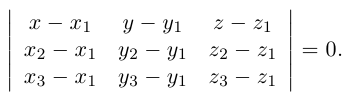
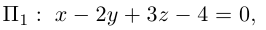
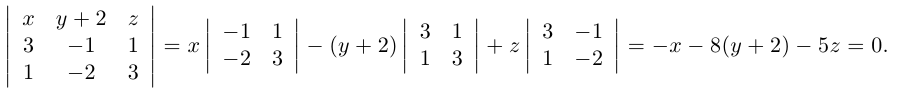
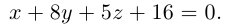
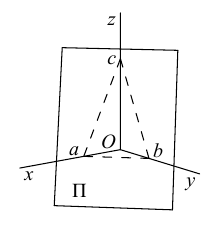
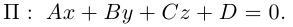
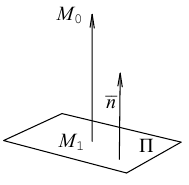
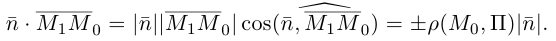
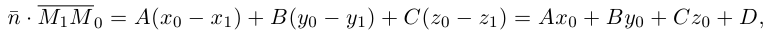
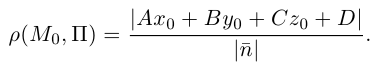
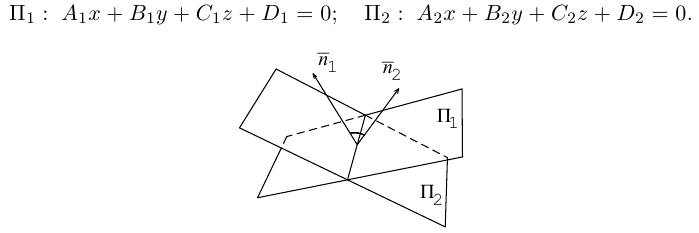
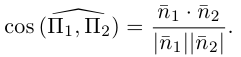
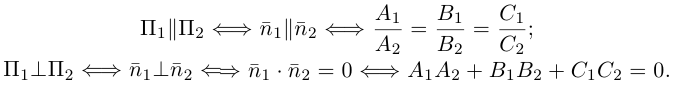
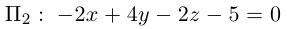
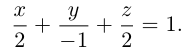
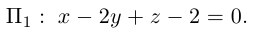
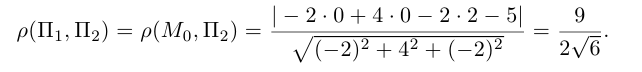
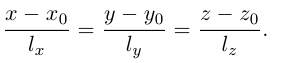
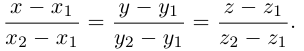
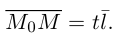
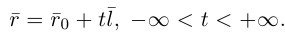
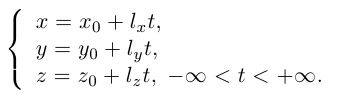
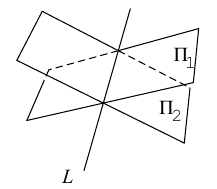
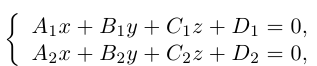
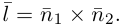
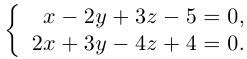
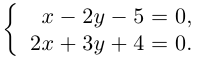
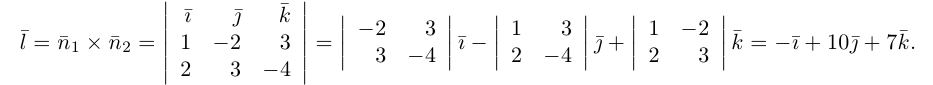
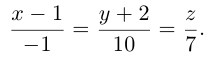
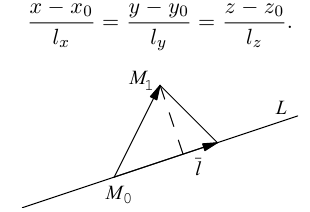
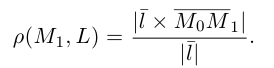
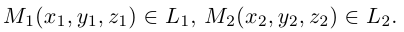
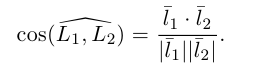
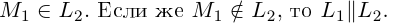
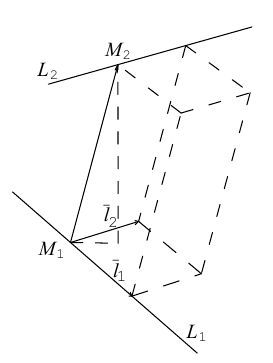
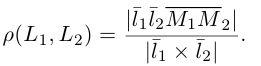
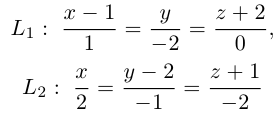
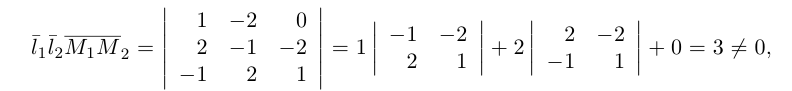
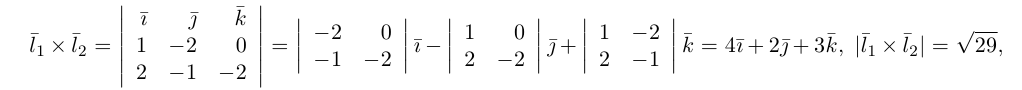
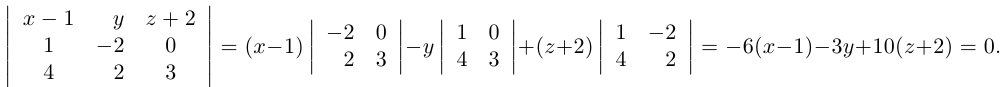
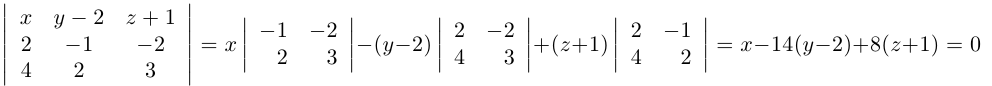
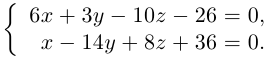
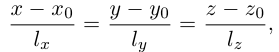
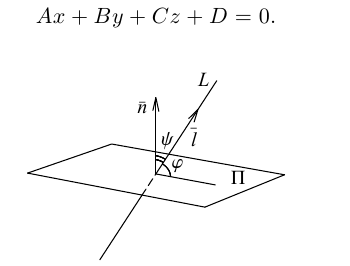
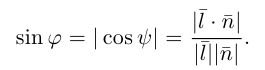
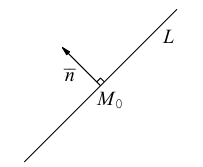
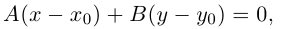
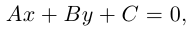
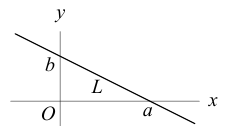
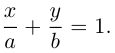
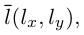
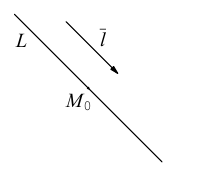
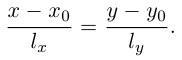
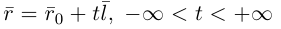
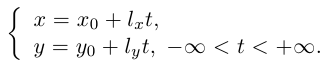
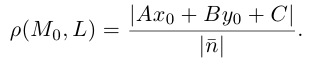
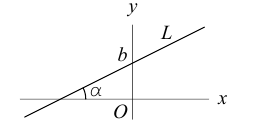
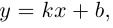
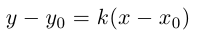
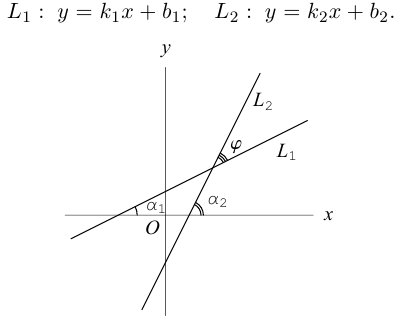
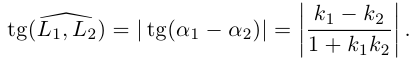
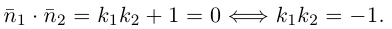
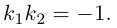
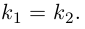
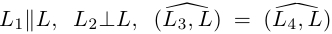
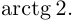
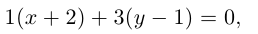
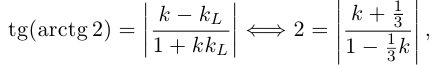
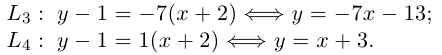
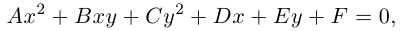
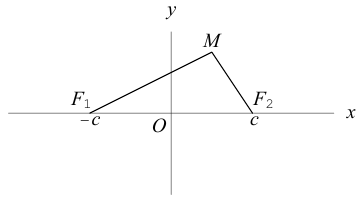
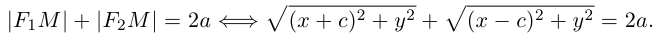
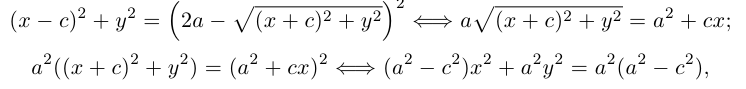
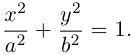
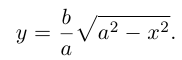
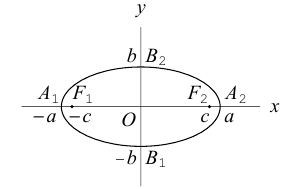
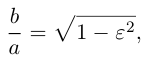
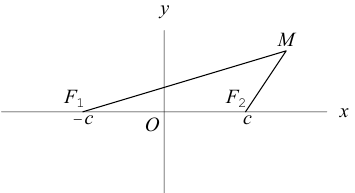
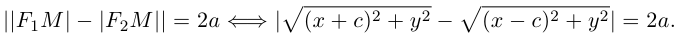
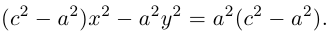
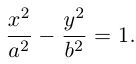
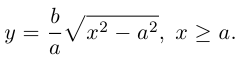
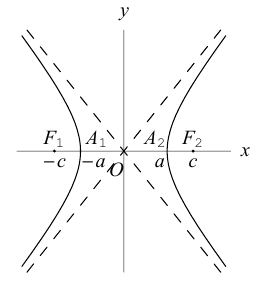
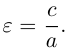
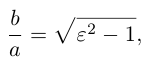
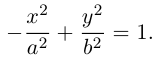
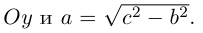
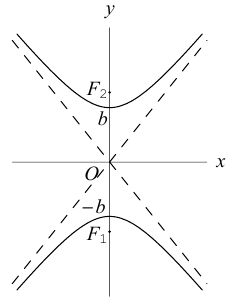
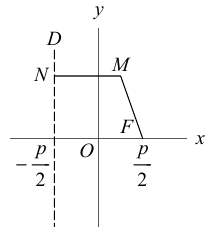
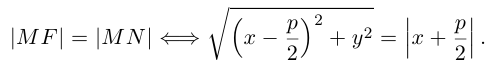
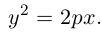
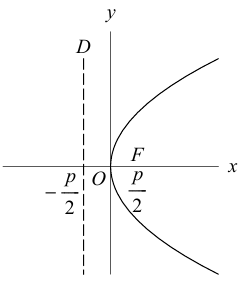
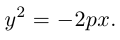
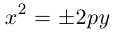
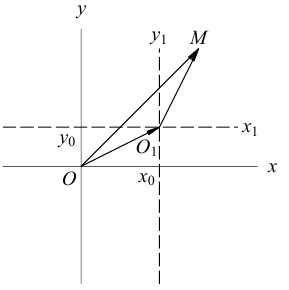
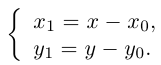
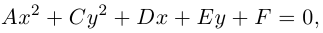
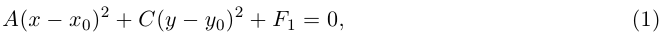
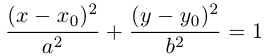
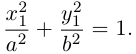
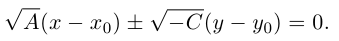
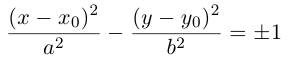
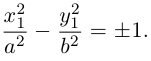
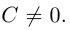
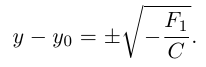
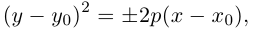
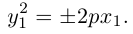
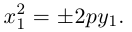
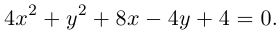
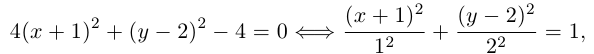
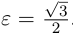
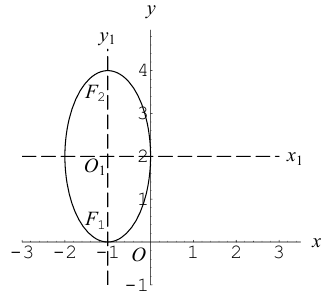
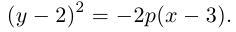
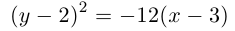
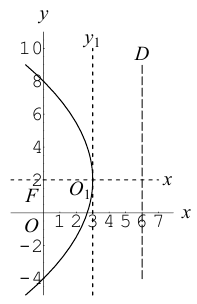
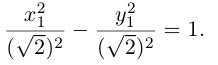
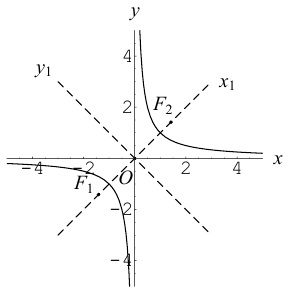
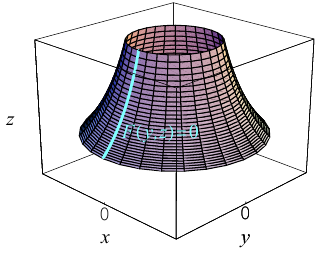
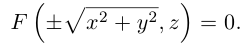
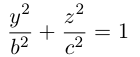
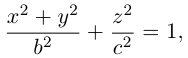
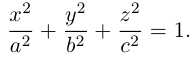
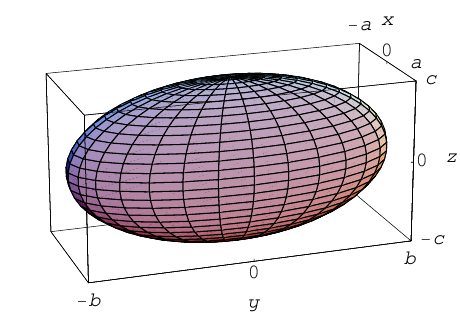
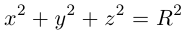
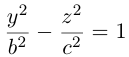
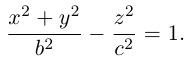
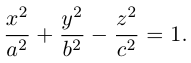
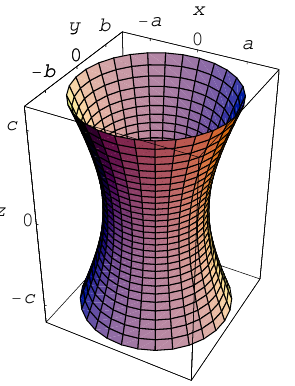
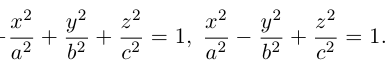
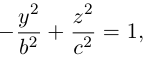
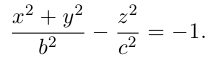
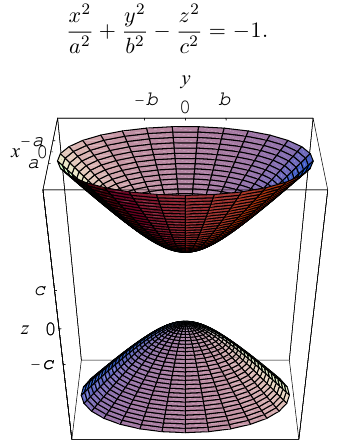
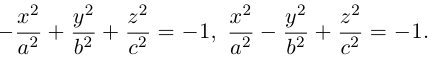
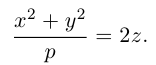
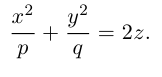
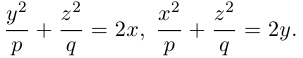
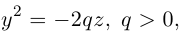
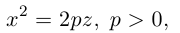
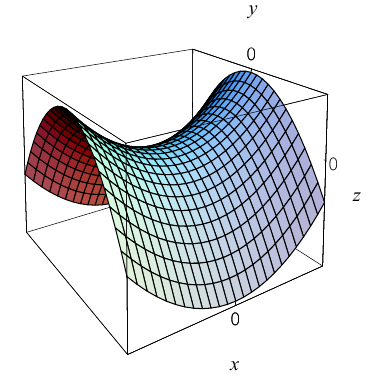
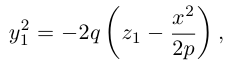
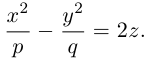
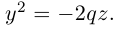
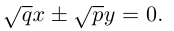
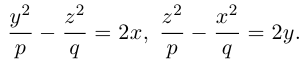
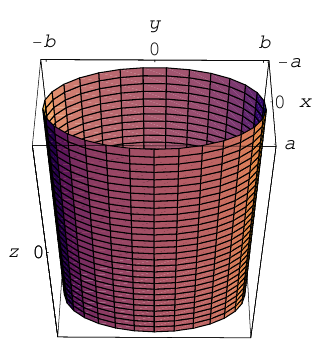
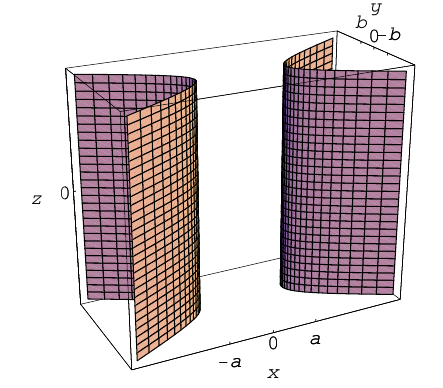
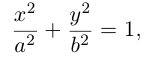
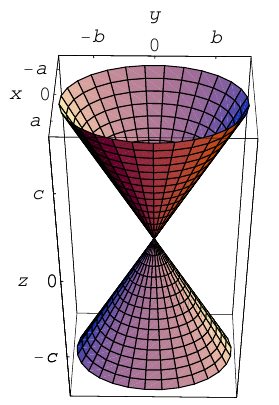
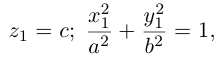
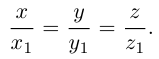
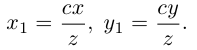
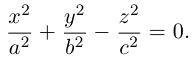
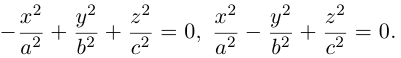
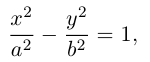
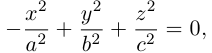
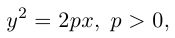
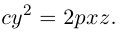
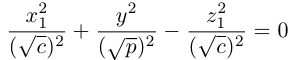
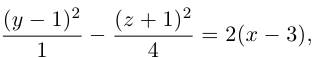
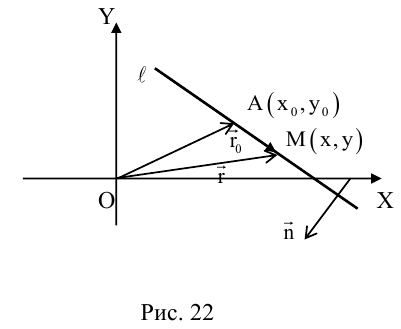
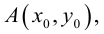
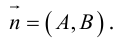


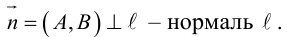
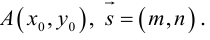


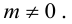
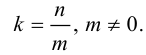
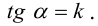
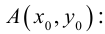


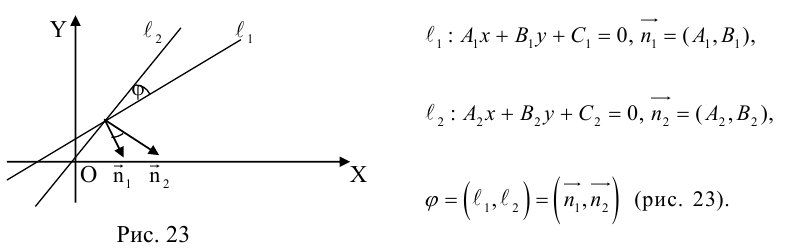
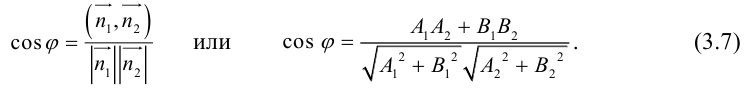
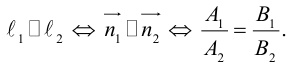
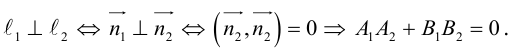
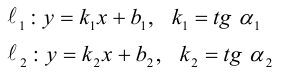
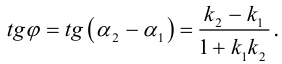
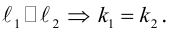
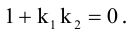
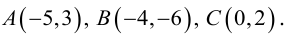
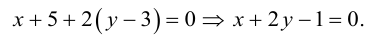
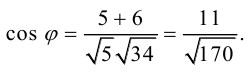
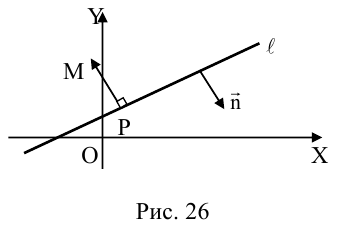
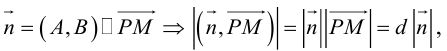
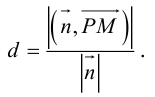

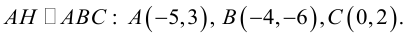
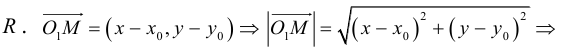


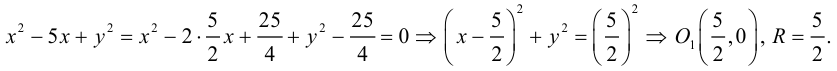
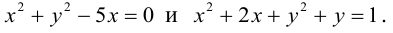
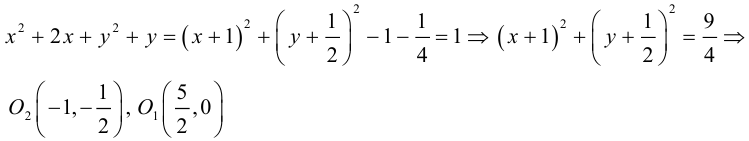
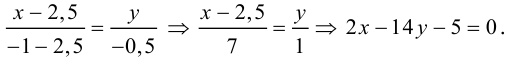
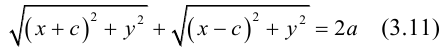
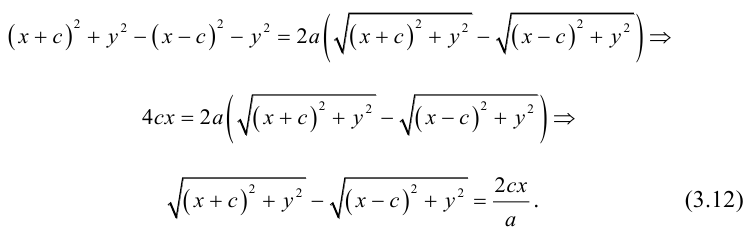
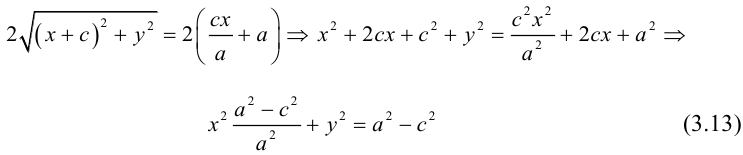

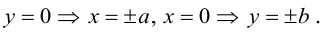
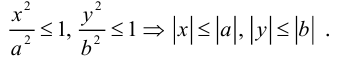

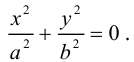
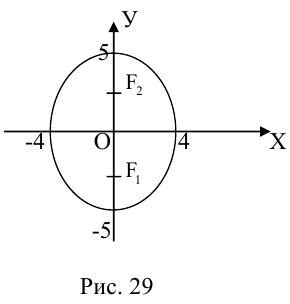
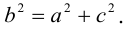
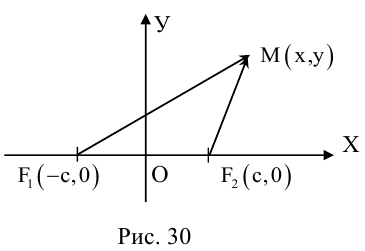
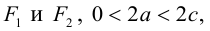
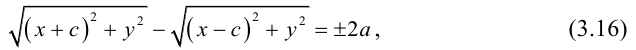


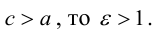
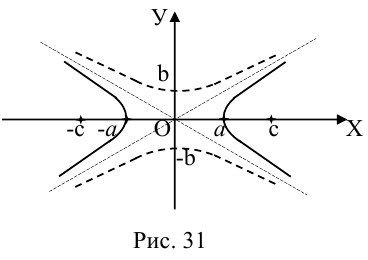

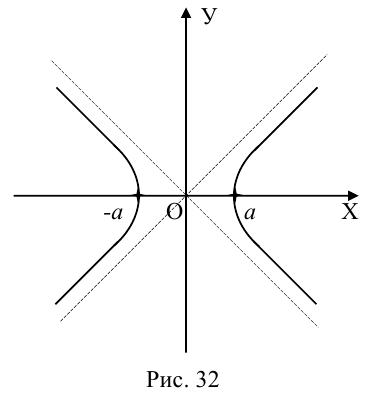
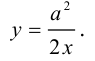
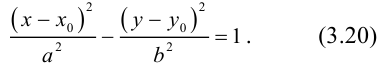
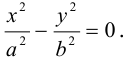
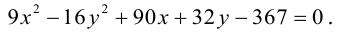
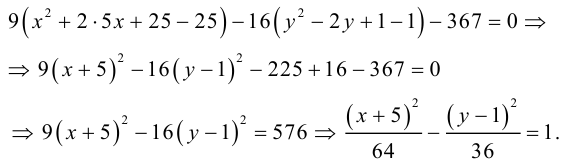
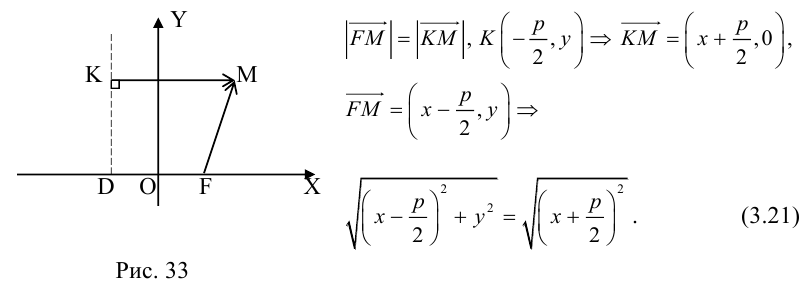
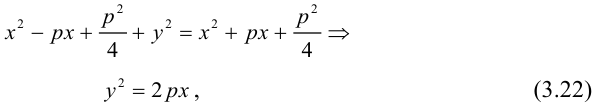
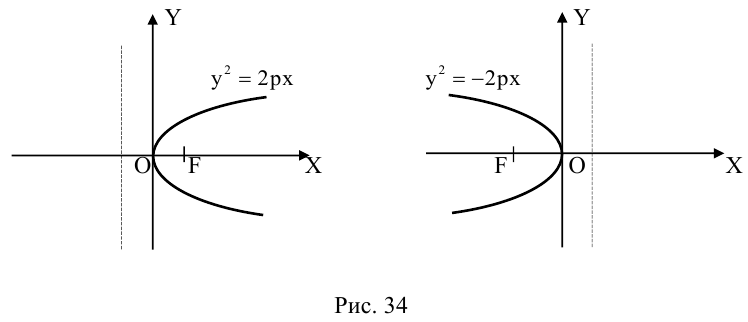
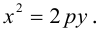
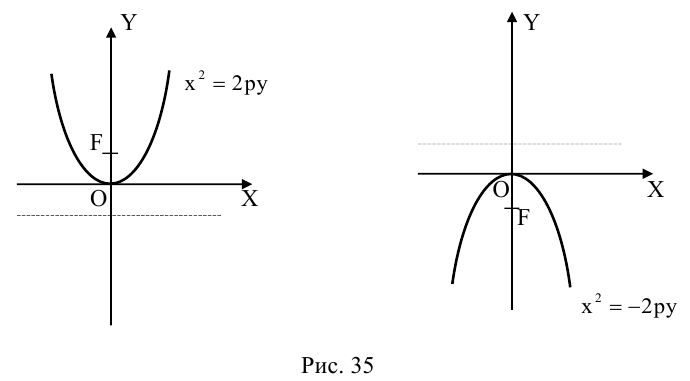
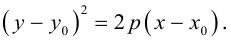
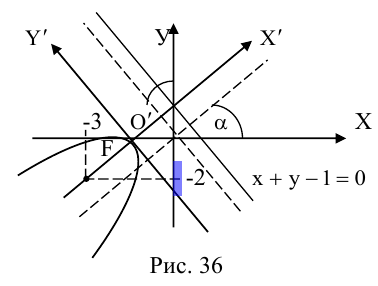
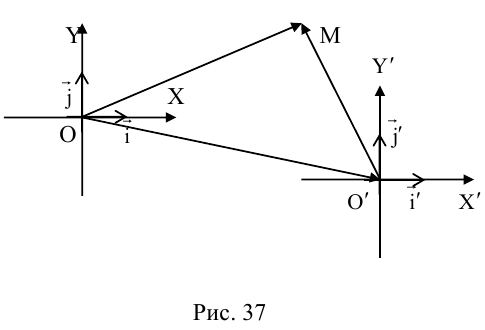
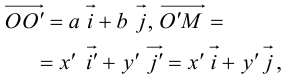
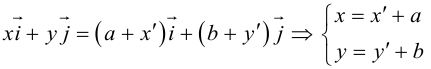

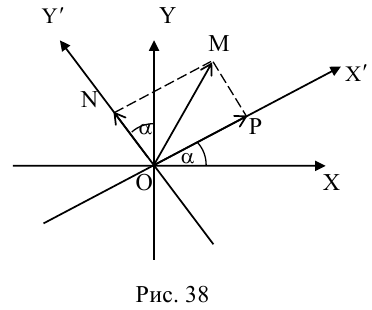

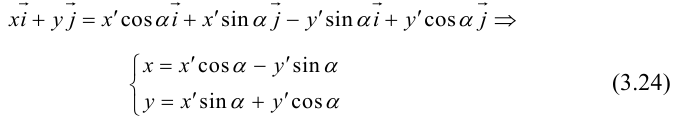
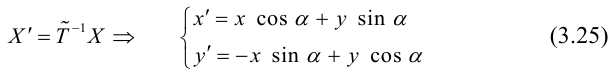
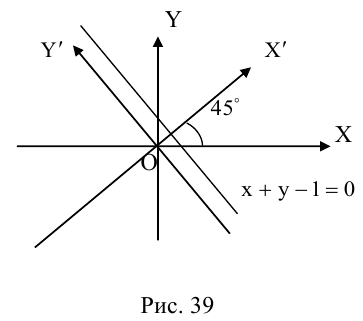
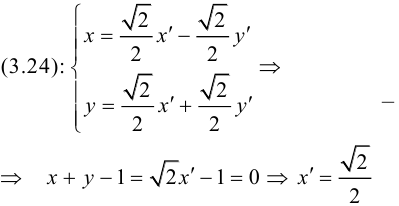

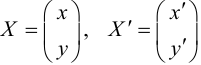
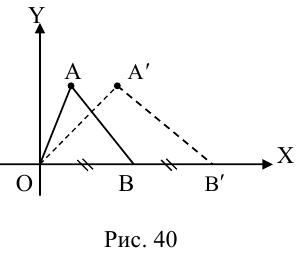
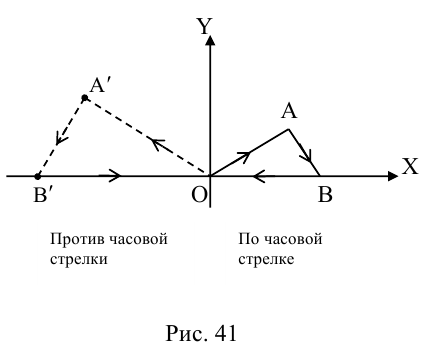
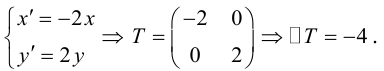
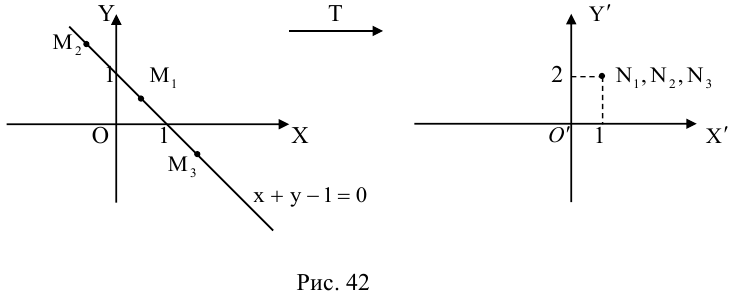
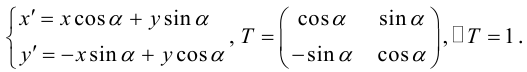
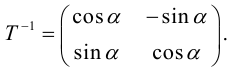
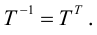
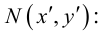

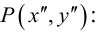

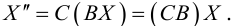
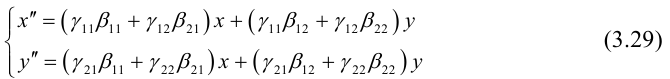
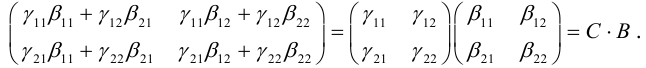
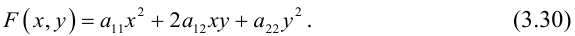
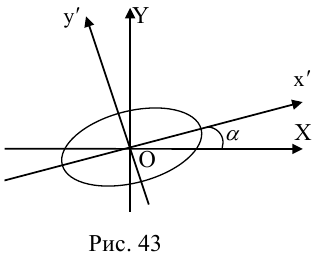
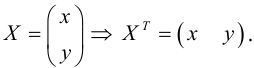
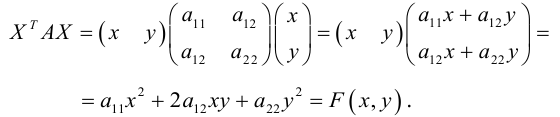

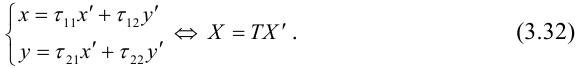
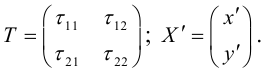

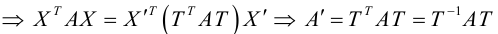
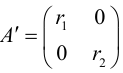
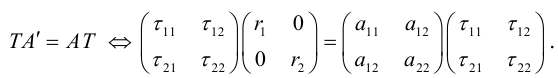
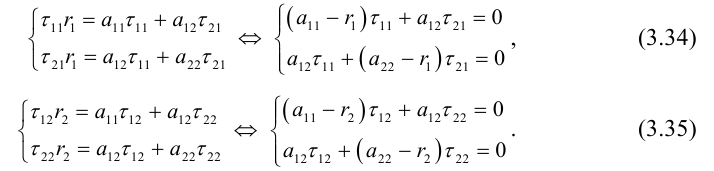
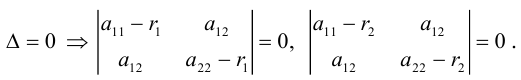
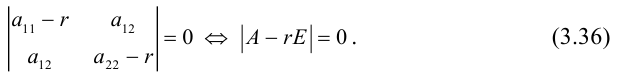
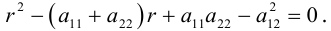
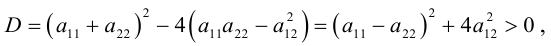
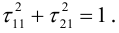
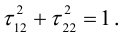
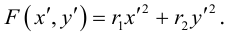
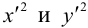 в каноническом виде квадратичной формы.
в каноническом виде квадратичной формы.  .При этом если ось
.При этом если ось сонаправлена с
сонаправлена с 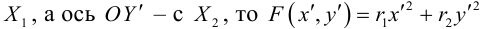 – канонический вид, который квадратичная форма имеет в системе
– канонический вид, который квадратичная форма имеет в системе  .
.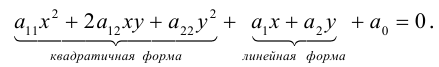
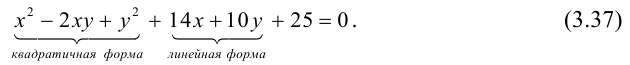
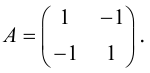
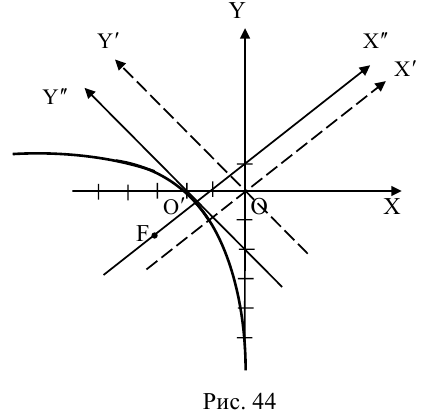
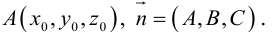
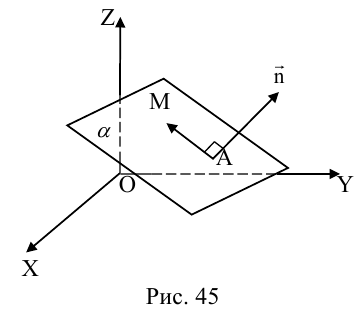
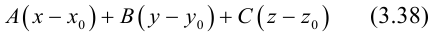

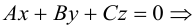 координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат.
координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат. 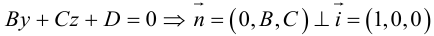 , так как
, так как 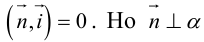 , значит, плоскость
, значит, плоскость  .
. 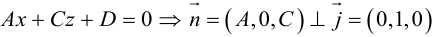 , так как
, так как 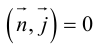 .Значит, плоскость
.Значит, плоскость  .
.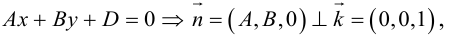 так как
так как 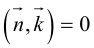 . Значит, плоскость
. Значит, плоскость  .
. 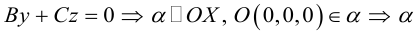 проходит через OX .
проходит через OX . 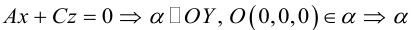 проходит через OY .
проходит через OY . 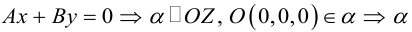 проходит через OZ .
проходит через OZ . 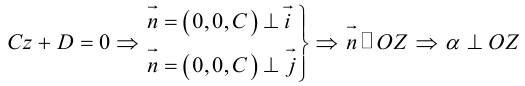 или
или  .
. 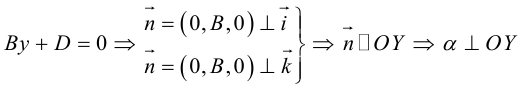 или
или  .
. 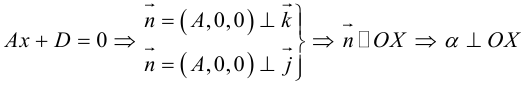 или
или 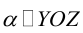 .
. 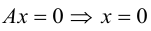 – плоскость YOZ .
– плоскость YOZ . 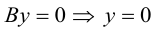 – плоскость XOZ .
– плоскость XOZ . 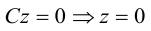 – плоскость XOY .
– плоскость XOY . 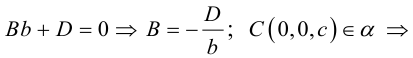
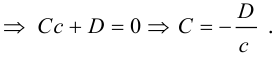
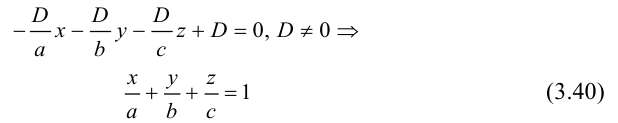
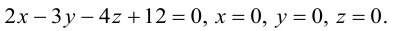
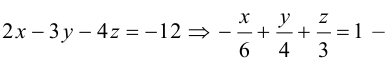
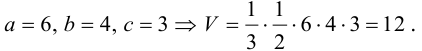
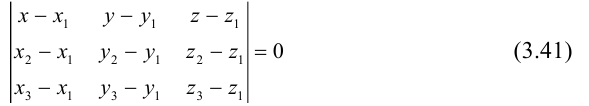
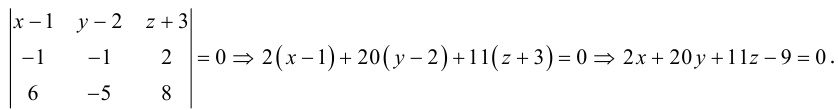
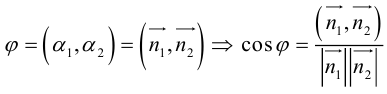
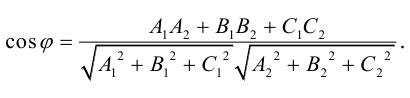
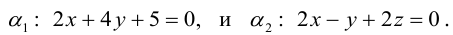
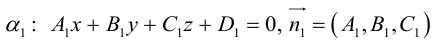
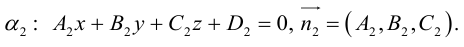
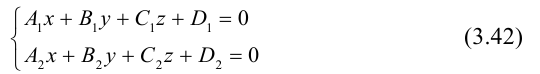

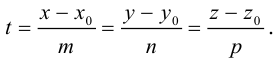

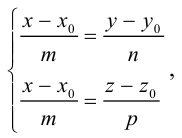
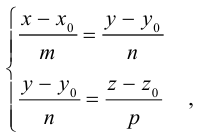

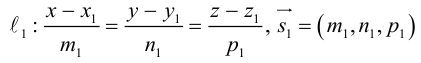
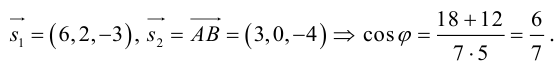
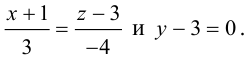
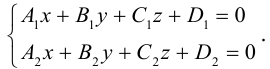
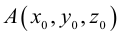 , лежащей на
, лежащей на