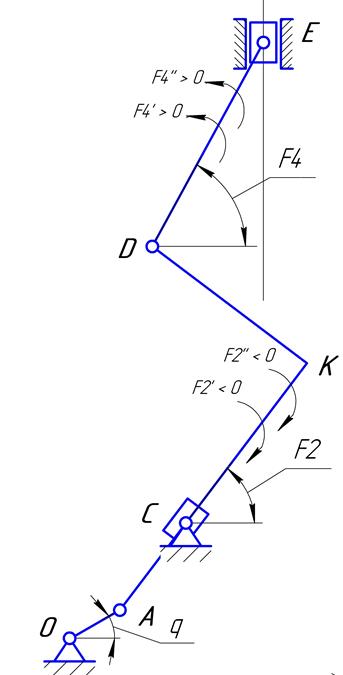
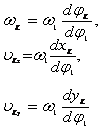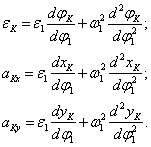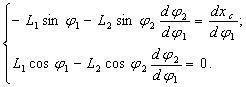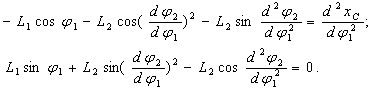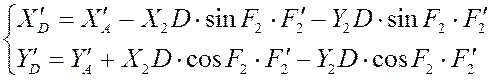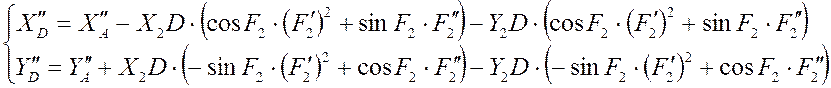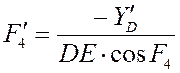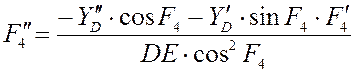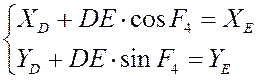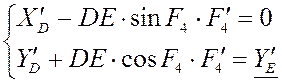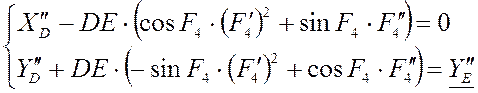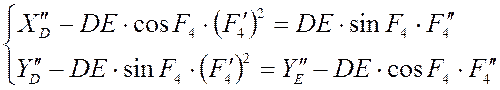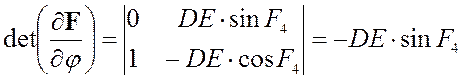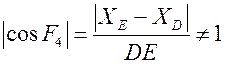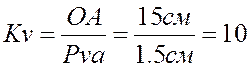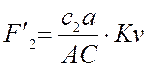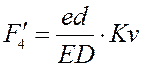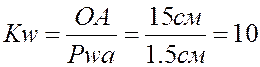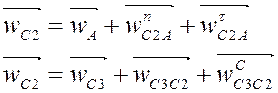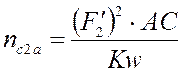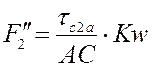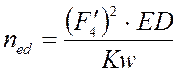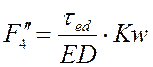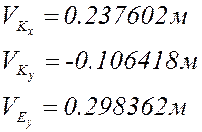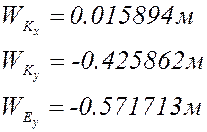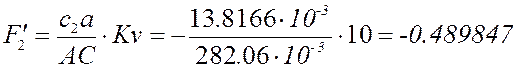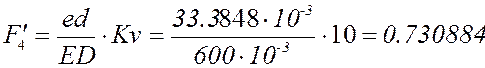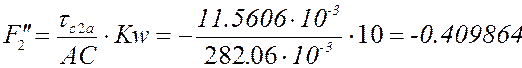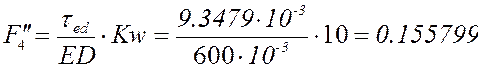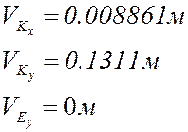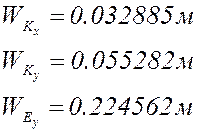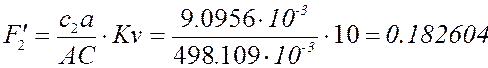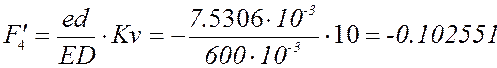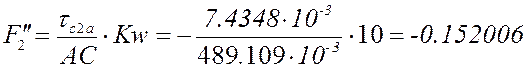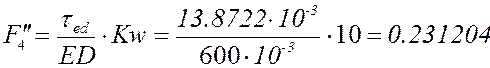Функция положения. Аналог скорости. Аналог ускорения
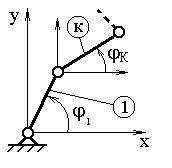
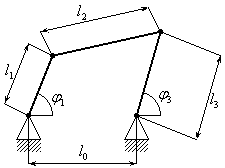
Положение любого звена механизма может
определяться параметрами: углом
относительно какой-либо координатной
оси или координатами ХК
и YК (рис.
3.12).
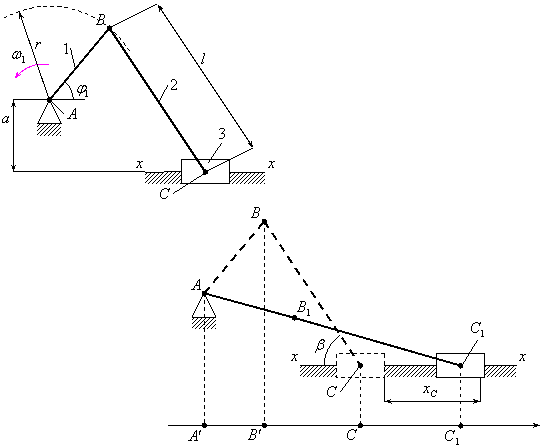
Рис. 3.12. Схема механизма
Функция положения – это
аналитическая зависимость положения
или координаты К-го звена (,
ХК или YК
) от положения ведущего звена
,
т.е.
или
и
,
где
,
XK
и YK
– координаты, определяющие
положение К-го звена (ведомого), а
угол
– угол, характеризующий положение
ведущего звена.
Аналог скорости. Угловая
скорость К-го звена определяется
зависимостью
,
(3)
где
– аналог скорости К-го звена
(первая передаточная функция) для
вращающегося звена, величина безразмерная;
и
–
аналоги скорости К-го звена,
движущегося поступательно, величины
безразмерные.
Аналог ускорения. Угловая
скорость К-го звена определяется
зависимостью, получаемой дифференцированием
уравнения (3) по dt:
.
При дифференцировании предполагается,
что угловая скорость К-го звена
определяется зависимостью
,
а угол
является функцией угла
:
.
Величина
– аналог ускорения К-го звена, совершающего
вращательное движение, величины
и
– аналоги ускорения К-го звена,
двигающегося поступательно, в проекциях
на оси X и Y.
Введение в кинематический анализ понятий
аналогов отделяет геометрические
свойства механизма от кинематических.
Величину
называют ещё передаточным отношением,
так как выражение
можно преобразовать, умножив и разделив
его на величину dt:
Отношение угловых скоростей в механике
называют передаточным отношением
.
Аналог скорости звена также называют
первой передаточной функцией.
Задачи кинематического анализа и пути
их аналитического решения приведены в
таблице.
|
Функции |
Задача о |
Задача об |
|
Определить |
Определение
Вычисление скоростей
|
Определение аналогов ускорений
Вычисление ускорений |
Как следует из приведенной таблицы, для
решения задачи о положениях
звеньев исследуемого механизма необходимо
найти функции положения (или
ХК и YК
), предварительно составив векторное
уравнение замкнутого векторного контура
кинематической цепи и уравнения проекций
его на координатные оси Х и Y.
Из этих уравнений находят функции
положения (зависимости положений
исследуемого звена от положения ведущего
звена). При известном (заданном) законе
движения ведущего звена задаются шагом
и вычисляют координаты исследуемых
звеньев (угловые координаты для
вращающегося звена и прямоугольные для
звена, совершающего возвратно-поступательное
движение).
Для решения задачи о скоростях
необходимо найти аналоги скоростей
исследуемых звеньев и, умножив их на
угловую скорость ведущего звена, получить
формулы расчета искомых скоростей.
Для решения задачи об ускорениях
находят также аналоги ускорений
звеньев и по формулам, приведенным в
таблице, находят величины ускорений.
Ниже приводится пример кинематического
анализа кривошипно-ползунного механизма
аналитическим методом.
Аналитическое
исследование кривошипно-ползунного
механизма
Аналитическое исследование
кривошипно-ползунного механизма
используется в двигателях внутреннего
сгорания, насосах, компрессорах.
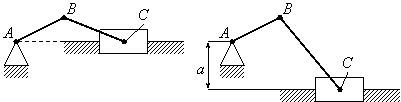
Различают две схемы кривошипно-ползунных
механизмов: нормальный или центральный
кривошипно-ползунный механизм (рис.3.13,
а) и дизоксиальный кривошипно-ползунный
механизм (рис.3.13, б).
а)
б)
Рис.3.13
Величина
называется смещением дизоксиальности.
Если в дизоксиальном кривошипно-ползунном
механизме сделать смещение дизоксиальности
равным нулю, то получится нормальный
кривошипно-ползунный механизм.
Кривошипно-ползунные механизмы
предназначены для преобразования
вращательного движения кривошипа в
поступательное движение ползуна (насосы,
компрессоры, механизмы шаговой подачи),
или для преобразования возвратно-поступательного
движения ползуна во вращательное
движение коромысла (двигатели внутреннего
сгорания).
Пример 4. Аналитическое
исследование механизма с ведущим
кривошипом.
Дано:
,
,
,
(рис.3.14).
Рис.3.14
Решение:
Скорость точки
равна нулю.
Модуль скорости точки
можно найти по формуле:
,
а линия действия вектора скорости точки
перпендикулярна звену
.
;
;
;
;
;
;
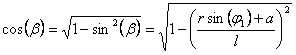
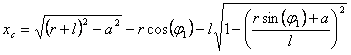
Получили формулу:
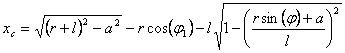
скорость точки
можно получить с помощью формулы
,
а ускорение точки
можно получить с помощью формулы
.
Понятия о мёртвых
положениях в кривошипно-ползунных
механизмах и способы их прохождения
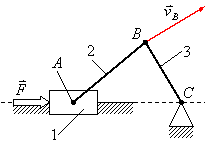
Рассмотрим случай, когда ведущим звеном
является ползун. В этом случае происходит
преобразование поступательного движения
ползуна во вращательное движение ползуна
(рис.3.15).
Рис.3.15
В таких механизмах, в момент, когда
кривошип и шатун находятся на одной
прямой, то вывести механизм из состояния
неподвижности ползун не может.
Работу точки
можно найти по формуле:
.
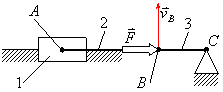
На рис.3.16 угол между силой
и вектором скоростью точки
составляет 90 градусов, следовательно
,
то есть как бы не была велика сила
вывести механизм из этого положения
она не может.
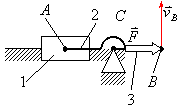
Положения механизма, представленные
на рис.3.16 и рис.3.17 из-за невозможности
движения под действием силы
принято называть мёртвым положением.
Рис.3.16
Рис.3.17
Существует два способа прохождения
мёртвых положений: динамический
и кинематический.
При динамическом методе на вал
кривошипа одевается маховик.
Маховик – колесо со
значительной массой, девяносто процентов
которой сосредоточено в ободе этого
колеса (рис.3.18).
Рис.3.18
Таким образом, маховик является
аккумулятором энергии, получаемой от
механизма, когда положение звеньев
представляет наилучшее для работы
состояние. Поскольку масса маховика
значительна, то при прохождении мёртвого
положения кинетическая энергия маховика
проворачивает кривошип. Дальше действует
сила ползуна.
Кинематический способ используется
в тех случаях, когда большие массы
маховиков недопустимы. Этот способ
заключается в том, что кривошипы
нескольких одинаковых механизмов жёстко
связаны между собой образуя коленчатый
вал. У этих кривошипов общая ось вращения,
но расположены они под углом друг к
другу, чтобы при мёртвом положении
одного механизма, другой имел более
благоприятное положение, и проворачивал
коленчатый вал остальных механизмов.
В этом случае также могут быть использованы
маховики, но они будут иметь очень
незначительную массу.
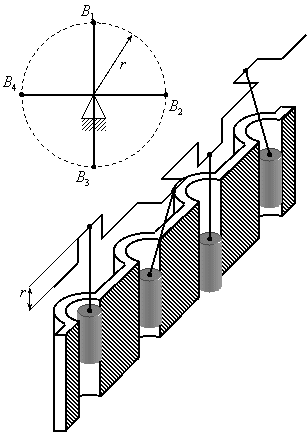
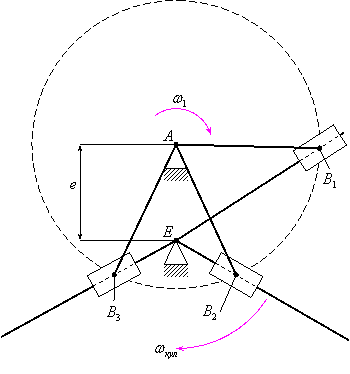
На рис.3.19 первый и третий механизмы
находятся в мёртвых положениях, а второй
и четвёртый механизмы находятся в
наилучших положениях.
Рис.3.19
Пример 5.
Используем метод замкнутых векторных
контуров (рис. 3.7).
Рис. 3.20. Замкнутый векторный контур
кривошипно-ползунного механизма
Решение:
Рассмотрим замкнутый векторный контур
OABCO. Соблюдая единообразие
отсчёта углов, определяющих положение
звеньев, составим векторное уравнение
.
(4)
Спроектируем (4) на координатные оси Х
и Y:
(5) – (6)
Решение задачи о положениях
Определим функции положения ползуна
и шатуна
.
Из (6) получаем
,
откуда
,
из (5) получаем
.
Решение задачи о скоростях
Определим аналог скорости ползуна
и
шатуна
,
для чего продифференцируем уравнение
(5) и (6):
(7) — (8)
Из (8) получаем аналог скорости шатуна
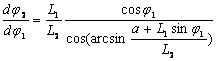
тогда угловая скорость шатуна
.
Из (7) получаем аналог скорости ползуна
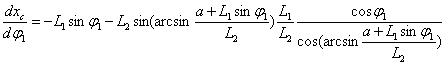
тогда скорость ползуна вычисляется по
формуле
.
Решение задачи об ускорениях
Определим аналоги ускорений шатуна
и ползуна
,
для чего продифференцируем уравнения
по
(7) и (8):
(9) — (10)
Из (10) получим аналог ускорения шатуна
,
тогда угловое ускорение шатуна можно
вычислить по формуле
.
Из (9) получим аналог ускорения ползуна
,
тогда ускорение ползуна можно вычислить
по формуле
.
Аналитическое
исследование шарнирного четырёхзвенного
механизма
Рис.3.21
При ведущем кривошипе рабочим ведомым
звеном является чаще всего коромысло
(рис.3.21). Чтобы найти зависимость угла
поворота ведомого звена от ведущего
аналитическим способом пользуются
следующей формулой (рис.3.22):
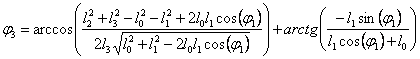
Рис.3.22
Аналитическое
исследование кривошипно-кулисного
механизма
Основным элементом кривошипно-кулисных
механизмов является кулиса.
Кулиса – подвижная направляющая
ползуна.
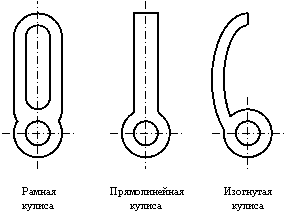
Кулисы бывают прямолинейные и изогнутые
(рис.3.23). Конструктивно они бывают
выполнены в виде стержней или рамных
направляющих.
Рис.3.23
По принципу действия кривошипно-кулисные
механизмы бывают следующих видов:
механизмы с возвратно-поступательным
вращением кулисы, механизмы с вращательным
движением кулисы.
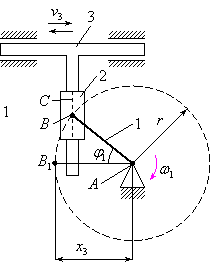
Рассмотрим механизм с поступательным
вращением кулисы (рис.3.24).
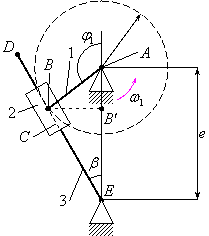
1 – кривошип.
2 – ползун (камень).
3 – кулиса.
;
;
.
Рис.3.24
Назначением таково механизма является
преобразование вращательного движения
кривошипа в возвратно-поступательное
движение кулисы.
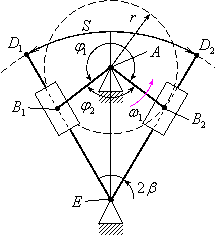
Кулисный механизм с вращающейся головкой
(рис.3.25).
Рис.3.25
1 – кривошип.
2 – ползун.
3 – качающаяся кулиса.
Этот механизм предназначен для
преобразования вращающегося движения
кривошипа в колебательное или вращательное
движение кулисы (рис.3.26).
Рис.3.26
Зададим
.
— угол поворота кривошипа при переходе
кулисы из крайнего правого в крайнее
левое положение.
— угол поворота кривошипа при переходе
кулисы из крайнего левого в крайнее
правое положение.
Очевидно, что угол
больше угла
.
Так как
,
то
,
а
;
или
.
Так как
,
то
.
Это означает, что прохождения кулисы
влево и вправо различны, то есть влево
кулиса двигается медленнее, чем вправо.
Средняя скорость точки
:
;
.
Путь
.
;
.
Найдём зависимость угла поворота кулисы
от угла поворота кривошипа:
;
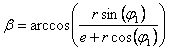
;
;
;
;
;
.
Выше были рассмотрены механизмы, у
которых радиус кривошипа
был меньше чем межцентровое расстояние
.
В этих механизмах кулиса совершала
колебательные движения.
Рассмотрим вариант, когда радиус
кривошипа будет больше межцентрового
расстояния
(рис.3.27).
В этом случае центр вращения кулисы –
точка
будет находиться внутри кривошипной
окружности, очерчиваемой шарниром
кривошипа. Такие механизмы имеют
вращающуюся кулису.
Так как радиус
величина переменная, то угловая скорость
кулисы
тоже будет величиной переменной. Верхнюю
часть окружности кулиса проходит
медленнее, чем нижнюю
Рис.3.27
Вопросы для
самопроверки
— Что называется «функцией положения»
для звена или точки механизма?
— В чем различие между кинематическими
и геометрическими характеристиками
механизма?
— Какие функции называются кинематическими
передаточными функциями механизма?
— Какие передаточные функции механизма
называются главными, а какие
вспомогательными?
— Перечислите методы геометро-кинематического
исследования механизмов?
— Напишите формулы, устанавливающие
связь между геометрическими и
кинематическими характеристиками
механизма?
— Изложите суть метода «проекций
векторного контура»?
— Что называется циклом?
— Что называется «центроидой», как
центроиды используются при кинематическом
исследовании механизма?
— Как метод кинематических диаграмм
применяется при кинематическом
исследовании механизмов?
— Как применяется метод преобразования
координат при решении прямой задачи о
положении точки выходного звена?
— Как кинематические характеристики
определяются экспериментально?
— Опишите последовательность кинематического
анализа плоского механизма.
— Запишите уравнения планов скоростей
и ускорений для любой структурной группы
II класса, содержащей внутреннюю
поступательную пару.
— Запишите уравнения планов скоростей
и ускорений для любой структурной группы
II класса, содержащей хотя бы одну внешнюю
поступательную пару.
— Как определяют величину и направление
ускорения Кориолиса?
— В каких случаях при построении планов
скоростей и ускорений применяют метод
подобия?
— По какому признаку можно установить,
является ли равномерным (или неравномерным)
относительное движение звеньев,
образующих поступательную пару?
— Цель кинематического анализа механизмов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
А.Н.Евграфов, Г.Н.Петров. Теория механизмов и машин. Лекция 4.
3. Кинематический анализ механизмов
После проведения геометрического анализа приступают к кинематическому. Задачей кинематического анализа является определение скоростей и ускорений точек механизма, угловых скоростей и угловых ускорений его звеньев при заданных законах изменения обобщенных скоростей и обобщенных ускорений
, т.е. первых и вторых производных по времени от обобщенных координат.
Пусть для одноподвижного механизма (W=1) определена функция положения некоторой точки М:
xМ=Пх(q) (2.18)
Дифференцируя (2.18) по времени, получим:
, (2.19)
где — обобщенная скорость, а
— аналог скорости или первая геометрическая передаточная функция. Отметим, что аналог скорости
является геометрической характеристикой механизма, в отличие от скорости, которая является кинематическим параметром. В частности, если обобщенная координата – угловая, то аналог скорости
имеет ту же размерность, что и функция положения Пх(q). В дальнейшем будет показано, что аналог скорости является важной характеристикой механизма, определяющей его качество.
Для определений ускорения точки М продифференцируем выражение (2.19) по времени:
, (2.20)
где — аналог ускорения или вторая геометрическая передаточная функция. Так же, как и аналог скорости, аналог ускорения является геометрической характеристикой механизма.
— обобщенное ускорение.
Часто мы будем ограничиваться рассмотрением случая:
= 0; тогда
.
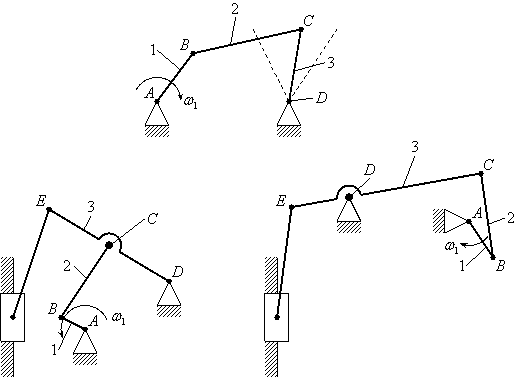
В качестве примера рассмотрим механизм с внутренним входом (рис. 2.9,а). Т
акие механизмы встречаются в гидро- или пневмоприводах: звено 3 – цилиндр, звено 2 – поршень и шток. Обобщенная входная q – это перемещение поршня относительно цилиндра. В этом случае оказывается, что расстояние между точками А и С является переменным: АС = l+q , где l = const. Особенностью такого механизма является то, что он содержит только одну трехзвенную одноподвижную структурную группу, которая присоединена к стойке (рис. 2.9, с). Отметим, что, поскольку кинематическая пара В – поступательная, то угол поворота звена 2 и звена 3 – один и тот же — 3. Одинаковыми у них будут также угловые скорости и угловые ускорения. Обозначим OA=l1; составим функцию положения звеньев 1 и 3:
(2.21)
Продифференцируем (2.21) по обобщенной координате q:

Обозначим аналоги угловой скорости первого и второго звена :
Нетрудно видеть, что относительно аналогов скорости система уравнений (2.22) является линейной:
(2.22’)
Отсюда несложно найти аналоги скорости:

Отметим, что знаменатель выражения (2.23) (якобиан) обращается в ноль при 1=3 n, n=0, 1, … . В этих случаях механизм попадает в особые положения (рис. 2.9, б), а аналог скорости . Поэтому механизм стремятся не доводить до этого положения. Например, в автомобилях-самосвалах опрокидывающуюся платформу, связанную со звеном 1, опускают на упор, не позволяющий механизму попасть в особое положение.

Для отыскания аналогов углового ускорения и
продифференцируем систему уравнений (2.22’) по обобщенной координате q:
(2.25)
Система уравнений (2.25) является линейной относительно аналогов ускорений:
(2.25’)
Отметим, что  — аналог кориолисова ускорения,
— аналог кориолисова ускорения,  — аналоги вращательных составляющих ускорений,
— аналоги вращательных составляющих ускорений,  — аналоги центростремительных составляющих ускорений; в уравнениях (2.25) стоят проекции этих аналогов соответственно на оси 0х и 0у. Напомним, что для того, чтобы получить сами значения ускорений, надо в соответствии с (2.20) и при условии
— аналоги центростремительных составляющих ускорений; в уравнениях (2.25) стоят проекции этих аналогов соответственно на оси 0х и 0у. Напомним, что для того, чтобы получить сами значения ускорений, надо в соответствии с (2.20) и при условии  умножить аналоги ускорений на
умножить аналоги ускорений на  .
.
Из (2.25’) несложно найти аналоги угловых ускорений звеньев 1 и 3:


Отметим, что в знаменателе выражений (2.26) и (2.27), как и в случае аналогов скоростей, стоит якобиан функций положений звеньев 1 и 3, т.е. при приближении к особому положению аналоги ускорений и
.
В многоподвижных механизмах функции положения являются функциями W обобщенных координат:
хМ = Пх(q1, q2, … , qW). (2.28)
Продифференцировав (2.28) по времени, получим выражение для скорости точки М:
(2.29)
Для получения ускорения точки М надо продифференцировать (2.29) по времени:

К
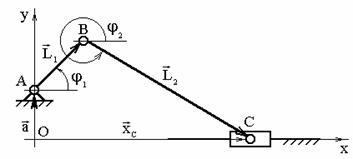
ак видно из (2.29) и (2.30), для отыскания скоростей и ускорений в многоподвижных механизмах надо определять первые и вторые частные производные от функции положения по всем обобщенным координатам, а также смешанные производные типа . Их определение рассмотрим на примере двухподвижного механизма (рис. 2.10).
Составим функцию положения:

В дальнейшем удобно представить (2.31) в более краткой форме:
(2.31’)
Возьмем производную от (2.31’) по обобщенной координате q1:

Из (2.32) можно найти производные и
:


Далее продифференцируем (2.31’) по обобщенной координате q2:

Из системы (2.35) найдем частные производные по q2:


(2.37)
Для того, чтобы найти вторые частные производные и
, можно продифференцировать по q1 выражения (2.33) и (2.34). Аналогично для отыскания производных
и
надо продифференцировать по q2 выражения (2.36) и (2.37). Для того, чтобы найти смешанные производные
и
, надо продифференцировать выражения (2.32) по q2 или (2.35) по q1, например:

Выражения для смешанных производных и
получите самостоятельно.
Повторить по лекции 4.
Задача геометрического анализа;
Аналог скорости;
Аналог ускорения;
Формулы (2.19) и (2.20).
6
ЛЕКЦИЯ 3. ГРАФО-АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ АНАЛОГОВ СКОРОСТЕЙ И УСКОРЕНИЙ ЗВЕНЬЕВ И ХАРАКТЕРНЫХ ТОЧЕК МЕХАНИЗМА
Целью лекции является определении аналогов скоростей и ускорений звеньев, а также характерных точек механизма графо-аналитически методом. Отметим, что алгоритм построений отличается универсальностью и простотой, а результат позволяет получать не только величины, но и направления скоростей и ускорений заданных точек звеньев механизма. Теоретические основания построения планов скоростей и ускорений были изложены О. Мором в 1870 г.
2.1. Порядок построения планов скоростей и ускорений звеньев механизма
Планами скоростей и ускорений механизма называют векторные изображения этих кинематических параметров, соответствующие заданному положению механизма, т. е. совокупности плоских пучков, лучи которого изображают абсолютные скорости или ускорения точек звеньев, а отрезки, соединяющие концы лучей, – относительные скорости или ускорения соответствующих точек звеньев при данном положении механизма. Векторы абсолютных скоростей или ускорений на каждом плане откладываются от одной точки – полюса, обозначаемого на плане скоростей р, на плане ускорений π.
При кинематическом исследовании механизма расчет и построения планов скоростей и ускорений начинают от ведущего звена, угловую скорость которого обычно принимают постоянной, по группам Ассура в порядке их присоединения.
Итак, известны положения звеньев механизма с указанием их размеров, задана угловая скорость начального звена 1, требуется найти для каждого звена механизма аналог его угловой или линейной скорости, а также проекции аналогов скоростей центров масс звеньев.
Решение задачи начинаем с определения величины аналога абсолютной линейной скорости кинематической пары А, начального звена – кривошипа 1, вокруг О1:
м. (1)
Напомним, что в системе СИ единица угловой скорости обозначается как рад/с или с–1, так как радиан есть безразмерная величина. Если задано число оборотов ведущего звена в минуту, т. е. частота вращения n, то для определения угловой скорости используется соотношение ω1=πn1/30.
Поскольку вектор линейной скорости кинематической пары, вращающейся вокруг неподвижного или мгновенного центра, сонаправлен с угловой скоростью звена, которому принадлежит пара, и перпендикулярен положению данного звена, то вектор скорости VAO1 перпендикулярен кривошипу занимающему пятое положение, а значит, образует с осью ОХ угол, равный λ=φ13+90º=117.77º.
Масштабный коэффициент плана аналогов скоростей механизма есть отношение аналога линейной скорости кинематической пары начального звена к отрезку, изображающему эту скорость на плане в миллиметрах.
Изобразим скорость VAO1 вектором (рис. 1), отложенным из некоторой точки р5, называемой полюсом плана скоростей. Числовой индекс 5 полюса, указывающий номер положения механизма, для которого строится план скоростей, в дальнейшем опустим.
Произвольно зададимся чертежным размером VAO1, обозначенным ра = 100 мм, и вычислим масштабный коэффициент плана аналогов скоростей:
, (2)
.
Для определения аналога скорости элемента кулисы 3, образующего кинематическую пару А3 с элементом кинематической пары камня 2, составим векторное выражение вида
, (3)
где относительным движением считаем поступательное движение кулисы вдоль камня со скоростью. Вращательное движение кулисы вокруг О2 отображаем на плане вектором аналога линейной скорости А3, , выстраиваемым из полюса плана аналога скоростей.
Векторное уравнение равносильно двум скалярным уравнениям: его можно заменить двумя уравнениями проекций векторов на координатные оси, лежащие в плоскости векторов. Следовательно, найдем неизвестные величины: и .
Рис. 1. План аналогов скоростей звеньев механизма в положении № 5
Пересечение прямых, построенных через полюс плана скоростей р перпендикулярно кулисе и через вершину вектора а параллельно кулисе, обозначим а3. Из плана скоростей, замеряя полученные векторы, определим
м; ; (4)
и .
Векторы аналогов скоростей выстраиваемого плана и имеют направления к точке плана скоростей, стоящей первой в буквенной последовательности обозначений, в частности к А3.
Поступательное движение камня 2 по кулисе 3 характеризуется скоростью , где .
Для определения скоростей кинематических пар сложных звеньев, обладающих тремя и более вершинами, используем теорему подобия: отрезки прямых линий, соединяющих точки одного и того же звена на плане механизма, и отрезки прямых линий, соединяющих концы векторов скоростей этих точек на плане скоростей, образуют подобные и сходственно расположенные фигуры.
Фигура на плане скоростей повернута относительно фигуры на плане механизма на 90°. Теорема подобия дает возможность определения любой скорости звена, если известны скорости двух точек этого звена.
Конструкция механизма такова, что кинематические пары А3 и С базисного звена 3 находятся по разные стороны от центра вращения О2 и при этом α=180°.
А так как аналог угловой скорости любой точки звена 3 в любом положении имеет определенное и одинаковое значение, векторы аналогов линейных скоростей кинематических пар А3 и С противоположны, а их величины представлены отрезками, пропорциональными длинам сторон звена l2 и l3.
Таким образом, чертежный размер вектора скорости кинематической пары С относительно О2 найдем из пропорции
, (5)
откуда , .
Аналог линейной скорости ползуна 5 относительно стойки F определим из векторного уравнения
,
где VDF׀׀l5 , а . (6)
Векторы и проводим через полюс р и координату с плана скоростей соответственно до пересечения в точке d.
Аналоги линейной скорости ползуна, его центра масс S5, а также угловой скорости шатуна 4 найдены из выражений
, ; (7)
и .
Так как центр масс шатуна S4 расположен на середине звена, его скорость
. (8)
Рис. 2. План аналогов ускорений звеньев механизма в положении № 5
Проекции вектора аналога скорости центра масс шатуна S4 принадлежат третьей координатной четверти, следовательно, они имеют отрицательные значения
м, м, (9)
где (pS4X), (pS4Y) – проекции скорости на координатные оси, определяемые из плана скоростей. Так же определяем проекции аналога скорости центра масс S3 кулисы.
Для определения знака аналога угловой скорости звена перенесем на звено вектор его скорости из плана, который покажет движение звена относительно центра его вращения.
Так, после переноса на шатун 4 установим, что относительно мгновенного центра вращения С звено движется против хода часовой стрелки и, следовательно, значение аналога угловой скорости будет положительным.
Задача об определении аналогов ускорений может быть решена графоаналитически, путем построения плана ускорений (рис. 2).
Уравнения, которые используются при построении плана ускорений механизма, отличаются от уравнений для плана скоростей только разложением полных ускорений на отдельные, взаимно перпендикулярные парные составляющие: нормальные – n и касательные – , кориолисовы – k (поворотные) и относительные – r (релятивные) ускорения.
Полное ускорение кинематической пары А есть геометрическая сумма двух составляющих: нормального и касательного аналогов ускорений:
, (10)
где нормальное , или центростремительное ускорение характеризует изменение вектора скорости по направлению при криволинейном движении, а тангенциальное или касательное ускорение характеризует изменение вектора скорости по модулю. Вектор направлен в сторону движения точки при возрастании скорости и в противоположную – при убывании скорости.
Нормальное ускорение направлено по линии (АО1) к центру вращения звена, а его модуль определяется из выражения
, (11)
.
По условию начальное звено имеет перманентное движение (φ’1=const, φ»1=0), поэтому модуль аналога касательного ускорения начального звена
, (12)
.
Примем точку π за полюс плана ускорений и отложим вектор, изображающий нормальное ускорение точки А в виде отрезка (πа) = 100 мм.
Тогда масштабный коэффициент плана аналогов ускорений найдем из соотношения
, (13)
.
Векторные выражения аналога полного ускорения кинематической пары А3 относительно О1 и О2 имеют вид
, (14)
. (15)
Модуль аналога нормального ускорения элемента кинематической пары А3 кулисы относительно стойки О2 вычислим следующим образом:
, (16)
.
На луче, параллельном положению кулисы 3, проходящем через полюс плана ускорений π и направленном к центру вращения кулисы, отложим отрезок
, (17)
.
Отметим, что только в кулисных механизмах кориолисово ускорение возникает на камне или на кулисе, когда они образуют поступательную кинематическую пару с качающимся ползуном 3 (рис. 3). В механизмах с качающимся ползуном кориолисово ускорение откладывается из полюса π плана аналогов ускорений звеньев механизма.
Рис. 3. Рычажный механизм с качающимся ползуном 3
Французским ученым Густавом Гаспаром Кориолисом в 1831 г. установлено существование вектора ускорения при любом движении тела во вращающейся системе, перпендикулярного оси вращения и скорости данного тела. Ученым было установлено, что кориолисово ускорение не зависит от положения тела [6].
В плоских механизмах вектор кориолисова ускорения расположен в плоскости действия векторов ускорений других звеньев.
При графическом определении аналогов скоростей направление вектора скорости соответствует движению кулисы относительно мгновенного центра – камня (рис. 4, а). В действительности камень перемешается по кулисе, а не наоборот, и направление его движения (рис. 4, б) относительно кулисы будет противоположным тому, как это показано на плане скоростей. Поэтому в исследуемом положении механизма при построении планов ускорений направление кориолисова ускорения по отношению к вектору нормального ускорения кривошипа будет встречным (см. рис. 2 и 4, д).
Подробно рассмотрим процедуру определения направления, модуля и масштаба кориолисова ускорения камня в пятом положении механизма.
Известно, что направление кориолисова ускорения определяется поворотом относительной скорости камня на 90° по направлению переносной угловой скорости ω2 кулисы вокруг опоры О2 (рис. 4, в). Однако значения указанных скоростей на данном этапе исследования не известны и потому определить действующее на звено кориолисово ускорение не представляется возможным.
а б в г д
Рис. 4. Определение кориолисова ускорения камня
Известно, что направление кориолисова ускорения и определяемого его аналога совпадают, так как совпадают направления скоростей звеньев и ускорений с направлениями соответствующих им аналогов скоростей и ускорений в любых конкретных положениях механизма.
Затем определим модуль аналога кориолисова ускорения, для чего значение аналога относительной скорости камня , равное аналогу скорости кулисы (рис. 4, а, б) или l’2, но противоположное ему по направлению, умножим на удвоенное значение аналога переносной угловой скорости звена, на котором находится камень, т. е. на φ’2.
Таким образом, полученный вектор аналога кориолисова ускорения, как указывалось выше, будет направлен навстречу вектору нормального ускорения кривошипа, и его значение определяется по формуле
, (18)
.
Проведем через точку а плана ускорений линию, перпендикулярную положению кулисы, и отложим на ней масштаб кориолисова ускорения (рис. 2):
, (19)
.
Через точки k и n2 плана ускорений проводим прямые, перпендикулярные векторам кориолисова ускорения и нормального соответственно. Место пересечения этих прямых определит положение а3 – окончание вектора искомого ускорения кинематической пары А3.
Модули аналогов углового ускорения кулисы и аналога линейного ускорения камня находим по формулам
, , (20)
, .
Если аналог полного ускорения кинематической пары А3 кулисы 3, расположенной на размере l2 от центра вращения О2, пропорционален отрезку (πа3), то отрезок, пропорциональный аналогу полного ускорения вершины кулисы С, найдем по теореме подобия:
, откуда , (21)
.
Известно, что плечи кулисы (А3О2) и (СО2) образуют угол α=180º, поэтому вектор аналога полного ускорения длиной (πс) откладываем от полюса плана ускорений в противоположную сторону так, чтобы данные ускорения образовывали угол, равный α.
Найдем значение аналога нормального ускорения шатуна 4:
, (22)
Вектор аналога нормального ускорения шатуна 4, параллельный положению звена, примыкает к точке с плана ускорений и направлен к мгновенному центру вращения кинематической паре С. Изображающий его на плане отрезок
, (23)
.
При построении планов аналогов ускорений показать векторы малых размеров не представляется возможным. Поэтому считаем, что координаты с и п4 на плане совпадают.
Через п4 проводим прямую тангенциального ускорения шатуна 4 перпендикулярно построенной линии положения аналога нормального ускорения , а через полюс π – вертикальную прямую положения полного аналога ускорения ползуна 5.
Точка d пересечения прямых определяет масштабы ускорений и , а затем модули искомых величин:
, (24)
,
, (25)
,
откуда аналоги углового ускорения звена 4 и линейного ускорения ползуна 5 равны
, . (26)
Для того чтобы определить проекции аналога ускорения центра масс звена, необходимо знать его координаты на звене.
По условию центр масс S3 кулисы расположен на расстоянии lO2S3 = 0.1 м от центра вращения О2. Для определения положения центра масс на плане ускорений составим пропорцию
, . (27)
На плане S3 принадлежит вектору ускорения .
Найдем проекции аналога ускорения центра масс звена 3 на координатные оси. Для этого измерим линейкой на плане ускорений соответствующие проекции вектора S»3, а затем умножим полученные величины на масштабный коэффициент плана аналога ускорения и поделим на квадрат обобщенной координаты механизма:
, , (28)
где (πS3)X и (πS3)Y – проекции S»3 аналога ускорения центра масс звена 3 на оси координатной системы с центром, совпадающим с полюсом π5. Так как вектор аналога скорости принадлежит третьей четверти координатной системы, его проекции отрицательны и, следовательно, S»3X<0 и S»3Y<0.
Составим таблицу значений величин кинематических параметров, найденных аналитически и графически, и убедимся в том, что отклонение между ними удовлетворяет рекомендуемому условию.
Таблица 2. Результаты расчета аналогов скоростей и ускорений звеньев
Величина
, м
, м
, м
, м
Аналитически
Графически
Отклонение
В заключение построим план аналогов скоростей (рис. 5) звеньев механизма с качающимся ползуном 3 (рис. 3), в котором кулиса 2 механизма вращается со скоростью относительно одноподвижной кинематической пары А и движется поступательно относительно опоры С или О со скоростью . Отметим, что мгновенный центр вращения кулисы А перемещается вокруг центра О со скоростью , масштаб ра которой выбирается произвольно.
Рис. 5. План аналогов скоростей механизма с качающимся ползуном
Аналог угловой и линейной скоростей звена 2 определим графо-аналитически из выражений
, м, (29)
что позволит далее определить модуль кориолисова ускорения.
В механизмах с качающимся ползуном вектор , обозначенный на плане отрезком (πk), откладывается от полюса плана π, и его направление совпадает с направлением вектора аналога скорости –– (pb), который повернут на 90° в сторону углового перемещения φ’2 звена 2. Укажем, что направление вращения относительно полюса р (рис. 5) определено направлением вектора – (ab), т. е. в рассматриваемом положении поворот следует провести против движения часовой стрелки.
Местоположение b на плане аналогов ускорений (рис. 6) определено пересечением векторов и , входящих в выражения суммы векторов
и . (30)
Рис. 6. План аналогов ускорений механизма с качающимся ползуном
Найденный масштаб векторов тангенциального ускорения , равный (n2b), и относительного , равный (kb), позволит определить аналоги углового и линейного ускорений кулисы соответственно:
, м. (31)
Для закрепления изложенного выше материала представим алгоритм определения кинематических параметров синусного механизма (рис. 7) и механизма с ведущей кулисой. Обе схемы механизмов включают две поступательных С, D и вращательных О, В пары.
При построении планов аналогов ускорений звеньев синусного механизма, в состав которого входит группа Ассура пятого вида, следует учесть то, что звено 2 механизма, структурно классифицируемое камнем, движется вдоль ползуна 3, совершающего поступательное гармоническое движение относительно опоры D. В таком случае на звено 2 не действует кориолисово (поворотное) ускорение, поскольку оно при описанных условиях движения звеньев 2 и 3 не возникает.
Рис. 7. Синусный механизм a), план аналогов скоростей b), ускорений звеньев c)
На рис. 8 показан механизм с ведущей кулисой 1 с присоединенной к ней группой Ассура четвертого вида. План аналогов скоростей звеньев механизма удовлетворяет выражению
. (32)
Воспользуемся найденными графически значениями аналогов скоростей
м, м (33)
и построим план аналогов ускорений, удовлетворяющий выражению
, (34)
где (мм).
Рис. 8. Механизм с ведущей кулисой а), план аналогов скоростей b) ускорений c)
Аналоги ускорения камня 2 и ползуна 3 вычисляются по формулам
м, м.
Одним из результатов исследований является определение силы Кориолиса Fк, действующей на тело i,
, (35)
где mi – масса тела, движущегося во вращающейся системе; – ускорение Кориолиса.
Несмотря на то, что действующая на Земле сила Кориолиса очень мала, она приводит к целому ряду весьма важных эффектов. Ее присутствие объясняет закон Бэра: у рек в северном полушарии, несущих свои воды к северному полюсу Земли, правый берег более крутой и подмытый, чем левый, а в южном полушарии – наоборот. В этом случае сила Кориолиса прижимает воду к берегу в направлении вращения Земли, т. е. к правому – в северном полушарии и к левому – в южном.
Сила Кориолиса приводит и к отклонению падающих тел к востоку. Этот эффект послужил одним их экспериментальных доказательств теории Кориолиса. В 1833 г. в Фрейбурской шахте немецкий физик Ф. Райх провел эксперименты, показавшие, что при свободном падении тел с высоты 158 м их отклонение в среднем, по проведенным 106 опытам, составляет 28,3 мм.
Аналог — скорость
Cтраница 1
Аналоги скоростей и ускорений часто применяются при динамическом анализе механизмов в тех случаях, когда предварительное их определение как характеристик, не зависящих от времени, облегчает нахождение законов движения начальных звеньев.
[1]
Аналогом скорости точки какого либо звена механизма является первая производная радиуса-вектора этой точки по обобщенной координате механизма. Аналогом угловой скорости звена механизма называется первая производная угловой координаты этого звена по обобщенной координате механизма.
[2]
Традиционно аналог скорости и перемещение выходного звена при заданном законе ускорения определяются интегрированием этого ускорения по обобщенной координате — углу поворота кулачка. Основные размеры кулачка определяются из условия ограничения угла давления графическими методами, в основе которых лежит построение диаграммы изменения аналога скорости в функции перемещения толкателя.
[3]
Величины аналогов скоростей и ускорений впервые были использованы Л. В. Ассуром при кинематическом исследовании механизмов.
[4]
Так как аналог скорости S2 в начале и конце фазы фп равен нулю ( рис. 26.12, б), то площади прямоугольников ADEF и FGHK.
[5]
Определим сначала аналоги скоростей и ускорений звеньев.
[6]
Так как аналоги скоростей и ускорений зависят только от обобщенной координаты и не зависят от времени, то кинематическое исследование механизмов можно вести чисто геометрическим путем. Для этого, если ведущее звено входит во вращательную пару, поворачивают его на углы р и определяют перемещения всех остальных звеньев.
[7]
Так как аналоги скоростей и ускорений зависят только от обобщенной координаты и не зависят от времени, то кинематическое исследование механизма можно вести чисто геометрическим путем. Для этого, если ведущее звено входит во вращательную пару, поворачивают его на углы ф и определяют перемещения всех остальных звеньев.
[8]
Определим сначала аналоги скоростей и ускорений звеньев.
[9]
Итак, аналоги скоростей и ускорений зависят только от обобщенной координаты и не зависят от времени; следовательно, кинематическое исследование можно проводить чисто геометрическим путем. Для этого, если ведущее звено вращается вокруг некоторой точки, поворачивают его на угол ф, считая от некоторого положения, принятого за начальное, и определяют перемещения всех остальных звеньев. Далее, если требуется определить скорости и ускорения &-го звена и принадлежащей ему точки М, то находят аналоги скоростей и ускорений сокср, е / сср, VMV, Мер и подставляют их значения в уравнения, приведенные выше: таким образом получаем значения истинных скоростей и ускорений.
[10]
Сначала находим аналог скорости центра ролика dsB / d ( p / i /, где г / di) / dcp — аналог угловой скорости коромысла. Значения / / откладываются на фазе подъема от центра вращения С, если кулачок и коромысло вращаются в противоположных направлениях, и к центру С, если они вращаются в одну сторону.
[11]
Если диаграмма аналога скорости имеет точки разрыва ( рис. 131, а), то в месте скачкообразного изменения скорости теоретически ускорение достигает бесконечности, бесконечно большими должны быть и динамические нагрузки. Такое явление называется жестким ударом. Такому удару подвергается и кулачок и толкатель. Практически вследствие упругости звеньев бесконечно большой динамической нагрузки не получается, но величина ее оказывается все-таки очень большой. Законы движения толкателя, при которых получаются жесткие удары, можно применять только в тихоходных механизмах.
[12]
Если диаграмма аналога скорости имеет точки разрыва ( рис. 131, а), то в месте скачкообразного изменения скорости теоретически ускорение достигает бесконечности, бесконечно большими должны быть и динамические нагрузки. Такое явление называется жестким ударом. Практически вследствие упругости звеньев бесконечно большой динамической нагрузки не получается, но величина ее оказывается все-таки очень большой. Законы движения толкателя, при которых получаются жесткие удары, можно применять только в тихоходных механизмах.
[13]
Внутри скобок стоят аналоги скоростей и si и wv, которые характеризуют передаточные свойства механизма. Из уравнения (4.21) следует, что приведенный момент инерции 1 У механизма от его закона движения не зависит и является характеристикой самого механизма.
[14]
Внутри скобок стоят аналоги скоростей vqsi и со, которые характеризуют передаточные свойства механизма. Из уравнения (4.21) следует, что приведенный момент инерции / vp механизма от его закона движения не зависит и является характеристикой самого механизма.
[15]
Страницы:
1
2
3
4
3) Дифференцируя
уравнения функции положения точки D по
q, мы получаем аналог скорости точки D:
Дифференцируя уравнения второй
раз, мы получаем аналог ускорения точки D:
4) Группа
ВВП:
Дифференцируя выражение 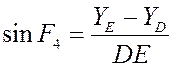
:
Дифференцируя уравнение второй
раз, мы получаем аналог углового ускорения :
Напомним уравнения геометрического анализа для группы ВВП:
Дифференцируя уравнения
геометрического анализа для группы ВВП по q, мы
получаем следующее:
Дифференцируя уравнения второй
раз, мы получаем следующее:
Приведём к более удобному виду:
Якобианом системы уравнений
группы ВВП будет являться определитель следующей матрицы:
Здесь 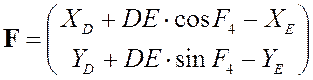
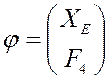
Когда якобиан
обращается в ноль, мы получаем:
Следовательно,
якобиан обращается в ноль при ,
. Это означает, что якобиан обращается в
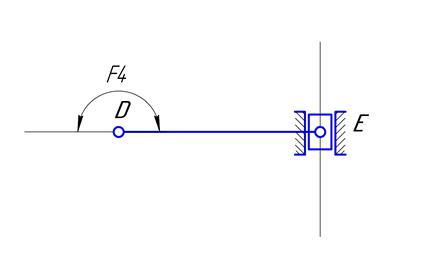
ноль в тех положениях, при которых шатун DE расположен перпендикулярно
вертикальной прямой, по которой ходит ползун E.
Это – особое (сингулярное) положение группы BBП. В
действительности же этого не происходит, так как не выполняется условие
существования группы ВВП:
Рис.3.1. Особое
положение группы ВВП
Аналог скорости и ускорения точки
E определяется по
формулам:
Все расчёты представлены в
приложении в протоколе MathCad.
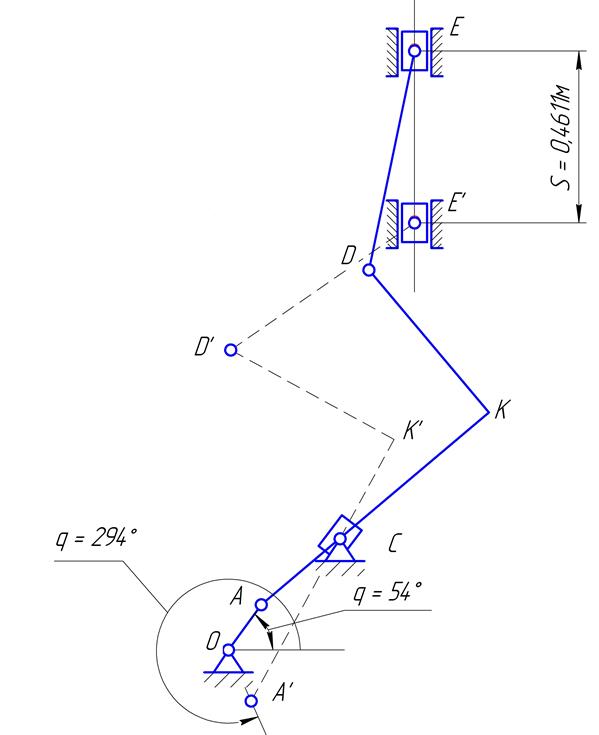
3.2.
Механизм в крайних положениях
Рис.3.2. Механизм в
крайних положениях
3.3.
Планы аналогов скоростей и ускорений
1) а)
План аналогов скоростей при .
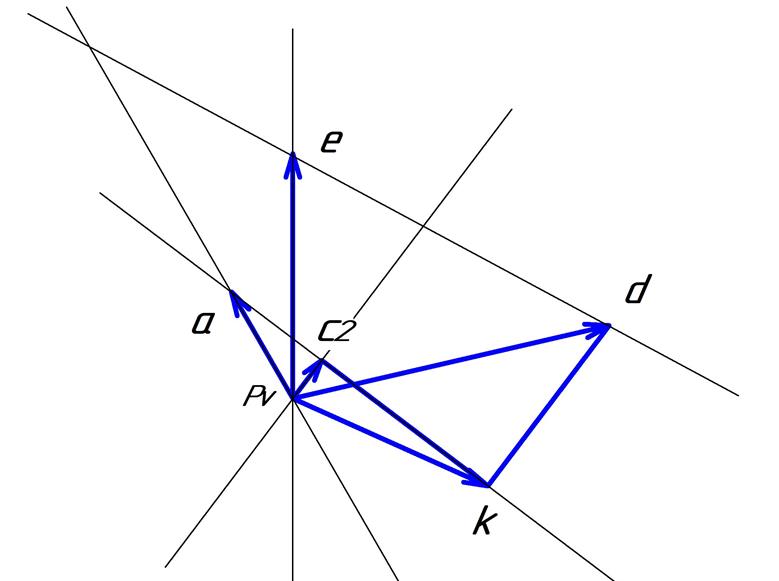
Рис.3.3.
План аналогов скоростей при
Для построения плана аналогов скоростей выберем полюс и масштаб:
Уравнение для группы ВПВ:
Точка C неподвижна
Аналог угловой скорости определяется выражением:
Уравнение для группы ВВП:
Аналог угловой скорости определяется выражением:
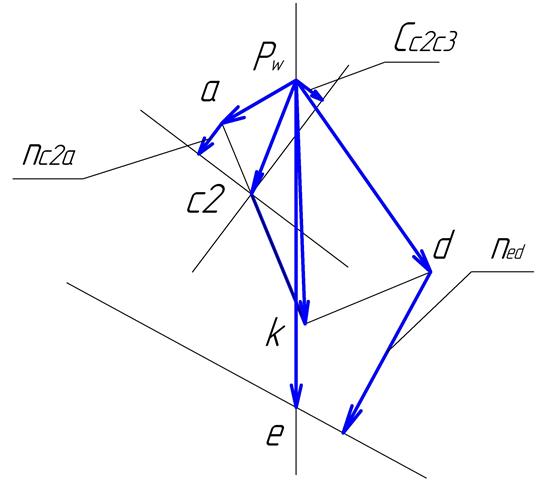
б) План аналогов ускорений при .
Рис.3.4.
План аналогов ускорений при
Для построения плана аналогов ускорений
выберем полюс и
масштаб:
Уравнения для группы ВПВ:
Точка C неподвижна
Тогда:
Аналог ускорения кориолиса точки С3относительно точки С2 определяется выражением:
Аналог нормальной составляющей
ускорения точки С2 относительно точки A определяется выражением:
Аналог углового ускорения определяется выражением:
Уравнение для группы ВВП:
Аналог нормальной составляющей
ускорения точки E относительно
точки D определяется
выражением:
Аналог углового ускорения определяется выражением:
Направление аналогов угловых
скоростей и ускорений показано на рис.3.5.
Рис.3.5. Направление
аналогов скоростей и ускорений при
Расчёт по представленным выше
формулам с учётом знаков (все линейные размеры в метрах):
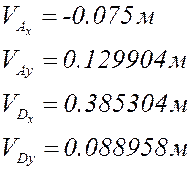
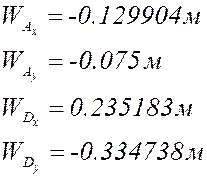
План аналогов скоростей и
ускорений в крайнем положении при представлен в приложении
2.
Расчёт для
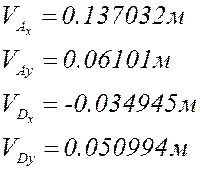
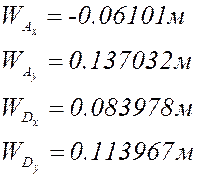
4.
Графики функции положения и её производных по обобщенной координате
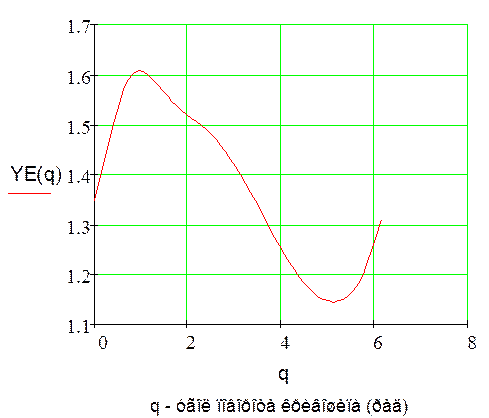
График функции положения
точки Е.
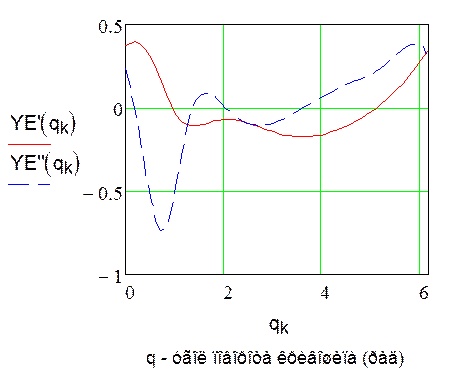
1.4.1. График
аналогов скорости и ускорения точки Е.
— аналог
скорости точки Е
— аналог
ускорения точки Е
5. Сравнение
результатов расчётов, полученных разными методами
При .