Как найти апофему зная площадь

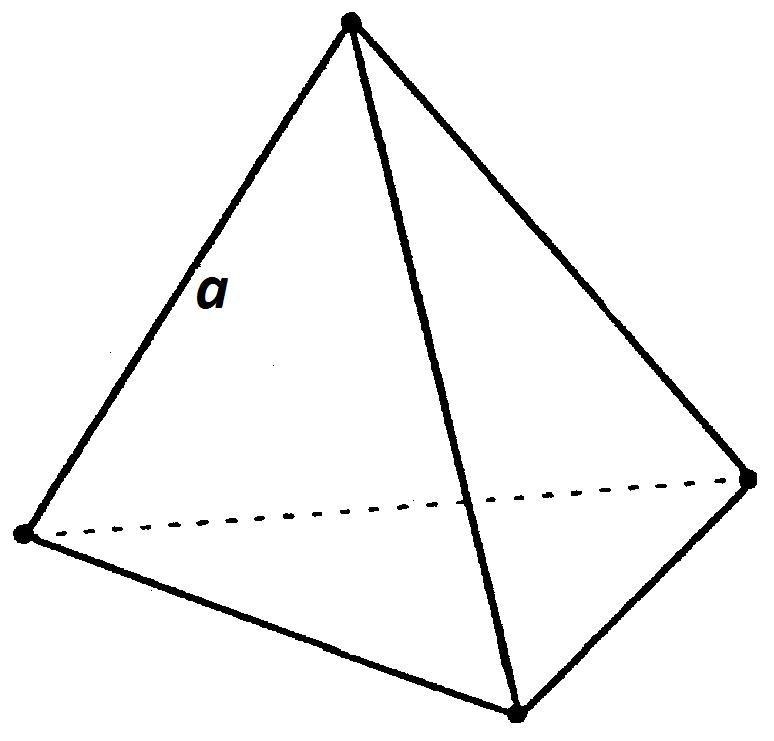
У треугольной пирамиды и в основании находится треугольник, и боковые грани являются треугольниками. То есть, апофема треугольной пирамиды — это обычная высота треугольника, который является боковой гранью.

Если речь о правильной пирамиде, то все боковые грани таковой являются равнобедренными треугольниками. Потому высота, проведенная к основанию, является медианой и биссектрисой.

Поэтому апофема определяется по теореме Пифагора, где ребро является гипотенузой, половина основания является первым катетом, а апофема — вторым.

Или же рассчитываем апофему, зная площадь боковой грани и основания: S= ah/2, h = 2S/a.

Апофема пирамиды. Формулы для апофемы правильной треугольной пирамиды

Пирамида — это пространственный полиэдр, или многогранник, который встречается в геометрических задачах. Основными свойствами этой фигуры являются ее объем и площадь поверхности, которые вычисляются из знания любых двух ее линейных характеристик. Одной из таких характеристик является апофема пирамиды. О ней пойдет речь в статье.

Фигура пирамида

Прежде чем приводить определение апофемы пирамиды, познакомимся с самой фигурой. Пирамида представляет собой многогранник, который образован одним n-угольным основанием и n треугольниками, составляющими боковую поверхность фигуры.

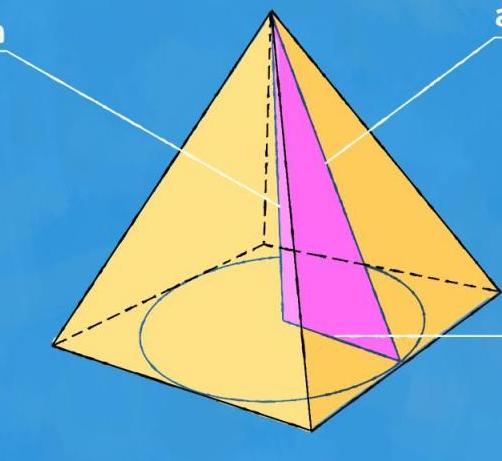
Всякая пирамида имеет вершину — точку соединения всех треугольников. Перпендикуляр, проведенный из этой вершины к основанию, называется высотой. Если высота пересекает в геометрическом центре основание, то фигура называется прямой. Пирамида прямая, имеющая равностороннее основание, называется правильной. На рисунке показана пирамида с шестиугольным основанием, на которую смотрят со стороны грани и ребра.

Апофема правильной пирамиды

Ее также называют апотемой. Под ней понимают перпендикуляр, проведенный из вершины пирамиды к стороне основания фигуры. По своему определению этот перпендикуляр соответствует высоте треугольника, который образует боковую грань пирамиды.

Поскольку мы рассматриваем пирамиду правильную с n-угольным основанием, то все n апофем для нее будут одинаковыми, поскольку таковыми являются равнобедренные треугольники боковой поверхности фигуры. Заметим, что одинаковые апофемы являются свойством правильной пирамиды. Для фигуры общего типа (наклонной с неправильным n-угольником) все n апофем будут разными.

Еще одним свойством апофемы пирамиды правильной является то, что она одновременно является высотой, медианой и биссектрисой соответствующего треугольника. Это означает, что она делит его на два одинаковых прямоугольных треугольника.

Треугольная пирамида и формулы для определения ее апофемы

В любой правильной пирамиде важными линейными характеристиками являются длина стороны ее основания, ребро боковое b, высота h и апофема h_b. Эти величины друг с другом связаны соответствующими формулами, которые можно получить, если начертить пирамиду и рассмотреть необходимые прямоугольные треугольники.

Правильная треугольная пирамида состоит из 4 треугольных граней, причем одна из них (основание) должна быть обязательно равносторонней. Остальные являются равнобедренными в общем случае. Апофему треугольной пирамиды можно определить через другие величины по следующим формулам:

Первое из этих выражений справедливо для пирамиды с любым правильным основанием. Второе выражение характерно исключительно для треугольной пирамиды. Оно показывает, что апофема всегда больше высоты фигуры.

Не следует путать апофему пирамиды с таковой для многогранника. В последнем случае апофемой называется перпендикулярный отрезок, проведенный к стороне многогранника из его центра. Например, апофема равностороннего треугольника равна √3/6*a.

Задача на вычисление апофемы

Пусть дана правильная пирамида с треугольником в основании. Необходимо вычислить ее апофему, если известно, что площадь этого треугольника равна 34 см 2 , а сама пирамида состоит из 4 одинаковых граней.

В соответствии с условием задачи мы имеем дело с тетраэдром, состоящим из равносторонних треугольников. Формула для площади одной грани имеет вид:

Откуда получаем длину стороны a:

Для определения апофемы h_b воспользуемся формулой, содержащей боковое ребро b. В рассматриваемом случае его длина равна длине основания, имеем:

Подставляя значение a через S, получим конечную формулу:

Мы получили простую формулу, в которой апофема пирамиды зависит только от площади ее основания. Если подставить значение S из условия задачи, то получим ответ: h_b ≈ 7,674 см.

Апофема правильной пирамиды, формула

Апофема правильной пирамиды находится по формуле

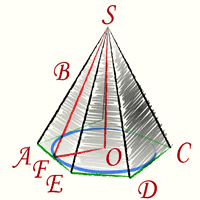
f — апофема правильной пирамиды (SF)
n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника (AB или BC или CD или DE или EA) — основания правильной пирамиды
h — высота правильной пирамиды (OS)

Апофема правильной пирамиды выводится из следующих формул

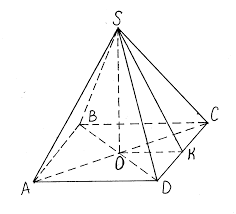
Синим цветом на рисунке изображена вписанная в основание правильной пирамиды окружность. Треугольник SFO прямоугольный. Его стороны: OS — высота правильной пирамиды ( h), OF — радиус вписанной окружности в правильный многоугольник (основание правильной пирамиды ( r)), SF — апофема правильной пирамиды ( f). По теореме Пифагора

подставив сюда только радиус вписанной окружности получается формула (1).

Апофема правильной треугольной пирамиды: формула и пример задачи

При изучении характеристик пространственных фигур в курсе стереометрии большое внимание уделяется таким свойствам, как площадь и объем. В то же время знать линейные параметры фигур важно, чтобы иметь возможность рассчитать указанные свойства. В данной статье ответим на вопрос, как найти апофему пирамиды правильной треугольной.

Какая фигура будет рассмотрена?

Треугольная пирамида с правильным основанием представляет собой фигуру в пространстве, которая ограничена одним равносторонним треугольником (основание) и тремя равнобедренными треугольниками (боковые стороны). Чтобы иметь возможность более четко представить эту пирамиду, покажем ее на рисунке.

Вам будет интересно: Зазноба — это . Значение слова

Важной точкой любой пирамиды является ее вершина, которая не принадлежит основанию. Если опустить перпендикуляр из нее на основание, то его длина будет высотой фигуры. В дальнейшем будем обозначать высоту буквой h. Высота правильной пирамиды падает точно в геометрический центр треугольника (точка пересечения его медиан, а также биссектрис и высот). Вторым линейным параметром, который следует знать, является длина стороны основания треугольной пирамиды, то есть длина стороны равностороннего треугольника. Обозначим ее буквой a.

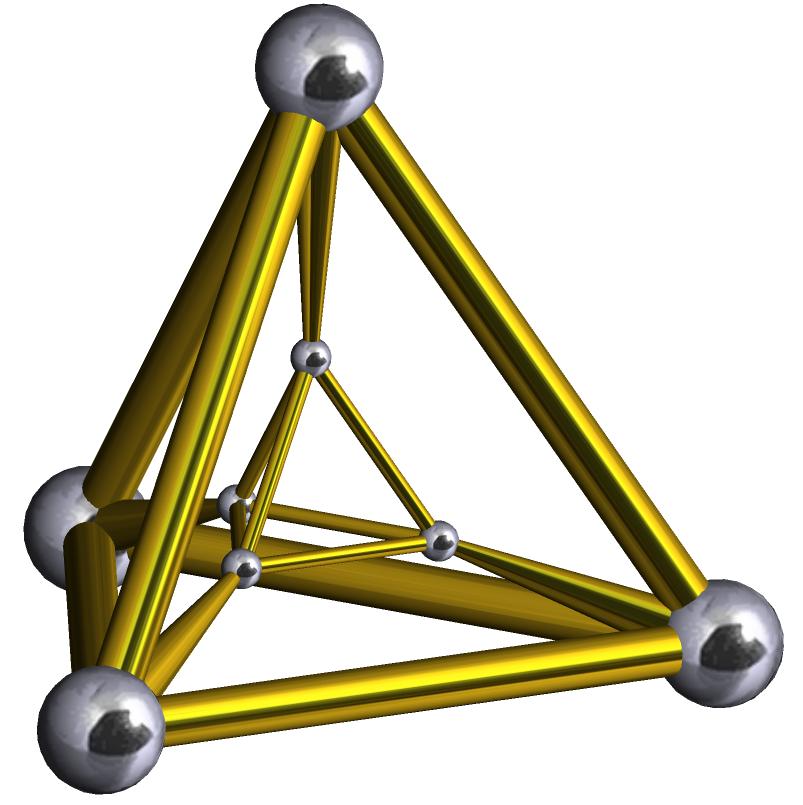
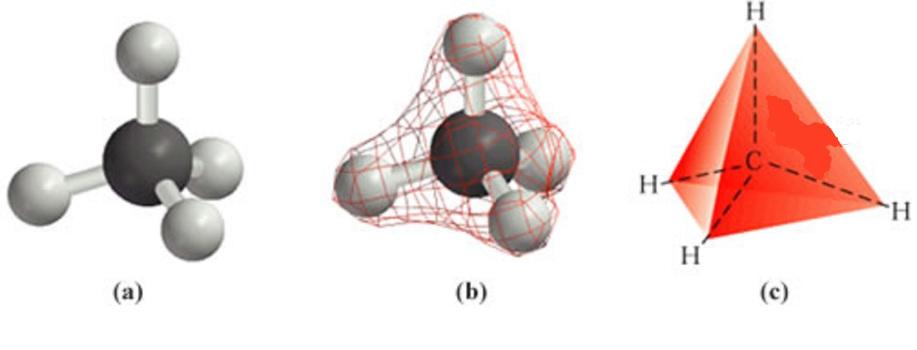
Треугольная пирамида имеет собственное название — тетраэдр. Тетраэдр не является чисто теоретической геометрической фигурой. Она также встречается в некоторых природных структурах. Так, в алмазе атом углерода соединен с четырьмя такими же атомами, которые образуют тетраэдр. Другой пример — это молекула метана, в которой углерод, соединенный с четырьмя атомами водорода, образует правильную треугольную пирамиду.

Формула апофемы пирамиды правильной треугольной

Перейдем непосредственно к вопросу статьи. Для треугольной пирамиды правильной апофемой называется любая из высот боковых треугольников, опущенная из вершины фигуры. Обозначим ее hb. Поскольку рассматриваемая фигура состоит из трех боковых треугольников, которые равны друг другу, то она имеет три одинаковых апофемы hb.

Определение длины апофемы не составляет большого труда. Предположим, что высота h и длина стороны a известны. Проводим высоту фигуры и рассматриваем треугольник прямоугольный, который находится внутри пирамиды и образован следующими сторонами:

• апофемой hb (гипотенуза);
• высотой h (один катет);
• 1/3 медианы m равностороннего треугольника (второй катет).

Длина медианы m треугольника в основании равна:

Пользуясь теоремой Пифагора, получаем формулу для длины апофемы hb:

Эта формула показывает, что длина апофемы hb для любых параметров треугольной пирамиды всегда больше ее высоты h.

Решение задачи на определение значения hb

Решим интересную задачу. Рассчитаем длину апофемы для тетраэдра, у которого все ребра равны друг другу.

Обозначим длину ребра буквой a. Она же является стороной треугольника в основании. Чтобы определить hb, необходимо найти h. Сделать это не сложно, если рассмотреть прямоугольный треугольник, образованный высотой h, ребром a и двумя третями медианы m. Получаем:

h = √(a2 — 4/9*m2) = √(a2 — 4/9*3/4*a2) = a*√(2/3)

Теперь применяем формулу для апофемы, получаем:

hb = √(a2/12 + h2) = √(a2/12 + 2/3*a2) = √3/2*a

Мы получили очевидный результат. Апофема правильной пирамиды треугольной равна длине медианы любого из равносторонних треугольников.

Пирамидой в стереометрии называется объёмная фигура, образуемая многоугольником и расположенной вне
его плоскости точкой. Эта точка соединена с точками в вершинах многоугольника отрезками, которые
называются рёбрами пирамиды. Сам многоугольник — это основание пирамиды. При треугольном
основании пирамида будет носить название треугольной, при четырёхугольном – четырёхугольной, и так
далее.

Приведём варианты вычисления апофемы правильной четырёхугольной пирамиды в зависимости от исходных
данных пространственной фигуры. Заданная пирамида обозначена SABCD, где S – вершина, а ABCD –
вершины квадрата в основании.

Вычисление апофемы при известных значениях высоты пирамиды и ребра основания

Апофема пирамиды при известных значениях её высоты SO и стороны квадрата в основании AD=DC=BC=AB
вычисляется по формуле гипотенузы для прямоугольного треугольника SOK. В этом треугольнике одним из
катетов будет высота SO, вторым – половинное значение заданной стороны основания OK=1/2 AD.
Значит: SK²= OK²+ SO² или SK= (1/2 AD) ²+ SO²)
или

L = √ (H² + (a / 2 tan45º)²)

где H — высота, a — ребро основания.

Пример. Пусть высота SO = 4, а сторона основания AD = 6. Тогда апофема L находится
следующим образом: L = √ (( 6 / 2)² + 4²) = 5

Вычисление апофемы при известном значении бокового ребра и ребра основания

При известном значении бокового ребра SD и стороны основания CD для нахождения апофемы SK также
используется теорема Пифагора. В этом случае рассматривается прямоугольный треугольник SKD,
гипотенузой которого выступает боковое ребро SD, одним из катетов – отрезок стороны основания DK, а
вторым – апофема SK. Первый катет равен половине стороны квадрата в основании, поскольку апофема
равнобедренного треугольника, коим является боковая грань пирамиды, является для него и медианой,
делящей основание пополам: DK = 1/2 DC. Отсюда следует, что SD²= DK²+ SK², а SK²= SD²- DK² или, подставляя, получаем выражение:
SK² = SD² — (1/2 DC)², откуда SK = √(SD² — (1/2 DC )²)
или

L = √ (b² — (a / 2)²)

где a — ребро основания, b — боковое ребро.

Пример. Пусть боковое ребро SD равно 5, а сторона основания – 6. Тогда, подставляя
указанные числовые значения, вычисляем значение апофемы: SK =5² – (6 / 2)² ) = 4.

Нахождение апофемы при заданной площади боковых поверхностей и известном ребре основания

Апофема при известной суммарной площади боковых поверхностей Sбок и значении ребра основания CD
вычисляется по следующей схеме. Вначале следует определить площадь каждой из четырёх граней, что
легко сделать, зная, что все они для правильной пирамиды равны между собой. Поэтому общая площадь
делится на четыре равные части: Ssdc = Sбок /4. Затем, при известном
значении площади боковой грани и ребра основания, по формуле площади равнобедренного треугольника
находится его высота, то есть искомая апофема: Ssdc = ½ SK * CD откуда
SK = 2Ssdc / CD. Или, подставляя выведенную площадь грани, SK = 2(Sбок /4) / CD. Преобразив, получаем: SK = Sбок /2CD
или

L = Sбок / 2a

где Sбок — площадь боковых поверхностей, a — ребро основания.

Пример. Допустим, в задаче задана общая площадь боковой поверхности правильной
четырёхугольной пирамиды Sбок = 48 и ребро основания CD = 6. Найдём, используя выведенную формулу,
значение апофемы: SK = 48 / 2 * 6 = 4.

Вычисление апофемы при заданной площади боковых поверхностей и площади основания

Апофема при известных значениях суммарной площади боковых поверхностей Sбок и площади основания Sосн
вычисляется следующим образом. В первую очередь следует найти ребро основания. Площадь основания
пирамиды – квадрата – является произведением двух его сторон либо квадратом стороны. Значит,
значение стороны основания вычисляем по формуле Sосн = CD² или CD = √Sосн. Теперь, зная суммарную площадь боковой поверхности
четырёхугольной пирамиды, делением на 4 находим площадь боковой грани – равнобедренного треугольника
SCD: Ssdc = Sбок / 4. Его площадь также вычисляется, как произведение
основания на высоту, делённое на два: Ssdc =½CD * SK или Sбок/4 =½CD * SK отсюда SK = 2 (Sбок / 4) / CD
или, сократив и подставив выражение для CD: SK = Sбок / 2 Sосн, где SK –
высота грани и искомая апофема.

L = Sбок / (2 * √Sосн)

где Sбок — площадь боковых поверхностей, Sосн — площадь основания.

Пример. Возьмём для примера численные значения, Sбок = 48 и Sосн = 36. Подставляя,
получаем результат: SK = 48 / (2 * √36) = 4.

Вычисление апофемы при заданной площади боковых поверхностей и радиусе описанной вокруг основания
окружности

Найдём апофему при известной площади боковых поверхностей Sбок и радиусе R описанной вокруг основания
ABCD окружности. Рассмотрим прямоугольный треугольник COD, образованный половинами диагоналей этого
квадрата CO и OD, равными заданному радиусу, и гранью в основании CD. Эта сторона в данном
треугольнике выступает гипотенузой. Её можно вывести из теоремы Пифагора: CD² = OD² + OC²,
откуда CD = √(OD²+OC²) или CD = √2R²= R√2.
Теперь определим площадь каждой боковой грани. Она находится путём деления площади полной боковой
поверхности пирамиды на 4: Ssdc = Sбок / 4. По формуле, связывающей
площадь равнобедренного треугольника SDC с его высотой и основанием, выделяем высоту-апофему: Ssdc =½CD * SK Или, подставляя выведенное выше выражение: Sбок/4 = ½CD * SK. Далее преобразовываем для выделения SK: SK=(2 Sбок/4) / CD или, подставляя выведенное для CD выражение и
сокращая, получаем: SK= Sбок / 2R * √2.

L = Sбок / 2R * √2

где Sбок — площадь боковых поверхностей, R — радиус описанной окружности.

Пример. Подставляя для примера числовые значения R = 3√2 и Sбок = 48, получаем в
результате значение апофемы: SK=48 / 2 * (3√2 * √2)=4.

Способ вычисления апофемы при известной площади боковых поверхностей и диагональ основания

Поскольку стороны квадрата ABCD в основании равны и угол между смежными сторонами прямой, значения
этих сторон можно найти, рассматривая прямоугольный треугольник ADC, где заданная диагональ AC
является гипотенузой, а неизвестные стороны AD и CD – равными катетами. Вычисляем их значения по
теореме Пифагора: AC² = AD² + CD² = 2CD² откуда CD = √(AC² / 2)  = AC / √2. Найденное
значение стороны основания позволяет найти апофему — высоту боковой грани SK — при
известной площади этой грани. Суммарная площадь боковой поверхности заданной фигуры Sбок даёт
возможность найти площадь каждой её боковой плоскости. То есть Sscd = Sбок / 4. А теперь Sscd иначе выразим через высоту и основание
грани: Sscd = 1/2 * (SK * CD) или, подставляя ранее выведенную формулу для
CD: Sscd = 1/2 * (SK * ( AC / √2). Теперь все данные кроме искомой апофемы
SK у нас присутствуют, поэтому преобразуем выражение, заменяя SSCD и сокращая: SK= 2 * √2 * Sscd / AC = 2 * √2 (Sбок / 4) / AC = Sбок * √2 / 2АС.

L = Sбок / (2 * √(D² / 2))

где Sбок — площадь боковых поверхностей, D — диагональ основания.

Пример. Допустим, диагональ в основании равна 6√2, а суммарная площадь боковых
граней – 48. Тогда, подставляя числовые значения в полученное выше выражение, вычисляем: SK = 48√2 / 2 * (6√2) = 4

Нахождение апофемы при заданной площади боковых поверхностей и известном периметре основания

Исходными данными, на которые можно опереться при вычислении апофемы для этой задачи, являются Sбок и
Росн. Известное значение периметра квадрата ABCD в основании пирамиды Росн даёт возможность найти
значение его сторон, которые равны между собой как стороны квадрата и находятся путём деления
периметра на 4 равные части: AB = BC = CD = AD = Рabcd / 4. Теперь ребро
CD, одновременно являясь основанием боковой грани SCD, позволяет вычислить её высоту SK – искомую
апофему, при известном значении боковой площади пирамиды. Площадь каждой из 4-х граней найдём путём
деления общей площади на равные части: Sscd= Sбок/4. Далее из формулы
площади равнобедренного треугольника SCD через высоту и основание найдём апофему SK.  Sscd = 1/2 * (SK * CD) или SK = 2* Sscd / CD. Подставляя
выведенные выше через общую площадь и периметр основания значения площади грани и ребро её основания
соответственно, получаем: SK = 2 * (Sбок / 4) / (Рabcd / 4). Или SK = 2Sбок / Рabcd

L = Sбок / (P / 2)

где Sбок — площадь боковых поверхностей, P — периметр основания.

Пример. Предположим, что площадь боковой поверхности Sбок равно 48, периметр
основания – 24. Подставляя данные числовые значения, получаем следующий результат: SK= 2 * (48 / 4) / (24 / 4) = 4.

Вычисление апофемы при заданных значениях площади полной поверхности пирамиды и ребра её
основания

Полная площадь поверхности Sполн в этом случае представляет собой сумму полной площади боковой
поверхности Sбок фигуры и площади квадрата в её основании – Sabcd, сторона которого CD задана
условием задачи. Апофему удобнее всего найти через площадь боковой грани, имея значение её
основания: Sscd = 1/2 * (SK * CD). Преобразуя формулу, получаем: SK = 2* Sscd / CD. Вычтя из площади полной поверхности пирамиды площадь
основания, которую можно найти при его заданном ребре, получаем полную площадь боковой поверхности:
Sполн= Sбок + Sabcd, откуда Sбок= Sполн — Sabcd. Здесь площадь квадрата в основании легко
найти, зная его ребро: Sabcd = CD² и тогда, подставляя: Sбок = Sполн — CD². Разделив Sбок на 4 равные части, получим
площадь боковой грани: Sбок / 4 = (Sполн- CD²) / 4= Sscd. Теперь,
подставив в формулу для вычисления высоты боковой грани найденное выражение, получим: SK = 2* ((Sполн — CD²) /4) / CD или, выполнив сокращение: SK = (Sполн — CD²) /2CD.

L = (Sпол / a — a) / 2

где Sполн — площадь полной поверхности, a — ребро основания.

Пример. Допустим, нам задана общая площадь фигуры S = 84, а ребро её основания – CD
= 6. Тогда, подставляя значения в полученное выражение, находим:
SK = (84 — 62) / (2 * 6) = 4.

Правильной пирамидой называется такая фигура, в основании которой лежит многоугольник с равными
сторонами, то есть правильный. При этом проекция вершины на его плоскость является центром вписанной
в это многоугольное основание и описанной вокруг него окружностей. Отличительными признаками
правильной четырёхугольной пирамиды являются квадрат в основании и лежащая в точке пересечения его
диагоналей проекция вершины на этот квадрат.

Боковые плоскости (грани) правильной пирамиды – равнобедренные треугольники. Основание каждого из них
одновременно является и стороной основания пирамиды.
Проведенная к основанию высота боковых
граней, имеющая для каждой из них одинаковое значение, называется апофемой. Это понятие применяется
при решении множества геометрических задач, в которых фигурирует правильная пирамида с квадратом в
основании. В зависимости от других исходных данных, апофема даёт возможность вычислить площадь
боковой поверхности фигуры, её высоту, длину ребер и сторону основания.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?