Как найти апостериорную вероятность события

Понимаем теорему Байеса

Время на прочтение
8 мин

Количество просмотров 35K

Перевод статьи подготовлен специально для студентов базового и продвинутого курсов «Математика для Data Science».

Теорема Байеса – одна из самых известных теорем в статистике и теории вероятности. Даже если вы не работаете с расчетами количественных показателей, вероятно, вам в какой-то момент пришлось познакомиться с этой теоремой во время подготовки к экзамену.

P(A|B) = P(B|A) * P(A)/P(B)

Вот так она выглядит, но что это значит и как работает? Сегодня мы это узнаем и углубимся в теорему Байеса.

Основания для подтверждения наших суждений

В чем вообще заключается смысл теории вероятности и статистики? Одно из наиболее важных применений относится к принятию решений в условиях неопределенности. Когда вы принимаете решение совершить какое-либо действие (если, конечно, вы человек разумный), вы делаете ставку на то, что после завершения этого действия оно повлечет за собой результат лучший, чем если бы этого действия не произошло… Но ставки – это вещь ненадежная, как же вы в конечном итоге принимаете решение делать ли тот или иной шаг или нет?

Так или иначе вы оцениваете вероятность успешного исхода, и, если эта вероятность выше определенного порогового значения, вы предпринимаете шаг.

Таким образом, возможность точно оценить вероятность успеха имеет решающее значение для принятия правильных решений. Несмотря на то, что случайность всегда будет играть определенную роль в конечном исходе, вам следует учиться правильно использовать эти случайности и оборачивать их в свою пользу с течением времени.

Именно здесь вступает в силу теорема Байеса – она дает нам количественную основу для сохранения нашей веры в исход действия по мере изменений окружающих факторов, что, в свою очередь, позволяет нам со временем совершенствовать процесс принятия решений.

Разберем формулу

Давайте еще раз посмотрим на формулу:

P(A|B) = P(B|A) * P(A)/P(B)

Здесь:

P(A|B) – вероятность наступления события А, при условии, что событие В уже случилось;
P(B|A) – вероятность наступления события В, при условии, что событие А уже случилось. Сейчас это выглядит как какой-то замкнутый круг, но мы скоро поймем, почему формула работает;
P(A) – априорная (безусловная) вероятность наступления события А;
P(B) – априорная (безусловная) вероятность наступления события В.

P(A|B) – это пример апостериорной (условной) вероятности, то есть такой, которая измеряет вероятность какого-то определенного состояния окружающего мира (а именно состояния, при котором произошло событие В). Тогда как P(A) – это пример априорная вероятности, которая может быть измерена при любом состоянии окружающего мира.

Давайте посмотрим на теорему Байеса в действии на примере. Предположим, что недавно вы закончили курс по анализу данных от bootcamp. Вы еще не получили ответа от некоторых компаний, в которых вы проходили собеседование, и начинаете волноваться. Итак, вы хотите рассчитать вероятность того, что конкретная компания сделает вам предложение об устройстве на работу, при условии, что уже прошло три дня, а они вам так и не перезвонили.

Перепишем формулу в терминах нашего примера. В данном случае, исход А (Offer) – это получения предложения о работе, а исход В (NoCall) – «отсутствие телефонного звонка в течение трех дней». Исходя из этого, нашу формулу можно переписать так:

P(Offer|NoCall) = P(NoCall|Offer) * P(Offer) / P(NoCall)

Значение P(Offer|NoCall) — это вероятность получения предложения при условии, что звонка нет в течение трех дней. Эту вероятность оценить крайне сложно.

Однако обратной вероятности, P(NoCall|Offer), то есть отсутствию телефонного звонка в течение трех дней, при учете, что в итоге вы получили предложение о работе от компании, вполне можно привязать какое-то значение. Из разговоров с друзьями, рекрутерами и консультантами вы узнаете, что эта вероятность небольшая, но иногда компания все же может сохранять тишину в течение трех дней, если она все еще планирует пригласить вас на работу. Итак, вы оцениваете:

P(NoCall|Offer) = 40%

40% — это неплохо и кажется, еще есть надежда! Но мы еще не закончили. Теперь нам нужно оценить P(Offer), вероятность выхода на работу. Все знают, что поиск работы – это долгий и трудный процесс, и возможно вам придется проходить собеседование несколько раз, прежде чем вы получите это предложение, поэтому вы оцениваете:

P(Offer) = 20%

Теперь нам осталось оценить P(NoCall), вероятность, что вы не получите звонок от компании в течение трех дней. Существует множество причин, по которым вам могут не перезвонить в течение трех дней – они могут отклонить вашу кандидатуру или до сих пор проводить собеседования с другими кандидатами, или рекрутер просто заболел и поэтому не звонит. Что ж, есть множество причин, по которым вам могли не позвонить, так что эту вероятность вы оцениваете как:

P(NoCall) = 90%

А теперь собрав это все вместе, мы можем рассчитать P(Offer|NoCall):

P(Offer|NoCall) = 40% * 20%/90% = 8.9%

Это довольно мало, так что, к сожалению, рациональнее оставить надежду на эту компанию (и продолжать отправлять резюме в другие). Если это все еще кажется немного абстрактным, не переживайте. Я чувствовал то же самое, когда впервые узнал про теорему Байеса. Теперь давайте разберемся, как мы пришли к этим 8,9% (имейте в виду, что ваша изначальная оценка в 20% уже была низкой).

Интуиция, стоящая за формулой

Помните, мы говорили о том, что теорема Байеса дает основания для подтверждения наших суждений? Так откуда же они берутся? Они берутся из априорной вероятности P(A), которая в нашем примере зовется P(Offer), по сути, это и есть наше изначальное суждение том, насколько вероятно, что человек получит предложение о работе. В нашем примере вы можете считать, что априорная вероятность – это вероятность того, что вы получите предложение о работе в тот же момент, когда покинете собеседование.

Появляется новая информация – прошло 3 дня, а компания вам так и не перезвонила. Таким образом мы используем другие части уравнения, чтобы скорректировать нашу априорную вероятность нового события.

Давайте рассмотрим вероятность P(B|A), которая в нашем примере называется P(NoCall|Offer). Когда вы впервые видите теорему Байеса, вы задаетесь вопросом: Как понять откуда взять вероятность P(B|A)? Если я не знаю, чему равна вероятность P(A|B), то каким магическом образом я должен узнать, чему равна вероятность P(B|A)? Я вспоминаю фразу, которую однажды сказал Чарльз Мангер:

«Переворачивайте, всегда переворачивайте!»
— Чарльз Мангер

Он имел в виду, что, когда вы пытаетесь решить сложную задачу, ее нужно перевернуть с ног на голову и посмотреть на нее под других углом. Именно это и делает теорема Байеса. Давайте переформулируем теорему Байеса в терминах статистики, чтобы сделать ее более понятной (об это я узнал отсюда):

Для меня, например, такая запись выглядит понятнее. У нас есть априорная гипотеза (Hypothesis) — о том, что мы получили работу, и наблюдаемые факты — доказательства (Evidence) – телефонного звонка нет в течение трех дней. Теперь мы хотим узнать вероятность того, что наша гипотеза верна, с учетом предоставленных фактов. Как бы решили выше, у нас есть вероятность P(A) = 20%.

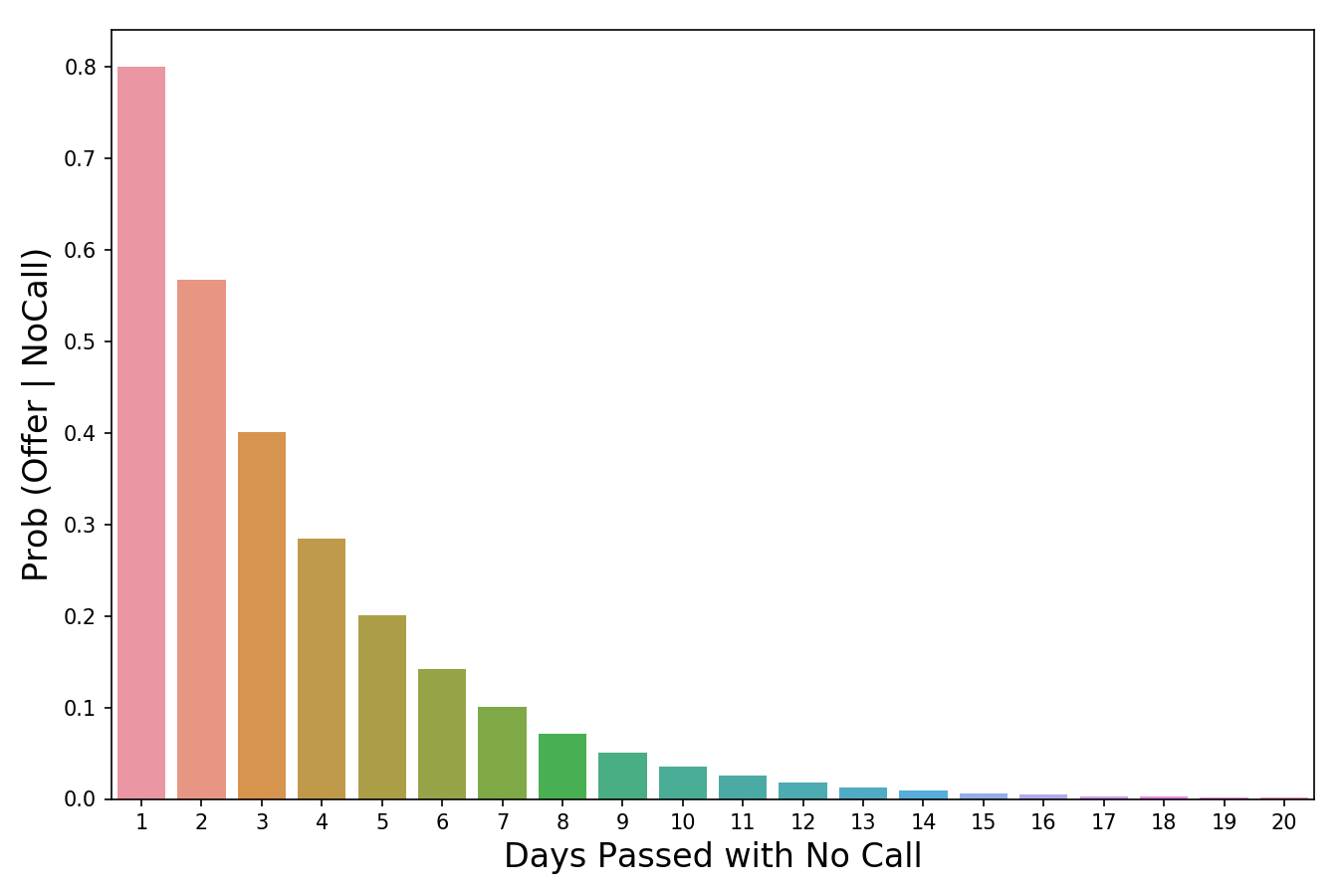
Время переворачивать все с ног на голову! Мы используем P(Evidence|Hypothesis), чтобы посмотреть на задачу с другой стороны и спрашиваем: «Какова вероятность наступления этих событий-доказательств в мире, где наша гипотеза верна?». Итак, если вернуться к нашему примеру, мы хотим знать, насколько вероятно, что, если нам не звонят в течение трех дней, нас все равно возьмут на работу. В изображении выше я пометил P(Evidence|Hypothesis), как “scaler” (скейлер), потому что это слово хорошо отражает суть значения. Когда мы умножаем его на априорное значение, он уменьшает или увеличивает вероятность события, в зависимости от того «вредит» ли какое-либо событие-доказательство нашей гипотезе. В нашем случае, чем больше дней проходит без звонка, тем меньше вероятность того, что нас позовут на работу. 3 дня тишины – это уже плохо (они сокращают нашу априорную вероятность на 60%), тогда как 20 дней без звонка полностью уничтожат надежду на получение работы. Таким образом, чем больше накапливается событий-доказательств (больше дней проходит без телефонного звонка), тем быстрее скейлер уменьшает вероятность. Скейлер – это механизм, который теорема Байеса использует для корректировки наших суждений.

Есть одна вещь, с которой я боролся в оригинальной версии этой статьи. Это была формулировка того, почему P(Evidence|Hypothesis) легче оценить, чем P(Hypothesis|Evidence). Причина этого заключается в том, что P(Evidence|Hypothesis) – это гораздо более ограниченная область суждений о мире. Сужая область, мы упрощаем задачу. Можно провести аналогию с огнем и дымом, где огонь – это наша гипотеза, а наблюдение дыма – событие, доказывающее наличие огня. P(огонь|дым) оценить сложнее, поскольку много чего может вызвать дым – выхлопные газы автомобилей, фабрики, человек, который жарит гамбургеры на углях. При этом P(дым|огонь) оценить проще, поскольку в мире, где есть огонь, почти наверняка будет и дым.

Значение вероятности уменьшается по мере того, сколько проходит дней без звонка.

Последняя часть формулы, P(B) или же P(Evidence) – это нормализатор. Как следует из названия, его цель – нормализовать произведение априорной вероятности и скейлера. Если бы у на не было нормализатора, мы бы имели следующее выражение:

Заметим, что произведение априорной вероятности и скейлера равно совместной вероятности. И поскольку одно из составляющих в нем P(Evidence), то на совместную вероятность повлияла бы маленькая частота событий.

Это проблема, поскольку совместная вероятность – это значение, включающее в себя все состояния мира. Но нам то не нужны все состояния, нам нужны только те состояния, которые были подтверждены событиями-доказательствами. Другими словами, мы живем в мире, где события – доказательства уже произошли, и их количество уже не имеет значения (поэтому мы не хотим, чтобы они влияли на наши расчеты в принципе). Деление произведения априорной вероятности и скейлера на P(Evidence) меняет его с совместной вероятности на условную(апостериорную). Условная вероятность учитывает только те состояния мира, в которых произошло событие-доказательство, именно этого мы и добиваемся.

Еще одна точка зрения, с которой можно взглянуть на то, почему мы делим скейлер на нормализатор, заключается в том, что они отвечают на два важных вопроса – и их отношение объединяет эту информацию. Давайте возьмем пример из моей недавней статьи про Байеса. Предположим, мы пытаемся выяснить, является ли наблюдаемое животное кошкой, основываясь на единственном признаке – ловкости. Все, что мы знаем, так это то, что животное, о котором мы говорим, проворное.

Скейлер говорит нам о том, у какого процента кошек хорошо с ловкостью. Это значение должно быть довольно высоким, допустим, 0.90.
Нормализатор говорит нам, какой процент животных ловок в принципе. Это значение должно быть средним, скажем, 0.50.
Отношение 0.90/0.50 = 1.8 говорит о том, что нужно изменить априорную вероятность, поскольку, если вы раньше считали иначе, настало время изменить свое мнение, поскольку вы скорее всего имеете дело с кошкой. Причина, по которой так можно считать заключается в том, что мы наблюдали некоторые доказательство того, что животное ловкое. Затем мы выяснили, что доля ловких кошек больше, чем доля ловких животных в целом. Учитывая, что на данный момент мы знаем только такую доказательную часть и ничего больше, разумно было бы пересмотреть наши убеждения в сторону мыслей о том, что мы все-таки наблюдаем кошку.

Подведем итог

Теперь, когда мы знаем, как трактовать каждую часть формулы, мы можем наконец собрать все воедино и посмотреть на то, что получилось:

Сразу после собеседования, мы устанавливаем априорную вероятность – шанс того, что нас возьмут на работу равен 20%.
Чем больше дней без звонка проходит, тем меньше становится вероятность того, что нас возьмут на работу. Например, после трех дней без звонка, мы считаем, что в мире, где мы эту работу можем получить, есть всего 40% вероятность того, что компания будет тянуть так долго, прежде чем вам позвонит. Умножаем скейлер на априорную вероятность и получаем 20% * 40% = 8%
Наконец, мы понимаем, что 8% было рассчитано для всех состояний, в которых может находиться мир. Но нас волнуют только те состояния, где нам не позвонили в течение трех дней. Для того, чтобы работать только с этими состояниями, мы принимаем за 90% априорную вероятность того, что в течение трех дней звонка не будет и получаем нормализатор. Мы делим ранее полученные 8% на нормализатор 8% / 90% = 8.9% и получаем окончательный ответ. Итого, при всех состояниях мира, если вы не получили звонка от компании в течение трех дней, вероятность получить работу составляет всего 8.9%.

Надеюсь, эта статья оказалась для вас полезной!

Источник

From Wikipedia, the free encyclopedia

The posterior probability is a type of conditional probability that results from updating the prior probability with information summarized by the likelihood via an application of Bayes’ rule.^[1] From an epistemological perspective, the posterior probability contains everything there is to know about an uncertain proposition (such as a scientific hypothesis, or parameter values), given prior knowledge and a mathematical model describing the observations available at a particular time.^[2] After the arrival of new information, the current posterior probability may serve as the prior in another round of Bayesian updating.^[3]

In the context of Bayesian statistics, the posterior probability distribution usually describes the epistemic uncertainty about statistical parameters conditional on a collection of observed data. From a given posterior distribution, various point and interval estimates can be derived, such as the maximum a posteriori (MAP) or the highest posterior density interval (HPDI).^[4] But while conceptually simple, the posterior distribution is generally not tractable and therefore needs to be either analytically or numerically approximated.^[5]

Definition in the distributional case[edit]

In variational Bayesian methods, the posterior probability is the probability of the parameters theta given the evidence , and is denoted .

It contrasts with the likelihood function, which is the probability of the evidence given the parameters: .

The two are related as follows:

Given a prior belief that a probability distribution function is and that the observations have a likelihood , then the posterior probability is defined as

${displaystyle p(theta |x)={frac {p(x|theta )}{p(x)}}p(theta )}$

^[6]

where p(x) is the normalizing constant and is calculated as

{displaystyle p(x)=int p(x|theta )p(theta )dtheta }

for continuous theta ,
or by summing
over all possible values of theta for discrete theta .^[7]

The posterior probability is therefore proportional to the product Likelihood · Prior probability.^[8]

Example[edit]

Suppose there is a school with 60% boys and 40% girls as students. The girls wear trousers or skirts in equal numbers; all boys wear trousers. An observer sees a (random) student from a distance; all the observer can see is that this student is wearing trousers. What is the probability this student is a girl? The correct answer can be computed using Bayes’ theorem.

The event is that the student observed is a girl, and the event is that the student observed is wearing trousers. To compute the posterior probability P(G|T) , we first need to know:

, or the probability that the student is a girl regardless of any other information. Since the observer sees a random student, meaning that all students have the same probability of being observed, and the percentage of girls among the students is 40%, this probability equals 0.4.
, or the probability that the student is not a girl (i.e. a boy) regardless of any other information ( is the complementary event to ). This is 60%, or 0.6.
, or the probability of the student wearing trousers given that the student is a girl. As they are as likely to wear skirts as trousers, this is 0.5.
, or the probability of the student wearing trousers given that the student is a boy. This is given as 1.
, or the probability of a (randomly selected) student wearing trousers regardless of any other information. Since (via the law of total probability), this is .

Given all this information, the posterior probability of the observer having spotted a girl given that the observed student is wearing trousers can be computed by substituting these values in the formula:

$P(G|T)={frac {P(T|G)P(G)}{P(T)}}={frac {0.5times 0.4}{0.8}}=0.25.$

An intuitive way to solve this is to assume the school has N students. Number of boys = 0.6N and number of girls = 0.4N. If N is sufficiently large, total number of trouser wearers = 0.6N+ 50% of 0.4N. And number of girl trouser wearers = 50% of 0.4N. Therefore, in the population of trousers, girls are (50% of 0.4N)/(0.6N+ 50% of 0.4N) = 25%. In other words, if you separated out the group of trouser wearers, a quarter of that group will be girls. Therefore, if you see trousers, the most you can deduce is that you are looking at a single sample from a subset of students where 25% are girls. And by definition, chance of this random student being a girl is 25%. Every Bayes theorem problem can be solved in this way.^[9]

Calculation[edit]

The posterior probability distribution of one random variable given the value of another can be calculated with Bayes’ theorem by multiplying the prior probability distribution by the likelihood function, and then dividing by the normalizing constant, as follows:

${displaystyle f_{Xmid Y=y}(x)={f_{X}(x){mathcal {L}}_{Xmid Y=y}(x) over {int _{-infty }^{infty }f_{X}(u){mathcal {L}}_{Xmid Y=y}(u),du}}}$

gives the posterior probability density function for a random variable given the data Y=y , where

Credible interval[edit]

Posterior probability is a conditional probability conditioned on randomly observed data. Hence it is a random variable. For a random variable, it is important to summarize its amount of uncertainty. One way to achieve this goal is to provide a credible interval of the posterior probability.^[11]

Classification[edit]

In classification, posterior probabilities reflect the uncertainty of assessing an observation to particular class, see also Class membership probabilities.
While statistical classification methods by definition generate posterior probabilities, Machine Learners usually supply membership values which do not induce any probabilistic confidence. It is desirable to transform or re-scale membership values to class membership probabilities, since they are comparable and additionally more easily applicable for post-processing.^[12]

References[edit]

^ Lambert, Ben (2018). «The posterior – the goal of Bayesian inference». A Student’s Guide to Bayesian Statistics. Sage. pp. 121–140. ISBN 978-1-4739-1636-4.
^ Grossman, Jason (2005). Inferences from observations to simple statistical hypotheses (PhD thesis). University of Sydney. hdl:2123/9107.
^ Etz, Alex (2015-07-25). «Understanding Bayes: Updating priors via the likelihood». The Etz-Files. Retrieved 2022-08-18.
^ Gill, Jeff (2014). «Summarizing Posterior Distributions with Intervals». Bayesian Methods: A Social and Behavioral Sciences Approach (Third ed.). Chapman & Hall. pp. 42–48. ISBN 978-1-4398-6248-3.
^ Press, S. James (1989). «Approximations, Numerical Methods, and Computer Programs». Bayesian Statistics : Principles, Models, and Applications. New York: John Wiley & Sons. pp. 69–102. ISBN 0-471-63729-7.
^ Christopher M. Bishop (2006). Pattern Recognition and Machine Learning. Springer. pp. 21–24. ISBN 978-0-387-31073-2.
^ Andrew Gelman, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari and Donald B. Rubin (2014). Bayesian Data Analysis. CRC Press. p. 7. ISBN 978-1-4398-4095-5.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ Ross, Kevin. Chapter 8 Introduction to Continuous Prior and Posterior Distributions | An Introduction to Bayesian Reasoning and Methods.
^ «Bayes’ theorem — C o r T e x T». sites.google.com. Retrieved 2022-08-18.
^ «Posterior probability — formulasearchengine». formulasearchengine.com. Retrieved 2022-08-19.
^ Clyde, Merlise; Çetinkaya-Rundel, Mine; Rundel, Colin; Banks, David; Chai, Christine; Huang, Lizzy. Chapter 1 The Basics of Bayesian Statistics | An Introduction to Bayesian Thinking.
^ Boedeker, Peter; Kearns, Nathan T. (2019-07-09). «Linear Discriminant Analysis for Prediction of Group Membership: A User-Friendly Primer». Advances in Methods and Practices in Psychological Science. 2 (3): 250–263. doi:10.1177/2515245919849378. ISSN 2515-2459. S2CID 199007973.

Пример: расчет апостериорной вероятности

Лес состоит из 20% дубов и 80% кленов. Предположим, известно, что 90 % дубов здоровы, а здоровы лишь 50 % клёнов. Предположим, что на расстоянии можно сказать, что конкретное дерево здорово. Какова вероятность того, что это дуб?

Напомним, что вероятность наступления события А при условии, что произошло событие В, равна:

Р(А|В) = Р(А) * Р(В|А) / Р(В)

В этом примере вероятность того, что дерево является дубом, при условии, что дерево здоровое, составляет:

P(Дуб|Здоровый) = P(Дуб) * P(Здоровый|Дуб) / P(Здоровый)

P(Дуб) = Вероятность того, что данное дерево является дубом, равна 0,2 , потому что 20% всех деревьев в лесу являются дубами.

P(Healthy) = Вероятность того, что данное дерево является здоровым, можно рассчитать как (0,20)*(0,9) + (0,8)*(0,5) = 0,58 .

P(Здоровый|Дуб) = Вероятность того, что дерево здоровое, учитывая, что это дуб, равна 0,9 , поскольку нам сказали, что 90% дубов здоровы.

Используя эти три числа, мы можем найти вероятность того, что дерево является дубом при условии, что оно здоровое:

P(Дуб|Здоровый) = P(Дуб) * P(Здоровый|Дуб) / P(Здоровый) = (0,2) * (0,9) / (0,58) = 0,3103 .

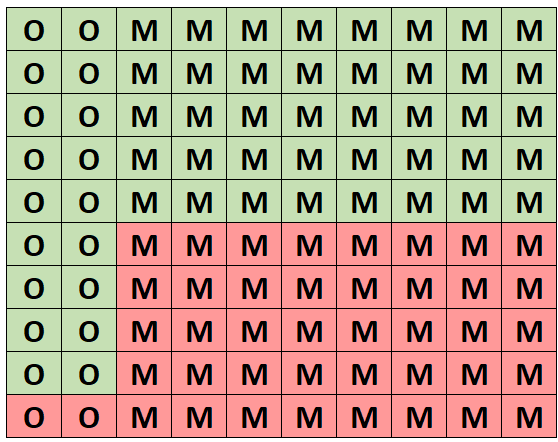
Для интуитивного понимания этой вероятности предположим, что следующая сетка представляет этот лес со 100 деревьями. Ровно 20 деревьев дубы и 18 из них здоровые. Остальные 80 деревьев — это клены, и 40 из них — здоровые.

(O = дуб, M = клен, зеленый = здоровый, красный = нездоровый)

Из всех деревьев ровно 58 здоровых и 18 из этих здоровых дубов. Таким образом, если мы знаем, что выбрали здоровое дерево, то вероятность того, что это дуб, составляет 18/58 = 0,3103 .

Когда следует использовать апостериорную вероятность?

Апостериорная вероятность используется в самых разных областях, включая финансы, медицину, экономику и прогнозирование погоды.

Весь смысл использования апостериорных вероятностей состоит в том, чтобы обновить предыдущее убеждение, которое у нас было о чем-то, как только мы получим новую информацию.

Напомним, что в предыдущем примере мы знали, что вероятность того, что данное дерево в лесу является дубом, составляет 20 %. Это известно как априорная вероятность.Если бы мы просто выбрали дерево наугад, то знали бы, что вероятность того, что это дуб, равна 0,20.

Однако, как только мы получили новую информацию о том, что выбранное нами дерево было здоровым, мы смогли использовать эту новую информацию, чтобы определить, что апостериорная вероятность того, что это дерево является дубом, вместо этого равнялась 0,3103.

В реальном мире люди постоянно сталкиваются с новой информацией. Эта новая информация помогает нам обновить наши прежние убеждения. С точки зрения статистики это означает, что мы можем генерировать апостериорные вероятности происходящих событий, что помогает нам получить более точное представление о мире и позволяет делать более точные прогнозы будущих событий.

Источник

Начнем с примера. В урне, стоящей перед вами, с равной вероятностью могут быть (1) два белых шара, (2) один белый и один черный, (3) два черных. Вы тащите шар, и он оказывается белым. Как теперь вы оцените вероятность этих трех вариантов (гипотез)? Очевидно, что вероятность гипотезы (3) с двумя черными шарами = 0. А вот как подсчитать вероятности двух оставшихся гипотез!? Это позволяет сделать формула Байеса, которая в нашем случае имеет вид (номер формулы соответствует номеру проверяемой гипотезы):

Скачать заметку в формате Word или pdf

х – случайная величина (гипотеза), принимающая значения: х₁ – два белых, х₂ – один белый, один черный; х₃ – два черных; у – случайная величина (событие), принимающая значения: у₁ – вытащен белый шар и у₂ – вытащен чёрный шар; Р(х₁) – вероятность первой гипотезы до вытаскивания шара (априорная вероятность или вероятность до опыта) = 1/3; Р(х₂) – вероятность второй гипотезы до вытаскивания шара = 1/3; Р(х₃) – вероятность третьей гипотезы до вытаскивания шара = 1/3; Р(у₁|х₁) – условная вероятность вытащить белый шар, в случае, если верна первая гипотеза (шары белые) = 1; Р(у₁|х₂) – вероятность вытащить белый шар, в случае, если верна вторая гипотеза (один шар белый, второй – черный) = ½; Р(у₁|х₃) – вероятность вытащить белый шар, в случае, если верна третья гипотеза (оба черных) = 0; Р(у₁) – вероятность вытащить белый шар = ½; Р(у₂) – вероятность вытащить черный шар = ½; и, наконец, то, что мы ищем – Р(х₁|у₁) – вероятность того, что верна первая гипотеза (оба шара белых), при условии, что мы вытащили белый шар (апостериорная вероятность или вероятность после опыта); Р(х₂|у₁) – вероятность того, что верна вторая гипотеза (один шар белый, второй – черный), при условии, что мы вытащили белый шар.

Вероятность того, что верна первая гипотеза (два белых), при условии, что мы вытащили белый шар:

Вероятность того, что верна вторая гипотеза (один белый, второй – черный), при условии, что мы вытащили белый шар:

Вероятность того, что верна третья гипотеза (два черных), при условии, что мы вытащили белый шар:

Что делает формула Байеса? Она дает возможность на основании априорных вероятностей гипотез – Р(х₁), Р(х₂), Р(х₃) – и вероятностей наступления событий – Р(у₁), Р(у₂) – подсчитать апостериорные вероятности гипотез, например, вероятность первой гипотезы, при условии, что вытащили белый шар – Р(х₁|у₁).

Вернемся еще раз к формуле (1). Первоначальная вероятность первой гипотезы была Р(х₁) = 1/3. С вероятностью Р(у₁) = 1/2 мы могли вытащить белый шар, и с вероятностью Р(у₂) = 1/2 – черный. Мы вытащили белый. Вероятность вытащить белый при условии, что верна первая гипотеза Р(у₁|х₁) = 1. Формула Байеса говорит, что так как вытащили белый, то вероятность первой гипотезы возросла до 2/3, вероятность второй гипотезы по-прежнему равна 1/3, а вероятность третьей гипотезы обратилась в ноль.

Легко проверить, что вытащи мы черный шар, апостериорные вероятности изменились бы симметрично: Р(х₁|у₂) = 0, Р(х₂|у₂) = 1/3, Р(х₃|у₂) = 2/3.

Вот что писал Пьер Симон Лаплас о формуле Байеса в работе Опыт философии теории вероятностей, вышедшей в 1814 г.:

Это основной принцип той отрасли анализа случайностей, которая занимается переходами от событий к причинам.

Почему формула Байеса так сложна для понимания!? На мой взгляд, потому, что наш обычный подход – это рассуждения от причин к следствиям. Например, если в урне 36 шаров из которых 6 черных, а остальные белые. Какова вероятность вытащить белый шар? Формула Байеса позволяет идти от событий к причинам (гипотезам). Если у нас было три гипотезы, и произошло событие, то как именно это событие (а не альтернативное) повлияло на первоначальные вероятности гипотез? Как изменились эти вероятности?

Я считаю, что формула Байеса не просто о вероятностях. Она изменяет парадигму восприятия. Каков ход мыслей при использовании детерминистской парадигмы? Если произошло событие, какова его причина? Если произошло ДТП, чрезвычайное происшествие, военный конфликт. Кто или что явилось их виной? Как думает байесовский наблюдатель? Какова структура реальности, приведшая в данном случае к такому-то проявлению… Байесовец понимает, что в ином случае результат мог быть иным…

Немного иначе разместим символы в формулах (1) и (2):

Давайте еще раз проговорим, что же мы видим. С равной исходной (априорной) вероятностью могла быть истинной одна из трех гипотез. С равной вероятностью мы могли вытащить белый или черный шар. Мы вытащили белый. В свете этой новой дополнительной информации следует пересмотреть нашу оценку гипотез. Формула Байеса позволяет это сделать численно. Априорная вероятность первой гипотезы (формула 7) была Р(х₁), вытащили белый шар, апостериорная вероятность первой гипотезы стала Р(х₁|у₁). Эти вероятности отличаются на коэффициент .

Событие у₁ называется свидетельством, в большей или меньшей степени подтверждающим или опровергающим гипотезу х₁. Указанный коэффициент иногда называют мощностью свидетельства. Чем мощнее свидетельство (чем больше коэффициент отличается от единицы), тем больше факт наблюдения у₁ изменяет априорную вероятность, тем больше апостериорная вероятность отличается от априорной. Если свидетельство слабое (коэффициент ~ 1), апостериорная вероятность почти равна априорной.

Свидетельство у₁ в = 2 раза изменило априорную вероятность гипотезы х₁ (формула 4). В то же время свидетельство у₁ не изменило вероятность гипотезы х₂, так как его мощность = 1 (формула 5).

В общем случае формула Байеса имеет следующий вид:

х – случайная величина (набор взаимоисключающих гипотез), принимающая значения: х₁, х₂, … , х_n. у – случайная величина (набор взаимоисключающих событий), принимающая значения: у₁, у₂, … , у_n. Формула Байеса позволяет найти апостериорную вероятность гипотезы х_i при наступлении события y_j. В числителе – произведение априорной вероятности гипотезы х_i – Р(х_i) на вероятность наступления события y_j, если верна гипотеза х_i – Р(y_j|х_i). В знаменателе – сумма произведений того же, что и в числителе, но для всех гипотез. Если вычислить знаменатель, то получим суммарную вероятность наступления события у_j (если верна любая из гипотез) – Р(y_j) (как в формулах 1–3).

Еще раз о свидетельстве. Событие y_j дает дополнительную информацию, что позволяет пересмотреть априорную вероятность гипотезы х_i. Мощность свидетельства – – содержит в числителе вероятность наступления события y_j, если верна гипотеза х_i. В знаменателе – суммарная вероятность наступления события у_j (или вероятность наступления события у_j усредненная по всем гипотезам). Если вероятность наступления события у_j выше для гипотезы x_i, чем в среднем для всех гипотез, то свидетельство играет на руку гипотезе x_i, увеличивая ее апостериорную вероятность Р(y_j|х_i). Если вероятность наступления события у_j ниже для гипотезы x_i, чем в среднем для всех гипотез, то свидетельство понижает, апостериорную вероятность Р(y_j|х_i) для гипотезы x_i. Если вероятность наступления события у_j для гипотезы x_i такая же, как в среднем для всех гипотез, то свидетельство не изменяет апостериорную вероятность Р(y_j|х_i) для гипотезы x_i.

Предлагаю вашему вниманию несколько примеров, которые, надеюсь, закрепят ваше понимание формулы Байеса.

Задача 1.[1] Имеется 3 урны; в первой 3 белых шара и 1 черный; во второй — 2 белых шара и 3 черных; в третьей — 3 белых шара. Некто подходит наугад к одной из урн и вынимает из нее 1 шар. Этот шар оказался белым. Найдите апостериорные вероятности того, что шар вынут из 1-й, 2-й, 3-й урны. Ответ 1.

Задача 2. Два стрелка независимо друг от друга стреляют по одной и той же мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8, для второго — 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку. Ответ 2.

Задача 3. Объект, за которым ведется наблюдение, может быть в одном из двух состояний: Н₁ = {функционирует} и Н₂ = {не функционирует}. Априорные вероятности этих состояний Р(Н₁) = 0,7, Р(Н₂) = 0,3. Имеется два источника информации, которые приносят разноречивые сведения о состоянии объекта; первый источник сообщает, что объект не функционирует, второй — что функционирует. Известно, что первый источник дает правильные сведения с вероятностью 0,9, а с вероятностью 0,1 — ошибочные. Второй источник менее надежен: он дает правильные сведения с вероятностью 0,7, а с вероятностью 0,3 — ошибочные. Найдите апостериорные вероятности гипотез. Ответ 3.

Задача 4.[2] Вероятность того, что человек страдает от определенного заболевания, равна 0,03. Медицинский тест позволяет проверить, так ли это. Если человек действительно болен, вероятность точного диагноза (утверждающего, что человек болен, когда он действительно болен) равна 0,9. Если человек здоров, вероятность ложноположительного диагноза (утверждающего, что человек болен, когда он здоров) равна 0,02. Допустим, что медицинский тест дал положительный результат. Какова вероятность того, что человек действительно болен? Ответ 4.

[1] Задачи 1–3 взяты из учебника Е.С.Вентцель, Л.А.Овчаров. Теория вероятностей и ее инженерные приложения, раздел 2.6 Теорема гипотез (формула Байеса).

[2] Задача 4 взята из книги Левин. Статистика для менеджеров с использованием Microsoft Excel, раздел 4.3 Теорема Байеса.

Источник

Что такое апостериорная вероятность?

Апостериорная вероятность относится к методу, основанному на байесовской интерпретации вероятности. Метод включает расчет новой вероятности путем обновления предыдущей вероятности в ответ на новые данные. По сути, это приложение теоремы Байеса.

Применяя теорему Байеса, существующая вероятность события становится априорной вероятностью (до наблюдения свидетельств), когда в наблюдение поступают новые свидетельства. Обновленная вероятность (вероятность, основанная на наблюдаемых данных) получается путем применения вероятности данных к предыдущей вероятности.

Оглавление

Что такое апостериорная вероятность?
- Объяснение апостериорной вероятности
- Формула
- Пример расчета
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи

Апостериорная вероятность относится к обновленной вероятности события, полученной путем применения нового сформированного свидетельства. Его основы подкреплены условной вероятностью и теоремой Байеса.
Формула для расчетов: P(A|B) = P(B|A)*P(A)/P(B)
Важными элементами являются априорная вероятность P(A), свидетельство P(B), P(B|A) – функция правдоподобия.
По мере появления новых данных и их интеграции в вычисления апостериорная вероятность может стать априорной для новой обновленной апостериорной вероятности.

Объяснение апостериорной вероятности

Апостериорная вероятность является важным инструментом для представления неопределенности конкретных событий. Он рассматривает все доступные данные, и когда он рассматривает последнюю информацию, чтобы пересчитать существующую вероятность, чтобы получить новую и отбросить предыдущую, он показывает, что его основы подкреплены концепцией условной вероятности. происходит конкретное событие, при условии, что ранее произошло другое событие. Он широко применим во многих областях, включая управление бизнес-рисками, страхование, личную жизнь, вычисления, политику и т. д., помогая физическим и юридическим лицам определять возможные результаты и принимать соответствующие практические решения. читать далее определяется теоремой Байеса. Пересмотренная вероятность зависит от условной и безусловной вероятности второго или нового события.

Его можно сравнить с мыслительным процессом человека. Выбор и выводы людей всегда чувствительны к новой информации, опыту или интуиции. Это преднамеренная процедура, которая тщательно рассматривает многочисленные варианты того, как событие может произойти или не произойти. При таком подходе на суждения людей о случайных результатах правильно влияют апостериорные факты в неоднозначной среде. Следовательно, этот метод важен в финансах, науке о данных, лекарствои т. д.

Формула

Формула апостериорной вероятности теоремы Байеса:

Где:

P(A|B) = вероятность возникновения события A при наличии свидетельства B (апостериорная вероятность).
P(A) = Вероятность наступления события A (априорная вероятность)
P(B) = Вероятность возникновения события B (свидетельство или предельная вероятность)
P(B|A) = вероятность возникновения события B при наличии свидетельства A (функция правдоподобия).
«|» означает «при условии»

Пример расчета

Представьте себе коробку, в которой 50% темного шоколада и 50% белого шоколада. Половина темного шоколада завернута в золотую бумагу, а другая половина в серебряную. Все белые конфеты завернуты в серебряную бумагу. Ребенок выбрал из коробки шоколад, завернутый в серебристую бумагу. Какова вероятность того, что выбранный — темный шоколад?

Событие D состоит в том, что выбранный шоколад темный.
Событие S состоит в том, что выбранный шоколад завернут в серебряную бумагу.

Согласно вариационным байесовским методам:

Апостериорная вероятность: P(темный шоколад|серебряная обертка): P(D|S): это вероятность того, что выбранный шоколад является «темным шоколадом», учитывая свидетельство «шоколад, завернутый в серебряную бумагу».
Функция правдоподобия: P(серебряная обертка|темный шоколад): P(S|D): вероятность доказательства с учетом параметра; вероятность серебряной обертки для данного типа шоколада — темный шоколад.
P(D): Вероятность того, что выбранный шоколад является «темным шоколадом», при отсутствии предварительной информации. Вероятность P(D) равна 50%, 0,5.
P(W): Вероятность того, что выбранный шоколад является «белым шоколадом», при отсутствии предварительной информации. Вероятность P(W) равна 50%, 0,5.
P(S|D): Вероятность шоколада, завернутого в серебряную бумагу, при условии, что это темный шоколад, равна 0,5 (50% темного шоколада покрыто золотой бумагой, а остальные 50% – серебряной).
P(S|W): вероятность шоколада, завернутого в серебряную бумагу, при условии, что это белый шоколад, равна 1 (поскольку все белые шоколадные конфеты завернуты в серебряную бумагу).
P(S): Вероятность случайного выбора шоколада завернута в серебряную бумагу без предварительной информации.
P(S): Вероятность случайного выбора шоколада завернута в серебряную бумагу без предварительной информации.

P(S)= P(S|D).P(D) + P(S|W).P(W)

=0,5*0,5 + 1*0,5

=0,75

Применение приведенных выше результатов в формуле для расчета апостериорной вероятности:

P(D|S)= P(S|D)*P(D)|P(S)

=0,5*0,5|0,75

=0,3333

=33,33%

Следовательно, вероятность того, что случайно выбранный шоколад будет «темным шоколадом», а свидетельство того, что обертка шоколада имеет серебристый цвет, составляет 33,33%. Академики также используют калькуляторы апостериорной вероятности для получения быстрых результатов.

Часто задаваемые вопросы (FAQ)

Что такое апостериорная вероятность?

Это относится к вероятности, полученной путем обновления предыдущей вероятности при наличии новых данных. Он основан на теореме Байеса.

Что такое формула апостериорной вероятности?

Проще говоря, это вероятность после добавления новых доказательств.
Формула является применением теоремы Байеса:

P(A|B)= P(B|A).P(A)/P(B)

Где P(A|B)= вероятность возникновения события A при наличии свидетельства B (апостериорная вероятность), P(A) = вероятность возникновения события A (априорная вероятность), P(B) = вероятность возникновения события B ( свидетельство), P(B|A) = вероятность возникновения события B при наличии свидетельства A (функция правдоподобия) и «|» означает «обеспеченный».

Что такое пример апостериорной вероятности?

Рассмотрим группу людей, 50% из которых работают (P(E)=0,5) и 40% женщин (P(W)=0,4). Учитывая, что она работает, условная вероятность того, что выбранный человек является женщиной, составляет 20% (P(W|E) = 0,2). Какова вероятность того, что человек, выбранный из группы, работает, если выбранный человек — женщина (P(E|W) =?).

P(E|W) = P(W|E) P(E)|P(W)
=0,20,5|0,4
=0,25
=25%

Понимаем теорему Байеса

Основания для подтверждения наших суждений

Разберем формулу

Интуиция, стоящая за формулой

Подведем итог

Definition in the distributional case[edit]

Example[edit]

Calculation[edit]

Credible interval[edit]

Classification[edit]

See also[edit]

References[edit]

Further reading[edit]

Пример: расчет апостериорной вероятности

Когда следует использовать апостериорную вероятность?

Что такое апостериорная вероятность?

Объяснение апостериорной вероятности

Формула

Пример расчета

Часто задаваемые вопросы (FAQ)

Рекомендуемые статьи