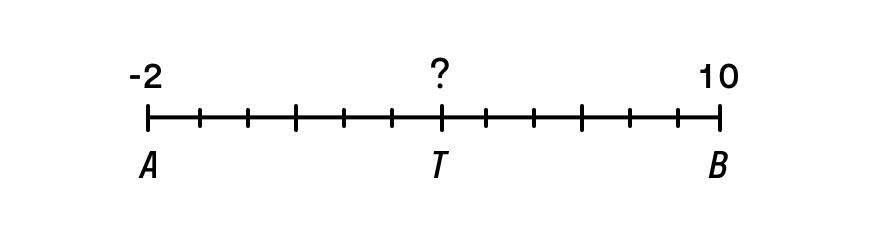Определение.
Середина отрезка — это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, …
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Формулы вычисления расстояния между двумя точками:
- Формула вычисления координат середины отрезка с концами A(xa, ya) и B(xb, yb) на плоскости:
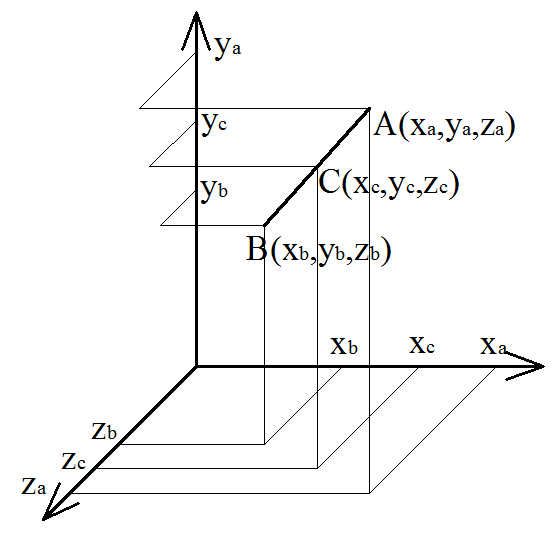
xc = xa + xb yc = ya + yb 2 2 - Формула вычисления координат середины отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в пространстве:
xc = xa + xb yc = ya + yb zc = za + zb 2 2 2
Примеры задач на вычисление середины отрезка
Примеры вычисления координат середины отрезка на плоскости
Пример 1.
Найти координаты точки С, середины отрезка AB заданного точками A(-1, 3) и B(6, 5).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4).
Пример 2.
Найти координаты точки В, если известны координаты точки C(1; 5), середины отрезка AB и точки A(-1, 3).
Решение.
xc =
xa + xb2
=> xb = 2xc — xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc — ya = 2·5-3=10-3=7
Ответ: B(3, 7).
Примеры вычисления координат середины отрезка в пространстве
Пример 3.
Найти координаты точки С середины отрезка AB заданного точками A(-1, 3, 1) и B(6, 5, -3).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
| zc = | za + zb | = | 1 + (-3) | = | -2 | = -1 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4, -1).
Пример 4.
Найти координаты точки В если известны координаты точки C(1, 5, 2), середины отрезка AB и точки A(-1, 3, 10).
Решение.
xc =
xa + xb2
=> xb = 2xc — xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc — ya = 2·5-3=10-3=7
zc =
za + zb2
=> zb = 2zc — za = 2·2-10=4-10=-6
Ответ: B(3, 7, -6).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Что такое отрезок
Чтобы изучить эту тему досконально, давайте начнем с самого простого: с определения отрезка.
Отрезок — это прямая, у которой есть начало и конец, или же прямая, которая соединяет две произвольные точки, не совпадающие друг с другом.
Отрезок называют заглавными буквами латинского алфавита по названию конечных точек. Причем можно расставлять буквы в любом порядке: АВ и ВА — равноценные варианты. Рассмотрите иллюстрацию, посчитайте и назовите все отрезки.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Что такое середина отрезка
Середина отрезка — это точка, которая находится на равном расстоянии от его концов. Иначе можно сказать так: это точка, которая делит отрезок пополам.
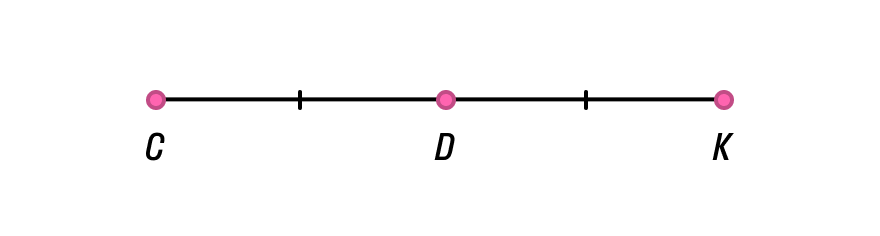
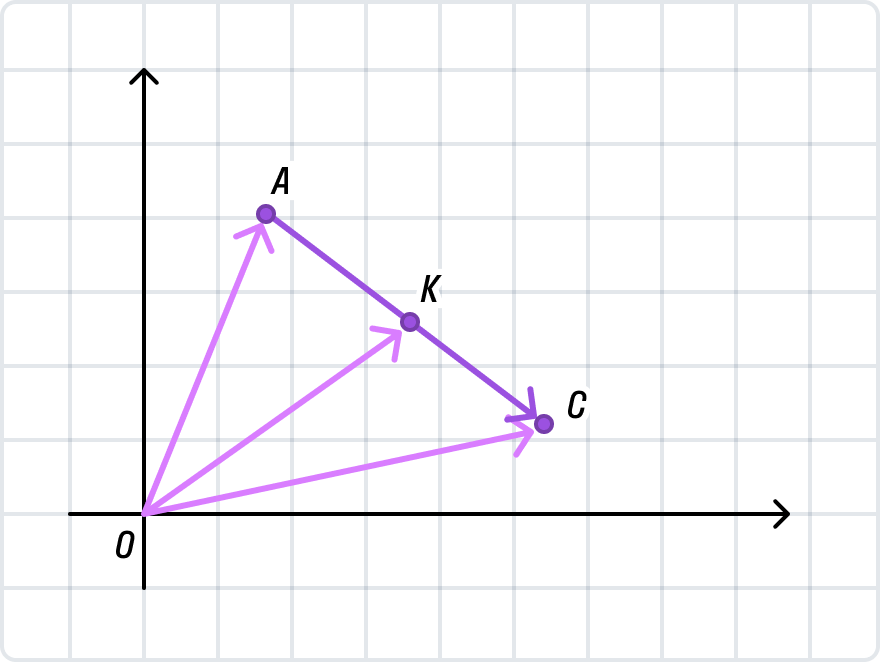
Так, на рисунке ниже D — середина отрезка СК, так как СD = DK. Обратите внимание, как на чертеже обозначаются равные по длине отрезки — мы ставим на них равное количество черточек.
Главный вопрос, который нас сегодня интересует, это координаты середины отрезка.
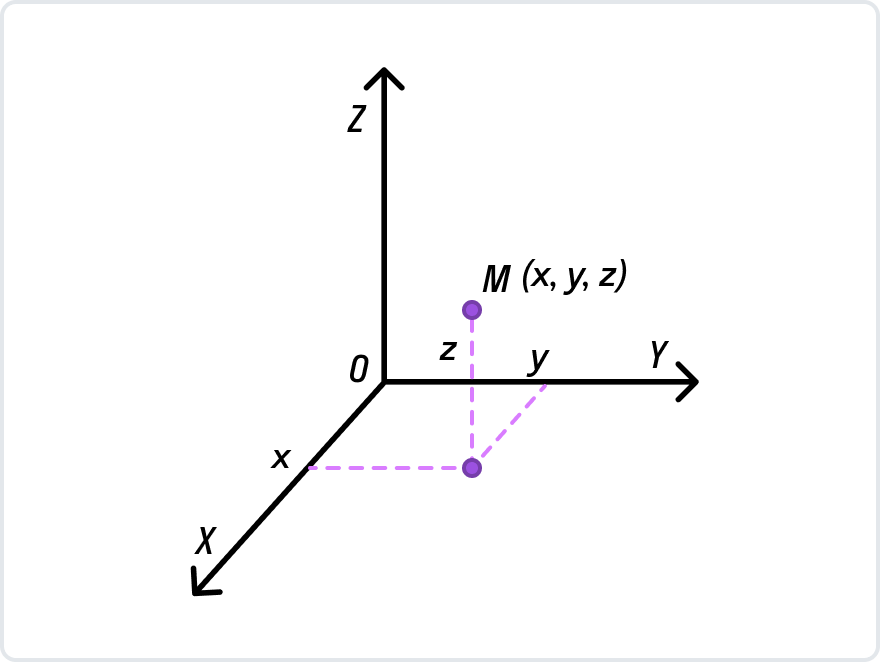
Координаты — это положение точки в пространстве.
Мы можем рассмотреть отрезок, который лежит на координатной прямой, тогда координата будет одна. В Декартовой системе координат оХУ будет две координаты, причем вначале записывают х, потом у. Например: С (5; 3): К (4; 8). Еще мы можем поместить отрезок в трехмерное пространство, тогда у каждой точки будет три координаты: х, у, z.
Кажется, что чем дальше, тем сложнее, но на самом деле это не совсем так. Хорошая новость: в каждом из случаев мы будем использовать один и тот же принцип, так что вы обязательно во всем разберетесь!
Как найти координаты середины отрезка на координатной прямой
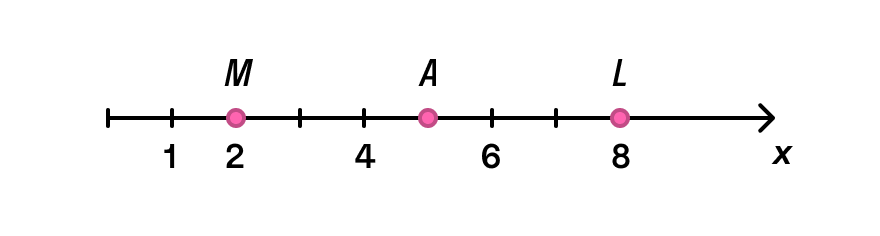
Изобразим горизонтальную координатную прямую оХ и отметим на ней две точки: М и L. Координату точки М запишем как Хм, точки L — соответственно XL. Поставим лежащую на отрезке точку А — середину ML, MA = LA.
Определим координаты точек: Хм = {2}, XL = {8}. Чтобы найти середину отрезка, воспользуемся формулой XA=(XM+XL)/2 и получим:
ХА = (2 + 8)/2 = 5.
Проверим, верна ли формула. Для этого определим координаты середины отрезка графическим методом.Действительно: фактическая координата точки А совпадает со значением, которое мы получили.
Подумайте, взяли ли мы эту формулу случайно или же ее можно вывести. Да, конечно, второй вариант верный — в математике не используют ничего непроверенного. Давайте посмотрим, каким образом можно доказать истинность формулы, тем более, что мы возьмем ее за основу при решении более сложных задач.
-
Точка А — это середина отрезка, а значит, MA = LA.
-
Расстояние между точками можно рассчитать через разность модулей их координат: │ХА – ХМ│=│ХL – ХА│.
-
Преобразуем правую часть, вынесем знак минуса: ХА – ХМ= — (ХА –ХL).
-
Перенесем ХА в левую часть, а все остальное — в правую: 2ХА= ХL+ ХМ.
-
Найдем ХА: ХА = (ХL + ХМ)/2.
Вот мы и вывели формулу координат середины отрезков! Чтобы лучше закрепить материал, сделаем пару заданий.
Задача 1
Определите координаты середины отрезка АВ, если ХА = –2, ХB = 10.
Решение
Обозначим точку середины отрезка буквой Т. Тогда Хт = (ХА + ХB)/2 = (–2 + 10)/2 = 4.
Ответ: Хк = {4}.
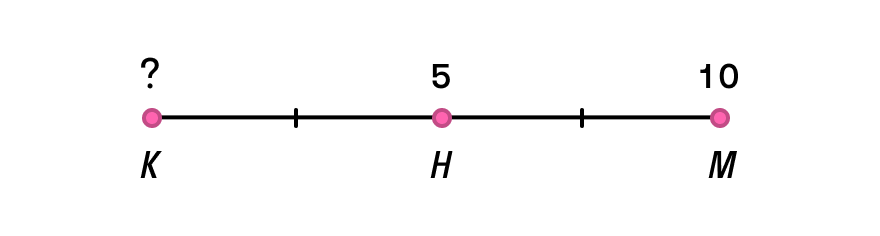
Задача 2
Определите координаты начала отрезка КМ с серединой в точке Н, если Хм = 5, Хн = 10.
Решение
Вначале запишем формулу для середины отрезка: Хн = (Хк + Хм)/2. Выразим Хк через нее:
Хн = (Хк + Хм)/2,
2Хн = (Хк + Хм),
2Хн – Хм = Хк,
Хк = 2Хн – Хм = 2 * 5 – 10 = 0.
Ответ: Хк = {0}
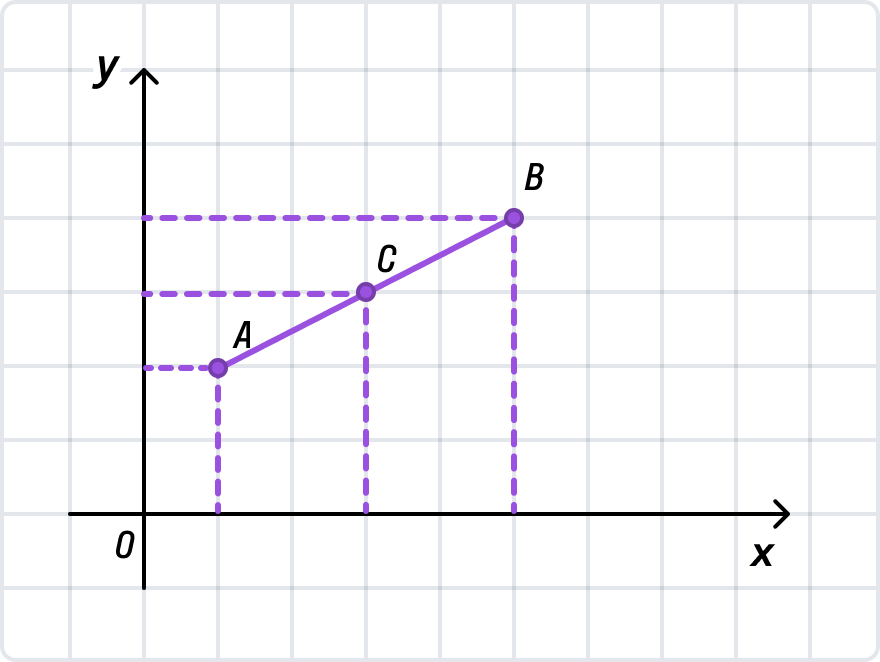
Как найти середину отрезка на плоскости
В Декартовой системе координат у каждой точки есть две координаты: по оси оХ и оУ. Изобразим отрезок АВ с координатами А (1; 3), В (3; 6) и точкой С — серединой отрезка.
Чтобы найти координаты точки С, мы воспользуемся уже известной нам формулой, но применим ее к каждой координате в отдельности. Вначале рассчитаем Хс:
Хс = (ХА + ХB)/2 = (1 + 3)/2 = 2.
Тогда УC = (УA + УB)/2 = (3 + 6)/2 = 4,5. Значит С (2; 4,5).
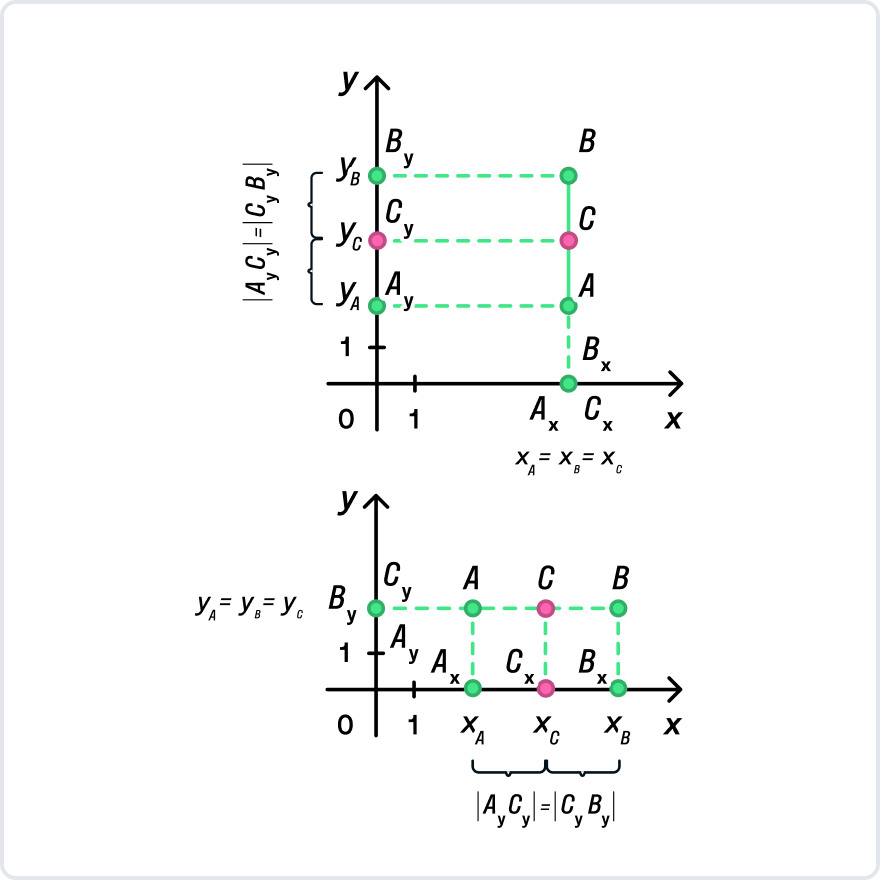
Не пугайтесь, если отрезок на чертеже параллелен оси оХ или оУ: мы четко идем по нашему алгоритму и ничего не меняем.
Важно заметить: если отрезок параллелен оси оУ, координаты концов и середины отрезка по оХ будут совпадать, ХА = ХС = ХВ. Если же отрезок параллелен оси оХ, совпадут координаты по оУ: УА = УВ = УС.
И вновь пришло время задачек. Давайте разберем несколько примеров решения.
Задача 3
В системе координат находятся две точки: С (–6; 4) и К (2; 8). Определите координаты середины отрезка.
Решение
Обозначим середину отрезка точкой О. Тогда:
ХО = (ХС + ХК)/2 = (–6 + 2)/2 = –2,
УО = (УС + УК)/2 = (4 + 8)/2 = 6.
Ответ: О (-2; 6).
Задача 4
Дан треугольник с вершинами АВС: А (-2; 4), В (4; 6), С (3; -5). Определите координаты точки М — медианы ВМ.
Решение
Медиана — отрезок, который проведен из вершины треугольника и делит противоположную сторону пополам. А значит, медиана ВМ делит на равные части сторону АС, АМ = МС. Тогда:
ХМ = (ХА + ХС)/2 = (–2 + 3)/2 = 0,5,
УМ = (УА + УС)/2 = (4 – 5)/2 = –0,5.
Ответ: М (0,5; –0,5).
Координаты середины отрезка в пространстве
Вспомните, чем пространство отличается от плоскости. Правильно, третьим измерением! В том смысле, что добавляется еще одна координатная ось: оZ. Как это выглядит, можно посмотреть на рисунке ниже.
При этом формула нахождения середины отрезка остается неизменной. Если мы изобразим в трехмерном пространстве отрезок АВ с серединой в точке С, тогда:
ХС = (ХА + ХВ)/2,
УС = (УА + УВ)/2,
ZС = (ZА + ZВ)/2.
Координаты середины отрезка через радиус-векторы его концов
По сути, этот способ нельзя назвать каким-то новым и уникальным. Он лишь еще раз доказывает истинность формулы координат середины отрезков, только через алгебру. Чтобы разобраться в нем, давайте сначала вспомним определение вектора.
Вектор — это направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Векторы — достаточно обширная тема. Чтобы разобраться в ней, не хватит и двух статей. Но сейчас мы с вами будем использовать всего несколько тезисов, которые помогут разобраться в теме.
-
Векторы можно изображать в системах координат оХУ и оХYZ, т. е. в двумерной и трехмерной.
-
Координаты начала и конца векторов записывают так же, как и для отрезков: (x; y) и (x; y; z).
-
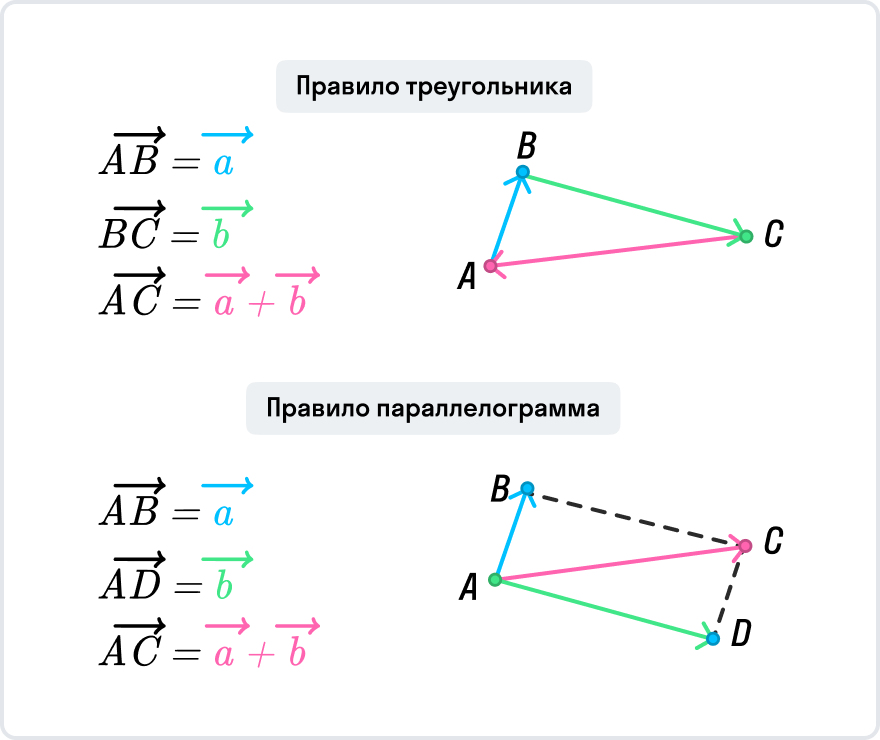
Сумму векторов можно найти по методу треугольника или параллелограмма. Картинка ниже поможет вам вспомнить, как ими пользоваться.
Радиус-вектор — вектор, который задает положение точки в пространстве относительно некоторой заранее фиксированной точки — начала координат.
Давайте разберемся, как доказать формулу для нахождения координаты середины отрезка через радиус-векторы его концов. В Декартовой системе координат нарисуем вектор
с серединой в точке К. Координаты точки А (ХА; УА; ZА), К (ХК; УК; ZК), С (ХС; УС; ZС).Проведем радиус-векторы
,
,
.
Согласно определению середины отрезка: ОК = ½(ОС + ОА). Координаты векторов ОА, ОК, ОС соответственно равны координатам точек А, К, С, так как координаты точки О (0; 0; 0).
ОА (ХА – 0, УА – 0, ZА – 0) = (ХА; УА; ZА),
ОК (ХК – 0, УК – 0, ZК – 0) = (ХК; УК; ZК,),
ОС (ХС– 0, УС – 0, ZС – 0) = (ХС; УС; ZС).
Тогда запишем равенство ОК = ½(ОС + ОА) через координаты:
ХК = 1/2(ХА + ХО),
УК = 1/2(УА + УО),
ZК = 1/2(ZА + ZО).
Напоследок мы сделаем небольшой перерыв, забудем про формулы и числа. Давайте подумаем, как можно найти середину отрезка, если мы не знаем координат его концов.
Например, нарисуем отрезок на песчаном пляже во время каникул. Определить точные координаты в таком случае будет достаточно сложно, правда? Вряд ли вы взяли с собой в отпуск набор линеек, чтобы вычислить длину отрезка. С подобным заданием вы могли столкнуться и на уроках геометрии, где учитель раздавал вам чистые нелинованные листы бумаги и просил найти середину отрезка без использования линейки.
Сейчас мы обучим вас волшебному методу, приготовьтесь! Все что вам понадобится — это циркуль. Нарисуем на бумаге отрезок АВ любой длины. Поставим иголку циркуля в точку А и начертим окружность с радиусом, равным АВ. Далее повторим действие — прочертим такую же окружность с центром в точке В.
Мы видим, что окружности пересеклись дважды: снизу и сверху. Если соединить эти две точки, эта прямая пересечет наш исходный отрезок ровно в его середине.
Скептики вспомнят наш пример с пляжем и скажут: «Линейку мы с собой в отпуск не берем, но и циркуль ведь тоже! Что вы скажете на это?» А ответим мы вот что: приходите на курсы по профильной математики в Skysmart! Там вы научитесь не только заменять настоящий циркуль на самодельный, но еще подготовитесь к экзаменам, разовьете логику и узнаете много всего интересного. Ждем вас на занятиях!
Обновлено: 24.05.2023
Отрезок — это множество точек прямой, которые лежат между двумя точками, называемыми концами отрезка. Точка, равноудаленная от концов отрезков, является серединой этого отрезка.
Определение координат середины отрезка
Если по условию заданы координаты концов отрезка, например, А (х1; у1; z1) и В (х2; у2; z2), то можно рассчитать координаты середины отрезка — точки О. Определение каждой координаты середины проводится сложением соответствующих координат концов отрезка и делением на 2.
Таким образом, абсцисса середины отрезка равна (х1 + х2) / 2, ордината — (у1 + у2) / 2 и аппликата — (z1 +z2) / 2, тогда координаты точки О (((х1 + х2) / 2), ((у1 + у2) / 2); ((z1 +z2) / 2)).
Определение середины отрезка графически
Для определение середины отрезка графически нужны:
- чертежный циркуль,
- линейка,
- карандаш.
Действия проводится в следующем порядке:
1) один конец циркуля с иглой устанавливается в любой конец отрезка;
2) раскрываем циркуль на расстояние визуально большее, чем половина отрезка и меньшее, чем весь отрезок;
3) проводим вторым концом циркуля с грифелем над отрезком дугу и под отрезком такую же дугу;
4) переносим иглу циркуля в другой конец отрезка;
5) вторым концом циркуля с грифелем над отрезком проводим дугу до пересечения с первой дугой над отрезком;
6) аналогично находим точку пересечения двух дуг под отрезком;
7) проводим через две полученные точки прямую;

Середина отрезка — это такая точка, которая делит отрезок (множество, которое состоит из двух точек, расположенных на прямой (концы отрезка), и точек, которые лежат между ними) на две равные части. Концы отрезка и его середину обычно обозначают латинскими буквами: A и B — концы, C — середина, C и D — концы, E — середина и т. д.
Зная координаты конца и начала отрезка, можно вычислить координаты его середины.
Пусть концы отрезка AB имеют координаты A (x₁; y₁) и B (x₂; y₂). Тогда координаты середины отрезка будут равны:
Зная координаты конца и начала отрезка, также можно вычислить расстояние, которое отделяет середину отрезка от его концов. Для этого необходимо вычислить длину отрезка по формуле:
|AB| = √((x₁ — x₂)² + (y₁ — y₂)²), а затем эту длину разделить на 2.
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.
Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:
Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:
Свойства длин отрезков:
-
Основное свойство длины отрезка: если точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример. Возьмём два отрезка CD и LM:
Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:
Значит длины отрезков равны, следовательно CD = LM.
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.
При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):
CA CA.
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):
CA > CB или CB AC.
Так как отрезки AB и AC имеют одинаковую длину, то
AB = AC.
Если при измерении отрезков их длины равны, то и отрезки равны.
Середина отрезка
Середина отрезка — это точка, делящая отрезок на две равные части.
В данной публикации мы рассмотрим, что из себя представляет отрезок, перечислим его основные свойства, а также приведем возможные варианты расположения двух отрезков по отношению друг к другу на плоскости.
Определение отрезка
Отрезок – это часть прямой, ограниченная двумя точками на ней.
У отрезка есть начало и конец, а расстояние между ними называется его длиной.
Обычно отрезок обозначается двумя большими латинским буквами, которые соответствуют точкам на прямой (или его концам), причем неважно в каком порядке. Например, AB или BA (эти отрезки совпадают).
Если же порядок важен, то такой отрезок называется направленным. В этом случае отрезки AB и BA не совпадают.
Средина отрезка – это точка (в нашем случае – C), которая делит его пополам или
Взаимное расположение отрезков
Два отрезка на плоскости, как и прямые, могут быть:
Примечание: в отличие от прямых, два отрезка могут быть не параллельным, и при этом не пересекаться.
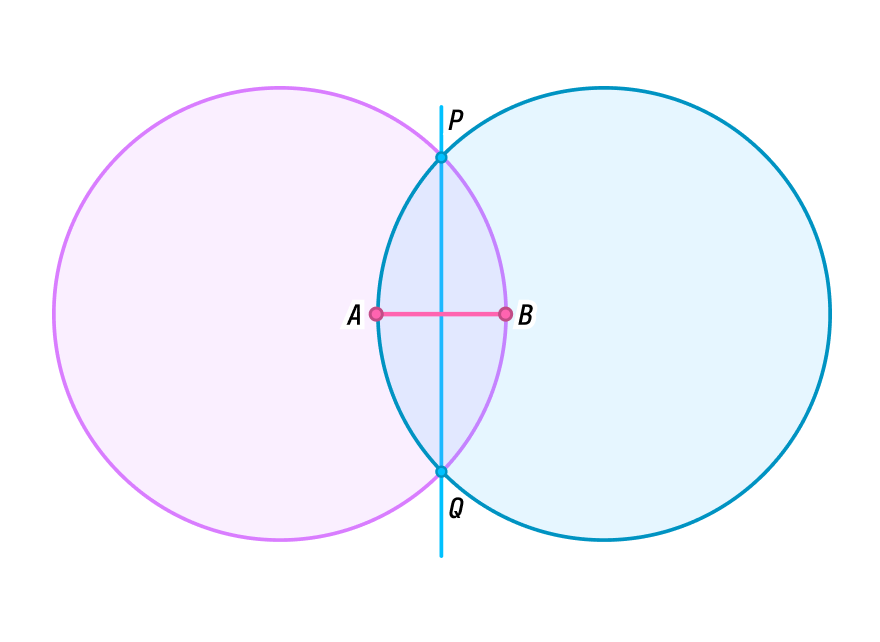
Дано: отрезок АВ.
Построить: середину АВ.
Решение:
Строим с помощью линейки произвольный отрезок АВ.
Далее с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В.
Получаем две точки пересечения данных окружностей. Обозначим их Р и Q. Проведем с помощью линейки через точки Р и Q прямую РQ.
Точку пересечения прямой РQ и отрезка АВ обозначим О.
Докажем, что точка О — искомая точка, т.е. точка О — середина отрезка АВ.
Рассмотрим треугольники РАQ и РВQ.
По построению АР = ВР, АQ = BQ (как радиусы одинаковых окружностей), PQ — общая, следовательно, РАQ =РВQ по 3 признаку равенства треугольников. Значит, по свойству равных треугольников АРО =ВРО, тогда РО — биссектриса АРВ.
В АРВ АР = ВР (как радиусы одинаковых окружностей), следовательно, АРВ — равнобедренный, тогда по свойству равнобедренного треугольника биссектриса РО АРВ и его медиана, следовательно, точка О — середина отрезка АВ. Что и требовалось доказать.
Читайте также:
- В чем заключается значение зеленой революции кратко
- Звезды как пыль краткое содержание
- Чем знаменит мадрид кратко и понятно
- Проблема соотношения обучения и воспитания в педагогической психологии кратко
- Кто открыл африку и в каком году кратко
Если через точку О в пространстве мы проведем три перпендикулярные прямые, назовем их, выберем направление, обозначим единичные отрезки, то мы получим прямоугольную систему координат в пространстве. Оси координат называются так: Ох – ось абсцисс, Оy – ось ординат и Оz – ось аппликат. Вся система координат обозначается – Oxyz. Таким образом, появляются три координатные плоскости: Оxy, Оxz, Оyz.
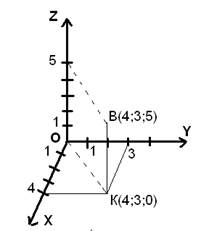
Приведем пример построения точки В(4;3;5) в прямоугольной системе координат (см. Рис. 1).
Рис. 1. Построение точки B в пространстве
Первая координата точки B – 4, поэтому откладываем на Ox 4, проводим прямую параллельно оси Oy до пересечения с прямой, проходящей через у=3. Таким образом, мы получаем точку K. Эта точка лежит в плоскости Oxy и имеет координаты K(4;3;0). Теперь нужно провести прямую параллельно оси Oz. И прямую, которая проходит через точку с аппликатой 5 и параллельна диагонали параллелограмма в плоскости Oxy. На их пересечении мы получим искомую точку B.
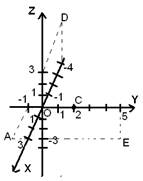
Рассмотрим расположение точек, у которых одна или две координаты равны 0 (см. Рис. 2).
Рис. 2.
Например, точка A(3;-1;0). Нужно продолжить ось Oy влево до значения -1, найти точку 3 на оси Ox, и на пересечении линий, проходящих через эти значения, получаем точку А. Эта точка имеет аппликату 0, а значит, она лежит в плоскости Oxy.
Точка C(0;2;0) имеет абсциссу и аппликату 0 – не отмечаем. Ордината равна 2, значит точка C лежит только на оси Oy, которая является пересечением плоскостей Oxy и Oyz.
Чтобы отложить точку D(-4;0;3) продолжаем ось Ox назад за начало координат до точки -4. Теперь восстанавливаем из этой точки перпендикуляр – прямую, параллельную оси Oz до пересечения с прямой, параллельной оси Ox и проходящей через значение 3 на оси Oz. Получаем току D(-4;0;3). Так как ордината точки равна 0, значит точка D лежит в плоскости Oxz.
Следующая точка E(0;5;-3). Ордината точки 5, аппликата -3, проводим прямые проходящие через эти значения на соответствующих осях, и на их пересечении получаем точку E(0;5;-3). Эта точка имеет первую координату 0, значит она лежит в плоскости Oyz.
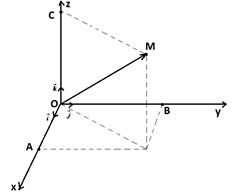
Начертим прямоугольную систему координат в пространстве Oxyz. Зададим в пространстве прямоугольную систему координат Oxyz. На каждой из положительных полуосей отложим от начала координат единичный вектор, т. е. вектор, длина которого равна единице. Обозначим единичный вектор оси абсцисс, единичный вектор оси ординат
, и единичный вектор оси аппликат
(см. рис. 1). Эти векторы сонаправлены с направлениями осей, имеют единичную длину и ортогональны – попарно перпендикулярны. Такие вектора называют координатными векторами или базисом.
Рис. 1. Разложение вектора по трем координатным векторам
Рис. 2.
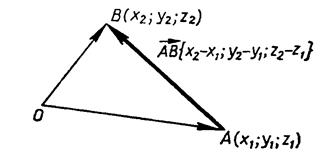
Возьмем точку A(x1;y1;z1) и точку B(x2;y2;z2) (см. рис. 3). Представим вектор как разность векторов
и
по свойству векторов. Причем,
и
— радиус-векторы, и их координаты совпадают с координатами концов этих векторов. Тогда мы можем представить координаты вектора
как разность соответствующих координат векторов
и
:
. Таким образом, координаты вектора мы можем выразить через координаты конца и начала вектора.
Рис. 3.
Рассмотрим примеры, иллюстрирующие свойства векторов и их выражение через координаты. Возьмем векторы ,
,
. Нас спрашивают вектор
. В данном случае найти
это значит найти координаты вектора , которые полностью его определяют. Подставляем в выражение вместо векторов соответственно их координаты. Получаем:
Теперь умножаем число 3 на каждую координату в скобках, и то же самое делаем с 2:
У нас получилась сумма трех векторов, складываем их по изученному выше свойству:
Ответ:
Пример №2.
Дано: Треугольная пирамида AOBC (см. рис. 4). Плоскости AOB, AOC и OCB – попарно перпендикулярны. OA=3, OB=7, OC=4; M — сер.AC; N — сер.OC; P – сер. CB.
Рис. 4.
Решение: Введем прямоугольную систему координат Oxyz с началом отсчета в точке O. По условию обозначаем точки A, B и C на осях и середины ребер пирамиды – M, P и N. По рисунку находим координаты вершин пирамиды: A(3;0;0), B(0;7;0), C(0;0;4).
Так как координаты вектора — это разность координат его конца и начала, получаем:
. Таким же образом находим координаты векторов
и
.
;
.
Чтобы найти координаты вектора , нужно сначала найти координаты точек M и N. По рисунку видно, что точка N имеет координаты
, так как она лежит на оси аппликат. Рассмотрим
. MN – средняя линия,
. Значит координата точки M по оси Oz 2. Теперь проведем из точки M перпендикуляр к оси Ox, координата 1,5. Точка M лежит в плоскости Oxz, значит по оси Oy координата 0. Получаем M(1,5;0;2). Теперь зная координаты точек M и N, считаем их разность:
.
Теперь найдем координаты точки P. Опустим перпендикуляр на плоскость Oxy, получаем значение 3,5 по оси ординат. И проведя перпендикуляр к оси Oz, получаем значение 2 по оси аппликат. Точка P имеет координаты (0;3,5;2). Зная координаты нужных точек, найдем координаты оставшихся векторов.
;
.
Вектора и
— радиус-векторы, значит, их координаты равны координатам концов этих векторов:
,
.
.
Пример 1. Задача на нахождение координат середины отрезка (рис. 1). Даны две точки: A(x1;y1z1), B(x2;y2;z2), C – середина AB. Найти: C(x;y;z).
Рис. 1. Координаты середины отрезка
Пример 2. Задача на нахождение модуля вектора через его координаты (рис. 2). Если у нас есть вектор , то его модуль вычисляется по формуле:
.
Рис. 2.
Рассмотрим вывод этой формулы.
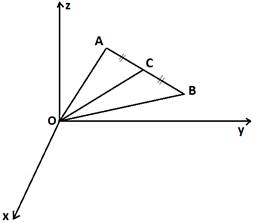
1) Начертим вектор и совместим его начало с началом координат, чтобы координаты точки M совпадали с координатами вектора.
2) Опустим перпендикуляр из точки M на плоскость Oxy, получаем точку K.
3) Рассмотрим . OA=x — первая координата точки M, отрезок AK=y – вторая координата точки M. Гипотенуза
,
— по теореме Пифагора.
4) Рассмотрим — прямоугольный, так как MK — перпендикуляр к плоскости Oxy.
, MK=z.
— по теореме Пифагора.
Пример 3. Задача на нахождение расстояния между точками, которые заданы координатами (рис. 3). Дано: A(x1;y1z1), B(x2;y2;z2). Найти: длину отрезка AB.
Рис. 3.
Решение:
1) Найдем координаты вектора .
.
2) Найдем модуль вектора по его координатам:
.
Задача №1.
Дано: A(-3;m;5), B(2;-2;n), C – середина AB, . Найти: m, n.
Решение: Так как , мы знаем две координаты точки C – (x;0;0). Запишем формулу середины отрезка для отрезка AB и его середины – C. Получаем три уравнения:
;
;
.
Ответ: ,
.
Задача №2.
Дано: M(-4;7;0), N(0;-1;2), C – середина MN. Найти: расстояние от начала координат до точки C.
Решение: Сначала найдем координаты точки C. Ее координаты равны полусумме соответствующих координат. .
Нужно найти расстояние от начала координат до точки C. Это значит, что мы должны найти длину отрезка OC или модуль вектора . Так как
— радиус-вектор, то координаты этого вектора равны координатам точки
. Воспользуемся формулой нахождения длины вектора по его координатам:
.
Достарыңызбен бөлісу:
Координаты точки середины отрезка в пространстве онлайн
Калькулятор рассчитывает координаты середины отрезка в пространстве по координатам конца отрезка с подробным порядком вычислений. В поля можно вводить целые или десятичные числа.
Введите координаты точки A
Введите координаты точки B
Определение середины отрезка
Середина отрезка — это точка которая лежит на отрезке, делит этот отрезок пополам и находится на равном расстоянии от начала и конца отрезка.
Формула расчёта координаты середины отрезка в пространстве
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
xc=(xa+xb)/2
yc=(ya+yb)/2
zc=(za+zb)/2
A(xa, ya, za), B(xb, yb, zb) — координаты концов отрезка
C(xc, yc, zc) — координаты середины отрезка
Разберём пример
Найдите координаты середины отрезка AC заданного точками A(4,5,7), C(10,11,5)
По формуле найдём координаты середины отрезка
x=(4+10)/2=7
y=(5+11)/2=8
z=(7+5)/2=6
Найдите координаты точки C середины отрезка AB заданного точками A(3,4,5), B(9,10,11)
xc=(3+9)/2=6
yc=(4+10)/2=7
yc=(5+11)/2=8
Найти координаты середины отрезка AB если A(3, 2, 4), B(1, 1, 5).
Найти координаты середины отрезка AB если A(2, 1, 1), B(6, 6, 0).
Найти координаты середины отрезка AB если A(3, 3, 6), B(2, 1, 5).
Найти координаты середины отрезка AB если A(3, 0, 2), B(1, 2, 5).
Похожие калькуляторы