Как найти аппроксимирующую прямую - Исправление недочетов и поиск решений вместе с Examum.ru

При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.

Аппроксимацией (приближением) функции f(x) называется нахождение такой функции (аппроксимирующей функции) g(x), которая была бы близка заданной. Критерии близости функций могут быть различные.

В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.

В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.

Пусть задан дискретный набор точек, называемых узлами интерполяции, а также значения функции в этих точках. Требуется построить функцию g(x), проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi.

В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом.

В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная.

В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию).

Аппроксимация линейной функцией

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.

Реализация на Си

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// Задание начального набора значений
double ** getData(int n) {
  double **f;
  f = new double*[2];
  f[0] = new double[n];
  f[1] = new double[n];
  for (int i = 0; i<n; i++) {
    f[0][i] = (double)i;
    f[1][i] = 8 * (double)i — 3;
    // Добавление случайной составляющей
    f[1][i] = 8*(double)i — 3 + ((rand()%100)-50)*0.05;
  }
  return f;
}
// Вычисление коэффициентов аппроксимирующей прямой
void getApprox(double **x, double *a, double *b, int n) {
  double sumx = 0;
  double sumy = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += x[0][i];
    sumy += x[1][i];
    sumx2 += x[0][i] * x[0][i];
    sumxy += x[0][i] * x[1][i];
  }
  *a = (n*sumxy — (sumx*sumy)) / (n*sumx2 — sumx*sumx);
  *b = (sumy — *a*sumx) / n;
  return;
}
int main() {
  double **x, a, b;
  int n;
  system(«chcp 1251»);
  system(«cls»);
  printf(«Введите количество точек: «);
  scanf(«%d», &n);
  x = getData(n);
  for (int i = 0; i<n; i++)
    printf(«%5.1lf — %7.3lfn», x[0][i], x[1][i]);
  getApprox(x, &a, &b, n);
  printf(«a = %lfnb = %lf», a, b);
  getchar(); getchar();
  return 0;
}

Результат выполнения
Запуск без случайной составляющей

Запуск со случайной составляющей

Построение графика функции

Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь.

Реализация на Си

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149

#include <windows.h>
const int NUM = 70; // количество точек
LONG WINAPI WndProc(HWND, UINT, WPARAM, LPARAM);
double **x; // массив данных
      // Определение коэффициентов линейной аппроксимации по МНК
void getApprox(double **m, double *a, double *b, int n) {
  double sumx = 0;
  double sumy = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += m[0][i];
    sumy += m[1][i];
    sumx2 += m[0][i] * m[0][i];
    sumxy += m[0][i] * m[1][i];
  }
  *a = (n*sumxy — (sumx*sumy)) / (n*sumx2 — sumx*sumx);
  *b = (sumy — *a*sumx) / n;
  return;
}
// Задание исходных данных для графика
// (двумерный массив, может содержать несколько рядов данных)
double ** getData(int n) {
  double **f;
  double a, b;
  f = new double*[3];
  f[0] = new double[n];
  f[1] = new double[n];
  f[2] = new double[n];
  for (int i = 0; i<n; i++) {
    double x = (double)i * 0.1;
    f[0][i] = x;
    f[1][i] = 8 * x — 3 + ((rand() % 100) — 50)*0.05;
  }
  getApprox(f, &a, &b, n); // аппроксимация
  for (int i = 0; i<n; i++) {
    double x = (double)i * 0.1;
    f[2][i] = a*x + b;
  }
  return f;
}
// Функция рисования графика
void DrawGraph(HDC hdc, RECT rectClient, double **x, int n, int numrow = 1) {
  double OffsetY, OffsetX;
  double MAX_X = 0;
  double MAX_Y = 0;
  double ScaleX, ScaleY;
  double min, max;
  int height, width;
  int X, Y;    // координаты в окне (в px)
  HPEN hpen;
  height = rectClient.bottom — rectClient.top;
  width = rectClient.right — rectClient.left;
  // Область допустимых значений X
  min = x[0][0];
  max = x[0][0];
  for (int i = 0; i<n; i++) {
    if (x[0][i] < min)
      min = x[0][i];
    if (x[0][i] > max)
      max = x[0][i];
  }
  double temp = max — min;
  MAX_X = max — min;
  OffsetX = min*width / MAX_X;  // смещение X
  ScaleX = (double)width / MAX_X; // масштабный коэффициент X
                  // Область допустимых значений Y
  min = x[1][0];
  max = x[1][0];
  for (int i = 0; i<n; i++) {
    for (int j = 1; j <= numrow; j++) {
      if (x[j][i] < min)
        min = x[j][i];
      if (x[j][i] > max)
        max = x[j][i];
    }
  }
  MAX_Y = max — min;
  OffsetY = max*height / (MAX_Y);  // смещение Y
  ScaleY = (double)height / MAX_Y; // масштабный коэффициент Y
                   // Отрисовка осей координат
  hpen = CreatePen(PS_SOLID, 0, 0); // черное перо 1px
  SelectObject(hdc, hpen);
  MoveToEx(hdc, 0, OffsetY, 0);  // перемещение в точку (0;OffsetY)
  LineTo(hdc, width, OffsetY);   // рисование горизонтальной оси
  MoveToEx(hdc, OffsetX, 0, 0);  // перемещение в точку (OffsetX;0)
  LineTo(hdc, OffsetX, height);  // рисование вертикальной оси
  DeleteObject(hpen);  // удаление черного пера
             // Отрисовка графика функции
  int color = 0xFF; // красное перо для первого ряда данных
  for (int j = 1; j <= numrow; j++) {
    hpen = CreatePen(PS_SOLID, 2, color); // формирование пера 2px
    SelectObject(hdc, hpen);
    X = (int)(OffsetX + x[0][0] * ScaleX);    // координаты начальной точки графика
    Y = (int)(OffsetY — x[j][0] * ScaleY);
    MoveToEx(hdc, X, Y, 0);  // перемещение в начальную точку
    for (int i = 0; i<n; i++) {
      X = OffsetX + x[0][i] * ScaleX;
      Y = OffsetY — x[j][i] * ScaleY;
      LineTo(hdc, X, Y);
    }
    color = color << 8; // изменение цвета пера для следующего ряда
    DeleteObject(hpen); // удаление текущего пера
  }
}
// Главная функция
int  WINAPI  WinMain(HINSTANCE  hInstance,
  HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow) {
  HWND hwnd;
  MSG msg;
  WNDCLASS w;
  x = getData(NUM); // задание исходных данных
  memset(&w, 0, sizeof(WNDCLASS));
  w.style = CS_HREDRAW | CS_VREDRAW;
  w.lpfnWndProc = WndProc;
  w.hInstance = hInstance;
  w.hbrBackground = CreateSolidBrush(0x00FFFFFF);
  w.lpszClassName = «My Class»;
  RegisterClass(&w);
  hwnd = CreateWindow(«My Class», «График функции»,
    WS_OVERLAPPEDWINDOW, 500, 300, 500, 380, NULL, NULL,
    hInstance, NULL);
  ShowWindow(hwnd, nCmdShow);
  UpdateWindow(hwnd);
  while (GetMessage(&msg, NULL, 0, 0)) {
    TranslateMessage(&msg);
    DispatchMessage(&msg);
  }
  return msg.wParam;
}
// Оконная функция
LONG WINAPI WndProc(HWND hwnd, UINT Message,
  WPARAM wparam, LPARAM lparam) {
  HDC hdc;
  PAINTSTRUCT ps;
  switch (Message) {
  case WM_PAINT:
    hdc = BeginPaint(hwnd, &ps);
    DrawGraph(hdc, ps.rcPaint, x, NUM, 2); // построение графика
    EndPaint(hwnd, &ps);
    break;
  case WM_DESTROY:
    PostQuitMessage(0);
    break;
  default:
    return DefWindowProc(hwnd, Message, wparam, lparam);
  }
  return 0;
}

Результат выполнения

Аппроксимация с фиксированной точкой пересечения с осью y

В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a.

В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
// Задание начального набора значений
double ** getData(int n) {
  double **f;
  f = new double*[2];
  f[0] = new double[n];
  f[1] = new double[n];
  for (int i = 0; i<n; i++) {
    f[0][i] = (double)i;
    f[1][i] = 8 * (double)i — 3;
    // Добавление случайной составляющей
    //f[1][i] = 8 * (double)i — 3 + ((rand() % 100) — 50)*0.05;
  }
  return f;
}
// Вычисление коэффициентов аппроксимирующей прямой
void getApproxA(double **x, double *a, double b, int n) {
  double sumx = 0;
  double sumx2 = 0;
  double sumxy = 0;
  for (int i = 0; i<n; i++) {
    sumx += x[0][i];
    sumx2 += x[0][i] * x[0][i];
    sumxy += x[0][i] * x[1][i];
  }
  *a = (sumxy — b*sumx) / sumx2;
  return;
}
int main() {
  double **x, a, b;
  int n;
  system(«chcp 1251»);
  system(«cls»);
  printf(«Введите количество точек: «);
  scanf(«%d», &n);
  x = getData(n);
  for (int i = 0; i<n; i++)
    printf(«%5.1lf — %7.3lfn», x[0][i], x[1][i]);
  b = 0;
  getApproxA(x, &a, b, n);
  printf(«a = %lfnb = %lf», a, b);
  getchar(); getchar();
  return 0;
}

Результат выполнения программы поиска коэффициента угла наклона аппроксимирующей прямой при фиксированном значении b=0:

Назад: Алгоритмизация

Источник

Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.

Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.

Аппроксимация функции одной переменной

Квадратичная аппроксимация

Аппроксимация степенной функцией

Показательная аппроксимация

Логарифмическая аппроксимация

Гиперболическая аппроксимация

Экспоненциальная аппроксимация

Точность вычисления

Знаков после запятой: 4

Коэффициент линейной парной корреляции

Средняя ошибка аппроксимации, %

Логарифмическая регрессия

Средняя ошибка аппроксимации, %

Гиперболическая регрессия

Средняя ошибка аппроксимации, %

Экспоненциальная регрессия

Средняя ошибка аппроксимации, %

Результат

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Линейная регрессия

Уравнение регрессии:

Коэффициент a:
$a&=frac{sum x_i sum y_i- nsum x_iy_i}{left(sum x_iright)^2-nsum x_i^2}$

Коэффициент b:
$b&=frac{sum x_i sum x_iy_i-sum x_i^2sum y_i}{left(sum x_iright)^2-nsum x_i^2}$

Коэффициент линейной парной корреляции:
$r_{xy}&=frac{nsum x_iy_i-sum x_isum y_i}{sqrt{left(nsum x_i^2-left(sum x_iright)^2right)!!left(nsum y_i^2-left(sum y_iright)^2 right)}}$

Коэффициент детерминации:
$R^2=r_{xy}^2$

Средняя ошибка аппроксимации:
$overline{A}=dfrac{1}{n}sumleft|dfrac{y_i-widehat{y}_i}{y_i}right|cdot100%$

Квадратичная регрессия

Уравнение регрессии:
$widehat{y}=ax^2+bx+c$

Система уравнений для нахождения коэффициентов a, b и c:
$begin{cases}asum x_i^2+bsum x_i+nc=sum y_i,,\[2pt] asum x_i^3+bsum x_i^2+csum x_i=sum x_iy_i,,\[2pt] asum x_i^4+bsum x_i^3+csum x_i^2=sum x_i^2y_i,;end{cases}$

Коэффициент корреляции:
$R= sqrt{1-frac{sum(y_i-widehat{y}_i)^2}{sum(y_i-overline{y})^2}}$ ,
где
$overline{y}= dfrac{1}{n}sum y_i$

Коэффициент детерминации:
R^2

Средняя ошибка аппроксимации:
$overline{A}=dfrac{1}{n}sumleft|dfrac{y_i-widehat{y}_i}{y_i}right|cdot100%$

Кубическая регрессия

Уравнение регрессии:
$widehat{y}=ax^3+bx^2+cx+d$

Система уравнений для нахождения коэффициентов a, b, c и d:
$begin{cases}asum x_i^3+bsum x_i^2+csum x_i+nd=sum y_i,,\[2pt] asum x_i^4+bsum x_i^3+csum x_i^2+dsum x_i=sum x_iy_i,,\[2pt] asum x_i^5+bsum x_i^4+csum x_i^3+dsum x_i^2=sum x_i^2y_i,,\[2pt] asum x_i^6+bsum x_i^5+csum x_i^4+dsum x_i^3=sum x_i^3y_i,;end{cases}$

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Степенная регрессия

Уравнение регрессии:
$widehat{y}=acdot x^b$

Коэффициент b:
$b=dfrac{nsum(ln x_icdotln y_i)-sumln x_icdotsumln y_i }{nsumln^2x_i-left(sumln x_iright)^2 }$

Коэффициент a:
$a=exp!left(dfrac{1}{n}sumln y_i-dfrac{b}{n}sumln x_iright)$

Показательная регрессия

Уравнение регрессии:
$widehat{y}=acdot b^x$

Коэффициент b:
$b=expdfrac{nsum x_iln y_i-sum x_icdotsumln y_i }{nsum x_i^2-left(sum x_iright)^2 }$

Коэффициент a:
$a=exp!left(dfrac{1}{n}sumln y_i-dfrac{ln b}{n}sum x_iright)$

Гиперболическая регрессия

Уравнение регрессии:
$widehat{y}=a + frac{b}{x}$

Коэффициент b:
$b=dfrac{nsumdfrac{y_i}{x_i}-sumdfrac{1}{x_i}sum y_i }{nsumdfrac{1}{x_i^2}-left(sumdfrac{1}{x_i}right)^2 }$

Коэффициент a:
$a=dfrac{1}{n}sum y_i-dfrac{b}{n}sumdfrac{1}{x_i}$

Логарифмическая регрессия

Уравнение регрессии:

Коэффициент b:
$b=dfrac{nsum(y_iln x_i)-sumln x_icdot sum y_i }{nsumln^2x_i-left(sumln x_iright)^2 }$

Коэффициент a:
$a=dfrac{1}{n}sum y_i-dfrac{b}{n}sumln x_i$

Экспоненциальная регрессия

Уравнение регрессии:
$widehat{y}=e^{a+bx}$

Коэффициент b:
$b=dfrac{nsum x_iln y_i-sum x_icdotsumln y_i }{nsum x_i^2-left(sum x_iright)^2 }$

Коэффициент a:
$a=dfrac{1}{n}sumln y_i-dfrac{b}{n}sum x_i$

Вывод формул

Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.

Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.

Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.

Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:

Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.

Используя формулу производной сложной функции, получим следующую систему уравнений:
$begin{cases} sum [y_i - F(x_i, a, b)]cdot F^prime_a(x_i, a, b)=0 \ sum [y_i - F(x_i, a, b)]cdot F^prime_b(x_i, a, b)=0 end{cases}$

Для функции вида частные производные равны:
,

Подставив производные, получим:
$begin{cases} sum (y_i - ax_i-b)cdot x_i=0 \ sum (y_i - ax_i-b)=0 end{cases}$

Далее:
$begin{cases} sum y_ix_i - a sum x_i^2-bsum x_i=0 \ sum y_i - asum x_i - nb=0 end{cases}$

Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.

Источник

Линейная аппроксимация комбинации линий по набору зашумленных точек

Время на прочтение
3 мин

Количество просмотров 7.5K

Постановка задачи

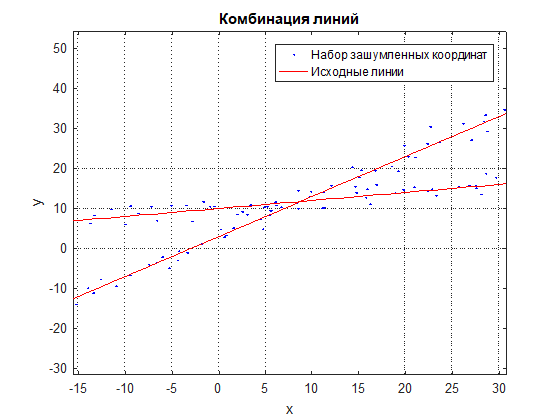
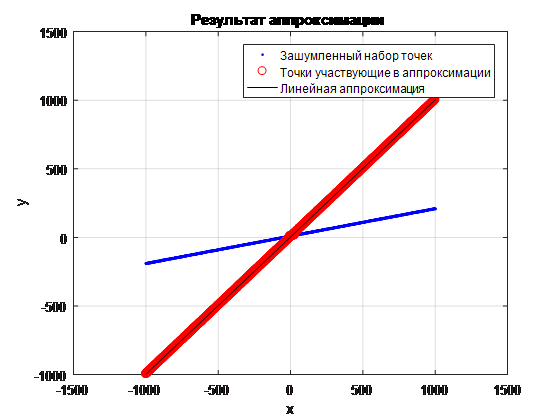
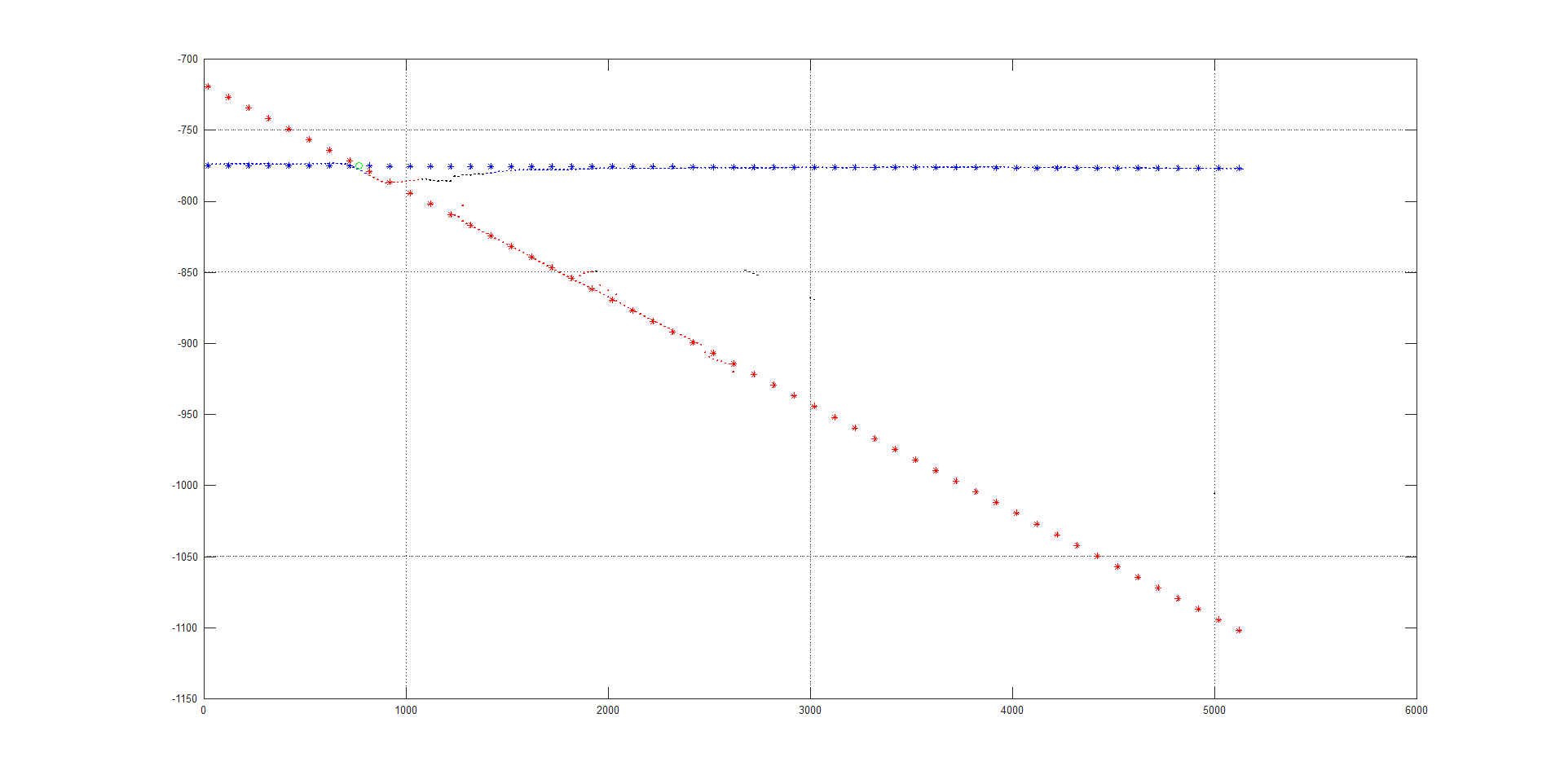
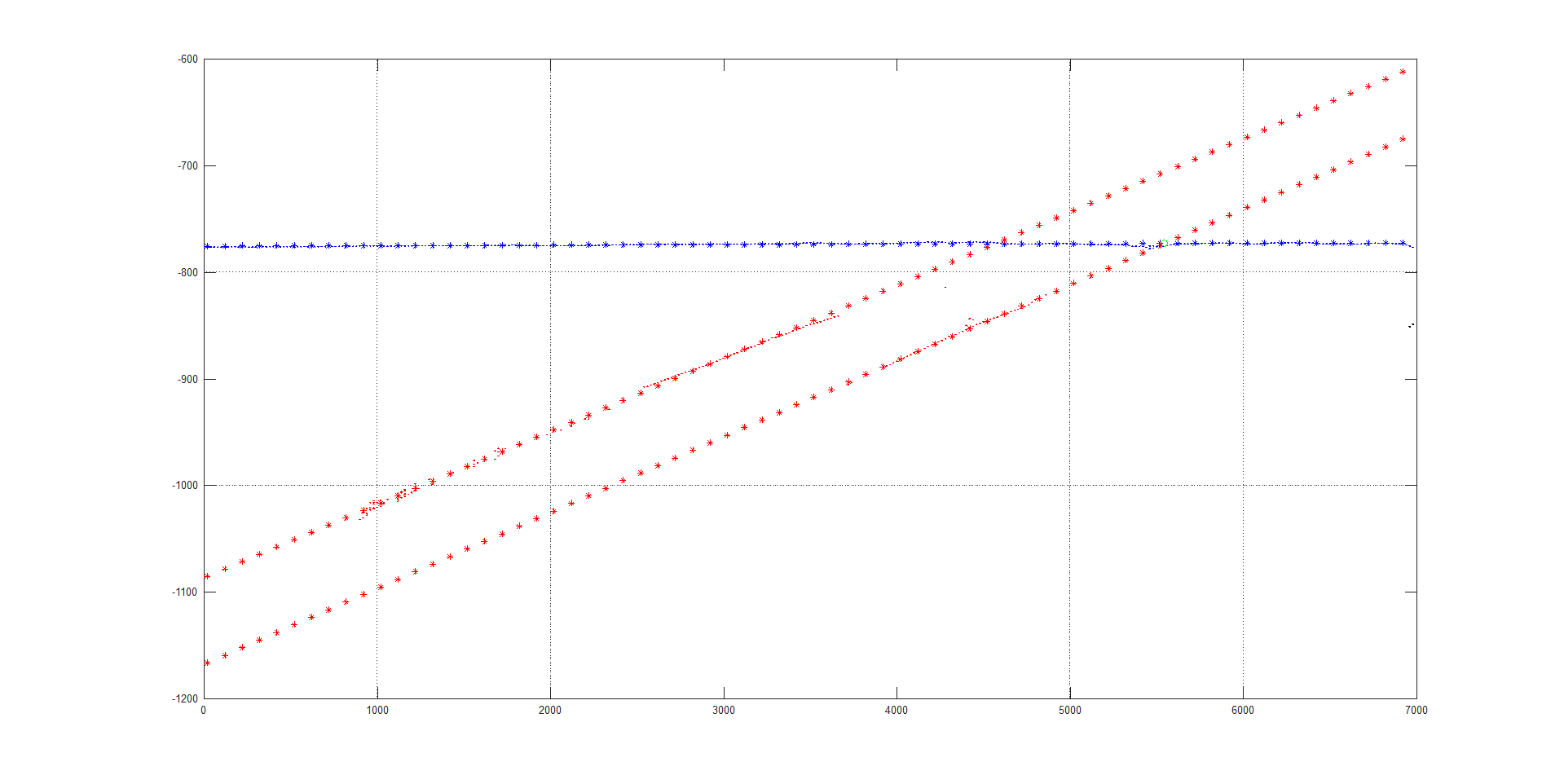
Рассмотрим задачу аппроксимации комбинации прямых линий по набору зашумленных координат точек, находящихся на данной комбинации линий (см. Рис. 1 и Рис. 2). Обычная формула линейной аппроксимации здесь не подойдет, так как точки перемешаны и результат будет некая усредненная линия между ними (см. Рис. 3).

Рис. 1 Комбинация линий и зашумленный набор координат

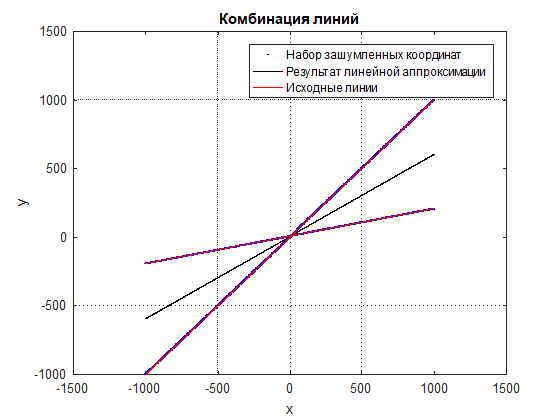
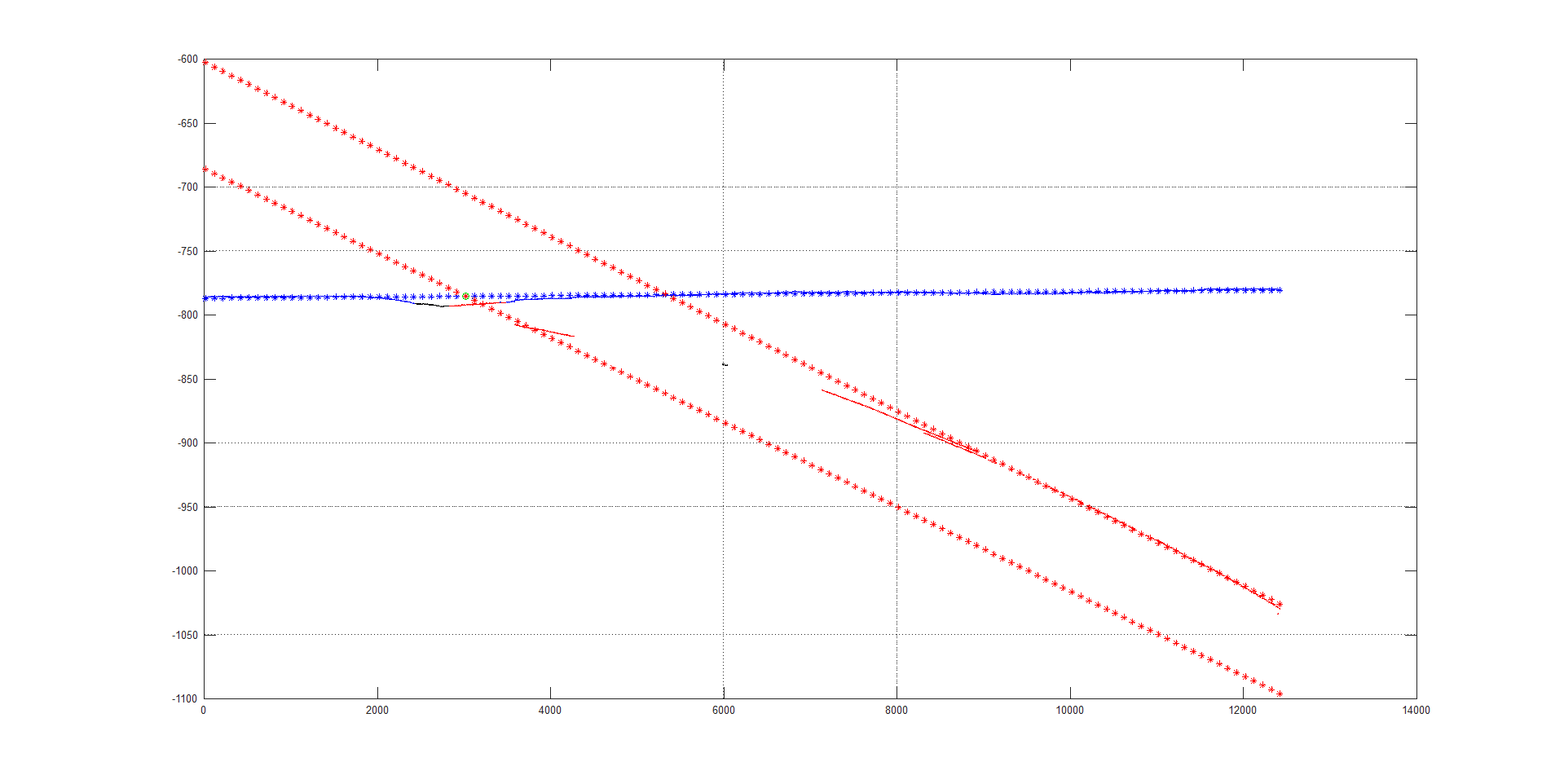
Рис. 2 Комбинация линий и зашумленный набор координат в увеличенном масштабе

Рис. 3 Результат линейной аппроксимации

Алгоритм

Единственный способ, который пришел в голову, это перебирать разные варианты линий. Т.е. перебираем все возможные углы, естественно на ограниченной сетке, от -90 градусов до +90 градусов (от -180 до 180 бессмысленно, т.к. линия симметрична относительно центра координат).

Таким образом, перебирая всевозможные варианты углов оцениваем тот угол наклона линии, при котором наибольшее количество точек находится на одинаковом расстоянии. Данный угол является искомым углом наклона линии, но он приблизительный, ввиду дискретности начального набора углов. Далее строим линейную аппроксимацию по полученному набору точек и получаем максимально приближенную аппроксимацию первой линии.

Для нахождения следующей линии, из рассмотрения убираются точки, использованные на предыдущем этапе. Таким образом, линия за линией, аппроксимируем все линии.

1. Набор рассматриваемых углов

На данном этапе необходимо разобраться какой набор углов будет перебираться. Зная особенности конкретной задачи можно подкорректировать данный набор углов, тем самым ускорив процесс детектирования линий. Так же можно учесть особенности угла наклона между линиями, то есть на каждом следующем шаге сужать диапазон перебираемых углов. В данной задаче будем использовать в лоб равномерный набор углов от -90 до 90 градусов с шагом 0.1 градуса.

2. Определение расстояния от точки до прямой

Для удобства перебора всевозможных вариантов линий, нам необходимо вывести формулу оценки кратчайшего расстояния от точки до линии.

Пусть уравнение линии и координаты точки, расстояние от которой измеряем, принимают следующие обозначения:

Тогда, так как кратчайшее расстояние от точки до линии это перпендикуляр к этой линии, получаем уравнение перпендикуляра, проходящего через заданную точку следующего вида:

Тогда, точка пересечения этих двух прямых:

Получаем расстояние от интересующей точки до точки пересечения:

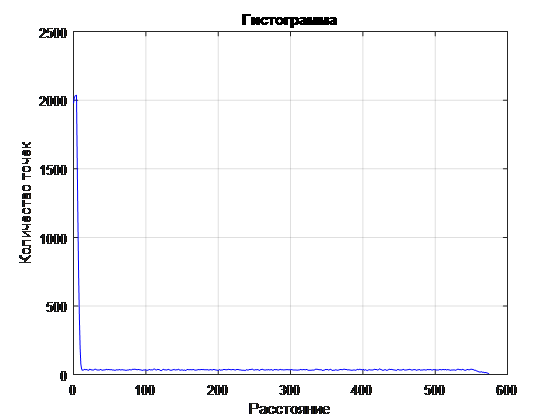
3. Построение гистограммы расстояний

Если мы построим просто гистограмму расстояний, она будет малоинформативной, поэтому нам необходимо построить гистограмму по скользящему окну, таким образом она будет более плавной и результат мы получим с меньшей ошибкой (см. Рис. 4-6).

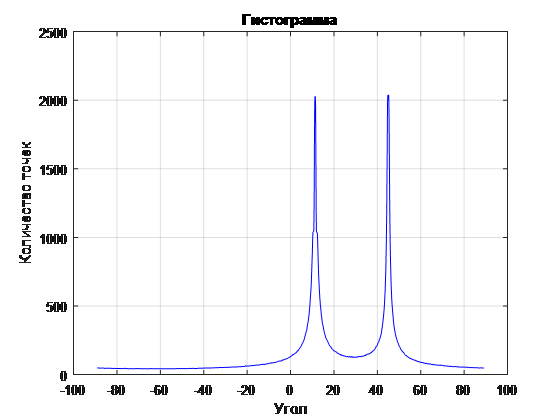
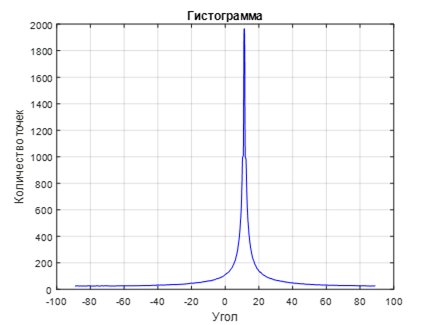
По построенной гистограмме определяем расстояние с максимальным количеством точек. По полученному набору максимального количества точек для каждого угла, строим зависимость количества точек и угла наклона линии (см. Рис. 7, 8). На Рис. 7 видно четких два пика, данные пики и есть углы наклона интересующих нас линий.

Рис. 4 Гистограмма расстояний (ошибочная линия)

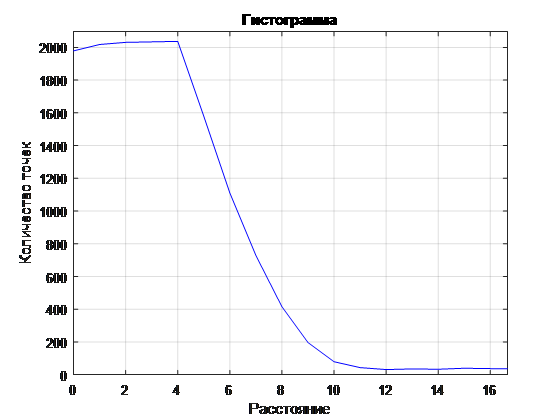
Рис. 5 Гистограмма расстояний (правильная линия)

Рис. 6 Увеличенная гистограмма расстояний (правильная линия)

Рис. 7 Гистограмма распределения максимального количества равноудаленных точек в зависимости от угла наклона рассматриваемой линии (Шаг 1)

Рис. 8 Гистограмма распределения максимального количества равноудаленных точек в зависимости от угла наклона рассматриваемой линии (Шаг 2)

4. Построение линейной аппроксимации

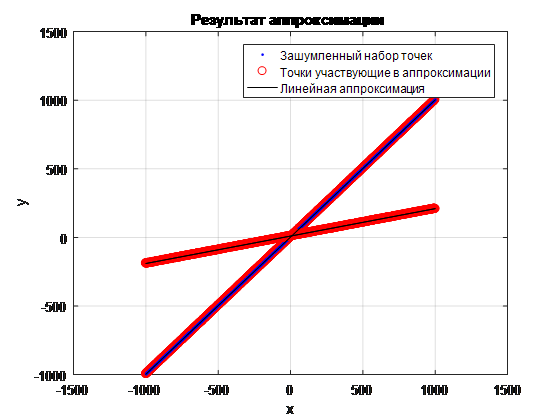
Полученный из гистограммы угол наклона линии является неточным, так как он был получен на фиксированной сетке углов. Для получения более точного угла наклона и смещения интересующей линии, необходимо выполнить линейную аппроксимацию полученного набора точек по следующим формулам (см. Рис. 9 и Рис. 10):

Рис. 9 Результат аппроксимации первой линии

Рис. 10 Результат аппроксимации второй линии

Примеры использования

Приведем примеры распознавания линий на произвольных наборах точек (см. Рис 11-13).

Рис. 11 Результат работы на произвольной выборке точек

Рис. 12 Результат работы на произвольной выборке точек

Рис. 13 Результат работы на произвольной выборке точек

Вывод

С помощью приведенного алгоритма можно детектировать прямые линии с относительно высокой скоростью и определять их параметры (наклон и смещение). Количество линий при этом может быть неограниченное количество.

Для успешного детектирования линий, желательно чтобы точки были максимально сильно разбросаны по координатной системе, так как если все точки будут рядом, то при процедуре перехода детектирования от одной линии к другой, точки новой линии будут отброшены ввиду их близости к линии с предыдущей итерации.

Основная цель данной статьи увидеть взгляд со стороны, встречались ли у кого-либо подобные задачи и как вы их решали. Вдруг есть способы, которые в один проход умеют детектировать эти линии. Увидеть какие-нибудь интересные решения, которые можно будет использовать в других задачах.

Источник

Экспериментальные
данные могут быть заданы в виде таблицы
n
пар чисел
X_i;
Y_i.
Аппроксимировать их, значит построить
функцию, которая пройдет как можно ближе
к заданным точкам. Существует много
численных методов решения этой задачи.
Некоторые из них запрограммированы в
пакете MathCad.
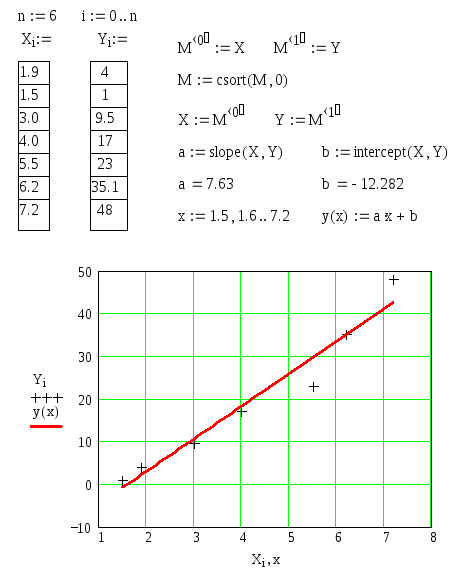
На рис. 25 приведен пример линейной
аппроксимации 7-ми пар чисел, занесенных
в массивы X_i,
Y_i.

Рис. 25

Линейная
аппроксимация предполагает построение
прямой y(x)
= ax+b,
проходящей через заданные точки.
Коэффициент а
можно получить с помощью функции
slope(X,Y),
свободный член получаем с помощью
функции intercept(X,Y).
Следует иметь в виду, что эти функции
работают с
упорядоченным по возрастанию
массивом X.
Для упорядочения обоих массивов
воспользуемся следующим приемом. Числа
Х
запишем в нулевой столбец двумерного
массива М,
числа Y
запишем в первый столбец этого массива.
Затем следует воспользоваться функцией
csort(M,0),
осуществляющей сортировку массива М
по возрастанию нулевого столбца. После
этого отсортированные пары чисел снова
переписываются в массивы X
и Y.
Теперь можно вычислить коэффициенты a
и b.
Для приведенного примера они получились
равными 7,63 и –12,282. Таким образом, искомая
аппроксимирующая прямая имеет вид у(х)
= 7,63х
– 12,282. В принципе можно считать, что
поставленная задача решена. Однако
можно еще построить график, подсчитать
абсолютную погрешность аппроксимации
по формуле _i
= Y_i–
y(X_i),
относительную погрешность по формуле

Задание
1. Повторите
линейную аппроксимацию вышеприведенного
примера. Постройте графики, подсчитайте
абсолютную и относительную погрешности
аппроксимации.

MathCad
имеет возможность осуществить нелинейную
аппроксимацию полиномом k-й
степени. Степень аппроксимирующего
полинома выбирается с помощью столбца,
содержащего члены полинома без
коэффициентов, начиная с низшей степени
(т.е. с нулевой). Аппроксимация полиномом
выполняется с помощью функции linfit(X,Y,
f), где f
– имя столбца, содержащего члены
полинома. Результатом выполнения этой
функции являются коэффициенты
аппроксимирующего полинома.

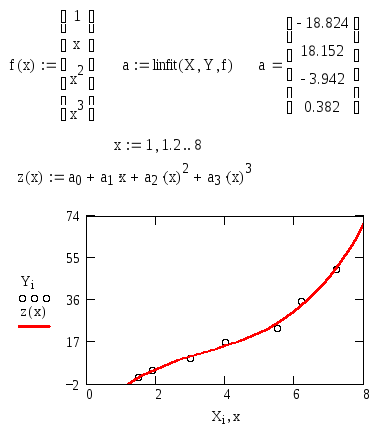
На
рис. 26 приведен пример аппроксимации
данных из предыдущего примера полиномом
3-й степени.

Рис. 26

Задание
2. Постройте
аппроксимирующие полиномы 2-й и 3-й
степени. Сравните погрешности линейной
аппроксимации с погрешностями
аппроксимации 2- и 3-й степеней. Постройте
на одном поле графики линейной
аппроксимации и аппроксимации 2-й и 3-й
степеней.

При анализе экспериментальных данных достаточно часто возникает необходимость в аппроксимации этих данных, т.е. нахождения приблизительной аналитической функции с необходимой точностью описывающей имеющиеся значения.
В ниже следующих программах на различных языках приводятся программы аппроксимации исходных данных линейной функцией по методу наименьших квадратов.

Далее приводится вариант программы на языке С (компилятор BORLAND C++ 3.1)

Show »

//***********************************************************
// Программа линейной аппроксимации табличной функции по МНК.
//***********************************************************
// Вводятся последовательно:
// - кол-во точек исходной функции
// - затем пары значений (абсцисса и ордината табличного значения)
// Внимание!!! Абсциссы не обязательно равноотстоящие.
// Контрольная точка №1: при вводе
// - 9
// - -26 66.7 -22 71 -16 76.3 -11 80.6 -5 85.7 3 92.9 10 99.4 25 113.6 42 125.1
// получаю
// 67.508 70.990 76.214 80.567 85.791 92.756 98.851 111.910 126.711
// Контрольная точка №2: при вводе
// - 3
// - 1 3 5 6 7 8
// получаю
// 2.929 6.214 7.857
// при этом а0=2.107143 а1=0.821428

#include <stdio.h>
#include <conio.h>
int n; // количество исходных точек аппроксимации
float mx[20]; // массив исходных значений абсцисс
float my[20]; // аналогично для ординат исходной табличной функции
int i; // переменная цикла
float a0,a1; // коэффициенты аппроксимирующей прямой Y=a0+a1*X
float sx=0, sy=0, sxy=0, sx2=0; // сюда буду накапливать суммы;
void main(void)
{ // 0
 clrscr(); //начальная очистка экрана
 puts("Введи количество исходных интерполируемых точек:");
 scanf("%d",&n);
 puts("Введи попарно сами исходные абсциссы (от меньших к большим) и ординаты:");
 // Ввод самих исходных значений
 for(i=0;i<=n-1; scanf("%f%f",&mx[i++],&my[i]));
 // Собственно получение искомых коээфициентов аппроксимирующей прямой
 for(i=0;i<=n-1;sx+=mx[i],sy+=my[i],sxy+=mx[i]*my[i],sx2+=mx[i]*mx[i],i++);
 a1=(sxy-sy*sx/n)/(sx2-sx*sx/n);
 a0=(sy-a1*sx)/n;
 puts("Результаты работы программы:");
 puts("номер абсцисса исх.ордината выч.ордината");
 for(i=0;i<=n-1; printf("%3d%10.3f%12.3f%14.3fn",i,mx[i++],my[i],a0+a1*mx[i]));
} // -0

Далее приводится текст программы на языке PASCAL. Проверено на компиляторах
PASCALABC 3.1 и PASCALABC.NET 2.2.

Show »

// AINTE002.CPP
//***********************************************************
// Программа линейной аппроксимации табличной функции по МНК.
//***********************************************************
// Вводятся последовательно:
// - кол-во точек исходной функции
// - затем пары значений (абсцисса и ордината табличного значения)
// Внимание!!! Абсциссы не обязательно равноотстоящие.
// Контрольная точка №1: при вводе
// - 9
// - -26 66.7 -22 71 -16 76.3 -11 80.6 -5 85.7 3 92.9 10 99.4 25 113.6 42 125.1
// получаю
// 67.508 70.990 76.214 80.567 85.791 92.756 98.851 111.910 126.711
// Контрольная точка №2: при вводе
// - 3
// - 1 3 5 6 7 8
// получаю
// 2.929 6.214 7.857
// при этом а0=2.107143 а1=0.821428

uses crt;
var 
n:integer; // количество исходных точек аппроксимации
mx: array[0..20] of real; // массив исходных значений абсцисс
my: array[0..20] of real; // аналогично для ординат исходной табличной функции
i:integer; // переменная цикла
a0,a1:real; // коэффициенты аппроксимирующей прямой Y=a0+a1*X
sx, sy, sxy, sx2:real; // сюда буду накапливать суммы;
begin // 0
 writeln('Введи количество исходных интерполируемых точек:');
 readln(n);
 writeln('Введи попарно сами исходные абсциссы (от меньших к большим) и ординаты:');
 // Ввод самих исходных значений
 // и получение искомых коээфициентов аппроксимирующей прямой
 for i:=0 to n-1 do
 begin
 read(mx[i],my[i]);
 sx:=sx+mx[i];
 sy:=sy+my[i];
 sxy:=sxy+mx[i]*my[i];
 sx2:=sx2+mx[i]*mx[i];
 end;
 a1:=(sxy-sy*sx/n)/(sx2-sx*sx/n);
 a0:=(sy-a1*sx)/n;
 writeln('Результаты работы программы:');
 writeln('номер абсцисса исх.ордината выч.ордината');
 for i:=0 to n-1 do
 writeln(i:3,mx[i]:10:3,my[i]:12:3,a0+a1*mx[i]:14:3);
end. // -0

Далее приводится текс программы на языке QBASIC в компиляторе
MS-DOS QBASIC 1.0.

Show »

'***********************************************************
' Программа линейной аппроксимации табличной функции по МНК.
'***********************************************************
' Вводятся последовательно:
' - кол-во точек исходной функции
' - затем пары значений (абсцисса и ордината табличного значения)
' Внимание!!! Абсциссы не обязательно равноотстоящие.
' Контрольная точка №1: при вводе
' - 9
' - -26 66.7 -22 71 -16 76.3 -11 80.6 -5 85.7 3 92.9 10 99.4 25 113.6 42 125.1
' получаю
' 67.508 70.990 76.214 80.567 85.791 92.756 98.851 111.910 126.711
' Контрольная точка №2: при вводе
' - 3
' - 1 3 5 6 7 8
' получаю
' 2.929 6.214 7.857
' при этом а0=2.107143 а1=0.821428

DIM n AS INTEGER ' количество исходных точек аппроксимации
DIM i AS INTEGER ' переменная цикла
DIM a0 AS SINGLE, a1 AS SINGLE' коэффициенты аппроксимирующей прямой Y=a0+a1*X
DIM sx AS SINGLE, sy AS SINGLE, sxy AS SINGLE, sx2 AS SINGLE' сюда буду накапливать суммы
INPUT "Введи количество исходных интерполируемых точек:", n
DIM mx(0 TO n - 1) AS SINGLE' массив исходных значений абсцисс
DIM my(0 TO n - 1) AS SINGLE' аналогично для ординат исходной табличной функции
PRINT "Введи попарно сами исходные абсциссы (от меньших к большим) и ординаты:"
' Ввод самих исходных значений
' и получение искомых коээфициентов аппроксимирующей прямой
FOR i = 0 TO n - 1
 INPUT mx(i), my(i)
 sx = sx + mx(i)
 sy = sy + my(i)
 sxy = sxy + mx(i) * my(i)
 sx2 = sx2 + mx(i) * mx(i)
NEXT i
a1 = (sxy - sy * sx / n) / (sx2 - sx * sx / n)
a0 = (sy - a1 * sx) / n
PRINT "Результаты работы программы:"
PRINT "номер абсцисса исх.ордината выч.ордината"
FOR i = 0 TO n - 1
 PRINT USING "### #######.### ######.### #########.###";i,mx(i),my(i),a0 + a1 * mx(i)
NEXT i
END

Далее приводится текст этой же программы, написанный на C# 4.0 в компиляторе Visual C# 2010 Express.

Show »

/***********************************************************
 Программа линейной аппроксимации табличной функции по МНК.
 Данные вводятся каждая на своей строке.
 Работа программы выглядит следующим образом:
Введи количество исходных интерполируемых точек:
3
Введи попарно сами исходные абсциссы (от меньших к большим) и ординаты каждое на
 отдельнй строке:'
1
3
5
6
7
8 
Результаты работы программы:
номер абсцисса исх.ордината выч.ордината
 001 1,000 3,000 2,929
 002 5,000 6,000 6,214
 003 7,000 8,000 7,857
***********************************************************/
using System;

namespace ConsoleApplication1
{
 class Program
 {
 static void Main(string[] args)
 {
 int n,i;
 float sx=0, sy=0, sxy=0, sx2=0, a1, a0;
 Console.WriteLine("Введи количество исходных интерполируемых точек:");
 n = int.Parse(Console.ReadLine());
 Console.WriteLine("Введи попарно сами исходные абсциссы (от меньших к большим) и ординаты:'");
 // заполнение с клавы массивов исходных данных
 float[] mx = new float[n];
 float[] my = new float[n];
 // собственно заполнение массивов в цикле необходимые вычисления
 for (i = 0; i < n; i++)
 {
 mx[i] = float.Parse(Console.ReadLine());
 my[i] = float.Parse(Console.ReadLine());
 sx+=mx[i];
 sy+=my[i];
 sxy+=mx[i] * my[i];
 sx2+=mx[i] * mx[i];
 }
 a1 = (sxy - sy * sx / n) / (sx2 - sx * sx / n);
 a0 = (sy - a1 * sx) / n;
 Console.Write("Результаты работы программы:n");
 Console.Write("номер абсцисса исх.ордината выч.ординатаn");
 for (i = 0; i < n; i++)
 Console.WriteLine(" {0:d3} {1:f3} {2:f3} {3:f3}", i+1, mx[i], my[i], a0 + a1 * mx[i]);
 Console.ReadLine(); // держит экран
 }
 }
}

Ниже приводится текст этой же программы составленный для интерпретатора Python 3.4.3.

Show »

#***********************************************************
# Программа линейной аппроксимации табличной функции по МНК.
#***********************************************************
# Вводятся последовательно:
# - кол-во точек исходной функции
# - затем пары значений (абсцисса и ордината табличного значения)
# Внимание!!! Абсциссы не обязательно равноотстоящие.
# Контрольная точка №2: при вводе
# - 3
# - 1 3 
# - 5 6
# - 7 8
# получаю
# 2.929 6.214 7.857
# при этом а0=2.107143 а1=0.821428
n= int(input('Введи кол-во исходных точек '))
print('Введи попарно сами исходные абсциссы (от меньших к большим) и ординаты:')
mmxy = [] # объявляю пустой список (в данном случае одномерный массив)
# цикл по вводу с клавы пар координат
sx=sy=sxy=sx2=0
for i in range(n): 
 # собствнно ввод с клавы через пробел
 (a,b)= list(map(float, input().split())) 
 mmxy.append(a)
 mmxy.append(b)
 sx+=a
 sy+=b
 sxy+=a*b
 sx2+=a*a
a1=(sxy - sy * sx / n) / (sx2 - sx * sx / n)
a0=(sy - a1 * sx) / n
print('Результаты работы программы:')
print(' номер абсцисса исх.ордината выч.ордината')
for i in range(n):
 print('%3d%10.3f%12.3f%14.3f'%(i+1,mmxy[2*i],mmxy[2*i+1],a0+a1*mmxy[2*i]),end='n')
input() # команда ДЕРЖИТ экран

Ниже приводится текст этой же программы составленный для компилятора Compaq Visual Fortran 2000.

Show »

! AINTE002.CPP
!***********************************************************
! Программа линейной аппроксимации табличной функции по МНК.
!***********************************************************
! Вводятся последовательно:
! - кол-во точек исходной функции
! - затем пары значений (абсцисса и ордината табличного значения)
! Внимание!!! Абсциссы не обязательно равноотстоящие.
! Контрольная точка №1: при вводе
! - 9
! - -26 66.7 -22 71 -16 76.3 -11 80.6 -5 85.7 3 92.9 10 99.4 25 113.6 42 125.1
! получаю
! 67.508 70.990 76.214 80.567 85.791 92.756 98.851 111.910 126.711
! Контрольная точка №2: при вводе
! - 3
! - 1 3 
! - 5 6
! - 7 8
! получаю
!nomer abscissa isx.ordinata wich.ordinata
! 001 1,000 3,000 2,929
! 002 5,000 6,000 6,214
! 003 7,000 8,000 7,857
! при этом а0=2.107143 а1=0.821428
real, dimension(0:20)::mmxy
integer i,n
real sx,sy,sxy,sx2! сюда буду накапливать суммы
real a0,a1 !вычисляемые коэффициенты
real a,b,kk
print*,'Wwedite kol-wo par ischodhix tochek'
read*,n
print*,'Wwedi poparno sami abscissi i ordinati:'
! Ввод самих исходных значений
! и получение искомых коээфициентов аппроксимирующей прямой
do 1 i=0,n-1
 read*,a,b
 mmxy(2*i)=a
 mmxy(2*i+1)=b
 sx = sx + a
 sy = sy + b
 sxy = sxy + a*b
 sx2 = sx2 + a*a
1 continue
a1 = (sxy - sy * sx / n) / (sx2 - sx * sx / n)
a0 = (sy - a1 * sx) / n
print*,'nomer abscissa isx.ordinata wich.ordinata'
do 2 i = 0,n - 1
 kk=a0 + a1 * mmxy(2*i)
 write(*,7)i,mmxy(2*i),mmxy(2*i+1),kk
7 format(' ',I3,F10.3,F12.3,F14.3)
2 continue 
end

Источник

Аппроксимация линейной функцией

Пример реализации

Построение графика функции

Аппроксимация с фиксированной точкой пересечения с осью y

Аппроксимация функции одной переменной

Линейная регрессия

Квадратичная регрессия

Кубическая регрессия

Степенная регрессия

Показательная регрессия

Гиперболическая регрессия

Логарифмическая регрессия

Экспоненциальная регрессия

Вывод формул

Линейная аппроксимация комбинации линий по набору зашумленных точек

Постановка задачи

Алгоритм

1. Набор рассматриваемых углов

2. Определение расстояния от точки до прямой

3. Построение гистограммы расстояний

4. Построение линейной аппроксимации

Примеры использования

Вывод

Оглавление