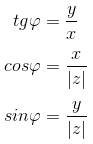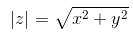Вычислить аргумент и модуль комплексного числа.
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки,
соответствующей данному комплексному числу и обозначается Arg(z) = φ
Из определения следуют следующие формулы:
Для числа z = 0 аргумент не определен.
Главным значением аргумента называется такое значение φ, что 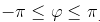
Обозначается: arg(z).
Свойства аргумента:
Модулем комплексного числа z = x + iy называется вещественное число |z| равное:
Для любых комплексных чисел z, z1, z2 имеют место следующие свойства модуля:
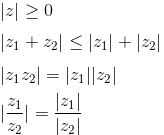
|
|
для пары комплексных чисел z1 и z2 модуль их разности |z1 − z2| равен расстоянию между соответствующими точками комплексной плоскости. |
Простое объяснение принципов решения частных производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения частных производных
Вычисление частной производной функции из нескольких переменных осуществляется по тем же правилам, что и функций с одной переменной. Разница лишь той, что другие переменные не участвуют дифференцировании (вычислении производной).
Проще говоря, чтобы найти частную производную функции по переменной
,переменную
будем считать константой (производная константы равна нулю), после чего находим производную функции по
с помощью таблицы производных элементарных функций –
. Готово!
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Примеры решения частных производных
Задача
Найти частные производные функции .
Решение
Частная производная функции по независимой переменной :
Производная суммы равна сумме производных. Производная от вычисляется по правилам вычислений производных функций одного аргумента, производная от слагаемого
вычисляется как производная от функции двух аргументов. При этом аргумент
считается константой. Производная от слагаемого
вычисляется как производная от константы.
.
Частная производная функции по независимой переменной :
Здесь вычисления также происходят по правилам вычисления производной суммы. Производная от вычисляется как производная от константы (независимым аргументом при этом считается
). Производная от слагаемого
вычисляется как производная от функции двух аргументов. При этом аргумент
считается константой, а
– независимым аргументом. Вычисление производной от слагаемого
осуществляется по правилам вычисления производных функций с одним аргументом.
.
Ответ
.
Задача
Найти частные производные функции .
Решение
Найдём частную производную функции по независимой переменной :
Функция является сложной. Производной показательной функции с основанием
является сама функция. Производная показателя степени вычисляется в при условии, что
является константой и равна
. Производная функции
равна произведению
и
. В результате получаем:
.
Найдём частную производную функции по независимой переменной :
По аналогии с предыдущим случаем производная функции будет равна произведению производных от функции и показателя её степени
:
Считая постоянной величиной, находим производную по независимому аргументу
:
.
Ответ
.
Задача
Найти частные производные функции .
Решение
Частная производная функции по независимой переменной будет равна производной от
. Производная от слагаемого
при этом будет равна нулю как производная от константы.
Частная производная функции по независимой переменной находится аналогичным образом, при этом предполагается, что
является константой.
Ответ
Задача
Найти частные производные функции .
Решение
Частная производная функции по независимой переменной
определяется слагаемым
. Производная второго слагаемого –
равна нулю, как производная от константы.
В свою очередь, частная производная функции по независимой переменной
будет определяться обоими слагаемым:
Таким образом, окончательно получаем:
Ответ
Задача
Найти частные производные функции .
Решение
При нахождении производной по независимой переменной , функцию
следует рассматривать как степенную. По правилу нахождения производной степенной функции получаем:
Производная по независимой переменной находится по правилу вычисления производной показательной функции, которая, в свою очередь, определяется по правилам нахождения производных сложных функций, т.к. переменная
входит в показатель степени виде функции
.
Производная показательной функции равна:
Производная показателя степени равна:
В результате получаем:
Ответ
Задача
Найти частные производные функции .
Решение
Частная производная по независимой переменной находится как сумма слагаемых:
Частная производная по независимой переменной находится как сумма слагаемых:
Ответ
Задача
Найти частные производные функции .
Решение
По правилу нахождения производной квадратного корня получаем, рассматривая как независимый аргумент:
Т.к. функция является сложной, то результат вычисления производной от квадратного корня – следует домножить на производную подкоренного выражения:
.
Рассматривая в качестве независимого аргумента, получаем:
По аналогии с предыдущим случаем, результат вычисления производной от квадратного корня – следует домножить на производную подкоренного выражения:
.
Ответ
Задача
Найти частные производные функции .
Решение
Данная функция является сложной, поэтому процесс нахождения производной данной функции целесообразно производить в несколько этапов.
Производная показательной функции с основанием равна самой себе. Далее необходимо найти производную показателя степени:
. В свою очередь аргумент функции арктангенс в данном случае также представляет собой сложную функцию:
. Результирующая производная будет равна произведению производных трёх функций:
и
.
Нахождение частной производной функции по аргументу :
Нахождение частной производной функции по аргументу :
Ответ
Задача
Найти частные производные первого и второго порядков функции .
Решение
Найдём частную производную первого порядка по аргументу :
Найдём частную производную второго порядка по аргументу :
Найдём частную производную первого порядка по аргументу :
Найдём частную производную второго порядка по аргументу :
Ответ
Задача
Найти частные производные первого и второго порядков функции .
Решение
Найдём частную производную первого порядка по аргументу :
Найдём частную производную второго порядка по аргументу :
Найдём частную производную первого порядка по аргументу :
Найдём частную производную второго порядка по аргументу :
Ответ
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Если для каждой пары $(x,y)$ значений двух независимых переменных из некоторой области ставится в соответствие определенное значение $z$, то говорят, что $z$ является функцией двух переменных $(x,y)$. Обозначение: $z=f(x,y)$.
В отношении функции $z=f(x,y)$ рассмотрим понятия общего (полного) и частного приращений функции.
Пусть дана функция $z=f(x,y)$двух независимых переменных $(x,y)$.
Замечание 1
Так как переменные $(x,y)$ являются независимыми, то одна из них может изменяться, а другая при этом сохранять постоянное значение.
Дадим переменной $x$ приращение $Delta x$, при этом сохраним значение переменной $y$ неизменным.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Тогда функция $z=f(x,y)$ получит приращение, которое будет называться частным приращением функции $z=f(x,y)$ по переменной $x$. Обозначение:
Аналогично дадим переменной $y$ приращение $Delta y$, при этом сохраним значение переменной $x$ неизменным.
Тогда функция $z=f(x,y)$ получит приращение, которое будет называться частным приращением функции $z=f(x,y)$ по переменной $y$. Обозначение:
Если же аргументу $x$ дать приращение $Delta x$, а аргументу $y$ — приращение $Delta y$, то получается полное приращение заданной функции $z=f(x,y)$. Обозначение:
Таким образом, имеем:
-
$Delta _{x} z=f(x+Delta x,y)-f(x,y)$ — частное приращение функции $z=f(x,y)$ по $x$;
-
$Delta _{y} z=f(x,y+Delta y)-f(x,y)$ — частное приращение функции $z=f(x,y)$ по $y$;
-
$Delta z=f(x+Delta x,y+Delta y)-f(x,y)$ — полное приращение функции $z=f(x,y)$.
Пример 1
Записать частные и полное приращение функции
[z=x+y.]
Решение:
По определению частного приращения найдем:
$Delta _{x} z=x+Delta x+y$ — частное приращение функции $z=f(x,y)$ по $x$;
$Delta _{y} z=x+y+Delta y$ — частное приращение функции $z=f(x,y)$ по $y$.
По определению полного приращения найдем:
$Delta z=x+Delta x+y+Delta y$ — полное приращение функции $z=f(x,y)$.
«Частное и полное приращение функции» 👇
Пример 2
Вычислить частные и полное приращение функции $z=xy$ в точке $(1;2)$ при $Delta x=0,1;, , Delta y=0,1$.
Решение:
По определению частного приращения найдем:
$Delta _{x} z=(x+Delta x)cdot y$ — частное приращение функции $z=f(x,y)$ по $x$
$Delta _{y} z=xcdot (y+Delta y)$ — частное приращение функции $z=f(x,y)$ по $y$;
По определению полного приращения найдем:
$Delta z=(x+Delta x)cdot (y+Delta y)$ — полное приращение функции $z=f(x,y)$.
Следовательно,
[Delta _{x} z=(1+0,1)cdot 2=2,2] [Delta _{y} z=1cdot (2+0,1)=2,1] [Delta z=(1+0,1)cdot (2+0,1)=1,1cdot 2,1=2,31.]
Замечание 2
Полное приращение заданной функции $z=f(x,y)$ не равно сумме ее частных приращений $Delta _{x} z$ и $Delta _{y} z$. Математическая запись: $Delta zne Delta _{x} z+Delta _{y} z$.
Пример 3
Проверить утверждение замечания для функции
[z=x+y.]
Решение:
$Delta _{x} z=x+Delta x+y$; $Delta _{y} z=x+y+Delta y$; $Delta z=x+Delta x+y+Delta y$ (получены в примере 1)
Найдем сумму частных приращений заданной функции $z=f(x,y)$
[Delta _{x} z+Delta _{y} z=x+Delta x+y+(x+y+Delta y)=2cdot (x+y)+Delta x+Delta y.]
Так как
[2cdot (x+y)+Delta x+Delta yne x+Delta x+y+Delta y,]
то
[Delta _{x} z+Delta _{y} zne Delta z.]
Определение 2
Если для каждой тройки $(x,y,z)$ значений трех независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией трех переменных $(x,y,z)$ в данной области.
Обозначение: $w=f(x,y,z)$.
Определение 3
Если для каждой совокупности $(x,y,z,…,t)$ значений независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией переменных $(x,y,z,…,t)$ в данной области.
Обозначение: $w=f(x,y,z,…,t)$.
Для функции от трех и более переменных, аналогично как для функции двух переменных определяются частные приращения по каждой из переменных:
-
$Delta _{z} w=f(x,y,z+Delta z)-f(x,y,z)$ — частное приращение функции $w=f(x,y,z,…,t)$ по $z$;
-
$…$
-
$Delta _{t} w=f(x,y,z,…,t+Delta t)-f(x,y,z,…,t)$ — частное приращение функции $w=f(x,y,z,…,t)$ по $t$.
Пример 4
Записать частные и полное приращение функции
[w=(x+y)cdot z.]
Решение:
По определению частного приращения найдем:
$Delta _{x} w=((x+Delta x)+y)cdot z$ — частное приращение функции $w=f(x,y,z)$ по $x$
$Delta _{y} w=(x+(y+Delta y))cdot z$ — частное приращение функции $w=f(x,y,z)$ по $y$;
$Delta _{z} w=(x+y)cdot (z+Delta z)$ — частное приращение функции $w=f(x,y,z)$ по $z$;
По определению полного приращения найдем:
$Delta w=((x+Delta x)+(y+Delta y))cdot (z+Delta z)$ — полное приращение функции $w=f(x,y,z)$.
Пример 5
Вычислить частные и полное приращение функции $w=xyz$ в точке $(1;2;1)$ при $Delta x=0,1;, , Delta y=0,1;, , Delta z=0,1$.
Решение:
По определению частного приращения найдем:
$Delta _{x} w=(x+Delta x)cdot ycdot z$ — частное приращение функции $w=f(x,y,z)$ по $x$
$Delta _{y} w=xcdot (y+Delta y)cdot z$ — частное приращение функции $w=f(x,y,z)$ по $y$;
$Delta _{z} w=xcdot ycdot (z+Delta z)$ — частное приращение функции $w=f(x,y,z)$ по $z$;
По определению полного приращения найдем:
$Delta w=(x+Delta x)cdot (y+Delta y)cdot (z+Delta z)$ — полное приращение функции $w=f(x,y,z)$.
Следовательно,
[Delta _{x} w=(1+0,1)cdot 2cdot 1=2,2] [Delta _{y} w=1cdot (2+0,1)cdot 1=2,1] [Delta _{y} w=1cdot 2cdot (1+0,1)=2,2] [Delta z=(1+0,1)cdot (2+0,1)cdot (1+0,1)=1,1cdot 2,1cdot 1,1=2,541.]
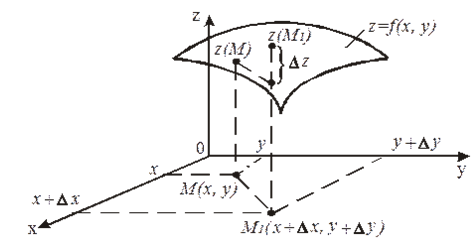
С геометрической точки зрения полное приращение функции $z=f(x,y)$ (по определению $Delta z=f(x+Delta x,y+Delta y)-f(x,y)$) равно приращению аппликаты графика функции $z=f(x,y)$ при переходе от точки $M(x,y)$ к точке $M_{1} (x+Delta x,y+Delta y)$ (рис. 1).
Рисунок 1.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Комплексные числа в тригонометрической
и показательной формах
Тригонометрическая форма комплексного числа
Каждому комплексному числу геометрически соответствует точка
на плоскости
. Но положение точки на плоскости, кроме декартовых координат
, можно зафиксировать другой парой — ее полярных координат
в полярной системе (рис. 1.3,a).
Величина является неотрицательной и для данной точки определяется единственным образом, а угол
может принимать бесчисленное множество значений (при этом
): если точке соответствует некоторое значение
, то ей также соответствуют значения
. Например, если для точки
(см. рис. 1.1) выбрать
, то ей соответствует любое
, в частности
при
. Если же выбрать
, то
, а при
получаем
.
Используя связь декартовых и полярных координат точки (рис. 1.3,б), из алгебраической формы записи комплексного числа
получаем тригонометрическую форму:
(1.3)
Показательная форма комплексного числа
Если обозначить комплексное число , у которого
, а
, через
, то есть
, то из (1.3) получим показательную форму записи комплексного числа:
(1.4)
Равенство называется формулой Эйлера.
Заметим, что геометрически задание комплексного числа равносильно заданию вектора
, длина которого равна
, то есть
, а направление — под углом
к оси
(рис. 1.3,б).
Модуль комплексного числа
Число — длина радиуса-вектора точки
называется модулем комплексного числа
. Обозначение:
.
Из рис. 1.3,б получаем формулу для нахождения модуля числа, заданного и алгебраической форме
(1.5)
Очевидно, что и
только для числа
.
С помощью правила вычитания запишем модуль числа , где
и
А это, как известно, есть формула для расстояния между точками и
.
Таким образом, число есть расстояние между точками
и
на комплексной плоскости.
Пример 1.13. Найти модули комплексных чисел:
Решение
Аргумент комплексного числа
Полярный угол точки
называется аргументом комплексного числа
. Обозначение:
.
В дальнейшем, если нет специальных оговорок, под будем понимать значение
, удовлетворяющее условию
. Так, для точки
(см. рис. 1.1)
.
Формулу для нахождения аргумента комплексного числа , заданного в алгебраической форме, получаем, используя связь декартовых и полярных координат точки
(см. рис. 1.3,б). Для точек, не лежащих на мнимой оси, т.е. для
, у которых
, получаем
; для точек мнимой положительной полуоси, т.е. для
, у которых
, имеем
; для точек мнимой отрицательной полуоси, т.е. для
, у которых
, соответственно
.
Аргумент числа — величина неопределенная.
Нахождение аргумента при сводится к решению тригонометрического уравнения
. При
, т.е. когда
— число действительное, имеем
при
и
при
. При
решение уравнения зависит от четверти плоскости
. Четверть, в которое расположена точка
, определяется по знакам
и
. В результате получаем:
(1.6)
При решении примеров удобно пользоваться схемой, которая изображена на рис. 1.5.
Пример 1.14. Найти аргументы чисел из примера 1.13.
Решение
Пример 1.15. Найти модуль и аргумент числа .
Решение. Находим . Так как
, т.е. точка расположена в четвертой четверти, то из равенства
получаем
(рис. 1.5).
Главное значение аргумента комплексного числа
Аргумент комплексного числа определяется неоднозначно. Это следует из неоднозначности задания величины угла для данной точки, а также из тригонометрической формы записи комплексного числа и свойства периодичности функций
и
.
Всякий угол, отличающийся от на слагаемое, кратное
, обозначается
и записывается равенством:
(1.7)
где — главное значение аргумента,
.
Пример 1.16. Записать и
для чисел
.
Решение. Числа и
— действительные, расположены на действительной оси (рис. 1.6), поэтому
числа и
— чисто мнимые, расположены на мнимой оси (рис. 1.6), поэтому
Пример 1.17. Записать комплексные числа из примера 1.16:
а) в тригонометрической форме;
б) в показательной форме.
Решение
Модули всех чисел, очевидно, равны 1. Поэтому, используя решение предыдущего примера и формулы (1.3) и (1.4), получаем:
а)
б) .
Пример 1.18. Записать в тригонометрической форме числа .
Решение
Числа и
записаны в алгебраической форме (заметим, что заданная запись числа
не является тригонометрической формой записи (сравните с (1.3)). Находим модули чисел по формуле (1.5):
Далее находим аргументы. Для числа имеем
и, так как
(точка расположена в третьей четверти), получаем
(см. рис. 1.5). Для числа
имеем
, или
, и, так как
(точка расположена в четвертой четверти (см. рис. 1.5)), получаем
.
Записываем числа и
в тригонометрической форме
Заметим, что для числа решение можно найти иначе, а именно используя свойства тригонометрических функций:
.
Число является произведением двух чисел. Выполнив умножение, получим алгебраическую форму записи (найдем
и
):
. Здесь, как и для числа
, при решении удобно использовать преобразования тригонометрических выражений, а именно
.
Рассуждая, как выше, найдем . Для числа
, записанного в алгебраической форме, получаем тригонометрическую форму:
Равенство комплексных чисел в тригонометрической форме
Условия равенства комплексных чисел получаем, используя геометрический смысл модуля и аргумента комплексного числа, заданного в тригонометрической форме. Так, для чисел
из условия
. очевидно, следует:
или
(1.8)
Аргументы равных комплексных чисел либо равны (в частности равны главные значения), либо отличаются на слагаемое, кратное .
Для пары сопряженных комплексных чисел и
справедливы следующие равенства:
(1.9)
Умножение комплексных чисел в тригонометрической форме
Зададим два комплексных числа в тригонометрической форме и
и перемножим их по правилу умножения двучленов:
или
Получили новое число , записанное в тригонометрической форме:
, для которого
.
Правило умножения. При умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:
(1.10)
В результате умножения чисел может получиться аргумент произведения, не являющийся главным значением.
Пример 1.19. Найти модули и аргументы чисел:
Решение
Каждое из заданных чисел записано в виде произведения. Найдем модули и аргументы сомножителей и воспользуемся правилом (1.10) умножения чисел, заданных в тригонометрической форме:
Для чисел и
находим модули и аргументы:
. Используя формулы (1.10), получаем
б) . Для числа
имеем:
; для числа
, и так как
(точка расположена в четвертой четверти), то
. Используя формулы (1.10), получаем
.
Заметим, что для решения этой задачи можно раскрыть скобки, записать каждое число в алгебраической форме, а затем найти и
, используя формулы (1.5), (1.6).
Деление комплексных чисел в тригонометрической форме
Рассмотрим частное комплексных чисел , заданных в тригонометрической форме. Из определения частного
имеем
и, применяя к произведению правило умножения (формулы (1.10)), получаем
.
Правило деления. Модуль частного, полученного в результате деления чисел, заданных в тригонометрической форме, равен частному от деления модуля числителя на модуль знаменателя, а аргумент частного равен разности аргументов делимого и делителя:
(1.11)
В результате деления чисел по формуле (1.11) может получиться аргумент честного, не являющийся главным значением.
Пример 1.20. Записать в тригонометрической форме комплексное число .
Решение. Обозначим . Для чисел
и
находим модули и аргументы:
(см. пример 1.19). По формуле (1.11) получаем
и
Возведение в степень комплексного числа в тригонометрической форме
Из определения степени и правила умножения чисел, записанных в тригонометрической форме (формула (1.10)), получаем
, где
.
Правило возведения в степень. При возведении в степень комплексного числа в эту степень возводится модуль числа, а аргумент умножается на показатель степени:
(1.12)
Записывая число в тригонометрической форме
, получаем формулу возведения в степень:
(1.13)
При это равенство принимает вид и называется формула Муавра
(1.14)
Пример 1.21. Найти модуль и аргумент комплексного числа .
Решение. Обозначим . Находим модуль и аргумент числа
. Поэтому
и
. Так как по определению для главного значения аргумента выполняется условие
, то
.
Пример 1.22. Записать в тригонометрической форме число .
Решение
Пример 1.23. Используя формулу Муавра, найти выражения для и
через тригонометрические функции угла
.
Решение
Из формулы (1.14) при имеем
. Возведем левую часть в степень, учитывая, что
(см. пример 1.8):
Используя условие равенства комплексных чисел, получаем:
Извлечение корня из комплексного числа в тригонометрической форме
Рассмотрим задачу извлечения корня из комплексного числа, заданного в показательной или тригонометрической форме , или
. Искомое число
также запишем в показательной форме:
. Используя определение операции извлечения корня
и условия (1.8), получаем соотношения
или
(1.15)
Правило извлечения корня. Чтобы извлечь корень из комплексного числа, нужно извлечь корень (арифметический) той же степени из модуля данного числа, а аргумент разделить на показатель корня:
(1.16)
Теперь можно записать число в показательной форме:
Если записать это соотношение в тригонометрической форме, то, учитывая периодичность тригонометрических функций, нетрудно убедиться, что выражение принимает только
различных значений. Для их записи достаточно в формуле (1.15) взять
последовательных значений
, например
. В результате получаем формулу извлечения корня из комплексного числа в тригонометрической форме, где
:
(1.17)
Замечания 1.1
1. Рассмотренная задача извлечения корня степени из комплексного числа равносильна решению уравнения вида
, где, очевидно,
.
Для решения уравнения нужно найти значений
, а для этого необходимо найти
и использовать формулу извлечения корня.
2. Исследование формулы (1.17) показывает, что все комплексные числа (значения
) имеют равные модули, т.е. геометрически расположены на окружности радиуса
. Аргументы двух последовательных чисел отличаются на
, так как
, т.е. каждое последующее значение
может быть получено из предыдущего
поворотом радиуса-вектора точки
на
.В этом заключается геометрический смысл формулы (1.17), что можно сформулировать следующим образом.
Точки, соответствующие значениям , расположены в вершинах правильного n-угольника, вписанного в окружность с центром в начале координат, радиус которой
, причем аргумент одного из значений
равен
(рис. 1.7).
Алгоритм решения комплексных уравнений вида z^n-a=0
1. Найти модуль и аргумент числа .
2. Записать формулу (1.17) при заданном значении .
3. Выписать значения корней уравнения , придавая значения
.
Пример 1.24. Решить уравнения: a) ; б)
.
Решение
Задача равносильна задаче нахождения всех значений корня из комплексного числа. Решаем в каждом случае по алгоритму.
а) Найдем .
1. Определим модуль и аргумент числа .
2. При полученных значениях и
записываем формулу (1.17):
Заметим, что справа стоит — арифметический корень, его единственное значение равно 1.
3. Придавая последовательно значения от 0 до 5, выписываем решения уравнения:
Геометрически соответствующие точки расположены в вершинах правильного шестиугольника, вписанного в окружность радиуса , одна из точек (соответствует
)
. Строим шестиугольник (рис. 1.8,в). Отметим свойства корней этого уравнения с действительными коэффициентами — его комплексные корни являются попарно сопряженными:
и
— действительные числа.
б) Найдем .
1. Определим модуль и аргумент числа .
2. По формуле (1.17) имеем
3. Выписываем корни .
Для геометрического представления решения уравнения достаточно изобразить одно значение, например (при
) — это точка окружности
, лежащая на луче
. После этого строим правильный треугольник, вписанный в окружность
(рис. 1.8,б).
Пример 1.25. Найти корень уравнения , для которого
.
Решение
Задача равносильна задаче нахождения при условие
.
1. Находим модуль и аргумент числа .
2. По формуле (1.17) имеем: .
3. Для нахождения искомого решения нет необходимости выписывать все значения корня. Нужно выбрать значение , при котором выполняется условие
(соответствующая точка — точка второй четверти). Удобно при этом использовать чертеж (рис. 1.9).
Условию поставленной задачи удовлетворяет корень (при
):
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
36.
Частные производные ФНП, их нахождение.
Частные производные ФДП, их геометрический
смысл. Примеры.
Частные
производные
Частной
производной по x функции z
= f(x,y) в
точке A(x0,y0)
называется предел отношения частного
приращения по x функции
в точке A к
приращению ∆x при
стремлении ∆x к
нулю.
Частные
производные функции z(x,y) находятся
по следующим формулам: Вторые
частные производные функции z(x,y) находятся
по формулам:
Смешанные
частные производные функции z(x,y) находятся
по формулам:
Частные
производные функции нескольких переменных
Ели
одному из аргументов функции z
= f(x,y) придать
приращение, а другой аргумент не изменять,
то функция получит частное
приращение по одному из аргументов: –
эточастное приращение функции z по
аргументу x; –
это частное приращение функции z по
аргументу у.
Частной
производной функции нескольких
переменных по
одному из её аргументов называется
предел отношения частного приращения
функции по этому аргументу к соответствующему
приращению аргумента при условии, что
приращение аргумента стремится к
нулю:
–
это частная производная функции z по
аргументу x;
–
это частная производная функции z по
аргументу у.
Чтобы
вычислить частную производную ФНП по
одному из её аргументов, нужно все другие
её аргументы считать постоянными и
проводить дифференцирование по правилам
дифференцирования функции одного
аргумента.
Пример
1.
z = 2x5 +
3x2y
+ y2 –
4x + 5y — 1
Пример
2.
Найти частные производные функции
z = f(x;y) в точке A(x0;y0).
Находим
частные производные:
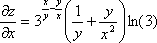

Найдем
частные производные в точке А(1;1)
Находим
вторые частные производные:


Найдем
смешанные частные производные:
Геометрический
смысл частных производных функции двух
переменных
Остановимся
на функции двух переменных.
Если
каждой паре значений x, y из
множества D ставится
в соответствие одно определённое
значение z из
множества E,
то z называется
функцией двух независимых друг от друга
переменных x и y и
обозначается z= f(x, y).
Множество D называется
областью определения функции z,
а множество E –
множеством её значений. Переменные x и y по
отношению к функции z называются
её аргументами.
Частным
значениям аргументов
Соответствует
частное значение функции
Пример
4.Область
определения функции S = xy,
выражающей зависимость площади
многоугольника от длин его сторон, может
быть записана двумя неравенствами
и
которые
определяют I квадрант на плоскости xOy.
Частное значение этой функции при x =
3, y =
5 составляет
В
общем случае область определения функции
двух переменных геометрически может
быть представлена некоторым множеством
точек (x; y)
плоскости xOy.
Подобно
тому, как функция y = f(x)
геометрически изображается графиком,
можно геометрически истолковать и
уравнение z = f(x, y).
Ставя
в соответствие каждой точке
аппликату z = f(x, y),
мы получим некоторое множество точек
(x; y; z)
трёхмерного пространства – чаще всего
некоторую поверхности. Поэтому
равенство z = f(x, y)
называют уравнением поверхности.
Пример
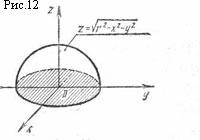
5. Пусть
задана функция
Её
область определения найдём из равенства
т.е.
Это
круг с центром в начале координат и
радиусом r.
Графиком функции
является
верхняя половина сферы
(разрешив
уравнение сферы относительно z,
получим две однозначные функции z:
и
Соседние файлы в папке Bilety
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #