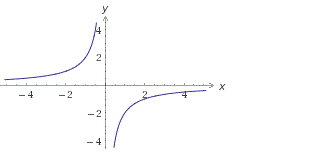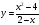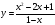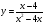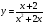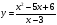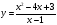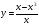Как найти аргумент дроби

Дробно-рациональная функция — это функция вида , где f(x) и g(x) — некоторые функции.
График дробно-рациональной функции представляет собой гиперболу.
Функция имеет две асимптоты — вертикальную и горизонтальную.
Определение.Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность:
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты

Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь , у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
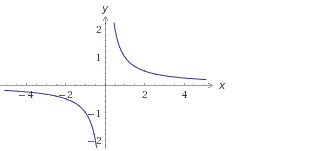
Построим график функции y=1/x:
D(y): х≠0
E(y): у≠0
y = k/x — нечетная

Построим график функции y=k/x:
При k=2 y=-2/x:
ООФ: х≠0
МЗФ: у≠0
y=k/x – нечетная

Пример1 . Построим график функции , т.е. представим ее в виде : выделим целую часть дроби, разделив числитель на знаменатель, мы получим:

.

Итак, . Мы видим, что график этой функции может быть получен из графика функции у=5/х с помощью двух последовательных сдвигов: сдвига гиперболы у=5/х вправо на 3 единицы, а затем сдвига полученной гиперболы  вверх на 2 единицы.

При этих сдвигах асимптоты гиперболы у=5/х также переместятся: ось х на 2 единицы вверх, а ось у на 3 единицы вправо.

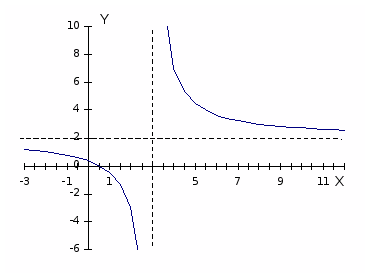
Для построения графика проведем в координатной плоскости пунктиром асимптоты: прямую у=2 и прямую х=3. Так как гипербола состоит из двух ветвей, то для построения каждой из них составим две таблицы: одну для х3 (т. е. первую слева от точки пересечения асимптот, а вторую справа от нее):

x	-7	-2	-1	0	1	2	2,5
y	1,5	1	0,75	0,33	-0,5	-3	-8

x	3,5	4	5	6	7	8	13
y	12	7	4,5	3,33	3,25	3	2,52

Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной линией, получим одну ветвь гиперболы. Аналогично (используя вторую таблицу) получим вторую ветвь гиперболы. График функции  изображен на рисунке 3.

Любую дробь  можно записать аналогичным образом, выделив ее целую часть. Следовательно, графики всех дробно-линейных функций являются гиперболами, различным образом сдвинутыми параллельно координатным осям и растянутыми по оси Оу.

Пример 2.

Построим график функции .

Поскольку мы знаем, что график есть гипербола, достаточно найти прямые, к которым приближаются ее ветви (асимптоты), и еще несколько точек.

Найдем сначала вертикальную асимптоту. Функция не определена там, где 2х+2=0, т.е. при х=-1. Стало быть, вертикальной асимптотой служит прямая х=-1.

Чтобы найти горизонтальную асимптоту, надо посмотреть, к чему приближаются значения функций, когда аргумент возрастает (по абсолютной величине), вторые слагаемые в числителе и знаменателе дроби  относительно малы. Поэтому

.

Стало быть, горизонтальная асимптота – прямая у=3/2.

Определим точки пересечения нашей гиперболы с осями координат. При х=0 имеем у=5/2. Функция равна нулю, когда 3х+5=0, т.е. при х=-5/3.

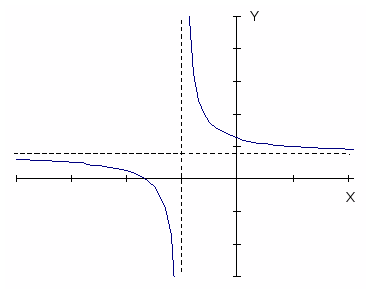
Отметив на чертеже точки (-5/3;0) и (0;5/2) и проведя найденные горизонтальную и вертикальную асимптоты, построим график (рис.4).

Вообще, чтобы найти горизонтальную асимптоту, надо разделить числитель на знаменатель, тогда y=3/2+1/(x+1), y=3/2 – горизонтальная асимптота.

Алгоритм построения графика дробно-рациональной функции, содержащей квадратный трехчлен.

1. Найти область определения функции.

2. Разложить на множители квадратный трехчлен.

3. Сократить дробь.

4. Построить график (параболу, гиперболу, кубическую параболу).

5. Исключить из графика точки, не входящие в область определения («выколотые» точки).

6. Найти значение функции в «выколотых» точках.

7. Определить, при каких значениях b прямая y=b имеет с графиком ровно одну общую точку.

ЗАДАНИЕ

Построить график функции (D(y), на графике – выколотые точки):

1. 

2. 

3. 

4. 

5. 

6. 

7. 

Содержание:

1. Комплексные числа
2. Алгебраическая форма комплексного числа
3. Действия над комплексными числами в алгебраической форме
4. Геометрическая интерпретация комплексного числа
5. Тригонометрическая форма комплексного числа
6. Действия над комплексными числами в тригонометрической форме
7. Показательная форма комплексного числа
8. Что такое комплексное число
9. Понятие о комплексном числе
10. Арифметические операции над комплексными числами
11. Отыскание комплексных корней уравнений

Комплексные числа

Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i² = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.

Алгебраическая форма комплексного числа

На множестве действительных чисел ряд алгебраических задач, в частности нахождение корней квадратных уравнений с отрицательным дискриминантом, не имеет решения. Введём некоторое навое число, которое будем считать решением уравнения х² + 1 = 0. Корень уравнения  х² + 1 = 0 или  х² = -1 называется мнимой единицей и обозначается буквой i. Таким образом i² = -1.

В некоторых технических дисциплинах мнимую единицу обозначают буквой j. В дальнейшем будем использовать оба обозначения.

Мнимая единица позволяет ввести числа нового вида, которые называют комплексными.

Комплексным числом называют выражение вида , где  — действительные числа, i — мнимая единица.

Число  называют действительной, а число  — мнимой частями комплексного числа. Комплексное число, как правило, обозначают буквой . Два комплексных числа  называют равными тогда и только тогда, когда , то есть когда равны их действительные части и коэффициенты при мнимой части. 

Понятия «больше» и «меньше» для комплексных чисел не определено. Комплексное число  называется нулём и обозначается 0; комплексное число  отождествляется с действительным числом ; комплексное число  называют чисто мнимым и обозначают . Число 0 является единым числом, которое одновременно и является действительным, и чисто мнимое.

Комплексные числа  называются сопряжёнными и обозначаются  и. Например, в числе , сопряжённым к нему будет число , а для числа  сопряжённым будет число .

Множество комплексных чисел принято обозначать буквой С. Запись комплексного числа в виде  называется алгебраической формой комплексного числа.

Действия над комплексными числами в алгебраической форме

Сложение, вычитание, умножение комплексных чисел в алгебраической форме по правилам соответствующих действий над многочленами.

Пример 1. Найти сумму и произведение комплексных чисел 

Решение: Сумму находим формальным сложением двучленов 

произведение находим перемножив двучлены  с последующей заменой .

Ответ: 

Легко увидеть, что слагаемое двух сопряжённых чисел является действительным числом:

Воспользуемся этим свойством для введения действия деления двух комплексных чисел.

При делении комплексных чисел , где  достаточно умножить числитель и знаменатель дроби  на число сопряжённое к знаменателю, то есть на 

Пример 2. Даны комплексные числа   и  Найдите разность  и частное 

Решение:

Находим разность вычитанием двучленов 

Чтобы найти частное  умножим числитель и знаменатель на число, сопряжённое к знаменателю:

Ответ: 

Действия над комплексными числами имеют следующие интересные свойства:

Доказательство выходит из определения сопряжённых чисел. Действительно, 

Аналогично доказываются и другие приведённые свойства.

Возведение комплексного числа в степень выполняется по формулам возведения двучлена в степень. При этом следует учитывать, что

Например:

Пример 3. Найти комплексное число  

Решение: 

Выполнив в знаменателе возведение в степень, получим:

Умножив числитель и знаменатель на число, сопряжённое к знаменателю, то есть на -5-12i, получим:

Ответ: z = i.

Геометрическая интерпретация комплексного числа

Каждому комплексному числу  можно поставить в соответствие упорядоченную пару действительных чисел  и наоборот. Такая упорядоченная пара действительных чисел определяет точку или вектор на плоскости.

Следовательно, комплексное число вида  изображается на координатной плоскости точкой  или вектором, начало которого совпадает с началом координат, а конец с т. М.

Сама координата плоскости называется при этом комплексной плоскости, ось абсцисс — действительной осью, ось ординат — мнимой осью.

Например, изобразим числа 

Представление комплексного числа как вектора на плоскости позволяет ввести понятие модуля и аргумента комплексного числа.

Модулем комплексного числа называют длину вектора, которая соответствует данному числу (обозначают r либо p).

Аргументом комплексного числа  называют величину угла  между положительным направлением действительной оси и вектора, который соответствует данному комплексному числу.

Рассмотрим рисунок:

На основе теоремы Пифагора получаем 

Например, комплексное число  имеет модуль равный 10, так как 

Аргумент комплексного числа , в отличии от модуля, вычисляется неоднозначно. Так аргументом числа 5 являются следующие углы  Среди бесконечного множества значений аргумента только одно принадлежит промежутку . Эти значения аргумента мы и будем вычислять.

Аргумент легко вычислить, если комплексное число расположено в I четверти. Действительно, согласно тригонометрическим соотношениям в прямоугольном треугольнике (рис. 2) имеем:

Если комплексные числа размещены в других четвертях, то необходимо провести дополнительные рассуждения. Рассмотрим рис. 3. Видим, что для

Таким образом, алгоритм нахождения аргумента комплексного числа следующий:

1.Определить коэффициент  заданного комплексного числа.

2. Найти  

3. Установить, в какой четверти расположено комплексное число.

4. Вычислить аргумент  согласно приведённым формулам.

Возможны и другие способы нахождения аргумента комплексного числа, например:

Пример 4. Найти аргумент комплексного числа 

Тригонометрическая форма комплексного числа

Рассмотрим рис. 2. Согласно тригонометрическим соотношениям в прямоугольном треугольнике числа  можно выразить через r и  таким образом:

Тогда комплексное число запишется в виде:

Запись комплексного числа в таком виде называется тригонометрической формой комплексного числа.

Следовательно, для того, чтобы перейти от алгебраической формы записи комплексного  числа  к тригонометрической, достаточно найти его модуль и аргумент.

Пример 5. Записать число  в тригонометрической форме.

Решение:

Найдём модуль 

Найдём острый угол 

Вектор, который соответствует данному комплексному числу принадлежит третьей четверти, поэтому аргумент равен  следовательно 

Ответ:

Для того, чтобы перейти от тригонометрической формы записи комплексного числа  к алгебраической, достаточно найти действительные числа  из формул 

Пример 6. Записать число  в алгебраической форме.

Найдём  и 

Ответ:

Действия над комплексными числами в тригонометрической форме

В тригонометрической форме записи комплексного числа выполняют действия умножения, деления, возведения в степень, извлечения корня n-й степени. Выведение формул, по которым выполняются действия, относительно просты и основываются на основных формулах тригонометрии.

Следовательно, при умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножают, а аргументы складывают; при делении — модули делят, а аргументы вычитают.

Правило умножения комплексных чисел автоматически распространяется на произвольное число множителей. Если взять равные множители 

Полученную формулу называют формулой Муавра.

Для извлечении корня n-й степени из комплексного числа  используют формулу:

где  арифметический корень, 

Пример 8. Вычислить  Ответ записать в алгебраической форме.

Решение: Находим:

Ответ: 

Пример 9. Вычислить

Решение: Запишем число в тригонометрической форме:

Пример 10. Вычислите . Ответ запишите в алгебраической и тригонометрической формах.

Решение: Запишем число -81 в тригонометрической форме:

Тогда:

Показательная форма комплексного числа

Рассматривая функцию  для комплексной переменной, известный математик Л. Эйлер установил соотношение 

Из заданной формулы следует, что каждое комплексное число  можно записать в виде  которое называется показательной формой записи.

Над комплексными числами в показательной форме выполняют те же действия что и в тригонометрической форме. Выведение формул, по которым выполняют действия основывается на основных свойствах степени.

Пусть , тогда:  

Пример 11. Представить число  в алгебраической форме.

Решение: Согласно условию задачи , поэтому

значит

Ответ:

Пример 12. Выполнить действия, результат записать в тригонометрической и показательной формах: 

Решение: Сначала выполним действия:

Теперь полученное число запишем в тригонометрической и показательной формах. Для этого найдём модуль и аргумент:

Тогда

Ответ: 

Что такое комплексное число

Комплексные числа — это числа вида , где  — вещественные числа, — мнимая единица, то есть число, для которого выполняется равенство: 

Понятие о комплексном числе

Процесс расширения понятия числа от натуральных к действительным был связан как с потребностями практики, так и с нуждами самой математики. Сначала для счета предметов использовались натуральные числа. Необходимость выполнения деления привела к понятию обыкновенной (и десятичной) дроби, необходимость выполнения вычитания — к понятиям нуля и отрицательного числа, необходимость извлечения корней из положительных чисел — к понятию иррационального числа.

Все перечисленные операции выполнимы на множестве действительных чисел. Однако остались и невыполнимые на этом множестве операции, например извлечение квадратного корня из отрицательного числа. Значит, имеется потребность в дальнейшем расширении понятия числа, в появлении новых чисел, отличных от действительных.

Геометрически действительные числа изображаются точками на координатной прямой: каждому действительному числу соответствует одна точка прямой («образ» действительного числа) и, обратно, каждая точка координатной прямой соответствует одному действительному числу. Координатная прямая сплошь заполнена образами действительных чисел, т. е., выражаясь фигурально, «на ней нет места для новых чисел». Возникает предположение о том, что геометрические образы новых чисел надо искать уже не на прямой, а на плоскости. Однако каждую точку М координатной плоскости ху можно отождествить с координатами этой точки. Поэтому естественно в качестве новых чисел ввести упорядоченные пары действительных чисел (упорядоченные в том смысле, что — разные точки, а значит, и разные числа).

Комплексным числом называют всякую упорядоченную пару действительных чисел

Два комплексных числа называют равными тогда и только тогда, когда

Арифметические операции над комплексными числами

Суммой комплексных чисел называют комплексное число

Например,

Комплексным нулем считают пару (0; 0). Числом, противоположным числу считают число обозначают его

Разностью комплексных чисел называют, как обычно, такое число Разность всегда существует и единственна. В самом деле, пусть Тогда  Это значит, что откуда находим

Таким образом, получаем следующее правило вычитания комплексных чисел:

Например, (9; 10) — (8; 12) = (9 — 8; 10 — 12) = (1;-2).

Произведением комплексных чисел  называют комплексное число

Например, если то

Арифметические операции над комплексными числами обладают теми же свойствами, что арифметические операции над действительными числами (см. п. 29).

Пусть Существует, и только одно, комплексное число такое, что Это число и называют, как обычно, частным от деления z на w.

Имеем Так как то должны выполняться равенства

Из этой системы двух уравнений с двумя переменными находим (см. п. 164)  Итак,

Получили следующее правило деления комплексных чисел: если то

Например,

Алгебраическая форма комплексного числа

Используя введенные в п. 45 определения сложения и умножения комплексных чисел, легко получить следующие равенства:

Условились вместо писать просто , а комплексное число (0; 1) обозначать буквой и называть мнимой единицей. Тогда равенство (1) принимает вид т. е.

а равенство (2) — вид

Запись называют алгебраической формой комплексного числа при этом число называют действительной частью комплексного числа z, a bi — его мнимой частью.

Например,

Если мнимая часть комплексного числа отлична от нуля, то число называют мнимым, если при этом = 0, т. е. число имеет вид bi, то его называют чисто мнимым, наконец, если у комплексного числа мнимая часть равна нулю, то получается действительное число .

Алгебраическая форма существенно облегчает выполнение арифметических операций над комплексными числами.

Сложение. Известно (см. п. 45), что

Выполнив сложение тех же чисел в алгебраической форме, считая и с + di обычными двучленами, находим

Сравнивая равенства (7) и (8), замечаем, что получился верный результат.

Вычитание. Известно (см. п. 45), что

Выполнив вычитание тех же чисел в алгебраической форме, считая и с + di обычными двучленами, находим

Сравнивая равенства (9) и (10), замечаем, что получился верный результат.

Умножение. Известно (см. п. 45), что

Выполнив умножение тех же чисел в алгебраической форме, считая  и с + di обычными двучленами, находим

Воспользуемся тем, что (см. равенство (5)); тогда В результате получаем

Сравнивая равенства (11) и (12), замечаем, что получился верный результат.

Деление. Известно (см. п. 45), что если  то

Выполним деление тех же чисел в алгебраической форме, считая и с + di обычными двучленами, a — обычной дробью. Умножив числитель и знаменатель этой дроби на с — di (предполагая, что значение дроби от этого не изменится), находим

Итак,

Сравнивая равенства (13) и (14), замечаем, что получился верный результат.

Подводя итоги, приходим к следующему важному практическому выводу: над комплексными числами, записанными в алгебраической форме, можно осуществлять все арифметические операции как над обычными двучленами, учитывая лишь, что  Чтобы преобразовать в комплексное число дробь вида  нужно числитель и знаменатель дроби умножить на число с — di; числа с + di и с — di называют комплексно-сопряженными.

Пример 1.

Вычислить

Решение: 

Применив формулу , получим

Пример 2.

Вычислить

Решение: 

Пример 3.

Найти действительные числа х и у такие, что выполняется равенство

Решение: 

Имеем  Тогда заданное равенство можно переписать в виде

Комплексные числа  равны тогда и только тогда, когда равны их действительные части ( = с) и коэффициенты при мнимых частях (Ь = d). Значит, приходим к системе уравнений

из которой находим (см. п. 164)

Пример 4.

Найти комплексные числа z, удовлетворяющие равенству

Решение: 

Будем искать комплексное число z в виде х + yi. Имеем

Из последнего равенства следует, что

Эта система имеет два решения (см. п. 164): (2; 3) и (-2; -3). Значит,

Пример 5.

Вычислить

Решение: 

Имеем (см. п. 58)        

Значит,  

Далее, имеем 

Значит,

Отыскание комплексных корней уравнений

Пусть > 0. Так как  Тем самым мы получаем возможность извлекать квадратные корни из отрицательных действительных чисел. Это позволяет находить не только действительные, но и мнимые корни уравнений.

Пример 1.

Решить уравнение

Решение.

Имеем (см. п. 137)  Итак,

Пример 2.

Решить уравнение

Решение.

Имеем Значит, либо х — 2 = 0, откуда находим  либо откуда находим  Итак,  

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

• Математика решение заданий и задач

Смотрите также дополнительные лекции по предмету «Математика»:

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а; если а равно нулю, а b не равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Как решать уравнения с дробями. Показательное решение уравнений с дробями.

Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.

Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.

Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.

Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45
x=45-20=25

Другой пример, когда неизвестное находится в знаменателе:

Уравнения такого типа называются дробно-рациональными или просто дробными.

Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:

• значение переменной, обращающее в 0 знаменатель, корнем быть не может;
• нельзя делить или умножать уравнение на выражение =0.

Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.

Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.

Например, требуется решить дробное уравнение:

Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.

Избавляемся от знаменателя путем умножения всех членов уравнения на х

И решаем обычное уравнение

5x – 2х = 1
3x = 1
х = 1/3

Решим уравнение посложнее:

Здесь также присутствует ОДЗ: х -2.

Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.

Для сокращения знаменателей требуется левую часть умножить на х+2, а правую — на 2. Значит, обе части уравнения надо умножать на 2(х+2):

Это самое обычное умножение дробей, которое мы уже рассмотрели выше

Запишем это же уравнение, но несколько по-другому

Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:

х = 4 – 2 = 2, что соответствует нашей ОДЗ

Для закрепления материала рекомендуем еще посмотреть видео.

Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Урок по теме «Решение дробных рациональных уравнений». 8-й класс

Разделы: Математика

Класс: 8

Цели урока:

• формирование понятия дробных рационального уравнения;
• рассмотреть различные способы решения дробных рациональных уравнений;
• рассмотреть алгоритм решения дробных рациональных уравнений, включающий условие равенства дроби нулю;
• обучить решению дробных рациональных уравнений по алгоритму;
• проверка уровня усвоения темы путем проведения тестовой работы.

• развитие умения правильно оперировать полученными знаниями, логически мыслить;
• развитие интеллектуальных умений и мыслительных операций — анализ, синтез, сравнение и обобщение;
• развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
• развитие критического мышления;
• развитие навыков исследовательской работы.

• воспитание познавательного интереса к предмету;
• воспитание самостоятельности при решении учебных задач;
• воспитание воли и упорства для достижения конечных результатов.

Тип урока: урок – объяснение нового материала.

Ход урока

1. Организационный момент.

Здравствуйте, ребята! На доске написаны уравнения посмотрите на них внимательно. Все ли из этих уравнений вы сможете решить? Какие нет и почему?

Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений».

2. Актуализация знаний. Фронтальный опрос, устная работа с классом.

А сейчас мы повторим основной теоретический материл, который понадобиться нам для изучения новой темы. Ответьте, пожалуйста, на следующие вопросы:

1. Что такое уравнение? (Равенство с переменной или переменными.)
2. Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель).
3. Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений. (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)
4. Что такое пропорция? (Равенство двух отношений.) Основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)
5. Какие свойства используются при решении уравнений? (1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)
6. Когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)

3. Объяснение нового материала.

Решить в тетрадях и на доске уравнение №2.

Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5).

х 2 -4х-2х+8 = х 2 +3х+2х+6

х 2 -6х-х 2 -5х = 6-8

Решить в тетрадях и на доске уравнение №4.

Какое дробно-рациональное уравнение можно попробовать решить, умножая обе части уравнения на знаменатель? (№6).

Теперь попытайтесь решить уравнение №7 одним из способов.

Комплексные числа

В математике кроме натуральных, рациональных и вещественных чисел имеется ещё один вид, называемый комплексными числами. Такое множество принято обозначать символом $ mathbb{C} $.

Рассмотрим, что из себя представляет комплексное число. Запишем его таким образом: $ z = a + ib $, в котором мнимая единица $ i = sqrt{-1} $, числа $ a,b in mathbb{R} $ вещественные. 

Если положить $ b = 0 $, то комплексное число превращается в вещественное. Таким образом, можно сделать вывод, что действительные числа это частный случай комплексных и записать это в виде подмножества $ mathbb{R} subset mathbb{C} $. К слову говоря также возможно, что $ a = 0 $.

Принято записывать мнимую часть комплексного числа как $ Im(z) = b $, а действительную $ Re(z) = a $.

Введем понятие комплексно-сопряженных чисел. К каждому комплексному числу $ z = a+ib $ существует такое, что $ overline{z} = a-ib $, которое и называется сопряженным. Такие числа отличаются друг от друга только знаками между действительной и мнимой частью.

Формы

Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:

1. Алгебраическая $ z = a+ib $
2. Показательная $ z = |z|e^{ivarphi} $
3. Тригонометрическая $ z = |z|cdot(cos(varphi)+isin(varphi)) $

Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.

Изображение

Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:

Видим, что $ a,b in mathbb{R} $ расположены на соответствующих осях плоскости. 

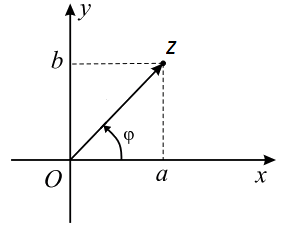
Комплексное число $ z = a+ib $ представляется в виде вектора $ overline{z} $.

Аргумент обозначается $ varphi $.

Модуль $ |z| $ равняется длине вектора  $ overline{z} $ и находится по формуле $ |z| = sqrt{a^2+b^2} $

Аргумент комплексного числа $ varphi $ нужно находить по различным формулам в зависимости от полуплоскости, в которой лежит само число.

Если:

1. $ a>0 $, то $ varphi = arctgfrac{b}{a} $
2. $ a<0, b>0 $, то $ varphi = pi + arctgfrac{b}{a} $
3. $ a<0, b<0 $, то $ varphi = -pi + arctgfrac{b}{a} $

Операции

Над комплексными числами можно проводить различные операции, а именно:

• Складывать и вычитать
• Умножать и делить
• Извлекать корни и возводить в степень
• Переводить из одной формы в другую 

Для нахождения суммы и разности складывается и вычитаются только соответствующие друг другу члены. Мнимая часть только с мнимой, а действительная только с действительной:

$$ z_1 + z_2 = (a_1+ib_1) + (a_2+ib_2) = (a_1 + a_2)+i(b_1 + b_2) $$

$$ z_1 — z_2 = (a_1+ib_1) — (a_2+ib_2) = (a_1 — a_2)+i(b_1 — b_2) $$

Умножение в алгебраической форме:

$$ z_1 cdot z_2 = (a_1+ib_1) cdot (a_2+ib_2) = (a_1 a_2 — b_1 b_2)+i(a_1 b_2 + a_2 b_1) $$

Умножение в показательной форме:

$$ z_1 cdot z_2 = |z_1|e^{ivarphi_1} cdot |z_2|e^{ivarphi_2} = |z_1|cdot|z_2|cdot e^{i(varphi_1 + varphi_2)} $$

Деление в алгебраической форме:

$$ frac{z_1}{z_2} = frac{a_1+ib_1}{a_2+ib_2} = frac{a_1 a_2 + b_1 b_2 }{a_2 ^2 + b_2 ^2} + i frac{a_2 b_1 — a_1 b_2}{a_2 ^2 + b_2 ^2} $$

Деление в показательной форме:

$$ frac{z_1}{z_2} = frac{|z_1|e^{ivarphi_1}}{|z_2|e^{ivarphi_2}} = frac{|z_1|}{|z_2|}e^{i(varphi_1 — varphi_2)} $$

Для возведения в степень необходимо умножить комплексное число само на себя необходимое количество раз, либо воспользоваться формулой Муавра:

$$ z^n = |z|^n(cos nvarphi+isin nvarphi) $$

Для извлечения корней необходимо также воспользоваться формулой Муавра:

$$ z^frac{1}{n} = |z|^frac{1}{n}bigg(cos frac{varphi + 2pi k}{n}+isin frac{varphi + 2pi k}{n}bigg), k=0,1,…,n-1 $$

Так же теория комплексных чисел помогает находить корни многочленов. Например, в квадратном уравнении, если $ D<0 $, то вещественных корней нет, но есть комплексные. В последнем примере рассмотрен данный случай.

Рассмотрим на практике комплексные числа: примеры с решением.

Примеры с решением

Пример 1

Перевести из алгебраической в тригонометрическую и показательную форму:$$ z = 4-4i $$

Решение

Для начала приступим к нахождению модуля комплексного числа: $$ |z| = sqrt{4^2 + (-4)^2} = sqrt{16 + 16} = sqrt{32} = 4sqrt{2} $$ Осталось найти аргумент: $$ varphi = arctg frac{b}{a} = arctg frac{-4}{4} = arctg (-1) = -frac{pi}{4} $$ Теперь составляем тригонометрическую запись комплексного числа, указанного в условии примера: $$ z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg) $$ Тут же можно записать показательную форму: $$ z = 4sqrt{2} e^{-frac{pi}{4}i} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg) $$ $$ z = 4sqrt{2} e^{-frac{pi}{4}i} $$

Пример 2

Вычислить сумму и разность заданных комплексных чисел: $$ z_1 = 3+i, z_2 = 5-2i $$

Решение

Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел: $$ z_1 + z_2 = (3+i) + (5-2i) = (3+5)+(i-2i) = 8 — i $$ Аналогично выполним вычитание чисел: $$ z_1 — z_2 = (3+i) — (5-2i) = (3-5)+(i+2i) = -2 + 3i $$

Ответ

$$ z_1 + z_2 = 8 — i; z_1 — z_2 = -2 + 3i $$

Пример 3

Выполнить умножение и деление комплексных чисел: $$ z_1 = 3+i, z_2 = 5-2i $$

Решение

$$ z_1 cdot z_2 = (3+i) cdot (5-2i) = $$ Просто на просто раскроем скобки и произведем приведение подобных слагаемых, так же учтем, что $ i^2 = -1 $: $$ = 15 — 6i + 5i -2i^2 = 15 — i — 2cdot(-1) = $$ $$ = 15 — i + 2 = 17 — i $$ Так, теперь разделим первое число на второе: $$ frac{z_1}{z_2} = frac{3+i}{5-2i} = $$ Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки: $$ = frac{(3+i)(5+2i)}{(5-2i)(5+2i)} = frac{15 + 6i + 5i + 2i^2}{25 + 10i — 10i -4i^2} = $$ $$ = frac{15 + 11i -2}{25 + 4} = frac{13 + 11i}{29} $$ Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы: $$ frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i $$

Ответ

$$ z_1 cdot z_2 = 17 — i; frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i $$

Пример 4

Возвести комплексное число $ z = 3+3i $ в степень: a) $ n=2 $ б) $ n=7 $

Решение

1) $ n = 2 $ Для возведения в квадрат достаточно умножить число само на себя: $$ z^2 = (3+3i)^2 = (3+3i)cdot (3+3i) = $$ Пользуемся формулой для умножения, раскрываем скобки и приводим подобные: $$ =9 + 9i + 3icdot 3 + 9i^2 = 9 + 18i — 9 = 18i $$ Получили ответ, что $$ z^2 = (3+i)^2 = 18i $$ 2) $ n = 7 $ В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую. Вычисляем значение модуля: $$ |z| = sqrt{3^2 + 3^2} = sqrt{9 + 9} = sqrt{18} = 3sqrt{2} $$ Найдем чем равен аргумент: $$ varphi = arctg frac{3}{3} = arctg(1) = frac{pi}{4} $$ Записываем в тригонометрическом виде: $$ z = 3sqrt{2}(cos frac{pi}{4} + isin frac{pi}{4}) $$ Возводим в степень $ n = 7 $: $$ z^7 = (3sqrt{2})^7 (cos frac{7pi}{4} + isin frac{7pi}{4}) = $$ Преобразуем в алгебраическую форму для наглядности: $$ =(3sqrt{2})^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = $$ $$ = 3^7 sqrt{2}^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = $$ $$ = 3^7 sqrt{2}^6 (1-i) = 3^7 cdot 8(1-i) = $$ $$ = 2187 cdot 8 (1-i) = 17496(1-i) $$

Ответ

$$ z^2 = (3+i)^2 = 18i $$ $$ z^7 = 17496(1-i) $$

Пример 5

Извлечь корень $ sqrt[3]{-1} $ над множеством $ mathbb{C} $

Решение

Представим число в тригонометрической форме. Найдем модуль и аргумент: $$ |z| = sqrt{(-1)^2 + 0^2} = sqrt{1+0} = sqrt{1}=1 $$ $$ varphi = arctg frac{0}{-1} +pi = arctg 0 + pi = pi $$ Получаем: $$ z = (cos pi + isin pi) $$ Используем знакомую формулу Муавра для вычисления корней любой степени: $$ z^frac{1}{n} = r^frac{1}{n}bigg(cos frac{varphi + 2pi k}{n}+isin frac{varphi + 2pi k}{n}bigg), k=0,1,…,n-1 $$ Так как степень $ n = 3 $, то по формуле $ k = 0,1,2 $: $$ z_0 = sqrt[3]{1} (cos frac{pi}{3}+isin frac{pi}{3}) = frac{1}{2}+ifrac{sqrt{3}}{2} $$ $$ z_1 = sqrt[3]{1} (cos frac{3pi}{3}+isin frac{3pi}{3}) = -1 $$ $$ z_2 = sqrt[3]{1} (cos frac{5pi}{3}+isin frac{5pi}{3}) = frac{1}{2} — ifrac{sqrt{3}}{2} $$

Ответ

$$ z_0 = frac{1}{2}+ifrac{sqrt{3}}{2} $$ $$ z_1 = -1 $$ $$ z_2 = frac{1}{2} — ifrac{sqrt{3}}{2} $$

Пример 6

Решить квадратное уравнение $ x^2 + 2x + 2 = 0 $ над $ mathbb{C} $

Решение

Решать будем по общей формуле, которую все выучили в 8 классе. Находим дискриминант $$ D = b^2 — 4ac = 2^2 — 4cdot 1 cdot 2 = 4-8 = -4 $$ Получили, что $ D=-4<0 $ и казалось бы, что решение можно заканчивать. Но нет! В нашем задании требуется решить уравнение над комплексным множеством, а то что дискриминант отрицательный означает только лишь отсутствие вещественных корней. А комплексные корни есть! Найдем их продолжив решение: $$ x_{1,2} = frac{-bpm sqrt{D}}{2a} = frac{-2pm sqrt{-4}}{2} = $$ Заметим, что $ sqrt{-4} = 2sqrt{-1} = 2i $ и продолжим вычисление: $$ = frac{-2 pm 2i}{2} = -1 pm i $$ Получили комплексно-сопряженные корни: $$ x_1 = -1 — i; x_2 = -1 — i $$ Как видите любой многочлен можно решить благодаря комплексным числам.

Ответ

$$ x_1 = -1 — i; x_2 = -1 — i $$

В статье «Комплексные числа: примеры с решением» было дано определение, основные понятия, формы записи, алгебраические операции и решение практических примеров.