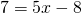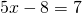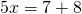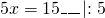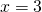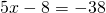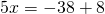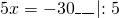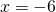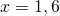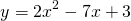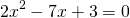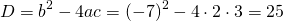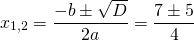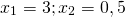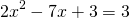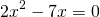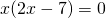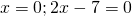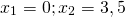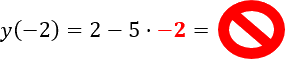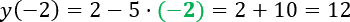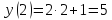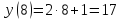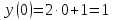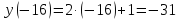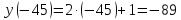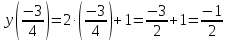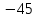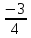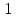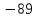Как найти аргумент при известной функции - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти значение аргумента по значению функции

Как найти значение аргумента по значению функции? Это можно сделать с помощью формулы функции.

Если формула задана формулой вида y=f(x), чтобы найти значение аргумента по значению функции, надо в формулу вместо y подставить заданное значение функции и решить получившееся уравнение относительно икса.

Примеры.

1) Линейная функция задана формулой y=5x-8. Найти значение аргумента, при котором значение функции равно 7; -38;0.

Решение:

При y=7

Поменяем местами левую и правую часть, чтобы запись выглядела в привычном виде (знаки при этом менять не надо):

Это — линейное уравнение. Неизвестное — в одну сторону, известные — в другую (при переносе слагаемых из одной части в другую знаки меняются на противоположные):

$[5x = 15___left| {:5} right.]$

Обе части уравнения делим на число, стоящее перед иксом:

Итак, при y=7 x=3.

При y= -38

$[5x = - 30___left| {:5} right.]$

При y= -38 x= -6.

При y=o

$[5x = 8___left| {:5} right.]$

При y=0 x=1,6.

2) При каком значении аргумента значение функции

$[y = 2{x^2} - 7x + 3]$

равно 0; 3?

Решение:

При y=0

$[2{x^2} - 7x + 3 = 0]$

Решаем квадратное уравнение.

$[D = {b^2} - 4ac = {( - 7)^2} - 4 cdot 2 cdot 3 = 25]$

$[{x_{1,2}} = frac{{ - b pm sqrt D }}{{2a}} = frac{{7 pm 5}}{4}]$

$[{x_1} = 3;{x_2} = 0,5]$

При y=0 x=3 и x=0,5.

При y=3

$[2{x^2} - 7x + 3 = 3]$

$[2{x^2} - 7x = 0]$

Это — неполное квадратное уравнение. Общий множитель x выносим за скобки

и решаем уравнение типа «произведение равно нулю»:

$[{x_1} = 0;{x_2} = 3,5]$

При y=3 x=0 и x=3,5.

Значение аргумента по заданному значению функции можно также найти с помощью графика. О том, как это сделать, мы будем говорить в следующий раз.

Источник

На чтение 4 мин Просмотров 5.4к.

Как найти значение аргумента по значению функции? Это можно сделать с помощью формулы функции.

1) Линейная функция задана формулой y=5x-8. Найти значение аргумента, при котором значение функции равно 7; -38;0.

Обе части уравнения делим на число, стоящее перед иксом:

2) При каком значении аргумента значение функции

Решаем квадратное уравнение.

При y=0 x=3 и x=0,5.

Это — неполное квадратное уравнение. Общий множитель x выносим за скобки

При y=3 x=0 и x=3,5.

В прошлый раз мы находили значение функции по значению аргумента с помощью формулы.

Рассмотрим, как по данному графику функции найти y по x.

1) Пользуясь графиком линейной функции, изображенной на рисунке 1, найдите значение функции,если значение аргумента равно 1; 3; -3, -1; 0.

Аргумент — это x, функция — y.

Найти значение функции по значению аргумента — значит, по данному значению x найти, чему равен y.

Начнём с x=1. На оси абсцисс Ox находим x=1. Чтобы найти соответствующее значение y, надо из точки на Ox идти либо вверх, либо вниз, чтобы попасть на график.

От x=1 идём вверх. От полученной точки на графике надо двигаться либо влево, либо вправо, чтобы попасть на ось Oy. В данном случае идем влево и попадаем с ординатой y=2 (стрелочки помогают увидеть направление движения).

Следовательно, при x=1 y=2.

Аналогично, если x=3, идем вверх до пересечения с графиком, затем влево до пересечения с осью ординат Oy.

Получаем, что при x=3 y=4.

Если x=-3, чтобы попасть на график функции, нужно идти вниз, затем — вправо, до пересечения с осью Oy.

При x=-1 ни вверх, ни вниз двигаться не надо — эта точка уже на графике функции. Следовательно, y=0.

Записываем: при x=-1 y=0.

При x=0 идем до графика вверх и попадаем в точку с ординатой y=2.

2) На рисунке 2 изображен график функции y=f(x).

Пользуясь графиком, найдите значение функции, если значение аргумента равно 1; 3; 5; 7; -1; -5.

Чтобы по графику функции найти y по x, сначала надо от точки с данной абсциссой попасть на график, двигаясь вверх либо вниз, а затем от точки на графике идти к оси Oy, двигаясь влево или вправо.

При x=1 идем до графика функции вверх, затем влево — на ось Oy. Попадаем в точку с ординатой y=2.

Пишем: при x=1 y=2.

При x равном -1 и -5 идем сначала вверх, затем — вправо.

При иксах равных 3; 5 и 7 идём вниз и влево.

Обратите внимание: различным значениям икса может соответствовать одно значение y:

Дана следующая функция y=f(x) :
y = 2x – 10, если x > 0
y = 0, если x = 0
y = 2 * |x| – 1, если x

Требуется найти значение функции по переданному x .

Получить с клавиатуры значение x .
Если x больше 0, то вычислить выражение 2*x-10 , результат присвоить переменной y .

Иначе если x равен 0, то присвоить y значение 0.

Иначе присвоить y результат выражения 2*|x|-1 .

Вывести значение y на экран.

var x , y : integer ;
begin
readln ( x ) ;
if x > 0 then y : = 2 * x – 10
else
if x = 0 then y : = 0
else y : = 2 * abs ( x ) – 1 ;

writeln ( y ) ;
end .

main ( ) <
int x , y ;
scanf ( «%d» , & x ) ;
if ( x > 0 ) y = 2 * x – 10 ;
else
if ( x == 0 ) y = 0 ;
else
y = 2 * abs ( x ) – 1 ;

printf ( «%d
» , y ) ;
>

x = input ( )
x = int ( x )

if x > 0 :
y = 2 *x – 10
elif x == 0 :
y = 0
else :
y = 2 * abs ( x ) – 1

В КуМир функция взятия модуля от числа возвращает вещественное значение. Поэтому используется функция int(), чтобы привести к целому, иначе присвоение невозможно.

Источник

Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».

После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.

В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.

Как получить значение функции

Рассмотрим задание.
Функция задана формулой «y = 2x − 1»

Вычислить «y» при «x = 15»
Найти значение «x», при котором
значение «y» равно «−19».

Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.

Запись решения выглядит следующим образом.

y(15) = 2 · 15 − 1 = 30 − 1 = 29

Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.

То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .

−19 = 2x − 1

Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.

Запомните!

Не забывайте про правило переноса в уравнениях.

При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.

−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18

Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.

−2x = 18 | · (−1)
2x = −18

Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .

2x = −18 | (: 2)
x = −9

Как проверить верно ли равенство для функции

Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».

Верно ли равенство
«f(−2) = −18»?

Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.

Важно!

Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.

Не забывайте использовать
правило знаков.

Неправильно

Правильно

С помощью расчетов мы получили
«f(−2) = 12».

Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.

Как проверить, что точка принадлежит графику функции

Рассмотрим функцию «y = x² −5x + 6»

Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).

Для этой задачи нет необходимости, строить график заданной функции.

Запомните!

Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).

Если получится верное равенство, значит, точка принадлежит функции.

Вернемся к нашему заданию. Подставим в функцию «y = x² − 5x + 6»
координаты точки (1; 2).

Вместо «x» подставим «1».
Вместо «y» подставим «2».

2 = 1² − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)

У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.

Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x² − 5x + 6»?

Вместо «x» подставим «0».
Вместо «y» подставим «1».

1 = 0² − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)

В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x² − 5x + 6»

Как получить координаты точки функции

С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.

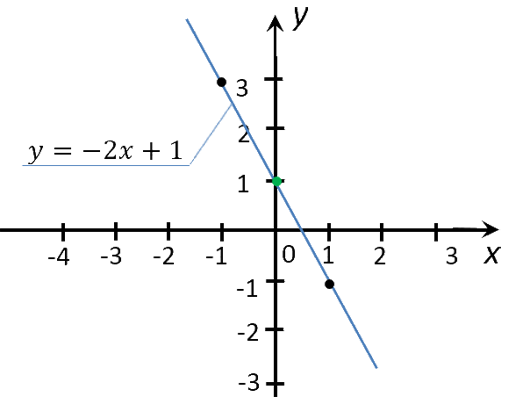
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.

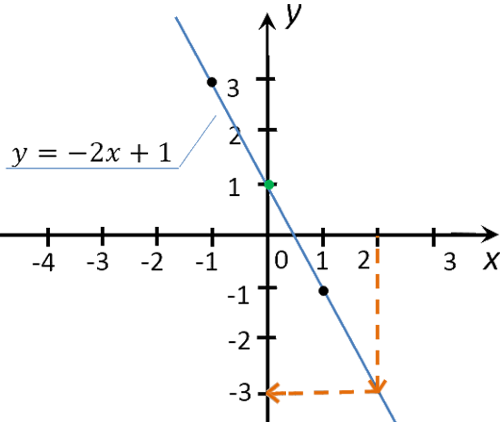
Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.

Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».

Полученное значение «−3» на оси «Oy» и будет искомым значением «y».

Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».

Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.

y(2) = −2 · 2 + 1 = −4 + 1 = −3

При расчетах мы также получили y = −3.

Значит, мы правильно получили координаты с графика функции.

Важно!

Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.

При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.

При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».

Только подстановка значений в формулу функции дает точные результаты.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

11 ноября 2018 в 15:46

Веточка Сакуры
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Веточка Сакуры
Профиль
Благодарили: 0

Сообщений: 1

Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= — x² — 8x.Найдите значение фун. в т. минимума (y min).

0
Спасибо thanks
Ответить

12 ноября 2018 в 3:25
Ответ для Веточка Сакуры

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

y_min= y(4) = -16.

0
Спасибо thanks
Ответить

17 сентября 2018 в 13:28

Alesger Mammedov
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Alesger Mammedov
Профиль
Благодарили: 0

Сообщений: 1

Добрый день помогите пожалуйста с задачкой
f(x²-3x)=3x²+5x-4
f(3)=?

0
Спасибо thanks
Ответить

17 сентября 2018 в 23:01
Ответ для Alesger Mammedov

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

f(3) = 26 ± 7√21

0
Спасибо thanks
Ответить

13 ноября 2016 в 6:43

Роман Безбородов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Роман Безбородов
Профиль
Благодарили: 0

Сообщений: 1

определите вид графика

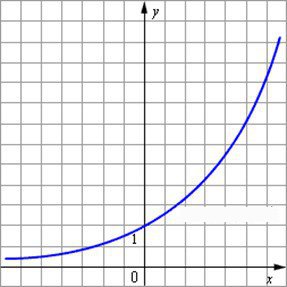
0
Спасибо thanks
Ответить

14 ноября 2016 в 17:30
Ответ для Роман Безбородов

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

y = a^x; a > 1.

0
Спасибо thanks
Ответить

7 сентября 2016 в 22:08

Иван Баранов
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Иван Баранов
Профиль
Благодарили: 0

Сообщений: 3

у=Х²+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10

0
Спасибо thanks
Ответить

8 сентября 2016 в 15:26
Ответ для Иван Баранов

Юлия Анарметова
(^-^)
Профиль
Благодарили: 0

Сообщений: 11

(^-^)
Юлия Анарметова
Профиль
Благодарили: 0

Сообщений: 11

аргумент это х значит у=(-2)²+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5

0
Спасибо thanks
Ответить

Источник

Как найти значение функции по значению аргумента

Как найти значение функции по значению аргумента? Это можно сделать с помощью формулы, задающей функцию.

Если функция задана формулой y=f(x), чтобы найти значение функции по данному значению аргумента, надо в формулу функции вместо каждого икса подставить это значение и вычислить значение y.

Пример.

1) Линейная функция задана формулой y=10x-7.

Найти значение функции, соответствующее значению аргумента, равному 3; -2,5; 1,4; 0.

Решение:

При x=3

при x=-2,5

при x=1,4

при x=0

2) Функция задана формулой

Найти значение функции при x, равном 10; -2; 1; 0.

Решение:

При x=10

при x=-2

при x=1

при x=0

Значение функции по данному значению аргумента можно найти также по графику. Как это сделать, мы рассмотрим в следующий раз.

www.algebraclass.ru

Как найти значение аргумента по значению функции

Как найти значение аргумента по значению функции? Это можно сделать с помощью формулы функции.

Примеры.

1) Линейная функция задана формулой y=5x-8. Найти значение аргумента, при котором значение функции равно 7; -38;0.

Решение:

При y=7

Обе части уравнения делим на число, стоящее перед иксом:

Итак, при y=7 x=3.

При y= -38

При y= -38 x= -6.

При y=o

При y=0 x=1,6.

2) При каком значении аргумента значение функции

равно 0; 3?

Решение:

При y=0

Решаем квадратное уравнение.

При y=0 x=3 и x=0,5.

При y=3

Это — неполное квадратное уравнение. Общий множитель x выносим за скобки

и решаем уравнение типа «произведение равно нулю»:

При y=3 x=0 и x=3,5.

www.algebraclass.ru

Как по значению аргумента найти соответствующее значение функции. ?

Как по значению аргумента найти соответствующее значение функции?
Аргумент — х, значение функции — y.
Нам известно некоторое значение аргумента, например, х = 2. Чтобы найти соответствующее ему значение функции нужно в формулу у = 6х + 12 вместо х подставить его значение, в нашем примере это число 2. Получаем:
у = 6*2 + 12 = 12 + 12 = 24
Итак, значению аргумента х = 2 соответствует значение функции у = 24.
Правило: чтобы по значению аргумента найти значение функции надо в формулу данной функции вместо х подставить его числовое значение.
б) Как найти значение аргумента, которому соответствует указанное значение функции?
Нам задано значение функции — y, например y = 6.
Чтобы найти значение аргумента, которому соответствует указанное значение функции нужно в формулу у = 6х + 12 вместо y подставить его значение, в нашем примере это число 6. Получаем уравнение:
6 = 6х + 12
6х = -6
х = -1
Итак, значению функции y = 6 соответствует значение аргумента х = -1.
Правило: чтобы по значению функции найти значение аргумента надо в формулу данной функции вместо y подставить его числовое значение.

подставляй найденный аргумент в условие и останется только одна переменная

Функцыя задана формулой y=5x-1.Найти значение функции, если значение аргумента равно -1.

а по графику как?

Большой ответ*

Надо подставить Х в формулу и решить
(получается уравнение)

touch.otvet.mail.ru

Вычислить значение функции — Мегаобучалка

Если у>0 ,вычислить и напечатать

Если у<0 ,напечатать ,y<0

Если у=0 ,вычислить и напечатать с=

Дано: b, c.

Если b=c, вычислить значения функций

где х изменяется на интервале от 0 до 5 с шагом 0,2.

Вывести на печать y,z,x.

Если b>c, вычислить .

Если b<c, вычисления закончить.

Если d 0, вывести на печать значения b,c.

Если d<0, вычисления закончить.

8. ВАРИАНТ

1.Вычислить

2. Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.

с заданной точностью e = 10^-4

Дано: a, b, x

Если a>b,вычислить и напечатать значение функции

Если ,вычислить z=

Если z=0,напечатать “z=0”

Если z>0,вычислить и напечатать

Если z<0,вычисления закончить.

Дано: y, c, a.

Вычислить .

Если ,вычислить .

Если ,вычислить и ввести на печать только положительные значения функции , где x изменяется на интервале от –1 до 3 с шагом 0,1.

Если , вычисления закончить.

Если ,вывести на печать “d<0”.

9. ВАРИАНТ

1.Вычислить

2.Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.

при x=0.2 с заданной точностью e = 10^-8

Дано: z, x

Вычислить

Если , вычислить

Если вычислить и напечатать

значение функции

Если , вычисления закончить.

4. Дано: а, b.

Вычислить

Если Вычислить

Если , напечатать значения a,b.

Если р>0, вычислить и напечатать

Если р<0, вычислить закончить.

Если P=0,вычислить функцию ,

где x изменяется на интервале от 1 до 5 с шагом 0,25;

Напечатать значения c,x,y.

10. ВАРИАНТ

1.Вычислить

. Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.

при x=0.7 с заданной точностью e = 10^-3
(отсчёт начинается с нулевого члена)

Дано:a, b.

Если , вычислить

Если вычислить

Если вычисления закончить.

Если ,вычислить и напечатать

Если ,напечатать “Y ”

Если , вычислить и напечатать

Дано:b,а

Если ,вычислить

Если , вычислить значение функции ,

где x изменяется на интервале от –5 до 7 с шагом 1.

Вывести на печать только y>0.

Если с>11,5 , вычислить и напечатать .

Если ,вычислить и напечатать .

11. ВАРИАНТ

1.Вычислить

с заданной точностью e = 10^-3

Дано: x ,y.

Вычислить

Если ,вычислить

Если t=0,напечатать x ,y

Если b>0, вычислить и напечатать

Если b<0, вычисления закончить

Еслиb=0, вычислить a=

Если a 0, вычислить и напечатать

Если a<0, вычислить закончить

Дано: а, b.

Если , вычислить

Если , напечатать значения a,b.

Если , вычисления закончить.

Если , вычислить значения функции ,

где х изменяется на интервале от –1 до 2 с шагом 0,1.

12. ВАРИАНТ

1.Вычислить

с заданной точностью e = 10^-4

Дано:a,b,c

Если a+b c, вычислить r= ,

Если a+b=c, вычисления закончить

Если r<0, вычислить z=

Если r=0, напечатать “r=0”

Если r>0, вычислить y=

Если z ,вычислить и напечатать ,

Если z<15, вычислить и напечатать

Дано: a, b.

Вычислить

Если , вычислить значение функции

где x изменяется на интервале от 0.5 до 1.5 с шагом 0.1

Вывести на печать c, y, x.

Если Z<0, вычислить

Если вычисления закончить.

Если , напечатать “f>0”.

Если , напечатать значение .

13. ВАРИАНТ

1.Вычислить

при x=5 с заданной точностью e = 10^-4

3. Дано: a, x, t, b, c, k=1, 2, 3,…..

Если , для функции ,

Определить и напечатать k, при котором z становится меньше a

Если b , вычислить y=

Если y< 0, напечатать ”y< 0”.

Если y³0, вычислить и напечатать

Дано: x, b, c.

Вычислить .

Если a>0,вычислить значения функции, ,

где x изменяется на интервале от -2 до 2 с шагом 0,2. Вывести на печать только y<0.

Если a<0,вычисления закончить.

Если a=0,вычислить и напечатать .

14. ВАРИАНТ

1.Вычислить

с заданной точностью e = 10^-3

Дано: x , y , c .

Если x = 0 . Напечатать “ x = 0 “ .

Если x > 0 . Вычислить

Если x < 0 . Вычисления закончить.

Если a > 0 . Вычислить

Если a 0 . Напечатать x , y , c .

Дано: a, P

Если а<P, вычислить и напечатать

Если а< P, вычислить и напечатать b=0.6

Если а=P, вычислить

где x изменяется на интервале от -3 до 3 с шагом 0,4

Вывести на печать значения x,y

15. ВАРИАНТ

1.Вычислить

с заданной точностью e = 10^-3

Дано:a,b,x

Если a>b,вычислить и напечатать значение функции

Если a<=b,вычислить z=

Если z=0,напечатать “z=0”

Если z>0,вычислить и напечатать

Если z<0,вычисления закончить.

Дано: b,а

Если b<a ,вычислить

Если , вычислить значение функции

, где x изменяется на интервале от –5 до 6 с шагом 1.

Вывести на печать только y>0.Если с>12,5 , вычислить и напечатать .

Если с 12,5 ,вычислить и напечатать .

16. ВАРИАНТ

1.Вычислить

с заданной точностью e = 10^-4

Дано:y,c

Вычислить

Если x=0, напечатать”x=0”

Если x>0, вычислить

Если x<0,вычисления закончить

Если a>=12,5 ,вычислить и напечатать

Если a<12,5 ,вычислить и напечатать b=

Дано: с

Вычислить .

Если а=0, напечатать с

Если a>0, вычислить и напечатать значения функции

, где x изменяется на интервале от –1 до 5 с шагом 0,5,

y изменяется на интервале от 2 до 2 с шагом .

Если a<0, вычислить .

Если P , вычислить .

Если <5,8, вычисления закончить.

17. ВАРИАНТ

1.Вычислить

2.Найти сумму членов ряда. На экран вывести значение суммы, число членов ряда, вошедших в сумму, и последний член ряда, вошедший в сумму. Точность считается достигнутой, если очередной член ряда окажется по модулю меньше заданного e.

с заданной точностью e = 10^-2

megaobuchalka.ru

Источник

7 класс.

Вычисление значений функции по формуле.

Итак, мы познакомились с функцией, узнали, что такое область определения и область значений функции. Теперь мы научимся находить значения функции по формуле, которой она задана, а также находить значения аргумента при известных значениях функции.

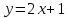
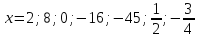
Рассмотрим пример функции: . Для того, чтобы найти значение функции, нужно знать значение аргумента. Эти значения могут быть заданы в условии задачи, а могут выбираться самостоятельно. Пусть заданы значения аргумента: . Для нахождения значений функции, необходимо подставить в формулу функции вместо х его значение (поочерёдно) и посчитать.

Для наглядности все значения удобно оформлять в таблице. В верхней строчке записываем значения х, а в нижней – значения у.

х
у

Если выбираем значения аргумента самостоятельно, то лучше это делать в порядке возрастания.

Чтобы найти значения аргумента при заданных значениях функции, сначала нужно выразить переменную х через переменную у из формулы, которой задана функция.

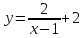
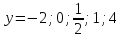
Например, дана функция . Нужно найти значения аргумента, если заданы значения функции: .

Решение. Сначала из формулы 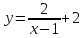выразим переменную х:

Теперь в эту формулу вместо у будем подставлять его значения:

Запишем все эти значения в таблицу.

х
у

Функция задана формулой . Найдите значения переменной у, если:
Функция задана формулой . Найдите значения переменной у, если:
Функция задана формулой . Найдите значения переменной у, если:
Функция задана формулой . Заполните таблицу, вычислив соответствующие значения функции.

x
y

Функция задана формулой . Заполните таблицу, вычислив соответствующие значения функции.

x
y

Функция задана формулой . Заполните таблицу, вычислив соответствующие значения функции.

x
y

Дана функция

Найдите: .

Дана функция

Найдите: .

Дана функция

Найдите: .

Функция задана формулой . Определите:

значение функции, если значение аргумента равно ;
значение аргумента, при котором значение функции равно .

Функция задана формулой . Определите:

значение функции, если значение аргумента равно ;
значение аргумента, при котором значение функции равно .

Дана функция . Найдите значение функции, если значение аргумента равно .
Дана функция . Найдите значение функции, если значение аргумента равно 1.
Дана функция . Найдите значение функции, если значение аргумента равно 3.
Дана функция . Найдите значение функции, если значение аргумента равно -3.
Найдите значение аргумента, при котором функция принимает значение .
Найдите значение аргумента, при котором функция принимает значение .
Найдите значение аргумента, при котором функция принимает значение .
Найдите значение аргумента, при котором функция принимает значение .
Дана функция . Найдите произведение значений функции

Дана функция . Найдите произведение значений функции

Дана функция . Найдите произведение значений функции .
Дана функция . Найдите произведение значений функции .
Для функции найдите значения и и сравните их.
Для функции найдите значения и и сравните их.
Для функции найдите значения и и сравните их.
Для функции найдите значения и и сравните их.

Функция задана формулой . Заполните таблицу:

х
у

Функция задана формулой . Заполните таблицу:

х
у

Длина (см) стального стержня при температуре изменяется по закону . На сколько миллиметров изменится длина стержня, если его температура повысится с до ?
Длина (см) медного стержня при температуре изменяется по закону . На сколько миллиметров изменится длина стержня, если его температура повысится с до ?
Составьте таблицу значений функции, заданной формулой , где , с шагом 1.
Составьте таблицу значений функции, заданной формулой , где , с шагом 1.

Источник