Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Длина радиус-вектора, который изображает заданное комплексное число $z=a+bi$, называется модулем данного комплексного числа.
Модуль заданного комплексного числа вычисляется по следующей формуле:
[r=|z|=|a+bi|=sqrt{a^{2} +b^{2} } .]
Пример 1
Вычислить модуль заданных комплексных чисел $z_{1} =13,, , z_{2} =4i,, , , z_{3} =4+3i$.
Решение:
Модуль комплексного числа $z=a+bi$ вычислим по формуле: $r=sqrt{a^{2} +b^{2} } $.
Для исходного комплексного числа $z_{1} =13$ получим $r_{1} =|z_{1} |=|13+0i|=sqrt{13^{2} +0^{2} } =sqrt{169} =13$
Для исходного комплексного числа $, z_{2} =4i$ получим $r_{2} =|z_{2} |=|0+4i|=sqrt{0^{2} +4^{2} } =sqrt{16} =4$
Для исходного комплексного числа $, z_{3} =4+3i$ получим $r_{3} =|z_{3} |=|4+3i|=sqrt{4^{2} +3^{2} } =sqrt{16+9} =sqrt{25} =5$
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Угол $varphi $, образованный положительным направлением вещественной оси и радиус-вектором $overrightarrow{OM} $, который соответствует заданному комплексному числу $z=a+bi$, называется аргументом данного числа и обозначается $arg z$.
Примечание 1
Модуль и аргумент заданного комплексного числа в явном виде используются при представлении комплексного числа в тригонометрической или показательной форме:
- $z=rcdot (cos varphi +isin varphi )$ — тригонометрическая форма;
- $z=rcdot e^{ivarphi } $ — показательная форма.
Пример 2
Записать комплексное число в тригонометрической и показательной формах, заданное следующими данными: 1) $r=3;varphi =pi $; 2) $r=13;varphi =frac{3pi }{4} $.
«Модуль и аргумент комплексного числа» 👇
Решение:
1) Подставим данные $r=3;varphi =pi $ в соответствующие формулы и получим:
$z=3cdot (cos pi +isin pi )$ — тригонометрическая форма
$z=3cdot e^{ipi } $ — показательная форма.
2) Подставим данные $r=13;varphi =frac{3pi }{4} $ в соответствующие формулы и получим:
$z=13cdot (cos frac{3pi }{4} +isin frac{3pi }{4} )$ — тригонометрическая форма
$z=13cdot e^{ifrac{3pi }{4} } $ — показательная форма.
Пример 3
Определить модуль и аргумент заданных комплексных чисел:
1) $z=sqrt{2} cdot (cos 2pi +isin 2pi )$; 2) $z=frac{5}{3} cdot (cos frac{2pi }{3} +isin frac{2pi }{3} )$; 3) $z=sqrt{13} cdot e^{ifrac{3pi }{4} } $; 4) $z=13cdot e^{ipi } $.
Решение:
Модуль и аргумент найдем, используя формулы записи заданного комплексного числа в тригонометрической и показательной формах соответственно
[z=rcdot (cos varphi +isin varphi );] [z=rcdot e^{ivarphi } .]
1) Для исходного комплексного числа $z=sqrt{2} cdot (cos 2pi +isin 2pi )$ получим $r=sqrt{2} ;varphi =2pi $.
2) Для исходного комплексного числа $z=frac{5}{3} cdot (cos frac{2pi }{3} +isin frac{2pi }{3} )$ получим $r=frac{5}{3} ;varphi =frac{2pi }{3} $.
3) Для исходного комплексного числа $z=sqrt{13} cdot e^{ifrac{3pi }{4} } $ получим $r=sqrt{13} ;varphi =frac{3pi }{4} $.
4) Для исходного комплексного числа $z=13cdot e^{ipi } $ получим $r=13;varphi =pi $.
Аргумент $varphi $ заданного комплексного числа $z=a+bi$ можно вычислить, используя следующие формулы:
[varphi =tgfrac{b}{a} ;cos varphi =frac{a}{sqrt{a^{2} +b^{2} } } ;sin varphi =frac{b}{sqrt{a^{2} +b^{2} } } .]
На практике для вычисления значения аргумента заданного комплексного числа $z=a+bi$ обычно пользуются формулой:
$varphi =arg z=left{begin{array}{c} {arctgfrac{b}{a} ,age 0} \ {arctgfrac{b}{a} +pi ,a
или решают систему уравнений
$left{begin{array}{c} {cos varphi =frac{a}{sqrt{a^{2} +b^{2} } } } \ {sin varphi =frac{b}{sqrt{a^{2} +b^{2} } } } end{array}right. $. (**)
Пример 4
Вычислить аргумент заданных комплексных чисел: 1) $z=3$; 2) $z=4i$; 3) $z=1+i$; 4) $z=-5$; 5) $z=-2i$.
Решение:
1) $z=3$
Так как $z=3$, то $a=3,b=0$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{0}{3} =arctg0=0.]
2) $z=4i$
Так как $z=4i$, то $a=0,b=4$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{4}{0} =arctg(infty )=frac{pi }{2} .]
3) $z=1+i$.
Так как $z=1+i$, то $a=1,b=1$. Вычислим аргумент исходного комплексного числа, решая систему (**):
[left{begin{array}{c} {cos varphi =frac{1}{sqrt{1^{2} +1^{2} } } =frac{1}{sqrt{2} } =frac{sqrt{2} }{2} } \ {sin varphi =frac{1}{sqrt{1^{2} +1^{2} } } =frac{1}{sqrt{2} } =frac{sqrt{2} }{2} } end{array}right. .]
Из курса тригонометрии известно, что $cos varphi =sin varphi =frac{sqrt{2} }{2} $ для угла, соответствующего первой координатной четверти и равного $varphi =frac{pi }{4} $.
4) $z=-5$
Так как $z=-5$, то $a=-5,b=0$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{0}{-5} +pi =arctg0+pi =0+pi =pi .]
5) $z=-2i$
Так как $z=-2i$, то $a=0,b=-2$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{-2}{0} =arctg(-infty )=frac{3pi }{2} .]
Примечание 3
Аргумент чисто мнимых чисел равен соответственно:
- $frac{pi }{2} $ с положительной мнимой частью;
- $frac{3pi }{2} $ с отрицательной мнимой частью.
Решение:
Число $z_{1} $ изображено точкой $(3;0)$, следовательно, длина радиус-вектора равна 3, т.е. $r=3$, а аргумент $varphi =0$ по примечанию 2.
Число $z_{2} $ изображено точкой $(-2;0)$, следовательно, длина соответствующего радиус-вектора равна 2, т.е. $r=2$, а аргумент $varphi =pi $ по примечанию 2.
Число $z_{3} $ изображено точкой $(0;1)$, следовательно, длина соответствующего радиус-вектора равна 1, т.е. $r=1$, а аргумент $varphi =frac{pi }{2} $ по примечанию 3.
Число $z_{4} $ изображено точкой $(0;-1)$, следовательно, длина соответствующего радиус-вектора равна 1, т.е. $r=1$, а аргумент $varphi =frac{3pi }{2} $ по примечанию 3.
Число $z_{5} $ изображено точкой $(2;2)$, следовательно, длина соответствующего радиус-вектора равна $sqrt{2^{2} +2^{2} } =sqrt{4+4} =sqrt{8} =2sqrt{2} $, т.е. $r=2sqrt{2} $, а аргумент $varphi =frac{pi }{4} $ по свойству прямоугольного треугольника.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Модуль и аргумент комплексного числа
Пусть задано комплексное число $ z = a+bi $.
| Формула |
| Модуль комплексного числа равен корню квадратному из суммы квадратов мнимой и действительной части и находится по формуле: $$ |z| = sqrt{a^2 + b^2} $$ |
Если комплексное число состоит только из действительной части $ z = a $, то его модуль равен $ |z| = |a| $.
Стоит заметить, что модуль комплексных чисел всегда неотрицательный $ |z| ge 0 $ и равен нулю $ |z| = 0 $, только в случае $ z = 0 $.
| Формула |
Аргумент комплексного числа обозначается $ varphi = arg z $ и зависит от полуплоскости, в которой лежат числа $a,b$:
|
Введите комплексное число
Пример 1 Пример 2 Правила ввода
| Пример 1 |
| Найти модуль и аргумент комплексного числа $ z = 3 — 4i $. |
| Решение |
|
Комплексное число состоит из действительной и мнимой части: $$ a = Re z = 3 $$ $$ b = Im z = -4 $$ Применяя формулу вычисления модуля получаем: $$ |z| = sqrt{a^2 + b^2} = sqrt{3^2 + (-4)^2} = sqrt{9+16} = 5 $$ Теперь вычисляем аргумент. Так как $a = 3 > 0$, то получаем аргумент: $$varphi = arctg frac{b}{a} = arctg frac{-4}{3} = -arctg frac{4}{3}.$$ |
| Ответ |
| $$ |z| = 5, varphi = -arctg frac{4}{3} $$ |
| Пример 2 |
| Найти модуль и аргумент комплексного числа $ z = 3i $ |
| Решение |
|
В данном случае отсутствует действительная часть, а вернее она равна нулю: $$ a = Re z = 0 $$ Мнимая часть комплексного числа равна: $$ b = Im z = 3 $$ Вычисляем модуль по уже известной формуле: $$ |z| = sqrt{a^2 + b^2} = sqrt{0^2 + 3^2} = sqrt{9} = 3 $$ А вот аргумент здесь попадает под правило при $a = 0, b>0$ и значит равен $$varphi = frac{pi}{2}.$$ |
| Ответ |
| $$ |z| = 3, varphi = frac{pi}{2} $$ |
| Пример 3 |
| Найти модуль и аргумент комплексного числа $$ z = 1+sqrt{3}i $$ |
| Решение |
|
Выписываем действительную и мнимую часть: $$ a = 1 $$ $$ b = sqrt{3} $$ Так как $ a > 0 $, то аргумент равен $$ varphi = arctg frac{sqrt{3}}{1} = arctg sqrt{3} = frac{pi}{3} $$ Находим модуль извлекая квадратный корень из суммы квадратов действительной и мнимой части: $$|z| = sqrt{1^2 + (sqrt{3})^2} = sqrt{1+3}=2.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ varphi = frac{pi}{3}, |z| = 2 $$ |
| Пример 4 |
| Найти аргумент комплексного числа $$ z = -1 + sqrt{3}i $$ |
| Решение |
|
Действительная часть $$ a = Re z = -1 $$ Мнимая часть $$ b = Im z = sqrt{3} $$ Так как $ a < 0 $ и $ b > 0 $, то пользуемся второй формулой: $$ varphi = arg z = pi + arctg frac{sqrt{3}}{-1} = pi + arctg (-sqrt{3}) = $$ $$ = pi — arctg(sqrt{3}) = pi — frac{pi}{3} = frac{2pi}{3}. $$ |
| Ответ |
| $$ varphi = frac{2pi}{3} $$ |
Модуль и аргумент комплексного числа, формулы
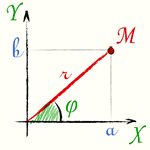 |
Длина вектора, изображающего комплексное число, называется модулем комплексного числа. |
[r = vert a + htmlStyle{color: MediumPurple;}{i} b vert = sqrt{a^2+b^2}]
Модуль действительного числа, совпадает с его абсолютным значением. Сопряженные комплексные числа a + i·b и a — i·b имеют один и тот же модуль.
Угол φ между осью абсцисс и вектором OM, изображающим комплексное число a + i·b, называется аргументом комплексного числа a + i·b
Каждое не равное нулю комплексное число имеет бесчисленное множество аргументов, отличающихся друг от друга на целое число полных оборотов (т.е. на 360°·k, где k — любое целое число). Аргумент комплексного числа связан с его координатами следующими формулами:
[ tg(φ) = frac{b}{a} ]
[ cos(φ) = frac{a}{sqrt{a^2+b^2}}]
[ sin(φ) = frac{b}{sqrt{a^2+b^2}}]
Однако ни одна из этих формул в отдельности не позволяет найти аргумент.
Для того чтобы найти аргумент комплексного числа, эти формулы надо использовать в совокупности,
а также учитывать номер четверти, на координатной плоскости,
в которой находится комплексное число.
Вычислить, найти модуль и аргумент комплексного числа по формулам (1, 2, 3, 4)
Модуль и аргумент комплексного числа |
стр. 75 |
|---|
Вычислить аргумент и модуль комплексного числа.
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки,
соответствующей данному комплексному числу и обозначается Arg(z) = φ
Из определения следуют следующие формулы:
Для числа z = 0 аргумент не определен.
Главным значением аргумента называется такое значение φ, что 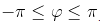
Обозначается: arg(z).
Свойства аргумента:
Модулем комплексного числа z = x + iy называется вещественное число |z| равное:
Для любых комплексных чисел z, z1, z2 имеют место следующие свойства модуля:
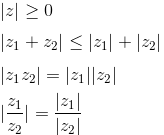
|
|
для пары комплексных чисел z1 и z2 модуль их разности |z1 − z2| равен расстоянию между соответствующими точками комплексной плоскости. |
Что такое комплексное число
Комплексное число — это выражение типа (z;=;a;+;ib). Здесь a и b будут являться любыми действительными числами, а i — специальным числом, называемым мнимой единицей. Действительная часть комплексного числа обозначается как (a;=;RE;z ), а мнимая часть — (b;=;Im;z).
Во множестве комплексных чисел содержится множество вещественных чисел. Если множество комплексных чисел — это всевозможные пары (x, y), то содержащееся в нем множество вещественных чисел — это пары (x, 0). Те же комплексные числа, которые задают пары (0, y) являются мнимыми.
Что такое модуль комплексного числа
Модуль комплексного числа — это длина вектора, который изображает комплексное число.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Любое комплексное число кроме 0 может быть выражено в тригонометрической форме.
(z;=;left|zright|;cdot;(cosleft(varphiright);+;isinleft(varphiright)))
В этом виде (left|zright|) — модуль комплексного числа z. Может обозначаться как p и r.
Если (left|zright|;=;r,) то r будет обозначать длину радиус-вектора точки M (x, y).
Вычисление модуля комплексного числа, если в алгебраической форме оно выглядит как z = x + iy, возможно по следующей формуле:
(left|zright|;=;sqrt{x^2;+;y^2})
То есть модуль комплексного числа можно вычислить как квадратный корень из суммы квадратов действительной и мнимой его частей.
Модуль комплексного числа имеет следующие свойства:
- Модуль не отрицателен — (left|xright|;geq;0). (left|xright|;=;0) только в том случае, если z = 0.
- Модуль суммы двух комплексных чисел будет меньше или равен сумме модулей: (left|z_1;+;z_2right|;leq;left|z_1right|;+;left|z_2right|.)
- Модуль результата умножения двух комплексных числе будет равен произведению модулей: (left|z_1;cdot;z_2right|;=;left|z_1right|;cdot;left|z_2right|.)
- Модуль результата деления двух комплексных чисел будет равняться частному модулей: (left|z_1;div;z_2right|;=;left|z_1right|;div;left|z_2right|.)
- Модуль неравенства комплексных чисел будет равен расстоянию между этими числами на комплексной плоскости: (left|z_1;-;z_2right|;=;sqrt{left(x_1;-;x_2right)^2;+;left(y_1;-;y_2right)^2}).
Что такое аргумент комплексного числа
Аргумент комплексного числа — это угол (varphi) радиус-вектора точки, соответствующей комплексному числу (z;:;varphi;=;arg;z) на комплексной плоскости. Этот угол измеряется в радианах.
Каждое комплексное число, которое не равно нулю, имеет бесконечное множество аргументов. Эти аргументы отличаются друг от друга на целое число полный оборотов — (360^circ;cdot;k) при k — любое число.
Связь аргумента комплексного числа с его координатами отражена в следующих формулах:
(tanleft(varphiright);=;frac ba)
(cosleft(varphiright);=;frac a{sqrt{a^2;+;b^2}})
(sinleft(varphiright);=;frac b{sqrt{a^2;+;b^2}})
Важно помнить, что ни одна из этих формул отдельно недостаточна для того, чтобы найти аргументы. Формулы используются в совокупности, а также учитывается номер четвертый на координатной плоскости, в которой находится комплексное число.
Аргумент может быть записан в тригонометрической форме. Для комплексного числа (z = x + iy), это будет выглядеть следующим образом:
(z;=;r;(cosleft(varphiright);+;i;sinleft(varphiright)))
Здесь (r) будет модулем комплексного числа (z), а (varphi) — arg z.
Важно отметить, arg z имеет смысл лишь при (z neq 0), комплексное число ноль не имеет аргумента.
Как вывести формулу модуля
В соответствии с теоремой Пифагора длина вектора с координатами a и b равна (sqrt{a^2;+;b^2}).
Так как именно эта величина называется модулем комплексного числа (z = a + bi), тогда (left|xright|;=;sqrt{a^2;+;b^2}).
Примеры решения задач
Задача
Найти модуль числа (z;=;-5;+;15i)
Решение
(x;=;Re;z;=;-15) — действительная часть, а (y;=;Im;z;=;15) — мнимая часть комплексного числа (z;=;-5;+;15i.)
Таким образом, модуль числа равен следующему выражению:
(r;=;sqrt{x^2;+;y^2};=sqrt{{(-5)}^2;+;15^2};=;sqrt{25;+;225};=;sqrt{250} )
Ответ: (r;=;sqrt{250})
Задача
Найти расстояние между числами (z_1;=;1;-;3i,;z_2;=;-2;+;2i) на комплексной плоскости.
Решение
Расстояние между двумя комплексными числами находятся как модуль разности комплексных чисел. Используем необходимую формулу:
(left|z_1;-;z_2right|;=;sqrt{{(x_1;-;x_2)}^2;+;left(y_1;-;y_2right)^2};=;sqrt{(1;-;{(-2))}^2;+;{(-2;-;2)}^2};=;sqrt{34})
Ответ: (sqrt{34})
Задача
Найти значение аргумента комплексного числа (sqrt{34}) и выразить его в тригонометрической форме.
Решение
Если действительно частью комплексного числа (z;=;1;+;sqrt{3i}) является число (x = Re z = 1), а мнимой частью является (y = Im z;=sqrt3), то аргумент можно вычислить по формуле:
(varphi;=;arg;z;=;arctg;frac yx;=;arctg;frac{sqrt3}1;=;arctg;sqrt3;=;frac{mathrmpi}3)
Теперь для нахождения тригонометрической формы записи комплексного числа необходимо найти модуль.
(r;=;sqrt{x^2;+;y^2};=;sqrt{1^2;+;{(sqrt3)}^2};=;sqrt{1+3};=;sqrt4;=;2)
Исходя из этого, тригонометрическая форма комплексного числа выглядит следующим образом:
(z;=;2;(cosleft(frac{mathrmpi}3right);+;i;sinleft(frac{mathrmpi}3right)))
Ответ: аргумент равен (frac{mathrmpi}3). Тригонометрическая форма записана выше.
Задача
Найти модуль и аргумент числа (z = 2 — i)
Решение
Найдем (left|zright|;=;sqrt{2^2;+;{(-;1)}^2};=;sqrt5.)
Так как (Re z = 2 > 0), (Im z = -1 < 0), точка расположена в 4 четверти. Тогда из равенства (tanleft(varphiright);=;-frac12) следует:
(varphi;=;arctanleft(-frac12right))
Ответ: (varphi;=;arctanleft(-frac12right))