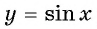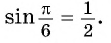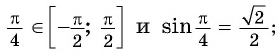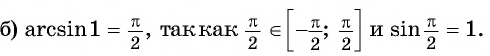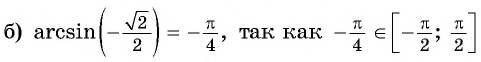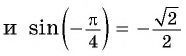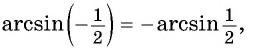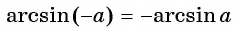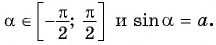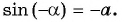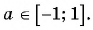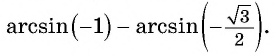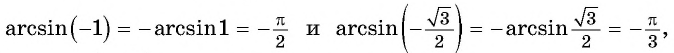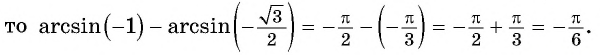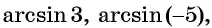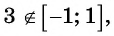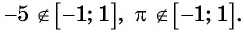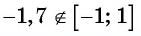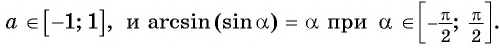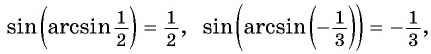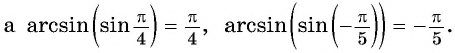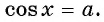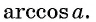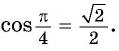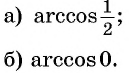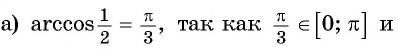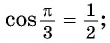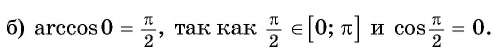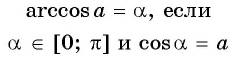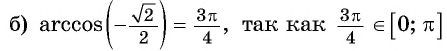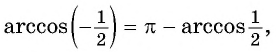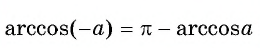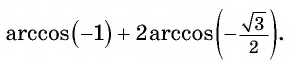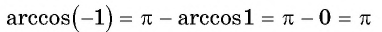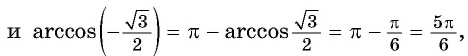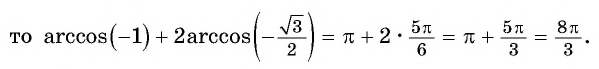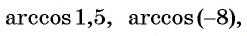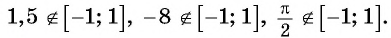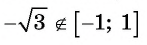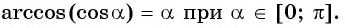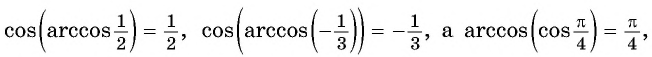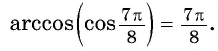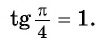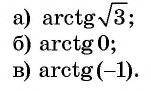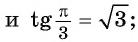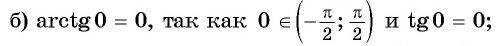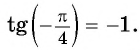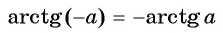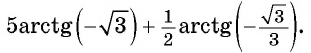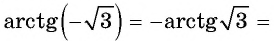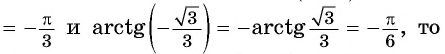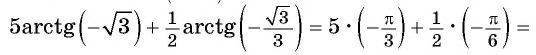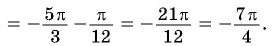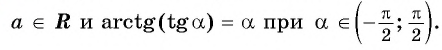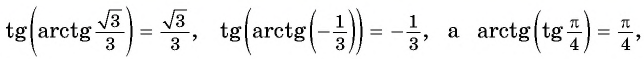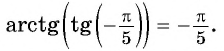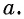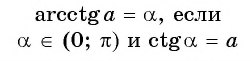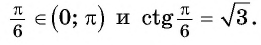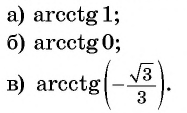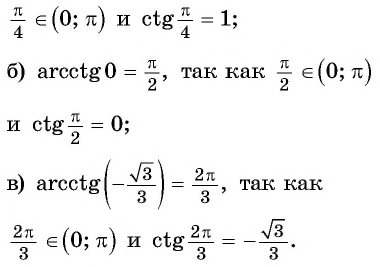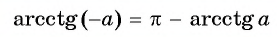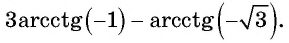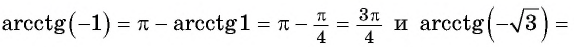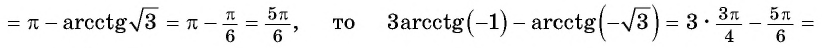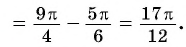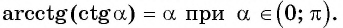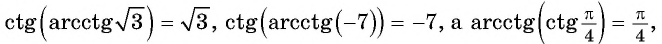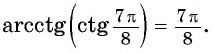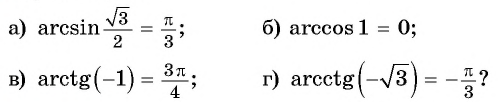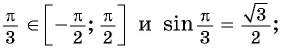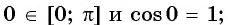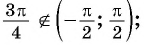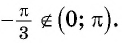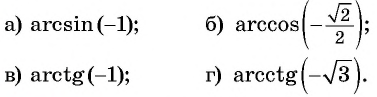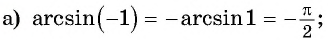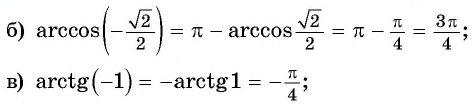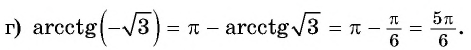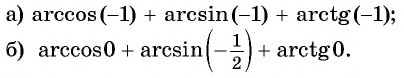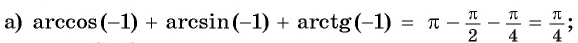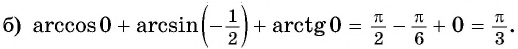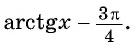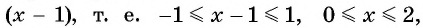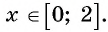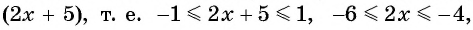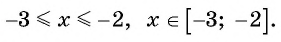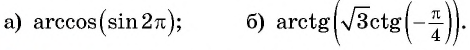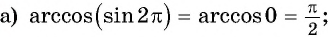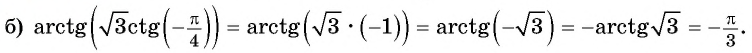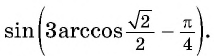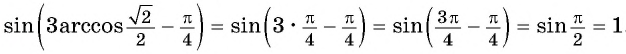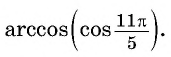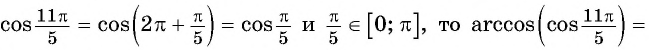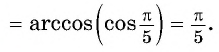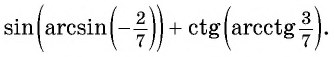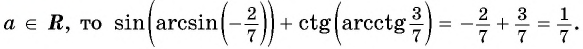Содержание:
При изучении тригонометрических функций часто возникает вопрос о нахождении значения аргумента, при котором значение функции равно заданному числу.
Нахождение значения аргумента
Например, найдем все значения аргумента, при которых значение функции
На единичной окружности найдем точки 
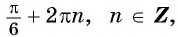
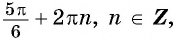
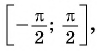
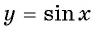
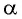
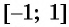
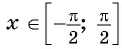
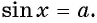
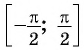
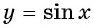
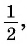
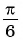
Определение Арксинуса
Определение:
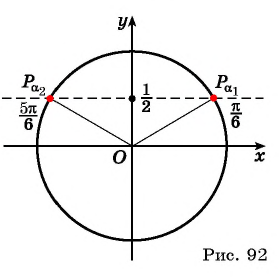
Арксинусом числа 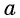
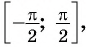
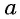
Этот угол обозначают 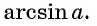
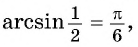
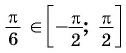
Пример №1
Вычислите:
Решение:
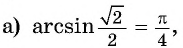
Пример №2
Найдите значение выражения:
Решение:
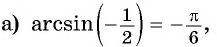
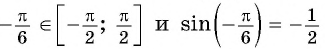
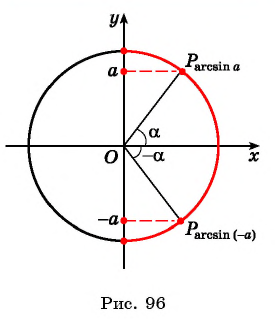
Заметим, что 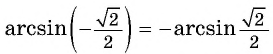
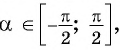
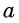
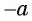
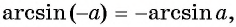
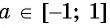
Пусть 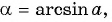
Так как точки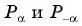
Поскольку 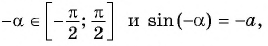
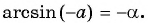
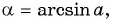
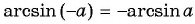
Воспользуемся полученным равенством и найдем значение выражения
Так как
Отметим, что областью определения выражения 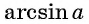
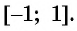
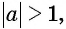
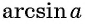
Например, выражения 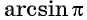
Выражение 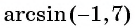
Из определения арксинуса числа следует, что 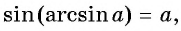
Например,
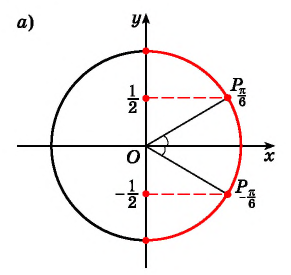
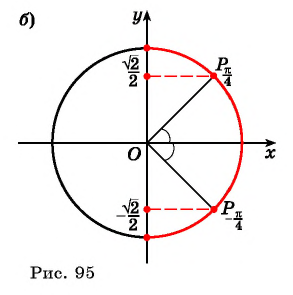
Рассмотрим промежуток 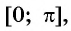
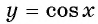
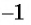
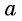
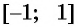
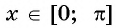
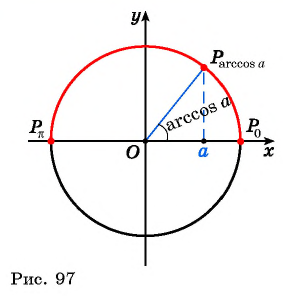
Определение Арккосинуса
Определение:
Арккосинусом числа 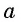
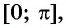
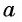
Этот угол обозначают
Например: 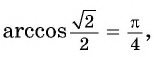
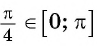
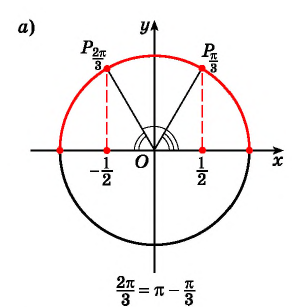
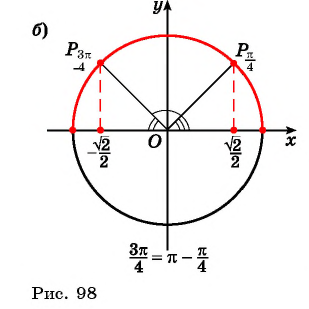
Пример №3
Вычислите:
Решение:
Пример №4
Найдите значение выражения:
Решение:
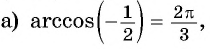
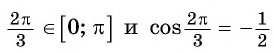
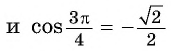
Заметим, что 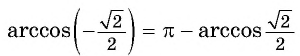
Пусть 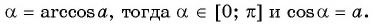
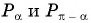
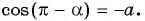
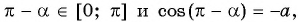
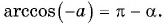
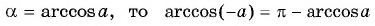
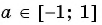
Воспользуемся полученным равенством и найдем значение выражения
Так как
Областью определения выражения 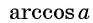
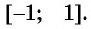
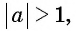
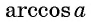
Так, выражения 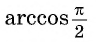
Выражение 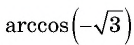
Из определения арккосинуса числа следует, что 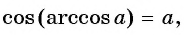
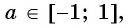
Например,
На промежутке монотонности 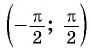
Определение Арктангенса
Определение:
Арктангенсом числа 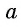
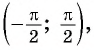
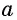
Этот угол обозначают 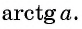
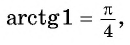
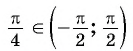
Пример №5
Вычислите:
Решение:
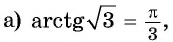
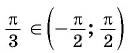
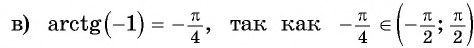
Для любого числа 
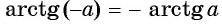
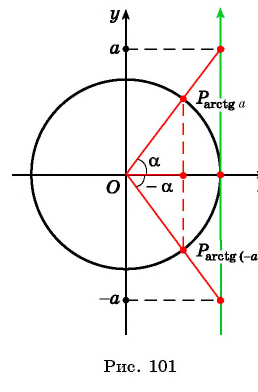
Пример №6
Найдите значение выражения
Решение:
Так как
Из определения арктангенса числа следует, что 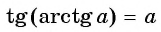
Например,
На промежутке монотонности 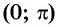
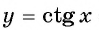
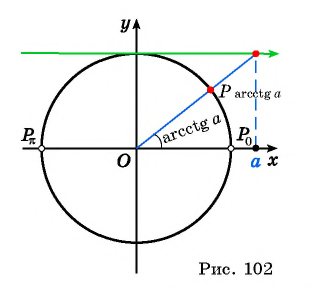
Определение Арккотангенса
Определение:
Арккотангенсом числа 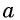
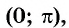
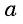
Этот угол обозначают 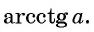
- Заказать решение задач по высшей математике
Пример №7
Вычислите:
Решение:
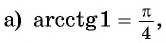
Для любого числа 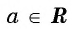
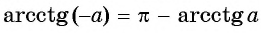
Пример №8
Найдите значение выражения
Решение:
Так как
Из определения арккотангенса числа следует, что 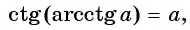
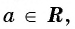
Например,
Примеры заданий и их решения
Пример №9
Верно ли, что:
Решение:
а) Верно, так как
б) верно, так как
в) неверно, так как
г) неверно, так как
Пример №10
Вычислите:
Решение:
Пример №11
Найдите значение выражения:
Решение:
Пример №12
Оцените значение выражения
Решение:
По определению арктангенса числа
Воспользуемся свойствами числовых неравенств и получим:
Пример №13
Найдите область определения выражения:
Решение:
а) По определению арксинуса числа 
б) По определению арккосинуса числа 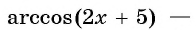
Пример №14
Найдите значение выражения:
Решение:
Пример №15
Вычислите
Решение:
Пример №16
Найдите значение выражения
Решение:
Воспользуемся формулой 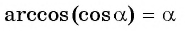
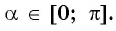
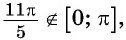
Так как
Пример №17
Найдите значение выражения
Решение:
Так как 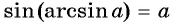
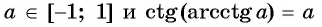
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
- Синус, косинус, тангенс суммы и разности
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
Сферы применения правил обратных тригонометрических функций
Определение
Тригонометрия — раздел математики, объясняющий зависимость между сторонами и углами треугольника, правила используют для расчета углов.
Изучая постулаты тригонометрических функций, ученики и студенты часто задаются вопросом, где эти знания могут пригодиться. Сфер применения достаточно много. Астрономы используют понятия для расчёта положения небесных объектов, тригонометрия помогает выполнять чертежи и создавать архитектурные шедевры, выстраивать модель биологических ритмов. В морской и воздушной навигации, акустике и оптике, в анализе финансового рынка, статистике, медицине, химии, во многих областях используются тригонометрические вычисления. Поэтому так важно научиться применять и выводить формулы самостоятельно.
Обратные функции тригонометрии
Обратными называются функции, которые ещё называют арксинус, арккосинус, арктангенс, арккотангенс.
Название данный вид тригонометрической зависимости, получил от соответствующей прямой функции с приставкой арк — дуга. Взаимосвязь просматривается между длиной дуги единичной окружности и соответствующим определённым отрезком.
Правила обратной функции справедливы в пределах интервалов, например,
формула арксинуса возможна при:
[arcsin (sin mathrm{x})=mathrm{x} text { при }-frac{pi}{2} leq mathrm{x} leq frac{pi}{2}]
[arccos (cos mathrm{x})=mathrm{x} text { при } 0 leq mathrm{x} leq pi]
и так далее.
Формулы с обратными функциями тригонометрии
Уже были рассмотрены обратные тригонометрические функции. Они, как и другие функции имеют между собой связи и зависимости, которые можно выразить в виде формул и использовать для решения задач.
В данной работе мы рассмотрим основные формулы, в которых применяются функции тригонометрии. Разберём их виды, деление на группы, доказательства и способы решения задач с их помощью.
Группировка основных понятий
Сначала проведём группировку формул, для того чтобы сделать более понятной логику объяснений. И объединим все правила и доказательства в одну статью.
Синус от арксинуса для [alpha in(-1 ; 1) sin (arcsin alpha)=alpha, cos (arccos alpha)=alpha]
Тангенса от арктангенса для [alpha in(-infty, infty) operatorname{tg}(operatorname{arctg} alpha)=alpha, operatorname{ctg}(operatorname{arctg} alpha)=alpha].
Указанное в данных выражениях легко выводится из самих определений обратных функций тригонометрии. При необходимости найти arcsin tg, можно использовать приведённые формулы.
Тангенс, арктангенс, котангенс, арккотангенс, синус, арксинус, косинус, арккосинус и формулы
[text{Для }-frac{pi}{2} leq alpha leq frac{pi}{2} arcsin (sin alpha)=alpha],
[text{Для } leq alpha leq pi arccos (cos alpha)=alpha],
[text{Для }-frac{pi}{2}<alpha<frac{pi}{2} operatorname{arctg}(operatorname{tg} alpha)=alpha],
[text{Для } 0<alpha<pi operatorname{arcctg}(operatorname{ctg} alpha)=alpha].
В данном примере собраны тригонометрические выражения, достаточно очевидные, которые можно вывести из определений функций тригонометрии. Необходимо обратить внимание, на то, что высказывания будут верны, если «а» (угол, или числовое значение) будет входить в определённый предел. Если условие не выполняется, расчёт будет не верен и формулу использовать нельзя.
Соотношение между собой обратных тригонометрических функций противоположных чисел
Рассмотрим важное определение:
Обратные функции тригонометрии можно выразить через аркфункции противоположного положительного числа.
[text{Для }alpha in operatorname{open}-1,1] text { arccis }(-alpha)= -operatorname{arc} sin alpha, quad operatorname{arc} cos (-alpha)=pi -a r c cos alpha]
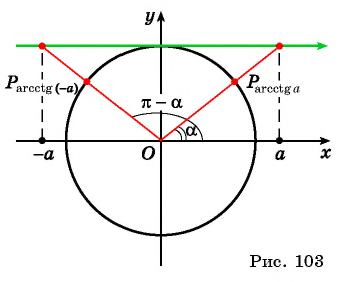
[text { Для } alpha in(-infty, infty) operatorname{arctg}(-alpha)= -operatorname{arctg} alpha, operatorname{arcctg}(-alpha)=pi-operatorname{arcctg} alpha]
Это значит, если расчёты имеют функции отрицательного числа, от них можно избавиться. Для этого необходимо преобразовать их в аркфункции положительных чисел. Такие вычисления проводить проще.
Формулы суммы: arcsin + arccos, arctg +arcctg
Правила суммы выглядят так:
Для [alpha in[-1,1] arcsin alpha+arccos alpha=frac{pi}{2}],
Для [alpha in[-infty, infty] operatorname{arctg} alpha+operatorname{arctg} alpha=frac{pi}{2}].
Отсюда видно, что arcsin определённого числа можно выразить через его arccos , и наоборот. Тоже правило касается и arctg и arcctg, которые выражаются аналогично.
Формулы связи между обратными и прямыми тригонометрическими функциями
Чтобы иметь возможность решить множество задач, требуется знание связей между прямыми тригонометрическими функциями, и их аркфункциями. Рассмотрим, как необходимо поступить, если нужно вычислить тангенс арксинуса. Ниже представлен список основных формул, которые помогут в решении таких задач.
| [-1 leq alpha leq 1], [sin (arcsin alpha)=alpha] |
[-1 leq alpha leq 1], [sin (arccos alpha) =sqrt{1-alpha^{2}}] |
[-infty leq alpha leq+infty], [sin (operatorname{arctg} alpha)=frac{alpha}{sqrt{1+alpha^{2}}}] |
[-infty leq alpha leq+infty], [sin (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}] |
| [-1 leq alpha leq 1], [cos (arcsin alpha)=sqrt{1-alpha^{2}}] |
[-1 leq alpha leq 1], [cos (arccos alpha)=alpha] |
[-infty leq alpha leq+infty], [cos (operatorname{arctg} alpha)=frac{1}{sqrt{1+a^{2}}}] |
[-infty leq alpha leq+infty], [cos (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}] |
| [-1<alpha<1], [operatorname{tg}(arcsin alpha)=frac{alpha}{sqrt{1-alpha^{2}}}] |
[alpha in(-1,0) cup(0,1)], [operatorname{tg}(arccos alpha)=frac{sqrt{1-a^{2}}}{alpha}] |
[-infty leq alpha leq+infty], [operatorname{tg}(operatorname{arctg} alpha)=alpha] |
[alpha neq 0], [operatorname{tg}(operatorname{arcctg} alpha)=frac{1}{alpha}] |
| [alpha in(-1,0) cup(0,1)], [operatorname{ctg}(arcsin alpha)=frac{sqrt{1-alpha^{2}}}{alpha}] |
[-1<alpha<1], [operatorname{ctg}(arccos alpha)=frac{alpha}{sqrt{1-a^{2}}}] |
[alpha neq 0], [operatorname{ctg}(operatorname{arctg} alpha)=frac{1}{alpha}] |
[-infty leq alpha leq+infty], [operatorname{ctg}(operatorname{arcctg} alpha)=alpha] |
Примеры 1 — 2
Нужно найти косинус арктангенса из 5.
Решение. Для этого необходимо воспользоваться формулой следующего вида: [cos (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}]
Подставим необходимое значение: [cos (operatorname{arctg} sqrt{5})=frac{1}{sqrt{1+sqrt{5^{2}}}}=frac{2}{sqrt{6}}]
Определить синус арккосинуса [frac{1}{2}]
Решение. Реализовать решение нам поможет формула: [sin (arccos alpha)=sqrt{1-alpha^{2}}]
Ставим значение и получаем: [sin left(arccos frac{1}{2}right)=sqrt{1-left(frac{1}{2}right)^{2}}=frac{sqrt{3}}{2}]
Заметим, что непосредственное вычисление приведёт к тому же ответу: [sin left(arccos frac{1}{2}right)=sin frac{pi}{3}=frac{sqrt{3}}{2}]
Для правильного вычисления значений прямых и обратных тригонометрических функций, стоит вспомнить начальные материалы.
Доказательство формул синуса от арккосинуса, арккотангенса и арктангенса
Чтобы вывести формулы и разобрать их более наглядно, необходимо применить основные тригонометрические тождества и правила обратных тригонометрических функций, которые были выведены ранее.
Доказательство формул 1
Используя тождества получим:
[sin ^{2} alpha+cos ^{2} alpha=1]
[1+operatorname{ctg}^{2} alpha=frac{1}{sin ^{2} alpha}]
Вспомним тот факт, что tg α *ctg α= 1, следовательно
[sin alpha=sqrt{1-cos ^{2} alpha}, 0 leq alpha leq pi]
[sin alpha=frac{operatorname{tg} alpha}{sqrt{1+operatorname{tg}^{2} alpha}},-frac{pi}{2}<alpha<frac{pi}{2}]
[sin alpha=frac{1}{sqrt{1+c t g^{2} alpha}}, 0<alpha<pi]
Результатом станет вывод синуса через подходящие аркфункции в заданном условии.
В математическое выражение вместо α, ставим arccos α, получаем в итоге формулу синуса арккосинуса.
Во втором случае вместо α подставляем arctg α, соответственно получаем формулу синуса арктангенса.
В третьем варианте проводим аналогичную операцию и подставляем arcctg α для выражения формулы синуса арккотангенса.
Нет времени решать самому?
Наши эксперты помогут!
Доказательство формул для тангенса, обратных функций(arcsin, arccos, arcctg)
В данном разделе рассмотрим доказательство закона тангенса обратных функций тригонометрии.
Доказательство формул 2
- Исходя из: [frac{sin alpha}{sqrt{1-sin alpha^{2}}},-frac{pi}{2}<alpha<frac{pi}{2}]Получим [operatorname{tg}(arcsin alpha)=frac{sin (arcsin alpha)}{sqrt{1-sin ^{2}(arcsin alpha)}}=frac{alpha}{sqrt{1-alpha^{2}}}]При условии [-1<alpha<1]
- Из выражения [operatorname{tg} alpha=frac{sqrt{1-cos ^{2} alpha}}{cos alpha}, alpha inleft[0, frac{pi}{2}right) cupleft(frac{pi}{2}, piright]]
Получаем [operatorname{tg}(arccos alpha)=frac{sqrt{1-cos ^{2}(arccos alpha)}}{cos (arccos alpha)}=frac{sqrt{1-alpha^{2}}}{alpha}] при условии [alpha in(-1,0) cup(0,1)]. - Исходя из [operatorname{tg} alpha=frac{1}{operatorname{ctg} alpha}, alpha inleft(0, frac{pi}{2}right) cupleft(frac{pi}{2}, piright)] получаем [operatorname{tg}(operatorname{arcctg} alpha)=frac{1}{operatorname{ctg}(operatorname{arcctg} alpha)}=frac{1}{alpha}] при условии, что [alpha neq 0].
Далее нам понадобятся понятия котангенсов арксинуса, арккосинуса, арктангенса. Напомним такое тригонометрическое равенство:
[operatorname{ctg} alpha=frac{1}{operatorname{tg} alpha}]
Применяя данное выражение можно вывести необходимые формулы, вставляя выражения тангенса обратных функций тригонометрии. Практически необходимо поменять местами числитель и знаменатель.
Выражение арксинуса с помощью арккосинуса, арктангенса и арккотангенса
Прямые и обратные функции в тригонометрии связаны между собой. Полученные в результате выведения формулы помогут найти связь и между обратными функциями тригонометрии, выразив одни аркфункции через другие. Рассмотрим примеры.
В первом случае меняем арксинус на арккосинус, а арктангенс на арккотангенс, получим следующие формулы арксинуса и арккосинуса:
[begin{aligned} &arcsin a=left{begin{array}{l} arccos sqrt{1-a^{2}}, 0 leq a leq 1 \ -arccos sqrt{1-a^{2}},-1 leq a<0 end{array}right. \ &arcsin a=operatorname{arctg} frac{a}{sqrt{1-a^{2}}},-1<a<1 \ &arcsin a=left{begin{array}{l} operatorname{arcctg} frac{sqrt{1-a^{2}}}{a}, 0<a leq 1 \ operatorname{arcctg} frac{sqrt{1-a^{2}}}{a}-pi,-1 leq a<0 end{array}right. end{aligned}]
Для арккосинуса также есть свои формулы:
[begin{aligned} &arccos a=left{begin{array}{l} arcsin sqrt{1-a^{2}}, 0 leq a leq 1 \ pi-arcsin sqrt{1-a^{2}},-1 leq a<0 end{array}right. \ &arccos a=left{begin{array}{l} operatorname{arctg} frac{sqrt{1-a^{2}}}{a}, 0<a leq 1 \ pi+operatorname{arctg} frac{sqrt{1-a^{2}}}{a},-1 leq a<0 end{array}right. \ &arccos a=operatorname{arcctg} frac{a}{sqrt{1-a^{2}}},-1<a<1 end{aligned}]
Выражения для арктангенса:
[begin{aligned} &operatorname{arctg} a=arcsin frac{a}{sqrt{1+a^{2}}},-infty<a<+infty\ &operatorname{arctg} a=left{begin{array}{l} arccos frac{1}{sqrt{1+a^{2}}}, a geq 0 \ -arccos frac{1}{sqrt{1+a^{2}}}, a<0 end{array}right.\ &operatorname{arctg} a=operatorname{arcctg} frac{1}{a}, a neq 0 end{aligned}]
Последний блок формул покажет преобразование арккотангенса через другие обратные функции тригонометрии:
[begin{aligned} &operatorname{arcctg} a=left{begin{array}{l} arcsin frac{1}{sqrt{1+a^{2}}}, a geq 0 \ pi-arcsin frac{1}{sqrt{1+a^{2}}}, a<0 end{array}right.\ &operatorname{arctg} a=arccos frac{a}{sqrt{1+a^{2}}},-infty<a<+infty\ &operatorname{arcctg} a=operatorname{arctg} frac{1}{a}, a neq 0 end{aligned}]
Рассмотренные формулы арксинуса, арккосинуса, арктангенса помогут в решении различных задач. Разберём доказательство с использованием основных определений обратных функций и ранее рассмотренных правил.
Возьмём arcsin [alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}},-1<alpha<1] для выведения доказательства.
Мы имеем выражение [operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}] — число, которое имеет значение от минус половины [pi] до плюс половины [pi]. Используя выражение синуса арктангенса, получаем следующее:
[sin left(operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}right)=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{sqrt{1+left(frac{alpha}{sqrt{1-alpha^{2}}}right)^{2}}}=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{sqrt{1+frac{alpha^{2}}{1-alpha^{2}}}}=frac{frac{alpha}{sqrt{1-alpha^{2}}}}{frac{1}{sqrt{1-alpha^{2}}}}=alpha]
Получается, что [operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}] с условием [-1<alpha<1] — арксинус числа [alpha].
Вывод: [arcsin alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}},-1<alpha<1].
Другие подобные формулы доказываются по аналогичной схеме.
Рассмотрим пример применения полученных истин.
Пример 3
Необходимо вычислить синус арккотангенса — [sqrt{3}]
Решение. Для того чтобы провести решение задачи, необходимо использовать формулу связи арккотангенса и арксинуса: [arcsin alpha=operatorname{arctg} frac{alpha}{sqrt{1-alpha^{2}}}]
Подставим в неё [alpha=-sqrt{3}] и получим [-frac{1}{2}].
Используя непосредственное вычисление ответ был бы такой же: [sin (operatorname{arcctg}(-sqrt{3}))=sin frac{5 pi}{6}=frac{1}{2}]
Можно использовать и следующую формулу:
[sin (operatorname{arcctg} alpha)=frac{1}{sqrt{1+a^{2}}}]
[sin (operatorname{arcctg}(-sqrt{3}))=frac{1}{sqrt{1+(-sqrt{3})^{2}}}=frac{1}{2}]
Другие формулы, в которых используются обратные функции тригонометрии
Разобраны основные функции, которые чаще всего используются для решения задач. Но представлены не все формулы с обратными тригонометрическими функциями, есть некоторые специфичные, употребляемые редко, но они тоже полезны. Учить их нет смысла, лучше вывести при необходимости.
Пример 4
Разберём для примера одну такую формулу. Выглядит она так:
[sin ^{2} frac{alpha}{2}=sqrt{frac{1-cos alpha}{2}}]
Если представленный угол имеет значение больше нуля, но меньше Пи, то получаем:
[sin frac{arccos alpha}{2}=sqrt{frac{1-cos (arccos alpha)}{2}}]
[Leftrightarrow sin frac{arccos alpha}{2}=frac{sqrt{1-alpha}}{2}]
Здесь мы выводим следующую готовую формулировку, арксинус которой выведен через арккосинус:
[frac{arccos alpha}{2}=arcsin sqrt{frac{1-alpha}{2}}]
В тексте рассмотрены лишь некоторые, самые популярные виды связей между прямыми и обратными функциями тригонометрии. Главное не выучить наизусть данные постулаты, а научиться их применять и выводить, исходя из уже известных определений.
Удобно использовать инженерный вид калькулятора, на котором есть, необходимые для вычислений тригонометрические формулы и функции.
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.
Сначала дадим определения.
Арксинусом числа а называется число , такое, что
Или, можно сказать, что это такой угол
, принадлежащий отрезку
, синус которого равен числу а.
Арккосинусом числа а называется число , такое, что
Арктангенсом числа а называется число , такое, что
Арккотангенсом числа а называется число , такое, что
Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.
Помните, мы уже встречались с обратными функциями.
Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.
Логарифм числа b по основанию a — такое число с, что
При этом
Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это
и
Мы не смогли бы записать их без специального символа арифметического квадратного корня.
Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число
Это показатель степени, в которую надо возвести 2, чтобы получить 7.
Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение
Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?
Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.
Угол, принадлежащий отрезку , синус которого равен
— это арксинус одной четвертой. И значит, серия решений нашего уравнения, соответствующая правой точке на тригонометрическом круге, — это
А вторая серия решений нашего уравнения — это
Подробнее о решении тригонометрических уравнений — здесь.
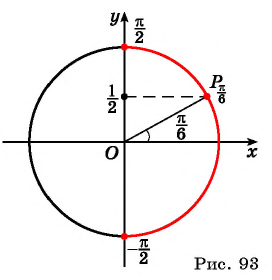
Осталось выяснить — зачем в определении арксинуса указывается, что это угол, принадлежащий отрезку ?
Дело в том, что углов, синус которых равен, например, , бесконечно много. Нам нужно выбрать какой-то один из них. Мы выбираем тот, который лежит на отрезке
.
Взгляните на тригонометрический круг. Вы увидите, что на отрезке каждому углу соответствует определенное значение синуса, причем только одно. И наоборот, любому значению синуса из отрезка
отвечает одно-единственное значение угла на отрезке
. Это значит, что на отрезке
можно задать функцию
принимающую значения от
до
Повторим определение еще раз:
Арксинусом числа a называется число , такое, что
Обозначение: Область определения арксинуса — отрезок
Область значений — отрезок
.
Можно запомнить фразу «арксинусы живут справа». Не забываем только, что не просто справа, но ещё и на отрезке .
Мы готовы построить график функции
Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.
Поскольку , следовательно, х лежит в пределах от -1 до 1.
Значит, областью определения функции y = arcsin x является отрезок
Мы сказали, что у принадлежит отрезку . Это значит, что областью значений функции y = arcsin x является отрезок
.
Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и
Как всегда при построении графика незнакомой функции, начнем с таблицы.
По определению, арксинус нуля — это такое число из отрезка , синус которого равен нулю. Что это за число? — Понятно, что это ноль.
Аналогично, арксинус единицы — это такое число из отрезка , синус которого равен единице. Очевидно, это
Продолжаем: — это такое число из отрезка
, синус которого равен
. Да, это
| 0 | |||||
| 0 |
Строим график функции
Свойства функции
1. Область определения
2. Область значений
3. , то есть эта функция является нечетной. Ее график симметричен относительно начала координат.
4. Функция монотонно возрастает. Ее наименьшее значение, равное —
, достигается при
, а наибольшее значение, равное
, при
5. Что общего у графиков функций и
? Не кажется ли вам, что они «сделаны по одному шаблону» — так же, как правая ветвь функции
и график функции
, или как графики показательной и логарифмической функций?
Представьте себе, что мы из обычной синусоиды вырезали небольшой фрагмент от до
, а затем развернули его вертикально — и мы получим график арксинуса.
То, что для функции на этом промежутке — значения аргумента, то для арксинуса будут значения функции. Так и должно быть! Ведь синус и арксинус — взаимно-обратные функции. Другие примеры пар взаимно обратных функций — это
при
и
, а также показательная и логарифмическая функции.
Напомним, что графики взаимно обратных функций симметричны относительно прямой
Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок
Арккосинусом числа a называется число , такое, что
Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке
Обозначение: Область определения арккосинуса — отрезок
Область значений — отрезок
Очевидно, отрезок выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно-единственное значение угла из промежутка
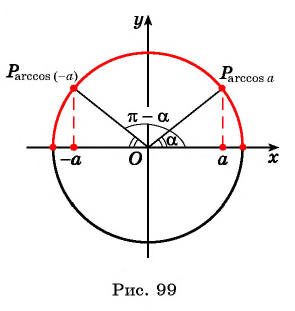
Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:
Построим график функции
Нам нужен такой участок функции , на котором она монотонна, то есть принимает каждое свое значение ровно один раз.
Выберем отрезок . На этом отрезке функция
монотонно убывает, то есть соответствие между множествами
и
взаимно однозначно. Каждому значению х соответствует свое значение у. На этом отрезке существует функция, обратная к косинусу, то есть функция у = arccosx.
Заполним таблицу, пользуясь определением арккосинуса.
Арккосинусом числа х, принадлежащего промежутку , будет такое число y, принадлежащее промежутку
, что
Значит, , поскольку
;
, так как
;
, так как
,
, так как
,
| 0 | |||||
| 0 |
Вот график арккосинуса:
Свойства функции
1. Область определения
2. Область значений
3.
Эта функция общего вида — она не является ни четной, ни нечетной.
4. Функция является строго убывающей. Наибольшее значение, равное , функция у = arccosx принимает при
, а наименьшее значение, равное нулю, принимает при
5. Функции и
являются взаимно обратными.
Следующие — арктангенс и арккотангенс.
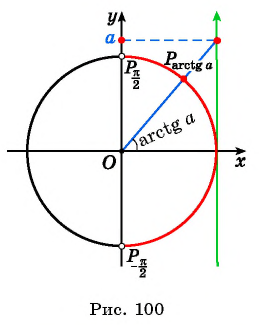
Арктангенсом числа a называется число , такое, что
Обозначение: . Область определения арктангенса — промежуток
Область значений — интервал
.
Почему в определении арктангенса исключены концы промежутка — точки ? Конечно, потому, что тангенс в этих точках не определён. Не существует числа a, равного тангенсу какого-либо из этих углов.
Построим график арктангенса. Согласно определению, арктангенсом числа х называется число у, принадлежащее интервалу , такое, что
Как строить график — уже понятно. Поскольку арктангенс — функция обратная тангенсу, мы поступаем следующим образом:
— Выбираем такой участок графика функции , где соответствие между х и у взаимно однозначное. Это интервал Ц На этом участке функция
принимает значения от
до
Тогда у обратной функции, то есть у функции , область, определения будет вся числовая прямая, от
до
а областью значений — интервал
Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.
, значит,
, значит,
, значит,
А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?
Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте
Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте
На рисунке — график функции
Свойства функции
1. Область определения
2. Область значений
3. Функция нечетная.
4. Функция является строго возрастающей.
5. Прямые и
— горизонтальные асимптоты данной функции.
6. Функции и
являются взаимно обратными — конечно, когда функция
рассматривается на промежутке
Аналогично, определим функцию арккотангенс и построим ее график.
Арккотангенсом числа a называется число , такое, что
График функции :
Свойства функции
1. Область определения
2. Область значений
3. Функция — общего вида, то есть ни четная, ни нечетная.
4. Функция является строго убывающей.
5. Прямые и
— горизонтальные асимптоты данной функции.
6. Функции и
являются взаимно обратными, если рассматривать
на промежутке
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Обратные тригонометрические функции и их графики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Функции с приставкой arc — это функции, обратные тригонометрическим. Например, для функции $sinα$ обратной функцией является её арксинус, записывается как $arcsinα$, а для функции косинуса обратной будет функция арккосинус, записывается как $arccosα$. Проще говоря, обратные тригонометрическим функции с приставкой $arc$ являются множеством значений углов $α$, от которых берётся какая-либо обычная тригонометрическая функция, также иногда функции с приставкой $arc$ используют как меру длины дуги, ограничивающей угол $α$.

Рисунок 1. Единичная окружность. Автор24 — интернет-биржа студенческих работ
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рассмотрим теперь непосредственно определения для функций арксинус, арккосинус, арктангенс и арккотангенс по отдельности.
Арксинус числа
Определение 1
Арксинус числа $x$ — это множество значений углов, для которых $sinα = x$. Также определение арксинуса можно записать так: $arcsin(x) = α$.
Рассмотрим рисунок 1, на котором изображена окружность с радиусом, равным единице. Как мы помним, $sinα$ — это отношение противолежащей стороны к гипотенузе, численно он равен длине стороны $AC$. Так как арксинус его обратная функция и есть не что иное как угол, от которого берётся синус, свойства арксинуса очень похожи на свойства синуса:
- Область определения функции арксинуса $D(y)= [-1;1 ]$, для синуса $D(y)= [-frac{π}{2};frac{π}{2} ]$;
- Область значения для арксинуса $E = [-frac{π}{2};frac{π}{2} ]$, для синуса $E = [-1;1 ]$
- Функции синуса и арксинуса обе возрастающие;
- Функции арксинуса и синуса обе нечётные, то есть: $arcsin(-x)= -arcsinx$;
- Функция $y=arcsin(x)$ равна нулю при $x=0$.
«Арксинус, арккосинус и арктангенс числа» 👇
График арксинуса выглядит следующим образом:
Рисунок 2. График арксинуса. Автор24 — интернет-биржа студенческих работ
Арккосинус числа
Определение 2
Арккосинус числа $x$ — это множество значений углов, для которых $cosα = x$, то есть это значение угла.
Свойства арккосинуса в сравнении с косинусом:
- Область определения функции арккосинуса $D(y)= [-1;1 ]$, для косинуса $D(y)= [0; π ]$;
- Область значения для арккосинуса $E = [0; π ]$, для косинуса $E = [-1;1 ]$;
- График функции арккосинуса симметричен относительно точки $(0; frac{ π}{2})$, следовательно, он не является ни чётным, ни нечётным, в отличии от функции косинуса, которая является чётной;
- График функции арккосинуса $y= arccos(x)$ является убывающим, это происходит на всей его области определения, так же, как и c графиком косинуса.
- Функция $y=arccos(x)$ равна нулю при $x=1$.
Рисунок 3. График арккосинуса. Автор24 — интернет-биржа студенческих работ
Арктангенс числа
Определение 3
Арктангенс числа $x$ — это множество значений углов, для которых $tgα = x$.
Свойства арктангенса:
- $D(y)= [-infty;1 ]$;
- $E = [-frac{π}{2};frac{π}{2} ]$;
- Данная функция нечётная;
- Функция $y= arctgx$ возрастающая на всей области определения;
- Функция $y= arctgx$ равна нулю при $x=0$.
Рисунок 4. График арктангенса. Автор24 — интернет-биржа студенческих работ
Арккотангенс
Определение 4
Арккотангенс числа $x$ — это множество значений углов, для которых $ctgα = x$.
Свойства функции арккотангенса:
- $D(y)= [-infty;1 ]$;
- $E = [0; π ]$;
- Данная функция не является ни чётной, ни нечётной;
- Функция $y= arcсtgx$ убывает на всей области определения;
Рисунок 5. График арккотангенса. Автор24 — интернет-биржа студенческих работ
Пример 1
Найдите значение следующих выражений: $arcsin(frac{1}{2}), arccos(-frac{sqrt{2}}{2}), arcctg(frac{sqrt{3}}{3}), arccos(-frac{1}{2})$.
Решение:
$arcsin(frac{1}{2}) = frac{π}{6}$
$arccos(frac{sqrt{2}}{2}) = frac{π}{4}$
$arcctg(frac{sqrt{3}}{3}) = frac{π}{4}$
Здесь мы имеем арккосинус отрицательного числа $arccos(-frac{-1}{2})$, для того чтобы его вычислить, необходимо прибегнуть к следующей формуле:
$arccos(-α) = π – arccos(α)$
$arccos(-frac{-1}{2}) = π – arccos(frac{-1}{2}) = π – frac{π}{3} = frac{2π}{3}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме