Как найти арктангенс в маткаде - Исправление недочетов и поиск решений вместе с Examum.ru

MathCAD. MatLab

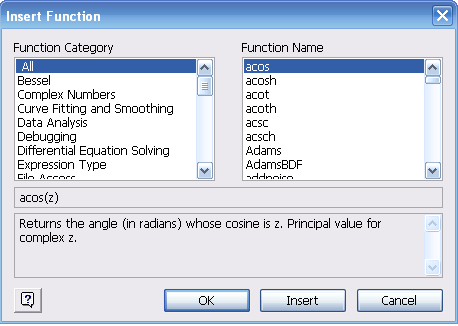
— Арктангенса нет на панелях инструментов, поэтому его нужно найти в специальном списке функций. Вызвать этот список можно либо сочетанием [Ctrl]+[E], либо выполнив команду Insert / Function (Вставка/Функция), либо при помощи специальной кнопки панели Standard (Стандартная). В открывшемся окне есть список категорий функций (Function Category), список самих функций выбранной категории (Function Name), а также окно информации о выбранной функции. По умолчанию определена категория All (Все) и в окне Function Name находится полный список всех встроенных функций MathCAD.
Очевидно, что арктангенс нужно искать в категории Trigonometric (Тригонометрические). Среди множества всевозможных тригонометрических функций находится 2 вида арктангенса (Atan и Atan2).
Для того чтобы определить, какой из них следует выбрать, прочитаем описание для каждого:
Atan(Z). »Returns the angle (in radians) whose tangent is z. Principal value for complex z.» »Возвращает угол (в радианах), для которого тангенс — это Z. Главное значение для комплексного Z».
Atan2(x,y). »Returns the angle (in radians) from the x-axis to a line containing the origin (0, 0) and the point (x, y). Both x and y must be real.» » Возвращает угол (в радианах) между осью x и линией, содержащей точку начала координат и точку (x,y). X и Y должны быть действительными».
Очевидно, нужно использовать первую функцию. Выбираем ее и нажимаем Ok.
2) Выражение введено, но параметры его вида, установленные по умолчанию, зачастую могут не удовлетворить пользователя. Для того чтобы отредактировать вид выражения, нужно при помощи команды Format/Equation (Формат/Уравнение) вызвать соответствующее меню.
Здесь вы можете определить цвет шрифта формул (Default equation color), выбрать стиль (Style name). При помощи кнопки Modify (Модифицировать) вы можете изменить стиль текста формул: выбрать тип, размер, начертание шрифта. Чтобы поменять параметры самой математической области, выполните правый щелчок мышью по любой точке редактируемой формулы и в открывшемся контекстном меню выберите пункт Properties (Свойства).

Как записать арктангенс в маткаде

Система MathCAD содержит большой набор встроенных элементарных функций. Функции задаются своими именами и значениями аргумента, заключёнными в круглых скобках. Функции, как и переменные, и числа, могут входить в состав математических выражений. В ответ на обращение к ним, функции возвращают вычисленные значения. Ниже представлены некоторые из этих функций.

1.2.1 Тригонометрические функции

sin (z) — синус . cos (z) — косинус
tan (z) — тангенс . sec (z) — секанс
csc (z) — косеканс . cot (z) — котангенс

1.2.2 Гиперболические функции

sinh (z) — гиперболический синус
cosh(z) — гиперболический косинус
tanh(z) — гиперболический тангенс
sech(z) — гиперболический секанс
csch(z) — гиперболический косеканс
coth(z) — гиперболический котангенс

1.2.3 Обратные тригонометрические функции

asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс

1.2.3 Обратные тригонометрические функции

asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс

1.2.4 Обратные гиперболические функции

asinh (z) — обратный гиперболический синус
acosh(z) — обратный гиперболический косинус
atanh(z) — обратный гиперболический тангенс

1.2.5 Показательные и логарифмические функции

exp (z) — экспоненциальная функция
ln (z) — натуральный логарифм
log (z) — десятичный логарифм

1.2.6 Функции с условиями сравнения

ceil (x) — наименьшее целое, большее или равное х
floor(x) — наибольшее целое, меньшее или равное х
mod(x,y) — остаток отделения х/у со знаком х
angle(x,y) — положительный угол с осью х для точки с координатами (х,у)

Как ввести arctg в mathcad

Как правильно записать Arcctg()

Как правильно записать F(x)
Как правильно записать F(x) чтоб реализовать метод простой итерации

Как правильно записать?
Записываю интеграл как есть ,а он выдаёт странное решение,помогите, как правильно записать?

Как записать правильно формулу?
не могу записать фор-лу,постоянно что-то горит красным..

Основные средства программы MathCAD

aequiv3

x:=1 , ,

x:=2 , $mu:=yfrac<z>+e^x$

y:=3.46 , z:=7.46 ,

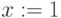
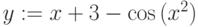
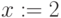
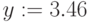
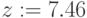
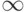
infty -бесконечность ( клавиши <Ctrl>+<Shift>+<z>);

— основание натурального логарифма (клавиша <е>);

; — число «пи» (вводится клавишами <Ctrl>+<Shift>+<p>);

— мнимая единица (вводится клавишами <1>, <i> или <1>, <j>);

— символ процента, <%>, эквивалентный 0,01.

t:=1i+1

2t=2+2i

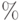
Набираемая формула всегда заключена в рамку. Не выходите из рамки, пока не закончили набор формулы!
Для набора формул пользуйтесь «Калькулятором» из «Математической палитры»

При наборе формул возможно появление ошибок набора. Кнопка на стандартной панели инструментов позволяет отменить последнее действие, выполненное при редактировании, т.е. вернуться к тексту, набранному ранее.

Встроенные функции MathCAD

x:=2

$mathbf= left( begin<array> <cccc>a_ <11>& a_ <12>& ldots & a_ <1n>\ a_ <21>& a_ <22>& ldots & a_<2n>\ ldots & ldots & ldots & ldots \ a_ <m1>& a_ <m2>& ldots & a_<mn>\ end <array>right)$

$left( begin<array> <cc>a_ <11>& a_ <12>\ a_ <21>& a_ <22>\ end <array>right) left( begin<array> <ccc>b_ <11>& b_ <12>& b_ <13>\ b_ <21>& b_ <22>& b_ <23>\ end <array>right) = left( begin<array> <ccc>a_<11>b_<11>+a_<12>b_ <21>& a_<11>b_<12>+a_<12>b_ <22>& a_<11>b_<13>+a_<12>b_ <23>\ a_<21>b_<11>+a_<21>b_ <21>& a_<21>b_<12>+a_<22>b_ <22>& a_<21>b_<13>+a_<22>b_ <23>\ end <array>right)$

Создаются матрицы при помощи кнопки палитры инструментов Matrix или команды Insert/Matrix (Рис.1.18, Рис.1.19, Рис.1.20). Появляется окно Insert matrix, где указывается количество строк, столбцов Rows и Columns.

Источник

Как в маткаде написать арктангенс

Этот раздел описывает тригонометрические, гиперболические и показательные функции Mathcad вместе с обратными им. Здесь также описываются встроенные функции Бесселя.

Тригонометрические функции и обратные им.

Тригонометрические функции Mathcad и обратные им определены для любого комплексного аргумента. Они также возвращают комплексные значения везде, где необходимо. Результаты для комплексных значений вычисляются с использованием тождеств:

Для применения этих функций к каждому элементу вектора или матрицы используйте оператор векторизации.

Обратите внимание, что все эти тригонометрические функции используют аргумент, выраженный в радианах. Чтобы перейти к градусам, используется встроенная единица deg. Например, чтобы вычислить синус 45 градусов, введите sin(45*deg).

Имейте в виду, что из-за ошибок округления, свойственных машинной арифметике, Mathcad может возвращать очень большое число в той точке, где находится особенность вычисляемой функции. Вообще, необходимо быть осторожным при вычислениях в окрестности таких точек.

sin(z)	Возвращает синус z. В прямоугольном треугольнике это — отношение длины противолежащего катета к длине гипотенузы.
cos(z)	Возвращает косинус z. В прямоугольном треугольнике это — отношение длины прилежащего катета к длине гипотенузы.
tan(z)	Возвращает (sin(z)/cos(z)), тангенс z. В прямоугольном треугольнике это — отношение длины противолежащего катета к длине прилежащего катета; z не должен быть кратным p /2 .
csc(z)	Возвращает 1/sin(z), косеканс z; z не должен быть кратным p .
sec(z)	Возвращает 1/cos(z), секанс z; z не должен быть кратным p /2.
cot(z)	Возвращает 1/tan(z), котангенс z; z не должен быть кратным p .

Обратные тригонометрические функции, приведенные ниже, возвращают угол в радианах между 0 и 2 p . Чтобы преобразовать этот результат в градусы, можно также пользоваться встроенной единицей deg или напечатать deg в поле единиц.

Из-за ошибок округления, свойственных машинной арифметике, в результате вычисления atan достаточно большого числа получается значение . Как правило, лучше всего избегать численных вычислений около таких особенностей.

asin(z)	Возвращает угол (в радианах), чей синус — z.
acos(z)	Возвращает угол (в радианах), чей косинус — z.
atan(z)	Возвращает угол (в радианах), чей тангенс — z.

Гиперболические функции sinh и cosh определяются формулами:

Эти функции также могут использовать комплексный аргумент и возвращать комплексные значения. Гиперболические функции тесно связаны с тригонометрическими функциями. Справедливы формулы:

sinh(iz)=isin(z)cosh(iz)=cos(z)

sinh (z)	Возвращает гиперболический синус z.
cosh (z)	Возвращает гиперболический косинус z.
tanh (z)	Возвращает sinh(z)/cosh(z), гиперболический тангенс z.
csch (z)	Возвращает 1/sinh(z), гиперболический косеканс z.
sech (z)	Возвращает 1/cosh(z), гиперболический секанс z.
coth (z)	Возвращает 1/tanh(z), гиперболический котангенс z.
asinh (z)	Возвращает число, чей гиперболический синус — z.
acosh (z)	Возвращает число, чей гиперболический косинус — z.
atanh (z)	Возвращает число, чей гиперболический тангенс — z.

Логарифмические и показательные функции

Логарифмические и показательные функции Mathcad могут использовать комплексный аргумент и возвращать комплексные значения. Значения экспоненциальной функции для комплексного аргумента вычисляются с применением формулы

e x+iy =e x (cos(y) + isin(y))

Вообще говоря, значения натурального логарифма даются формулой

ln(x + iy)=ln|x + iy|+ atan(y/x)i + 2n p i

В Mathcad функция ln возвращает значение, соответствующее n = 0. А именно:

ln(x + iy)=ln|x + iy|+ atan(y/x)i

Оно называется основным значением логарифма. Рисунок 1 иллюстрирует некоторые основные свойства логарифма.

На Рисунке 1 показано, как можно использовать эти функции для вычисления логарифма по любому основанию.

Рисунок 1: Использование логарифмических функций.

Эти функции обычно возникают как решения для волнового уравнения, подчиненного цилиндрическим граничным условиям.

Функции Бесселя первого и второго рода, J_n(x) и Y_n(x), являются решениями для дифференциального уравнения

Модифицированные функции Бесселя первого и второго рода, I_n(x) и K_n(x), являются решениями для немного видоизмененного уравнения:

J0(x)	Возвращает J₀(x); x вещественный.
J1(x)	Возвращает J₁(x); x вещественный.
Jn(m, x)	Возвращает J_n(x); x вещественный, 0m100.
Y0(x)	Возвращает Y₀(x); x вещественный, x > 0.
Y1(x)	Возвращает Y₁(x); x вещественный, x > 0.
Yn(m, x)	Возвращает Y_n(x). x > 0, 0m100
I0(x)	Возвращает I₀(x); x вещественный.
I1(x)	Возвращает I₁(x); x вещественный.
In(m, x)	Возвращает I_n(x); x вещественный, 0m100.
K0(x)	Возвращает K₀(x); x вещественный, x > 0.
K1(x)	Возвращает K₁(x); x вещественный, x > 0.
Kn(m, x)	Возвращает K_n(x). x > 0, 0m100

Следующие функции возникают в широком круге задач.

x должен быть вещественным. G (z) Возвращает значение эйлеровой гамма-функции в z. Для вещественного z значения этой функции совпадают со следующим интегралом:

Для комплексных z значения — аналитическое продолжение вещественной функции. Гамма-функция Эйлера неопределена для z= 0,-1,-2, .

Гамма-функция Эйлера удовлетворяет рекуррентному соотношению

Откуда следует для положительных целых z:

Интеграл ошибок часто возникает в статистике. Он может также быть использован для определения дополнения интеграла ошибок по формуле:

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник статьи: http://old.exponenta.ru/SOFT/MATHCAD/UsersGuide/chapter12/12_2.asp

Как задать арктангенс в маткаде

10.4. Тригонометрические функции (Trigonometric)

acos(z) —арккосинус;
acot(z) — котангенс;
acsc(z) — арккосеканс (листинг 10.4);
angle(x,y) — угол между точкой (х,у) и осью ох;
asec(z) — арксеканс;
asin(z) — арксинус (листинг 10.4);
atan (z) — арктангенс;
atan2(x,y) — угол, отсчитываемый от оси ОХ до точки (х,у) (листинг 10.5);
cos(z) —косинус;
cot(z) — котангенс;
csc(z) — косеканс (листинг 10.4);
sec(z) —секанс;
sin(z) — синус (листинг 10.4);
tan(z) — тангенс;

z — безразмерный скаляр.

Аргумент тригонометрических функций и результат обратных тригонометрических функций выражаются в радианах. Чтобы использовать значение угла в градусах, его необходимо перевести в радианы (листинг 10.6). Аргумент тригонометрических функций может быть комплексным.

Листинг 10.4. Примеры тригонометрических функций

Листинг 10.5. Примеры расчета угла между прямой и осью OX

Листинг 10.6. Расчет тригонометрических функций в градусах

Листинг 10.4. Примеры тригонометрических функций

Листинг 10.5. Примеры расчета угла между прямой и осью OX

Листинг 10.6. Расчет тригонометрических функций в градусах

Когда тот или иной физик использует понятие «физический вакуум», он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.

Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.

Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование «моря» двух компенсирующих друг друга энергий в вакууме — положительной и отрицательной, а также «моря» компенсирующих друг друга частиц — виртуальных (то есть кажущихся) электронов и позитронов в вакууме.

Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом — присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.

БАЗОВЫЕ ОПЕРАЦИИ.
РАНЖИРОВАННЫЕ ПЕРЕМЕННЫЕ. ФУНКЦИИ. ГРАФИКИ
МАССИВЫ

1 Запуск. Формульные и текстовые области

Запуск Mathcad: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).

Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:

Для ввода математических символов: View / Toolbars / Math (Вид / Панели инструментов / Математическая).

Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!

Перемещение курсора — клавиша Пробел. Изменение направления уголка — клавиша Insert (Ins).

«:=» — «присвоить» — задать выражение (число или формулу)

«=» — «вычислить» подсчитать и вывести значение выражения.

Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.

2 Ранжированные переменные. Функции. Графики

В Mathcad существует тип переменных, принимающих не одно, а множество значений. Такие переменные носят название ранжированных или дискретных. Ранжированная переменная – переменная, которая принимает ряд значений при каждом ее использовании, причем каждое значение отличается от соседнего на постоянную величину, называемую шагом.

Ранжированная переменная общего вида определяется выражением:

Имя := x1, x2 .. xn

Здесь Имя – задаваемое пользователем имя ранжированной переменной;
x1 – первое значение ранжированной переменной;
x2 – второе значение ранжированной переменной (x2 = x1 + Dx — первое значение плюс шаг);
xn – последнее значение ранжированной переменной.
Значения x1 и x2 разделяются запятой, двоеточие представляет собой единый оператор, указывающий на изменение переменной в заданных пределах. Он вводится с клавиатуры клавишей «;» или выбирается с палитры математических инструментов Matrix (Векторы и матрицы) (кнопка — Range Variable).

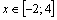
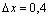
Например, если переменная изменяется в интервале с шагом , то она задается в виде

Шаг изменения значений ранжированной переменной в явном виде обычно не задается, он определяется как x2 – x1.

Функции в системе Mathcad можно условно разделить на две группы: встроенные и функции пользователя. Встроенные функции изначально заданы в системе разработчиками. Имя функции вводится с клавиатуры, обычно в нижнем регистре. Полный перечень встроенных функций можно получить, выполнив команду Function (Функция) главного меню Insert (Вставка), или нажав на кнопку панели инструментов. При этом появляется окно, где справа перечислены возможные категории функций, а слева – список функций из выделенной категории.

Среди наиболее часто используемых функций можно указать:

sin(z) — синус z (z задается в радианах);
cos(z) — косинус z;
tan(z) — тангенс z;
cot(z) — котангенс z;
exp(z) – экспоненциальная функция, значение е (основание натурального логарифма) в степени z;
ln(z) – натуральный логарифм z;
log(z) – десятичный логарифм числа z;
log(z, b) – логарифм числа z по основанию b;
acos(z) – арккосинус z;
acot(z) – арккотангенс z;
asin(z) – арксинус z;
atan(z) – арктангенс z.

Функция пользователя сначала должна быть определена, а затем к ней можно обращаться при вычислениях, записи алгебраических выражений, построении графиков и т. п. Функция пользователя определяется

Имя(список аргументов) := Выражение

Сначала задается имя функции, в круглых скобках указывается список аргументов функции (перечень используемых переменных), разделяемых запятыми. Затем вводится оператор присваивания. Справа от него записывается выражение, содержащее доступные системе операторы, операнды и функции с аргументами, указанными в списке аргументов.

Обращение к функции осуществляется по ее имени с подстановкой на место аргументов констант, переменных, определенных до обращения к функции, и выражений.

Основные виды графиков и инструменты для работы с ними находятся на палитре математических инструментов Graph (График).

Для построения графика функции одной переменной в декартовой системе координат в Mathcad:

определяется функция пользователя;
задается ранжированная переменная на некотором диапазоне с мелким шагом;
вставляется шаблон двумерного графика X-Y Plot;
в знакоместо по оси абсцисс записывается имя переменной, а в знакоместо по оси ординат — функция или имя ранее определенной функции;
производится щелчок левой клавишей мыши вне области графика.

Примечание — Для построения в одной координатной плоскости графиков двух и более функций их имена или определяющие выражения перечисляются в знакоместе по оси ординат через запятую.

Массив в пакете Mathcad – это совокупность конечного числа упорядоченных пронумерованных элементов, которая может иметь уникальное имя. Обычно используют одномерные (векторы) и двумерные (матрицы) массивы, содержащие числовые, символьные или строковые данные.

– вектор-столбец; – вектор-строка.

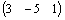
Порядковый номер элемента называется индексом. Местоположение элемента в массиве задается одним индексом для вектора и двумя – для матрицы. Номер первого элемента массива определяется значением системной переменной ORIGIN. По умолчанию ORIGIN = 0 и может принимать только целые значения. Изменение значения этой системной переменной осуществляется последовательностью команд Math / Options… / Built-In Variables / Array Origin (ORIGIN) (Математика / Параметры / Встроенные переменные / Начальный индекс массивов) или переопределением в документе, например:

Существует несколько способов создания массивов.

1-й способ. Использование панели Matrix (Матрицы).

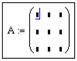
Сначала набирается имя массива и оператор присваивания, например, 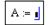. Далее на панели Math (Математика) выбираем кнопку Matrix (Матриц):

Далее указываем количество ее строк m (Rows) и столбцов n (Columns) матрицы. Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-строку, а при n = 1 – вектор-столбец.

На месте курсора появится шаблон, в знакоместа которого вводятся значения элементов массива:

2-й способ. Использование ранжированной переменной.

Целочисленные ранжированные переменные используются для задания индексов и позволяют создавать массивы в следующем порядке:

определяется системная переменная ORIGIN;
задается ранжированная переменная (переменные) для нумерации элементов;
индексированной переменной присваиваются значения элементов массива через запятую или в виде явной формулы.

Обращаться к отдельным элементам вектора или матрицы можно, используя нижний индекс, принимающий только целочисленные значения. Для ввода нижнего индекса после имени вектора или матрицы нажимается клавиша «[» (прямая открывающая скобка) либо используется пиктограмма с палитры математических инструментов Matrix. Для элемента матрицы указываются через запятую два индекса, обозначающих номер строки и номер столбца соответственно.

Для работы с векторами и матрицами система Mathcad имеет ряд специальных операторов и команд (представленных в таблице 1), используя которые не следует забывать об общих правилах матричного исчисления.

Таблица 1 – Команды палитры инструментов Matrix (Матрица)

Источник статьи: http://mnogotolka.ru/info/kak-zadat-arktangens-v-matkade/

Источник

0 / 0 / 0

Регистрация: 18.05.2017

Сообщений: 1

Посчитать значение арктангенса в градусах

22.11.2017, 18:28. Показов 10657. Ответов 2

Доброго времени суток
В процессе решения возник вопрос: как сделать, чтобы в правой части арктангенс появился в численном значении и при том в градусах?

1501 / 1022 / 159

Регистрация: 12.06.2012

Сообщений: 2,084

23.11.2017, 09:46

Прикрепите к сообщению файл Mathcad в архиве.

1767 / 971 / 180

Регистрация: 24.02.2013

Сообщений: 2,790

Записей в блоге: 12

23.11.2017, 09:50

См.картинку.

Миниатюры

Источник

Продолжение табл. П.1

Операция		Клавиши			Пример
Нижний индекс матрицы или вектора	[			A1,2
Сумма элементов вектора		Ctrl + 4
Транспонирование матрицы		Ctrl + 1			MT
Диапазон изменения в цикле		;		A	0..100
Добавить график в двумерных декар-	Shift + 2
товых координатах
Добавить график в трехмерных де-	Ctrl + 2
картовых координатах
Добавить график в двумерных круго-	Ctrl + 7
вых координатах
Добавить график линий уровня		Ctrl + 5
Добавить линию для подпрограммы	]
Определить переменную в подпро-	{			см. рис.
грамме
					П.15
Условный оператор if		}

Цикл for		Ctrl + “
	Таблица П.2

					Описание
Функция	Обращение
Тригонометрические функции
Синус	sin(x)
Косинус	cos(x)		х – аргумент (в радиа-
Тангенс	tan(x)		нах)
Котангенс	cot(x)
Арксинус	asin(x)		х – аргумент
				( −1 ≤ x ≤1)
Арккосинус	acos(x)
				х – аргумент
Арктангенс	atan(x)
Гиперболические функции
Синус гиперболический	sinh(x)
Косинус гиперболический		cosh(x)	х – аргумент (в радианах)
Тангенс гиперболический		tanh(x)
		157

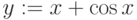
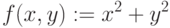
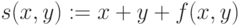
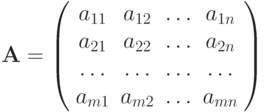
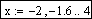
Источник