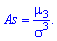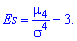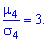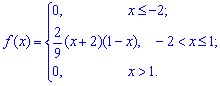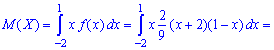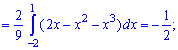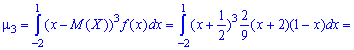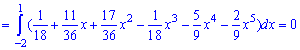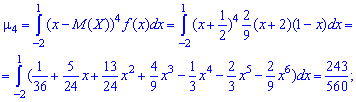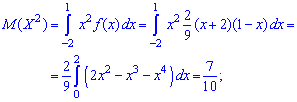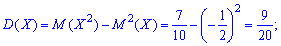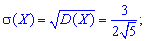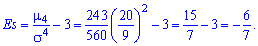Коэффициент асимметрии. Эксцесс распределения
Краткая теория
При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.
Асимметрией теоретического распределения называют отношение
центрального момента третьего порядка к кубу среднего квадратического
отклонения:
Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию. Асимметрия положительна,
если «длинная часть» кривой распределения расположена справа от математического
ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева
от математического ожидания.
На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию
,
а кривая II – отрицательную (левостороннюю)
.
Кроме вышеописанного коэффициента, для характеристики асимметрии
рассчитывают также показатель асимметрии Пирсона:
Коэффициент асимметрии Пирсона характеризует асимметрию только в
центральной части распределения, поэтому более распространенным и более точным
является коэффициент асимметрии, рассчитанный на основе центрального момента третьего
порядка.
Для оценки «крутости», т. е. большего или меньшего подъема кривой
теоретического распределения по сравнению с нормальной кривой, пользуются
характеристикой — эксцессом.
Эксцессом (или коэффициентом эксцесса) случайной величины
называется число:
Число 3 вычитается из отношения
потому, что для наиболее часто встречающегося
нормального распределения отношение
.
Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные — отрицательным
эксцессом.
Примеры решения задач
Задача 1
Для заданного
вариационного ряда вычислить коэффициенты асимметрии и эксцесса.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим расчетную
таблицу
Средняя:
Найдем моду — варианту, которой соответствует наибольшая частота.
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии Пирсона:
Коэффициент асимметрии можно найти по формуле:
Центральный момент
3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Центральный момент
4-го порядка:
Получаем:
Задача 2
Для заданного
вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и
эксцесса методом произведений, используя условные моменты.
Решение
Составим расчетную таблицу
Перейдем к условным вариантам
В качестве ложного нуля возьмем
3-ю варианту
0
Условные варианты вычислим по
формуле:
где
4
(разность между соседними вариантами)
Условный момент 1-го порядка:
Средняя:
Условный момент 2-го порядка:
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент асимметрии можно найти
по формуле:
Условный момент 3-го порядка:
Центральный момент 3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Условный момент 4-го порядка:
Центральный момент 4-го порядка:
Получаем:
Асимметрия и эксцесс
В прикладных
задачах, например в математической
статистике, при теоретическом изучении
эмпирических
распределений, отличающихся от
нормального распределения, возникает
необходимость количественных оценок
этих различий. Для этой цели введены
специальные безразмерные характеристики.
Определение 6.
Асимметрией
теоретического распределения называется
отношение центрального момента третьего
порядка к кубу среднего квадратического
отклонения:
Определение 7.
Эксцессом
теоретического распределения называется
величина, определяемая равенством
где μ4
— центральный момент четвертого порядка.
Для нормального
распределения
As
= Еk
= 0. При
отклонении от нормального распределения
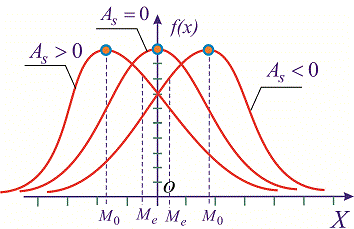
асимметрия положительна, если «длинная»
и более пологая часть кривой распределения
расположена справа от точки на оси
абсцисс, соответствующей моде; если
эта часть кривой расположена слева от
моды, то асимметрия отрицательна (рис.
18.7, а, б).
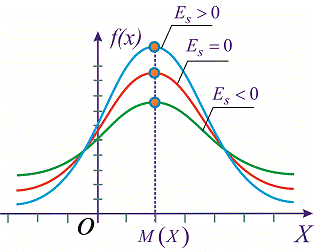
Эксцесс характеризует
«крутизну» подъема кривой
распределения по сравнению с нормальной
кривой: если эксцесс положителен, то
кривая имеет более высокую и острую
вершину;
в случае
отрицательного эксцесса сравниваемая
кривая имеет более низкую и пологую
вершину (рис. 18.7, в).
Следует иметь в
виду, что при использовании указанных
характеристик сравнения опорными
являются предположения об одинаковых
величинах математического ожидания и
дисперсии для нормального и
теоретического распределений.
Пример 5.
Пусть дискретная случайная величина Х
задана законом следующего распределения:
Найти асимметрию
и эксцесс теоретического распределения.
Решение.
Найдем сначала математическое ожидание
случайной величины:
Затем вычисляем
начальные и центральные моменты 2, 3 и
4-го порядков и среднее квадратическое
отклонение (см. формулы (18.27)-(18.31)):
Теперь по формулам
(18.45) и (18.46) находим искомые величины:
В данном случае
«длинная» часть кривой распределения
расположена справа от моды, причем
сама кривая является несколько более
островершинной, чем нормальная кривая
с теми же величинами математического
ожидания и дисперсии.
18.6. Некоторые элементы математической статистики Задачи математической статистики
Первой задачей
математической статистики является
указание методов сбора и группировки
статистических сведений, которые
получены в результате экспериментов
или наблюдений. Вторая задача — это
разработка методов анализа статистических
данных: оценки неизвестных вероятности
события, а также функции и параметров
распределения; оценка зависимости
случайной величины от других случайных
величин; проверка статистических гипотез
о виде и величинах параметров
неизвестного распределения. Рассмотрим
некоторые из этих вопросов.
Выборки
На практике сплошное
исследование (каждого объекта из
интересующей нас совокупности) проводят
крайне редко. К тому же если эта
совокупность содержит большое число
объектов или исследование объекта
требует нарушения его функционального
стандарта, то сплошное исследование
нереально. В таких случаях из всей
совокупности случайно отбирают
ограниченное число объектов и
подвергают их исследованию.
Введем основные
понятия, связанные с выборками.
Генеральной
совокупностью
называется совокупность объектов, из
которых производится выборка. Выборочной
совокупностью (выборкой)
называется совокупность случайно
отобранных объектов из генеральной
совокупности. Число объектов в совокупности
называется ее объемом.
Пример 1.
Пусть из 2000 изделий отобрано для
обследования 100 изделий. Тогда объем
генеральной совокупности N
= 2000, а объем
выборки п
= 100.
Выборку можно
осуществлять двумя способами. Если
после исследования объект из выборки
возвращается в генеральную совокупность,
то такая выборка называется повторной;
если объект не возвращается в генеральную
совокупность, то выборка называется
бесповторной.
Выборка называется
репрезентативной
(представительной), если по ее данным
можно достаточно уверенно судить об
интересующем признаке генеральной
совокупности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
The measure of skewness tells us the direction and the extent of skewness. In symmetrical distribution the mean, median, and mode are identical. the more the mean moves away from the mode, the larger the asymmetric or skewness.
Before learning let’s learn more about Mean, Median, and Mode first.
Mean
Mean is the average of the numbers in the data distribution, It is calculated by adding up all the values in the dataset and dividing the sum by the number of values in the dataset.
Mean= Sum of all values in Dataset / Total number of values
Example: Find the mean of a dataset of exam scores: 70, 80, 85, 90, and 95.
Solution:
Mean = (70 + 80 + 85 + 90 + 95) / 5 = 84
So the mean of this dataset is 84.
Median
When arranging all the data in order (ascending and descending) the comes in the middle of the data is called the median.
Median is the middle value of a dataset when the values are arranged in order from smallest to largest.
Examples for Odd Numbers in the Dataset
Example 1: Find the median of a dataset of exam scores: 70, 85, 80, 95, 90
Solution:
Firstly arrange all no. in order from smallest to largest: 70, 80, 85, 90, 95.
The mid value is 85. so, the median is 85.
Example 2: Find the median of a dataset: 5, 10, 15, 20, 25.
Solution:
Firstly arrange all no. in order from smallest to largest: 5, 10, 15, 20, 25.
The mid value is 15. so, the median is 15.
If there are an even number of values in the dataset, the median is calculated by taking the average of the two middle values.
Examples for Even Numbers in the Dataset
Example 1: Find the median of a dataset of exam scores: 70, 80, 85, 90.
Solution:
The median is calculated as (80 + 85) / 2 = 82.5
So the median of this dataset is 82.5.
Example 2: Find the median of a dataset: 2, 4, 6, 8, 10, 12.
Solution:
Firstly, we need to find the middle two numbers. So, 6, and 8 are mid values of the dataset
Median = (6 +
/ 2 = 7
So the median of this dataset is 7.
Mode
most frequently used number in data is called the mode of the data.
Example 1: We have a data set representing the number of pets owned by 10 people: 3, 1, 0, 2, 1, 1, 4, 2, 2, 1. Find the mode.
Solution:
So, the value that appears most frequently in the data set is 1. the value 1 appears four times. Therefore, the mode of this data set is 1.
Skewness Formula
The skewness formula is discussed in the image below,
Type of Skewness
Various types of skewness used in mathematics are,
- Positive Skewness
- Negative Skewness
- Zero Skewness
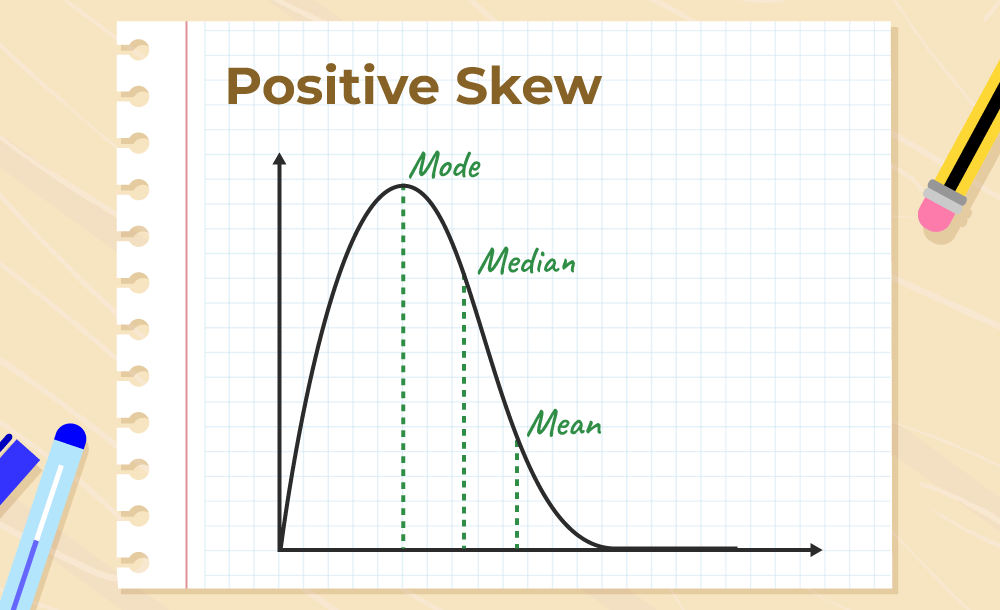
Positive Skewness
Positive Skewness means the tail on the right side of the distribution is longer. The mean and median will be greater than the mode.
Condition for positive skewness = Mean > Median >Mode
The positive curve of skewness is shown in the image below,
Let’s take an example of the income distribution where a few people earn very high incomes and the majority earn lower incomes. so, this is often positively skewed. Analyzing skewed data can provide valuable insights into the underlying causes and potential solutions or interventions.
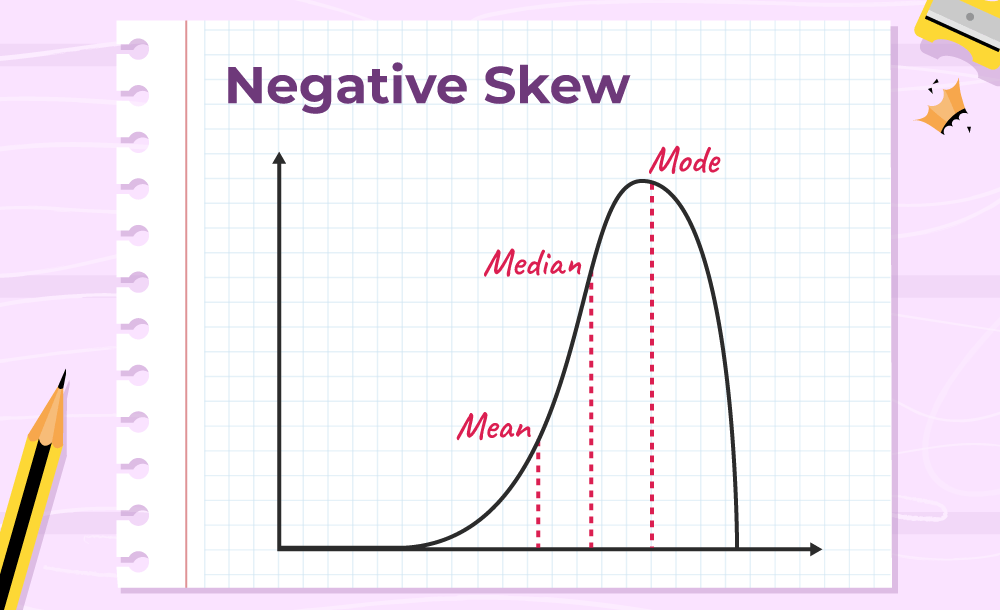
Negative Skewness
Negative Skewness means when the tail of the left side of the distribution is longer than the tail on the right side. The mean and median will be less than the mode.
Condition for negative skewness is Mode > Median > Mean
The curve shows negative skewness in the image below,
Let’s take an example of a match, during the match most of the players of a particular team scored runs above 50 and only a few of them scored below 10. In such a case, the data is generally represented with the help of a negatively skewed distribution. And this data is helpful to analyze the game’s performance.
Zero Skewness
It is also known as a “symmetric distribution”.It signifies that distribution of data is evenly distributed around the mean, with no long tails on either end of the distribution
Condition for zero skewness is Mean = Mode = Median
The curve for zero skews is shown in the image below,
Methods to Measure Skewness
Skewness can be measured using Karl Pearson’s Coefficient of Skewness.
Karl Pearson’s Co-efficient of Skewness
The formula for measuring Skewness using Karl Pearson’s Co-efficient is discussed below in the image,
Conditions
- Mean = Mode = Median, then the coefficient of skewness is zero for symmetrical distribution.
- Mean > Mode, then the coefficient of skewness will be positive.
- Mean < Mode, then the coefficient of skewness will be negative.
Karl person`s coefficient of skewness has a positive sign for the positively skewed and a negative sign for the negatively skewed.
Read More,
- Bayes’ Theorem
- Mean
Solved Examples on Skewness Formula
Example 1: Find the skewness for the given Data ( 2,4,6,6)
Solution:
Mean of Data = (2 + 4 + 6 + 6) / 4
= 18 / 4
= 4.5
Number of terms (n) = 4 (even)
Median of Data = {[n / 2]th + [n / 2 + 1]th}/2 term
= [(4 /2)th term + (4/2 +1)th term] / 2
= [2nd term + 3rd term] / 2
= [4+6]/2
= 10/2
Median of Data = 5
Mode of Data = Highest Frequency term = 6 (frequency 2)
S.D. = √[(2 – 5)2 + (4-5)2 + (6-5)2 + (6-5)2/4]
= √[(9 + 1 + 1 + 1)/4]
= √(3)
= 1.732
Skewness = 3(Mean – Median)/S.D.
By Applying Skewness Formula,
Skewness = 3(4.5 – 5)/1.732
= 3(-0.5)/ 1.732
Skewness = – 0.866
So, the skewness of these data is negative.
Example 2: A boy collects some rupees in a week as follows (25,28,26,30,40,50,40) and finds the skewness of the given Data in question with the help of the skewness formula.
Solution:
Mean of Data = (25+28+26+30+40+50+40) / 7
= 239 / 7
= 34.14
Number of terms (n) =7 (odd)
Arrange Data in ascending order = 25,26 ,28,30,40,40,50
The median of data is = 30
Mode of Data = Highest Frequency term = 40 (frequency 2)
S.D = √(1/7 – 1) x ((25 – 34.1429)2 + (28 – 34.1429)2 + (26 – 34.1429)2 + (30 – 34.1429)2 + (40 – 34.1429)2 +(534.1429)2 + (40 – 34.1429)2)
= √(1/6) x ((-9.1429)2 + (-6.1429)2 + (-8.1429)2 + (-4.1429)2 + (5.8571)2 + (15.8571)2 + (5.8571)2)
= √(0.1667) x ((83.5926) + (37.7352) + (66.3068) + (17.1636) + (34.3056) + (251.4476) + (34.3056))
= √(0.1667) x 524.8571
= √87.4762
. = 9.3529Skewness = 3(Mean – Median)/S.D.
By Applying Skewness Formula,
Skewness = 3(34.14 – 30)/9.3529
= 1.32
Skewness = 1.32
So skewness for these data is positive
Example 3: Attendance of all classes of a school are as follows find their skewness?
1st (35), 2nd(32), 3rd(38), 4th(39), 5th(43)
| Class Name | Number of students |
|---|---|
| 1 st | 35 |
| 2 nd | 32 |
| 3 rd | 38 |
| 4 th | 39 |
| 5 th | 45 |
Solution:
Mean of Data = (35 + 32 + 38 + 39 + 42)/5
= 186/5
= 37.2
Number of terms (n) = 5 (odd)
Arrange Data in ascending order = 32,35,38,39,42
Median of Data = 38
S.D. = √(1/5 – 1) x ((35 – 37.2)2 + (32 – 37.2)2 + (38 – 37.2)2 + (39 – 37.2)2 + (42 – 37.2)2)
= √(1/4) x ((-2.2)2 + (-5.2)2 + (0.8)2 + (1.8)2 + (4.8)2)
= √(0.25) x ((4.84) + (27.04) + (0.64) + (3.24) + (23.04))
= √(0.25) x 58.8
= √14.7
= 3.8341Skewness = ∑(yi – ymean) / (n – 1) x (sd)³
Skewness =((35 – 37.2)³ + (32 – 37.2)³ + (38 – 37.2)³ + (39 – 37.2)³ + (42 – 37.2)³) / (5 – 1)³ x 3.8341
Skewness = ((-2.2)³ + (-5.2)³ + (0.8)³ + (1.8)³ + (4.8)³ )/ (4)³ x 3.8341
Skewness =((-10.648) + (-140.608) + (0.512) + (5.832) + (110.592)) / 64 x 3.8341
Skewness =-34.32 / 245.3824
Skewness = -0.1522
So, the skewness of these data is negative.
FAQs on Skewness
Q1: Can skewness be zero?
Answer:
Yes, skewness can be zero. This occurs when the distribution is perfectly symmetrical. It is possible if there are an equal number of values on the left and right sides of the mean.
Q2: What does positive skewness mean?
Answer:
Positive skewness means the distribution is skewed to the right. There are more values on the right side of the mean than on the left side.
Condition for Positive Skewness = Mean > median >mode
Q3: What does negative skewness mean?
Answer:
Negative skewness means the distribution is skewed to the left. There are more values on the left side of the mean than on the right side.
Condition for negative skewness = Mode > median > mean
Q4: How is skewness used in finance and investment analysis?
Answer:
In finance and investment analysis, skewness is used to measure the degree of asymmetry in returns on investment. Skewed returns can have an impact on portfolio management and risk management strategies, and understanding the skewness of a particular investment can help investors to make better-informed decisions.
Q5: What is the formula for calculating skewness?
Answer:
The formula used to calculate Skewness is,
Skewness Formula= 3(Mean – Median)/S.D.
Q6: How is skewness used in hypothesis testing?
Answer:
Skewness is used in hypothesis testing to determine whether a sample of data is normally distributed or not. If the skewness value is close to zero, the data is likely to be normally distributed. If the skewness value is positive or negative, the data is likely to be skewed and may require non-parametric tests for hypothesis testing.
В прикладных задачах, например в математической статистике, при теоретическом изучении Эмпирических распределений, отличающихся от нормального распределения, возникает необходимость количественных оценок этих различий. Для этой цели введены специальные безразмерные характеристики.
Определение 6. Асимметрией теоретического распределения называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
Определение 7. Эксцессом теоретического распределения называется величина, определяемая равенством
Где μ4 — центральный момент четвертого порядка.
Для нормального распределения As = Еk = 0. При отклонении от нормального распределения асимметрия положительна, если «длинная» и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствующей моде; если эта часть кривой расположена слева от моды, то асимметрия отрицательна (рис. 18.7, А, б).
Эксцесс характеризует «крутизну» подъема кривой распределения по сравнению с нормальной кривой: если эксцесс положителен, то кривая имеет более высокую и острую вершину; в случае отрицательного эксцесса сравниваемая кривая имеет более низкую и пологую вершину (рис. 18.7, В).
Следует иметь в виду, что при использовании указанных характеристик сравнения опорными являются предположения об одинаковых величинах математического ожидания и дисперсии для нормального и теоретического распределений.
Пример 5. Пусть дискретная случайная величина Х задана законом следующего распределения:
Найти асимметрию и эксцесс теоретического распределения.
Решение. Найдем сначала математическое ожидание случайной величины:
Затем вычисляем начальные и центральные моменты 2, 3 и 4-го порядков и среднее квадратическое отклонение (см. формулы (18.27)-(18.31)):
Теперь по формулам (18.45) и (18.46) находим искомые величины:
В данном случае «длинная» часть кривой распределения расположена справа от моды, причем сама кривая является несколько более островершинной, чем нормальная кривая с теми же величинами математического ожидания и дисперсии.
| < Предыдущая | Следующая > |
|---|
Вычисление асимметрии и эксцесса позволяет установить симметричность распределения случайной величины 
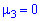
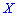
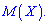
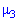
Центральный момент четвертого порядка используется для определения эксцесса, характеризует плосковершиннисть или гостровершиннисть плотности вероятности 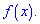
Число 3 вычитается для сравнения отклонения от центрального закона распределения (нормального закона), для которого подтверждается равенство:
Итак, 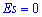
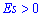
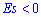
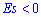
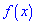
Приведу Вам один из распространенных примеров.
Пример 1. Дана плотность вероятностей:
Вычислить асимметрию и эксцесс 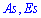
Решение. Вычисляем математическое ожидание случайной величины
после этого — третий момент инерции
Поскольку момент нулевой 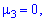
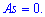
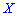
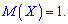
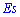
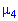

По найденным значениям вычисляем дисперсию
после нее среднее матиматичне отклонения
Окончательно получим
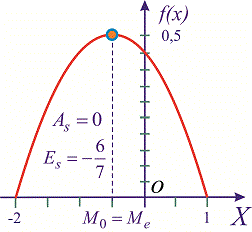
отрицательный эксцесс, что указывает на пологость функции распределения. Сам график функции с найденными величинами приведен на рисунку ниже
—————————————
Хорошо разберите приведенный пример, все другие подобные. Найти асимметрию и эксцесс довольно легко тем, кто хорошо умеет интегрировать и не спешит при вычислениях.

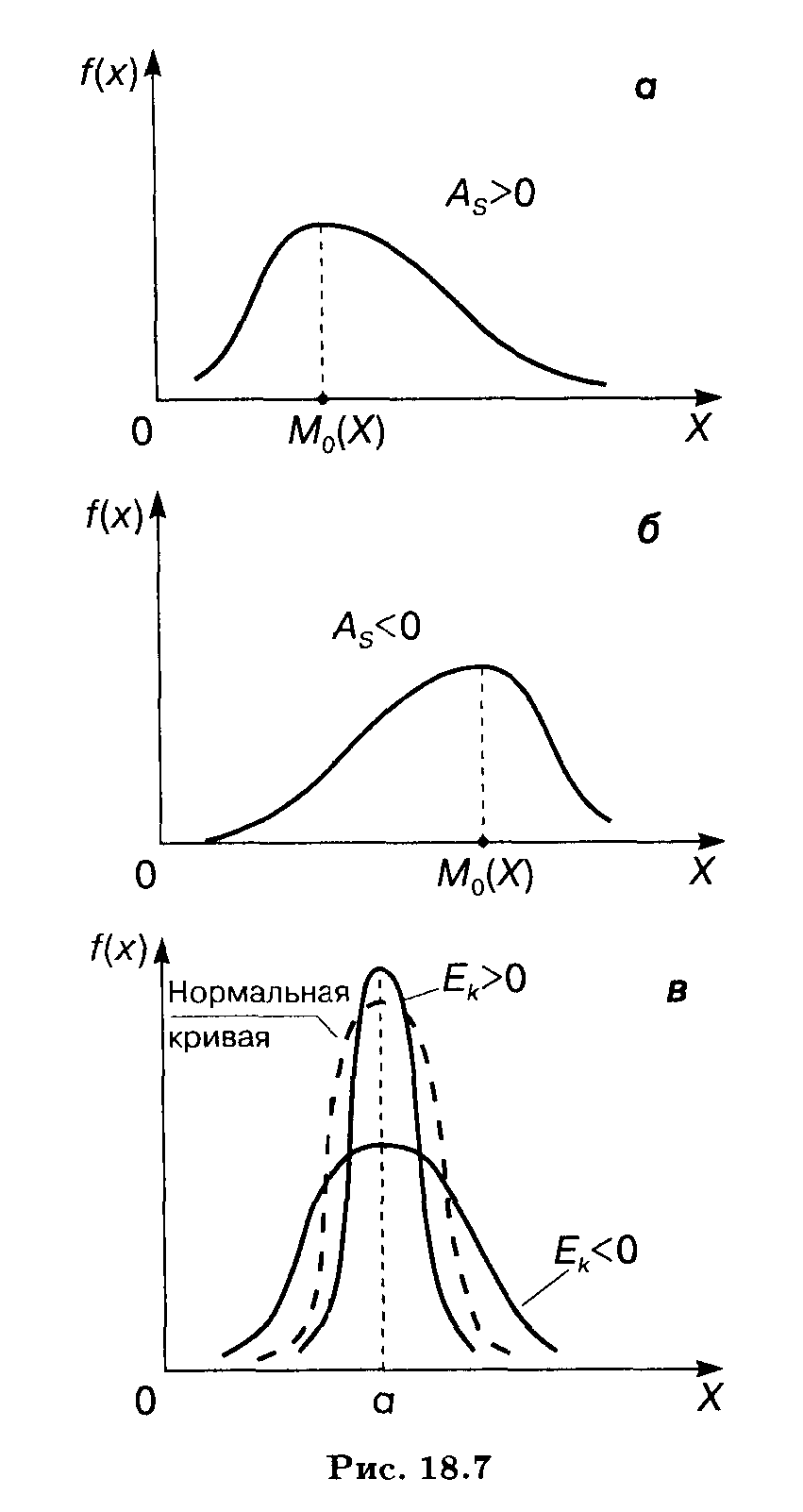


 / 2 = 7
/ 2 = 7