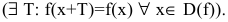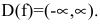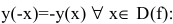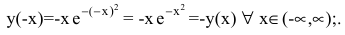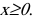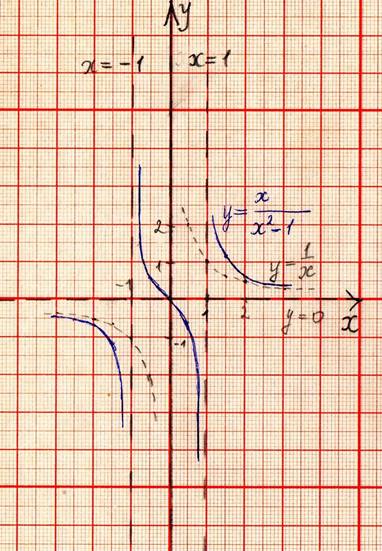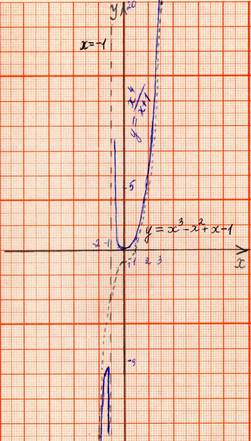Асимптоты графика функции. График дробно-линейной функции
Асимптоты графика функции. График дробно-линейной функции.
В этой статье мы рассмотрим, что такое асимптота графика функции, и как ее находить.
Асимптота – это прямая, к которой бесконечно близко приближается график функции.
Асимптоты бывают горизонтальные, вертикальные и наклонные.
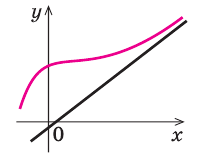
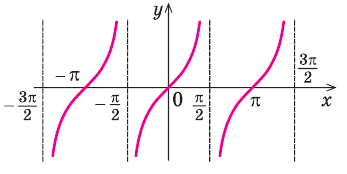
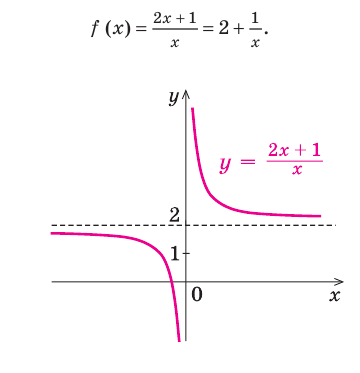
Если мы посмотрим на хорошо известный нам график функции 


В общем случае горизонтальная асимптота — это прямая, параллельная оси OX. Уравнение горизонтальной асимптоты имеет вид 




То есть 
Вертикальная асимптота — это прямая, параллельная оси OY. Уравнение вертикальной асимптоты имеет вид 




В некоторых случаях для построения графика функции бывает достаточно найти асимптоты графика.
Рассмотрим дробно-линейную функцию. В общем виде уравнение дробно-линейной функции имеет вид: 
График дробно-линейной функции — это гипербола. Как мы знаем, гипербола имеет две асимптоты: горизонтальную и вертикальную.
Заметим, что при 


Степень 





График дробно-линейной функции 
Для этого достаточно найти точки пересечения графика с осями координат.
Точка пересечения с осью OX (y=o): 
Точка пересечения с осью OY (x=0): 
Построим график функции 
Найдем горизонтальную и вертикальную асимптоты.
Уравнение горизонтальной асимптоты: 
уравнение вертикальной асимптоты (ноль знаменателя):
Найдем точки пересечения с осями координат:
С осью ОХ: 
с осью OY(x=0): 
То есть график функции 
И, наконец, наклонная асимптота. Наклонная асимптота — это к прямая, к кторой стремится график функции на бесконечности.
Уравнение наклонной асимптоты имеет вид 
Коэффициенты 

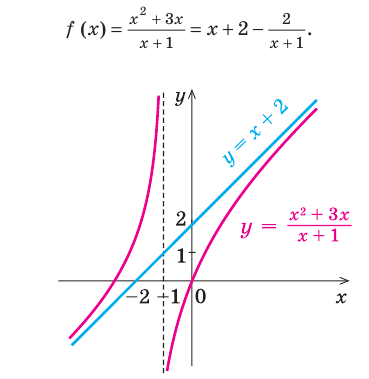
Найдем асимптоты графика функции
1. Начнем с области определения функции. Функция 


2. Степень числителя дроби 


3. Попробуем найти наклонную асимптоту.
(Предел функции равен отношению коэффициентов при максимальных степенях 


Итак, уравнение наклонной асимптоты:
График функции 
И.В. Фельдман, репетитор по математике.
Содержание:
Понятие асимптоты:
Асимптота кривой — это прямая, к которой неограниченно приближается кривая при ее удалении в бесконечность.
Вертикальные асимптоты

Вертикальная асимптота 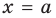
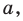
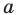
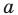
Примеры вертикальных асимптот графиков функций
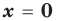
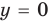
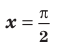
Наклонные и горизонтальные асимптоты
I. Если 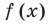
Примеры:
При 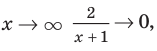
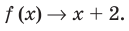
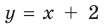
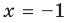
При 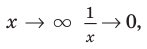
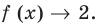
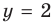
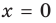
II. В общем случае уравнения наклонных и горизонтальных асимптот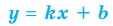
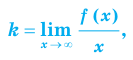
Понятие асимптоты
Если кривая 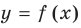
Асимптоты могут быть вертикальными, горизонтальными или наклонными.
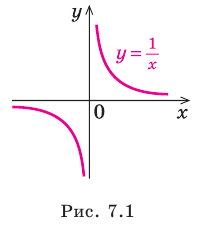
Например, для графика функции 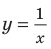
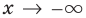
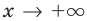
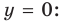
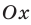
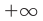
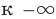
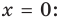
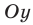
Если рассмотреть функцию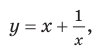
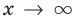
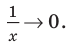
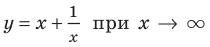
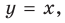
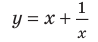
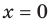
Следует отметить, что не любая кривая имеет асимптоту, поэтому не у каждого графика функции будет асимптота. Но исследование функции на наличие у ее графика асимптот позволяет уточнить свойства функции и поведение ее графика.
Вертикальные асимптоты
Если прямая 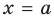
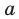

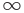
Например, у функции 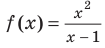
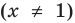

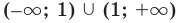

Аналогично
Таким образом, прямая 

Отметим, что не всегда в точке разрыва области определения функция будет иметь вертикальную асимптоту. Например, функция 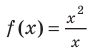
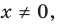
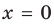
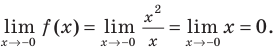
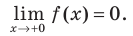
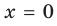
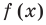
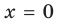
Наклонные и горизонтальные асимптоты
Наклонные и горизонтальные асимптоты довольно просто находятся для графиков дробно-рациональных функций, у которых степень числителя на единицу больше степени знаменателя (или равна степени знаменателя). Для этого достаточно выделить целую часть заданной дроби и использовать определение асимптоты.
Например, еще раз рассмотрим функцию 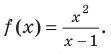
При 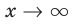
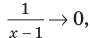
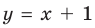
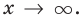
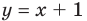
Рассмотрим, как находятся наклонные и горизонтальные асимптоты в общем случае.
Пусть наклонной (или горизонтальной) асимптотой графика функции 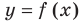

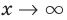
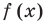
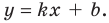
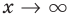
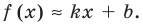
Эта равенство не нарушится, если обе его части разделить на 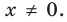
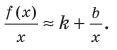
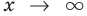
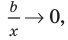
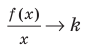
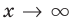
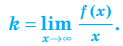
Возвращаясь к формуле (1), получаем, что при 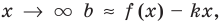
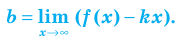
Формулы (2) и (3) дают возможность находить наклонные и горизонтальные асимптоты для графика любой функции 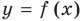
Отметим, что если у графика функции 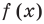
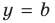
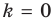
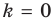
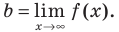
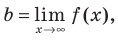
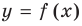
- Заказать решение задач по высшей математике
Пример:
Пользуясь общими формулами, найдите наклонную асимптоту графика функции
Решение:
Будем искать наклонную асимптоту в виде 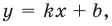
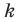
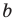
Асимптотой графика данной функции будет прямая 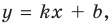
Пример:
Найдите асимптоты графика функции
Решение:
Область определения функции: 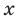
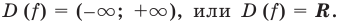
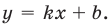
Таким образом, заданная функция имеет только горизонтальную асимптоту 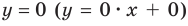
Иногда график функции 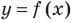
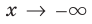
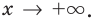
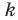
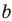
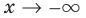
Как найти асимптоты графика функции
При исследовании поведения функции на бесконечности или вблизи точек разрыва часто оказывается, что расстояние между точками графика функции и точками некоторой прямой стремится к нулю при неограниченном удалении точек графика от начала координат. Прямая, к которой стремится кривая в бесконечно удаленной точке, называется асимптотой графика. Различают вертикальные и наклонные асимптоты. Прямая 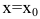
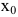
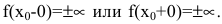
Внимание! Непрерывные на множестве действительных чисел функции вертикальных асимптот на имеют.
Для того чтобы график функции y=f(x) имел наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы
Частным случаем наклонной асимптоты (k=0) является горизонтальная асимптота.
Пример:
Найти асимптоты графика функции
Решение:
Функция 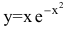
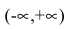
Получаем горизонтальную асимптоту y=0.
Общее исследование функции и построение графика
С помощью производной функции можно провести ее полное исследование и построить график этой функции. При этом рекомендуется использовать следующую схему.
- Найти область определения функции D(f).
- Исследовать функцию на четность
нечетность
периодичность
- Исследовать функцию на непрерывность, найти точки разрыва.
- Найти асимптоты графика функции.
- Исследовать функцию на монотонность, найти точки экстремума.
- Найти интервалы выпуклости и вогнутости, точки перегиба функции.
- Используя результаты проведенного исследования, построить график функции (можно вычислить координаты точек пересечения с осями координат).
Пример:
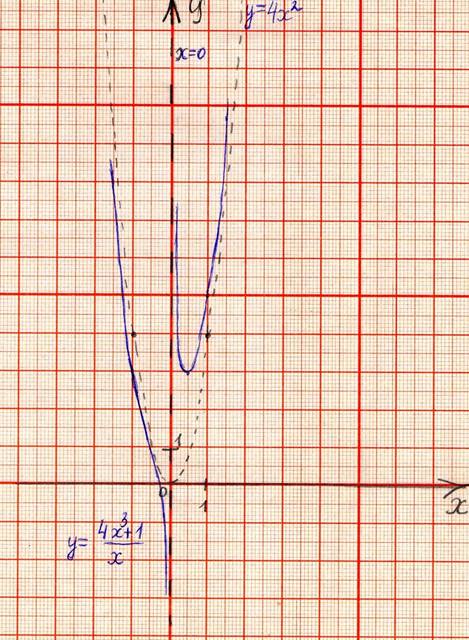
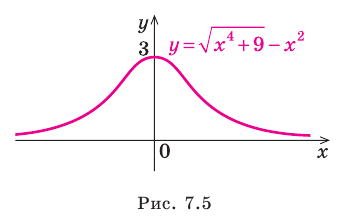
Провести полное исследование функции 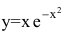
Решение:
Область определения функции — вся числовая прямая:
Функция непериодическая. Она нечетная, т.к. область определения симметрична относительно начала координат и
Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для
Функция непрерывна в области определения как композиция основных элементарных функций. Поскольку 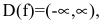
Строим график функции, используя результаты исследования.
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
- Иррациональные уравнения
- Иррациональные неравенства
- Производная в математике
- Как найти производную функции
«Асимптоты дробно-рациональных функций»
Секция: математика
Автор:
Мантрова Марина
Николаевна,
учитель математики
МБУ «Школа № 11»
г.о. Тольятти
Самарской обл.
Тольятти
2022
СОДЕРЖАНИЕ.
Введение……………………………………………………………………………3
Раздел 1. Теоретические
сведения об асимптотах…………………………………5
1. Понятие
асимптоты………………………………………….……………..5
2. Виды
асимптот графиков………………………………………………….5
3. Связь
между наклонной и горизонтальной асимптотами……………….6
4. Правила
нахождения асимптот……………………………………………….7
Раздел 2. Образцы
дробно-рациональных функций, при построении графиков которых асимптотами
являются параболы и гиперболы………………….…..10
1. Задача
№ 1405, Берман……………………………………………………10
2. Задача
№ 1215, Минорский………………………………………………11
3. Задача
№ 1217, Минорский………………………………………………13
4. Задача
№1400, Берман……………………………………………………15
5. Задача
№5…………………………………………………………………17
Выводы……………………………………………………………………………20
Литература……………………………………………………………………….21
ВВЕДЕНИЕ.
Графики
функций являются неотъемлемой частью школьного курса математики. От точности их
построения зависит, насколько правильно будут определены свойства тех или иных
функций. Для более точного построения графиков необходимо выявить наличие у них
асимптот.
Цель
работы — выяснить, могут ли графики дробно-рациональных функций асимптотически
приближаться к кривым: параболам и гиперболам.
Для достижения
цели исследования поставлены конкретные задачи:
1.
Изучить
состояние вопроса по источникам информации.
2. Выдвинуть
гипотезу о том, что в качестве асимптот могут выступать параболы и гиперболы.
3. Экспериментально
проверить свою гипотезу в процессе построения графиков.
При решении
сформулированных задач были использованы следующие методы: изучение и
анализ литературы по проблеме исследования, наблюдение, синтез, индукция.
Объектом
исследования являются графики дробно-рациональных функций.
Предмет
исследования: асимптоты.
РАЗДЕЛ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ОБ АСИМПТОТАХ.
1.
Понятие асимптоты.
Асимптотой
кривой называется прямая, расстояние до которой от точки, лежащей на кривой,
стремится к нулю при неограниченном удалении этой точки по кривой от начала
координат или, что то же, когда расстояние точки от начала координат
неограниченно растет. [1,
с 238]
2.
Виды асимптот графиков.
Вертикальная
Вертикальная
асимптота — прямая вида при условии
существования предела .
Как правило, при
определении вертикальной асимптоты ищут не один предел, а два односторонних
(левый и правый). Это делается с целью определить, как функция ведёт себя по
мере приближения к вертикальной асимптоте с разных сторон. Итак, для того,
чтобы ветвь кривой у=f(х) имела вертикальную асимптоту х=а,
необходимо и достаточно, чтобы выполнялось одно из соотношений:
. [2,c.391]
Горизонтальная
Горизонтальная
асимптота — прямая вида при условии
существования предела
.
Наклонная
Наклонная
асимптота — асимптота, не перпендикулярная оси Ох. Уравнение этой
асимптоты должно иметь вид . [2, с.392]
Если существуют
конечные пределы
,
,
то кривая у=f(х) имеет
асимптоту . [1, с. 239]
Замечание: функция может
иметь не более двух наклонных (горизонтальных) асимптот!
Замечание: Если хотя бы
один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при
(или
) не
существует!
3.
Связь
между наклонной и горизонтальной асимптотами
Если при
вычислении предела , то очевидно, что
наклонная асимптота совпадает с горизонтальной. Какова же связь между этими
двумя видами асимптот?
Дело в том, что
горизонтальная асимптота является частным случаем наклонной при , и из выше указанных
замечаний следует, что
А. Функция
имеет или только одну наклонную асимптоту, или одну горизонтальную асимптоту,
или одну наклонную и одну горизонтальную, или две наклонных, или две
горизонтальных, либо же вовсе не имеет асимптот.
Б. Существование
указанных в п. А. асимптот напрямую связано с существованием соответствующих
пределов.
4. Правила
нахождения асимптот.
Алгоритм
нахождения асимптот через пределы:
1. Нахождение
вертикальных асимптот.
2. Нахождение
двух пределов
3. Нахождение
двух пределов
если в п. 2., то
, и предел
ищется по формуле
горизонтальной асимптоты,
Наклонная асимптота может быть получена также путем выделения
целой части из рациональной дроби [3, с.240]. Для кривой у=Р(х)/G(х) существует
наклонная асимптота при условии, что степень многочлена Р(х) на единицу больше
степени многочлена G(х) [3, с.240].
Рассмотрим конкретный пример: Задача №1409, Берман[4,]
Построить график функции у=.
Преобразуем функцию к виду у= и выделим из неё целую
часть
=
, где целая часть
и есть наклонная
асимптота.
Можно было её найти и через пределы.
У=кх+b,
у= — наклонная асимптота.
Проведём полное исследование функции для построения её
графика.
D(у)=, следовательно х=-1
вертикальная асимптота.
,
при
х=0, х=-1, х=-3.
|
х |
|
-3 |
|
-1 |
|
0 |
|
|
У |
|
|
|
Не |
|
0 |
|
|
|
+ |
0 |
— |
не |
+ |
0 |
+ |
|
Точка |
Точка |
Точка |
Дополнительные точки:
|
х |
-2 |
-0,5 |
1 |
2 |
|
у |
-4 |
-0,25 |
|
|
:
Используя исследование функции, строим её график.
Рассмотренный
выше пример показывает, как искать наклонные асимптоты для графиков
дробно-рациональных функций: надо представить, если это возможно, данную
функцию в виде суммы линейной функции и функции, бесконечно малой при
х→∞. Тогда график линейной функции и будет наклонной асимптотой. Из
разобранного примера видно, что наклонная асимптота к графику рациональной
функции существует, если степень числителя на единицу больше степени
знаменателя.[3, c.137 – 138]
Изучая
учебное пособие для углубленного изучения математики Виленкина
Н. Я. « Алгебра и математический анализ для 10 класса» [3], я
нашла задание № 300, в котором говорится найти параболу, к которой
неограниченно приближаются при х→∞ графики следующих: функций: [3]
У
меня возник вопрос, а что будет, если степень числителя на 2 или 3 единицы
больше знаменателя, или на 1,2 единицы меньше степени знаменателя? Ответа на
свой вопрос в книжных источниках и интернете найти не удалось. После анализа
сборников задач по высшей математике [4], [5] я нашла ряд функций,
которые меня заинтересовали. Например,
у=, у=
, у=
, у=
. Более подробно
рассмотрим эти функции в следующем разделе и попробуем к ним применить метод
выделения целой части для нахождения криволинейных асимптот.
РАЗДЕЛ 2. ОБРАЗЦЫ
ДРОБНО-РАЦИОНАЛЬНЫХ ФУНКЦИЙ, ПРИ ПОСТРОЕНИИ ГРАФИКОВ КОТОРЫХ АСИМПТОТАМИ ЯВЛЯЮТСЯ
ПАРАБОЛЫ И ГИПЕРБОЛЫ.
1. Задача
№ 1405, Берман. [4]
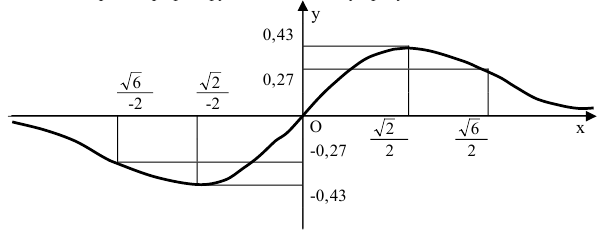
Построить график функции
у= .
По аналогии с рассмотренным
выше примером выделим целую часть из дроби .
Можно
предположить, что —
это асимптота, но явно, что это не линейная функция, а квадратичная. Проверим,
действительно ли это так экспериментальным путём. Построим график функции,
опираясь на её исследование, и график предполагаемой асимптоты.
D(у)= , поэтому х=0 –
вертикальная асимптота.
=
=0, если х=0,5.
=0,
если х=0, х=
.
|
х |
|
|
|
0 |
|
0,5 |
|
|
у |
|
0 |
|
Не сущ. |
|
3 |
|
|
|
— |
|
— |
Не |
— |
0 |
+ |
|
|
+ |
0 |
— |
Не |
+ |
+ |
|
|
Точка |
Точка |
Точка |
Дополнительные точки:
Таблица для асимптоты у=:
|
Х |
-2 |
-1 |
0 |
1 |
2 |
|
у |
16 |
4 |
0 |
4 |
16 |
На основании исследования функции строим её график и
её асимптоты.
Вывод: очевидно, что график функции у= действительно приближается к квадратичной параболе у=4х2
2. Задача
№ 1215, Минорский. [5]
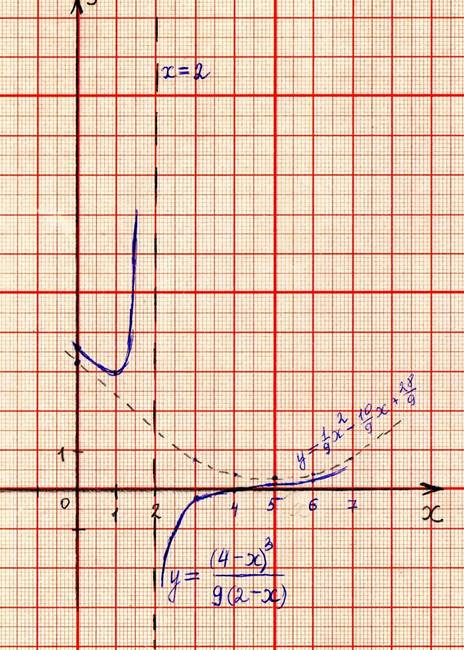
Построить график функции у= .
Преобразуем функцию к виду у= и выделим из дроби целую
часть .
Предположим, что целая часть — это параболическая
асимптота данного графика. Убедимся в этом на практике.
D(у)= , значит х=2 – вертикальная
асимптота.
=0, если х=1 и
х=4.
|
Х |
|
1 |
|
2 |
|
4 |
|
|
У |
|
3 |
|
Не |
|
0 |
|
|
|
— |
0 |
+ |
Не |
+ |
0 |
+ |
|
Точка |
Точка |
Точка |
Дополнительные точки:
|
Х |
0 |
1 |
3 |
4 |
5 |
6 |
|
у |
|
3 |
— |
0 |
|
|
Таблица для параболической асимптоты у= :
Вершина
|
х |
3 |
4 |
5 |
6 |
|
у |
|
|
|
|
Используя результаты исследования функции, строим её
график и асимптоты.
Вывод: убеждаемся, что у= квадратичная парабола является асимптотой для графика функции у=
3. Задача
№ 1217, Минорский. [5]
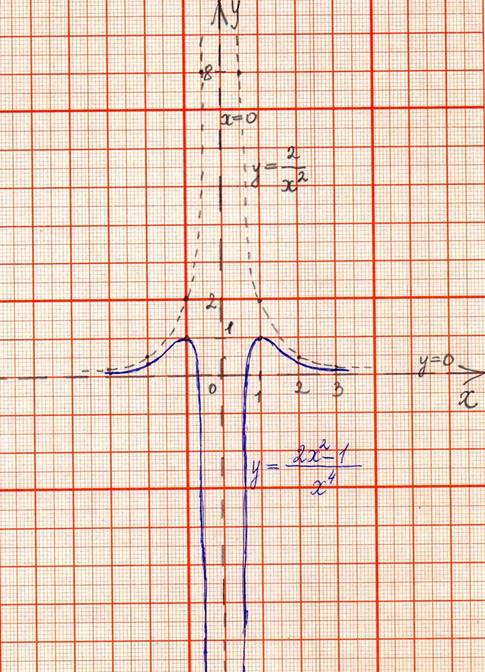
Построить график функции У=.
Преобразуем функцию к
виду у = . Предположим,
что
у= гиперболическая асимптота.
Проверим это, выполнив построения.
D(у)=. Следовательно, х=0 – вертикальная асимптота.
Найдём к=
b=
Значит, у=0 =
горизонтальная асимптота.
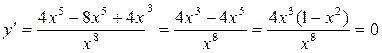
если х=1, х= -1, х=0.
Вычислим
|
х |
|
-1 |
|
0 |
|
1 |
|
|
у |
|
1 |
|
Не |
|
1 |
|
|
|
+ |
0 |
— |
Не |
+ |
0 |
— |
|
Точка |
Точка |
Точка |
Дополнительные точки:
|
Х |
1 |
2 |
3 |
0,5 |
|
у |
1 |
|
|
-8 |
Таблица для асимптоты у=
|
Х |
1 |
2 |
3 |
0,5 |
|
у |
2 |
0,5 |
|
8 |
Вывод: график функции у= имеет
гиперболическую асимптоту у=
4. Задача
№1400, Берман. [4]
Провести полное исследование данной функции и
начертить её график
У= .
Приведём данную функцию к виду у= .
Можно предположить, что у= является
криволинейной асимптотой для данного графика. Проверим это экспериментальным
путём, сделав полное исследование функции, построив её график и асимптоту у= .
D(у)= , следовательно х=1 и х=-1 –
вертикальные асимптоты.
Найдём к=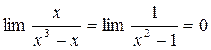
в= 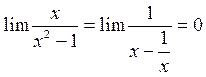
У=0 – горизонтальная асимптота.
Вычислим 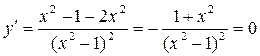
значения х.
|
Х |
|
-1 |
|
1 |
|
|
У |
|
Не |
|
Не |
|
|
|
— |
Не |
— |
Не |
— |
|
Точка |
Точка |
Дополнительные точки для построения данного графика:
|
Х |
0 |
0,5 |
1,5 |
2 |
2,5 |
3 |
|
у |
0 |
— |
1,2 |
|
0,48 |
0,375 |
Таблица для построения асимптоты:
|
Х |
0,5 |
1 |
1,5 |
2 |
|
у |
2 |
1 |
|
0,5 |
Основываясь на исследовании, построим график функции.
Вывод:
кривая у=(гипербола) служит асимптотой для графика
функции у=.
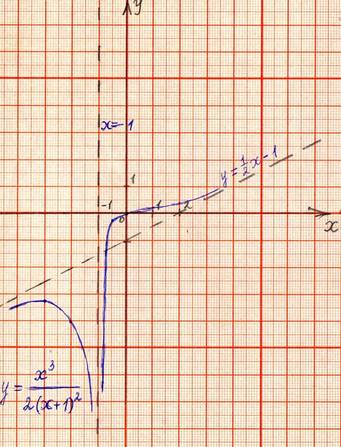
5. Задача 5. Попробую
сама взять дробно – рациональную функцию, у которой степень числителя на 3
единицы больше степени знаменателя .
Найдём асимптоту путём
выделения целой части.. Значит, g(x)=
— асимптота.
Таблица точек для построения асимптоты:
|
Х |
0 |
1 |
2 |
3 |
-1 |
-2 |
|
у |
-1 |
0 |
5 |
20 |
-4 |
-15 |
Проведём исследование функции при помощи аппарата
производной.
при х=0 и х=-
.
|
Х |
|
|
|
-1 |
|
0 |
|
|
|
+ |
0 |
|
Не |
|
0 |
+ |
|
у |
|
-9,5 |
|
Не |
|
0 |
|
|
Точка |
Точка |
Точка |
Дополнительные точки для построения функции :
|
х |
-2 |
-1,5 |
-0,5 |
0,5 |
1 |
2 |
|
у |
-16 |
-10,1 |
-0,125 |
0,04 |
0,5 |
5,3 |
Вывод:
график функции приближается к кубической асимптоте g(x)=
.
ВЫВОДЫ.
Таким образом, на основании проделанной работы мною были сделаны следующие
выводы:
1. Графики
дробно рациональных функций могут иметь не только асимптоты, представленные
линейной функцией, но и кривые линии, к которым они асимптотически приближаются:
квадратичную, кубическую параболы, а также гиперболы.
2. Если
степень многочлена числителя больше степени многочлена знаменателя на 2
единицы, то асимптотой будет квадратичная парабола, если разность степеней
равна 3 единицам, то асимптотой будет кубическая парабола. Логически можно
предположить, что если разница между степенью многочлена числителя больше
степени многочлена знаменателя на четное число единиц, то асимптотой будет
квадратичная парабола, ветви которой ближе к оси ординат; если же эта разность
составляет нечетное число, например 5, 7, 9, то асимптотой будет парабола вида
кубической, ветви которой приближены к оси ординат.
3. Если
степень многочлена числителя меньше степени многочлена знаменателя на 1(также
все нечетные числа) единицу, то асимптотой будет нечётная гипербола, а если
степень знаменателя на 2 (все четные числа) единицы больше степени числителя,
то асимптотой будет чётная гипербола.
4. Знание
криволинейных асимптотических линий необходимо тогда, когда дробная рациональная
функция не имеет прямолинейных асимптот. Криволинейные асимптотические линии
позволяют точнее построить график той или иной функции.
ЛИТЕРАТУРА.
1.
Игнатьева
А. В. и др. Курс высшей математики /А. В. Игнатьева, Т. И. Краснощекова, В. Ф.
Смирнов; Под редакцией П.И.Романовского. – 2-е изд. – М.: «Высшая школа», 1968.
— 670с.
2.
Уваренков
И.М., Малер М.З. Курс математического анализа. — Том 1. — М.: «Просвещение»,
1966. — 640с.
3.
Виленкин
Н. Я. и др. Алгебра и математический анализ для 10 класса: Учеб. пособие для
учащихся школ и классов с углубл. изуч. математики / Н.Я.Виленкин,
О.С.Ивашев–Мусатов, С.И. Шварцбурд. – 4-е изд. — М.: «Просвещение», 1995. —
335с.
4.
Берман
Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для высш.
учеб. заведений. — 17-е изд. – М.: «Наука», 1972. — 412с.
5.
Минорский
В.П. Сборник задач по высшей математике: Учеб. пособие для студ. высш. технич.
учеб. заведений – 12-е изд., стереотип. — М.: «Наука», 1978. — 352с.
Вертикальная
асимптота.
Если выполнено
хотя бы одно из условий
,
,
то прямую
называют вертикальной асимптотой
графика функции
.
Невертикальная
асимптота.
Прямую
называют
невертикальной асимптотой графика
функции
при
,
если
.
Если
,
то асимптоту называют наклонной, а если
,
то асимптоту
называют горизонтальной.
Аналогично вводится
понятие асимптоты при
.
Для того чтобы
прямая
была асимптотой графика функции
при
,
необходимо и достаточно, чтобы существовали
конечные пределы

.
Аналогично находится
асимптота при
.
Исследование
асимптот при
и при
как правило проводят отдельно.
В некоторых частных
случаях возможно совместное исследование
асимптот при
и при
,
например, для
1) рациональных
функций;
2) четных и нечетных
функций, для графиков которых исследование
можно проводить на части области
определения.
Следует отметить,
что метод вычисления пределов для
нахождения асимптот не позволяет оценить
взаимное расположение графика функции
и его асимптоты. Для определения взаимного
положения графика и асимптоты можно
пользоваться следующими правилами.
1) Если функция
имеет асимптоту при
,
дифференцируема и строго выпукла вниз
на луче
,
то график функции лежит выше асимптоты.
2) Если функция
имеет асимптоту при
,
дифференцируема и строго выпукла вверх
на луче
,
то график функции лежит ниже асимптоты.
3) Могут быть другие
случаи поведения графика функции при
стремлении к асимптоте. Например,
возможно, что, график функции бесконечное
число раз пересекает асимптоту.
Аналогичное
утверждение справедливо и при
.
До исследования
свойств выпуклости графика функции
взаимное расположения графика функции
и его асимптоты можно определить по
знаку
в методе выделения главной части.
Метод выделения
главной части.
Для нахождения асимптоты выделяем
главную часть функции при
.
Аналогично при
.
Главную часть
дробно рациональной функции
удобно находить, выделяя целую часть
дроби.
Главную часть
иррациональной функции
при решении практических примеров
удобно находить используя методы
представления функции формулой Тейлора
при
.
Главную часть
иррациональных функций вида
и
удобно находить соответственно методом
выделения полного квадрата или полного
куба подкоренного выражения.
Примеры
5.1.
Найти асимптоты графика функции

Прямая
— вертикальная асимптота.
Наклонная асимптота.
Найдем угловой коэффициент
и свободный член
по формулам
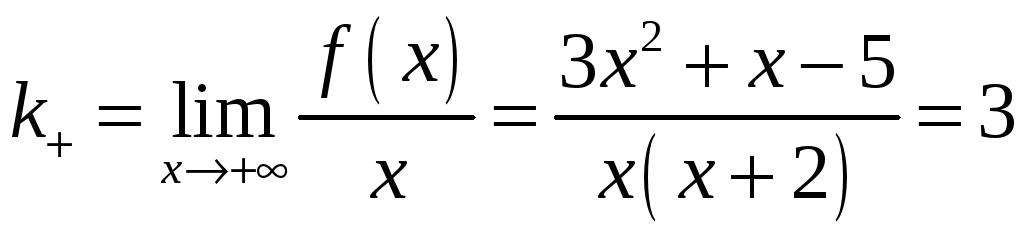
Таким образом,
прямая
— наклонная асимптота.
Найдем асимптоту
методом выделения главной части
дробно-рациональной функции. Выполняя
деление «столбиком», получаем
То есть,

Таким образом,
прямая
— наклонная асимптота.
5.2. Найти
асимптоты линии:

Вертикальных и
горизонтальных асимптот нет.
Выражая уравнение
линии в явном виде :.
Тогда

.
В итоге имеем 2
наклонных асимптоты:
.
5.3.
Найти асимптоты линии:
.
Выразим уравнение
линии в явном виде:
.
Так как

то прямая
— наклонная асимптота.
5.4. Найти
асимптоты функции:
Так как функция
не определена в точках
=
1,
то
— вертикальные асимптоты.
Найдём наклонную
асимптоту: угловой коэффициент прямой
и
число
найдём, применяя формулы:

.

Получили:
—
наклонная асимптота.
5.5. Найти
наклонную асимптоту графика функции

Так как

то по формуле
Тейлора получаем
и прямая
является искомой асимптотой. ◄
5.6. Найти
наклонные асимптоты графика функции
при
и
.
В подкоренном
выражении выделим полный квадрат
.
Так как график
функции
симметричен относительно прямой
и
то
при
.
Значит, прямая
является асимптотой при
,
а прямая
— асимптотой при
.
◄
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Анализ дробно-рациональной функции. Асимптоты, экстремум
Функция $y=frac{k}{x}$ . Гипербола. Свойства.
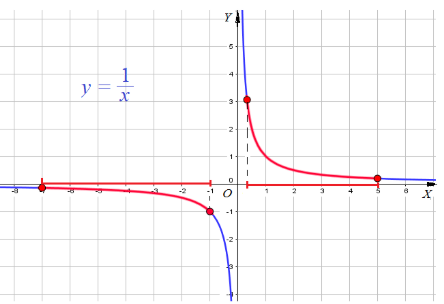
Пример 1: Построить график для функции $y=frac{1}{x}$, $fleft(xright)=frac{1}{x}$
- Вычислим значения функции в разнознаковых точках и нанесем точки с вычисленными координатами в системе $XOY$.
- $fleft(1right)=1$ $fleft(frac{1}{2}right)=2$ $fleft(-1right)=-1$ $x=-frac{1}{2}$ $fleft(-frac{1}{2}right)=-2$ $fleft(2right)=frac{1}{2}$ $fleft(frac{1}{4}right)=4$ $fleft(-frac{1}{4}right)=-4$ $fleft(4right)=frac{1}{4}$ $fleft(1right)=8$ $fleft(-4right)=-frac{1}{4}$ $fleft(-frac{1}{8}right)=-8$ .
- Точки Графика $(1;1)$, $(2;1/2)$, $(4;1/4)$, $(1/2;2)$, $(1/4;4)$, $(1/8;8)$, $(-1;-1)$, $(-2;-1/2)$, Еще точки: $(-4;-1/4)$, $(-1/2;-2)$, $(-1/4;-4)$, $(-1/8;-8)$ . По всем точкам построим кривые — график функции $y=frac{1}{x}$
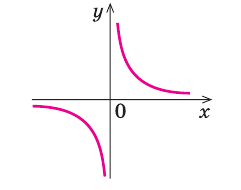
- График имеет разрыв по вертикальной линии $x=0$. Ветви графика прижимаются к горизонтальной линии $y=0$.
Графиком функции $y=frac{k}{x}$ $kne0$ является гипербола , ветви прижимаются к асимптотическим линиям.
- если коэффициент $k > 0$ , в I и III координатных четвертях. Точка $(0;0)$ — центр симметрии.
- если $k < 0$ , то во II и IV координатных четвертях. Точка $(0;0)$ — центр симметрии.
- Асимптоты: Вертикальная асимптота, линия $x=0$, Горизонтальная асимптота, линия $y=0$
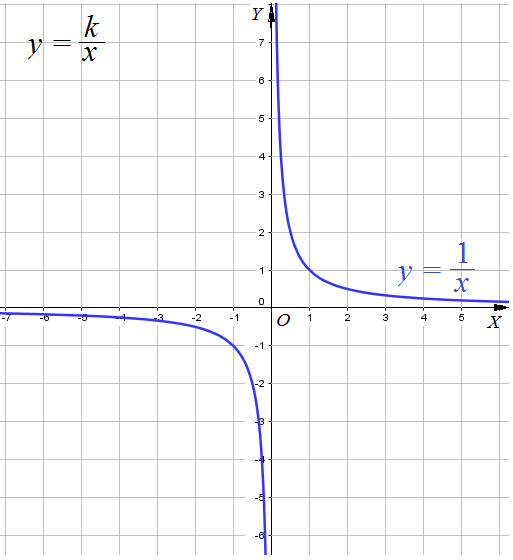
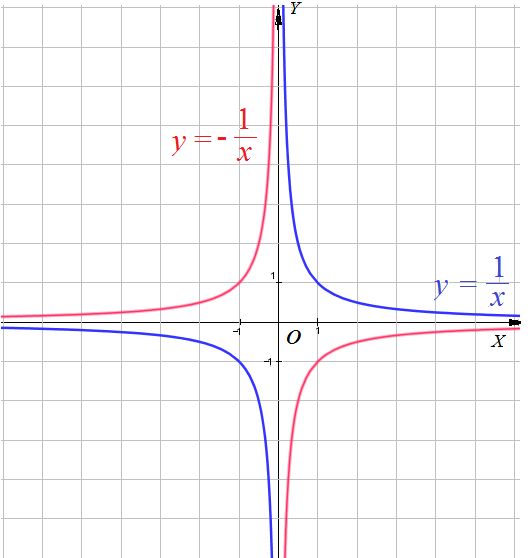
Cвойства функции $y=frac{k}{x}$ при $k > 0$ ( ветви гиперболы расположены в первом и третьем координатных углах) .
Свойство 1: Область Определения Функции — вся числовая прямая , кроме $x=0$. Свойство 2: $y > 0$ при $x > 0$; $y < 0$ при $x < 0$. Свойство 3: Функция убывает на промежутках $( — ∞ ; 0 )$ и $( 0 ; + ∞)$ Свойство 4: Функция не ограничена ни снизу, ни сверху. Свойство 5: Ни наименьшего, ни наибольшего значений $у$ у функций нет. Свойство 6: Функция непрерывна на $( — ∞ ; 0 )$ и $( 0 ; + ∞)$. Свойство 7: Область значений функции — $( — ∞ ; 0 )$ U $( 0 ; + ∞)$. имеет разрыв в точке $x=0$.
Cвойства функции $y=frac{k}{x}$ при $k < 0$ (ветви гиперболы расположены во втором и четвертом координатных углах).
Свойство 1: Область Определения Функции — вся числовая прямая , кроме $x=0$. Свойство 2: $y > 0$ при $x < 0$ ; $y < 0$ при $x > 0$. Свойство 3: Функция возрастает на промежутках $( — ∞ ; 0 )$ и $( 0 ; + ∞)$ Свойство 4: Функция не ограничена ни снизу, ни сверху. Свойство 5: Ни наименьшего, ни наибольшего значений $у$ у функций нет. Свойство 6: Функция непрерывна на $( — ∞ ; 0 )$ и $( 0 ; + ∞)$ Свойство 7: Область значений функции — объединение $( — ∞ ; 0 )$ U $( 0 ; + ∞)$ . имеет разрыв в точке $x=0$.
Метод Замены для построения Графика Функции.
Мысль: Умеем строить график функции попроще … используем его для построения функции при «сдвинутых» аргументах и значениях.
Как построить график функции $y=kcdot fleft(xright)$, если известен график функции $y=fleft(xright)$.
- График $y=5cdot fleft(xright)$: Расстянуть вертикально вверх по оси $OY$ 5 раз все, что над $OX$ графика $y=fleft(xright)$ , $k$ раза.
- График $y=5cdot fleft(xright)$: Расстянуть вертикально вниз по оси $OY$ 5 раз все, что под $OX$ графика $y=fleft(xright)$ , $k$ раза.
- График $y=frac{1}{3}cdot fleft(xright)$: Сжать по вертикали, оси $OY$ график $y=fleft(xright)$ 3 раза.
- Еще способ: Перемасштабирование. Для $y=5cdot fleft(xright)$ … построить $y=fleft(xright)$, изменить масштаб: «1» станет «5», «-2» станет «-10», и т.д.
Как построить график функции $y=-fleft(xright)$, если известен график функции $y=fleft(xright)$.
- Эти функции принимают ровно противоположные значения. Значит: график $y=fleft(xright)$ надо отразить по оси $OX$, «перевернуть».
Как построить график функции $y=fleft(x+lright)$, если известен график функции $y=fleft(xright)$.
- Построить график $y=fleft(x+lright)$, где $l > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OX$ на $l$ единиц масштаба влево.
- Построить график $y=fleft(x-lright)$, где $l < 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OX$ на $l$ единиц масштаба вправо.
Как построить график функции $y=fleft(xright)+m$, если известен график функции $y=fleft(xright)$.
- Построить график $y=fleft(xright)+m$, где $m > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OY$ на $m$ единиц масштаба вверх;
- Построить график $y=fleft(xright)-m$, где $m > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OY$ на $m$ единиц масштаба вниз.
Как построить график функции $y=fleft(x+lright)+m$, если известен график функции $y=fleft(xright)$.
- График функции $y=fleft(x+lright)+m$ можно получить из графика $y=fleft(xright)$ параллельными сдвигами по осям $OX$ и $OY$.
График Дробной Функции.
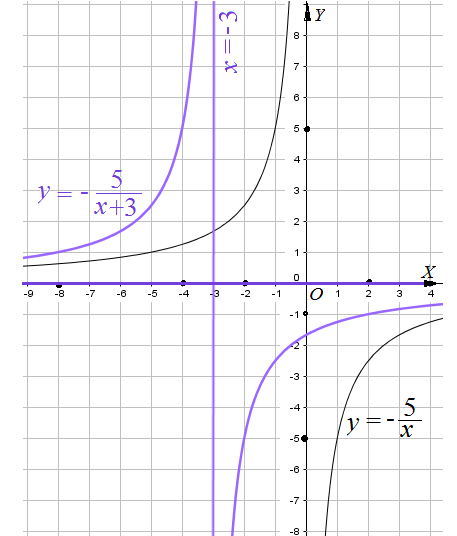
Пример 2: Построить график функции $y=-frac{5}{x+3}$ .
- сначала построим график функции $y=-frac{5}{x}$ … от графика $y=frac{1}{x}$ … отразим от $OX$ и растянем по вертикали 5 раз.
- сдвинем получившуюся гиперболу вдоль оси $OX$ на $3$ единицы влево, получится требуемый график.
- это гипербола с асимптотами $x=-3$; $y=0$. «почему так?» — как мы строим графики?
- берем несколько $x$ — точек и находим для каждого свои $y$ — значения в соответствии «с формулой функции».
- По точкам проводим график. Очевидно, если, скажем, $x=0,52$ функция $y=-frac{5}{x+3}$ дает какое-то значение,
- … то, конечно для $x=3,52$ другая функция, $y=-frac{5}{x}$ дает ровно такое же значение.
- значит, точки графиков будут различаться на $3$ единицы по $x$ — координате и совпадать по $y$ — координате.
- Ровно так и для всех точек. «Сравни две функции и вообрази их графики: каковы различия и что общего? «
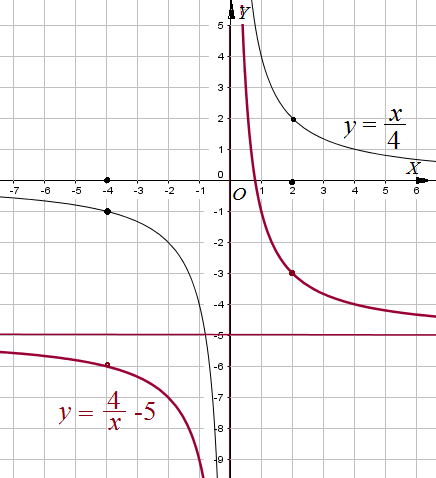
Пример 3: Построить график функции $y=frac{4}{x}-5$ .
- Сначала надо построить график функции $y=frac{4}{x}$ . Гиперболу $y=frac{1}{x}$ «растянем» четыре раза.
- Сдвинуть получившуюся гиперболу вдоль оси $OY$ на $5$ клеточек вниз. Т.к. каждое значение должно отличаться на 5 единиц.
- получится требуемый график. Это гипербола с асимптотами $x=0$; $y=-5$.
- Важно знать где пересекается с нулем. Решение, корень $frac{4}{x}-5=0$ дает абсциссу $x=0.8$. Точка графика $left(0,8;0right)$.
- Исследование: Найдем производное: $left(frac{4}{x}-5right)’=-frac{4}{x^2}$. Нигде не = 0, Экстремума нет!
- Производная для всех $x$ (кроме $0$) отрицательна — значит всюду убывает.
- Область Определения: $D_f=left(-infty;0right)+left(0;+inftyright)$ Область значений $E_f=left(-infty; -5right)+left(-5;+inftyright)$
- Знакопостоянство: $+Z_f=left(-infty;0,8right)$ — функция отрицательна, $-Z_f=left(0,8;+inftyright)$ — функция положительна.
- Монотонность: $+M_f=left(-infty;-3right)+left(-3;0right)$ — возрастает $-M_f=left(0;3right)+left(3;+inftyright)$ — функция убывает
Вертикальная асимптота ( $x=0$,) проходит в полюсе, точке разрыва функции. Точка обнуления знаменателя. Параллельно $OY$.
Горизонтальная асисмптота ( $y=-5$ ), линия, на которую «ложится» график при значениях $х$ около $+-infty$. Параллельно $OX$.
Гипербола — график простой дроби, две асимптоты делят на 4 четверти, ветви гиперболы «зажаты — прижаты» к асимптотическим линиям .
Наклонная асимптота — линия типа $y=2x+3$, к которой «прижимаются» ветви графика «на» или «около» + — бесконечнoсти.
Пример 4: Построить график функции $y=frac{x-5}{x^2-25}$
- Если выражение функции упрощается, то следует это сделать. Ибо получится функция проще, легче вычисляемая и рисуемая.
- Тождественное преобразование, сокращение $frac{x-5}{x^2-25}=frac{x-5}{(x+5)(x-5)}=frac{1}{x+5}$. Так, что график $y=frac{1}{x+5}$ ?
- Не спеши! Мы сократили на $x-5$ , которое незаконно для $x=5$. Нарушается О.Д.З — в исходной функции нет места $x=5$.
- Значит: можем строить гиперболу $y=frac{1}{x+5}$ взамен нашей $y=frac{x-5}{x^2-25}$, но «без точки $x=5$».
- Точка $x=5$ разрывает «гладкий» график гиперболы. Она называется «выколотая точка с координатами $left(5;0,1right)$».
Важно уметь исследовать функцию — график около точек разрыва. + / — поблизости. Куда тянется?
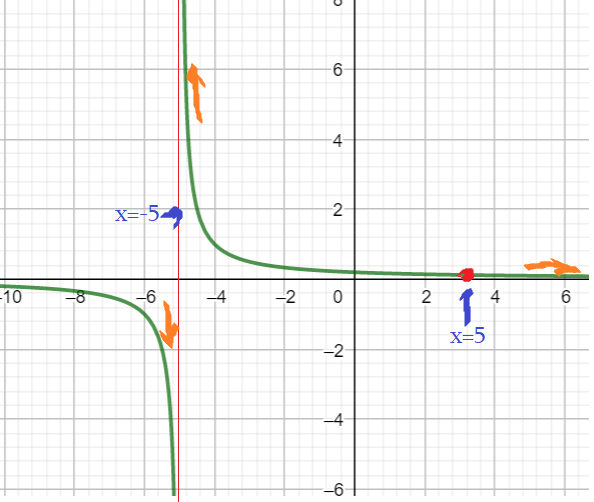
- Исследуем около $x=-5$. Возьмем «близкие» точки $-5,01$ и $-4,99$. Вычислим приближенные значения.
- Чуть левее … $fleft(-5,01right)=frac{-5,01-5}{(-5,01)^2-5^2}approx -100$. Чуть правее … $fleft(-4,99right)=frac{-4,99-5}{(-4,99)^2-5^2}approx 100$.
- Прямая $x=-5$ — вертикальная асимптота. Ветвь слева прижимается «вниз», к $-infty$ . А справа поднимается вверх к $+infty$.
- Около $x=5$. Чуть левее $fleft(4,99right)=frac{4,99-5}{4,99^2-5^2}approx0,101$. $fleft(5,01right)=frac{5,01-5}{5,01^2-5^2}approx0,099$.
- Значит, $x=5$ точка разрыва, на графике выколотая точка $left(5;0,1right)$. Т.к. в ней $y=frac{1}{5+5}=0,1$.
- «О нулях»: при $x=0$ $y=0,2$ . Но функция нигде не обнуляется, $yne0$. Прямая $y=0$ — горизонтальная асимптота.
- Анализ: Найдем производное: $left(frac{x-5}{x^2-25}right)’=left(frac{1}{x+5}right)’=-frac{1}{left(x+5right)^2}$
- Производная не равна нулю нигде и всюду отрицательна. Экстремума нет, Всюду убывающая функция.
- Область Определения функции: $D_f=left(-infty;-5right)+left(-5;5right)+left(5;+inftyright)$ .
- Знакопостоянство: $+Z_f=left(-5;5right)+left(5;+inftyright)$ — функция положительна. $-Z_f=left(-infty;-5right)$ — функция отрицательна
- Монотонность: $+M_f=varnothing $ — нет роста. $-M_f=left(-infty;-5right)+left(-5;5right)+left(5;+inftyright)$ — функция убывает
- Область значений $E_f=left(-infty;0right)+left(0;0,8right)+left(0,8;inftyright)$
Пример 5: Построить график функции $y=frac{x^2-16}{x+4}$
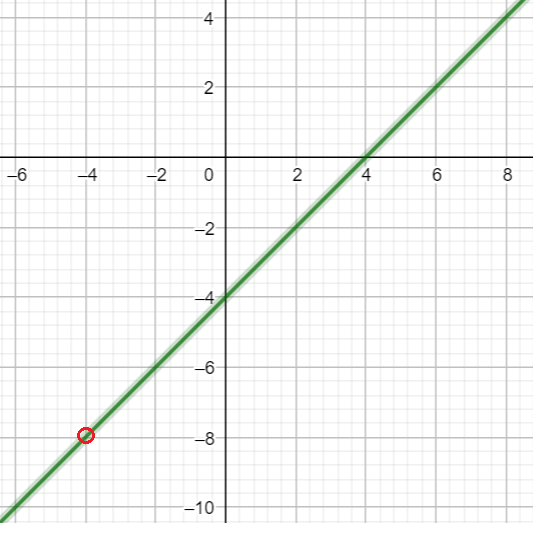
- О.Д.З функции $xne-4$. Оговорив это, со спокойной совестью сократим $y=frac{x^2-16}{x+4}=x-4$.
- График нашей функции — прямая линия $y=x-4$ с выколотой точкой $left(-4;-8right)$ при $x=-4$.
- «Близко чуть левее»: $x=-4,01$ значение $fleft(-4,01right)=frac{(-4,01)^2-16}{-4,01+4}=-8,01$. Ближе? … Предел $approx-8$.
- «О нулях». при $x=0$ $y=-4$ . Обнуление функции $y=0$ при $x=4$ — пересечение с $x$ — осью.
- Анализ: Найдем производное: $left(frac{x^2-16}{x+4}right)’=left(x-4right)’=1$
- Производное всюду равно 1. Постоянный рост. Кроме разрыва, конечно. Нет точки Экстремума.
- Область Определения: $D_f=left(-infty;-4right)+left(4;+inftyright)$ Область значений $E_f=left(-infty;-8right)+left(-8;inftyright)$
- Знакопостоянство: $+Z_f=left(4;+inftyright)$ — функция положительна. $-Z_f=left(-infty;4right)$ — функция отрицательна
- Монотонность: $+M_f=left(-infty;-4right)+left(-4;inftyright)$ — возрастает
График Дробно — Рациональной Функции.
Определение: дробно-рациональной порядка $left(n;mright)$ называется функция вида $y=frac{acdot x^n+5x^3-x+c}{bcdot x^m-4x^2-7x+d}$
Числитель — многочлен степени $n$ , знаменатель — многочлен степени $m$ . Общий вид: $y=frac{Pleft(xright)}{Qleft(xright)}$
Нули функции — корни числителя $Pleft(xright)=0$ , Асимптоты (полюсы) — корни знаменателя $Qleft(xright)=0$.
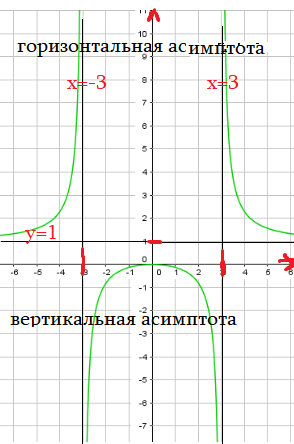
Пример 6: Построить график функции $y=frac{x^2}{x^2-9}$.
- Функция $fleft(xright)=frac{x^2}{x^2-9}$ — четная: $fleft(xright)=fleft(xright)$ $fleft(8right)=fleft(-8right)$ — Слева и справа от $OY$ симметрично.
- Вычисления: $fleft(-4right)=frac{left(-4right)^2}{left(-4right)^2-9}=frac{16}{7}approx2,3$ $fleft(-10right)=frac{100}{91}approx 1,1$ $fleft(-5right)=frac{25}{16}approx 1,6$ $fleft(-3,5right)=frac{12.25}{3,25}approx 3,8$
- $fleft(-2right)=fleft(2right)=frac{4}{-5}approx -0,8$ $fleft(-1right)=fleft(1right)approx -0,1$ $fleft(3,5right)approx 3,8$ $fleft(4right)approx 2,3$ $fleft(5right)approx 1,6$ $fleft(10right)approx 1,1$
- Наша функция имеет нули в точке $x=0$ , а вертикальные асимтоты — линии $x=-3$ , $x=3$
- Асимптота — прямая линия, к которой «прижимается» график функции, «подходя» к ней бесконечно близко.
- Чему равно $frac{x^2}{x^2-9}$ при очень больших $x$ ? $xapproxpm1000$ ? Конечно, $yapprox1$ горизонтальная асимптота $y=1$ .
- Анализ графика: 1) Обнуляется при $x=0$ . 2) Значение в нуле : $y=frac{x^2}{x^2-9}$ в $x=0$ равно $y=0$.
- 3) Поведение в разрывах: «чуть левее» полюса $xapprox-3-0,01$ значение $y > 0$ — «большое положительное».
- «чуть правее» разрыва $xapprox-3+0,01$ значение функции «большое отрицательное».
- Поведение около другого разрыва: когда $x$ «чуть левее» , например $xapprox3-0,01$ , то $y < 0$ ;
- когда $x$ «чуть правее» , например $xapprox3+0,01$ , то $y > 0$.
- 4) Поведение на бесконечности: при $xapproxpminfty$ значение «ложится» около $yapprox1$.
- 5) Область определения функции — все точки оси $x$ , кроме $x=pm3$
- 6) Функция положительна $y > 0$ на интервалах $x < -3$ , $x > 3$.
- 7) Функция отрицательна $y < 0$ на интервалах $-3 < x < 0$ , $0 < x < 3$.
Исследование Функции:
- Найдем производное: $left(frac{x^2}{x^2-9}right)’=frac{2xleft(x^2-9right)-x^2cdot2x}{left(x^2-9right)^2}=frac{-18x}{left(x^2-9right)^2}$
- Производное равно нулю дает точку Экстремума: $x=0$. Точка Максимума.
- Производная отрицательна — значит убывает $x > 0$. Производная положительна, значит возрастает: $x < 0$
- Область Определения: $D_f=left(-infty;-3right)+left(-3;3right)+left(3;+infty8right)$ — область определения функции.
- Знакопостоянство: $+Z_f=left(-infty;-3right)+left(3;+inftyright)$ — функция положительна. $-Z_f=left(-3;3right)$ — функция отрицательна
- Монотонность: $+M_f=left(-infty;-3right)+left(-3;0right)$ — возрастает $-M_f=left(0;3right)+left(3;+inftyright)$ — функция убывает
- Область значений $E_f=left(-infty;0right)+left(1;inftyright)$
пробaп 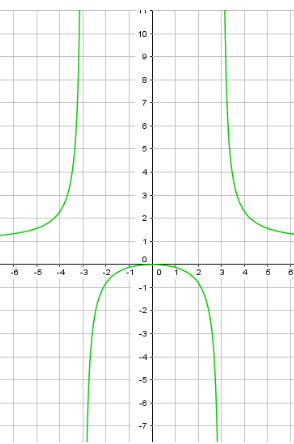
Пример 7: Анализ графика функции $y=frac{4x^2-5x-6}{2x^2-3x+1}$
- нули — точки обнуления числителя $4x^2-5x-6=0$ $x=2$ $x=-frac{3}{4}$
- Представление: $frac{4x^2-5x-6}{2x^2-3x+1}=frac{2cdot left(2x^2-3x+1right)+x-8}{2x^2-3x+1}=2+frac{x-8}{2x^2-3x+1}=2+frac{x-8}{left(2x-1right)left(x-1right)}=2+frac{15}{2x-1}-frac{7}{x-1}$
- разрыв (полюс): $2x^2-3x+1=0$ вертикальные асимптоты — $x=1$ и $x=0,5$.
- при $xapproxpm infty$ значение «ложится» около $yapprox2$. $-frac{30}{left(2x-1right)^2}+frac{7}{left(x-1right)^2}$ $x=0,75$ $x=15,24$
- Производное: $left(2+frac{15}{2x-1}-frac{7}{x-1}right)’=-frac{30}{left(2x-1right)^2}+frac{7}{left(x-1right)^2}=frac{-2x^2+32x-23}{left(2x-1right)^2cdotleft(x-1right)^2}$
- Или так: $left(frac{4x^2-5x-6}{2x^2-3x+1}right)’=frac{left(4x^2-5x-6right)’cdotleft(2x^2-3x+1right)-left(4x^2-5x-6right)cdotleft(2x^2-3x+1right)’}{left(2x^2-3x+1right)^2}=frac{left(8x-5right)cdotleft(2x^2-3x+1right)-left(4x^2-5x-6right)cdotleft(4x-3right)}{left(2x^2-3x+1right)^2}=frac{-2x^2+32x-23}{left(2x^2-3x+1right)^2}$
- Уравнение Экстремумов: $frac{-2x^2+32x-23}{left(2x^2-3x+1right)^2}=0$. $-2x^2+32x-23=0$. $x=8pm0,5sqrt{210}$
- Производная отрицательна на интервалах $-M_f=left(-infty;0,5right)+left(0,5;8-0,5sqrt{210}right)+left(8+0,5sqrt{210};inftyright)$. Убывает.
- Производная положительна на интервалах $+M_f=left(8-0,5sqrt{210};1right)+left(1;8+0,5sqrt{210}right)$. Возрастает.
- Точка Минимума: $x=8-0,5sqrt{210}$ $xapprox0,75$ . Точка Максимума: $x=8+0,5sqrt{210}$ $xapprox15,25$
- Область Определения: $D_f=left(-infty;0,5right)+left(0,5;1right)+left(1;+inftyright)$ .
- Знакопостоянство: $+Z_f=left(-infty;-0,75right)+left(0,5;1right)+left(2;+inftyright)$ — положительна. $-Z_f=left(-0,75;0right)+left(1;2right)$ — отрицательна.
- Область значений (приближенно!) $E_fapproxleft(-infty;2,001right)+left(60;inftyright)$
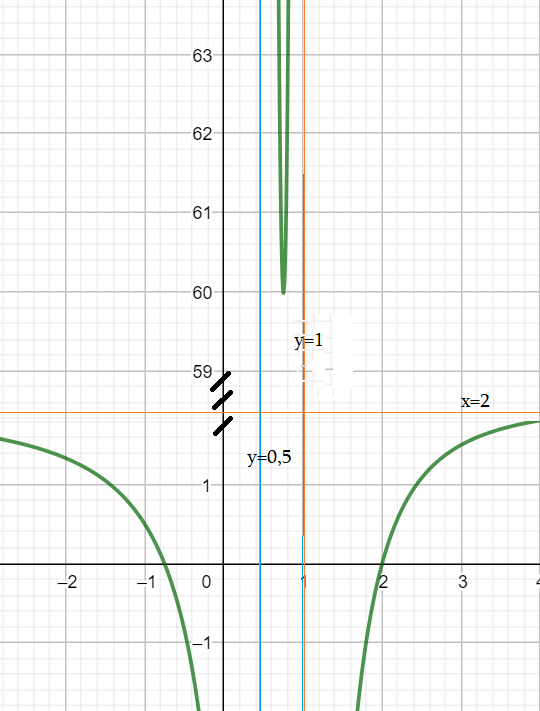
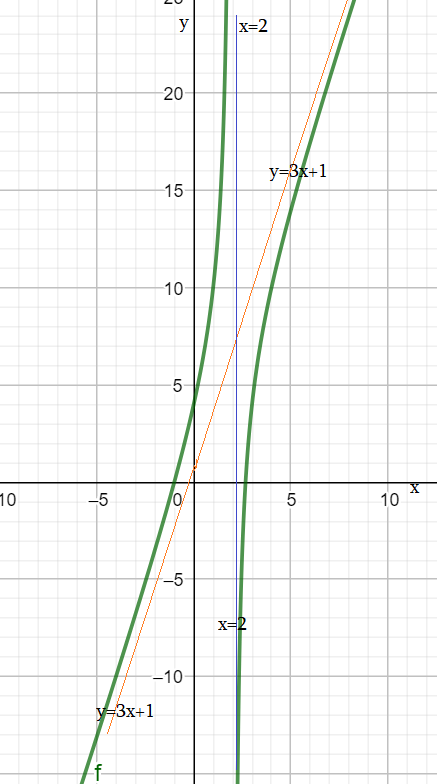
Пример 8: Анализ графика функции $y=frac{3x^2-5x-8}{x-2}$
- нули — точки обнуления числителя $3x^2-5x+8=0$ $x=-1$ $x=frac{8}{3}approx2,7$
- разрыв (полюс): $x-2=0$ вертикальные асимптоты — $x=2$ .
- «чуть левее»: $fleft(2-10^{-7}right)=frac{3cdotleft(2-10^{-7}right)^2-5left(2-10^{-7}right)-8}{2-10^{-7}-2}=frac{3cdot4-5cdot2-8-12cdot10^{-7}+5cdot10^{-7}+3cdotleft(10^{-7}right)^2}{-10^{-7}}approx6cdot10^7$ Значит, уходит к $+infty$
- Чуть правее: $fleft(2+10^{-7}right)=frac{3cdotleft(2+10^{-7}right)^2-5left(2+10^{-7}right)-8}{2+10^{-7}-2}=frac{3cdot4-5cdot2-8+12cdot10^{-7}-5cdot10^{-7}+3cdotleft(10^{-7}right)^2}{10^{-7}}approx-6cdot10^7$ …. бежит к $-infty$
- Представим нашу функцию по-другому : $frac{3x^2-5x-8}{x-2}=frac{3x^2-6x+x-2-6}{x-2}=3x+1-frac{6}{x-2}$
- Видно, что при больших $x=2$ она «почти совпадает» с линейной функцией $3x+1$. «прижимается к ней».
- $y=3x+1$ — наклонная асимптота нашей функции.
- Найдем производное: $left(frac{3x^2-5x-8}{x-2}right)’=frac{left(6x-5right)left(x-2right)-1cdotleft(3x^2-5x-8right)}{(x-2)^2}=frac{3x^2-12x+18}{(x-2)^2}=frac{3left(x^2-4x+6right)}{(x-2)^2}$
- Производное нигде не равно нулю, нет Экстремума: Производное всюду положительно, значит, возрастает.
- Область Определения: $D_f=left(-infty;2right)+left(2;+inftyright)$ . Полюс в $x=2$ .
- Знакопостоянство: $+Z_f=left(-1;2right)+left(frac{8}{3};+inftyright)$ — функция положительна. $-Z_f=left(-infty;-1right)+left(-1;frac{8}{3}right)$ — функция отрицательна
- Монотонность: $+M_f=left(-infty;2right)+left(2;inftyright)$ — всюду возрастает
- Область значений $E_f=left(-infty;+inftyright)$
Графический способ решения уравнений
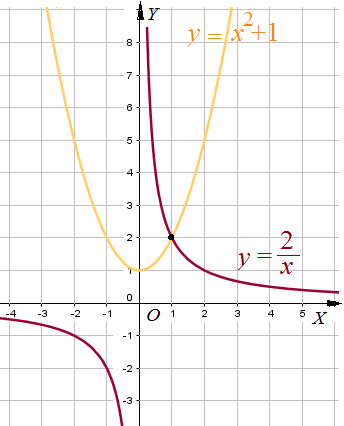
Пример 9: Решить уравнение $frac{2}{x}=x^2+1$ графическим способом.
- Построим гиперболу $y=frac{2}{x}$ и параболу $y=x^2+1$ . Равенство означает пересечение.
- Левая функция и правая функция приобретают одинаковые значения … графики этих функций пересекаются.
- По чертежу видно, что графики пересекаются в точке с координатами $left(1;2right)$. ответ: $x=1$.
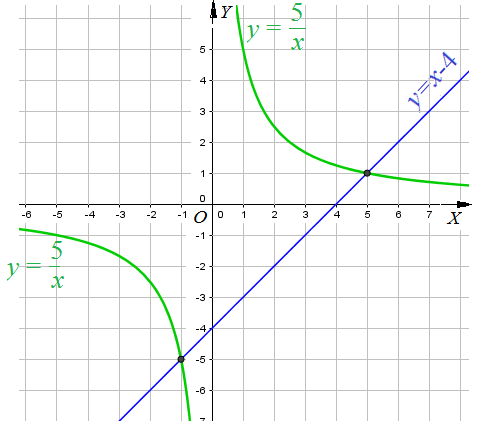
Пример 10: Решить уравнение $frac{5}{x}=x-4$.
- Построим их графики: гиперболу $y=frac{5}{x}$ и прямую $y=x-4$. пересекаются ?
- Гипербола и прямая пересекаются в точках $(-1;-5)$ и $(5;1)$. ответ: $x_1=-1$; $x_2=5$.
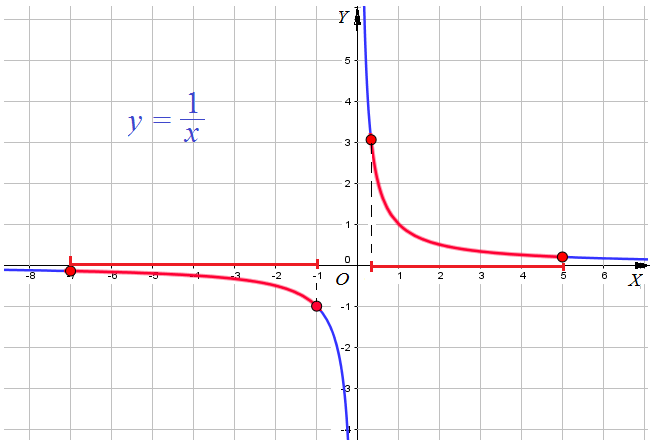
Пример 11: Найти наименьшее и наибольшее значения функции $y=frac{1}{x}$ на отрезках а) $left[frac{1}{3};5right]$ и б) $left[-7;-1right]$.
- Построим график функции $y=frac{1}{x}$ .
- Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $left[frac{1}{3};5right]$.
- Для выделенной части графика находим: наименьшее значение $y=frac{1}{5}$ при $x=5$ , наибольшее $y=3$ при $x=frac{1}{3}$.
- Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $left[-7;-1right]$.
- Для выделенной части графика находим: наименьшее значение $y=-frac{1}{7}$ при $x=-7$ наибольшее $y=-1$ при $x=-1$.














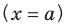
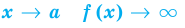
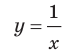
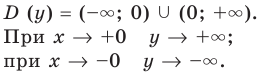
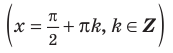
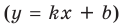
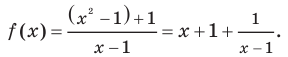
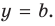
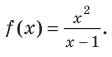
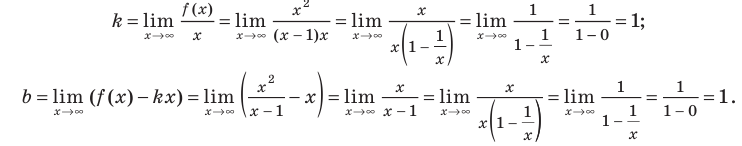
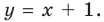
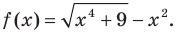
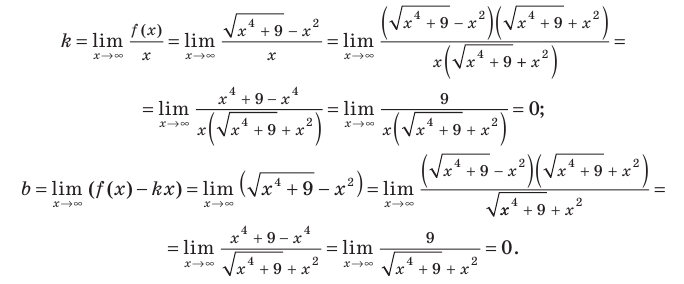
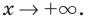
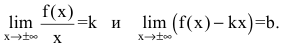
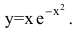
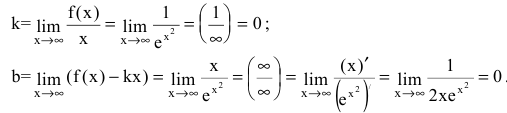
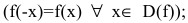 нечетность
нечетность 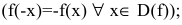 периодичность
периодичность