Атмосферное давление и его измерение
- Опыт Торричелли
- Эксперименты Отто фон Герике
- Как взвесить воздух в школьной лаборатории?
- Измерение атмосферного давления с помощью барометров
- Атмосферное давление на различных высотах
- Задачи
п.1. Опыт Торричелли
История открытия атмосферного давления тесно связана с объяснением действия насосов.
Простейшие насосы были известны еще со времен Аристотеля, который утверждал, что вода поднимается за поршнем потому, что «природа не терпит пустоты». Однако при сооружении фонтанов во Флоренции в 1638 г. оказалось, что вода поднимается чуть выше 10 м в трубе высотой 12 м и останавливается, сколько бы её ни качали, не заполняя оставшуюся в трубе «пустоту».
Галилео Галилей, к которому обратись за помощью, предложил разобраться с этой проблемой своему ученику – Эванджелиста Торричелли. После серии опытов Торричелли пришел к выводу: вес водяного столба в трубе насоса поддерживается давлением воздуха, действующего на свободную поверхность воды в резервуаре.
Поскольку речь шла о столбе жидкости, возникла замечательная идея: плотность ртути в 13,6 раз больше плотности воды, следовательно, ртутный столб таким же весом будет в 13,6 раз короче и можно перейти от громоздких опытов на стройплощадке к лабораторным исследованиям.
 |
Для опыта понадобились: 1) стеклянная трубка длиной 1 м, запаянная с одного конца; 2) колба с ртутью; 3) широкая чашка. Описание опыта Торричелли: |
Заметим, что такое неосторожное обращение с опаснейшим веществом вызывает сегодня недоумение. Однако техника безопасности при работе с ртутью была в те времена не на высоте. Вероятно, именно из-за этих опытов Торричелли прожил всего 39 лет.
На основании полученных результатов Торричелли пришел к следующему выводу:
Давление столба ртути уравновешивает атмосферное давление на поверхность ртути в чашке: (p_text{ртути}=p_text{атм}). Поэтому, измеряя высоту ртутного столба, мы узнаем атмосферное давление.
| «Мы живем на дне воздушного океана».
Эванджелиста Торричелли (1608-1647), |
 |
Идеи о том, что планету окружает атмосфера, воздух имеет вес и оказывает давление на поверхность Земли, были достаточно смелыми, и понадобилось некоторое время, чтобы их приняли современники.
п.2. Эксперименты Отто фон Герике
В 1654 году Отто фон Герике провел в Магдебурге масштабный эксперимент для демонстрации силы давления воздуха и изобретенного им воздушного насоса.
Вот как сам Герике описывал этот опыт:
«Я заказал два медных полушария диаметром в три четверти магдебургского локтя. К одному полушарию приделали кран, через который можно было выкачивать воздух с помощью воздушного насоса. К полушариям прикрепили кольца и продели в них канаты, привязанные к упряжи лошадей. Я велел соединить полушария, чтобы образовался шар, и вложить между полушариями кожаное кольцо, пропитанное смесью воска со скипидаром, — оно не пропускало воздух внутрь полушарий.
Когда воздух из полушарий выкачали, давление наружного воздуха прижало их друг к другу так сильно, что 16 лошадей не могли разнять их. Но стоило поворотом крана открыть доступ воздуху внутрь полушарий – и их можно было разнять руками».
Опыт с магдебургскими полушариями стал убедительным доказательством существования, как атмосферы, так и вакуума – безвоздушной «пустоты» внутри полушарий.
В 1657 году Герике построил водяной барометр, с помощью которого в 1660 году предсказал надвигающуюся бурю за 2 часа до её появления. В 1663 году изобрел электростатический генератор, изучал свойства электричества, описал отталкивание одноименно заряженных предметов. Будучи сторонником гелиоцентрической системы, занимался также астрономией.
Герике был выдающимся ученым, инженером, мыслителем и общественным деятелем своей эпохи. Как ученый, он особо подчеркивал важность эксперимента для формирования научного знания.
| «Философы, которые держатся исключительно за свои умозрения и аргументы, оставляя в стороне опыт, никогда не могут прийти к достоверным и справедливым выводам относительно явлений внешнего мира, и мы видим немало примеров, что человеческий разум, когда он не обращает внимания на результаты, добытые опытом, оказывается от истины дальше, чем Земля от Солнца».
Отто фон Герике (1602-1686), |
 |
п.3. Как взвесить воздух в школьной лаборатории?
Опыты Торричелли и Герике являются доказательством того, что воздух имеет вес.
В школьной лаборатории, используя несложное оборудование, можно также взвесить воздух. Для этого понадобятся:
1) прочная стеклянная колба; 2) пробка с трубкой и зажимом; 3) насос; 4) весы
Вывод: Отклонение стрелки весов равно массе откачанного воздуха.
п.4. Измерение атмосферного давления с помощью барометров
Еще в XVII веке, измеряя атмосферное давление по высоте ртутного или водного столба, исследователи заметили, что оно не остается постоянным: перед хорошей погодой давление растет, а перед ненастьем – падает. Значит, по изменению атмосферного давления можно достаточно уверенно предсказывать погоду. В эпоху освоения новых океанов и континентов такое умение было бесценным для моряков и путешественников.
Так появились барометры – приборы для измерения атмосферного давления.
Жидкостные барометры
 |
Самые простые барометры – жидкостные, в которых давление измеряется высотой столба жидкости: $$ p_text{атм}=rho gh $$ Ртутный барометр с трубкой длиной 1 м и миллиметровой шкалой был предложен Торричелли. Носить такой прибор с собой затруднительно из-за его размеров, к тому же ртуть ядовита, а вероятность вытекания высока. Водные барометры в различных городах строили Герике, Паскаль и многие другие ученые; основным элементом этих приборов была труба длиной 11-12 м. Это были капитальные сооружения, пользоваться которыми можно было только на месте постройки. |
Барометры-анероиды
Электронные барометры
 |
В наше время широко применяются электронные барометры. В них может быть вмонтирована традиционная гофрированная коробка с дальнейшей обработкой деформаций с помощью микропроцессора. Выпускаются также электронные барометры без коробки с электронным датчиком давления.  Модуль измерения атмосферного давления на основе датчика BMP-280 от BOSCH (цена менее $2) Результаты измерений выводятся на экран прибора в мм рт.ст. или в гектопаскалях (показания красным цветом на приборе, представленном на рисунке – 1013,9 гПа). |
п.5. Атмосферное давление на различных высотах
Воздух имеет массу, следовательно, он имеет вес и оказывает давление на поверхность под ним. Плотность воздуха очень сильно зависит от его температуры и влажности, а также от высоты над уровнем моря.
Как известно, расстояние между молекулами газа в несколько раз больше размера молекул, поэтому газы хорошо сжимаются (см. §16 данного справочника). В результате слои атмосферы у поверхности Земли, сжатые всеми слоями, расположенными выше, имеют большую плотность. Чем больше плотность газа, тем чаще молекулы сталкиваются между собой и различными поверхностями, т.е. тем большее давление газ создаёт.
Получается, что давление атмосферы наибольшее у поверхности Земли и постепенно уменьшается с высотой.
Атмосферное давление на различных высотах над уровнем моря
У поверхности Земли на уровне моря плотность сухого воздуха при 15°С равна 1,2250 кг/м3.
Масса одного кубометра такого воздуха (m=1,2250 text{кг}), а его вес (P=mgapprox 12 text{Н}).
Давление столба воздуха высотой 1 м: (papprox 12 text{Па}).
Давление столба воздуха высотой 1 км без учета изменения плотности: (p_1approx 12 text{кПа}).
Давление столба воздуха всей атмосферы, измеренное на поверхности Земли: $$ p_text{атм}=101,3 text{кПа} $$
Можем оценить высоту этого столба, не учитывая изменение давления с высотой $$ h=frac{p_text{атм}}{rho g}=frac{101 300}{1,2250cdot 9,8}approx 8400 (text{м})=8,4 (text{км}) $$
Если мы поднимемся на 1 км вверх, давление уменьшится на $$ p_1approx 12 text{кПа}approx 90 text{мм рт.ст.} $$
Эта величина неточная, но она может использоваться для быстрой оценки уменьшения давления с ростом высоты.
С другой стороны, зная более точную зависимость давления от высоты, можно построить прибор, который будет измерять давление, а показывать высоту. Такие приборы называют высотомерами (альтиметрами). Их используют в авиации, космонавтике и для высокогорных экспедиций.
п.6. Задачи
Задача 1. Скольким паскалям равно атмосферное давление в 730 мм рт.ст.? Выразите это давление в гектопаскалях. Какую погоду можно прогнозировать при таком давлении: ясную или пасмурную?
Дано:
(h=730 text{мм}=0,73 text{м})
(rho=13600 text{кг/м}^3)
(g=9,8 text{м/с}^2)
__________________
(p-?)
begin{gather*} p=rho gh,\[7pt] p=13600cdot 9,8cdot 0,73=97294,4 (text{Па})approx (text{гПа}) end{gather*} Это – пониженное давление. Можно прогнозировать пасмурную погоду.
Ответ: 973 гПа; прогноз – пасмурная погода
Задача 2. В эксперименте Отто фон Герике использовались медные полушария диаметром 35 см. Определите, сколько лошадей могут разорвать эти полушария, если один конец закрепить неподвижно на стене, а лошади будут тянуть другой конец с силой тяги (800 text{Н}) каждая. Площадь поверхности шара радиусом (R) рассчитывается по формуле (S=4pi R^2). Давление атмосферы примите равным 760 мм рт.ст. Давление внутри шаров примите равным двум третям атмосферного (удавалось выкачать треть воздуха).
Сколько лошадей понадобится, если лошади будут тянуть с обеих сторон?
Дано:
(D=35 text{см}=0,35 text{м})
(F_0=800 text{Н})
(p=760 text{мм рт.ст.}=101300 text{Па})
(p_text{вн}=frac 23 p)
__________________
(N-?, N’-?)
Площадь поверхности шара через диаметр $$ S=4pi R^2=4picdotleft(frac D2right)^2=pi D^2 $$ Сила давления на шар, составленный из полушарий $$ F=(p-p_text{вн})S=left(p-frac 23 pright)S=frac 13pcdot pi D^2 $$ Если один конец закреплен, то понадобится (N=frac{F}{F_0}) лошадей $$ N=frac{pcdot pi D^2}{3F_0} $$ Получаем $$ N=frac{101300cdot picdot 0,35^2}{3cdot 800}approx 16 $$ Если лошади будут тянуть в оба конца, то их понадобится в 2 раза больше $$ N’=2N=32 $$ Таким образом, используя по 8 лошадей с каждой стороны, даже при несовершенных насосах и изоляции швов в XVII веке, Герике ничем не рисковал.
Ответ: 16; 32
Задача 3. Определите глубину шахты, если на ее дне барометр показывает давление 109 кПа, а на поверхности Земли – 104 кПа. Примите плотность воздуха равной 1,3 кг/м3, g≈10 м/с2.
Дано:
(p=109cdot 10^3 text{Па})
(p_0=104cdot 10^3 text{Па})
(rho=1,3 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(h-?)
Давление на дне равно сумме давления на поверхности и давления столба воздуха $$ p=p_0+rho gh $$ Высота столба воздуха begin{gather*} h=frac{p-p_0}{rho g} end{gather*} Получаем: $$ h=frac{(109-104)cdot 10^3}{1,3cdot 10}approx 385 (text{м}) $$ Ответ: 385 м
Задача 4. Какова высота небоскреба, если у его входа барометр показывает 760 мм рт.ст., а на крыше – 740 мм рт.ст. Примите плотность воздуха равной 1,29 кг/м3.
Дано:
(h_1=760 text{мм}=0,76 text{м})
(h_2=740 text{мм}=0,74 text{м})
(rho_text{рт}=13600 text{кг/м}^3)
(rho=1,29 text{кг/м}^3)
__________________
(H-?)
Давление на входе $$ p_1=rho_text{рт}gh_1, $$ давление на крыше $$ p_2=rho_text{рт}gh_2. $$ Давление на входе равно сумме давления на крыше и давления столба воздуха высотой (H). $$ p_1=p_2+rho gH $$ Высота небоскреба begin{gather*} H=frac{p_1-p_2}{rho g}=frac{rho_text{рт}gh_1-rho_text{рт}gh_2}{rho g}\[7pt] H=frac{rho_text{рт}}{rho}(h_1-h_2) end{gather*} Получаем $$ H=frac{13600}{1,29}(0,76-0,74)approx 211 (text{м}) $$ Ответ: 211 м
Задача 5*. В трубке, запаянной с верхнего конца, удерживается столбик ртути высотой 20 см. Атмосферное давление – 760 мм рт.ст. Каково давление воздуха в верхней части трубки? Выразите ответ в мм рт.ст. и гектопаскалях.
Примите g=9,8 м/c2
Дано:
(h=20 text{см}=0,2 text{м})
(h_0=760 text{мм}=76 text{см})
(rho=13600 text{кг/м}^3)
(g=9,8 text{м/с}^2)
__________________
(p-?)
Если бы в верхней части не было воздуха, то высота столбика ртути определялась бы атмосферным давлением и равнялась бы 760 мм = 76 см.
В данном случае давление атмосферы уравновешивается суммой давления столбика ртути и давления воздуха вверху $$ p_text{атм}=rho gh+p $$ Давление воздуха вверху $$ p=p_text{атм}-rho gh=rho gh_0-rho gh=rho g(h_0-h) $$ В миллиметрах ртутного столба $$ p=h_0-h=760-200=560 text{мм рт.ст.} $$ В гектопаскалях $$ p=13600cdot 9,8cdot 0,56=74636,8 (text{Па})approx 746 (text{гПа}) $$ Ответ: 560 мм рт.ст.; 746 гПа
Атмосферное давление
Атмосферное давление — это сила, с которой давит на единицу земной поверхности столб воздуха, простирающийся от поверхности земли до верхней границы атмосферы. Атмосферное давление является одной из важнейших характеристик состояния атмосферы и одним из основных физических свойств воздуха, связанных с его плотностью и температурой.
Плотность есть отношение массы вещества к его объему. Так, 1 м3 воды при температуре 4°С имеет массу 1 т, а 1 м3 воздуха при 0°С и нормальном давлении имеет массу 1,293 кг. Следовательно, при указанных условиях плотность воды составляет 1000 кг/м3, а плотность воздуха 1,293 кг/м3. Таким образом, плотность воздуха примерно в 800 раз меньше плотности воды.
Плотность атмосферы быстро уменьшается с высотой. Половина всей массы атмосферы сосредоточена в <нижнем ее слое до высоты около 5,5 «м. На высоте 300 км плотность ее уже в 4-Ю10 раз меньше, чем на уровне моря. С дальнейшим увеличением высоты разреженность газов продолжает увеличиваться, и без четко выраженной верхней границы атмосфера постепенно переходит в межпланетное пространство.
Атмосферное давление обычно измеряется высотой ртутного столба в трубке барометра. Давление атмосферы удерживает столб ртути в трубке на определенной высоте. На уровне моря высота ртутного столба в трубке в среднем около 760 мм. При этом масса ртутного столба сечением в 1 см2 составляет примерно 76-13,6=1,0336 кг. Это означает, что атмосферное давление на уровне моря обычно около 1,033 кг/см2.
Атмосферное давление долгое время выражали в миллиметрах (мм) ртутного столба, т. е. линейной мерой измеряли силу. Чтобы измерять давление в единицах силы, в 1930 г. была установлена новая международная единица давления — бар (от древнегреческого барос — тяжесть), равная давлению 1 млн. дин на площадь 1 см2, что соответствует 750,1 мм рт. ст. В практике в качестве единицы давления использовалась тысячная часть бара —миллибар. С 1980 г. в качестве международной единицы для измерения атмосферного давления принят паскаль (Па) —давление, вызываемое силой в 1 ньютон на площадь 1 м2:
1 Па = 1 Н/м2 = Ю-5 бар = 0,01 мбар.
Для практических целей используют гектопаскаль (гПа). Поскольку до сих пор шкала приборов для измерения атмосферного давления градуирована в миллиметрах или миллибарах (мбар), то надо знать их соотношение:
1 гПа = 1 мбар =0,75 мм рт. ст.
Ускорение свободного падения на земном шаре увеличивается от экватора к полюсам и уменьшается с высотой. Чтобы исключить зависимость высоты ртутного столба, уравновешивающего атмосферное давление, от этих факторов, измеренное атмосферное давление приводят к ускорению свободного падения на широте 45° и на уровне моря. Давление, равное массе ртутного столба высотой 760 мм, имеющего температуру 0,0 °С и находящегося на широте 45° и на уровне моря, называют нормальным атмосферным давлением. Оно округленно составляет 1013 гПа.
Рекомендуемые материалы
Для измерения атмосферного давления применяют барометры. На наземных метеорологических станциях используют станционные чашечные барометры, а для полевых, экспедиционных, судовых, самолетных и тому подобных измерений предназначены барометры-анероиды. Для непрерывной записи атмосферного давления предназначен барограф.
Изменение давления с высотой. Барическая ступень
Непосредственные наблюдения и теоретические соображения показывают, что плотность и давление воздуха уменьшаются с высотой. Если на уровне моря давление составляет в среднем1 примерно 1013 гПа, то на высоте 5,5 км оно уже около 500 гПа, а на высоте 20 км — менее 50 гПа.
Изменение давления с высотой характеризуют барической ступенью. Барическая ступень есть то расстояние по вертикали, на котором давление меняется на 1 гПа. Барическая ступень может быть вычислена по формуле:
/г = 8291(1+0,0040 м/гПа,
где р — давление (в гПа) и I — температура (в °С) в той же точке, для которой вычисляется барическая ступень.
Допустим, что давление составляет 1000 гПа, температура 5° С. Тогда
* я
= — (1 + 0,004 • 5) = 8,0 (1 + 0,02) « 8 м/гПа.
Следовательно, при заданных исходных условиях давление уменьшается на 1 гПа при подъеме примерно на 8 м.
Вместе с этой лекцией читают «8 Организация интерфейса МП».
Как видно из формулы, барическая ступень несколько изменяется при изменении температуры и давления воздуха (табл. 2) . Например, при давлении 1000 гПа и изменении температуры от — 40 до 40° С барическая ступень возрастает на 2,6 м/гПа. При 0° С ее значение равно 8 м/гПа.
Зная барическую ступень, атмосферное давление, температуру воздуха и высоту над уровнем моря в одном из двух пунктов, лежащих на разной высоте, можно по разности давлений в этих пунктах определить разность их высот, а отсюда найти и высоту второго пункта над уровнем моря. Этот способ определения высоты пункта называется барометрическим, нивелированием.. Барометрическое нивелирование бывает необходимо при экспедиционных исследованиях в горных местностях для приближенного определения высоты различных форм рельефа.
Изменчивость давления на поверхности Земли. Горизонтальный барический градиент
Атмосферное давление в разных точках земной поверхности в один и тот же момент неодинаково, так как оно зависит от степени нагревания или охлаждения воздуха над этими точками, от характера имеющихся над ними воздушных течений и ряда других причин. Информацию об атмосферном давлении дают метеорологические станции. Поскольку они расположены на разных высотах, а давление зависит от высоты места, то его значения, измеренные на разных станциях, нельзя непосредственно сравнивать между собой. Их нужно сначала привести к какой-либо одинаковой высоте. За такую высоту принят уровень моря.
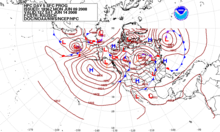
Чтобы получить наглядное представление о распределении давления по земному шару, на географическую карту наносят давление, измеренное в одно и то же время в разных пунктах и приведенное к уровню моря. Затем пункты, в которых давление одинаково, соединяют плавными линиями. Эти линии называют изобарами. Описанный способ картирования распределения давления по территории позволяет устанавливать расположение областей пониженного и повышенного давления на земном шаре! (рис. 2) и наблюдать за их передвижением, что имеет важное значение для прогноза погоды.
Изменение давления вдоль горизонтали, направленной перпендикулярно к изобарам в сторону от высокого давления к низкому, приходящееся на расстояние в 100 км, называют горизонтальным, барическим градиентом. Эта величина обычно составляет около 1—2 гПа/100 км. Горизонтальный барический градиент вызывает горизонтальное движение воздуха, т. е. ветер.
Валентина Николаевна Норина
Эксперт по предмету «География»
преподавательский стаж — 38 лет
Задать вопрос автору статьи
Понятие об атмосферном давлении
Любой газ, входящий в состав атмосферы, характеризуется плотностью, температурой и давлением. Если заключить его в сосуд, то он будет давить на стенки этого сосуда, потому что молекулы газа двигаются и создают давление, действуя на стенки сосуда с определенной силой. Скорость движения молекул в сосуде можно увеличить при повышении температуры, тогда увеличится и давление. Любая точка атмосферы или поверхности Земли характеризуется определенной величиной атмосферного давления. Эта величина будет равна весу вышележащего столба воздуха.
Определение 1
Атмосферное давление – это напор атмосферы на единицу площади земной поверхности.
Единицей измерения атмосферного давления являются граммы на кв. см, а нормальным считается давление, равное $760$ мм рт. столба или $1, 033$ кг/см кв. Эту величину принято считать за одну атмосферу.
Замечание 1
В результате постоянного движения масса воздуха в том или ином месте меняется и там, где воздуха больше, давление повышается. Движение воздуха связано с изменением температуры – нагретый от земной поверхности воздух расширяется и поднимается вверх, растекаясь в стороны. Результатом является понижение давления у поверхности Земли.
Воздух над холодной поверхностью охлаждается, уплотняется, становится тяжелым и опускается вниз – давление возрастает. Земная поверхность нагревается неодинаково, а это приводит к образованию разных областей атмосферного давления, которые имеют строго широтную зональность в распределении.
Материки и океаны на Земле расположены неравномерно, они по-разному получают и отдают солнечное тепло, поэтому пояса высокого и низкого давления распределены над поверхностью не ровными полосами. Кроме этого в результате наклона земной оси к плоскости орбиты Северное и Южное полушария получают разное количество тепла.
«Атмосферное давление» 👇
Эти особенности привели к тому, что на планете сформировалось несколько поясов атмосферного давления:
- Низкое давление на экваторе;
- Высокое давление в тропиках;
- Низкое давление над умеренными широтами;
- Высокое давление над полюсами.
Распределение давления на поверхности показано на географических картах специальным условным знаком, который называется изобара.
Определение 2
Изобары – это линии, соединяющие точки земной поверхности с одинаковым давлением.
С атмосферным давлением очень тесно связаны погода и климат той или иной местности. Безоблачная, безветренная, сухая погода характерна для высокого атмосферного давления и, наоборот, низкое давление сопровождается облачностью, осадками, ветрами, туманами.
Открытие атмосферного давления
То, что воздух давит на наземные предметы, люди замечали еще в глубокой древности. Давление вызывало ветер, который двигал парусные суда и вращал крылья ветряных мельниц. Но, доказать, что воздух имеет собственный вес, долго не удавалось и только в $ XVII$ весомость воздуха была доказана с помощью опыта, поставленного итальянцем Э. Торричелли. Опыту предшествовал случай во дворце герцога Тосканского в $1640$ г, задумавшего устроить фонтан. Вода для фонтана должна была поступать из озера, расположенного неподалеку, но выше $32$ футов, т.е. $10,3$ м она не поднималась. Торричелли провел целую серию долгих опытов, в результате которых было доказано, что воздух имеет вес, а давление атмосферы уравновешивается столбом воды в $32$ фута.
В $1643$ г. Торричелли совместно с В. Вивиани проводит опыт по измерению атмосферного давления с помощью трубки, запаянной с одного конца и наполненной ртутью. Трубка опускалась в сосуд, где тоже была ртуть, не запаянным концом вниз и столб ртути в трубке падал до отметки $760$ мм – это был уровень ртути в сосуде.
В сосуде остается свободная поверхность, на которую действует атмосферное давление. После снижения столбика ртути в трубке над ртутью остается пустота – давление столба ртути в трубке на уровне поверхности ртути в сосуде должно равняться атмосферному давлению. Высота столба в миллиметрах над свободной поверхностью ртути измеряет давление атмосферы прямо в миллиметрах ртутного столба. Трубка Торричелли, стала первым ртутным барометром для измерения давления атмосферы.
Столб воздуха от уровня моря до верхней границы атмосферы давит на площадку в один сантиметр с такой же силой, как гиря весом $1 кг 33 г. $ Все живые организмы этого давления не ощущают, потому что оно уравновешивается их внутренним давлением. Внутреннее давление живых организмов не изменяется.
Изменение атмосферного давления
С высотой атмосферное давление изменяется, оно начинает падать. Происходит это, потому что газы сильно сжимаемы. Сильно сжатый газ имеет большую плотность и сильнее давит. С удалением от поверхности Земли сжатость газов ослабевает, плотность уменьшается, а, следовательно, и давление, которое они могут производить. Давление уменьшается на $1$ миллиметр ртутного столба при подъеме на каждые $10,5$ м.
Пример 1
Атмосферное давление на высоте $2200$ м над уровнем моря составляет $545$ мм ртутного столба. Определить давление на высоте $3300$ м.
Решение: с высотой атмосферное давление понижается на $1$ мм ртутного столба через каждые $10,5$ м, поэтому
Определим разницу высот: $3300 – 2205 = 1095$ м
Находим разницу атмосферного давления: $1095 м div 10,5 = 104,3$ мм рт. столба
Определяем атмосферное давление на высоте $3300 мdiv 545 мм – 104,3 мм = 440,7$ мм рт. столба.
Ответ: атмосферное давление на высоте $3300$ м составляет $440,7$ мм ртутного столба.
Атмосферное давление изменяется и в течение суток, т.е. имеет свой суточный ход. При максимальной температуре днем атмосферное давление понижается, а в ночное время, когда температура воздуха становится ниже – давление увеличивается. В этом ходе давления просматривается два максимума (около $10$ и $22$ часов) и два минимума (около $4$ и $16$ часов). Очень четко эти изменения проявляются в тропических широтах, где суточные колебания составляют $3$-$4$ мбар. Нарушение правильности суточного хода давления в тропиках, говорит о приближении тропического циклона.
Замечание 2
Изменение давления в течение суток связано с температурой воздуха и зависит от её изменений. Годовые изменения зависят от нагревания материков и океанов в летний период и их охлаждения в зимнее время. Летом область пониженного давления создается на суше, а область повышенного давления над океаном.
Влияние атмосферного давления на организм человека
Процессы, происходящие в атмосфере, оказывают значительное влияние на организм человека, который вынужден перенастраивать свои биологические системы. Значительная часть людей сильно реагируют на изменение атмосферного давления, с понижением которого падает давление в артериях человека. С ростом атмосферного давления – растет давление артериальное, поэтому часто в ясную, сухую, жаркую погоду, многие испытывают головную боль.
Здоровые люди годовые колебания атмосферного воздуха переносят легко и незаметно, а у больных ухудшается самочувствие, наблюдаются приступы стенокардии, чувство страха, нарушение сна.
На атмосферное давление реагирует кожа и слизистые оболочки. С ростом давления увеличивается раздражение их рецепторов и в результате уменьшается содержание кислорода в крови. С повышенным атмосферным давлением связывают обострение бронхиальной астмы. Быстрое снижение атмосферного давления может привести к развитию патологических явлений в организме человека, связанных с кислородным голоданием тканей и, прежде всего, головного мозга.
Человек не может повлиять на погоду, но помочь себе пережить этот период совсем не сложно. При резких перепадах атмосферного давления необходимо максимально снизить физическую нагрузку на свой организм и использовать соответствующие лекарственные препараты.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
From Wikipedia, the free encyclopedia
«Air pressure» redirects here. For the pressure of air in other systems, see Pressure.
Atmospheric pressure, also known as barometric pressure (after the barometer), is the pressure within the atmosphere of Earth. The standard atmosphere (symbol: atm) is a unit of pressure defined as 101,325 Pa (1,013.25 hPa), which is equivalent to 1,013.25 millibars,[1] 760 mm Hg, 29.9212 inches Hg, or 14.696 psi.[2] The atm unit is roughly equivalent to the mean sea-level atmospheric pressure on Earth; that is, the Earth’s atmospheric pressure at sea level is approximately 1 atm.
In most circumstances, atmospheric pressure is closely approximated by the hydrostatic pressure caused by the weight of air above the measurement point. As elevation increases, there is less overlying atmospheric mass, so atmospheric pressure decreases with increasing elevation. Because the atmosphere is thin relative to the Earth’s radius—especially the dense atmospheric layer at low altitudes—the Earth’s gravitational acceleration as a function of altitude can be approximated as constant and contributes little to this fall-off. Pressure measures force per unit area, with SI units of pascals (1 pascal = 1 newton per square metre, 1 N/m2). On average, a column of air with a cross-sectional area of 1 square centimetre (cm2), measured from the mean (average) sea level to the top of Earth’s atmosphere, has a mass of about 1.03 kilogram and exerts a force or «weight» of about 10.1 newtons, resulting in a pressure of 10.1 N/cm2 or 101 kN/m2 (101 kilopascals, kPa). A column of air with a cross-sectional area of 1 in2 would have a weight of about 14.7 lbf, resulting in a pressure of 14.7 lbf/in2.
Mechanism[edit]
Atmospheric pressure is caused by the gravitational attraction of the planet on the atmospheric gases above the surface and is a function of the mass of the planet, the radius of the surface, and the amount and composition of the gases and their vertical distribution in the atmosphere.[3][4] It is modified by the planetary rotation and local effects such as wind velocity, density variations due to temperature and variations in composition.[5]
Mean sea-level pressure[edit]
Map showing atmospheric pressure in mbar or hPa
15-year average mean sea-level pressure for June, July, and August (top) and December, January, and February (bottom). ERA-15 re-analysis.
The mean sea-level pressure (MSLP) is the atmospheric pressure at mean sea level (PMSL). This is the atmospheric pressure normally given in weather reports on radio, television, and newspapers or on the Internet. When barometers in the home are set to match the local weather reports, they display pressure adjusted to sea level, not the actual local atmospheric pressure.
The altimeter setting in aviation is an atmospheric pressure adjustment.
Average sea-level pressure is 1,013.25 hPa (29.921 inHg; 760.00 mmHg). In aviation weather reports (METAR), QNH is transmitted around the world in hectopascals or millibars (1 hectopascal = 1 millibar), except in the United States, Canada, and Japan where it is reported in inches of mercury (to two decimal places). The United States and Canada also report sea-level pressure SLP, which is adjusted to sea level by a different method, in the remarks section, not in the internationally transmitted part of the code, in hectopascals or millibars.[6] However, in Canada’s public weather reports, sea level pressure is instead reported in kilopascals.[7]
In the US weather code remarks, three digits are all that are transmitted; decimal points and the one or two most significant digits are omitted: 1,013.2 hPa (14.695 psi) is transmitted as 132; 1,000 hPa (100 kPa) is transmitted as 000; 998.7 hPa is transmitted as 987; etc. The highest sea-level pressure on Earth occurs in Siberia, where the Siberian High often attains a sea-level pressure above 1,050 hPa (15.2 psi; 31 inHg), with record highs close to 1,085 hPa (15.74 psi; 32.0 inHg). The lowest measurable sea-level pressure is found at the centres of tropical cyclones and tornadoes, with a record low of 870 hPa (12.6 psi; 26 inHg).
Surface pressure [edit]
Surface pressure is the atmospheric pressure at a location on Earth’s surface (terrain and oceans). It is directly proportional to the mass of air over that location.
For numerical reasons, atmospheric models such as general circulation models (GCMs) usually predict the nondimensional logarithm of surface pressure.
The average value of surface pressure on Earth is 985 hPa.[8] This is in contrast to mean sea-level pressure, which involves the extrapolation of pressure to sea level for locations above or below sea level. The average pressure at mean sea level (MSL) in the International Standard Atmosphere (ISA) is 1,013.25 hPa, or 1 atmosphere (atm), or 29.92 inches of mercury.
Pressure (P), mass (m), and acceleration due to gravity (g) are related by P = F/A = (m*g)/A, where A is the surface area. Atmospheric pressure is thus proportional to the weight per unit area of the atmospheric mass above that location.
Altitude variation[edit]
Variation in atmospheric pressure with altitude, computed for 15 °C and 0% relative humidity.
This plastic bottle was sealed at approximately 4,300 metres (14,000 ft) altitude, and was crushed by the increase in atmospheric pressure, recorded at 2,700 metres (9,000 ft) and 300 metres (1,000 ft), as it was brought down towards sea level.
Pressure on Earth varies with the altitude of the surface, so air pressure on mountains is usually lower than air pressure at sea level. Pressure varies smoothly from the Earth’s surface to the top of the mesosphere. Although the pressure changes with the weather, NASA has averaged the conditions for all parts of the earth year-round. As altitude increases, atmospheric pressure decreases. One can calculate the atmospheric pressure at a given altitude.[9] Temperature and humidity also affect the atmospheric pressure. Pressure is proportional to temperature and inversely proportional to humidity. And it is necessary to know both of these to compute an accurate figure. The graph on the rightabove was developed for a temperature of 15 °C and a relative humidity of 0%.
At low altitudes above sea level, the pressure decreases by about 1.2 kPa (12 hPa) for every 100 metres. For higher altitudes within the troposphere, the following equation (the barometric formula) relates atmospheric pressure p to altitude h:

. The values in these equations are:
| Parameter | Description | Value |
|---|---|---|
| h | Height above mean sea level | m |
| p0 | Sea level standard atmospheric pressure | 101,325 Pa |
| L | Temperature lapse rate, = g/cp for dry air | ~ 0.00976 K/m |
| cp | Constant-pressure specific heat | 1,004.68506 J/(kg·K) |
| T0 | Sea level standard temperature | 288.16 K |
| g | Earth-surface gravitational acceleration | 9.80665 m/s2 |
| M | Molar mass of dry air | 0.02896968 kg/mol |
| R0 | Universal gas constant | 8.314462618 J/(mol·K) |
Local variation[edit]
Hurricane Wilma on 19 October 2005. The pressure in the eye of the storm was 882 hPa (12.79 psi) at the time the image was taken.
Atmospheric pressure varies widely on Earth, and these changes are important in studying weather and climate. Atmospheric pressure shows a diurnal or semidiurnal (twice-daily) cycle caused by global atmospheric tides. This effect is strongest in tropical zones, with an amplitude of a few hectopascals, and almost zero in polar areas. These variations have two superimposed cycles, a circadian (24 h) cycle, and a semi-circadian (12 h) cycle.
Records[edit]
The highest adjusted-to-sea level barometric pressure ever recorded on Earth (above 750 meters) was 1,084.8 hPa (32.03 inHg) measured in Tosontsengel, Mongolia on 19 December 2001.[10] The highest adjusted-to-sea level barometric pressure ever recorded (below 750 meters) was at Agata in Evenk Autonomous Okrug, Russia (66°53′ N, 93°28′ E, elevation: 261 m, 856 ft) on 31 December 1968 of 1,083.8 hPa (32.005 inHg).[11] The discrimination is due to the problematic assumptions (assuming a standard lapse rate) associated with reduction of sea level from high elevations.[10]
The Dead Sea, the lowest place on Earth at 430 metres (1,410 ft) below sea level, has a correspondingly high typical atmospheric pressure of 1,065 hPa.[12] A below-sea-level surface pressure record of 1,081.8 hPa (31.95 inHg) was set on 21 February 1961.[13]
The lowest non-tornadic atmospheric pressure ever measured was 870 hPa (0.858 atm; 25.69 inHg), set on 12 October 1979, during Typhoon Tip in the western Pacific Ocean. The measurement was based on an instrumental observation made from a reconnaissance aircraft.[14]
Measurement based on the depth of water[edit]
One atmosphere (101.325 kPa or 14.7 psi) is also the pressure caused by the weight of a column of freshwater of approximately 10.3 m (33.8 ft). Thus, a diver 10.3 m underwater experiences a pressure of about 2 atmospheres (1 atm of air plus 1 atm of water). Conversely, 10.3 m is the maximum height to which water can be raised using suction under standard atmospheric conditions.
Low pressures, such as natural gas lines, are sometimes specified in inches of water, typically written as w.c. (water column) gauge or w.g. (inches water) gauge. A typical gas-using residential appliance in the US is rated for a maximum of 1⁄2 psi (3.4 kPa; 34 mbar), which is approximately 14 w.g. Similar metric units with a wide variety of names and notation based on millimetres, centimetres or metres are now less commonly used.
Boiling point of liquids[edit]
Pure water boils at 100 °C (212 °F) at earth’s standard atmospheric pressure. The boiling point is the temperature at which the vapour pressure is equal to the atmospheric pressure around the liquid.[15] Because of this, the boiling point of liquids is lower at lower pressure and higher at higher pressure. Cooking at high elevations, therefore, requires adjustments to recipes[16] or pressure cooking. A rough approximation of elevation can be obtained by measuring the temperature at which water boils; in the mid-19th century, this method was used by explorers.[17] Conversely, if one wishes to evaporate a liquid at a lower temperature, for example in distillation, the atmospheric pressure may be lowered by using a vacuum pump, as in a rotary evaporator.
Measurement and maps[edit]
An important application of the knowledge that atmospheric pressure varies directly with altitude was in determining the height of hills and mountains, thanks to reliable pressure measurement devices. In 1774, Maskelyne was confirming Newton’s theory of gravitation at and on Schiehallion mountain in Scotland, and he needed to measure elevations on the mountain’s sides accurately. William Roy, using barometric pressure, was able to confirm Maskelyne’s height determinations, the agreement being to be within one meter (3.28 feet). This method became and continues to be useful for survey work and map making.[18]
See also[edit]
- Atmospheric density – Mass per unit volume of earths atmosphere
- Atmosphere of Earth – Gas layer surrounding Earth
- Barometric formula – Formula used to model how air pressure varies with altitude
- Barotrauma – Injury caused by pressure – physical damage to body tissues caused by a difference in pressure between an air space inside or beside the body and the surrounding gas or liquid.
- Cabin pressurization – Process to maintain internal air pressure in aircraft
- Cavitation – Low-pressure voids formed in liquids
- Collapsing can – an aluminium can is crushed by the atmospheric pressure surrounding it
- Effects of high altitude on humans – Environmental effects on physiology
- High-pressure area – In meteorology, an anticyclone
- International Standard Atmosphere – Atmospheric model, a tabulation of typical variations of principal thermodynamic variables of the atmosphere (pressure, density, temperature, etc.) with altitude, at middle latitudes.
- Low-pressure area – Area with air pressures lower than adjacent areas
- Meteorology – Interdisciplinary scientific study of the atmosphere focusing on weather forecasting
- NRLMSISE-00, an empirical, global reference atmospheric model of the Earth from ground to space
- Plenum chamber – Chamber containing a fluid under pressure
- Pressure – Force distributed over an area
- Pressure measurement – Analysis of force applied by a fluid on a surface
- Standard atmosphere (unit) – Unit of pressure defined as 101325 Pa
- Horse latitudes – Latitudes 30–35 degrees north and south of the Equator
References[edit]
- ^ «Statement (2001)». BIPM. Retrieved 2022-03-19.
- ^ International Civil Aviation Organization. Manual of the ICAO Standard Atmosphere, Doc 7488-CD, Third Edition, 1993. ISBN 92-9194-004-6.
- ^ «atmospheric pressure (encyclopedic entry)». National Geographic. Archived from the original on 28 February 2018. Retrieved 28 February 2018.
- ^ «Q & A: Pressure – Gravity Matters?». Department of Physics. University of Illinois Urbana-Champaign. Archived from the original on 28 February 2018. Retrieved 28 February 2018.
- ^ Jacob, Daniel J. (1999). Introduction to Atmospheric Chemistry. Princeton University Press. ISBN 9780691001852. Archived from the original on 2021-10-01. Retrieved 2020-10-15.
- ^ Sample METAR of CYVR Archived 2019-05-25 at the Wayback Machine Nav Canada
- ^ Montreal Current Weather, CBC Montreal, Canada, archived from the original on 2014-03-30, retrieved 2014-03-30
- ^ Jacob, Daniel J. Introduction to Atmospheric Chemistry Archived 2020-07-25 at the Wayback Machine. Princeton University Press, 1999.
- ^ A quick derivation relating altitude to air pressure Archived 2011-09-28 at the Wayback Machine by Portland State Aerospace Society, 2004, accessed 05032011
- ^ a b World: Highest Sea Level Air Pressure Above 750 m, Wmo.asu.edu, 2001-12-19, archived from the original on 2012-10-17, retrieved 2013-04-15
- ^ World: Highest Sea Level Air Pressure Below 750 m, Wmo.asu.edu, 1968-12-31, archived from the original on 2013-05-14, retrieved 2013-04-15
- ^ Kramer, MR; Springer C; Berkman N; Glazer M; Bublil M; Bar-Yishay E; Godfrey S (March 1998). «Rehabilitation of hypoxemic patients with COPD at low altitude at the Dead Sea, the lowest place on earth» (PDF). Chest. 113 (3): 571–575. doi:10.1378/chest.113.3.571. PMID 9515826. Archived from the original (PDF) on 2013-10-29.
- ^ Court, Arnold (1969). «Improbable Pressure Extreme: 1070 Mb». Bulletin of the American Meteorological Society. 50 (4): 248–50. JSTOR 26252600.
- ^ Chris Landsea (2010-04-21). «Subject: E1), Which is the most intense tropical cyclone on record?». Atlantic Oceanographic and Meteorological Laboratory. Archived from the original on 6 December 2010. Retrieved 2010-11-23.
- ^ Vapour Pressure, Hyperphysics.phy-astr.gsu.edu, archived from the original on 2017-09-14, retrieved 2012-10-17
- ^ High Altitude Cooking, Crisco.com, 2010-09-30, archived from the original on 2012-09-07, retrieved 2012-10-17
- ^ Berberan-Santos, M. N.; Bodunov, E. N.; Pogliani, L. (1997). «On the barometric formula». American Journal of Physics. 65 (5): 404–412. Bibcode:1997AmJPh..65..404B. doi:10.1119/1.18555.
- ^ Hewitt, Rachel, Map of a Nation – a Biography of the Ordnance Survey ISBN 1-84708-098-7
External links[edit]
- 1976 Standard Atmosphere from NASA
- Source code and equations for the 1976 Standard Atmosphere
- A mathematical model of the 1976 U.S. Standard Atmosphere
- Calculator using multiple units and properties for the 1976 Standard Atmosphere
- Calculator giving standard air pressure at a specified altitude, or altitude at which a pressure would be standard
- Current map of global mean sea-level pressure
- Calculate pressure from altitude and vice versa
Experiments[edit]
- Movies on atmospheric pressure experiments from Georgia State University’s HyperPhysics website – requires QuickTime
- Test showing a can being crushed after boiling water inside it, then moving it into a tub of ice-cold water.
Сегодня разбираем еще один запрос пользователя — Атмосферное давление, в котором нас просят вычислить атмосферное давление. В виду отсутствия дополнительной информации в запросе, я предположил, что нужно рассчитывать атмосферное давление в зависимости от высоты над уровнем моря.
Зависимость давления газа от высоты определяется так называемой барометрической формулой
,
где
— разность высот, м
— молярная масса воздуха, 29 г/моль (в расчете используется 0.029 кг/моль)
— универсальная газовая постоянная, 8.31 Дж/(мольК)
— ускорение силы тяжести, 9.81 м/(сс)
— температура воздуха (К)
Кстати, еще тема атмосферного давления развивается здесь Барометрическое нивелирование и здесь Зависимость температуры кипения воды от высоты над уровнем моря.
Ниже калькулятор — вводим давление на высоте уровня моря (можно оставить по умолчанию; 760 миллиметров ртутного столба — это нормальное атмосферное давление), температуру и высоту, получаем результат.
Зависимость давления от высоты над уровнем моря
Давление на уровне моря (мм.рт.ст.)
Температура воздуха (градусы Цельсия)
Высота над уровнем моря (метры)
Давление на заданной высоте (мм.рт.ст.)