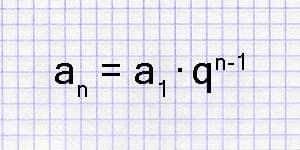Геометрическая прогрессия — это числовая последовательность, в которой все ее члены расположены в порядке, подчиняющемся определенной закономерности. Формула геометрической прогрессии определяет, что каждое следующее число будет получено умножением предыдущего на знаменатель прогрессии — постоянное число, не меняющее свое значение в пределах одной последовательности.
bn=b1 q(n-1)
В зависимости от знаменателя прогрессии, выписанные члены геометрической прогрессии могут давать различный вид ряда. Если знаменатель является числом положительным, больше 1 (k > 1), тогда он будет увеличивать значение каждого следующего числа. Такая прогрессия будет монотонно возрастать на протяжении всего ряда. Если знаменатель — положительный, но находится между 0 и 1 (0 < k < 1), тогда он будет каждый раз уменьшать значение следующего члена, и такая прогрессия будет называться бесконечно убывающая геометрическая прогрессия.
Если для все возрастающей последовательности, можно только найти сумму первых членов геометрической прогрессии, то сумма членов бесконечно убывающей прогрессии будет равна вполне конкретному числовому значению, которое может рассчитать калькулятор. Третий случай представлен отрицательным знаменателем (k < 0), тогда прогрессия становится знакочередующейся, то есть первые члены геометрической прогрессии определяют порядок знаков для всей последовательности чисел. Как знаменатель геометрической прогрессии, так и первый член геометрической прогрессии по определению не могут быть равны нулю.
Существует всего несколько формул геометрической прогрессии, из которых можно вывести все необходимые для решения конкретных задач:
• Формула первого члена геометрической прогрессии;
• Формула n члена геометрической прогрессии;
• Формула суммы первых членов геометрической прогрессии;
• Формула суммы бесконечно убывающей геометрической прогрессии;
• Формула знаменателя геометрической прогрессии.
Таким образом, если условиями задана геометрическая прогрессия с хотя бы двумя параметрами из всех выше представленных, для нее можно будет найти любую из всех прочих переменных.
Геометрическая прогрессия
- Понятие геометрической прогрессии
- Формула n-го члена геометрической прогрессии
- Свойства геометрической прогрессии
- Сумма первых n членов геометрической прогрессии
- Примеры
п.1. Понятие геометрической прогрессии
Геометрической прогрессией называют числовую последовательность, каждый член которой bn, начиная со второго, равен произведению предыдущего члена bn-1 и некоторого постоянного числа q: $$ mathrm{ b_n=b_{n-1}q, ninmathbb{N}, n ge 2, qne 0, qne 1, b_1ne 0 } $$ Число q называют знаменателем геометрической прогрессии.
Например:
1. Последовательность 1, 3, 9, 27, … является геометрической прогрессией с b1 = 1, q = 3.
2. Последовательность (mathrm{9, -3, 1, -frac13, frac19,…}) является геометрической прогрессией с b1 = 9, (mathrm{q=-frac13}).
п.2. Формула n-го члена геометрической прогрессии
По определению геометрической прогрессии мы получаем рекуррентную формулу для n-го члена: bn = bn-1q. Из неё можно вывести аналитическую формулу:
b2 = b1q, b3 = b2q = (b1q)q = b1q2, b4 = b3q = (b1q2)q = b1q3,…
Получаем:
bn = b1qn-1
Например:
Найдём b5, если известно, что (mathrm{b_1=frac12, q=2}).
По формуле n-го члена получаем: (mathrm{b_5=b_1q^4=frac12cdot 2^4=2^3=8})
п.3. Свойства геометрической прогрессии
Свойство 1. Экспоненциальный рост/падение
Геометрическая прогрессия с положительными первым членом и знаменателем b1 > 0, q > 0 является показательной функцией вида f(n) = kqn: $$ mathrm{ b_n=frac{b_1}{q}q^n } $$
При b1 > 0, q > 1 прогрессия экпоненциально растёт
При b1 > 0, 0 < q < 1 прогрессия экпоненциально падает
Свойство 2. Признак геометрической прогрессии
Для того чтобы числовая последовательность была геометрической прогрессией необходимо и достаточно, чтобы каждый её член, начиная со второго, был средним геометрическим предыдущего и последующего членов: $$ mathrm{ left{b_nright} — text{геометрическая прогрессия} Leftrightarrow b_n=sqrt{b_{n-1}b_{n+1}}, ninmathbb{N}, n geq 2 } $$ Следствие: аждый член прогрессии является средним геометрическим двух равноудалённых от него членов: $$ mathrm{ b_n=sqrt{b_{n-k}b_{n+k}}, ninmathbb{N}, kinmathbb{N}, n geq k+1 } $$
Например:
Найдём b9, если известно, что (mathrm{b_7=frac{1}{16}, b_{11}=4})
По следствию из признака геометрической прогрессии: (mathrm{b_9=sqrt{b_7b_{11}}=sqrt{frac{1}{16}cdot 4}=frac12})
Свойство 3. Равенство сумм индексов
Если {bn} – геометрическая прогрессия, то из равенства сумм индексов следует равенство произведений членов: $$ mathrm{ m+k=p+q Rightarrow b_mb_k=b_pb_q } $$ Следствие: произведение членов, равноудалённых от концов прогрессии, является постоянной величиной: $$ mathrm{ b_1b_n = b_2b_{n-1}=b_3b_{n-2}=… } $$
Например:
Найдём b6, если известно, что b2 = 5, b4 = 10, b8 = 40
По равенству сумм индексов b2b8 = b4b6
Откуда (mathrm{b_6=frac{b_2b_8}{b_4}=frac{5cdot 40}{10}=20})
п.4. Сумма первых n членов геометрической прогрессии
Сумма первых n членов геометрической прогрессии равна $$mathrm{ S_n=frac{b_nq-b_1}{q-1}, qne 1} $$
Если учесть, что bn = b1qn-1, получаем ещё одну формулу для суммы: $$mathrm{ S_n=b_1frac{q^n-1}{q-1}, qne 1} $$
Например:
Найдём сумму первых 10 степеней двойки: 2 + 22 + 23 + … + 210
В этом случае b1 = 2, q = 2, n = 10
Получаем: (mathrm{ S_{10}=2cdot frac{2^{10}-1}{2-1}=2cdot (1024-1)=2046})
п.5. Примеры
Пример 1. Найдите знаменатель геометрической прогрессии и сумму первых 10 членов, если:
а) b5 = 9, b8 = 243
Найдём отношение $$ mathrm{ frac{b_8}{b_5}=frac{b_1cdot q^7}{b_1cdot q^4}=q^3, frac{b_8}{b_5}=frac{243}{9}=27=3^3, q^3=3^3Rightarrow q = 3 } $$ Найдём 1-й член: $$ mathrm{ b_1=frac{b_5}{q^4}=frac{9}{3^4}=frac{3^2}{3^4}=frac{1}{3^2}=frac19 } $$ Сумма: $$ mathrm{ S_{10}=b_1frac{q^{10}-1}{q-1}=frac{3^{10}-1}{9cdot 2}=frac{29524}{9}=3280frac49 } $$ Ответ: q = 3, S10 = (mathrm{3280frac49})
б) b1 = 3, bn = 96, Sn = 189
По формуле суммы: $$ mathrm{ S_{n}=frac{b_nq-b_1}{q-1}Rightarrow 189 =frac{96q-3}{q-1}Rightarrow 189(q-1)=96q-3Rightarrow 93q=186Rightarrow q = 2 } $$ Сумма: $$ mathrm{ S_{10}=b_1frac{q^{10}-1}{q-1}=3cdot frac{2^{10}-1}{2-1}=3cdot 1023=3069 } $$ Ответ: q = 2, S10 = 3069
Пример 2. Между числами (mathrm{40frac12 text{и} 5frac13}) вставьте такие четыре числа, чтобы они вместе с данными числами образовали геометрическую прогрессию.
По условию (mathrm{b_1=40frac12, b_6=5frac13}) $$ mathrm{ frac{b_6}{b_1}=q^5, frac{b_6}{b_1}=5frac13 : 40frac12=frac{16}{3} : frac{81}{2}=frac{16}{3} cdot frac{2}{81}=frac{32}{243}=frac{2^5}{3^5}=left(frac23right)^5 } $$ Знаменатель (mathrm{q=frac23})
Находим промежуточные члены прогрессии: begin{gather*} mathrm{ b_2=b_1q=40frac12cdotfrac23=frac{81}{2}cdot frac23=27, b_3=b_2q=27cdotfrac23=18, }\ mathrm{ b_4=b_3q=18cdotfrac23=12, b_5=b_4q=12cdotfrac23=8 } end{gather*} Ответ: 27, 18, 12 и 8
Пример 3. Найдите первый и последний члены геометрической прогрессии, если: $$ left{ begin{array}{ l } mathrm{b_4-b_2=0,6} & \ mathrm{b_5-b_3=1,2} & \ mathrm{S_n=12,7} & end{array}right. $$ Заметим, что b4=b2q2, b5=b3q2. Для первых двух уравнений получаем: $$ left{ begin{array}{ l } mathrm{b_2q^2-b_2=0,6} & \ mathrm{b_3q^2-b-3=1,2} & end{array}right. Rightarrow left{ begin{array}{ l } mathrm{b_2(q^2-1)=0,6} & \ mathrm{b_3(q^2-1)=1,2} & end{array}right. $$ Делим второе уравнение на первое: $$ mathrm{ frac{b_3(q^2-1)}{b_2(q^2-1)}=frac{1,2}{0,6}Rightarrowfrac{b_3}{b_2}=q=2 } $$ Подставляем найденное значение знаменателя прогрессии в первое уравнение: $$ mathrm{ b_2(2^2-1)=0,6 Rightarrow b_2=frac{0,6}{3}=0,2 Rightarrow b_1=frac{b_2}{q}=frac{0,2}{2}=0,1 } $$ Для третьего уравнения можем записать: begin{gather*} mathrm{ S_n=b_1frac{q^n-1}{q-1}=0,1cdotfrac{2^n-1}{2-1}=frac{2^n-1}{10}=12,7 Rightarrow 2^n-1=127 Rightarrow }\ mathrm{ Rightarrow 2^n=128=2^7 Rightarrow n=7 } end{gather*} 7-й член b7 = b1q6 = 0,1 · 26 = 6,4
Ответ: b1 = 0,1; b7 = 6,4
Пример 4. В геометрической прогрессии, все члены которой положительны, сумма первого и второго членов равна 48, а сумма третьего и четвёртого членов равна 12. Найдите значение n, при котором Sn = 63. $$ text{По условию} left{ begin{array}{ l } mathrm{b_1+b_2=48} & \ mathrm{b_3+b_4=12} & \ mathrm{S_n=63} & end{array}right. $$ Заметим, что b3 = b1q2, b_4=b_2q2. Второе уравнение можно переписать в виде: $$ mathrm{ b_3+b_4=b_1q^2+b2q^2=underbrace{(b_1+b_2)}_{=48} q^2=12 Rightarrow q^2=frac{12}{48}=frac14 Rightarrow q=frac12 } $$ Берём положительное значение q, т.к. по условию все члены положительны.
Из первого уравнения $$ mathrm{ b_1+b_2=b_1(1+q)=48 Rightarrow b_1=frac{48}{1+frac12}=48cdotfrac23=32 } $$ Для третьего уравнения можем записать: begin{gather*} mathrm{ S_n=b_1frac{q^n-1}{q-1}=b_1frac{1-q^n}{1-q}=32cdotfrac{1-frac{1}{2^n}}{1-frac12}=64left(1-frac{1}{2^n}right)=63 }\ mathrm{ 64-frac{64}{2^n}=63 Rightarrow 1=frac{2^6}{2^n} Rightarrow n=6 } end{gather*} Ответ: 6
Пример 5. Бактерия, попав в организм, делится надвое каждые 20 мин. Сколько бактерий будет в организме через сутки?
Сутки – это 24 · 60 = 1440 мин, или n = 1440 : 20 = 72 цикла деления.
По условию необходимо найти
N = N0 · 2n, где N0 = 1
N = 272 = 4 722 366 482 869 645 213 696 ≈ 4,7 · 1021
Ответ: 4,7 · 1021 бактерий
Калькулятор геометрической прогрессии
Геометрическая прогрессия – такая последовательность чисел, в которой каждое следующее число получается путем умножения предыдущего на знаменатель прогрессии. Пример такой прогрессии: 4, 8, 16, 32, 64, где первый член – 4, знаменатель – 2, количество членов – 5. Если первый член прогрессии и ее знаменатель > 0, то это – возрастающая последовательность. Если знаменатель от нуля до единицы, то последовательность убывает.
Свойства геометрической прогрессии
Зная соседние члены, знаменатель q можно найти по формуле:
q = bn+1bn.
Скопировать «Геометрическая прогрессия»:
Последние вычисления
Комментарии к калькулятору
Количество комментариев: 2
21.10.2020
Лена
Получила 5!
18.10.2020
Лена
Во, как раз нам по домашке ГП задали, сейчас посчитаем)
Геометрической прогрессией называют числовую последовательность, каждый следующий член которой получается из предыдущего умножением его на постоянное число, не равное нулю.
Это число называют знаменателем геометрической прогрессии и обозначают буквой (q).
Например, последовательность (3); (6); (12); (24); (48)… является геометрической прогрессией, потому что каждый следующий элемент отличается от предыдущего в два раза (иначе говоря, может быть получен из предыдущего умножением его на два):

Как и любую последовательность, геометрическую прогрессию обозначают маленькой латинской буквой. Числа, образующие прогрессию, называют ее членами (или элементами). Их обозначают той же буквой, что и геометрическую прогрессию, но с числовым индексом, равным номеру элемента по порядку.
Например, геометрическая прогрессия (b_n = {3; 6; 12; 24; 48…}) состоит из элементов (b_1=3); (b_2=6); (b_3=12) и так далее. Иными словами:
|
порядковый номер элемента |
(1) |
(2) |
(3) |
(4) |
(5) |
… |
|
обозначение элемента |
(b_1) |
(b_2) |
(b_3) |
(b_4) |
(b_5) |
… |
|
значение элемента |
(3) |
(6) |
(12) |
(24) |
(48) |
… |
Если вы поняли вышеизложенную информацию, то уже сможете решить большинство задач на эту тему.
Пример (ОГЭ): Геометрическая прогрессия задана условиями (b_1=-2); (q=7). Найдите (b_4).
Решение:
|
|
Зная первый член и знаменатель, последовательно вычисляем элементы, пока не дойдем до нужного. |
|
|
Можно писать ответ. |
Ответ: (-686).
Пример (ОГЭ): Даны первые три члена прогрессии (324); (-108); (36)…. Найдите (b_5).
Решение:
|
|
Чтобы продолжить последовательность, нам нужно знать знаменатель. Найдем его из двух соседних элементов: на что нужно умножить (324), чтоб получилось (-108)? |
|
(324·q=-108) |
Отсюда без проблем вычисляем знаменатель. |
|
(q=-) (frac{108}{324})(=-) (frac{1}{3}) |
Теперь мы легко находим нужный нам элемент. |
|
|
Готов ответ. |
Ответ: (4).
Пример: Прогрессия задана условием (b_n=0,8·5^n). Какое из чисел является членом этой прогрессии:
а) (-5) б) (100) в) (25) г) (0,8) ?
Решение: Из формулировки задания очевидно, что одно из этих чисел точно есть в нашей прогрессии. Поэтому мы можем просто вычислять ее члены по очереди, пока не найдем нужное нам значение. Так как у нас прогрессия задана формулой n-го члена, то вычисляем значения элементов, подставляя разные (n):
(n=1); (b_1=0,8·5^1=0,8·5=4) – такого числа в списке нет. Продолжаем.
(n=2); (b_2=0,8·5^2=0,8·25=20) – и этого тоже нет.
(n=3); (b_3=0,8·5^3=0,8·125=100) – а вот и наш чемпион!
Ответ: (100).
Пример (ОГЭ): Даны несколько идущих последовательно друг за другом членов геометрической прогрессии …(8); (x); (50); (-125)…. Найдите значение элемента, обозначенного буквой (x).
Решение:
|
|
Найти (x), можно, например, умножив (8) на знаменатель прогрессии. Однако мы его не знаем, поэтому сначала найдем знаменатель из двух известных соседних членов. |
|
(50·q=-125) |
|
|
(q=-) (frac{125}{50})(=-)(2,5) |
Теперь вычисляем икс, умножая (8) на (-2,5). |
|
|
Задача решена. |
Ответ: (-20).
Пример (ОГЭ): Прогрессия задана условиями (b_1=7), (b_{n+1}=2b_n). Найдите сумму первых (4) членов этой прогрессии.
Решение:
|
(b_1=7), |
Мы знаем первый элемент и имеем рекуррентное соотношение — формулу для вычисления следующего элемента по предыдущему. |
|
|
(n=1); (b_{1+1}=2b_1 :: ⇔ :: b_2=2·7=14) |
Теперь найдем сумму. |
|
|
(S_4=b_1+b_2+b_3+b_4=) |
Ответ готов. |
Ответ: (105).
Пример (ОГЭ): Известно, что в геометрической прогрессии (b_6=-11), (b_9=704). Найдите знаменатель (q).
Решение:
|
|
Из схемы слева видно, что чтобы «попасть» из (b_6) в (b_9) – мы делаем три «шага», то есть три раза умножаем (b_6) на знаменатель прогрессии. Иными словами (b_9=b_6·q·q·q=b_6·q^3). |
|
(b_9=b_6·q^3) |
Подставим известные нам значения. |
|
(704=(-11)·q^3) |
«Перевернем» уравнение и разделим его на ((-11)). |
|
(q^3=) (frac{704}{-11})(::: ⇔ ::: )(q^3=-) (64) |
Какое число в кубе даст (-64)? |
|
(q=-4) |
Ответ найден. Его можно проверить, восстановив цепочку чисел от (-11) до (704). |
|
|
Все сошлось — ответ верен. |
Ответ: (-4).
Важнейшие формулы
Как видите, большинство задач на геометрическую прогрессию можно решать чистой логикой, просто понимая суть (это вообще характерно для математики). Но иногда знание некоторых формул и закономерностей ускоряет и существенно облегчает решение. Мы изучим две такие формулы.
Формула (n)-го члена: (b_n=b_1·q^{n-1}), где (b_1) – первый член прогрессии; (n) – номер искомого элемента; (q) – знаменатель прогрессии; (b_n) – член прогрессии с номером (n).
С помощью этой формулы можно, например, решить задачу из самого первого примера буквально в одно действие.
Пример (ОГЭ): Геометрическая прогрессия задана условиями (b_1=-2); (q=7). Найдите (b_4).
Решение:
|
(b_4=b_1·q^3) |
Нам нужен четвертый член, вот и вычисляем его сразу, напрямую, не находя всех промежуточных. |
|
|
(b_4=(-2)·7^3=(-2)·343=-686). |
Готов. |
Ответ: (-686).
Этот пример был простым, поэтому формула нам облегчила вычисления не слишком сильно. Давайте разберем задачку чуть посложнее.
Пример: Геометрическая прогрессия задана условиями (b_1=20480); (q=frac{1}{2}). Найдите (b_{12}).
Решение:
|
(b_{12}=b_1·q^{11}) |
Действуем как в предыдущей задаче. |
|
|
(b_4=20480·(frac{1}{2})^{11}=20480·frac{1}{2048}=10.) |
Есть ответ. |
Ответ: (10).
Конечно, возводить (frac{1}{2}) в (11)-ую степень не слишком радостно, но всё же проще чем (11) раз делить (20480) на два.
Сумма (n) первых членов: (S_n=)( frac{b_1·(q^n-1)}{q-1}), где (b_1) – первый член прогрессии; (n) – количество суммируемых элементов; (q) – знаменатель прогрессии; (S_n) – сумма (n) первых членов прогрессии.
Пример (ОГЭ): Дана геометрическая прогрессия (b_n), знаменатель которой равен (5), а первый член (b_1=frac{2}{5}). Найдите сумму первых шести членов этой прогрессии.
Решение:
|
(S_6=)( frac{b_1·(q^6-1)}{q-1}) |
Все данные есть, сразу вычисляем ответ. |
|
(S_6=)( frac{frac{2}{5}·(5^6-1)}{5-1})(=)( frac{frac{2}{5}·15624}{4})(=) |
Ответ готов. |
Ответ: (1562,4).
И вновь мы могли решить задачу «в лоб» – найти по очереди все шесть элементов, а затем сложить результаты. Однако количество вычислений, а значит и шанс случайной ошибки, резко возросли бы.
Для геометрической прогрессии есть еще несколько формул, которые мы не стали рассматривать тут из-за их низкой практической пользы. Вы можете найти эти формулы здесь.
Возрастающие и убывающие геометрические прогрессии
У рассмотренной в самом начале статьи прогрессии (b_n = {3; 6; 12; 24; 48…}) знаменатель (q) больше единицы и поэтому каждый следующий член больше предыдущего. Такие прогрессии называются возрастающими.
Если же (q) меньше единицы, но при этом положителен (то есть, лежит в пределах от нуля до единицы), то каждый следующий элемент будет меньше чем предыдущий. Например, в прогрессии (4); (2); (1); (0,5); (0,25)… знаменатель (q) равен (frac{1}{2}).

Эти прогрессии называются убывающими. Обратите внимание, что ни один из элементов такой прогрессии не будет отрицателен, они просто становятся всё меньше и меньше с каждым шагом. То есть, мы будем постепенно приближаться к нулю, но никогда его не достигнем и за него не перейдем. Математики в таких случаях говорят «стремиться к нулю».
Отметим, что при отрицательном знаменателе элементы геометрической прогрессии будут обязательно менять знак. Например, у прогрессии (5); (-15); (45); (-135); (675)… знаменатель (q) равен (-3), и из-за этого знаки элементов «мигают».

Смотрите также:
Числовая последовательность
Арифметическая прогрессия
Формулы геометрической прогрессии с примерами
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
Другими словами, последовательность (bn) – геометрическая последовательность, если для натурального n выполняются условия:
bn+1= bn×q,
где q некоторое число, которое называется знаменатель прогрессии, и bn≠0
Примером такой последовательности может быть ряд чисел 2; 10; 50; 250;…., откуда видно, что каждое последующее больше предыдущего в пять раз, значит, каждый член равен предыдущему, умноженному на одно и то же число 5. Или, например, ряд чисел 20; -2; 0,2; -0,02……, где видно, что каждое последующее умножали на одно и то же число (-0,1).
Так как по определению геометрической прогрессии мы имеем одно и то же число, то это и есть число q. Оно называется «знаменатель» геометрической прогрессии. Он находится путем деления соседних членов – последующего на предыдущий, то есть q=bn+1bn. Знаменатель не может быть равным нулю!
Для того чтобы задать геометрическую прогрессию, надо знать ее первый член и знаменатель. Например, если b1=4, q=3, то получим прогрессию: 4; 12; 36; ….и так далее. Ну, а зная первый член и знаменатель, можно найти любой член геометрической прогрессии: b2=b1q; b3=(b1q)q=b1q2; b4==((b1q)q)q=b1q3. Так можно продолжать и дальше, но из этих записей видно, что можно найти n-ый член геометрической последовательности, если умножить первый член на знаменатель, степень которого на 1 меньше порядкового номера искомого члена, то есть bn=b1 qn−1 . Мы получили формулу n-ого члена геометрической прогрессии.
Формула n-ого члена геометрической прогрессии
bn=b1 ×qn−1
Рассмотри на примерах применение формулы bn=b1 qn−1 для указанного члена геометрической прогрессии.
Пример №1. Найти четвертый член геометрической прогрессии, если известно, что b1=6, q=3. Составляем формулу для b4:
b4=b1 q4−1=b1 q3
Подставляем в формулу значения, указанные в задании и вычисляем результат: b4=6×33=162.
Найти шестой член геометрической прогрессии 2; -6;……. Здесь для нахождения b6 надо знать знаменатель q. Для его нахождения надо -6 разделить на 2, получим -3, то есть q=-3. Теперь составляем формулу для b6, подставляем значения и вычисляем ответ:
b6=b1 q6−1=b1 q5=2×(−3)5=−486
Свойство геометрической прогрессии
Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего ее членов. Формула:
b2n=bn−1×bn+1
Верным является и утверждение, обратное данному: если в последовательности чисел, отличных от нуля, квадрат каждого члена, начиная со второго, равен произведению предыдущего и последующего членов, то эта последовательность чисел является геометрической прогрессией.
Другими словами, с помощью данной формулы можно найти неизвестный член геометрической прогрессии, соседние члены которого известны. Рассмотрим применение данного свойства на примерах.
Пример №2. Найти b5, если задана геометрическая прогрессия, в которой b4=32, b6=128. Составляем формулу, подставляем в нее значения и вычисляем:
b25=b5−1×b5+1=b4 ×b6 =32×128=4096
Этим действием мы нашли квадрат пятого члена геометрической прогрессии, поэтому извлекаем квадратный корень из числа 4096 для нахождения значения b5: b5=√4096=64
Найти у, если дана геометрическая прогрессия …..24; у; 96. Видим, что у находится между соседними известными числами 24 и 96. Поэтому, следуя свойству, умножаем данные числа и извлекаем квадратный корень из полученного числа: у=√24×96=√2304=48.
Формула суммы n первых членов геометрической прогрессии
Формула суммы членов геометрической прогрессии с известными членами
Sn=bnq−b1q−1 , где q≠1
Для нахождения суммы по данной формуле нужно знать первый и последний член геометрической прогрессии, а также ее знаменатель.
Также есть вторая формула, по которой можно находить сумму нескольких первых членов прогрессии, зная только первый ее член и знаменатель:
Формула суммы членов геометрической прогрессии с известным первым членом и знаменателем
Sn=b1(qn−1)q−1, где q≠1
Рассмотрим применение данных формул на примере, решив его двумя способами.
Пример №3. Найти сумму пяти первых членов геометрической прогрессии, если известно, что b1=2; b5=162; q=-3.
Способ №1 (первая формула). Составим формулу для нахождения S5:
S5=b5q−b1q−1
Подставим значения b1=2; b5=162 и найдем результат:
S5=162(−3)−2−3−1=−486−2−4=−488−4=122
Способ №2 (вторая формула).
Sn=b1(qn−1)q−1
Для решения нам нужен первый член и знаменатель: b1=2; q=-3. Составим формулу:
S5=b1(q5−1)q−1
Подставим в формулу данные значения и вычислим сумму:
S5=2((−3)5−1)−3−1=2(−243−1)−4=−488−4=122
Таким образом, мы увидели, что у нас получился один и тот же результат 122 в обоих способах решения. Выбор формулы зависит от данных в условии задачи.
Задание OM1420222
У Кати есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 400 см, а после каждого следующего отскока от асфальта подлетал на высоту в 2 раза меньше предыдущей. После какого по счету отскока высота, на которую подлетит попрыгунчик, станет меньше 20 см?
Определим, к какой последовательности относится наша задача. По условию имеем, что после каждого следующего отскока от асфальта подлетал на высоту в 2 раза меньше предыдущей. Это геометрическая прогрессия. Теперь выпишем, что известно по условию и определим, что надо найти: первый член прогрессии b1=400, знаменатель q=12, n – количество отскоков, значит, найти надо n при bn<20.
Подставим в формулу n-ого члена геометрической прогрессии наши данные:
bn=b1qn-1=400∙(12)n−1<20
Разделим обе части неравенства на 400: (12)n−1<120
Будем рассматривать случаи, начиная с n=3: (12)3−1<120; (12)2<120; (14)<120 неверно
При n=4: (12)4−1<120; (12)3<120; (18)<120 неверно
При n=5: (12)5−1<120; (12)4<120; (116)<120 неверно
При n=6: (12)6−1<120; (12)5<120; (132)<120 верно. Следовательно, после 6 отскока высота, на которую подлетит попрыгунчик, станет меньше 20 см.
К данной задаче можно сделать проверку, а также она является простейшим способом для её решения. Рассмотрим этот способ:
1 отскок – 400 см
2 отскок – 200 см (разделили на 2, так как по условию сказано, что с каждым отскоком высота уменьшалась в 2 раза)
3 отскок – 100 см
4 отскок – 50 см
5 отскок – 25 см
6 отскок – 12,5 см, а это меньше, чем 20 см, как требуется в условии. Поэтому пишем в ответ число 6.
Ответ: 6
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 6.4k