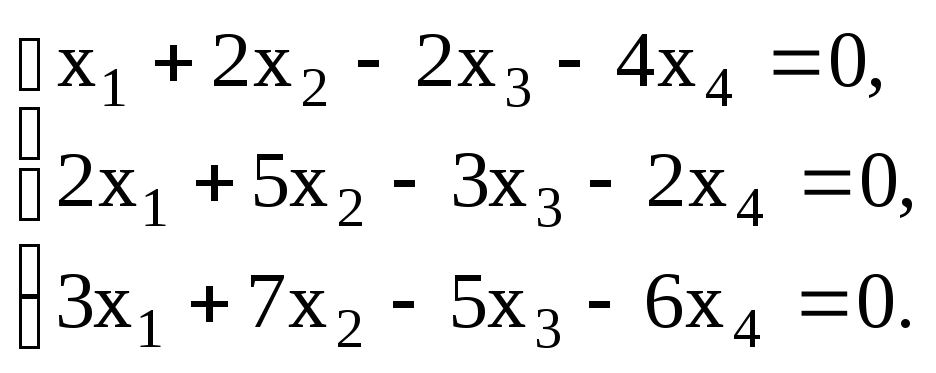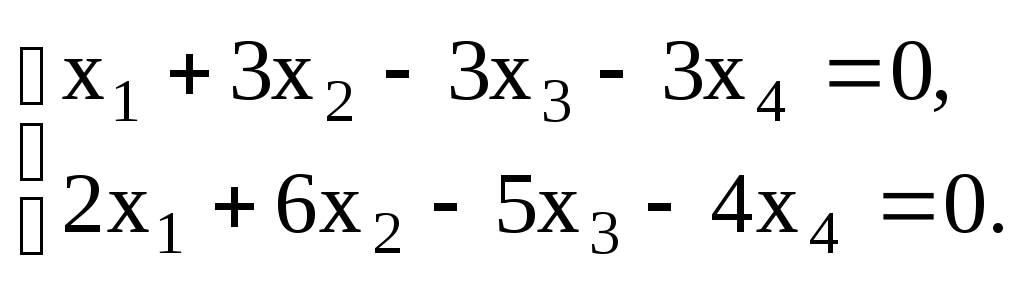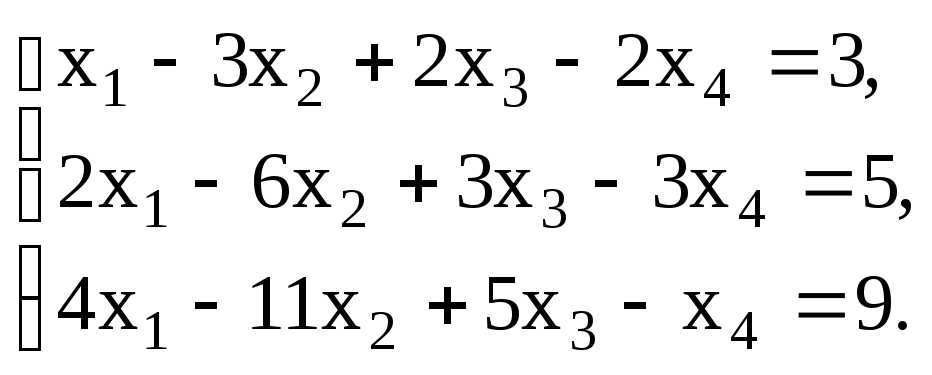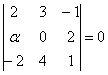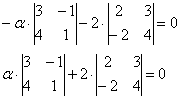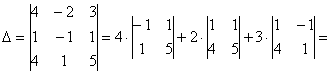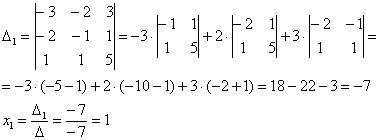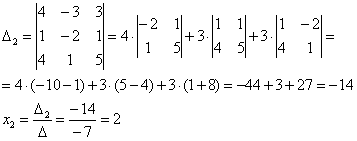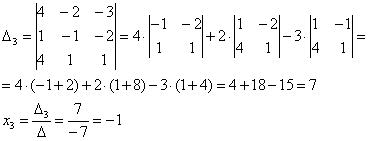Как найти координаты вектора в базисе
Решение:
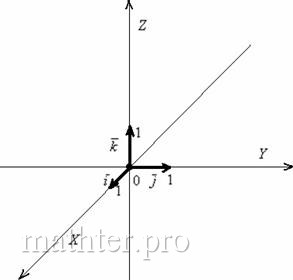
Записываем матрицу перехода А:
и находим ее определитель
<>0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f1 , f2 , f3 линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:
Обратная матрица А -1
Находим координаты вектора х относительно нового базиса.
Пример №1 . Даны векторы a<1;2;1>, b<2;-2;1>, c <1;-2;0>и d <0;3;1>. Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c
Пример №2 . Даны векторы 


Пример №3 . Даны два линейных преобразования:
х’1 = a11x1 + a12x2 + a13x3, х»1 = b11x’1 + b12x’2 + b13x’3,
х’2 = a21x1 + a22x2 + a23x3, х»2 = b21x’1 + b22x’2 + b23x’3,
х’3 = a31x1 + a32x2 + a33x3, х»3 = b31x’1 + b32x’2 + b33x’3,
Средствами матричного исчисления найти преобразование, выражающее х»1, x»2, x»3 через х1, х2, х3.
х’1 = 4x1 + 3x2 + 5x3, х»1 = — x’1 + 3x’2 — 2x’3,
х’2 = 6x1 + 7x2 + x3, х»2 = — 4x’1 + x’2 + 2x’3,
х’3 = 9x1 + x2 + 8x3, х»3 = 3x’1 — 4x’2 + 5x’3,
Решение. Используя калькулятор, получаем:
Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .
| A -1 = -1/182 |
|
Матрицу Х ищем по формуле:
| X = A -1 ·B = -1/182 |
|
* | = |
|
Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e 1= AB , e 2= AC , e 3= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e 1, e 2, e 3)
Решение. Пункты (а-д) решаются через онлайн калькулятор.
Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид 
Решим полученную систему уравнений.
Алгоритм нахождения базиса системы векторов
Для того чтобы найти базис системы векторов Av А2. А , необходимо:
1) составить соответствующую системе векторов однородную систему уравнений
2) привести эту систему к равносильной разрешенной системе вида
- 3) записать базис системы векторов Б = (АрА2, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
- 4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора
в разрешенной системе уравнений, т.е.
Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г.
Пример 3.3. Найти ранг и базис системы векторов
разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.
Решение. Составим систему уравнений A t ay + А2х2 + . + А„хп = 0, которая в координатной записи имеет вид
Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.
Разрешенная система имеет вид
В базис системы векторов включаем 1-й и 2-й векторы Б: = (AVA2), которые соответствуют разрешенным неизвестным х1 и х2. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.
Запишем разложения векторов по базису. Коэффициентами разложения вектора А3 являются координаты вектора А’3 = (3, -2), т.е. коэффициенты при х3 в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х3 А3 = ЗЛ1 — 2Аг Аналогично, коэффициентами разложения вектора А4 являются координаты вектора А’4 = (4, 1) А4 = 4Ау + 1 Ат
Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я94 = 1.
Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
http://bstudy.net/719717/estestvoznanie/algoritm_nahozhdeniya_bazisa_sistemy_vektorov
http://zaochnik.com/spravochnik/matematika/vektory/vektornoe-prostranstvo/
Линейной
комбинацией векторов
называется вектор
,
где λ1, … , λm– произвольные коэффициенты.
Система
векторов
называется
линейно зависимой, если существует ее
линейная комбинация, равная,
в которой есть хотя бы один ненулевой
коэффициент.
Система
векторов
называется
линейно независимой, если в любой ее
линейной комбинации, равной,
все коэффициенты нулевые.
Базисом
системы векторов
называется
ее непустая линейно независимая
подсистема, через которую можно выразить
любой вектор системы.
П р
и м е р 2. Найти базис системы векторов=
(1, 2, 2, 4),=
(2, 3, 5, 1),=
(3, 4, 8, -2),=
(2, 5, 0, 3) и выразить остальные векторы
через базис.
Р е
ш е н и е. Строим матрицу, в которой
координаты данных векторов располагаем
по столбцам. Приводим ее к ступенчатому
виду.
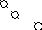



Базис
данной системы образуют векторы
,
,
,
которым соответствуют ведущие элементы
строк, выделенные кружками. Для выражения
векторарешаем уравнениеx1
+x2
+
x4=
.
Оно сводится к системе линейных
уравнений, матрица которой получается
из исходной перестановкой столбца,
соответствующего,
на место столбца свободных членов.
Поэтому для решения системы используем
полученную матрицу в ступенчатом виде,
сделав в ней необходимые перестановки.
Последовательно
находим:
x4
= 0;
x2
= 2;
x1
+ 4 = 3, x1
= -1;
=
—+2
.
Замечание
1. Если требуется выразить через базис
несколько векторов, то для каждого из
них строится соответствующая система
линейных уравнений. Эти системы будут
отличаться только столбцами свободных
членов. Поэтому для их решения можно
составить одну матрицу, в которой будет
несколько столбцов свободных членов.
При этом каждая система решается
независимо от остальных.
Замечание
2. Для выражения любого вектора достаточно
использовать только базисные векторы
системы, стоящие перед ним. При этом
нет необходимости переформировывать
матрицу, достаточно поставить вертикальную
черту в нужном месте.
У п
р а ж н е н и е 2. Найти базис системы
векторов и выразить остальные векторы
через базис:
а)
=
(1, 3, 2, 0),=
(3, 4, 2, 1),=
(1, -2, -2, 1),=
(3, 5, 1, 2);
б)
=
(2, 1, 2, 3),=
(1, 2, 2, 3),=
(3, -1, 2, 2),=
(4, -2, 2, 2);
в)
=
(1, 2, 3),=
(2, 4, 3),=
(3, 6, 6),=
(4, -2, 1);=
(2, -6, -2).
-
3. Фундаментальная система решений
Система
линейных уравнений называется однородной,
если все ее свободные члены равны нулю.
Фундаментальной
системой решений однородной системы
линейных уравнений называется базис
множества ее решений.
Пусть
дана неоднородная система линейных
уравнений. Однородной системой,
ассоциированной с данной, называется
система, полученная из данной заменой
всех свободных членов на нули.
Если
неоднородная система совместна и
неопределенна, то ее произвольное
решение имеет вид fн
+ 1fо1+
… + kfоk
,гдеfн– частное
решение неоднородной системы иfо1,
… , fоk–
фундаментальная система решений
ассоциированной однородной системы.
П р
и м е р 3. Найти частное решение
неоднородной системы из примера 1 и
фундаментальную систему решений
ассоциированной однородной системы.
Р е
ш е н и е. Запишем решение, полученное
в примере 1, в векторном виде и разложим
получившийся вектор в сумму по свободным
параметрам, имеющимся в нем, и фиксированным
числовым значениям:
= (x1,
x2,
x3,
x4) =
(–2a + 7b –
2, a, –2b + 1, b) = (–2a,
a, 0, 0) + (7b, 0, –2b, b) + +(–
2, 0, 1, 0) = a(-2, 1, 0, 0) + b(7, 0, -2, 1) + (–
2, 0, 1, 0).
Получаемfн=(–
2, 0, 1, 0), fо1= (-2, 1, 0,
0), fо2= (7, 0, -2, 1).
Замечание.
Аналогично решается задача нахождения
фундаментальной системы решений
однородной системы.
У п
р а ж н е н и е 3.1 Найти фундаментальную
систему решений однородной системы:
а)
б)
в)
2x1 –
x2
+3x3=
0.
У п
р а ж н е н и е 3.2. Найти частное решение
неоднородной системы и фундаментальную
систему решений ассоциированной
однородной системы:
а)
б)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
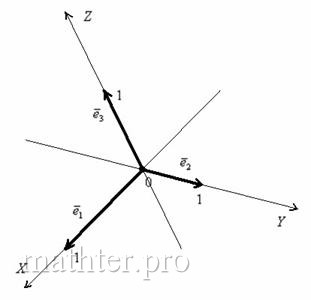
1.8.4. Базис и система координат пространства
Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Тем не менее, рекомендую внимательно
прочитать вводную часть, так как появятся новые термины и понятия.
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в
помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса
потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний
палец. Это будут векторы , они смотрят в разные стороны, имеют
разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов!
Кстати, не нужно демонстрировать такое
преподавателям, как ни крути пальцами, а от определений никуда не деться =)
Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно
прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас
пропало одно из измерений – высота. Такие векторы являются компланарными, и совершенно понятно, что базиса трёхмерного пространства они не
создают.
Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не
делайте этого с пальцами, так отрывался только Сальвадор Дали =)).
Определение: векторы называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если
такой плоскости не существует, то и векторы будут не компланарны.
Три компланарных вектора всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова
представим, что они лежат в одной плоскости. Во-первых, векторы мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно
выразить через любой вектор. Во втором случае, если, например, векторы не коллинеарны, то третий вектор выражается через них единственным образом:
(почему?).
Справедливо и противоположное утверждение: три некомпланарных вектора всегда линейно независимы, то есть никоим образом
не выражаются друг через друга.
И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.
Определение: базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов, взятых в определённом порядке, при этом любой вектор пространства единственным
образом раскладывается по данному базису , где
– координаты вектора
в этом базисе. Также говорят, что вектор
представлен в виде линейной комбинации базисных векторов.
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки (начала отсчёта) и любых трёх линейно
независимых векторов:
Выбранное (где угодно) начало координат , и некомпланарные векторы
, взятые в
определённом порядке, задают аффинную систему координаттрёхмерного пространства:
Наиболее привычным и удобным частным случаем аффинной системы координаявляется «школьная» система. Начало координат и ортонормированный
базис задают декартову прямоугольную систему
координат пространства:
Ось абсцисс изображают под углом в
по отношению к другим осям (к оси ординат
и оси аппликат
).
Популярный «тетрадный» масштаб: 1 ед. = 2 клетки по осям и 1 ед. = диагональ одной клетки – по оси
.
И перед тем как перейти к практическим заданиям, вновь систематизируем теоретическую информацию:
Для трёх векторов пространства эквиваленты следующие утверждения:
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.
Противоположные высказывания, думаю, понятны.
Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5), и оставшиеся
практические задания параграфа будут носить ярко выраженный алгебраический характер. Повесим на гвоздь геометрическую клюшку и начнём
орудовать бейсбольной битой линейной алгебры:
Три вектора пространства компланарны тогда и только
тогда, когда определитель, составленный из
координат данных векторов, равен нулю: 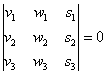
Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (результат не
изменится). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
Задача 42
Проверить, образуют ли векторы базис трёхмерного пространства:
а)
б)
Фактически всё решение сводится к вычислению
определителей:
а) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке):

, значит, векторы
линейно независимы (не компланарны) и образуют базис трёхмерного пространства.
Ответ: данные векторы образуют базис.
б) Это пункт для самостоятельного решения. Не пропускаем! Для проверки правильности вычислений определителей я приложил к
книге Алгебраический Калькулятор.
Решим творческую задачку:
Задача 43
При каком значении параметра векторы
будут компланарны?
Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен
нулю:
По существу, требуется решить уравнение с определителем. Определитель выгоднее всего раскрыть по второй строке:
Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:
Ответ: при
Здесь легко выполнить проверку, для этого нужно подставить полученное значение в исходный определитель и убедиться, что
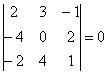
И в заключение параграфа рассмотрим ещё одну типовую задачу, которая встречается в подавляющем большинстве контрольных работ по алгебре и
геометрии:
Задача 44
Даны векторы . Показать, что векторы
образуют базис трехмерного пространства и найти координаты вектора
в этом базисе.
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе.
Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать свой базис. И первый этап полностью совпадает с решением Задачи 42 –
необходимо проверить, действительно ли векторы линейно
независимы. Для этого нужно вычислить определитель, составленный из координат векторов :
, значит, векторы
линейно независимы и образуют базис трехмерного пространства.
! Важно: координаты векторов обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.
Теперь вспомним теоретическую часть: если векторы образуют
базис, то любой вектор можно единственным способом разложить по
данному базису: , где
– координаты вектора в базисе
.
Поскольку наши векторы образуют базис трёхмерного
пространства (это уже доказано), то вектор можно единственным
образом разложить по данному базису:
, где
– координаты вектора
в
базисе .
И по условию требуется найти координаты .
Для удобства объяснения поменяю части местами: . В целях
нахождения следует расписать данное равенство
покоординатно:
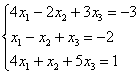
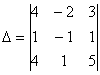
в правую часть записываем координаты вектора .
Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое
требование.
Главный определитель системы уже найден:
, значит, система имеет единственное решение.
Дальнейшее дело техники:
и ещё один определитель:
Таким образом:
– разложение вектора
по базису
.
Ответ:
Такая же задача для самостоятельного решения:
Задача 45
Даны векторы . Показать, что в
екторы образуют базис и найти координаты вектора
в этом базисе. Систему линейных уравнений решить методом Крамера.
Полное решение и примерный образец чистового оформления в конце книги. Для самоконтроля используйте тот же Алгебраический
Калькулятор, где есть макет с автоматическим расчётом системы по правилу Крамера.


| Оглавление |
Автор: Aлeксaндр Eмeлин
Содержание:
- n-мерный вектор и векторное пространство
- Линейные (векторные) n — мерные пространства
- Линейные операции над n — измеримыми векторами
- Скалярное произведение двух векторов
- Линейная зависимость и независимость векторов
- Базис n -мерного пространства. Разложение вектора по базису
- Переход к новому базису. Нахождение базисных решений системы линейных алгебраических уравнений
- Однородная система уравнений. Особенности решения
n-мерный вектор и векторное пространство
Множество всех векторов, которые мы рассматривали на плоскости или в пространстве и для которых определены операции сложения векторов, умножение вектора на число являются простыми примерами векторного пространства.
Определение 1. Упорядоченное множество n действительных чисел, записанных в виде (a1, a2, a3, …, an) называется n- мерным вектором. Числа a1, a2, a3, …, an называются координатами вектора 

Понятие n-мерного вектора широко используется в экономике, например, некоторый набор товаров можно охарактеризовать вектором 

Если у n-мерного вектора одна координата равна единице, а все остальные равны нулю, то такой вектор называется единичным. Очевидно, что существует n различных единичных векторов
исходящих из начала координат — точки О. Все определения и действия для двумерных и трехмерных векторов, заданных в координатной форме, распространяются и на n-мерные векторы (n ≥ 4).
Два n-мерных вектора равны тогда и только тогда, когда их соответствующие компоненты равны.
Вектор 

Суммой двух n-мерных векторов 




Произведением вектора 


Вектор, у которого все координаты равны нулю, называется нулевым вектором и обозначается
Операции над произвольными векторами удовлетворяют свойствам:
1. 
2. 
3. 
4. 
5. 
6. Существует нулевой вектор 


7. Для произвольного вектора 

8. 

Определение. Множество векторов с действительными координатами, в
котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие выше приведенным восьми свойствам, называется векторным пространством.
Замечания. Если под векторами 

Линейным пространством, например, множество всех алгебраических многочленов, степени которых не превышают натуральное число n. Если множество всех многочленов точно равно натуральному числу n, то не будет линейным пространством, потому что сумма двух многочленов может оказаться многочленом, степень которого меньше n.
Линейные (векторные) n — мерные пространства
Линейные 
В школьном курсе математики понятие вектора обозначалось как направленный отрезок. Положение (расположение) вектора на прямой 


Математический подход к изучению различных явлений (процессов) окружающего мира, в том, числе и экономических, требует обобщения понятия вектора, связано с увеличением количества его координат. Такое обобщение не подразумевает геометрической интерnретации, но является удобным для математического моделирования.
Вектором размерности 






Согласно определению 



Нулевым вектором 

Два вектора 

Линейные операции над n — измеримыми векторами
1. Суммой 



Следовательно:
Следствие. Для любого вектора 
2. Произведением вектора 




Следствие. Если 



Векторы 


Суммой взаимно противоположных векторов есть нулевой вектор той же размерности.
Разность векторов 



Векторы 




Если 
прямой или на параллельных прямых.
В частном случае, когда 

где 


Совокупность всех 


Скалярное произведение двух векторов
Аналогично тому, как рассматривался произведение матриц вводят понятие скалярного произведения векторов 


Скалярным произведением двух 
Действие умножения для получения скалярного произведения обозначают точкой между векторами:
Произведение 
На основе скалярного произведения приведем определение понятий, которые вводились для векторов размерностью 
Длиной 


то есть
Единичным 


Возведение любого ненулевого вектора к единичному называется его нормированием.
Среди единичных векторов выделяют векторы, для которых одна из координат равна единице, а все остальные — нулю. Такие векторы обозначают маленькой буквой 



В частности, в трехмерном пространстве эти векторы называются ортами координатных осей, они имеют собственные обозначения:
Кутом между двумя векторами 


Согласно (4.9) скалярное произведение можно рассматривать как общую числовую характеристику двух векторов.
Свойства скалярного произведения:
Линейное пространство, для которого определено скалярное произведение векторов со свойствами (4.10), называется евклидовым пространством.
В тeopии линейных пространств любое множество векторов одинаковой размерности называется системой векторов.
Пусть имеем систему, которая состоит из 







С помощью этой системы векторов систему линейных алгебраических уравнений с 
или кратко:
Действительно, если по правилам сложения векторов и умножения на скаляр умножить каждый вектор 


Замечания. На основе тeopии 
Линейная зависимость и независимость векторов
Пусть имеется система векторов 






Векторы называются линейно зависимыми, если хотя бы один из векторов системы является линейной комбинацией других. В противном случае, когда в системе векторов нет ни одного, который был бы линейной комбинацией других, векторы называются линейно независимыми.
Теорема 4.1 (про линейную зависимость системы векторов). Если среди чисел 

то система векторов 
Доказательство. Пусть в равенстве (4.14) среди чисел 

Отсюда получаем:
а согласно (4.13) это означает, что система векторов 

Последствие из теоремы 4.1 (о линейной независимости системы векторов).
Система векторов есть линейно независимой, если векторное равенство
выполняется только в случае 
Доказательство. Предположим, что система векторов линейно независима, и при этом существуют 

Одной из основных задач теории линейных пространств является задача исследования системы векторов на линейную независимость, то есть выяснения вопрос о том, какова есть заданная система векторов — линейно зависимой или линейно независимой.
Решение этой задачи сводится к решению систем линейных уравнений.
Запишем равенство (4.14) в координатной форме:
выполним умножение векторов системы на скаляры

По следствием из теоремы 4.1 система векторов линейно независимая, если система однородных уравнений (4.15) имеет только тривиальное решение: 

Проведем исследование на линейную независимость системы векторов:
Запишем векторное равенство:
Отсюда получаем систему уравнений:
Вычислим определитель основной матрицы системы:
Поскольку 

Преобразование основной матрицы системы по методу Жордана-Гаусса позволяет определить количество линейно независимых векторов в заданной системе векторов:
Ранг матрицы системы 
Подставляя найденные коэффициенты в векторное равенство (4.14), получим
Таким образом, векторы 





В линейной алгебре широко применяется система п единичных векторов 



Рассмотрим питания о наибольшее количество векторов, которое может содержать линейно независимая система 
Выберем из пространства 

запишем векторное равенство
и соответствующую ей однородную линейную систему 

Для ответа на поставленный вопрос будем исходить из сравнения количества векторов системы 

1. Если количество векторов больше измеримости пространства 


2. Если количество векторов равно размерности пространства 


Из проведенного анализа следует, что наибольшее количество линейно независимых векторов равно размерности линейного пространства.
Базис n -мерного пространства. Разложение вектора по базису
Понятие 






Теорема 4.2 (о разложении 
Произвольный вектор 


Доказательство. Согласно определению линейной комбинации системы векторов (4.13) надо показать существование единого набора цифр 

Представим векторы 

и запишем соответствующую систему линейных уравнений:
Поскольку определитель основной матрицы системы отличается от нуля (по условию векторы 
Представление вектора 


Система 



Запись 


Определение базиса пространства и разложения вектора по базису можно выполнять одновременно, аналогично тому, как выбор базисных неизвестных и нахождения решений СЛАУ осуществляли при применении методов Гаусса и Жордана-Гаусса.
Осуществить разложение вектора 

Для решения задачи представим вектор 


где 


Представим векторы 


Проверку на линейную независимость векторов 


Для этого запишем расширенную матрицу системы и проведем ее преобразования по методу Жордана-Гаусса:
Поскольку элементарными преобразования на месте основной матрицы системы получено единичную матрицу третьего порядка, то определитель исходной матрицы отличен от нуля, и система векторов 



Следовательно, координатами вектора 

В другом базисе вектор 

Любой вектор с 
Переход к новому базису. Нахождение базисных решений системы линейных алгебраических уравнений
Представим произвольный вектор 

где 

Выясним, как можно осуществить переход от одного базиса линейного пространства к другому и найти координаты вектора 
Пусть в пространстве 


Запишем систему (4.17) в матричном виде: 
Неособенная матрица 


Можно показать, что зависимость между координатами вектора в разных базисах определяется формулами:
где 

Переход к новому базису широко используется в задачах линейного программирования и в других задачах математических методов в экономике.
Задан вектор 







В предыдущем примере было показано, что векторы 
Матрица перехода от базиса 



Транспонируем матрицу 
Для нее существует обратная матрица, поскольку 
По соотношению (4.18) определяем координаты вектора 


Рассмотрим разложение вектора по новому базису для нахождения базисных решений СЛАУ.
Запишем систему линейных алгебраических уравнений в векторной форме
где коэффициентами при неизвестных системы являются векторы 





Система линейных уравнений называется сводной к единичному базису, если среди векторов 

В общем случае, если количество векторов, образующих базис, меньше количества векторов системы 
Таким образом, для нахождения всех базисных решений системы можно предложить такой алгоритм:
1) сводим систему линейных уравнений элементарными преобразованиями к единичному базису;
2) находим значения неизвестных, что соответствуют данном базису, то есть координаты вектора 
3) выполняем преобразование системы уравнений с целью введения в базис других векторов системы. Тогда координаты вектора 
Заметим, что максимальное количество базисных решений равно количеству сопряжений с 


Найдем все базисные решения системы линейных уравнений
В векторной форме система уравнений имеет вид
где
Среди заданных векторов 

Есть четыре вектора двумерного пространства, среди которых необходимо определить базисные. Поскольку наибольшее количество линейно независимых векторов в этом пространстве равно двум, то все четыре вектора не могут быть линейно независимыми. Сводим систему линейных уравнений к единичному базису. Запишем матрицу коэффициентов системы в таблице 4.1 и выполним элементарные преобразования этой системы по методу Жордана-Гаусса.
Сведение системы уравнений к единичному базису Таблица 4.1
По результатам последней операции получено единичную матрицу.
Следовательно, векторы 








Количество базисов для данного примера определяется количеством соединений из четырех векторов 

В таблице 4.2 первым из базисных решений системы приведено именно то, которое получили в таблице 4.1.
Нахождение базисных решений Таблица 4.2
Заметим, что среди шестерых базисных решений данной системы линейных уравнений только 

В рамках учебной дисциплины 


Однородная система уравнений. Особенности решения
Рассмотрим векторный подход к нахождению общего решения систем линейных уравнений (1.9):
где 


В векторной форме система однородных линейных уравнений имеет вид:
где 




Если ранг основной матрицы меньше количества неизвестных 
Пусть коэффициенты при неизвестных 
где 

По свойству 3 (п. 3.2) любая линейная комбинация решений однородной системы также является решением этой системы.
Фундаментальной системой решений однородной системы уравнений называется такая линейно независимая система векторов 
Теорема 4.3 (пpo фундаментальную систему решений). Однородная система уравнений (4.20) имеет фундаментальную систему решений, количество векторов которой равно 

Доказательство. Предоставим свободным неизвестным 

(Конечно, при 
Выражения базисных неизвестных 


Вектор
где 
Если числа 


Следовательно, для нахождения общего решения однородной системы уравнений выполняем следующее:
1. Выражает базисные неизвестные системы (4.20) через свободные.
2. Предоставляем значение свободным 
3. Подставляемые в (4.21) последовательно значение свободных неизвестных (4.22), находим базисные неизвестные, получая таким образом фундаментальную систему решений:
4. Записываем общее решение системы как линейную комбинацию фундаментальных решений (4.23).
Найдем фундаментальную систему решений однородной системы уравнений:
Чтобы выразить базисные неизвестные системы через свободные неизвестные, воспользуемся методом Жордана-Гаусса. Выполняем элементарные преобразования основной матрицы системы для получения в ней единичной матрицы:
Выбираем за базисные неизвестные 


Если свободным неизвестным последовательно предоставить значения 





Общее решение системы уравнений в векторной форме находим как линейную комбинацию фундаментальных решений, а именно:
где
Тогда общее решение однородной системы уравнений, составленный из фундаментальных решений системы, имеет вид:
Замечания. Аналогично можно представить общее решение и неоднородной системы уравнений, которая имеет множество решений.
Пусть система неоднородных уравнений
совместима, но ранг матрицы системы меньше количества неизвестных 
где 
— общее решение (4.22) соответствующей однородной системы уравнений (4.20).
Найдем общее решение неоднородной системы уравнений:
Если праве части всех уравнений положить равными нулю, то получим однородной систему уравнений (4.24), общее решение которой определен в предыдущем примере:
где
Найдем произвольный частное решение неоднородной системы. Например, возьмем свободные неизвестные равными нулю: 



где
или
Такое представление общего решения неоднородной системы линейных алгебраических уравнений обобщается на произвольные неоднородные системы, которые имеют множество решений.
Лекции:
- Исследовать ряд на абсолютную сходимость
- Комплексные числа: примеры решения
- Уравнение окружности и прямой
- Область определения функции примеры решения
- Неопределенный интеграл
- Объемы многогранников
- Приложения определенного интеграла
- Дифференциальное вычисление функции одной переменной
- Решение слау
- Каноническое уравнение параболы
Базис векторов и линейные действия над векторами аналитическим путём (теория и решение задач)
Базис – это неопределённое количество векторов в векторном пространстве, и абсолютно любой из этих векторов может создавать линейную комбинацию.
Помощь в написании работы
Базис векторов
Система линейно независимых векторов пространства, за которыми можно разложить произвольный вектор – это и есть базис векторов или этого пространства.
Так, согласно доказательству (3), произвольные три некомпланарные векторы ,
,
, образуют в трёхмерном пространстве базис, по которому, согласно формуле (2) можно единственным образом разложить произвольный вектор
пространства. Векторы
,
,
, которые образуют базис называются базисными.
Будем считать, что базисные векторы ,
,
сведены к точке
.
Числ , про которые упоминалось в разделах “линейно зависимая и линейно независимые системы векторов”, называют координатами вектора в заданном базисе, и пишут:
.
Аналогично, на плоскости базис образуют какие-то два неколлинеарные векторы, а любой некомпланарный с ними может быть разложен по этому базису.
Базисным вектором на прямой линии может быть любой ненулевой вектор.Согласно свойствам линейных операций над векторами, следует, что при сложении и вычитании векторов в данном базисе прибавляются и отнимаются их соответствующие координаты, а при умножении вектора на число умножаются не это число координаты вектора, то есть:
.
.
.
Векторы равны, когда у них одинаковые соответствующие координаты.
Линейные действия над векторами аналитическим путём
Если раньше линейные действия над векторами осуществлялись графически, то теперь эти операции можно выполнять аналитически, не пользуясь рисунком. Давайте вспомним и сформулируем линейные действия:
Чтобы прибавлять (отнимать) два вектора, необходимо прибавить (отнять) их соответствующие координаты, то есть:
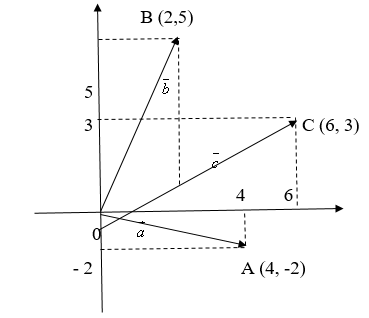
Приведём пример:
Найти сумму векторов и
, заданных на плоскости
.
Решение:
Согласно правилу 1 у нас получается:
= (6, 3).
Построим эти векторы: .
Рис. 3
Мы видим, что четырёхугольник OABC – параллелограмм. Координаты вектора мы сначала получили путём вычислений (аналитически), без помощи рисунка. Рисунок только подтверждает правило параллелограмма при прибавлении векторов, поэтому дальше рисунками будем пользоваться для наглядности.
Чтобы умножить вектор на число, необходимо каждую из его координат умножить на это число:
Дан вектор Найти
Решение:
Согласна правилу 2 у нас получается:
Геометрическое изображение смотрите на рис. 4.
Рис. 4
Два вектора равны, если у них равны соответствующие координаты:
.
Теперь вы понимаете, как получить координаты вектора не только графическим путём, но и аналитическим. В дальнейшем у вас не возникнет сложностей по этому поводу.
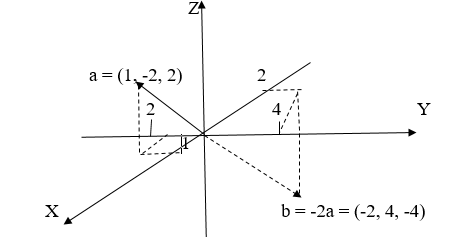
Как найти базис вектора, пример
В некотором базисе заданы своими координатами векторы и
Разложить вектор
по базису, который образовался из векторов
и
Решение:
Разложение вектора по базису
и
имеет такой вид:
где числа и
– неизвестные. Чтобы их найти, подставим в последнее равенство координаты векторов
и
, а тогда воспользуемся свойствами 1 и 2:
Согласно свойству 3 про равенство векторов, получим систему уравнений:
Первое равенство умножаем на 1, а второе на (- 2) и в итоге у на получается:
.
Значит, ответ у нас выходит: