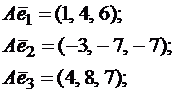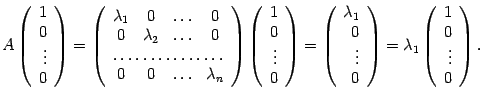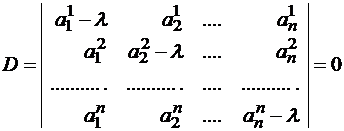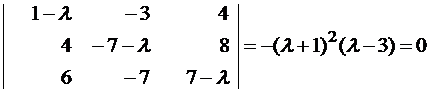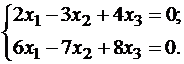Пусть линейный оператор . Рассмотрим в
произвольный базис
. Пусть в этом базисе линейному оператору
соответствует матрица
. Существует ли такой базис в пространстве
, в котором матрица линейного оператора
была бы диагональной?
Очевидно, если такой базис существует, то по Свойству 1 (п. 3.6) диагонализация матрицы произойдет в результате преобразование подобия.
Имеет место следующая
Теорема. Если в существует базис из собственных векторов линейного оператора
то матрица
линейного оператора будет диагональной в этом базисе.
Выясним, при каких условиях существует базис из собственных векторов линейного оператора.
Пусть – собственные значения линейного оператора
кратностей
, причём
. Если для каждого
существует
собственных векторов – решений ФСР соответствующей однородной СЛАУ, то существует базис из собственных векторов, а значит, матрицу
линейного оператора
можно привести к диагональному виду. В частности, если
, т. е. спектр линейного оператора простой, то базис из собственных векторов существует. Однако, если среди корней характеристического уравнения найдётся хотя бы одна пара комплексно-сопряжённых, то в вещественном линейном пространстве не существует базиса из собственных векторов.
Покажем, например, что, если спектр простой, то матрица линейного оператора в базисе из собственных векторов будет диагональной.
Рассмотрим квадратную матрицу , в столбцах которой стоят координаты собственных векторов
, соответствующих собственным значениям
. Это означает, что матрица
является матрицей перехода к базису из собственных векторов. Очевидно, в этом случае
, т. е. матрица
– невырожденная, и для неё существует обратная –
Из определения собственных векторов линейного оператора следует, что
(16)
Где – векторы-столбцы, соответствующие собственным векторам
линейного оператора
. Равенство (16) можно записать в более компактной форме:
(17)
Где – диагональная матрица, у которой на главной диагонали расположены собственные числа
т. е.
Умножим обе части равенства (17) слева на матрицу :
или
(18)
Это означает, что матрица линейного оператора при переходе к базису из собственных векторов станет диагональной в результате преобразования подобия (18).
Пример 14. Найти собственные значения и собственные векторы линейного оператора , заданного в некотором базисе матрицей
. Построить, если это возможно, базис из собственных векторов линейного оператора и найти матрицу
линейного оператора в этом базисе. Выполнить проверку.
Решение. Составим характеристическое уравнение:
Найдём собственные векторы линейного оператора:

;

Собственные значения линейного оператора различны, значит, собственные векторы линейно независимы, т. е. образуют базис. В этом базисе матрица
линейного оператора
будет диагональной:
.
Матрица перехода к базису из собственных векторов .
Проверим правильность проведенных вычислений. По формуле (7) Найдём
:
.
Тогда
Ответ: .
Пример 15. Линейный оператор в некотором базисе задан матрицей
Существует ли базис из собственных векторов линейного оператора
?
Решение. Составим характеристическое уравнение:
Собственные значения линейного оператора Найдём соответствующие им собственные векторы:

. Все остальные собственные векторы имеют вид
. Это означает, что базис из собственных векторов не существует.
Пример 16. Найти собственные векторы и собственные значения линейного оператора , заданного в некотором базисе матрицей

к диагональному виду?
Решение. Составим характеристическое уравнение:
Т. е.
Или
Собственные значения линейного оператора Найдём собственные векторы:
Эта система эквивалентна следующей:
Т. е. ФСР этой системы состоит из одного решения, например,
и
соответствует собственный вектор
. Другие собственные векторы, соответствующие собственным значениям
и
, могут быть получены из
умножением на произвольное вещественное число. Например,

Так как 
значит,
линейно зависимы, значит, совокупность собственных векторов
также линейно зависима, т. е. собственные векторы линейного оператора не образуют базис в
. Поэтому матрица
не может быть приведена к диагональному виду.
Литература: [3, 4, 5, 7, 10].
| < Предыдущая | Следующая > |
|---|
Собственные числа и собственные векторы линейного оператора
Наиболее
просто устроены матрицы диагонального
вида

Возникает вопрос, нельзя ли найти базис,
в котором матрица линейного оператора
имела бы диагональный вид. Такой базис
существует.
Пусть дано линейное
пространство Rnи действующий в
нем линейный оператор A; в этом случае
оператор A переводит Rnв себя, то
есть A:Rn→ Rn.
Определение.Ненулевой
вектор
называется
собственным вектором оператора A, если
оператор A переводит
в
коллинеарный ему вектор, то есть
.
Число λ называется собственным значением
или собственным числом оператора A,
соответствующим собственному вектору
.
Отметим некоторые свойства собственных
чисел и собственных векторов.
1. Любая
линейная комбинация собственных векторов
оператора
A, отвечающих одному и тому же собственному
числу λ, является собственным вектором
с тем же собственным числом.
2.
Собственные векторы
оператора
A с попарно различными собственными
числами λ1, λ2, …, λmлинейно независимы.
3. Если собственные
числа λ1=λ2= λm= λ, то
собственному числу λ соответствует не
более m линейно независимых собственных
векторов.
Итак, если имеется nлинейно
независимых собственных векторов
,
соответствующих различным собственным
числам λ1, λ2, …, λn, то
они линейно независимы, следовательно,
их можно принять за базис пространства
Rn. Найдем вид матрицы линейного
оператора A в базисе из его собственных
векторов, для чего подействуем оператором
A на базисные векторы:


Таким образом, матрица линейного
оператора A в базисе из его собственных
векторов имеет диагональный вид, причем
по диагонали стоят собственные числа
оператора A.
Существует ли другой
базис, в котором матрица имеет диагональный
вид? Ответ на поставленный вопрос дает
следующая теорема.
Теорема.Матрица
линейного оператора A в базисе
(i
= 1..n) имеет диагональный вид тогда и
только тогда, когда все векторы базиса
— собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Пусть
дан вектор
,
где x1, x2, …, xn— координаты
вектора
относительно
базиса
и
—
собственный вектор линейного оператора
A, соответствующий собственному числуλ, то есть
.
Это соотношение можно записать в
матричной форме
.
(*)
Уравнение
(*) можно рассматривать как уравнение
для отыскания
,
причем
,
то есть нас интересуют нетривиальные
решения, поскольку собственный вектор
не может быть нулевым. Известно, что
нетривиальные решения однородной
системы линейных уравнений существуют
тогда и только тогда, когда det(A — λE) = 0.
Таким образом, для того, чтобы λ было
собственным числом оператора A необходимо
и достаточно, чтобы det(A — λE) = 0.
Если
уравнение (*) расписать подробно в
координатной форме, то получим систему
линейных однородных уравнений:

где
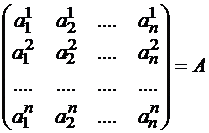
матрица линейного оператора.
Система (1) имеет ненулевое
решение, если ее определитель D равен
нулю
Получили
уравнение для нахождения собственных
чисел.
Это уравнение называется
характеристическим уравнением, а его
левая часть — характеристическим
многочленом матрицы (оператора) A. Если
характеристический многочлен не имеет
вещественных корней, то матрица A не
имеет собственных векторов и ее нельзя
привести к диагональному виду.
Пусть
λ1, λ2, …, λn— вещественные
корни характеристического уравнения,
причем среди них могут быть и кратные.
Подставляя по очереди эти значения в
систему (1), находим собственные векторы.
Пример 12.Линейный
оператор A действует в R3по закону
,
где x1, x2, .., xn— координаты
вектора
в
базисе
,
,
.
Найти собственные числа и собственные
векторы этого оператора.Решение.Строим матрицу этого оператора: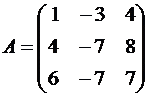
Составляем систему для определения
координат собственных векторов:
характеристическое уравнение и решаем
его:
λ1,2= -1, λ3= 3.
Подставляя
λ = -1 в систему, имеем: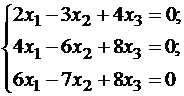

как

то зависимых переменных два, а свободное
одно.
Пусть x1— свободное
неизвестное, тогда

эту систему любым способом и находим
общее решение этой системы:

система решений состоит из одного
решения, так как n — r = 3 — 2 = 1.
Множество
собственных векторов, отвечающих
собственному числу λ = -1, имеет вид:
,
где x1— любое число, отличное от
нуля. Выберем из этого множества один
вектор, например, положив x1= 1:
.
Рассуждая аналогично, находим
собственный вектор, отвечающий
собственному числу λ = 3:
.
В пространстве R3базис состоит
из трех линейно независимых векторов,
мы же получили только два линейно
независимых собственных вектора, из
которых базис в R3составить нельзя.
Следовательно, матрицу A линейного
оператора привести к диагональному
виду не можем.
Пример 13.Дана матрица

1. Доказать, что вектор
является
собственным вектором матрицы A. Найти
собственное число, соответствующее
этому собственному вектору.
2. Найти
базис, в котором матрица A имеет
диагональный вид.Решение.1. Если
,
то
—
собственный вектор
Вектор (1, 8, -1) — собственный вектор.
Собственное число λ = -1.
Диагональный
вид матрица имеет в базисе, состоящем
из собственных векторов. Один из них
известен. Найдем остальные.
Собственные
векторы ищем из системы:
уравнение:

(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ2— 1) = 0
λ1= -3, λ2= 1, λ3= -1.
Найдем собственный вектор, отвечающий
собственному числу λ = -3: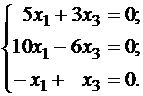
матрицы этой системы равен двум и равен
числу неизвестных, поэтому эта система
имеет только нулевое решение x1=
x3= 0. x2здесь может быть
любым, отличным от нуля, например, x2= 1. Таким образом, вектор (0,1,0) является
собственным вектором, отвечающим λ =
-3. Проверим:
Если λ = 1, то получаем систему

матрицы равен двум. Последнее уравнение
вычеркиваем.
Пусть x3— свободное
неизвестное. Тогда x1= -3x3,
4x2= 10x1— 6x3= -30x3— 6x3, x2= -9x3.
Полагая
x3= 1, имеем (-3,-9,1) — собственный
вектор, отвечающий собственному числу
λ = 1. Проверка:
Так как собственные числа действительные
и различны, то векторы, им отвечающие,
линейно независимы, поэтому их можно
принять за базис в R3. Таким образом,
в базисе
,
,
матрица
A имеет вид: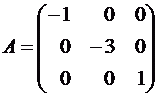
Не всякую матрицу линейного оператора
A:Rn→ Rnможно привести к
диагональному виду, поскольку для
некоторых линейных операторов линейно
независимых собственных векторов может
быть меньше n. Однако, если матрица
симметрическая, то корню характеристического
уравнения кратности m соответствует
ровно m линейно независимых векторов.
Определение.Симметрической
матрицей называется квадратная матрица,
в которой элементы, симметричные
относительно главной диагонали, равны,
то есть в которой
.Замечания.1. Все собственные
числа симметрической матрицы вещественны.
2. Собственные векторы симметрической
матрицы, соответствующие попарно
различным собственным числам, ортогональны.
В качестве одного из многочисленных
приложений изученного аппарата,
рассмотрим задачу об определении вида
кривой второго порядка.
Матрица
линейного преобразования в базисе из
собственных векторов
В
разделе «Матрица
линейного преобразования»
мы выяснили, что каждое линейное
преобразование
-мерного
линейного пространства в фиксированном
базисе задается матрицей. Если меняется
базис, то, как правило, меняется и матрица.
Возникает вопрос, нельзя ли найти базис,
в котором матрица линейного преобразования
имеет наиболее простой вид. В общем
случае выбрать такой базис довольно
сложно. Это связано с нахождением
нормальной жордановой формы матрицы,
изложение которого можно найти в более
обстоятельных учебниках по линейной
алгебре, например, в [4],
[5].
Следующая теорема отвечает на этот
вопрос в более простом случае.
Теорема
19.2
Пусть
—
линейное преобразование
-мерного
линейного пространства. Матрица линейного
преобразования имеет диагональный вид
|
|
(19.5) |
тогда
и только тогда, когда векторы базиса
являются собственнными векторами
преобразования
,
соответствующими собственным числам
.
Доказательство.
Пусть преобразование
имеет
линейно
независимых собственных векторов
,
соответствующих собственным числам
.
Так как векторы
линейно
независимы, то они образуют базис. Найдем
матрицу преобразования
в
этом базисе. Ее первый столбец является
координатным столбцом вектора
.
Так как
—
собственный вектор, то
Координатный
столбец этого вектора

Второй столбец матрицы
является
координатным столбцом вектора
.
Так как
—
собственный вектор, то
Координатный
столбец этого вектора
Вычисляя аналогично остальные столбцы,
получаем, что матрица линейного
преобразования
в
базисе
имеет
вид (19.5).
Первая часть теоремы доказана.
Пусть
в некотором базисе
матрица
линейного преобразования имеет
вид (19.5).
Найдем образ вектора
.
Этот вектор имеет координатный столбец

его образ имеет координатный столбец
Следовательно,
—
собственное число преобразования
,
а
—
соответствущий ему собственный вектор.
Аналогично находим, что любой базисный
вектор
является
собственным вектором преобразования
,
соответствующим собственному числу
.
Следствие
19.2
Если
у матрицы
порядка
существует
набор из
линейно
независимых собственнных векторов,
соответствующих собственным числам
,
то матрица
подобна
диагональной матрице с числами
на
диагонали.
Теорема
19.3
Пусть
собственные векторы
преобразования
соответствуют
собственным числам
,
среди которых нет равных друг другу.
Тогда система векторов
является
линейно независимой.
Доказательство.
Воспользуемся методом математической
индукции по числу векторов. Если
,
то утверждение теоремы следует из того,
что собственный вектор — ненулевой.
Пусть
утверждение верно для системы векторов
.
Составим линейную комбинацию векторов
и
приравняем ее к нулю
|
|
(19.6) |
К
обеим частям применим преобразование
По
определению линейного преобразования
получим
Так
как
—
собственные векторы, то
Умножим
равенство (19.6)
на
и
вычтем из последнего равенства. Получим
Так
как по предположению индукции векторы
линейно
независимы, то
По
условию
,
следовательно,
.
Подставим эти значения в (19.6),
получим
.
Получили, что из равенства (19.6)
следует
,
то есть векторы
линейно
независимы.
Следствие
19.3
Если
матрица
порядка
имеет
попарно
различных собственных чисел, то она
подобна диагональной матрице.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
06.02.2016667.14 Кб351.doc
- #
- #
- #
- #
- #
Собственные числа и собственные векторы линейного оператора
Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x 1, x 2, . x m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x 1, x 2, . x m оператора A с попарно различными собственными числами λ1, λ2, …, λm линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x 1, x 2, . x n, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 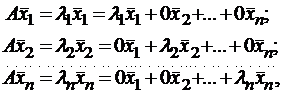

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе < ε i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
Пример №1 . Линейный оператор A действует в R3 по закону A· x =(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, . xn — координаты вектора x в базисе e 1=(1,0,0), e 2=(0,1,0), e 3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e 1=(1,4,6)
A· e 2=(-3,-7,-7)
A· e 3=(4,8,7) 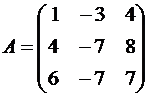
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
Пример №2 . Дана матрица 
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор
Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой ai k =ak i .
Замечания .
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Собственные числа, собственные векторы матриц и квадратичные формы
Проблема собственных чисел играет существенную роль не только в линейной алгебре, но и в других разделах математики, а также во многих прикладных областях (в менеджменте, психологии, юриспруденции).
Пусть задана квадратная матрица А размера (n X п), элементами которой являются действительные числа (R) и вектор неизвестных X размера (n X 1):
Предположим, что X — это некоторое неизвестное действительное число.
Если X и ненулевой вектор X удовлетворяют уравнению
то X называется собственным числом или собственным значением матрицы А, а X — собственным вектором этой же матрицы, соответствующим X.
Преобразуем уравнение (2.15) к следующему виду:
где Е — единичная матрица.
называется характеристической матрицей.
Так как по условию вектор неизвестных X не равен нулю, то среди его координат х , х2, . хп должна быть хотя бы одна ненулевая. А для того, чтобы система линейных однородных уравнений (2.16) имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен нулю (это следует из теоремы Кронекера-Капелли).
Число X = Xfc, где к = 1, п будет собственным числом только в том случае, если матрица (ХкЕ -А) — вырожденная.
Уравнение (2.17) называется характеристическим уравнением матрицы А и представляет собой алгебраическое уравнение степени п относительно X:
Уравнение (2.18) имеет п корней Xv Х2, Хп. Множество всех корней уравнения (2.18) называется спектром матрицы А.
Заметим, что уравнение det (А — ХЕ) = 0 имеет те же корни, что и уравнение (2.17), т. е.
Каждому собственному значению спектра матрицы А ставится в соответствие собственный вектор, определенный с точностью до скалярного множителя. Если Хк есть кратный корень характеристического уравнения, то для произвольной квадратной матрицы число соответствующих собственных векторов может быть не равно кратности корня. С геометрической точки зрения собственный вектор определяет в пространстве некоторое направление (прямую, проходящую через начало координат), которое в результате преобразования не изменяется и вдоль которого пространство испытывает растяжение или сжатие в X раз.
Полином Х п + р^” -1 + . + рп = 0 называют характеристическим полиномом. Коэффициенты рк (k = 1, п) можно вычислить по следующим рекуррентным формулам [57]:
Здесь SpA = S акк — след матрицы (сумма элементов, стоя-
щих на главной диагонали матрицы А). Заметим, что р = (-1)” X X det А. При отыскании собственных чисел даже для матриц невысокого порядка неизбежно большое количество вычислений. Для общего случая нельзя предложить оптимальный способ нахождения собственных чисел и собственных векторов матрицы.
Рассмотрим случай, когда собственные числа находятся сразу исходя из вида матрицы (исходная матрица либо диагональная, либо верхняя или нижняя треугольная). В этом случае собственные числа 2. п совпадают с элементами главной диагонали исходной матрицы ап, а22. апп.
Пусть задана верхняя треугольная матрица А размера (n X п):
Отсюда видно, что собственные числа равны:
С появлением ЭВМ получили распространение итерационные методы нахождения собственных чисел, которые не используют вычисление характеристического полинома. К этим способам относятся: степенной метод, метод обратных итераций, QR-алгоритм, метод вращений Якоби, QL-алгоритм и др. Причем применение конкретного итерационного метода зависит от вида исходной матрицы А [4].
Теперь рассмотрим конкретные примеры.
Пример 2.8. Дана матрица А размера (3 X 3)
Найти собственные числа и собственные векторы матрицы А.
Из условия задачи видно, что матрица А является верхней треугольной матрицей. Поэтому собственными числами данной матрицы будут элементы ее главной диагонали
Теперь найдем соответствующие найденным собственным числам собственные векторы. Для этого мы используем уравнение (2.16).
Для Х1 = -4 получаем
Далее раскроем матричное уравнение (2.20)
В результате получим
Так как матрица этой системы вырождена, то она имеет ненулевые решения, которые имеют вид:
т. е. получены искомые собственные вектора для Для Х2 = Х3 = 1 получаем
ил*
В результате получаем
т. е. это уравнение имеет ненулевые решения, которые и будут искомыми собственными векторами для 2.
Эти решения запишем в виде
Пример 2.9. Дана матрица А размера (2 X 2). Найти собственные числа и собственные матрицы А
Запишем характеристическое уравнение (2.17) для данного случая
Теперь найдем собственные векторы исходной матрицы А, соответствующие .1 = 1 и Х2 = -4.
В подробной записи получим
Так как определитель полученной матрицы равен нулю, то она имеет ненулевые решения, которые и являются собственными векторами Xv которые мы и находим
Из первого уравнения системы получаем х2 = 2xv Из второго уравнения системы получаем х2 = 2xv т. е. она имеет бесконечное множество решений. И искомый собственный вектор Xj будет иметь вид
Аналогично, для Х2 = -4 находим
В заключение приведем два полезных правила [38]:
1) сумма собственных чисел матрицы А равна следу этой матрицы, т. е.
2) произведение собственных чисел матрицы А равно определителю этой матрицы
Кратко рассмотрим квадратичные формы.
Квадратичной формой называется однородный многочлен второй степени от нескольких пременных. Обозначим их xv х2, . х .
Квадратичную форму в общем виде можно записать так:
В качестве примера рассмотрим квадратичную форму трех переменных:
Введем обозначения:
Тогда квадратичная форма примет вид
Дополнительно вводим симметричную матрицу В, вектор X.
В этом случае квадратичная форма примет вид
Последняя формула представляет собой матрично-векторный вид квадратичной формы.
А в общем случае получим:
где Ь..— коэффициенты при х 2 для всех i = 1, 2, n, a b’j = Ц< равны полусуммам коэффициентов при элементах, содержащих произведения х. х. и х. х< при всех г, j = 1, 2,п, г ^ j.
Матрица В является матрицей квадратичной формы.
В качестве примера запишем в матрично-векторном виде квадратичную форму
В данном случае получаем:
Матрица данной квадратичной формы принимает вид А ее матрично-векторная запись такова:
Собственные векторы матрицы
Онлайн калькулятор нахождение собственных чисел и собственных векторов — Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования.
Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.
http://studref.com/549305/matematika_himiya_fizik/sobstvennye_chisla_sobstvennye_vektory_matrits_kvadratichnye_formy
http://allcalc.ru/node/648
Собственные числа и собственные векторы линейного оператора
Наиболее просто устроены матрицы диагонального вида 
Пусть дано линейное пространство Rn и действующий в нем линейный оператор A; в этом случае оператор A переводит Rn в себя, то есть A:Rn
→ Rn.
Определение. Ненулевой вектор x называется собственным вектором оператора A, если оператор A переводит x в коллинеарный ему вектор, то есть A·x = λ·x. Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x.
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x1, x2, …, xm оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x1, x2, …, xm оператора A с попарно различными собственными числами λ1, λ2, …, λm
линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x1, x2, …, xn, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 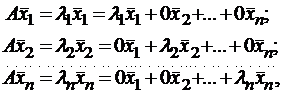

Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе {εi} (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Пусть дан вектор x=(x1, x2, …, xn), где x1, x2, …, xn — координаты вектора x относительно базиса {ε1, ε2, …, εn} и x — собственный вектор линейного оператора A, соответствующий собственному числу λ, то есть A·x=λ·x. Это соотношение можно записать в матричной форме
x·(A-λ·E). (*)
Уравнение (*) можно рассматривать как уравнение для отыскания x, причем x ≠ 0, то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A — λE) = 0. Таким образом, для того, чтобы λ было собственным числом оператора A необходимо и достаточно, чтобы det(A — λE) = 0.
Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений:
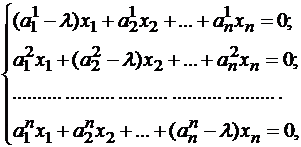
где 
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
Получили уравнение для нахождения собственных чисел.
Это уравнение называется характеристическим уравнением, а его левая часть — характеристическим многочленом матрицы (оператора) A. Если характеристический многочлен не имеет вещественных корней, то матрица A не имеет собственных векторов и ее нельзя привести к диагональному виду.
Пусть λ1, λ2, …, λn — вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.
Пример №1. Линейный оператор A действует в R3 по закону A·x=(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, .., xn — координаты вектора x в базисе e1=(1,0,0), e2=(0,1,0), e3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A·e1=(1,4,6)
A·e2=(-3,-7,-7)
A·e3=(4,8,7)
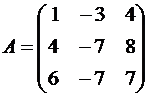
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
λ1,2 = -1, λ3 = 3.
Подставляя λ = -1 в систему, имеем:
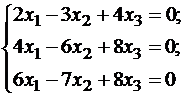
Так как 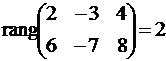
Пусть x1 — свободное неизвестное, тогда 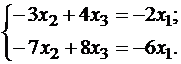

Множество собственных векторов, отвечающих собственному числу λ = -1, имеет вид: (x1, 2x1, x1)=x1(1,2,1), где x1 — любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x1 = 1: x1=(1,2,1).
Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу λ = 3: x2=(1,2,2).
В пространстве R3 базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в R3 составить нельзя. Следовательно, матрицу A линейного оператора привести к диагональному виду не можем.
Пример №2. Дана матрица 
1. Доказать, что вектор x=(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A·x=λ·x, то x — собственный вектор
Вектор (1, 8, -1) — собственный вектор. Собственное число λ = -1.
Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные.
Собственные векторы ищем из системы:
(2-λ)x1+3x3=0;
10x1-(3+λ)x2-6x3=0;
-x1-(2+λ)x3=0;
Характеристическое уравнение: 
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ2 — 1) = 0
λ1 = -3, λ2 = 1, λ3 = -1.
Найдем собственный вектор, отвечающий собственному числу λ = -3:
5x1+3x3=0;
10x1-6x3=0;
-x1+x3=0;
Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение x1 = x3 = 0. x2 здесь может быть любым, отличным от нуля, например, x2 = 1. Таким образом, вектор (0,1,0) является собственным вектором, отвечающим λ = -3. Проверим:
Если λ = 1, то получаем систему
Ранг матрицы равен двум. Последнее уравнение вычеркиваем.
Пусть x3 — свободное неизвестное. Тогда x1 = -3x3, 4x2 = 10x1 — 6x3 = -30x3 — 6x3, x2 = -9x3.
Полагая x3 = 1, имеем (-3,-9,1) — собственный вектор, отвечающий собственному числу λ = 1. Проверка:
Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в R3. Таким образом, в базисе f1=(1,8,-1), f2=(0,1,0), f3=(-3,-9,1) матрица A имеет вид:

Не всякую матрицу линейного оператора A:Rn→ Rn можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше n. Однако, если матрица симметрическая, то корню характеристического уравнения кратности m соответствует ровно m линейно независимых векторов.
Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой aik=aki.
Замечания.
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Перейти к онлайн решению своей задачи
Ответы с готовыми решениями:
Преобразовать к каноническому виду квадратичную форму и найти ОНБ, в котором эта форма имеет канонический вид
Кто-нибудь знает, как решить эту задачу, пожалуйста.
Спасибо.
Преобразовать к каноническому…
Матрица линейного оператора
Найдите матрицу линейного оператора А в базисе e1,e2, если оператор А переводит вектор e1+2e2 в…
Вырожденная матрица линейного оператора
Если предположить, что матрица линейного оператора в произвольном базисе вырождена, что из этого…
Матрица оператора линейного преобразования
Дана матрица М линейного преобразования φ в базисе e1, e2. Найти матрицу преобразования φ в…
1