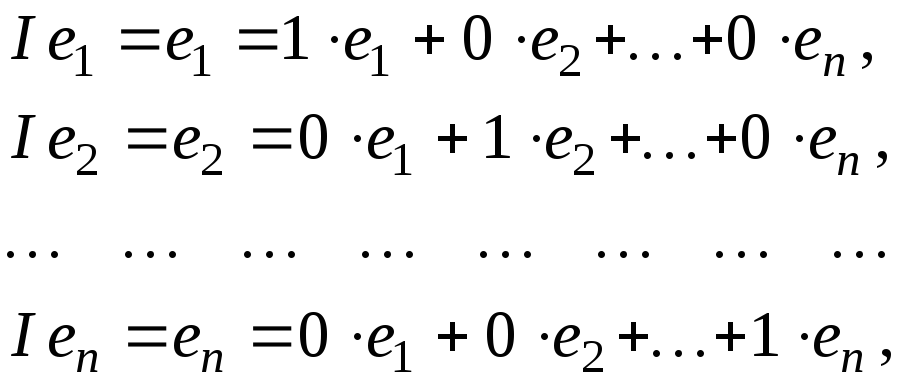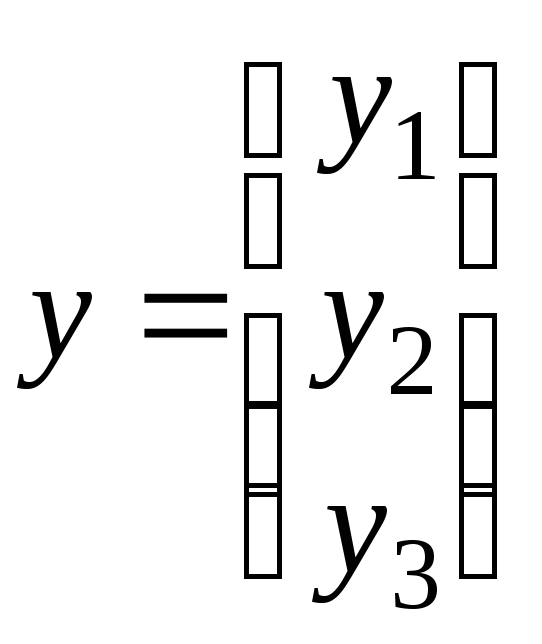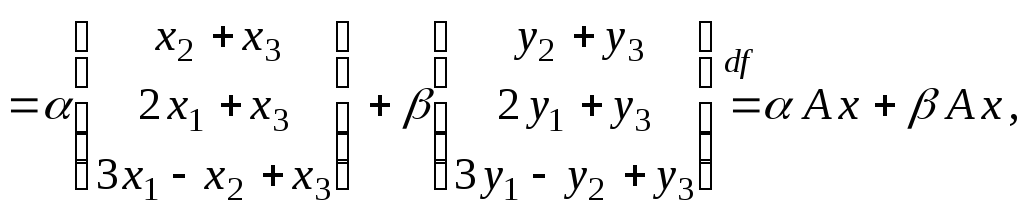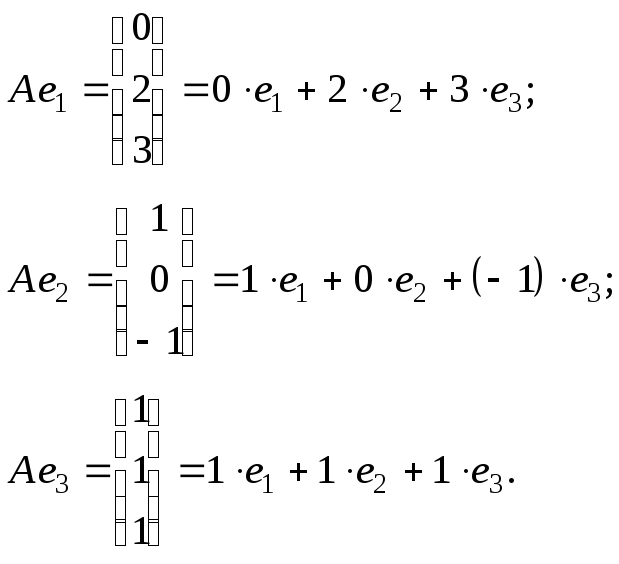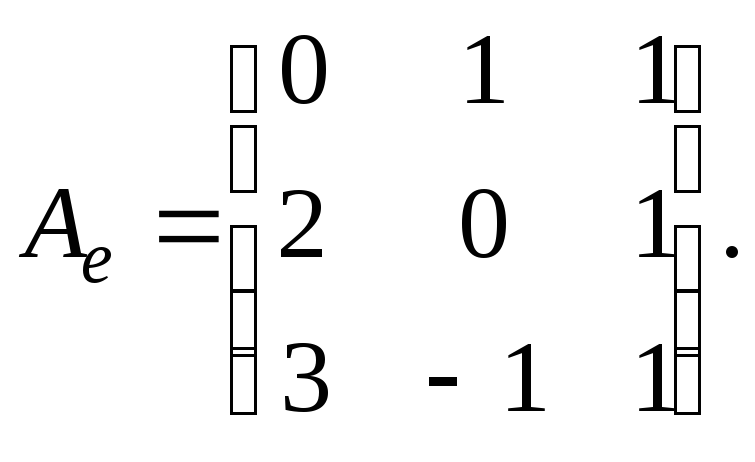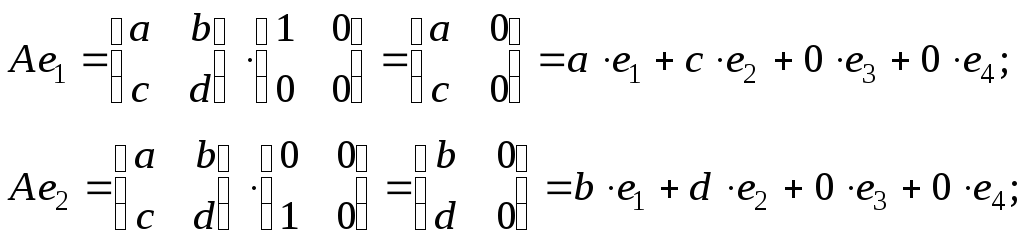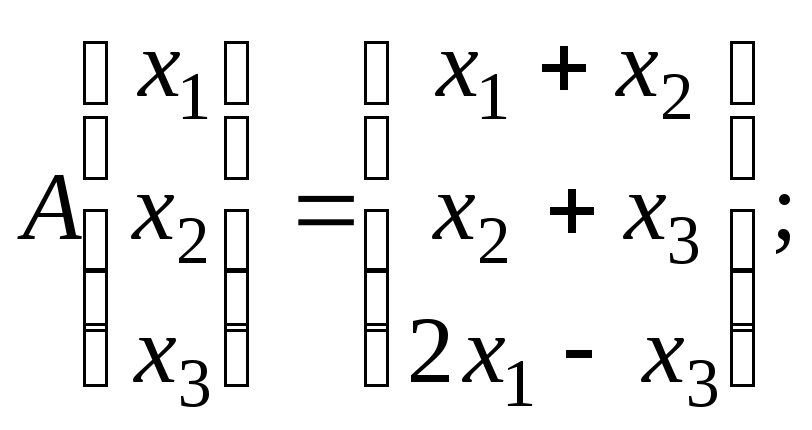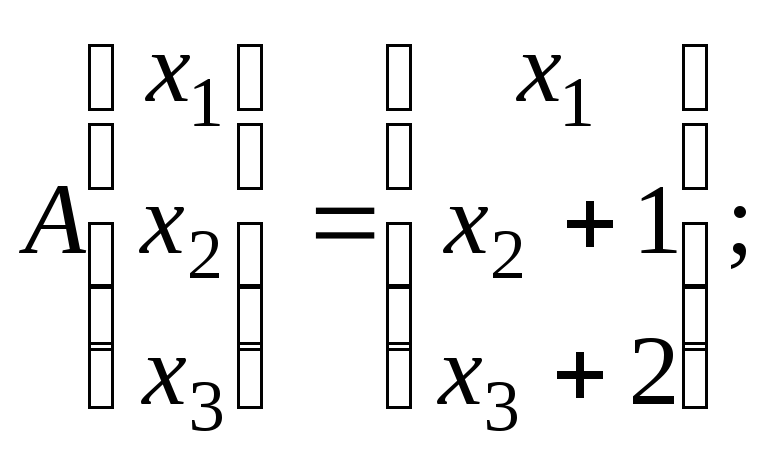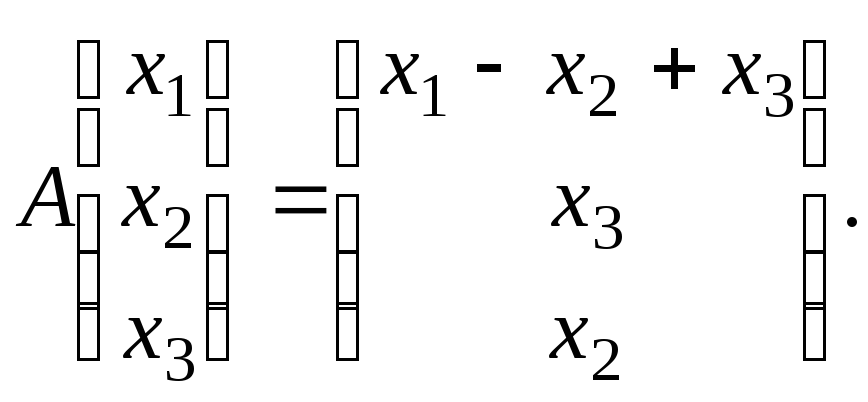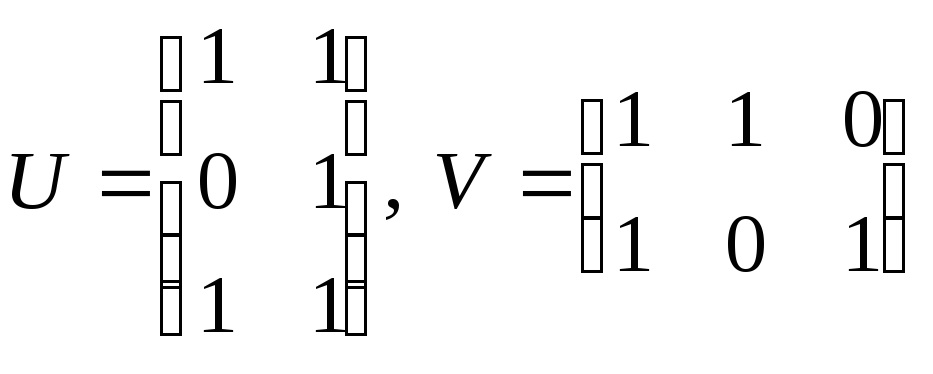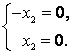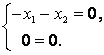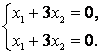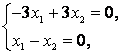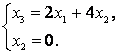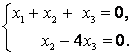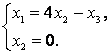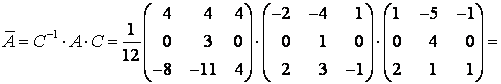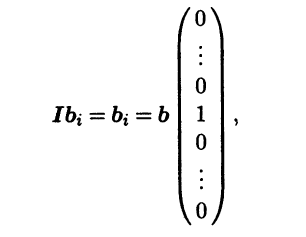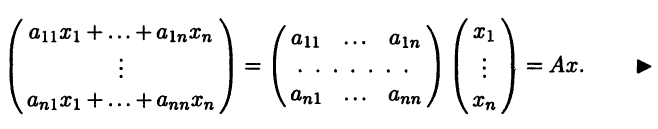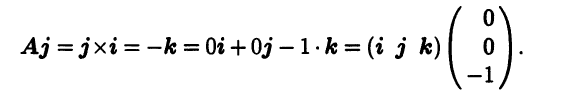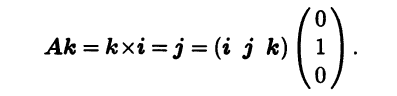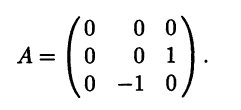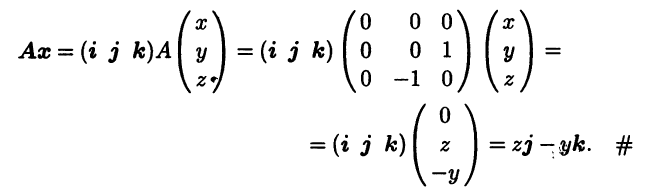Как найти базис матрицы линейного оператора - Исправление недочетов и поиск решений вместе с Examum.ru

Светлой
памяти

Чубича
Михаила Петровича

посвящается

§ 7.1. Определение линейного оператора.

Матрица линейного оператора

Пусть

и
— линейные пространства над одним и тем
же полем .
Будем говорить, что из
пространства

в пространство

действует оператор

или, что то же самое, отображение

,
преобразование
,
если каждому вектору
по какому — либо правилу поставлен в
соответствии определенный вектор
из .

Наиболее
простыми являются линейные операторы.
Отображение
называется линейным
оператором
(линейным
преобразованием),
действующим из
в ,
если оно удовлетворяет следующим двум
условиям:

;

,
.

Совокупность
условий 1 и 2 равносильна следующему
условию:

.
(7.1.1)

Обозначим
через
множество всех линейных операторов,
действующих из линейного пространства

в линейное пространство .
Два линейных оператора
и
из
называются равными,
если

(7.1.2)

Множество
будет линейным пространством над полем
,
если определить сумму

операторов

и произведение

оператора

на число

соотношениями

(7.1.3)

(7.1.4)

Нулевым
вектором пространства
будет нулевой
оператор
из
в,
т.е. оператор, переводящий любой вектор

линейного пространства
в нулевой вектор линейного пространства
.

В
случае, когда ,
линейный оператор

называется линейным преобразованием
пространства .

Пусть
—
оператор из ,
и пусть и
—
фиксированные базисы линейных пространств
исоответственно.
Разложим векторы
по базису :

,
(7.1.5)

Из
коэффициентов этих разложений составим
—
матрицу

(7.1.6)

Матрица

называется матрицей
линейного оператора

в паре базисов и
.
Заметим, что столбцами матрицы
служат столбцы координат векторов
в базисе ,
т.е. строки коэффициентов из разложений
(7.1.5).

Если

,
то при нахождении матрицы линейного
оператора фиксируются векторы одного
базиса ,
по которому раскладываются .
Записанные столбцами коэффициенты
разложений образуют квадратную матрицу

порядка .

Равные
линейные операторы в одном и том же
базисе имеют одинаковые матрицы.

Матрицей
суммы линейных операторов в фиксированных
базисах является сумма матриц слагаемых
операторов в тех же базисах.

При
умножении линейного оператора на число
его матрица умножается на то же число.

Если

и

—
соответственно,
—
и
—
мерное линейные пространства над одним
полем
,
то линейное пространство

изоморфно
линейному пространству
—
матриц с элементами из
с
операциями сложения матриц и умножения
их на числа из поля
.

Пример
1.
Оператор
называется
тождественным
(единичным)
оператором,
если

(7.1.7)

Покажите
линейность оператора
и постройте его матрицу в базисе .

Решение.
В силу того, что

убеждаемся
в линейности тождественного оператора.
Поскольку

получаем,
что

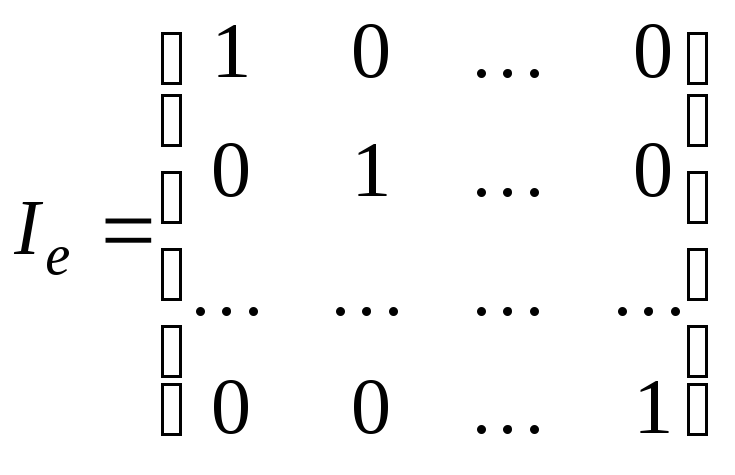
В
любом базисе тождественный оператор
имеет единичную матрицу.

Пример
2.
Докажите, что преобразование

пространства

линейно и найдите его матрицу в
каноническом базисе.

Решение.
Пусть

и

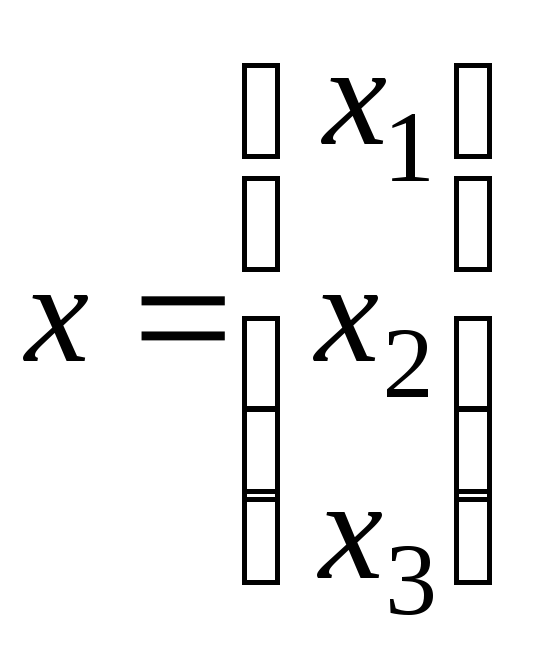
— произвольные векторы из .
Тогда

т.
е. преобразование
пространства
линейно. Канонический базис линейного
пространства
составляют векторы

.
Из определения оператора
вытекает, что

Таким
образом,

Пример
3.
Покажите, что умножение квадратных
матриц второго порядка слева на данную
матрицу
является линейным преобразованием
пространства
и найдите матрицу этого преобразования
в базисе, состоящем из матриц

Решение.
По определению преобразования
для любых матриц
и любых чисел
имеем:

Перейдем
к построению матрицы оператора
в данном базисе. В силу того, что

получаем:

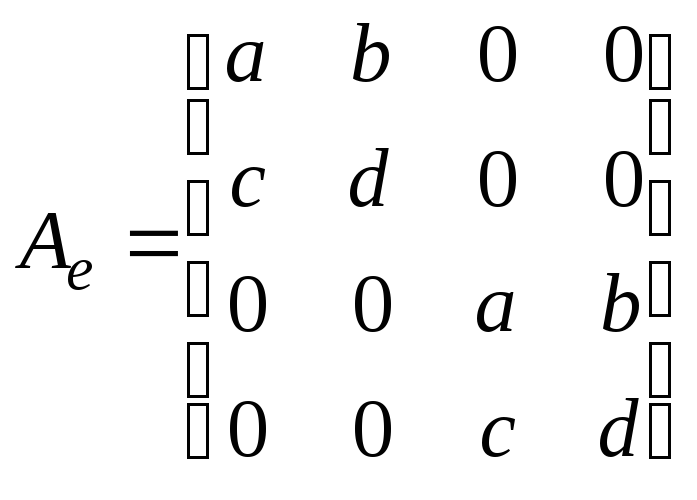
7.1.1.
Какую матрицу имеет нулевой оператор
в любых базисах пространств
и ?

7.1.2.
Линейное пространство
является прямой суммой подпространств

и .
Докажите, что оператор
пространства ,
который каждому вектору
с разложением ,
где ,
ставит в соответствие вектор
этого разложения, является линейным.
Оператор
называется оператором
проектирования
пространства
на
параллельно .

Найдите
матрицу этого оператора в базисе,
полученном объединением базисов
подпространств
и .

7.1.3.
Линейное пространство
является прямой суммой подпространств

и .
Докажите, что оператор ,
который каждому вектору
с разложением ,
где ,
ставит в соответствие вектор ,
является линейным. Оператор
называется отражением
пространства
в
параллельно .

Найдите
матрицу этого оператора в базисе,
полученном объединением базисов
подпространств
и .

7.1.4.
Докажите, что всякий линейный оператор,
действующий в одномерном пространстве,
сводится к умножению всех векторов
пространства на фиксированное (для
данного оператора) число.

7.1.5.
Верно ли, что линейный оператор переводит:

а)
линейно зависимую систему векторов в
линейно зависимую;

б)
линейно независимую систему векторов
в линейно независимую?

7.1.6.
Выясните, какие из следующих преобразований
пространства
линейны, и в случае линейности найдите
их матрицы в каноническом базисе:

а)

б)

в)

г)

7.1.7.
Укажите, какие из приведенных преобразований
пространства
являются линейными операторами, и
найдите их матрицы в базисе .
Каждое преобразование описывается
своим действием на произвольный многочлен
:

а)

б)

в)
,
где
и
— фиксированные числа, причем ;

г)

Этот оператор в дальнейшем называется
оператором
дифференцирования.

7.1.8.
Какова матрица оператора дифференцирования,
действующего в линейном пространстве
,
в базисе ,
где
— действительное число?

7.1.9.
Покажите, что умножение квадратных
матриц второго порядка справа на данную
матрицу
является линейным преобразованием
пространства ,
и найдите матрицу этого преобразования
в базисе, состоящем из матриц :

7.1.10.
Проверьте линейность оператора ,
заданного формулой ,
где
и постройте матрицу этого оператора в
базисах

7.1.11.
В пространстве
фиксирован базис, состоящий из матриц

(в
указанном порядке). Запишите в этом
базисе матрицу оператора транспонирования,
т.е. оператора, который каждой матрице

ставит в соответствие транспонированную
матрицу.

Как
изменится эта матрица, если в базисе
поменять местами векторы
и ?

Соседние файлы в папке Задачник-2

Источник

Задание 1. Линейный оператор преобразует векторы , , в векторы , , . Найти матрицу линейного оператора.

Решение. Матрицы

, и

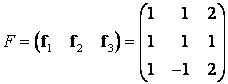
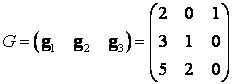
Связаны между собой соотношением , откуда .

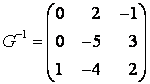
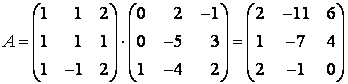
Так как , то , а искомая матрица линейного оператора .

Ответ: .

< Предыдущая		Следующая >

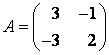
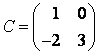
Задание 2. Пусть линейный оператор в базисе задан матрицей . Найти матрицу этого линейного оператора в базисе , если матрица является матрицей перехода от базиса к базису .

Решение. Матрицы и линейного оператора , заданного в разных базисах, связаны между собой соотношением . Так как , то

.

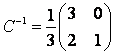
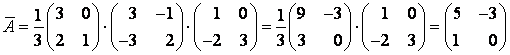
Ответ: .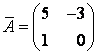

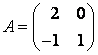
Задание 3. Линейный оператор в базисе задан матрицей . Найти матрицу этого линейного оператора в базисе , если , .

Решение. Связь между матрицами и линейного оператора в разных базисах определяется формулой , где – матрица перехода от базиса к базису .

Составим матрицу : , тогда и, следовательно,

.

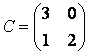
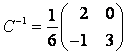
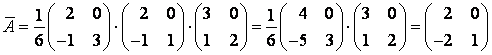
Ответ: .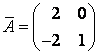

Задание 4. Линейный оператор в базисе задан матрицей . Найти матрицу этого линейного оператора в базисе , если , .

Решение. Матрицы и связаны между собой соотношением , где – матрица перехода от базиса к базису .

Составим матрицу : , тогда и, следовательно,

Ответ: .

Задание 5. Найти собственные значения и собственные векторы линейного оператора , заданного в некотором базисе матрицей .

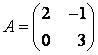
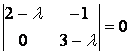
Решение. Для нахождения собственных значений линейного оператора составим характеристическое уравнение , т. е. . Раскрывая определитель, получим , т. е. , .

По определению называется собственным вектором линейного оператора , соответствующим собственному значению , если .

Найдём собственные векторы и , соответствующие собственным значениям и .

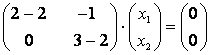
При получим: , что равносильно такой однородной системе уравнений:

Если – базисная переменная, а – свободная, то .

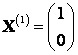
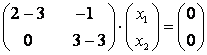
При : , что равносильно однородной системе уравнений

Пусть – базисная переменная, – свободная. Примем , тогда , а следовательно, .

Так как собственные векторы соответствуют различным собственным значениям, то они должны быть линейно независимы. Проверим линейную независимость полученных собственных векторов 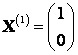и .

Составим матрицу . Так как , то собственные векторы и линейно независимы.

Ответ: собственные числа , ; собственные векторы , .

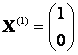
Задание 6. Привести матрицу 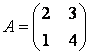линейного оператора к диагональному виду.

Решение. Матрица линейного оператора будет диагональной в базисе из собственных векторов, если такой базис существует. Найдём собственные значения и собственные векторы линейного оператора.

Запишем характеристическое уравнение: 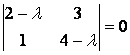, т. е. или , откуда получаем , .

Найдём собственные векторы И .

При получим: , что соответствует следующей однородной системе уравнений:

Пусть – базисная переменная, – свободная. Полагая , получим .

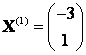
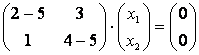
При : . Соответствующая однородная система уравнений имеет вид:

Откуда . Пусть – базисная переменная, – свободная, примем тогда , а, следовательно, .

Собственные векторы и отвечают различным собственным значениям, поэтому они линейно независимы, т. е. могут составить базис. Матрица линейного оператора в базисе из собственных векторов и имеет диагональный вид: .

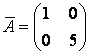
Можно проверить полученный результат. Так как , где матрица в случае перехода к базису из собственных векторов и имеет вид , следовательно,

,

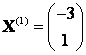
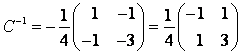
Тогда

.

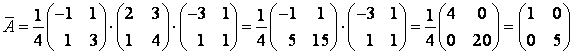
Ответ: .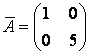

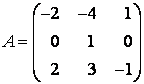
Задание 7. Найти собственные значения и собственные векторы линейного оператора , заданного в некотором базисе матрицей . Построить, если это возможно, базис из собственных векторов и найти матрицу этого линейного оператора в базисе из собственных векторов.

Решение. Запишем характеристическое уравнение:

,

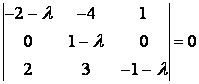
Т. е. ,

, откуда получаем , , .

Найдём собственные векторы линейного оператора.

При : , тогда соответствующая однородная система уравнений примет вид:

или

Что равносильно такой системе:

Пусть и – базисные переменные, – свободная. Полагая , получим .

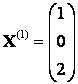
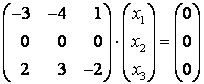
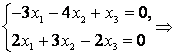
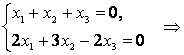
При : , или, переходя к однородной системе уравнений, получим

Пусть и – базисные переменные, – свободная. Если , то .

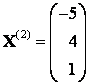
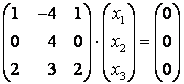
При получим: , и однородная система уравнений примет вид:

Пусть и – базисные переменные, – свободная. Тогда если , то . Найденные собственные векторы соответствуют различным собственным значениям, поэтому они линейно независимы, значит, существует базис из собственных векторов. Матрица перехода к такому базису , тогда

.

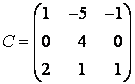
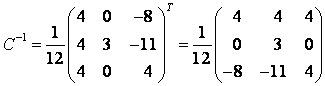
Матрица линейного оператора в базисе из собственных векторов имеет вид: .

Можно сделать проверку полученных результатов:

.

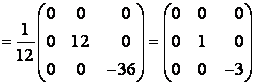
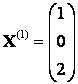
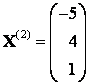
Ответ: , , ; , , ; матрица линейного оператора в базисе из собственных векторов .

< Предыдущая Следующая >

Источник

Пример 4.3 более глубок, чем это может показаться с первого взгляда. Фактически любой линейный оператор можно интерпретировать как линейный оператор, описанный в этом примере, т.е. действие линейного оператора сводится к умножению столбца координат вектора на матрицу. Поясним это подробнее.

Пусть задан линейный оператор А: L → L, т.е. линейное преобразование n-мерного линейного пространства L в себя. Выберем базис b = (b₁ … b_n) в L. Действие линейного оператора полностью определено, если известны образы векторов базиса. Действительно, если вектор х имеет координаты х = (x₁ … х_n)^T , то

Ах = A(x₁b₁ + … + х_nb_n) = x₁(Ab₁) +… + х_n(Аb_n),

т.е., зная векторы Ab_i, мы можем найти образ любого вектора x линейного пространства L.

Рассмотрим действие линейного оператора А на векторы базиса b. Обозначим столбцы координат векторов Ab_ix в базисе через а_i, a_i = (а_1i … а_in) , i = 1,n. Тогда

Ab_i = ba_i, i = 1,n.

Определение 4.4. Матрицу А = (а₁ … a_n), составленную из координатных столбцов векторов Ab₁, … , Ab_n в базисе b = (b₁ … b_n) называют матрицей линейного оператора А в базисе b.

Матрица линейного оператора А: L → L является квадратной, ее порядок совпадает с размерностью линейного пространства L.

Рассмотрим несколько примеров линейных операторов и их матриц.

Пример 4.7. Матрицей нулевого оператора Θ: L → L независимо от выбора базиса является нулевая матрица соответствующего типа. Действительно, образом любого вектора в случае нулевого оператора является нулевой вектор. Поэтому матрица нулевого оператора в любом базисе должна состоять из нулевых столбцов.

Пример 4.8. Матрица тождественного оператора I также не зависит от выбора базиса и в любом базисе является единичной. Действительно, взяв произвольный базис b = (b₁ … b_n), заключаем, что при i = 1,n

где единица в последнем столбце стоит на i-м месте. Видно, что столбец координат вектора Ib_i является i-м столбцом единичной матрицы.

Теорема 4.3. Пусть А: L → L — линейный оператор. Тогда столбец у координат вектора у = Ах в данном базисе b линейного пространства L равен произведению Ах матрицы А оператора А в базисе b на столбец х координат вектора x в том же базисе: у = Ах.

◄ Выберем произвольный вектор х = х₁b₁ + … + х_nb_n. Его образом будет вектор

у = Ах = A(x₁b₁ + … + x_nb_n) = x₁(Ab₁) + … + х_n(Аb_n) = x₁(a₁₁b₁ + … + a_n1b_n) + … + x_n(a_1nb₁ + … + a_nnb_n) =
(а₁₁x₁ + … + a_1nx_n)b₁ + … + (a_n1x₁ + … + a_nnx_n)b_n.

Столбец координат вектора Ax в базисе b имеет вид

Запись у = Ах из формулировки теоремы 4.3 удобно называть матричной формой записи действия линейного оператора А в базисе b.

Замечание 4.1. Выкладки, приведенные в доказательстве теоремы, можно упростить, если использовать матричные обо-значения и правила выполнения матричных операций. Полагая, что строка образов базисных векторов (Ab₁ … Ab_n) получается «умножением» строки векторов b слева на оператор А:

(Аb₁ … Аb_n) = Аb,

получаем

Ab = (Ab₁ … Ab_n) = (ba₁ … ba_n) = b(a₁ … а_n) = bА,

так как ba_i — матричная запись разложения вектора Ab_i по базису b, i = 1,n. Здесь мы использовали технику операций с блочными матрицами.

Взяв произвольный вектор х = bх, получаем

Ах = А(bх) = (Аb)х = (bА)х = b(Ах).

Это означает, что столбец Ах является столбцом координат вектора Ах.

Пример 4.9. Рассмотрим отображение А: V₃ → V₃, которое каждый вектор х преобразует в его векторное произведение Ах = х × i на орт i оси Ох. В силу свойств векторного произведения это отображение — линейный оператор. Найдем матрицу А этого линейного оператора в (правом) ортонорми- рованном базисе i, j, k. Для этого надо найти образы базисных векторов и разложить их по тому же базису. Поскольку Ai = i × i = 0, то первый столбец в матрице А нулевой. Далее получаем второй столбец матрицы А:

Затем третий столбец:

Итак, матрица А имеет вид

Действие линейного оператора А на вектор х можно теперь записать как умножение столбца координат (х у z)^T вектора х слева на матрицу оператора:

Матрица линейного оператора полностью характеризует линейный оператор. В то же время, какую бы квадратную матрицу порядка n мы ни взяли, она будет матрицей некоторого линейного оператора в заданном базисе n-мерного линейного пространства (см. пример 4.3). Таким образом, между линейными операторами, действующими в данном n-мерном линейном пространстве L и квадратными матрицами порядка n существует соответствие, которое является взаимно однозначным, что и утверждает следующая теорема.

Теорема 4.4. Пусть b — произвольный базис в n-мерном линейном пространстве L. Различным линейным операторам А и В, действующим в пространстве L, соответствуют и различные матрицы в базисе b. Любая квадратная матрица А порядка n является матрицей некоторого линейного оператора, действующего в линейном пространстве L.

◄ Если матрицы А и В операторов А и В в базисе b совпадают, то, согласно теореме 4.3, для любого вектора х со столбцом координат х

Ах = bАх = bВх = Вх,

т.е. образы произвольного вектора при двух отображениях совпадают. Следовательно, совпадают и сами отображения.

Пусть А = (a_ij) — произвольная квадратная матрица порядка n. Определим отображение А: L → L согласно формуле А(х) = bАх, где х — столбец координат вектора х. Несложно проверить, что заданное таким образом отображение является линейным оператором. Действительно, для любых векторов х,у ∈ L и любых действительных чисел λ, μ

А(λx + μу) = bА(λх + μу) = λ(bАx) + μ(bАу) = λА(х) + μА(у).

В этой выкладке мы использовали теорему 1.3 и свойства умножения матриц. Вычислив для i = 1,n столбец координат образа i-го вектора из базиса b

где единица стоит в i-й строке, убеждаемся, что он совпадает с i-м столбцом матрицы А и поэтому матрица заданного линейного оператора совпадает с исходной матрицей А. ►

Теорема 4.5. Ранг матрицы линейного оператора А: L → L совпадает с рангом этого оператора.

◄ Образ imA линейного оператора А представляет собой линейную оболочку системы векторов Ab₁, …, Ab_n, где b₁, …, b_n — некоторый базис линейного пространства L. Размерность линейного подпространства imA, представляющая собой ранг оператора, совпадает с максимальным количеством линейно независимых векторов в системе Ab₁, … , Ab_n и равна
максимальному количеству линейно независимых столбцов в матрице А, составленной из столбцов координат этих векторов. Но матрица А является матрицей оператора А. Значит, dim imA совпадает с рангом матрицы оператора А в указанном базисе. Поскольку понятие ранга линейного оператора не зависит от выбора базиса, то и ранг его матрицы в любом базисе один и тот же. ►

Замечание 4.2. Связь между линейными операторами и матрицами, вскрытая доказанными теоремами, позволяет дать геометрическую интерпретацию системе линейных алгебраических уравнений (СЛАУ). Если СЛАУ записать в матричной форме Ах = b, то матрицу А можно связать с некоторым линейным оператором А, а столбцы х и b интерпретировать как столбцы координат векторов x и b. Мы приходим к операторному уравнению, Ах = b, решение которого означает определение вектора х по его образу b. В частном случае b = 0 СЛАУ однородна, а решение операторного уравнения означает определение ядра оператора. Отметим, что тривиальное решение х = 0 однородной СЛАУ Ах = 0 соответствует нулевому вектору, всегда входящему в ядро оператора.

Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ

Источник

Линейные операторы (преобразования)

Определение линейных операторов (преобразований)

Линейным преобразованием (линейным оператором) линейного пространства {V} называется линейное отображение mathcal{A}colon Vto V пространства {V} в себя.

Поскольку линейное преобразование является частным случаем линейного отображения, к нему применимы все понятия и свойства, рассмотренные для отображений: инъективность, сюръективность, биективность, обратимость, ядро, образ, дефект, ранг и т.д.

Матрицей линейного оператора (преобразования) mathcal{A}colon Vto V в базисе $mathbf{e}_1,ldots,mathbf{e}_n$ пространства {V} называется квадратная матрица , составленная из координатных столбцов образов базисных векторов $mathcal{A}(mathbf{e}_1),ldots,mathcal{A}(mathbf{e}_n)$ , найденных относительно базиса $mathbf{e}_1,ldots,mathbf{e}_n$ .

Матрица биективного линейного оператора (преобразования) обратима, т.е. невырождена. Поэтому биективное (обратимое) преобразование называют также невырожденным.

Примеры линейных операторов (преобразований)

1. Обозначим mathcal{O}colon Vto V — нулевое преобразование n-мерного пространства {V} , которое ставит в соответствие любому вектору mathbf{v}in V нулевой элемент boldsymbol{o} пространства {V} . Это преобразование не является инъективным, сюръективным, биективным, обратимым. Матрица нулевого преобразования (в любом базисе) нулевая, ядро преобразования ker mathcal{O}=V , образ преобразования operatorname{im} mathcal{O}={boldsymbol{o}} , дефект d=n , ранг r=0 .

2. Обозначим mathcal{E}colon Vto V — тождественное преобразование n-мерного пространства {V} , которое ставит в соответствие каждому вектору mathbf{v}in V этот же вектор mathcal{E}(mathbf{v})=mathbf{v} . Это преобразование является инъективным, сюръективным, биективным, обратимым. Матрица тождественного преобразования (в любом базисе) единичная n-го порядка, ядро преобразования ker mathcal{E}={boldsymbol{o}} , образ преобразования operatorname{im} mathcal{E}=V , дефект d=0 , ранг r=n .

3. Обозначим $mathcal{Z}_{boldsymbol{o}}colon Vto V$ — центральную симметрию n-мерного пространства (относительно нулевого вектора ), т.е. преобразование, которое каждому вектору ставит в соответствие противоположный ему вектор: $mathcal{Z}_{boldsymbol{o}}(mathbf{v})=-mathbf{v}$ . Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Матрица преобразования противоположна единичной (в любом базисе): Z_0=E ; ядро преобразования $ker mathcal{Z}_{boldsymbol{o}}={boldsymbol{o}}$ , образ преобразования $operatorname{im} mathcal{Z}_{boldsymbol{o}}=V$ , дефект d=o , ранг r=n .

4. Обозначим $mathcal{H}_{lambda}colon Vto V$ — гомотетию n-мерного пространства {V} (с коэффициентом lambda ), т.е. преобразование, которое каждому вектору ставит в соответствие коллинеарный ему вектор: $mathcal{H}_{lambda} (mathbf{v})=lambdacdot mathbf{v}$ . Это преобразование линейное. При lambdane0 оно инъективное, сюръективное, биективное, обратимое. Матрица преобразования пропорциональна единичной (в любом базисе): $H_{lambda}=lambdacdot E$ , ядро преобразования $ker mathcal{H}_{lambda}= {boldsymbol{0}}$ , образ преобразования $operatorname{im} mathcal{H}_{lambda}= V$ , дефект d=0 , ранг r=n . При $lambda=0colon, mathcal{H}_{0}=mathcal{O}$ (см. пункт 1); при $lambda=1colon, mathcal{H}_1= mathcal{E}$ (см. пункт 2); при $lambda=-1colon, mathcal{H}_{(-1)}= mathcal{Z}_{boldsymbol{o}}$ (см. пункт 3).

5. Рассмотрим линейное пространство V_2 радиус-векторов (с общим началом в точке ), принадлежащих одной плоскости (рис. 9.1). Обозначим $mathcal{R}_{varphi}colon V_2to V_2$ — поворот вокруг точки (на угол varphi в положительном направлении (против часовой стрелки)). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу поворота в стандартном ортонормированием базисе vec{i},vec{j} . Раскладывая образы $vec{i},'= mathcal{R}_{varphi}(vec{i}),~ vec{j},'= mathcal{R}_{varphi}(vec{j})$ базисных векторов по базису, получаем

Линейное пространство радиус-векторов

$begin{cases} vec{i},'= vec{i}cdot cosvarphi+vec{j}cdot sinvarphi,,\ vec{j},'= -vec{i}cdot sinvarphi+ vec{j}cdot cosvarphi,.end{cases}$

Составляем матрицу (9.1) преобразования (оператора), записывая найденные координаты образов по столбцам:

$R_{varphi}= begin{pmatrix}cosvarphi&-sinvarphi\ sinvarphi& cosvarphi end{pmatrix}!.$

Ядро оператора (преобразования) $ker mathcal{R}_{varphi}={boldsymbol{o}}$ , образ преобразования $operatorname{im} mathcal{R}_{varphi}=V_2$ , дефект d=0 , ранг r=2 . При varphi=2pi k,~ kin mathbb{Z}colon $mathcal{R}_{2pi k}= mathcal{E}$ (см. пункт 2); при varphi=pi+2pi k,~ kin mathbb{Z}colon $mathcal{R}_{pi+2pi k}= mathcal{Z}_{boldsymbol{o}}$ (см. пункт 3).

6. Обозначим $mathcal{D}colon P_n(mathbb{R})to P_{n}(mathbb{R})$ — оператор дифференцирования, который каждому многочлену степени не выше и ставит в соответствие его производную, рассматриваемую как многочлен степени не выше ncolon, mathcal{D}(p(x))= p'(x) . Это преобразование линейное, неинъективное, несюръективное, небиективное, необратимое. Квадратная матрица ((n+l)-го порядка) преобразования в стандартном базисе имеет вид

$D=begin{pmatrix} 0&1&0&cdots&0\ 0&0&2&cdots&0\ vdots&vdots&vdots& ddots&vdots\ 0&0&0&cdots&n\ 0&0&0&cdots&0 end{pmatrix}!.$

Ядро преобразования $ker mathcal{D}=P_0(mathbb{R})$ — пространство многочленов нулевой степени, образ $operatorname{im} mathcal{D}=P_{n-1}(mathbb{R})$ — пространство многочленов степени не выше (n-1) , дефект d=1 , ранг r=1, $dim P_n(mathbb{R})=n+1$ .

Рассмотрим преобразование $mathcal{D}colon T_{omega}(mathbb{R})to T_{omega} (mathbb{R})$ линейного пространства тригонометрических многочленов (частоты omegane0 ) с действительными коэффициентами: $T_{omega}(mathbb{R})= operatorname{Lin} (sinomega t,cosomega t)$ , т.е. $T_{omega}(mathbb{R})$ — множество функций вида f(t)=asinomega t+bcosomega t , где a,bin mathbb{R} . Заметим, что это множество является двумерным вещественным линейным пространством. Стандартный базис пространства $T_{omega}(mathbb{R})$ образуют функции $mathbf{e}_1(t)=sinomega t,$ $mathbf{e}_2(t)=cosomega t$ , поскольку они линейно независимы (тождественное равенство нулю asinomega t+bcosomega tequiv0 возможно только в тривиальном случае a=b=0 ). При дифференцировании функции f(t) получаем функцию f'(t)=-bomega sinomega t+aomegacosomega t того же вида. Следовательно, преобразование $mathcal{D}colon T_{omega}(mathbb{R})to T_{omega} (mathbb{R})$ определено. Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу преобразования в стандартном базисе $mathbf{e}_1(t)=sinomega t,$ $mathbf{e}_2(t)=cosomega t$ . Раскладывая образы базисных векторов, получаем

$begin{aligned} mathcal{D}(mathbf{e}_1)&= omegacosomega t= 0cdotsinomega t+omegacosomega t,,\[5pt] mathcal{D}(mathbf{e}_2)&= -omegasinomega t= -omegasinomega t+0cdotcosomega t,.end{aligned}$

Составляем матрицу (9.1) преобразования, записывая найденные координаты образов по столбцам: $D=begin{pmatrix}0&-omega\ omega&0end{pmatrix}$ . Ядро преобразования ker mathcal{D}= {boldsymbol{o}(t)} — нулевое подпространство, образ $operatorname{im} mathcal{D}=T_{omega}(mathbb{R})$ , дефект d=0 , ранг r=2 , boldsymbol{o}(t)= 0cdotsinomega t+0cdotcosomega t .

Аналогичными свойствами обладает преобразование $mathcal{D}colon T_{omega} (mathbb{C})to T_{omega}(mathbb{C})$ , где $T_{omega}(mathbb{C})= operatorname{Lin} (sinomega t,cosomega t)$ — множество функций вида asinomega t+bcosomega t с комплексными коэффициентами ain mathbb{C} и bin mathbb{C} . Множество $T_{omega}(mathbb{C})$ является двумерным комплексным линейным пространством.

7. Пусть линейное пространство разлагается в прямую сумму подпространств V=L_1oplus L_2 . Обозначим $Pi_{L_1}colon Vto V$ — оператор проектирования на подпространство L_1 параллельно подпространству L_2 , который каждому вектору $mathbf{v}=mathbf{v}_1+mathbf{v}_2$ , где $mathbf{v}_1in L_1,~ mathbf{v}_2in L_2$ , ставит в соответствие его составляющую (проекцию) $mathbf{v}_1in L_1$ , т.е. $Pi_{L_1}(mathbf{v}_1+mathbf{v}_2)= mathbf{v}_1$ (рис.9.2). Это преобразование линейное. При L_1ne V оно неинъективное, несюръективное, небиективное, необратимое. Ядро преобразования $ker Pi_{L_1}=L_2$ , образ преобразования $operatorname{im} Pi_{L_1}=L_1$ , дефект $d=dim{L_2}$ , Ранг $r=dim{L_1}$ ,. При $L_1=Vcolon, Pi_V=mathcal{E}$ ; при $L_2=Vcolon, Pi_{{boldsymbol{o}}}= mathcal{O}$ .

Оператор проектирования на подпространство параллельно подпространству

8. Пусть линейное пространство разлагается в прямую сумму подпространств V=L_1oplus L_2 . Обозначим $mathcal{Z}_{L_1}colon Vto V$ — оператор отражения в подпространстве L_1 параллельно подпространству L_2 (или преобразование симметрии относительно подпространства L_1 параллельно подпространству L_2 ), который каждому вектору $mathbf{v}=mathbf{v}_1+ mathbf{v}_2$ , где $mathbf{v}_1in L_1,~ mathbf{v}_2in L_2$ , ставит в соответствие вектор $(mathbf{v}_1-mathbf{v}_2)$ , т.е. $mathcal{Z}_{L_1} (mathbf{v}_1+mathbf{v}_2)= mathbf{v}_1-mathbf{v}_2$ (рис. 9.3). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Ядро преобразования $ker mathcal{Z}_{L_1}={boldsymbol{o}}$ , образ преобразования $operatorname{im} mathcal{Z}_{L_1}=V$ , дефект d=0 , ранг r=dim{V} . При $L_1=Vcolon, mathcal{Z}_{L_1}= mathcal{E}$ .

Матрицы линейного оператора (преобразования) в разных базисах

Найдем связь матриц одного и того же линейного оператора (преобразования) в разных базисах.

Пусть в базисе $(mathbf{e})=(mathbf{e}_1,ldots,mathbf{e}_n)$ преобразование mathcal{A}colon Vto V имеет матрицу $mathop{A}limits_{(mathbf{e})}$ , а в базисе $(mathbf{f})=(mathbf{f}_1,ldots, mathbf{}_n)$ — матрицу $mathop{A}limits_{(mathbf{f})}$ . Если — матрица перехода от базиса к базису , то

$mathop{A}limits_{(mathbf{f})}= S^{-1}cdot mathop{A}limits_{(mathbf{e})} cdot S.$

(9.4)

Докажем формулу (9.4). Пусть векторы mathbf{v} и mathbf{w} в базисах (mathbf{e}) и (mathbf{f}) имеют координатные столбцы $mathop{v}limits_{(mathbf{e})}, mathop{v}limits_{(mathbf{f})}$ и $mathop{w}limits_{(mathbf{e})}, mathop{w}limits_{(mathbf{f})}$ соответственно. Если w=mathcal{A}(mathbf{v}) , то по формуле (9.2) имеем

$mathop{w}limits_{(mathbf{e})}= mathop{A}limits_{(mathbf{e})}cdot mathop{v}limits_{(mathbf{e})},qquad mathop{w}limits_{(mathbf{f})}= mathop{A}limits_{(mathbf{f})}cdot mathop{v}limits_{(mathbf{f})}.$

Подставляя в первое равенство связи координат векторов в разных базисах $mathop{v}limits_{(mathbf{e})}= Scdot mathop{v}limits_{(mathbf{f})},$ $mathop{w}limits_{(mathbf{e})}= Scdot mathop{w}limits_{(mathbf{f})}$ получаем $Scdot mathop{w}limits_{(mathbf{f})}= mathop{A}limits_{(mathbf{e})}cdot Scdot mathop{v}limits_{(mathbf{f})}$ или, учитывая обратимость матрицы Scolon $mathop{w}limits_{(mathbf{f})}= S^{-1}cdot mathop{A}limits_{(mathbf{e})}cdot Scdot mathop{v}limits_{(mathbf{f})}$ . Сравнивая последнее равенство с $mathop{w}limits_{(mathbf{f})}= mathop{A}limits_{(mathbf{f})}cdot mathop{v}limits_{(mathbf{f})}$ , убеждаемся в справедливости (9.4).

Замечания 9.2

1. Матрицы линейного преобразования в разных базисах оказываются подобными. И наоборот, любые две подобные матрицы являются матрицами некоторого линейного преобразования, найденными относительно разных базисов.

2. Для матриц преобразований справедливы свойства, рассмотренные ранее. В частности, при фиксированном базисе матрица суммы преобразований равна сумме их матриц, матрица произведения преобразования на число равна произведению матрицы преобразования на это же число, матрица композиции преобразований равна произведению матриц преобразований, матрица обратного преобразования является обратной для матрицы обратимого преобразования.

Алгебра линейных операторов (преобразований)

Рассмотрим множество mathcal{L}(V) — линейных преобразований (операторов) n-мерного линейного пространства . Напомним, что два преобразования mathcal{A}colon Vto V и mathcal{B}colon Vto V называются равными, если mathcal{A}(mathbf{v})= mathcal{B}(mathbf{v})~ forall mathbf{v}in V .

На множестве mathcal{L}(V) определены две линейные операции: сложение преобразований и умножение преобразования на число, поскольку в результате этих операций получается линейное преобразование.

Нетрудно показать, что эти операции удовлетворяют условиям:

1. mathcal{A}+mathcal{B}= mathcal{B}+mathcal{A}quad forall mathcal{A},mathcal{B}in mathcal{L}(V) ;

2. mathcal{A}+(mathcal{B}+mathcal{C})= (mathcal{A}+mathcal{B})+mathcal{C}quad forall mathcal{A},mathcal{B},mathcal{C}in mathcal{L}(V) ;

3. существует нулевое преобразование mathcal{O}inmathcal{L}(V) такое, что mathcal{A}+mathcal{O}=mathcal{A}~ forall mathcal{A}in mathcal{L}(V) ;

4. для каждого преобразования mathcal{A} существует противоположное преобразование (-mathcal{A})=(-1)cdot mathcal{A} такое, что mathcal{A}+(-mathcal{A})=mathcal{O} ;

5. lambdacdot(mathcal{A}+mathcal{B})= lambdacdot mathcal{A}+lambdacdot mathcal{B}~ forall mathcal{A},mathcal{B}in mathcal{L}(V) и любого числа lambda ;

6. (lambda+mu)cdot mathcal{A}= lambdacdot mathcal{A}+mucdot mathcal{A}~ forall mathcal{A}in mathcal{L}(V) и любых чисел lambda,,mu ;

7. lambdacdot (mucdot mathcal{A})=(lambdamu)cdot mathcal{A}~ forall mathcal{A}in mathcal{L}(V) и любых чисел lambda,,mu ;

8. 1cdot mathcal{A}quad forall mathcal{A}in mathcal{L}(V) .

В условиях 5-7 говорится о числах из того же числового поля, над которым определено линейное пространство {V} .

Условия 1-8 повторяют аксиомы линейного пространства. Поэтому множество mathcal{L}(V) с линейными операциями является линейным пространством. Если пространство {V} вещественное (комплексное), то и пространство вещественное (комплексное).

Найдем размерность пространства mathcal{L}(V) . При фиксированном базисе имеется взаимно однозначное соответствие между линейными преобразованиями и их матрицами, причем это соответствие сохраняет линейные операции. Следовательно, пространство mathcal{L}(V) изоморфно пространству $M_{ntimes n}$ — квадратных матриц n-го порядка. Размерность пространства $M_{ntimes n}$ равна n^2 . По теореме 8.3:

$dimmathcal{L}(V)= dim M_{ntimes n}=n^2,$ то есть $dimmathcal{L}(V)= (dim{V})^2.$

Кроме линейных операций в множестве mathcal{L}(V) определена операция умножения элементов. Произведением преобразований mathcal{A} и mathcal{B} назовем их композицию, т.е. mathcal{A}mathcal{B}= mathcal{A}circ mathcal{B} . В результате композиции линейных преобразований получается линейное преобразование. Операция умножения удовлетворяет следующим условиям:

1. mathcal{A}(mathcal{B}mathcal{C})= (mathcal{A}mathcal{B})mathcal{C}quad forall mathcal{A},mathcal{B},mathcal{C}in mathcal{L}(V) ;

2. mathcal{A}(mathcal{B}+mathcal{C})= mathcal{A}mathcal{B}+mathcal{A} mathcal{C} quad forall mathcal{A},mathcal{B},mathcal{C}in mathcal{L}(V) ;

3. (mathcal{A}+mathcal{B})mathcal{C}= mathcal{A}mathcal{C}+mathcal{B}mathcal{C} quad forall mathcal{A},mathcal{B},mathcal{C}in mathcal{L}(V) ;

4. существует тождественное преобразование mathcal{E} такое, что mathcal{A} mathcal{E}= mathcal{E}mathcal{A}= mathcal{A}~ forall mathcal{A}in mathcal{L}(V) .

Первое условие выражает ассоциативность операции умножения, условия 2 и 3 — законы дистрибутивности, условие 4 — существование нейтрального элемента. Множество mathcal{L}(V) с операциями сложения и умножения элементов является кольцом с единицей (вообще говоря, некоммутативное, так как в общем случае mathcal{A} mathcal{B}ne mathcal{B}mathcal{A} ).

Операции умножения операторов (преобразований) и произведения операторов на число (из заданного числового поля) удовлетворяют условию:

5. (lambdacdot mathcal{A})mathcal{B}= mathcal{A}(lambdacdot mathcal{B})= lambdacdot (mathcal{A}mathcal{B}).

Линейное пространство, которое является кольцом, удовлетворяющим условию 5, называется алгеброй. Поэтому множество mathcal(V) называют алгеброй линейных операторов (преобразований).

Многочлены от линейного оператора (преобразования)

В алгебре mathcal(V) можно определить целую неотрицательную степень оператора mathcal{A}colon Vto V , полагая по определению

$mathcal{A}^0=mathcal{E},quad mathcal{A}^1=mathcal{A},quad mathcal{A}^2=mathcal{A}mathcal{A},ldots, mathcal{A}^n=mathcal{A}^{n-1}mathcal{A}.$

Пусть p(lambda)=a_m lambda^m+ldots+a_1 lambda+a_0 — многочлен переменной lambda . Многочленом p(mathcal{A}) от линейного преобразования называется преобразование $p(mathcal{A})= a_m mathcal{A}^m+ldots+ a_1 mathcal{A}+ a_0 mathcal{E}$ .

Многочлен p(lambda)=a_m lambda^m+ldots+a_1 lambda+a_0 называется аннулирующим для линейного преобразования mathcal{A} , если p(mathcal{A})= mathcal{O} — нулевое преобразование. Заметим, что у каждого линейного преобразования mathcal{A}colon Vto V n-мерного линейного пространства существует аннулирующий многочлен степени не выше n^2 . Действительно, система из (n^2+1) элементов $mathcal{E}, mathcal{A},ldots,mathcal{A}^{n^2}$ линейного пространства mathcal{L}(V) линейно зависима (так как $dimmathcal{L}(V)=n^2$ ). Поэтому существуют такие числа $a_0,a_1,ldots,a_{n^2}$ , не все равные нулю одновременно, что $a_{n^2} mathcal{A}^{n^2}+ ldots+ a_1 mathcal{A}+a_0 mathcal{E}=mathcal{O}$ . Следовательно, многочлен $p(lambda)= a_{n^2}lambda^{n^2}+ldots+ a_1 lambda+a_0$ — аннулирующий для преобразования .

Замечания 9.3

1. При фиксированном базисе каждому преобразованию (оператору) можно сопоставить его матрицу. Свойства линейных операций 1-8, записанные для матриц преобразований, повторяют свойства линейных операций с матрицами, а свойствам 1-5 произведения операторов отвечают свойства операции умножения матриц.

2. При фиксированном базисе многочлен p(mathcal{A}) от линейного преобразования имеет матрицу p(A)=a_m A^m+ldots +a_1A+a_0E , где — матрица преобразования в том же базисе. Поэтому свойства многочленов от матриц переносятся на многочлены от линейного преобразования. В частности, многочлены от одного преобразования перестановочны:

$begin{aligned}p(mathcal{A})cdot q(mathcal{A})&= Biggl(sum_{i=1}^{m}a_i mathcal{A}^iBiggr)cdot Biggl(sum_{j=1}^{k}b_j mathcal{A}^jBiggr)= sum_{i=1}^{m} sum_{j=1}^{k} a_ib_j mathcal{A}^{i+j}=\[2pt] &= sum_{j=1}^{k} sum_{i=1}^{m} b_ja_i mathcal{A}^{j+i}= Biggl(sum_{j=1}^{k}b_j mathcal{A}^jBiggr)cdot Biggl(sum_{i=1}^{m} a_{i}mathcal{A}^iBiggr)= q(mathcal{A})cdot p(mathcal{A}). end{aligned}$

3. Функции от матриц определяются при помощи многочленов от матриц. Поэтому можно определить функции от линейных преобразований.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

§ 7.1. Определение линейного оператора.

Матрица линейного оператора

Линейные операции над векторами

Базис. Cкалярное произведение

Векторное и смешанное произведения векторов

Декартова система координат. прямая на плоскости

Плоскость в пространстве

Прямая в пространстве

Кривые второго порядка — I

Кривые второго порядка — II

Поверхности второго порядка

Матрицы и операции с ними

Обратная матрица

Ранг матрицы

Системы линейных алгебраических уравнений

Свойства решений однородных и неоднородных СЛАУ

Линейные операторы (преобразования)

Определение линейных операторов (преобразований)

Примеры линейных операторов (преобразований)

Матрицы линейного оператора (преобразования) в разных базисах

Алгебра линейных операторов (преобразований)

Многочлены от линейного оператора (преобразования)