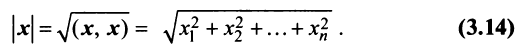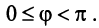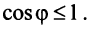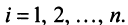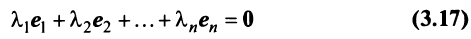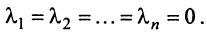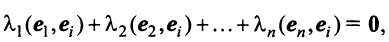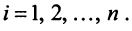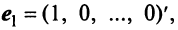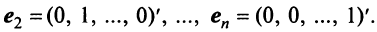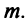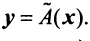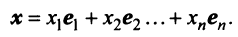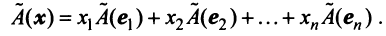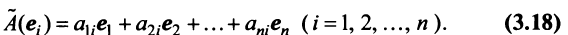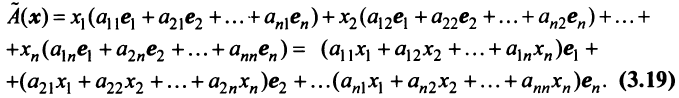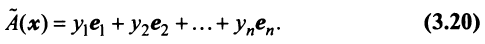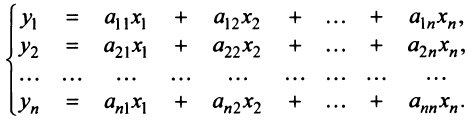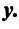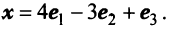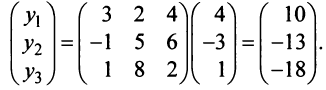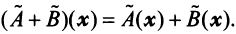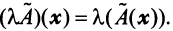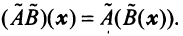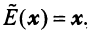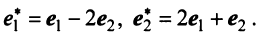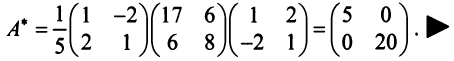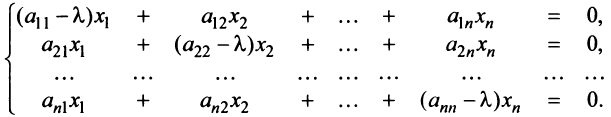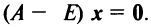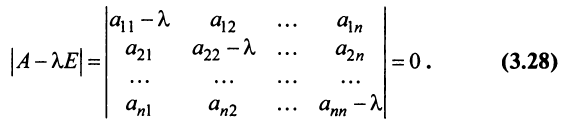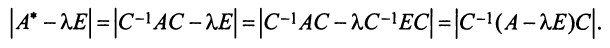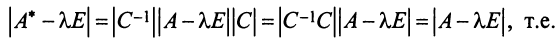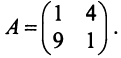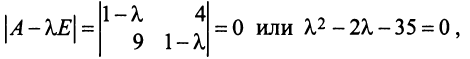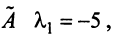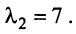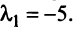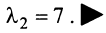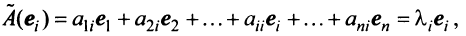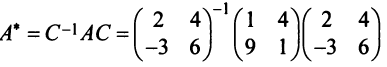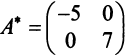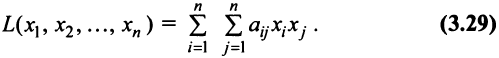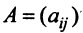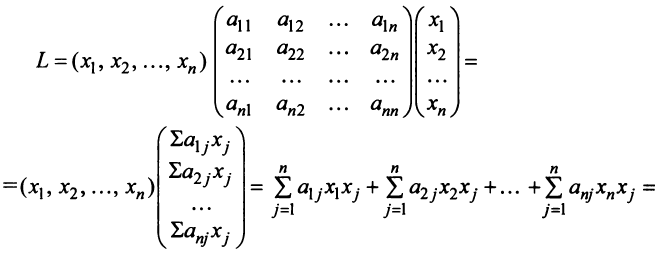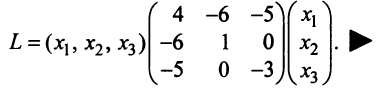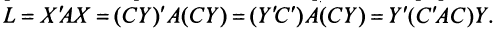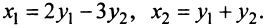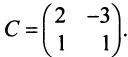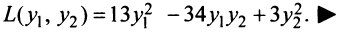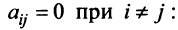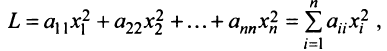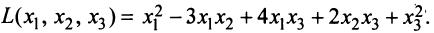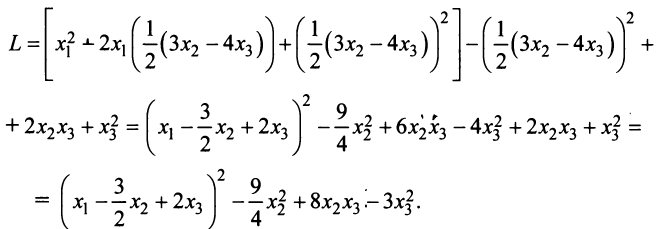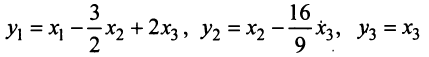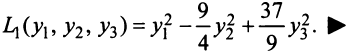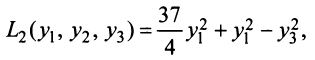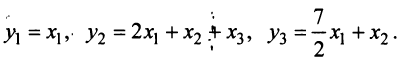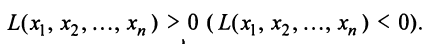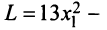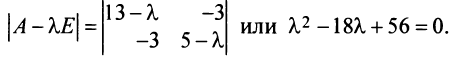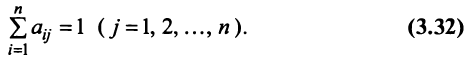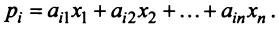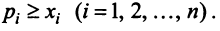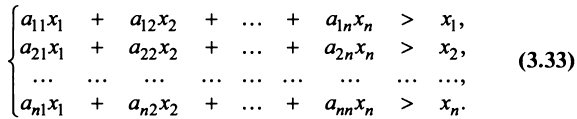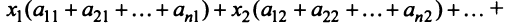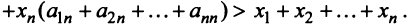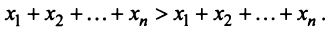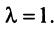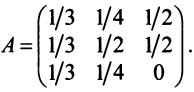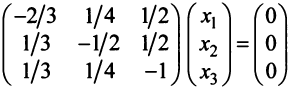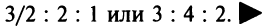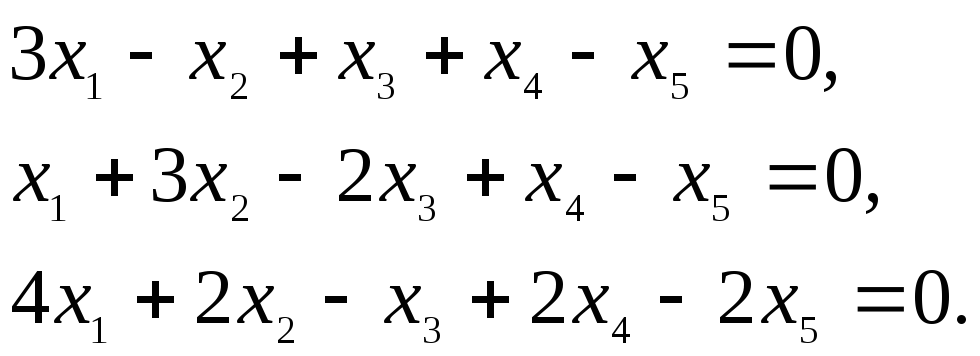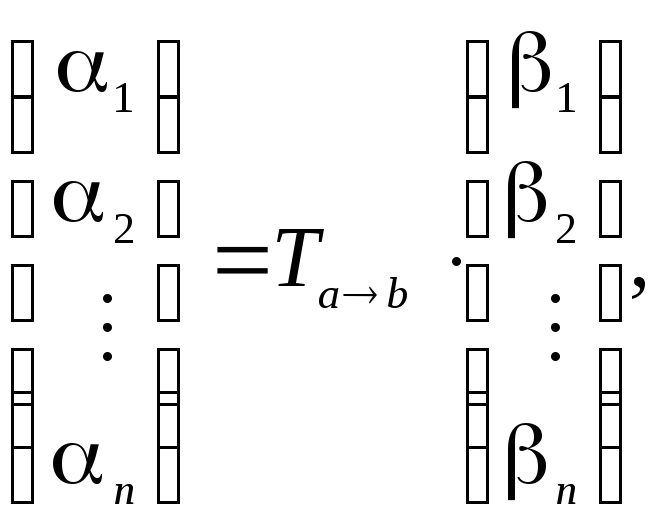Алгоритм нахождения базиса системы векторов
Для того чтобы найти базис системы векторов Av А2. А , необходимо:
1) составить соответствующую системе векторов однородную систему уравнений
2) привести эту систему к равносильной разрешенной системе вида
- 3) записать базис системы векторов Б = (АрА2, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
- 4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора
в разрешенной системе уравнений, т.е.
Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г.
Пример 3.3. Найти ранг и базис системы векторов
разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.
Решение. Составим систему уравнений A t ay + А2х2 + . + А„хп = 0, которая в координатной записи имеет вид
Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.
Разрешенная система имеет вид
В базис системы векторов включаем 1-й и 2-й векторы Б: = (AVA2), которые соответствуют разрешенным неизвестным х1 и х2. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.
Запишем разложения векторов по базису. Коэффициентами разложения вектора А3 являются координаты вектора А’3 = (3, -2), т.е. коэффициенты при х3 в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х3 А3 = ЗЛ1 — 2Аг Аналогично, коэффициентами разложения вектора А4 являются координаты вектора А’4 = (4, 1) А4 = 4Ау + 1 Ат
Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я94 = 1.
Как найти базис данной системы векторов
Определение базиса.Система векторов образует базис, если:
1) она линейно-независима,
2) любой вектор пространства через нее линейно выражается.
Пример 1.Базис пространства : .
2. В системе векторов базисом являются векторы: , т.к. линейно выражается через векторы .
Замечание.Чтобы найти базис данной системы векторов необходимо:
1) записать координаты векторов в матрицу,
2) с помощью элементарных преобразований привести матрицу к треугольному виду,
3) ненулевые строки матрицы будут являться базисом системы,
4) количество векторов в базисе равно рангу матрицы.
Теорема Кронекера-Капелли
Теорема Кронеккера–Капелли дает исчерпывающий ответ на вопрос о совместности произвольной системы линейных уравнений с неизвестными
Теорема Кронеккера–Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы, .
Алгоритм отыскания всех решений совместной системы линейных уравнений вытекает из теоремы Кронеккера–Капелли и следующих теорем.
Теорема. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Алгоритм решения произвольной системы линейных уравнений:
1. Найдем ранги основной и расширенной матриц системы. Если они не равны ( ), то система несовместна (не имеет решений). Если ранги равны ( , то система совместна.
2. Для совместной системы найдем какой-нибудь минор, порядок которого определяет ранг матрицы (такой минор называют базисным). Составим новую систему из уравнений, в которых коэффициенты при неизвестных, входят в базисный минор (эти неизвестные называют главными неизвестными), остальные уравнения отбросим. Главные неизвестные с коэффициентами оставим слева, а остальные неизвестных (их называют свободными неизвестными) перенесем в правую часть уравнений.
3. Найдем выражения главных неизвестных через свободные. Получаем общее решение системы.
4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образомнаходим частные решения исходной системы уравнений.
Линейное программирование. Основные понятия
Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.
Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.
Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующихсистему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называетсядопустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.
Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).
В общей постановке задача линейного программирования выглядит следующим образом:
Имеются какие-то переменные х = (х1 , х2 , … хn ) и функция этих переменных f(x) = f (х1 , х2 , … хn ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:
В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что
а) функция f(x) является линейной функцией переменных х1 , х2 , … хn
б) область G определяется системой линейных равенств или неравенств.
Математическая модель любой задачи линейного программирования включает в себя:
Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
http://megaobuchalka.ru/10/21983.html
http://zaochnik.com/spravochnik/matematika/vektory/vektornoe-prostranstvo/
Содержание:
Векторы на плоскости и в пространстве:
Обобщим некоторые сведения о векторах, известные в основном из школьного курса геометрии.
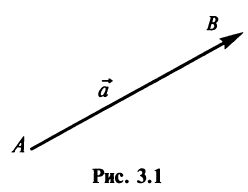
Вектором называется направленный отрезок
Векторы могут обозначаться как двумя прописными буквами, так и одной строчной с чертой или стрелкой, либо выделяться жирным шрифтом, например:
Длиной (или модулем) 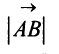
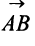
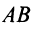
Векторы, лежащие на одной прямой или на параллельных прямых, называются коминеарными.
Если начало и конец вектора совпадают, например 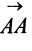
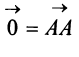
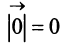
Произведением вектора 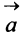
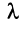
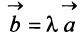
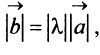
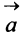
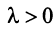
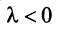
Противоположным вектором 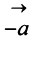
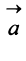
Рис. 32
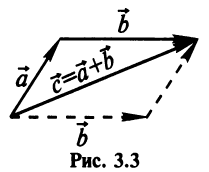
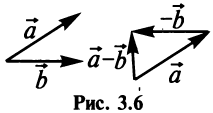
Суммой двух векторов 

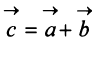




Очевидно, что вектор 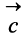


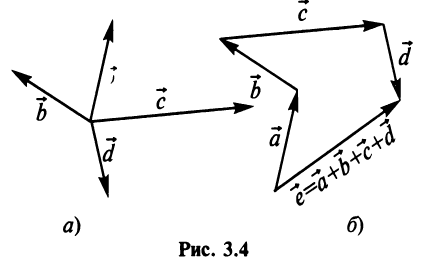
Аналогично определяется сумма нескольких векторов. Так, например, сумма четырех векторов 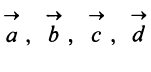
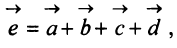

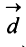
Нетрудно убедиться. что вектор 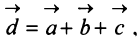


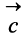
Разностью двух векторов 


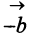

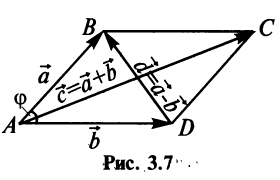
Легко убедиться в том, что в параллелограмме, построенном на векторах 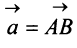
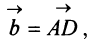


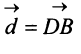
Перенесем вектор 

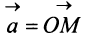
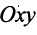
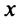
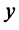
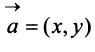
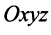
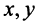
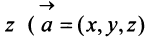
В соответствии с определениями, приведенными выше, нетрудно показать, что суммой и разностью векторов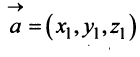
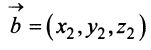
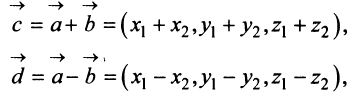
а произведение вектора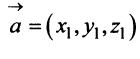
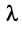
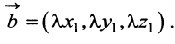
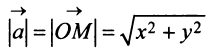
Определение. Скалярным произведением 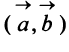


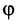
Выразим скалярное произведение через координаты векторов 

Из треугольника 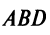
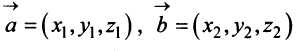
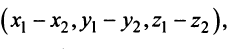
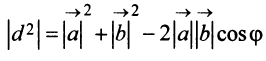
Учитывая формулу длины вектора (3.1) найдем
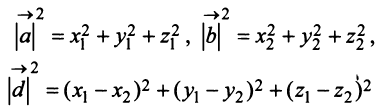
т.е. скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Заметим, что при 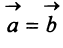
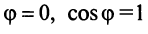
т.е. скалярный квадрат вектора равен квадрату его длины.
В частности, расстояние 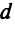
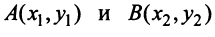
Поэтому
Угол между векторами

Пример:
Даны векторы
Найти: а)векторы 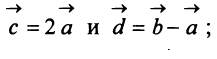
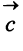
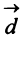
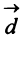
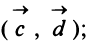
Решение:
а) По определению
б) По формуле (3.1) найдем длины векторов
в) По формуле (3.4) скалярный квадрат равен квадрату модуля вектора, т.е.
г) По формуле (3.3) скалярное произведение
д) По формуле (3.6) угол между векторами 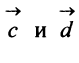
 >мерный вектор и векторное пространство
>мерный вектор и векторное пространство
Множества всех плоских или пространственных векторов, рассмотренных выше, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства.
Определение.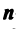
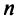
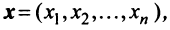
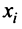
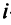
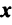
Понятие 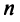
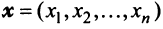
Два 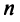
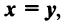
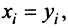
Суммой двух векторов одинаковой размерности п называется вектор 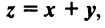
Произведением вектора 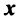
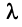
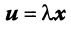
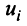
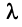
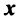
Линейные операции над любыми векторами удовлетворяют следующим свойствам:
— коммутативное (переместительное) свойство суммы:
— ассоциативное (сочетательное) свойство суммы;
— ассоциативное относительно числового множителя свойство;
— дистрибутивное (распределительное) относительно суммы векторов свойство;
—дистрибутивное относительно суммы числовых множителей свойство;
- Существует нулевой вектор
такой, что
для любого вектора
(особая роль нулевого вектора);
- Для любого вектора
существует противоположный вектор
такой, что
для любого вектора
(особая роль числового множителя 1).
Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствам (рассматриваемым как аксиомы), называется векторным пространством.
Следует отметить, что под 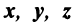
Линейным пространством является, например, множество всех алгебраических многочленов степени, не превышающей натурального числа 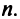
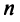
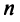
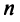
Из определения векторного (линейного) пространства, в частности из аксиом 1-8, вытекает существование единственного нулевого вектора, равного произведению произвольного вектора 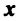
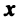
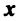
Размерность и базис векторного пространства
Понятия линейной комбинации, линейной зависимости и независимости векторов вводятся аналогично тому, как это было сделано в § 1.6 для строк матрицы.
Определение. Вектор 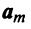

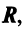
где 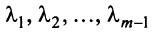
Определение. Векторы 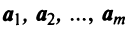
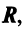
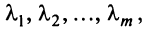
В противном случае векторы 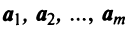
Из приведенных выше определений следует, что векторы 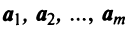
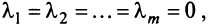
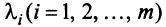
Можно показать (аналогично § 1.6), что если векторы 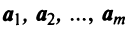
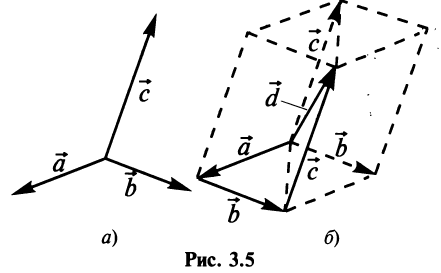
Примером линейно независимых векторов являются два не-коллинеарных, т.е. не параллельных одной прямой, вектора 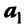
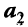
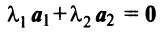
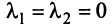
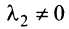
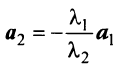
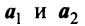
Отметим некоторые свойства векторов линейного пространства:
- Если среди векторов
имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например,
то равенство (3.8) справедливо при
- Если часть векторов
являются линейно зависимыми, то и все эти векторы — линейно зависимые. Действительно, если, например, векторы
линейно зависимы, то справедливо равенство
в котором не все числа равны нулю. Но тогда с теми же числами
и
будет справедливо равенство (3.8).
Пример:
Выяснить, являются ли векторы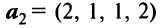
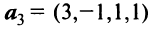
Решение:
Составим векторное равенство 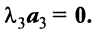
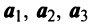
Задача свелась таким образом к решению системы:
Решая систему методом Гаусса (см. § 2.3), приведем ее к виду:
откуда найдем, бесконечное множество ее решений 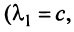
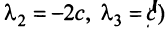
Итак, для ‘данных векторов условие (3.8) выполняется не только при 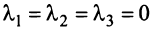
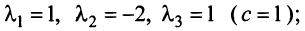
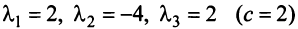
Определение. Линейное пространство 
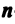
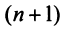
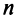

Определение. Совокупность 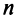
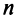

Теорема. Каждый вектор 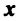

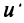

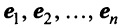
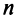

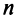
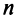
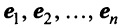
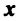
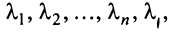
При этом 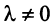
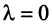
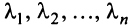
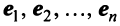
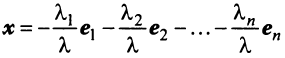
где
Это выражение 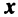
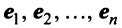
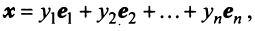
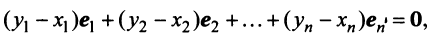
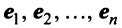
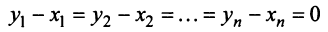
Равенство (3.9) называется разложением вектора 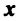
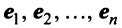
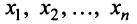
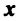
Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, — противоположные по знаку координаты.
Важное значение имеет следующая теорема.
Теорема. Если 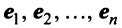

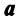
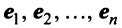

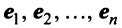

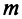

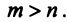
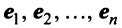
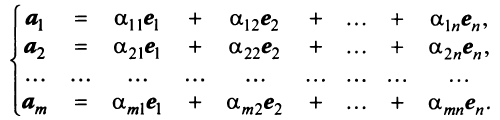
Ранг этой матрицы не превосходит 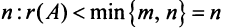
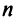
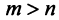
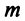
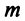
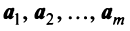

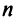
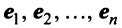
Пример:
В базисе 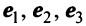
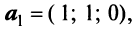
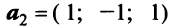
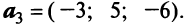
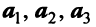
Решение:
Векторы 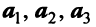
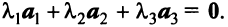
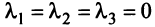
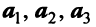
Переход к новому базису
Пусть в пространстве 
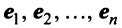
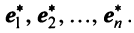
Полученная система означает, что переход от старого базиса 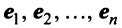
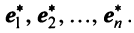
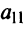
причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.
Матрица 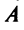
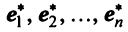
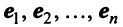
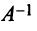
Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор 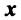
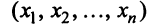
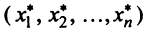
Подставив значения 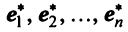
т.е. в матричной форме
Пример:
По условию примера 3.3 вектор 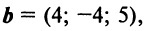
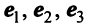
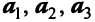
Решение:
Выразим связь между базисами:
Матрица перехода от базиса 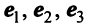
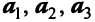
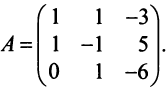
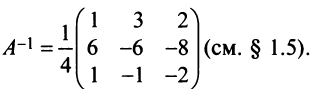
т.е. новые координаты вектора 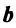
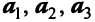
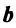
Евклидово пространство
Выше мы определили линейное (векторное) пространство, в котором можно складывать векторы и умножать их на числа, ввели понятие размерности и базиса, а теперь в данном пространстве введем метрику, т.е. способ измерять длины и углы. Это можно, например, сделать, если ввести понятие скалярного произведения.
Определение. Скалярным произведением двух векторов 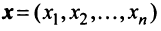
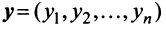
Скалярное произведение имеет экономический смысл. Если 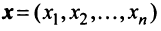
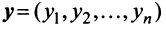
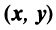
Скалярное произведение имеет следующие свойства:
— коммутативное свойство;
— дистрибутивное свойство;
— для любого действительного числа;
если
— ненулевой вектор;
, если
— нулевой вектор.
Определение. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется евклидовым пространством.
Длиной (нормой) вектора 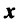
Имеют место следующие свойства длины вектора:
1. 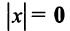
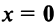
2. 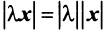
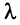
3.
(неравенство Коши—Буняковского);
4. 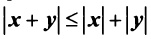
Угол 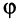
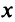
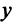

Такое определение вполне корректно, так как согласно неравенству Коши—Буняковского (3.15) 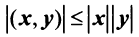
Два вектора называются ортогональными, если их скалярное произведение равно нулю. Очевидно, что нулевой вектор ортогонален любому другому вектору. Из определения следует, что если два ненулевых вектора ортогональны, то угол между ними равен 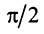
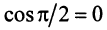
Векторы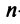
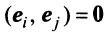
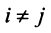
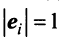
Для установления корректности приведенного определения необходимо убедиться в том, что входящие в него векторы 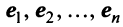
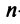

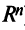
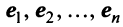
справедливо лишь при
Действительно, умножая скалярно равенство (3.17) на любой вектор 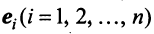
откуда, учитывая, что 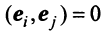
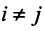
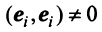
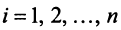
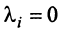
Сформулируем теперь (без доказательства) основную теорему.
Теорема. Во всяком 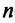
Примером ортонормированного базиса является система 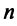
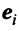
Линейные операторы
Одно из фундаментальных понятий матричной алгебры — понятие линейного оператора.
Рассмотрим два линейных пространства: 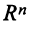
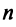
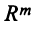
Определение. Если задан закон (правило), по которому каждому вектору 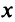
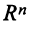
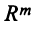
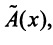
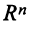
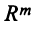
Оператор (преобразование) называется линейным, если для любых векторов 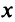
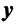
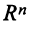
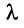
Вектор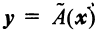
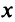
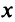
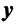
Если пространства 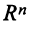
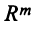
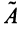
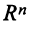
Выберем в пространстве 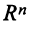
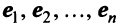
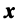
В силу линейности оператора 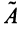
Поскольку 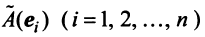
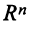
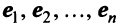
Тогда
С другой стороны, вектор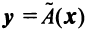
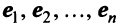
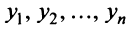
Ввиду единственности разложения вектора по базису равны правые части равенства (3.19) и (3.20), откуда
Матрица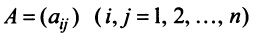
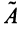
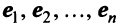
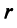
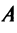
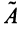
Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице 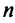
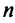
Связь между вектором 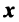
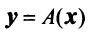
где 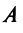
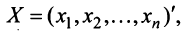
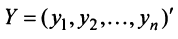
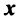
Пример:
Пусть в пространстве 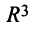
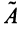
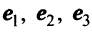
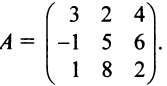
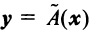
Решение:
По формуле (3.21) имеем
Следовательно, 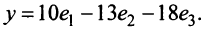
Определим действия над линейными операторами.
Суммой двух линейных операторов 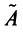
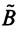
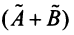
Произведением линейного оператора 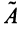
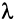
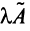
Произведением линейных операторов 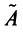
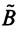
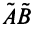
Можно убедиться в том, что операторы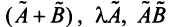
Определим нулевой оператор 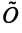
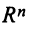
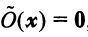
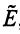
Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.
Теорема. Матрицы 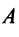
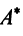
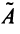
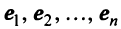
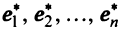
где 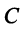

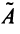
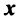
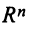
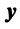
(в новом базисе). Так как 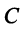
Умножим равенство (3.24) слева на матрицу 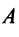
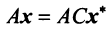
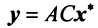
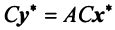
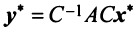
Пример:
В базисе 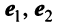
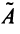
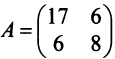
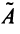
Решение:
Матрица перехода здесь 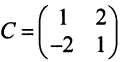
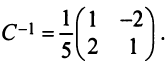
Собственные векторы и собственные значения линейного оператора
Определение. Вектор 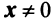
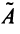
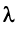
Число 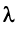
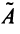
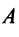
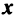
Из определения следует, что собственный вектор под действием линейного оператора 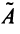
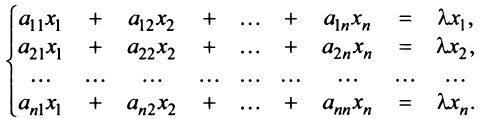
Равенство (3.26) можно записать в матричной форме:
где вектор 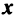
Перепишем систему так, чтобы в правых частях были нули:
или в матричном виде
Полученная однородная система всегда имеет нулевое решение 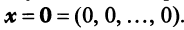
Определитель 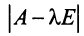
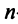
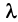
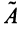
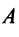
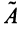
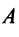
Характеристический многочлен линейного оператора не зависит от выбора базиса. В самом деле, преобразуем характеристический многочлен 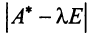
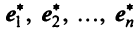
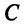
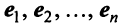
Учитывая, что определитель произведения квадратных матриц одинакового порядка равен произведению определителей этих матриц (см. §1.4), получим
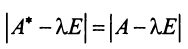
Пример:
Найти собственные значения и собственные векторы линейного оператора 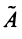
Решение:
Составляем характеристическое уравнение
откуда собственные значения линейного оператора
Находим собственный вектор 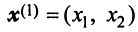
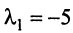
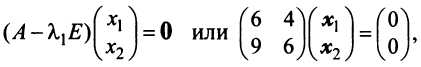
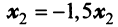
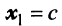
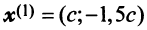
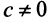
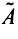
Аналогично можно убедиться в том, что векторы 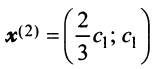
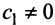
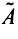
Наиболее простой вид принимает матрица 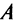
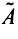
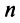
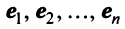
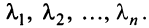
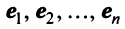
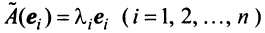
откуда 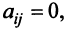
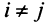
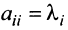
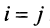
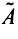
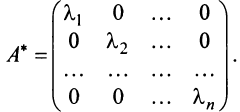
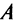
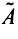
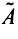
Можно доказать, что если линейный оператор имеет 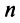
- Заказать решение задач по высшей математике
Пример:
Привести матрицу 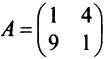
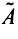
Решение:
В примере 3.7 были найдены собственные значения матрицы 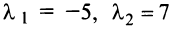
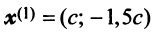
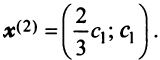
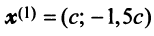
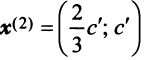
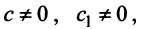
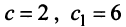
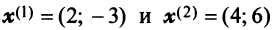
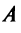
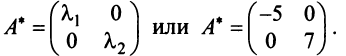
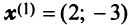
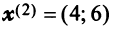
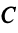
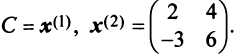
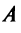
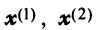
или после вычислений (которые мы опускаем)
т.е. получим ту же диагональную матрицу, элементы которой по главной диагонали равны собственным значениям матрицы 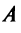
Квадратичные формы
При решении различных прикладных задач часто приходится исследовать квадратичные формы.
Определение. Квадратичной формой 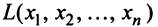
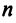
Предполагаем, что коэффициенты квадратичной формы 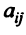
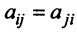
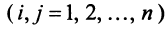
где 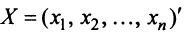
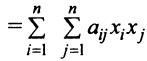
Пример:
Дана квадратичная форма 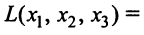
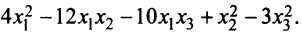
Решение:
Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 4, 1, -3, а другие элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому
Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.
Пусть матрицы-столбцы переменных 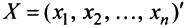
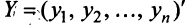
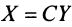
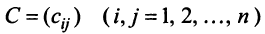
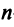
, Итак, при невырожденном линейном преобразовании 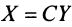
Пример:
Дана квадратичная форма 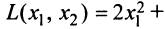
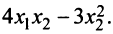
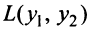
Решение:
Матрица данной квадратичной формы 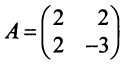
Следовательно, по (3.31) матрица искомой квадратичной формы 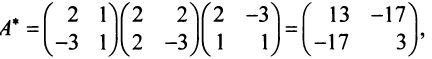
Следует отметить, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.
Квадратичная форма 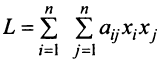
а ее матрица является диагональной. Справедлива следующая теорема.
Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Пример:
Привести к каноническому виду квадратичную форму
Решение:
Вначале вьделим полный квадрат при переменной 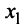
Теперь выделяем полный квадрат при переменной 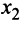
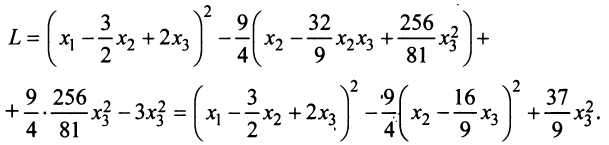
приводит данную квадратичную форму к каноническому виду
Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.
Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.
Например, квадратичную форму 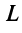
применив невырожденное линейное преобразование
Как видим, число положительных и отрицательных коэффициентов (соответственно два и один) сохранилось.
Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Квадратичная форма 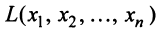
Так, например, квадратичная форма 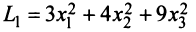
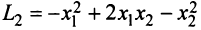
Теорема. Для того чтобы квадратичная форма 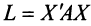
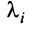
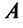
В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.
Теорема. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. 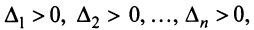

Пример:
Доказать, что квадратичная форма 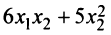
Решение:
Первый способ. Матрица 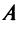
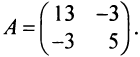
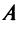
Решая уравнение, найдем 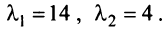
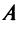
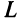
Второй способ. Так как главные миноры матрицы 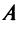
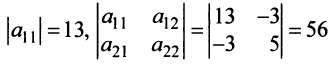
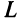
Линейная модель обмена
В качестве примера математической модели экономического процесса, приводящейся к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).
Пусть имеется 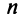
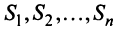
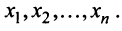
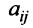
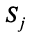
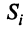
Рассмотрим матрицу
которая получила название структурной матрицы торговли. В соответствии с (3.32) сумма элементов любого столбца матрицы 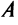
Для любой страны 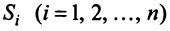
Для сбалансированной торговли необходима бездефицитность торговли каждой страны 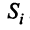
Если считать, что 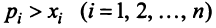
Сложив все неравенства системы (3.33), получим после группировки
Учитывая (3.32), выражения в скобках равны единице, и мы приходим к противоречивому неравенству
Таким образом, неравенство 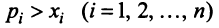
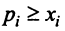
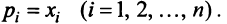
Вводя вектор 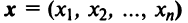
В котором вектор х записан в виде вектор-столбца, т.е. задача свелась к отысканию собственного вектора матрицы 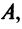
Пример:
Структурная матрица торговли трех стран 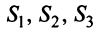
Найти соотношение национальных доходов стран для сбалансированной торговли.
Решение:
Находим собственный вектор 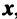
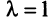
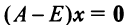
методом Гаусса. Найдем 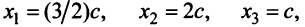
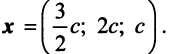
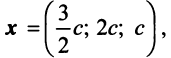
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды
- Степенные ряды
Фундаментальным
вопросом теории линейных пространств
является вопрос о том, можно ли, а если
можно, то как, произвольный вектор
пространства представить в виде линейной
комбинации фиксированного набора
векторов из этого пространства. Далее
мы получим ответ на этот вопрос.
Система
линейно независимых векторов
векторного пространства
называетсябазисом
этого пространства, если любой вектор
из
может быть представлен в виде линейной
комбинации векторов этой системы, т.е.
для каждого векторасуществуют вещественные числа
такие, что имеет место равенство
.
Это
равенство называется разложением
вектора
по базису
,
а числаназываютсякоординатами
вектора
относительно базиса
(или в базисе)
.
Утверждение
Базисом
линейного пространства решений
однородной системы является ее
фундаментальная система решений.
ТЕОРЕМА
(о единственности разложения по базису).
Каждый вектор
пространства
может быть разложен по базису
единственным
образом, т.е. координаты каждого вектора
в базисе
определяются однозначно.
Главное
значение базиса заключается в том, что
операции сложения векторов и умножения
их на числа при задании базиса превращаются
в соответствующие операции над числами
– координатами этих векторов. А именно,
справедлива следующая
ТЕОРЕМА.
При сложении
двух любых векторов линейного пространства
их координаты (относительно любого
базиса пространства) складываются; при
умножении
произвольного вектора на любое число
все координаты этого вектора умножаются
на.
Типовой
пример
Исследуем
вопрос о базисе пространства
,
введенного ранее при рассмотрении
Типовой примеров векторных пространств.
Покажем, чтоэлементов
указанного пространства образуют базис.
►Во-первых,
эти векторы линейно независимы. Проверка
линейной независимости набора
состоит в определении значений
,
при которых возможно равенство
.
Но в
силу только что доказанной теоремы
,
а
последний вектор является нулевым лишь
при условии
.
Во-вторых, всякий векторзаведомо представим в виде линейной
комбинации векторов:
и, значит, набор
образует базис. ◄
Векторное
пространство
называется
-мерным,
если в нем существуютлинейно независимых векторов, а любые
векторов уже являются линейно зависимыми.
При этом числоназываетсяразмерностьюпространства
.
Размерность
векторного пространства, состоящего
из одного нулевого вектора, принимается
равной нулю.
Размерность
пространства
обычно обозначают символом
.
Векторное
пространство
называетсябесконечномерным, если
в нем существует любое число линейно
независимых векторов. В этом случае
пишут.
Выясним
связь между понятиями базиса и размерности
пространства.
ТЕОРЕМА.Если
– векторное пространство размерности
,
то любыелинейно независимых векторов этого
пространства образуют его базис.
ТЕОРЕМА.Если векторное пространство
имеет базис, состоящий из
векторов, то
.
Утверждение
Rn=n.
Типовые примеры
-
Образуют
ли базис в пространстве R3
векторы
?
►По
определению базис составляют линейно
независимые векторы. Линейная зависимость
(или независимость) определяется исходя
из анализа равенства нулю линейной
комбинации этих векторов:
.
Последнее
векторное уравнение после записи его
по компонентам представляет собой
систему трёх однородных уравнений
относительно
.
Согласно схеме исследования линейной
зависимости векторов вычислим
определитель матрицы, составленной из
координат векторов
Определитель
системы равен нулю, следовательно, она
имеет нетривиальное решение и это
означает, что исходная группа векторов
линейно зависима и не образует базис в
R3. ◄
2.Найти
размерность и один из базисов линейного
пространства решений однородной системы:
►Представленная
система состоит из трёх уравнений и
содержит 5 неизвестных. Выпишем матрицу
системы и упростим её с помощью
элементарных преобразований, сначала
поменяв местами строки 1 и 2, а затем
вычитая новую первую строку, умноженную
на 3 и 4, соответственно из второй и
третьей строк :
Видно,
что ранг матрицы
равен 2. Следовательно, две неизвестные
являются главными, а три — свободными.
Значит ФСР системы содержит 5-2=3 линейно
независимых решения. Выберем в качестве
главных.
Это можно сделать, т.к. минор 2-го порядка,
составленный из коэффициентов при этих
неизвестных, отличен от нуля. Система,
соответствующая преобразованной
матрице, имеет вид
Отсюда,
выражая главные неизвестные через
свободные, получим общее решение
Или иначе:

Фундаментальная
совокупность решений является базисом
линейного пространства решений исходной
системы и в данном случае имеет вид
Размерность
искомого пространства равна 3.◄
Матрицей
переходаот базисак базису
называется матрица вида
где
для каждого
в
-ом
столбце стоят координатывектора
в базисе
.
Утверждение
Координаты
вектора
в базисе
и координаты
этого же вектора в базисе
связаны равенством
где
— матрица перехода от базиса
к базису
.
Утверждение.
Матрица перехода
от базиса
к базису
и матрица обратного перехода
от базиса
к базису
связаны равенством
=
.
Типовые
примеры
1.Найти координаты векторав базисе
,
если известно
►В
соответствии с определением матрица
перехода от базиса
к базису
есть
.
Обозначим
координаты вектора
в базисе
через
,
а в базисечерез
.
Искомые координатысвязаны с известными координатами
следующим соотношением:

Видно,
что для получения координат
необходимо вычислить матрицу, обратную
.
Используя стандартную процедуру, имеем
.
Вычислим теперь координаты
:
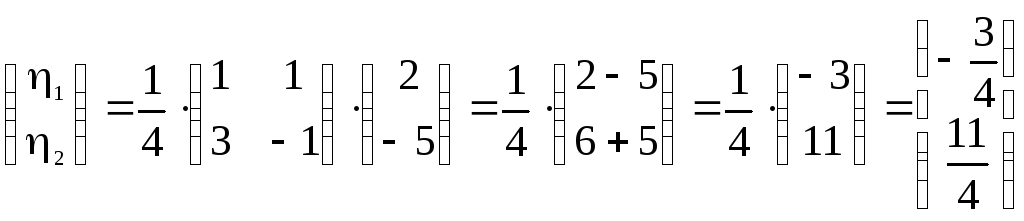
◄
-
Найти матрицу
перехода от базиса
к базису
по данным разложениям этих векторов
в базисе:
.
►Чтобы
построить матрицу
перехода
от базисак базису
,
необходимо найти разложение векторовпо базису
.
Сделаем это, представивв виде разложения по
с неизвестными координатами, которые
требуется определить:
,
или с
учётом вида этих векторов в базисе
.
Откуда для координат
имеем
Теперь,
зная разложение
по
,
выпишем матрицу:
.◄
5. Линейные оболочки
и подпространства
Подпространством линейного пространства
называется множество векторов из
такое, что для любых двух векторов
и
из
и любых двух вещественных чисел
и
линейная комбинация
также принадлежит
.
Утверждение. Подпространство само
является линейным пространством.
Линейной оболочкойсистемы векторовназывается множество всех линейных
комбинаций векторов.
Обозначается.
Утверждение. Линейная оболочка системы
векторов является подпространством.
Пересечениемдвух подпространстви
называется множество всех векторов,
принадлежащих одновременно и,
и
.
Обозначается
.
Суммой двух подпространстви
называется множество всех векторов
,
представимых в виде,
где,
.
Обозначается
.
Утверждение. Сумма и пересечение
подпространств
и
являются линейными пространствами, и
их размерности связаны равенством
+
=
+
.
Сумма
двух подпространств называется прямой
суммой, если
пересечение этих подпространств состоит
только из нулевого вектора.
Типовой пример
Найти размерность и какой-нибудь базис
суммы и пересечения подпространств,
порождённых векторами
.
►Вычислим вначале размерность
подпространств. С этой целью установим,
являются ли линейно независимыми
векторы, порождающие данные подпространства.
Для подпространства
,
порождённого векторами,
равенство нулю линейной комбинации,
эквивалентное системе уравнений,
достигается лишь при условии.
Следовательно, векторылинейно независимы и размерность
подпространстваравна 2:
.
Для подпространства,
порождённого векторами,
проводя аналогичный анализ, получим.
Вычислим теперь размерность пересечения
подпространств
и
.
По определению векторы, составляющие
пересечение, принадлежат одновременно
обоим подпространствам. Произвольный
векторподпространства
является линейной комбинацией базисных
векторов:
.
Аналогично для подпространстваимеем
,
тогда условие принадлежности пересечению
естьили
.
Это условие представляет собой систему
уравнений относительно коэффициентов
.
Составим матрицу системы и упростим её
с помощью элементарных преобразований:
Как видно ранг системы равен 3. Значит
ФСР состоит из одного линейно независимого
вектора. Найдём его, решив систему
уравнений, соответствующих последней
матрице, получим
,
откуда
.
Полагая свободное неизвестное
,
для остальных имеем
.
Итак, пересечение подпространствимеет
один базисный вектор
.
Размерность пересечения
.
Следовательно, в соответствии с равенством
размерность суммы подпространств
.
В качестве базиса суммы подпространств
можно взять, например, векторы,
дополненные вектором.
В линейной независимости векторовубедиться нетрудно.◄

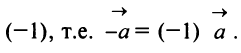
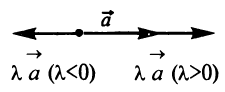
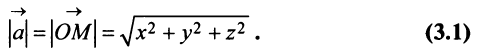
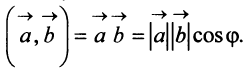
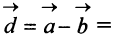
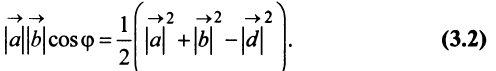
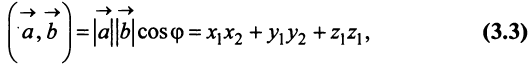
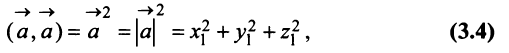
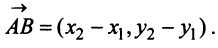
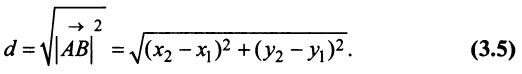
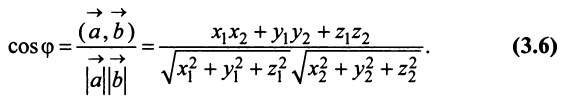
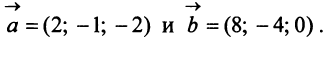
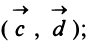
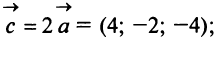
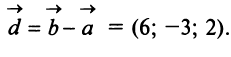
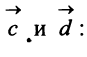
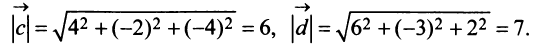
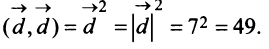
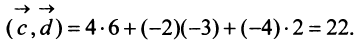
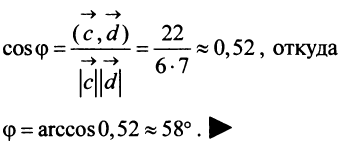
 >мерный вектор и векторное пространство
>мерный вектор и векторное пространство
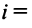
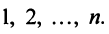
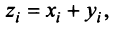
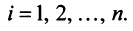
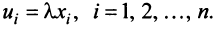
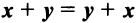 — коммутативное (переместительное) свойство суммы:
— коммутативное (переместительное) свойство суммы: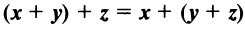 — ассоциативное (сочетательное) свойство суммы;
— ассоциативное (сочетательное) свойство суммы;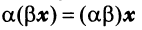 — ассоциативное относительно числового множителя свойство;
— ассоциативное относительно числового множителя свойство;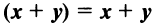 — дистрибутивное (распределительное) относительно суммы векторов свойство;
— дистрибутивное (распределительное) относительно суммы векторов свойство;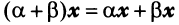 —дистрибутивное относительно суммы числовых множителей свойство;
—дистрибутивное относительно суммы числовых множителей свойство;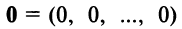 такой, что
такой, что 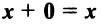 для любого вектора
для любого вектора 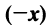 такой, что
такой, что 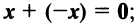
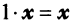 для любого вектора
для любого вектора 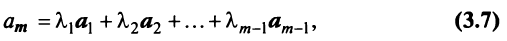
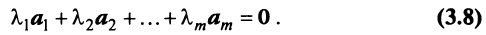
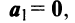 то равенство (3.8) справедливо при
то равенство (3.8) справедливо при 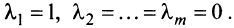
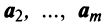 линейно зависимы, то справедливо равенство
линейно зависимы, то справедливо равенство 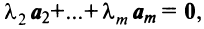 в котором не все числа равны нулю. Но тогда с теми же числами
в котором не все числа равны нулю. Но тогда с теми же числами 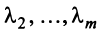 и
и 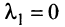 будет справедливо равенство (3.8).
будет справедливо равенство (3.8).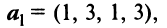
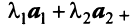
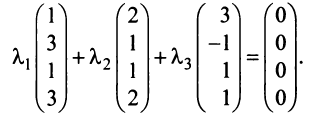
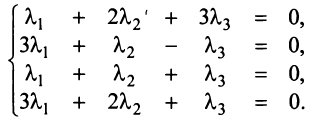
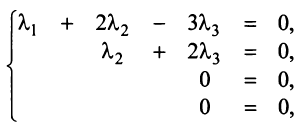
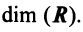
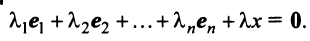
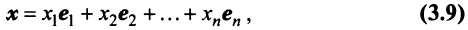
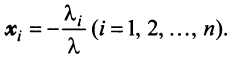
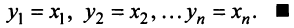
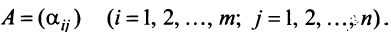


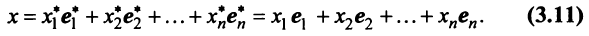
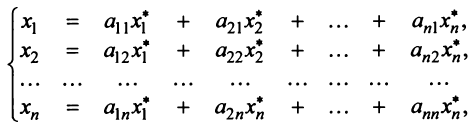
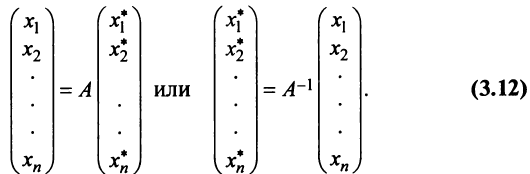
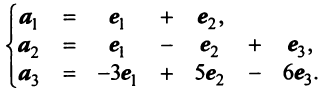
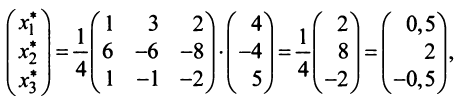
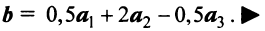
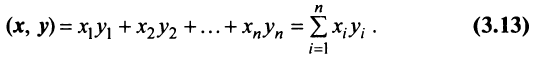
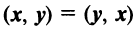 — коммутативное свойство;
— коммутативное свойство;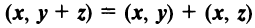 — дистрибутивное свойство;
— дистрибутивное свойство;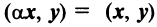 — для любого действительного числа;
— для любого действительного числа;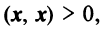 если
если 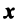 — ненулевой вектор;
— ненулевой вектор; 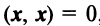 , если
, если