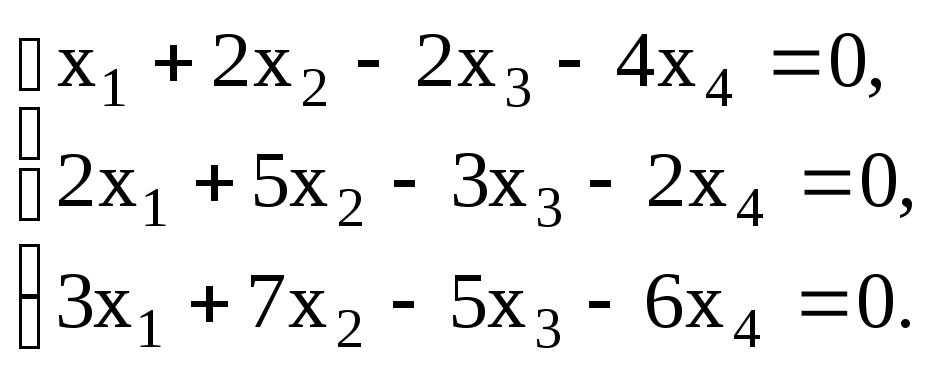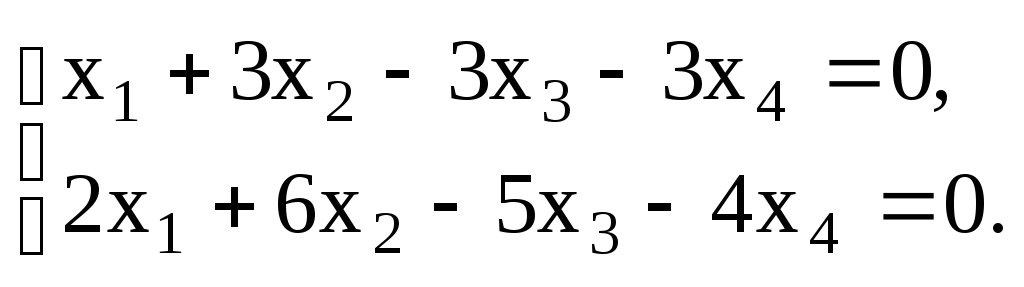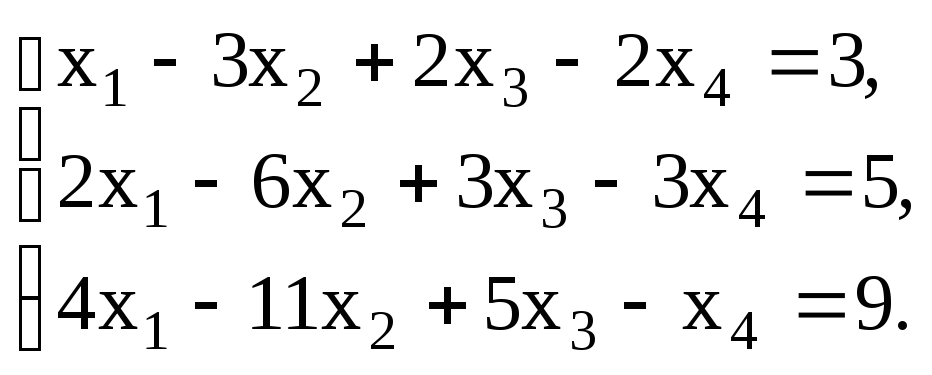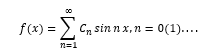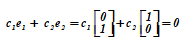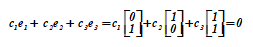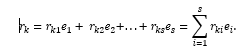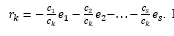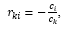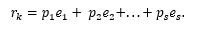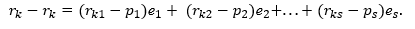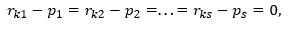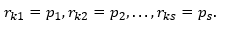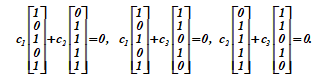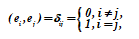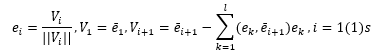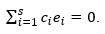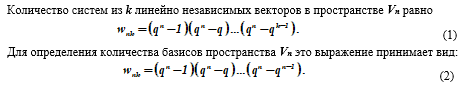Как найти базис множества векторов - Исправление недочетов и поиск решений вместе с Examum.ru

Линейной
комбинацией векторов
называется вектор,
где λ₁, … , λ_m– произвольные коэффициенты.

Система
векторов
называется
линейно зависимой, если существует ее
линейная комбинация, равная,
в которой есть хотя бы один ненулевой
коэффициент.

Система
векторов
называется
линейно независимой, если в любой ее
линейной комбинации, равной,
все коэффициенты нулевые.

Базисом
системы векторов
называется
ее непустая линейно независимая
подсистема, через которую можно выразить
любой вектор системы.

П р
и м е р 2. Найти базис системы векторов=
(1, 2, 2, 4),=
(2, 3, 5, 1),=
(3, 4, 8, -2),=
(2, 5, 0, 3) и выразить остальные векторы
через базис.

Р е
ш е н и е. Строим матрицу, в которой
координаты данных векторов располагаем
по столбцам. Приводим ее к ступенчатому
виду.

~~~.

Базис
данной системы образуют векторы
,,,
которым соответствуют ведущие элементы
строк, выделенные кружками. Для выражения
векторарешаем уравнениеx₁+x₂+
x₄=.
Оно сводится к системе линейных
уравнений, матрица которой получается
из исходной перестановкой столбца,
соответствующего,
на место столбца свободных членов.
Поэтому для решения системы используем
полученную матрицу в ступенчатом виде,
сделав в ней необходимые перестановки.

Последовательно
находим:

x₄
= 0;

x₂
= 2;

x₁
+ 4 = 3, x₁
= -1;

=
—+2.

Замечание
1. Если требуется выразить через базис
несколько векторов, то для каждого из
них строится соответствующая система
линейных уравнений. Эти системы будут
отличаться только столбцами свободных
членов. Поэтому для их решения можно
составить одну матрицу, в которой будет
несколько столбцов свободных членов.
При этом каждая система решается
независимо от остальных.

Замечание
2. Для выражения любого вектора достаточно
использовать только базисные векторы
системы, стоящие перед ним. При этом
нет необходимости переформировывать
матрицу, достаточно поставить вертикальную
черту в нужном месте.

У п
р а ж н е н и е 2. Найти базис системы
векторов и выразить остальные векторы
через базис:

а)
=
(1, 3, 2, 0),=
(3, 4, 2, 1),=
(1, -2, -2, 1),=
(3, 5, 1, 2);

б)
=
(2, 1, 2, 3),=
(1, 2, 2, 3),=
(3, -1, 2, 2),=
(4, -2, 2, 2);

в)
=
(1, 2, 3),=
(2, 4, 3),=
(3, 6, 6),=
(4, -2, 1);=
(2, -6, -2).

3. Фундаментальная система решений

Система
линейных уравнений называется однородной,
если все ее свободные члены равны нулю.

Фундаментальной
системой решений однородной системы
линейных уравнений называется базис
множества ее решений.

Пусть
дана неоднородная система линейных
уравнений. Однородной системой,
ассоциированной с данной, называется
система, полученная из данной заменой
всех свободных членов на нули.

Если
неоднородная система совместна и
неопределенна, то ее произвольное
решение имеет вид f_н
+ ₁f_о1+
… + _kf_о_k
,гдеf_н– частное
решение неоднородной системы иf_о1,
… , f_о_k–
фундаментальная система решений
ассоциированной однородной системы.

П р
и м е р 3. Найти частное решение
неоднородной системы из примера 1 и
фундаментальную систему решений
ассоциированной однородной системы.

Р е
ш е н и е. Запишем решение, полученное
в примере 1, в векторном виде и разложим
получившийся вектор в сумму по свободным
параметрам, имеющимся в нем, и фиксированным
числовым значениям:

= (x₁,
x₂,
x₃,
x₄) =
(–2a + 7b –
2, a, –2b + 1, b) = (–2a,
a, 0, 0) + (7b, 0, –2b, b) + +(–
2, 0, 1, 0) = a(-2, 1, 0, 0) + b(7, 0, -2, 1) + (–
2, 0, 1, 0).

Получаемf_н=(–
2, 0, 1, 0), f_о1= (-2, 1, 0,
0), f_о2= (7, 0, -2, 1).

Замечание.
Аналогично решается задача нахождения
фундаментальной системы решений
однородной системы.

У п
р а ж н е н и е 3.1 Найти фундаментальную
систему решений однородной системы:

а)

б)

в)
2x₁–
x₂
+3x₃=
0.

У п
р а ж н е н и е 3.2. Найти частное решение
неоднородной системы и фундаментальную
систему решений ассоциированной
однородной системы:

а)

б)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 — x 1 ) · e ( 1 ) + ( x

2 — x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 — x 2 ) , . . . , ( x

n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 — 1 1 3 2 — 5 2 1 — 3

1 — 1 1 0 5 — 8 0 3 — 5

1 — 1 1 0 5 — 8 0 0 — 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x

1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x

1 ∆ = — 1 — 1 = 1 ∆ x

2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x

2 ∆ = — 1 — 1 = 1 ∆ x

3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

Алгоритм нахождения базиса системы векторов

Для того чтобы найти базис системы векторов A_v А₂. А , необходимо:

1) составить соответствующую системе векторов однородную систему уравнений

2) привести эту систему к равносильной разрешенной системе вида

3) записать базис системы векторов Б = (А_рА₂, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора

в разрешенной системе уравнений, т.е.

Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г.

Пример 3.3. Найти ранг и базис системы векторов

разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.

Решение. Составим систему уравнений A _t ay + А₂х₂ + . + А„х_п = 0, которая в координатной записи имеет вид

Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.

Разрешенная система имеет вид

В базис системы векторов включаем 1-й и 2-й векторы Б_: = (A_VA₂), которые соответствуют разрешенным неизвестным х₁ и х₂. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.

Запишем разложения векторов по базису. Коэффициентами разложения вектора А₃ являются координаты вектора А’₃ = (3, -2), т.е. коэффициенты при х₃ в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х₃ А₃ = ЗЛ₁ — 2А_г Аналогично, коэффициентами разложения вектора А₄ являются координаты вектора А’₄ = (4, 1) А₄ = 4А_у + 1 А_т

Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я₉₄ = 1.

Как найти базис системы векторов примеры. Как найти базис данной системы векторов

Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:

или в развернутом виде .

Будем решать эту систему методом Гаусса, не меняя местами строки и столбцы, и, кроме того, выбирая главный элемент не в верхнем левом углу, а по всей строке. Задача состоит в том, чтобы выделить диагональную часть преобразованной системы векторов .

Разрешенная система векторов, равносильная исходной, имеет вид

Векторы а 1 1 , а 3 1 , а 4 1 образуют диагональную систему. Следовательно, векторы а 1 , а 3 , а 4 образуют базис системы векторов а 1 , а 2 , а 3 , а 4 , а 5 .

Разложим теперь векторы а 2 и а 5 по базису а 1 , а 3 , а 4 . Для этого сначала разложим соответствующие векторы а 2 1 и а 5 1 по диагональной системе а 1 1 , а 3 1 , а 4 1 , имея в виду, что коэффициентами разложения вектора по диагональной системе являются его координаты x i .

Векторы а 2 и а 5 разлагаются по базису а 1 , а 3 , а 4 с теми же коэффициентами, что и векторы а 2 1 и а 5 1 по диагональной системе а 1 1 , а 3 1 , а 4 1 (те коэффициенты x i ). Следовательно,

Задания. 1 .Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:

2. Найти все базисы системы векторов:

В геометрии вектор понимается как направленный отрезок, причем векторы, полученные один из другого параллельным переносом, считаются равными. Все равные векторы рассматриваются как один и тот же вектор. Начало вектора можно поместить в любую точку пространства или плоскости.

Если в пространстве заданы координаты концов вектора : A (x 1 , y 1 , z 1), B (x 2 , y 2 , z 2), то

Аналогичная формула имеет место на плоскости. Это значит, что вектор можно записать в виде координатной строки. Операции над векторами, – сложение и умножение на число, над строками выполняются покомпонентно. Это дает возможность расширить понятие вектора, понимая под вектором любую строку чисел. Например, решение системы линейных уравнений, а также любой набор значений переменных системы, можно рассматривать как вектор.

Над строками одинаковой длины операция сложения выполняется по правилу

(a 1 , a 2 , … , a n ) + (b 1 , b 2 , … , b n ) = (a 1 + b 1 , a 2 + b 2 , … , a n + b n ). (2)

Умножение строки на число выполняется по правилу

l(a 1 , a 2 , … , a n ) = (la 1 , la 2 , … , la n ). (3)

Множество векторов-строк заданной длины n с указанными операциями сложения векторов и умножения на число образует алгебраическую структуру, которая называется n-мерным линейным пространством .

Линейной комбинацией векторов называется вектор , где λ 1 , . , λ m – произвольные коэффициенты.

Система векторов называется линейно зависимой, если существует ее линейная комбинация, равная , в которой есть хотя бы один ненулевой коэффициент.

Система векторов называется линейно независимой, если в любой ее линейной комбинации, равной , все коэффициенты нулевые.

Таким образом, решение вопроса о линейной зависимости системы векторов сводится к решению уравнения

Если у этого уравнения есть ненулевые решения, то система векторов линейно зависима. Если же нулевое решение является единственным, то система векторов линейно независима.

Для решения системы (4) можно для наглядности векторы записать не в виде строк, а в виде столбцов.

Тогда, выполнив преобразования в левой части, придем к системе линейных уравнений, равносильной уравнению (4). Основная матрица этой системы образована координатами исходных векторов, расположенных по столбцам. Столбец свободных членов здесь не нужен, так как система однородная.

Базисом системы векторов (конечной или бесконечной, в частности, всего линейного пространства) называется ее непустая линейно независимая подсистема, через которую можно выразить любой вектор системы.

Пример 1.5.2. Найти базис системы векторов = (1, 2, 2, 4), = (2, 3, 5, 1), = (3, 4, 8, –2), = (2, 5, 0, 3) и выразить остальные векторы через базис.

Решение . Строим матрицу, в которой координаты данных векторов располагаем по столбцам. Это матрица системы x 1 + x 2 + x 3 + x 4 =. . Приводим матрицу к ступенчатому виду:

Базис данной системы векторов образуют векторы , , , которым соответствуют ведущие элементы строк, выделенные кружками. Для выражения вектора решаем уравнение x 1 + x 2 + x 4 = . Оно сводится к системе линейных уравнений, матрица которой получается из исходной перестановкой столбца, соответствующего , на место столбца свободных членов. Поэтому при приведении к ступенчатому виду над матрицей будут сделаны те же преобразования, что выше. Значит, можно использовать полученную матрицу в ступенчатом виде, сделав в ней необходимые перестановки столбцов: столбцы с кружками помещаем слева от вертикальной черты, а столбец, соответствующий вектору , помещаем справа от черты.

Замечание . Если требуется выразить через базис несколько векторов, то для каждого из них строится соответствующая система линейных уравнений. Эти системы будут отличаться только столбцами свободных членов. При этом каждая система решается независимо от остальных.

У п р а ж н е н и е 1.4. Найти базис системы векторов и выразить остальные векторы через базис:

а) = (1, 3, 2, 0), = (3, 4, 2, 1), = (1, –2, –2, 1), = (3, 5, 1, 2);

б) = (2, 1, 2, 3), = (1, 2, 2, 3), = (3, –1, 2, 2), = (4, –2, 2, 2);

в) = (1, 2, 3), = (2, 4, 3), = (3, 6, 6), = (4, –2, 1); = (2, –6, –2).

В заданной системе векторов базис обычно можно выделить разными способами, но во всех базисах будет одинаковое число векторов. Число векторов в базисе линейного пространства называется размерностью пространства. Для n -мерного линейного пространства n – это размерность пространства, так как это пространство имеет стандартный базис = (1, 0, … , 0), = (0, 1, … , 0), … , = (0, 0, … , 1). Через этот базис любой вектор = (a 1 , a 2 , … , a n ) выражается следующим образом:

= (a 1 , 0, … , 0) + (0, a 2 , … , 0) + … + (0, 0, … , a n ) =

A 1 (1, 0, … , 0) + a 2 (0, 1, … , 0) + … + a n (0, 0, … ,1) = a 1 + a 2 +… + a n .

Таким образом, компоненты в строке вектора = (a 1 , a 2 , … , a n ) – это его коэффициенты в разложении через стандартный базис.

Прямые на плоскости

Задача аналитической геометрии – применение к геометрическим задачам координатного метода. Тем самым задача переводится в алгебраическую форму и решается средствами алгебры.

Когда мы разбирали понятия n -мерного вектора и вводили операции над векторами, то выяснили, что множество всех n -мерных векторов порождает линейное пространство. В этой статье мы поговорим о важнейших связанных понятиях – о размерности и базисе векторного пространства. Также рассмотрим теорему о разложении произвольного вектора по базису и связь между различными базисами n -мерного пространства. Подробно разберем решения характерных примеров.

Навигация по странице.

Понятие размерности векторного пространства и базиса.

Понятия размерности и базиса векторного пространства напрямую связаны с понятием линейно независимой системы векторов, так что рекомендуем при необходимости обращаться к статье линейная зависимость системы векторов, свойства линейной зависимости и независимости.

Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

Приведем некоторые рассуждения, основываясь на этих определениях.

Рассмотрим пространство n -мерных векторов.

Покажем, что размерность этого пространства равна n .

Возьмем систему из n единичных векторов вида

Примем эти векторы в качестве строк матрицы А . В этом случае матрица А будет единичной матрицей размерности n на n . Ранг этой матрицы равен n (при необходимости смотрите статью ). Следовательно, система векторов линейно независима, причем к этой системе нельзя добавить ни одного вектора, не нарушив ее линейной независимости. Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы являются базисом этого пространства .

Из последнего утверждения и определения базиса можно сделать вывод, что любая система n -мерных векторов, число векторов в которой меньше n , не является базисом .

Теперь переставим местами первый и второй вектор системы . Легко показать, что полученная система векторов также является базисом n -мерного векторного пространства. Составим матрицу, приняв ее строками векторы этой системы. Эта матрица может быть получена из единичной матрицы перестановкой местами первой и второй строк, следовательно, ее ранг будет равен n . Таким образом, система из n векторов линейно независима и является базисом n -мерного векторного пространства.

Если переставить местами другие векторы системы , то получим еще один базис.

Если взять линейно независимую систему не единичных векторов, то она также является базисом n -мерного векторного пространства.

Таким образом, векторное пространство размерности n имеет столько базисов, сколько существует линейно независимых систем из n n -мерных векторов.

Если говорить о двумерном векторном пространстве (то есть, о плоскости), то ее базисом являются два любых не коллинеарных вектора. Базисом трехмерного пространства являются три любых некомпланарных вектора.

Рассмотрим несколько примеров.

Являются ли векторы базисом трехмерного векторного пространства?

Исследуем эту систему векторов на линейную зависимость. Для этого составим матрицу, строками которой будут координаты векторов, и найдем ее ранг:

Таким образом, векторы a , b и c линейно независимы и их количество равно размерности векторного пространства, следовательно, они являются базисом этого пространства.

Может ли система векторов быть базисом векторного пространства?

Эта система векторов линейно зависима, так как максимальное число линейно независимых трехмерных векторов равно трем. Следовательно, эта система векторов не может быть базисом трехмерного векторного пространства (хотя подсистема исходной системы векторов является базисом).

Убедитесь, что векторы

могут быть базисом четырехмерного векторного пространства.

Составим матрицу, приняв ее строками исходные векторы:

Найдем :

Таким образом, система векторов a, b, c, d линейно независима и их количество равно размерности векторного пространства, следовательно, a, b, c, d являются его базисом.

Исходные векторы действительно являются базисом четырехмерного пространства.

Составляют ли векторы базис векторного пространства размерности 4 ?

Даже если исходная система векторов линейно независима, количество векторов в ней недостаточно для того, чтобы быть базисом четырехмерного пространства (базис такого пространства состоит из 4 векторов).

Нет, не составляет.

Разложение вектора по базису векторного пространства.

Пусть произвольные векторы являются базисом n -мерного векторного пространства. Если к ним добавить некоторый n -мерный вектор x , то полученная система векторов будет линейно зависимой. Из свойств линейной зависимости мы знаем, что хотя бы один вектор линейно зависимой системы линейно выражается через остальные. Иными словами, хотя бы один из векторов линейно зависимой системы раскладывается по остальным векторам.

Так мы подошли к очень важной теореме.

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Пусть — базис n -мерного векторного пространства. Добавим к этим векторам n -мерный вектор x . Тогда полученная система векторов будет линейно зависимой и вектор x может быть линейно выражен через векторы : , где — некоторые числа. Так мы получили разложение вектора x по базису. Осталось доказать, что это разложение единственно.

Предположим, что существует еще одно разложение , где — некоторые числа. Отнимем от левой и правой частей последнего равенства соответственно левую и правую части равенства :

Так как система базисных векторов линейно независима, то по определению линейной независимости системы векторов полученное равенство возможно только тогда, когда все коэффициенты равны нулю. Поэтому, , что доказывает единственность разложения вектора по базису.

Коэффициенты называются координатами вектора x в базисе .

После знакомства с теоремой о разложении вектора по базису, мы начинаем понимать суть выражения «нам задан n -мерный вектор ». Это выражение означает, что мы рассматриваем вектор x n -мерного векторного пространства, координаты которого заданы в некотором базисе. При этом мы понимаем, что этот же вектор x в другом базисе n-мерного векторного пространства будет иметь координаты, отличные от .

Рассмотрим следующую задачу.

Пусть в некотором базисе n -мерного векторного пространства нам задана система из n линейно независимых векторов

и вектор . Тогда векторы также являются базисом этого векторного пространства.

Пусть нам требуется найти координаты вектора x в базисе . Обозначим эти координаты как .

Вектор x в базисе имеет представление . Запишем это равенство в координатной форме:

Это равенство равносильно системе из n линейных алгебраических уравнений с n неизвестными переменными :

Основная матрица этой системы имеет вид

Обозначим ее буквой А . Столбцы матрицы А представляют собой векторы линейно независимой системы векторов , поэтому ранг этой матрицы равен n , следовательно, ее определитель отличен от нуля. Этот факт указывает на то, что система уравнений имеет единственное решение, которое может быть найдено любым методом, например, или .

Так будут найдены искомые координаты вектора x в базисе .

Разберем теорию на примерах.

В некотором базисе трехмерного векторного пространства заданы векторы

Убедитесь, что система векторов также является базисом этого пространства и найдите координаты вектора x в этом базисе.

Чтобы система векторов была базисом трехмерного векторного пространства нужно, чтобы она была линейно независима. Выясним это, определив ранг матрицы A , строками которой являются векторы . Ранг найдем методом Гаусса

следовательно, Rank(A) = 3 , что показывает линейную независимость системы векторов .

Итак, векторы являются базисом. Пусть в этом базисе вектор x имеет координаты . Тогда, как мы показали выше, связь координат этого вектора задается системой уравнений

Подставив в нее известные из условия значения, получим

Решим ее методом Крамера:

Таким образом, вектор x в базисе имеет координаты .

В некотором базисе четырехмерного векторного пространства задана линейно независимая система векторов

Известно, что . Найдите координаты вектора x в базисе .

Так как система векторов линейно независима по условию, то она является базисом четырехмерного пространства. Тогда равенство означает, что вектор x в базисе имеет координаты . Обозначим координаты вектора x в базисе как .

Система уравнений, задающая связь координат вектора x в базисах и имеет вид

Подставляем в нее известные значения и находим искомые координаты :

Связь между базисами.

Пусть в некотором базисе n -мерного векторного пространства заданы две линейно независимые системы векторов

то есть, они тоже являются базисами этого пространства.

Если — координаты вектора в базисе , то связь координат и задается системой линейных уравнений (об этом мы говорили в предыдущем пункте):

, которая в матричной форме может быть записана как

Аналогично для вектора мы можем записать

Предыдущие матричные равенства можно объединить в одно, которое по сути задает связь векторов двух различных базисов

Аналогично мы можем выразить все векторы базиса через базис :

Матрицу называют матрицей перехода от базиса к базису , тогда справедливо равенство

Умножив обе части этого равенства справа на

получим

Найдем матрицу перехода, при этом не будем подробно останавливаться на нахождении обратной матрицы и умножении матриц (смотрите при необходимости статьи и ):

Осталось выяснить связь координат вектора x в заданных базисах.

Пусть в базисе вектор x имеет координаты , тогда

а в базисе вектор x имеет координаты , тогда

Так как левые части последних двух равенств одинаковы, то мы можем приравнять правые части:

Если умножить обе части справа на

С другой стороны

(найдите обратную матрицу самостоятельно).
Два последних равенства дают нам искомую связь координат вектора x в базисах и .

Матрица перехода от базиса к базису имеет вид
;
координаты вектора x в базисах и связаны соотношениями

или
.

Мы рассмотрели понятия размерности и базиса векторного пространства, научились раскладывать вектор по базису и обнаружили связь между разными базисами n-мерного пространства векторов через матрицу перехода.

Лекции по алгебре и геометрии. Семестр 1.

Лекция 9. Базис векторного пространства.

Краткое содержание: система векторов, линейная комбинация системы векторов, коэффициенты линейной комбинации системы векторов, базис на прямой, плоскости и в пространстве, размерности векторных пространств на прямой, плоскости и в пространстве, разложение вектора по базису, координаты вектора относительно базиса, теорема о равенстве двух векторов, линейные операции с векторами в координатной форме записи, ортонормированная тройка векторов, правая и левая тройки векторов, ортонормированный базис, основная теорема векторной алгебры.

Глава 9. Базис векторного пространства и разложение вектора по базису.

п.1. Базис на прямой, на плоскости и в пространстве.

Определение. Любое конечное множество векторов называется системой векторов.

Определение. Выражение , где
называется линейной комбинацией системы векторов
, а числа
называются коэффициентами этой линейной комбинации.

Пусть L, Р и S – прямая, плоскость и пространство точек соответственно и
. Тогда
– векторные пространства векторов как направленных отрезков на прямой L, на плоскости Р и в пространстве S соответственно.

называется любой ненулевой вектор
, т.е. любой ненулевой вектор коллинеарный прямой L:
и
.

Обозначение базиса
:
– базис
.

Определение. Базисом векторного пространства
называется любая упорядоченная пара неколлинеарных векторов пространства
.

, где
,
– базис
.

Определение. Базисом векторного пространства
называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства
.

– базис
.

Замечание. Базис векторного пространства не может содержать нулевого вектора: в пространстве
по определению, в пространстве
два вектора будут коллинеарные, если хотя бы один из них нулевой, в пространстве
три вектора будут компланарные, т.е будут лежать в одной плоскости, если хотя бы один из трех векторов будет нулевой.

п.2. Разложение вектора по базису.

Определение. Пусть – произвольный вектор,
– произвольная система векторов. Если выполняется равенство

то говорят, что вектор представлен в виде линейной комбинации данной системы векторов. Если данная система векторов
является базисом векторного пространства, то равенство (1) называется разложением вектора по базису
. Коэффициенты линейной комбинации
называются в этом случае координатами вектора относительно базиса
.

Теорема. (О разложении вектора по базису.)

Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.

Доказательство. 1) Пусть L произвольная прямая (или ось) и
– базис
. Возьмем произвольный вектор
. Так как оба вектора и коллинеарные одной и той же прямой L, то
. Воспользуемся теоремой о коллинеарности двух векторов. Так как
, то найдется (существует) такое число
, что
и тем самым мы получили разложение вектора по базису
векторного пространства
.

Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису
векторного пространства
:

и
, где
. Тогда
и используя закон дистрибутивности, получаем:

Так как
, то из последнего равенства следует, что
, ч.т.д.

2) Пусть теперь Р произвольная плоскость и
– базис
. Пусть
произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую , на которой лежит вектор , прямую
, на которой лежит вектор . Через конец вектора проведем прямую параллельную вектору и прямую параллельную вектору . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма
, и
,
,
– базис ,
– базис
.

Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа
, что

и
. Отсюда получаем:

и возможность разложения по базису доказана.

Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора по базису
векторного пространства
:
и
. Получаем равенство

Откуда следует
. Если
, то
, а т.к.
, то
и коэффициенты разложения равны:
,
. Пусть теперь
. Тогда
, где
. По теореме о коллинеарности двух векторов отсюда следует, что
. Получили противоречие условию теоремы. Следовательно,
и
, ч.т.д.

3) Пусть
– базис
и пусть
произвольный вектор. Проведем следующие построения.

Отложим все три базисных вектора
и вектор от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы
, плоскость
и плоскость
; далее через конец вектора проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:

По правилу сложения векторов получаем равенство:

. (1)

По построению
. Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число
, такое что
. Аналогично,
и
, где
. Теперь, подставляя эти равенства в (1), получаем:

и возможность разложения по базису доказана.

Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису
:

Заметим, что по условию векторы
некомпланарные, следовательно, они попарно неколлинеарные.

Возможны два случая:
или
.

а) Пусть
, тогда из равенства (3) следует:

. (4)

Из равенства (4) следует, что вектор раскладывается по базису
, т.е. вектор лежит в плоскости векторов
и, следовательно, векторы
компланарные, что противоречит условию.

б) Остается случай
, т.е.
. Тогда из равенства (3) получаем или

Так как
– базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что
и
, ч.т.д.

1) Существует взаимно однозначное соответствие между множеством векторов векторного пространства
и множеством действительных чисел R.

2) Существует взаимно однозначное соответствие между множеством векторов векторного пространства
и декартовым квадратом

3) Существует взаимно однозначное соответствие между множеством векторов векторного пространства
и декартовым кубом
множества действительных чисел R.

Доказательство. Докажем третье утверждение. Первые два доказываются аналогично.

Выберем и зафиксируем в пространстве
какой-нибудь базис
и устроим отображение
по следующему правилу:

т.е. каждому вектору поставим в соответствие упорядоченный набор его координат.

Так как при фиксированном базисе каждый вектор имеет единственный набор координат, то соответствие, задаваемое правилом (6) действительно является отображением.

Из доказательства теоремы следует, что различные векторы имеют различные координаты относительно одного и того же базиса, т.е. отображение (6) является инъекцией.

Пусть
произвольный упорядоченный набор действительных чисел.

Рассмотрим вектор
. Этот вектор по построению имеет координаты
. Следовательно, отображение (6) является сюръекцией.

Отображение, которое одновременно инъективное и сюръективное является биективным, т.е. взаимно однозначным, ч.т.д.

Теорема. (О равенстве двух векторов.)

Два вектора равны тогда и только тогда, когда равны их координаты относительно одного и того же базиса.

Доказательство сразу же вытекает из предыдущего следствия.

п.3. Размерность векторного пространства.

Определение. Число векторов в базисе векторного пространства называется его размерностью.

Обозначение:
– размерность векторного пространства V.

Таким образом, в соответствие с этим и предыдущими определениями, имеем:

1)
– векторное пространство векторов прямой L.

– базис
,
,
,
– разложение вектора
по базису
,
– координата вектора относительно базиса
.

2)
– векторное пространство векторов плоскости Р.

– базис
,
,
,
– разложение вектора
по базису
,
– координаты вектора относительно базиса
.

3)
– векторное пространство векторов в пространстве точек S.

– базис
,
,
– разложение вектора
по базису
,
– координаты вектора относительно базиса
.

Замечание. Если
, то
и можно выбрать базис
пространства
так, что
– базис
и
– базис
. Тогда
, и
, .

Таким образом, любой вектор прямой L, плоскости Р и пространства S можно разложить по базису
:

Обозначение. В силу теоремы о равенстве векторов, мы можем отождествить любой вектор с упорядоченной тройкой действительных чисел и писать:

Это возможно лишь том случае, когда базис
фиксирован и нет опасности спутаться.

Определение. Запись вектора в виде упорядоченной тройки действительных чисел называют координатной формой записи вектора:
.

п.4. Линейные операции с векторами в координатной форме записи.

Пусть
– базис пространства
и
– два его произвольных вектора. Пусть
и
– запись этих векторов в координатной форме. Пусть, далее,
– произвольное действительное число. В этих обозначениях имеет место следующая теорема.

Теорема. (О линейных операциях с векторами в координатной форме.)

2)
.

Другими словами, для того, чтобы сложить два вектора нужно сложить их соответствующие координаты, а чтобы умножить вектор на число, нужно каждую координату данного вектора умножить на данное число.

Доказательство. Так как по условию теоремы , , то используя аксиомы векторного пространства, которым подчиняются операции сложения векторов и умножения вектора на число, получаем:

Аналогично доказывается второе равенство.

п.5. Ортогональные векторы. Ортонормированный базис.

Определение. Два вектора называются ортогональными, если угол между ними равен прямому углу, т.е.
.

Обозначение:
– векторы и ортогональны.

Определение. Тройка векторов
называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е.
,
.

Определение. Тройка векторов
называется ортонормированной, если она ортогональная и длины всех векторов равны единице:
.

Замечание. Из определения следует, что ортогональная и, следовательно, ортонормированная тройка векторов является некомпланарной.

Определение. Упорядоченная некомпланарная тройка векторов
, отложенных от одной точки, называется правой (правоориентированной), если при наблюдении с конца третьего вектора на плоскость, в которой лежат первые два вектора и , кратчайший поворот первого вектора ко второму происходит против часовой стрелки. В противном случае тройка векторов называется левой (левоориентированной).

Здесь, на рис.6 изображена правая тройка векторов
. На следующем рис.7 изображена левая тройка векторов
:

Определение. Базис
векторного пространства
называется ортонормированным, если
ортонормированная тройка векторов.

Обозначение. В дальнейшем мы будем пользоваться правым ортонормированным базисом
, см. следующий рисунок.

Выражение вида называется линейной комбинацией векторов A 1 , A 2 . A n с коэффициентами λ 1, λ 2 . λ n .

Определение линейной зависимости системы векторов

Система векторов A 1 , A 2 . A n называется линейно зависимой , если существует ненулевой набор чисел λ 1, λ 2 . λ n , при котором линейная комбинация векторов λ 1 *A 1 +λ 2 *A 2 +. +λ n *A n равна нулевому вектору , то есть система уравнений: имеет ненулевое решение.
Набор чисел λ 1, λ 2 . λ n является ненулевым, если хотя бы одно из чисел λ 1, λ 2 . λ n отлично от нуля.

Определение линейной независимости системы векторов

Система векторов A 1 , A 2 . A n называется линейно независимой , если линейная комбинация этих векторов λ 1 *A 1 +λ 2 *A 2 +. +λ n *A n равна нулевому вектору только при нулевом наборе чисел λ 1, λ 2 . λ n , то есть система уравнений: A 1 x 1 +A 2 x 2 +. +A n x n =Θ имеет единственное нулевое решение.

Проверить, является ли линейно зависимой система векторов

1. Составляем систему уравнений :

2. Решаем ее методом Гаусса . Преобразования Жордано системы приведены в таблице 29.1. При расчете правые части системы не записываются так как они равны нулю и при преобразованиях Жордана не изменяются.

3. Из последних трех строк таблицы записываем разрешенную систему, равносильную исходной системе:

5. Задав по своему усмотрению значение свободной переменной x 3 =1, получаем частное ненулевое решение X=(-3,2,1).

Ответ: Таким образом, при ненулевом наборе чисел (-3,2,1) линейная комбинация векторов равняется нулевому вектору -3A 1 +2A 2 +1A 3 =Θ. Следовательно, система векторов линейно зависимая .

Свойства систем векторов

Свойство (1)
Если система векторов линейно зависимая, то хотя бы один из векторов разлагается по остальным и, наоборот, если хотя бы один из векторов системы разлагается по остальным, то система векторов линейно зависимая.

Свойство (2)
Если какая-либо подсистема векторов линейно зависимая, то и вся система линейно зависимая.

Свойство (3)
Если система векторов линейно независимая, то любая ее подсистема линейно независимая.

Свойство (4)
Любая система векторов, содержащая нулевой вектор, линейно зависимая.

Свойство (5)
Система m-мерных векторов всегда является линейно зависимой, если число векторов n больше их размерности (n>m)

Базис системы векторов

Базисом системы векторов A 1 , A 2 . A n называется такая подсистема B 1 , B 2 . B r (каждый из векторов B 1 ,B 2 . B r является одним из векторов A 1 , A 2 . A n) , которая удовлетворяет следующим условиям:
1. B 1 ,B 2 . B r линейно независимая система векторов;
2. любой вектор A j системы A 1 , A 2 . A n линейно выражается через векторы B 1 ,B 2 . B r

r — число векторов входящих в базис.

Теорема 29.1 О единичном базисе системы векторов.

Если система m-мерных векторов содержит m различных единичных векторов E 1 E 2 . E m , то они образуют базис системы.

Алгоритм нахождения базиса системы векторов

Для того, чтобы найти базис системы векторов A 1 ,A 2 . A n необходимо:

Составить соответствующую системе векторов однородную систему уравнений A 1 x 1 +A 2 x 2 +. +A n x n =Θ
Привести эту систему

Свежие записи

Вкусные букеты из овощей и фруктов с поздравлениями Человеку, который имеет свой плей л.

Петровская икона Богоматери, некий «700-летний юбилей свт Человеку, который имеет свой плей л.

Как женить на себе мужчину рака Человеку, который имеет свой плей л.

Автоковрики EVA: Как шить? Человеку, который имеет свой плей л.

Медитация на омоложение и усиление привлекательности Правила эффективной медитации Человеку, который имеет свой плей л.

источники:

http://bstudy.net/719717/estestvoznanie/algoritm_nahozhdeniya_bazisa_sistemy_vektorov

http://myfd.ru/kak-naiti-bazis-sistemy-vektorov-primery-kak-naiti-bazis/

Источник

При проведении научных и прикладных исследование часто создаются модели, в которых рассматриваются точки и/или векторы определенных пространств. Например, в моделях шифров на эллиптических кривых используются аффинные и проективные пространства. К проективным прибегают тогда, когда необходимо ускорить вычисления, так как в формулах манипулирования с точками эллиптической кривой выводимых в рамках проективного пространства отсутствует операция деления на координату, которую в случае аффинного пространства обойти не удается.

Операция деления как раз одна из самых «дорогих» операций. Дело в том, что в алгебраических полях, а соответственно и в группах операция деления вообще отсутствует и выход из положения (когда не делить нельзя) состоит в том, что операцию деления заменяют умножением, но умножают не на саму координату, а на обращенное ее значение. Из этого следует, что предварительно надо привлекать расширенный алгоритм Евклида НОД и кое что еще. Одним словом, не все так просто как изображают авторы большинства публикаций о ЕСС. Почти все, что по этой теме опубликовано и не только в Интернете мне знакомо. Мало того, что авторы не компетентны и занимаются профанацией, оценщики этих публикаций плюсуют авторов в комментариях, т. е. не видят ни пробелов, ни явных ошибок. Про нормальную же статью пишут, что она уже 100500-я и от нее нулевой эффект. Так все пока на Хабре устроено, анализ публикаций делается огромный, но не качества содержания. Здесь возразить нечего — реклама двигатель бизнеса.

Линейное векторное пространство

Изучение и описание явлений окружающего мира с необходимостью приводит нас к введению и использованию ряда понятий таких как точки, числа, пространства, прямые линии, плоскости, системы координат, векторы, множества и др.

Пусть r_<3> = <r1, r2, r3> вектор трехмерного пространства, задает положение одной частицы (точки) относительно начала координат. Если рассматривать N элементов, то описание их положения требует задания 3∙N координат, которые можно рассматривать как координаты некоторого вектора в 3N-мерном пространстве. Если рассматривать непрерывные функции и их совокупности, то приходим к пространствам, размерность которых равна бесконечности. На практике часто ограничиваются использованием лишь подпространства такого бесконечномерного пространства функции координат, обладающего конечным числом измерений.

Пример 1. Ряд Фурье — пример использования пространства функций. Рассмотрим разложение произвольной функции в ряд Фурье

Его можно трактовать как разложение «вектора» f(x) по бесконечному набору «ортогональных» базисных векторов sinпх

Это пример абстрагирования и распространения понятия вектора на бесконечное число измерений. Действительно, известно, что при -π≤x≤π

Существо дальнейшего рассмотрения не пострадает, если мы отвлечемся от размерности абстрактного векторного пространства – будь — то 3, 3N или бесконечность, хотя для практических приложений больший интерес представляет конечномерные поля и векторные пространства.

Набор векторов r1, r2,… будем называть линейным векторным пространством L, если сумма любых двух его элементов тоже находится в этом наборе и если результат умножения элемента на число С также входит в этот набор. Оговоримся сразу, что значения числа С могут быть выбраны из вполне определенного числового множества Fр – поля вычетов по модулю простого числа р, которое считается присоединенным к L.

Пример 2. Набор из 8 векторов, составленных из n =5 -разрядных двоичных чисел
r0 = 00000, r1 = 10101, r2 = 01111, r3 = 11010, r4 = 00101, r5 = 10110, r6 = 01001, r7 = 11100 образует векторное пространство L, если числа С є {0,1}. Этот небольшой пример позволяет убедиться в проявлении свойств векторного пространства, включенных в его определение.

Суммирование этих векторов выполняется поразрядно по модулю два, т. е. без переноса единиц в старший разряд. Отметим, что если все С действительные (в общем случае С принадлежат полю комплексных чисел), то векторное пространство называют действительным.

Формально аксиомы векторного пространства и записываются так:
r1 + r2 = r2 + r1 = r3; r1, r2, r3 є L – коммутативность сложения и замкнутость;
(r1 + r2) + r3 = r1 + (r2 + r3) = r1 + r2 + r3 – ассоциативность сложения;
ri + r0 = r0 + ri = ri; ∀i, ri, r0 є L–существование нейтрального элемента;
ri +(- ri) = r0, для ∀i существует противоположный вектор (-ri) є L;
1∙ ri = ri ∙1 = ri существование единицы для умножения;
α (β∙ri) = (α∙β)∙ri; α, β, 1, 0 – элементы числового поля F, ri є L; умножение на скаляры ассоциативно; результат умножения принадлежит L;
(α + β) ri = α∙ri + β∙ri; для ∀i, ri є L, α, β – скаляры;
а (ri + rj) = ari + arj для всех а, ri, rj є L;
a∙0 = 0, 0∙ri = 0; (-1) ∙ ri = – ri.

Размерность и базис векторного пространства

При изучении векторных пространств представляет интерес выяснение таких вопросов, как число векторов, образующих все пространство; какова размерность пространства; какой наименьший набор векторов путем применения к нему операции суммирования и умножения на число позволяет сформировать все векторы пространства? Эти вопросы основополагающие и их нельзя обойти стороной, так как без ответов на них утрачивается ясность восприятия всего остального, что составляет теорию векторных пространств.

Оказалось, что размерность пространства самым тесным образом связана с линейной зависимостью векторов, и с числом линейно независимых векторов, которые можно выбирать в изучаемом пространстве многими способами.

Линейная независимость векторов

Набор векторов r1, r2, r3 … rр из L называют линейно независимым, если для них соотношение

выполняется только при условии одновременного равенства

.
Все

$с_k$ , k = 1(1)p, принадлежат числовому полю вычетов по модулю два
F = {0, 1}.
Если в некотором векторном пространстве L можно подобрать набор из р векторов, для которых соотношение

выполняется, при условии, что не все

одновременно, т.е. в поле вычетов оказалось возможным выбрать набор

$с_k$ , k =1(1)р, среди которых есть ненулевые, то такие векторы

$r_i$ называются линейно зависимыми.

Пример 3. На плоскости два вектора

$е_1$ = <0, 1>^T и

$е_2$ = <1, 0>^T являются линейно независимыми, так как в соотношении (T-транспонирование)

невозможно подобрать никакой пары чисел

коэффициентов не равных нулю одновременно, чтобы соотношение было выполнено.
Три вектора

$е_1$ = <0, 1>^T,

$е_2$ = <1, 0>^T,

$е_3$ = <1, 1>^T образуют систему линейно зависимых векторов, так как в соотношении

равенство может быть обеспечено выбором коэффициентов

, не равных нулю одновременно. Более того, вектор

является функцией

$ е_1$ и

(их суммой), что указывает на зависимость

$ e_3 $ от

$е_1$ и

$е_2 $ . Доказательство общего случая состоит в следующем.

Пусть хотя бы одно из значений

$с_k$ , k = 1(1)р, например,

, а соотношение выполнено. Это означает, что векторы

$r_k$ , k = 1(1)р, линейно зависимы

Выделим явным образом из суммы вектор r_р

Говорят, что вектор r_р является л и н е й н о й комбинацией векторов

или r_р через остальные векторы выражается линейным образом, т.е. r_р линейно зависит от остальных. Он является их функцией.

На плоскости двух измерений любые три вектора линейно зависимы, но любые два неколлинеарных вектора являются независимыми. В трехмерном пространстве любые три некомпланарных вектора линейно независимы, но любые четыре вектора всегда линейно зависимы.

Зависимость/независимость совокупности {

${e_1, e_2, e_3, ..., e_n}$ } векторов часто определяют, вычисляя определитель матрицы Грама (ее строки скалярные произведения наших векторов). Если определитель равен нулю, среди векторов имеются зависимые, если определитель отличен от нуля — векторы в матрице независимы.

Определителем Грама (грамианом) системы векторов

${displaystyle mathbf {e} _{1},;mathbf {e} _{2},;ldots ,mathbf {e} _{n}}mathbf{e}_1,;mathbf{e}_2,;ldots,mathbf{e}_n$

в евклидовом пространстве называется определитель матрицы Грама этой системы:

${displaystyle {begin{vmatrix}langle e_{1},;e_{1}rangle &langle e_{1},;e_{2}rangle &ldots &langle e_{1},;e_{n}rangle \langle e_{2},;e_{1}rangle &langle e_{2},;e_{2}rangle &ldots &langle e_{2},;e_{n}rangle \ldots &ldots &ldots &ldots \langle e_{n},;e_{1}rangle &langle e_{n},;e_{2}rangle &ldots &langle e_{n},;e_{n}rangle \end{vmatrix}},}begin{vmatrix} langle e_1,;e_1rangle & langle e_1,;e_2rangle & ldots & langle e_1,;e_nrangle \ langle e_2,;e_1rangle & langle e_2,;e_2rangle & ldots & langle e_2,;e_nrangle \ ldots & ldots & ldots & ldots \ langle e_n,;e_1rangle & langle e_n,;e_2rangle & ldots & langle e_n,;e_nrangle \ end{vmatrix},$

где

${displaystyle langle e_{i},;e_{j}rangle }langle e_i,;e_jrangle{displaystyle langle e_{i},;e_{j}rangle }langle e_i,;e_jrangle$ — скалярное произведение векторов

${displaystyle mathbf {e} _{i}}mathbf{e}_i$ и

${displaystyle mathbf {e} _{j}}mathbf{e}_j$ .

Размерность и базис векторного пространства

Размерность s = d (L) пространства L определяется как наибольшее число векторов в L, образующих линейно независимый набор. Размерность – это не число векторов в L, которое может быть бесконечным и не число компонентов вектора.

Пространства, имеющие конечную размерность s ≠ ∞, называются конечномерными, если
s = ∞, – бесконечномерными.

Ответом на вопрос о минимальном числе и составе векторов, которые обеспечивают порождение всех векторов линейного векторного пространства является следующее утверждение.

Любой набор s линейно независимых векторов в пространстве L образует его б а з и с. Это следует из того, что любой вектор

$r_k$ линейного s-мерного векторного пространства L может быть представлен единственным способом в виде линейной комбинации векторов базиса.

Зафиксируем и обозначим символом

$е_i $ , i = 1(1)s, один из наборов, образующих базис пространства L. Тогда

Числа r_ki, i = 1(1)s называются координатами вектора

$r_k $ в базисе

$е_i $ , i = 1(1)s, причем r_ki = (

$е_i $ ,

$r_k $ ).
Покажем единственность представления

$r_k $ . Очевидно, что набор

$ r_k $ является зависимым, так как

$е_i$ , i = 1(1)s – базис. Другими словами, существуют такие

не равные одновременно нулю, что

.
При этом пусть

, ибо если

, то хоть одно из

, было бы отлично от нуля и тогда векторы

$ e_i $ , i = 1(1)s, были бы линейно зависимы, что невозможно, так как это базис. Следовательно,

Полагая

, будем иметь
Используя прием доказательства «от противного», допустим, что записанное представление

$r_k $ не единственное в этом базисе и существует другое

Тогда запишем отличие представлений, что, естественно, выражается как

Очевидно, что правая и левая части равны, но левая представляет разность вектора с самим собой, т. е. равна нулю. Следовательно, и правая часть равна нулю. Векторы

, i = 1(1)s линейно независимы, поэтому все коэффициенты при них могут быть только нулевыми. Отсюда получаем, что

а это возможно только при

Выбор базиса. Ортонормированность

Векторы называют нормированными, если длина каждого из них равна единице. Этого можно достичь, применяя к произвольным векторам процедуру нормировки.

Векторы называют ортогональными, если они перпендикулярны друг другу. Такие векторы могут быть получены применением к каждому из них процедуры ортогонализации. Если для совокупности векторов выполняются оба свойства, то векторы называются ортонормированными.

Необходимость рассмотрения ортонормированных базисов вызвана потребностями использования быстрых преобразований как одно –, так и многомерных функций. Задачи такой обработки возникают при исследовании кодов, кодирующих информационные сообщения в сетях связи различного назначения, при исследовании изображений, получаемых
посредством автоматических и автоматизированных устройств, в ряде других областей, использующих цифровые представления информации.

Определение. Совокупность n линейно независимых векторов n-мерного векторного
пространства V называется его базисом.

Теорема. Каждый вектор х линейного n-мерного векторного пространства V можно представить, притом единственным образом, в виде линейной комбинации векторов базиса. Векторное пространство V над полем F обладает следующими свойствами:
0·х = 0 (0 в левой части равенства – нейтральный элемент аддитивной группы поля F; 0 в правой части равенства – элемент пространства V, являющийся нейтральным единичным элементом аддитивной группы V, называемый нулевым вектором);
(– 1)·х = –х; –1є F; x є V; –x є V;
Если α·х = 0єV, то при х ≠ 0 всегда α = 0.
Пусть Vn(F) – множество всех последовательностей (х1, х2, …, хn) длины n с компонентами из поля F, т.е. Vn(F) ={x, таких, что х = (х1, х2, …, хn), хi є F;
i =1(1)n }.

Сложение и умножение на скаляр определяются следующим образом:
x + y =(x1 + y1, x2 + y2, …, xn + yn);
α·х = (α·х1, α·х2,…, α·хn), где у = (у1, у2,…, уn),
тогда Vn(F) является векторным пространством над полем F.

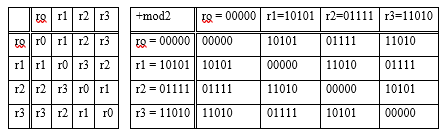
Пример 4. В векторном пространстве rо = 00000, r1 = 10101, r2 = 11010, r3 = 10101 над полем F2 = {0,1} определить его размерность и базис.
Решение. Сформируем таблицу сложения векторов линейного векторного пространства

В этом векторном пространстве V= {rо,r1,r2,r3} каждый вектор в качестве противоположного имеет самого себя. Любые два вектора, исключая rо, являются линейно независимыми, в чем легко убедиться
c1·r1 + c2·r2 = 0; c1·r1 + c3·r3 = 0; c2·r2 + c3·r3 = 0;

Каждое из трех соотношений справедливо только при одновременных нулевых значениях пар коэффициентов сi, сj є {0,1}.

При одновременном рассмотрении трех ненулевых векторов один из них всегда является суммой двух других или равен самому себе, а r1+r2+r3=rо.

Таким образом, размерность рассматриваемого линейного векторного пространства равна двум s = 2, d(L) = s = 2, хотя каждый из векторов имеет пять компонентов. Базисом пространства является набор (r1, r2). Можно в качестве базиса использовать пару (r1, r3).

Важным в теоретическом и практическом отношении является вопрос описания векторного пространства. Оказывается, любое множество базисных векторов можно рассматривать как строки некоторой матрицы G, называемой порождающей матрицей векторного пространства. Любой вектор этого пространства может быть представлен как линейная комбинация строк матрицы G ( как, например, здесь).

Если размерность векторного пространства равна k и равна числу строк матрицы G, рангу матрицы G, то очевидно, существует k коэффициентов с q различными значениями для порождения всех возможных линейных комбинаций строк матрицы. При этом векторное пространство L содержит q^k векторов.

Множество всех векторов из ℤpn с операциями сложения векторов и умножения вектора на скаляр из ℤp есть линейное векторное пространство.

Определение. Подмножество W векторного пространства V, удовлетворяющее условиям:
Если w1, w2 є W, то w1+ w2 є W,
Для любых α є F и w є W элемент αw є W,
само является векторным пространством над полем F и называется подпространством векторного пространства V.

Пусть V есть векторное пространство над полем F и множество W ⊆ V. Множество W есть подпространство пространства V, если W по отношению к линейным операциям, определенным в V, есть линейное векторное пространство.

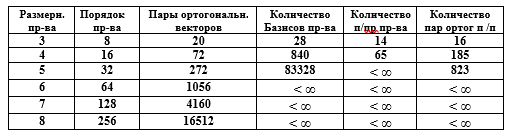
Таблица. Характеристики векторных пространств

Компактность матричного представления векторного пространства очевидна. Например, задание L векторов двоичных 50-разрядных чисел, среди которых 30 векторов образуют базис векторного пространства, требует формирования матрицы G[30,50], а описываемое количество векторов превышает 10⁹, что в поэлементной записи представляется неразумным.

Все базисы любого пространства L разбиваются подгруппой Р невырожденных матриц с det G > 0 на два класса. Один из них (произвольно) называют классом с положительно ориентированными базисами (правыми), другой класс содержит левые базисы.

В этом случае говорят, что в пространстве задана ориентация. После этого любой базис представляет собой упорядоченный набор векторов.

Если нумерацию двух векторов изменить в правом базисе, то базис станет левым. Это связано с тем, что в матрице G поменяются местами две строки, следовательно, определитель detG изменит знак.

Норма и скалярное произведение векторов

После того как решены вопросы о нахождении базиса линейного векторного пространства, о порождении всех элементов этого пространства и о представлении любого элемента и самого векторного пространства через базисные векторы, можно поставить задачу об измерении в этом пространстве расстояний между элементами, углов между векторами, значений компонентов векторов, длины самих векторов.

Действительное или комплексное векторное пространство L называется нормированным векторным пространством, если каждый вектор r в нем может быть сопоставлен действительному числу || r || – модулю вектора, норме. Единичный вектор – это вектор, норма которого равна единице. Нулевой вектор имеет компонентами нули.

Определение. Векторное пространство называется унитарным, если в нем определена бинарная операция, ставящая каждой паре ri, rj векторов из L в соответствие скаляр. В круглых скобках (ri, rj) записывается (обозначается) скалярное или внутреннее произведение ri и rj, причем
1. (ri, rj) = ri ∙ rj;
2. (ri, rj) = (rj ∙ ri)*, где * указывает на комплексное сопряжение или эрмитову симметрию;
3. (сri, rj) = с(ri ∙ rj) – ассоциативный закон;
4. (ri + rj, rk) = (ri ∙ rk)+ (rj ∙ rk)– дистрибутивный закон;
5. (ri, rk) ≥ 0 и из (ri, rj ) = 0 следует ri = 0.

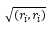
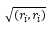
Определение. Положительное значение квадратного корня называют нормой (или длиной, модулем) вектора ri. Если = 1, то вектор ri называют нормированным.

Два вектора ri, rj унитарного векторного пространства L взаимно ортогональны, если их скалярное произведение равно нулю, т.е. (ri, rj) = 0.

При s = 3 в линейном векторном пространстве в качестве базиса удобно выбирать три взаимно перпендикулярных вектора. Такой выбор существенно упрощает ряд зависимостей и вычислений. Этот же принцип ортогональности используется при выборе базиса в пространствах и других размерностей s > 3. Использование введенной операции скалярного произведения векторов обеспечивает возможность такого выбора.

Еще большие преимущества достигаются при выборе в качестве базиса векторного пространства ортогональных нормированных векторов – ортонормированного базиса. Если не оговорено специально, то далее всегда будем считать, что базис еi, i = 1(1)s выбран именно таким образом, т.е.

, где ij — символ Кронекера (1823 — 1891).

В унитарных векторных пространствах такой выбор всегда реализуем. Покажем реализуемость такого выбора.

Определение. Пусть S = {v1, v2,…, vn} есть конечное подмножество векторного пространства V над полем F.
Линейная комбинация векторов из S есть выражение вида а1∙v1 + а2∙v2 +…+ аn∙vn, где каждое аi ∊ F.

Оболочка для множества S (обозначение {S}) есть множество всех линейных комбинаций векторов из S. Оболочка для S есть подпространство пространства V.

Если U есть пространство в V, то U натянуто на S (S стягивает U), если {S}=U.
Множество векторов S линейно зависимо над F, если в F существуют скаляры а1, а2,…, аn, не все нули, для которых а1∙v1+ а2∙v2 +…+ аn∙vn = 0. Если таких скаляров не существует, то множество векторов S линейно независимо над F.

Если векторное пространство V натянуто на линейно независимую систему векторов S (или система S стягивает пространство V), то система S называется базисом для V.

Приведение произвольного базиса к ортонормированному виду

Пусть в пространстве V имеется не ортонормированный базис ē_i, i = 1(1)s. Обозначим норму каждого вектора базиса символом

Известно следующее утверждение [11]. Если ē_i, i = 1(1)s – произвольная конечная или счетная система линейно независимых векторов в унитарном векторном пространстве, то существует ортонормированная система ē_i, i = 1(1)s, порождающая то же самое линейное пространство (многообразие).

В основу процедуры приведения базиса к ортонормированному виду положен процесс ортогонализации Грама — Шмидта, который в свою очередь, реализуется рекуррентными формулами

В развернутом виде алгоритм ортогонализации и нормирования базиса содержит следующие условия:

Делим вектор ē₁, на его норму; получим нормированный вектор ē_i=ē₁/(||ē₁ ||);
Формируем V2 = ē₂ — (ē₁, ē₂)e₁ и нормируем его, получим е₂. Ясно, что тогда
(е1, е2) ~ (е1, е2) – (е1, ē₂)( е1, е1) = 0;
Построив V3 = ē₃– (e1, ē₃)e1 – (e2, ē₃) e2 и нормируя его, получим е3.

Для него имеем сразу же (е1, е3) = (е2, е3) = 0.
Продолжая такой процесс, получим ортонормированный набор ē_i, i = 1(1)s. Этот набор содержит линейно независимые векторы, поскольку все они взаимно ортогональны.
Убедимся в этом. Пусть выполняется соотношение

Если набор ē_i, i = 1(1)s зависимый, то хотя бы один сj коэффициент не равен нулю сj ≠ 0.

Умножив обе части соотношения на еj, получаем
(ej, c1∙e1 ) + (ej, c2∙e2 )+ …+ ( ej, cj∙ej ) +…+ ( ej, cs∙rs ) = 0.
Каждое слагаемое в сумме равно нулю как скалярное произведение ортогональных векторов, кроме (ej ,cj∙ej), которое равно нулю по условию. Но в этом слагаемом
(ej, ej) = 1 ≠ 0, следовательно, нулем может быть только cj.
Таким образом, допущение о том, что cj ≠ 0 неверно и набор является линейно независимым.

Пример 5. Задан базис 3-х мерного векторного пространства:
{<-1, 2 ,3, 0>,<0, 1, 2, 1>,<2,-1,-1,1>}.
Скалярное произведение определено соотношением:
(<x1,x2,x3,x4>,<y1,y2,y3,y4>) = x1∙y1+x2∙y2+x3∙y3+x4∙y4.
Процедурой ортогонализации Грама — Шмидта получаем систему векторов:
а1 = <-1, 2, 3, 0>; a2 = <0, 1, 2, 1>-4<-1, 2, 3,0>/7=<4,-1, 2, 7>/7;
a3 =<2, -1, -1, 1>+½<-1, 2, 3, 0> — <4, -1, 2, 7>/5 =<7, 2, 1, -4>/10.
(a1,a2)= (1+4+9+0) = 14;
a1^E =a1/√14;
a2-(a1^E,a2)∙a1^E=a2-(8/√14)(a1/√14)=a2 — 4∙a1/7;
Третий вектор читателю предлагается обработать самостоятельно.

Нормированные векторы получают вид:
a1^E =a1/√14;
a2^E =<4, -1, 2, 7>/√70;
a3^E =<7, 2, 1,-4>/√70;

Ниже в примере 6 дается подробный развернутый процесс вычислений получения ортонормированного базиса из простого (взятого наугад).

Пример 6. Привести заданный базис линейного векторного пространства к ортонормированному виду.
Дано: векторы базиса

Подпространства векторных пространств

Структура векторного пространства

Представление объектов (тел) в многомерных пространствах весьма непростая задача. Так, четырехмерный куб в качестве своих граней имеет обычные трехмерные кубы, и в трехмерном пространстве может быть построена развертка четырехмерного куба. В некоторой степени «образность» и наглядность объекта или его частей способствует более успешному его изучению.

Сказанное позволяет предположить, что векторные пространства можно некоторым образом расчленять, выделять в них части, называемые подпространствами. Очевидно, что рассмотрение многомерных и тем более бесконечномерных пространств и объектов в них лишает нас наглядности представлений, что весьма затрудняет исследование объектов в таких
пространствах. Даже, казалось бы, такие простые вопросы, как количественные характеристики элементов многогранников (число вершин, ребер, граней, и т. п.) в этих пространствах решены далеко не полностью.

Конструктивный путь изучения подобных объектов состоит в выделении их элементов (например, ребер, граней) и описании их в пространствах меньшей размерности. Так четырехмерный куб в качестве своих граней имеет обычные трехмерные кубы и в трехмерном пространстве может быть построена развертка четырехмерного куба. В некоторой степени
«образность» и наглядность объекта или его частей способствует более успешному их изучению.

Если L – расширение поля К, то L можно рассматривать как векторное (или линейное) пространство над полем К. Элементы поля L (т. е. векторы) образуют по сложению абелеву группу. Кроме того, каждый «вектор» а є L может быть умножен на «скаляр» r є K, и при этом произведение ra снова принадлежит L (здесь ra – просто произведение в смысле операции поля L элементов r и а этого поля). Выполняются также законы
r∙(a+b) = r∙a+r∙b, (r+s)∙a = r∙a + r∙s, (r∙s)∙a = r∙(s∙a) и 1∙а = а, где r,s є K, a,b є L.

Сказанное позволяет предположить, что векторные пространства можно некоторым образом расчленять, выделять в них части, называемые подпространствами. Очевидно, что основным результатом при таком подходе является сокращение размерности выделяемых подпространств. Пусть в векторном линейном пространстве L выделены подпространства L1 и L2. В качестве базиса L1 выбирается меньший набор еi, i = 1(1)s1, s1 < s, чем в исходном L.

Оставшиеся базисные векторы порождают другое подпространство L2, называемое «ортогональным дополнением» подпространства L1. Будем использовать запись L = L1 + L2. Она означает не то, что все векторы пространства L принадлежат либо L1, либо L2,, а то, что любой вектор из L можно представить в виде суммы вектора из L1 и ортогонального ему вектора из L2.
Разбивается не множество векторов векторного пространства L, а размерность d(L) и набор базисных векторов. Таким образом, подпространством L1 векторного пространства L называется множество L1, его элементов (меньшей размерности), само являющееся векторным пространством относительно введенных в L операций сложения и умножения на число.

Каждое линейное векторное подпространство Li – содержит нулевой вектор и вместе с любыми своими векторами содержит и все их линейные комбинации. Размерность любого линейного подпространства не превосходит размерности самого исходного пространства.

Пример 7. В обычном трехмерном пространстве подпространствами являются все прямые (размерность s =1) линии, плоскости (размерность s = 2), проходящие через начало координат. В пространстве Рn многочленов степени не выше n подпространствами будут, например, все Рk при k < n, так как складывая и умножая на числа многочлены степени, не выше k, снова будут получаться такие же многочлены.

Однако, каждое из пространств Рп содержится в качестве подпространств в пространстве Р всех многочленов с вещественными коэффициентами, а это последнее является подпространством пространства С непрерывных функций.

Матрицы одинакового типа над полем действительных чисел также образуют линейное векторное пространство, так как для них выполняются все аксиомы векторных пространств. Векторное пространство L2 наборов длины n, каждый из которых ортогонален подпространству L1 наборов длины п, образует подпространство L2, называемое нулевым пространством для L1. Другими словами, каждый вектор из L2 ортогонален каждому вектору из L1 и наоборот.

Оба подпространства L1 и L2 являются подпространствами векторного пространства L наборов длины п. В теории кодирования [4] каждое из подпространств L1 и L2 порождает линейный код, двойственный по отношению к коду, порожденному другими подпространства-ми. Если L1 есть (п, k)-код, то L2 — это (п, п – k)-код. Если код является векторным пространством строк некоторой матрицы, то двойственный к нему код — нулевое пространство этой матрицы и наоборот.

Важным вопросом при изучении векторных пространств Vn является установление их структуры (строения). Другими словами, интерес представляют элементы, их совокупности (подпространства размерности 1<k<п ), а также их отношения (упорядоченность, вложенность и т.п.). Будем считать заданным векторное пространство Vn над конечным полем GF(q), образованным q = р r элементами, где р — простое число, r — целое.
Известны следующие результаты.

Количества подпространств векторного пространства

Приведем следующее обоснование. Каждый вектор v1 ≠ 0 из системы k линейно независимых ( v1,v2,…,vk ) векторов может быть выбран qⁿ – 1 способами. Следующий вектор v2 ≠ 0 не может быть выражен линейно через v1, т.е. может быть выбран qⁿ – q способами и т.д.

Последний вектор vk ≠ 0 также линейно не выражается через предыдущие выбранные векторы v1,v2,…,vk и, следовательно, может быть выбран qⁿ – q^k – 1 способами. Общее число способов для выбора совокупности векторов v1,v2,…,vk, таким образом, определится как произведение числа выборов отдельных векторов, что и дает формулу (1). Для случая, когда k = п, имеем wп = wn, n и из формулы (I) получаем формулу (2).

Важные обобщающие результаты о размерностях подпространств.
Совокупность всех наборов длины n, ортогональных подпространству V1 наборов длины n, образует подпространство V2 наборов длины n. Это подпространство V2 называется нулевым пространством для V1.
Если вектор ортогонален каждому из векторов, порождающих подпространство V1, то этот вектор принадлежит нулевому пространству для V1.
Примером (V1) может служить множество 7-разрядных векторов порождающей матрицы (7,4)-кода Хемминга, с нулевым подпространством (V2) 7-разрядных векторов, образующих проверочную матрицу этого кода.

Если размерность подпространства (V1) наборов длины n равна k, то размерность нулевого подпространства (V2) равна n — k.

Если V2 — подпространство наборов длины n и V1 — нулевое пространство для V2, то (V2) — нулевое пространство для V1.

Пусть U∩V обозначает совокупность векторов, принадлежащих одновременно U и V, тогда U∩V является подпространством.

Пусть U⊕V обозначает подпространство, состоящее из совокупности всех линейных комбинаций вида au +bv, где u є U, v є V, a b — числа.

Сумма размерностей подпространств U∩V и U⊕V равна сумме размерностей подпространств U и V.

Пусть U2 — нулевое подпространство для U1, а V2 -нулевое пространство для V1. Тогда U2∩V2 является нулевым пространством для U1⊕V1.

Заключение

В работе рассмотрены основные понятия векторных пространств, которые часто используются при построении моделей анализа систем шифрования, кодирования и стеганографических, процессов, протекающих в них. Так в новом американском стандарте шифрования использованы пространства аффинные, а в цифровых подписях на эллиптических кривых и аффинные и
проективные (для ускорения обработки точек кривой).

Об этих пространствах в работе речь не идет (нельзя валить все в одну кучу, да и объем публикации я ограничиваю), но упоминания об этом сделаны не зря. Авторы, пишущие о средствах защиты, об алгоритмах шифров наивно полагают, что понимают детали описываемых явлений, но понимание евклидовых пространств и их свойств без всяких оговорок переносится в другие пространства, с другими свойствами и законами. Читающая аудитория вводится в заблуждение относительно простоты и доступности материала.

Создается ложная картина действительности в области информационной безопасности и специальной техники (технологий и математики).

В общем почин мною сделан, насколько удачно судить читателям.

Литература

1. Авдошин С.М., Набебин А.А. Дискретная математика. Модулярная алгебра, криптография, кодирование. — М.: ДМК Пресс, 2017. -352 с.
2. Акимов О.Е. Дискретная математика.Логика, группы, графы- М.: Лаб.Баз. Зн., 2001. -352 с.
3. Андерсон Д.А. Дискретная математика и комбинаторика.- М.: Вильямс, 2003. -960 с.
4. Берлекэмп Э. Алгебраическая теория кодирования. -М.: Мир,1971.- 478 с.
5. Ваулин А.Е. Дискретная математика в задачах компьютерной безопасности. Ч 1- СПб.: ВКА им. А.Ф. Можайского, 2015. -219 с.
6. Ваулин А.Е. Дискретная математика в задачах компьютерной безопасности. Ч 2- СПб.: ВКА им. А.Ф. Можайского, 2017. -151 с.
7. Горенстейн Д. Конечные простые группы. Введение в их классификацию.-М.: Мир,1985.- 352 с.
7. Грэхем Р., Кнут Д., Пташник О. Конкретная математика.Основание информатики.-М.: Мир,1998.-703 с.
9. Елизаров В.П. Конечные кольца.- М.: Гелиос АРВ,2006. — 304 с.
Иванов Б.Н. Дискретная математика: алгоритмы и программы-М.: Лаб.Баз. Знаний., 2001. -280 с.
10. Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения-М.: Вузовская книга, 2000.-280 с.
11. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров.-М.: Наука, 1973.-832 с.
12. Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т.1 -М.: Мир,1988. — 430 с.
13. Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т.2 -М.: Мир,1988. — 392 с.
14. Ляпин Е.С., АйзенштатА.Я., Лесохин М.М., Упражнения по теории групп.- М.: Наука,1967.-264 с.
15. Муттер В.М. Основы помехоустойчивой телепередачи информации. -Л. Энергоатомиздат,1990.- 288 с.
16. Набебин А.А.Дискретная математика.- М.: Лаб.Баз. Знаний., 2001. -280 с.
17. Новиков Ф.А. Дискретная математика для программистов.- СПб.: Питер, 2000. -304 с.
18. Розенфельд Б.А. Многомерные пространства.-М.: Наука,1966.-648 с.
18. Холл М. Теория групп.-М.: Изд. ИЛ, 1962.- 468 с.
19. Шиханович Ю.А. Группы, кольца, решётки. — СПб.: Кирцидели,2006. — 368 с.
20. Шнеперман Л.Б. Курс алгебры и теории чисел в задачах и упражнениях: В 2-х ч Ч.2.-Мн.: Выш. шк., 1987. -256 с.
21. Шнеперман Л.Б. Сборник задач по алгебре и теории чисел.- Минск: Дизайн ПРО, 2000. -240 с.

Источник

Все курсы > Линейная алгебра > Занятие 2

Продолжим работать в том же ноутбуке⧉

Определение

С понятием вектора тесно связано понятие векторного или линейного пространства (vector space, linear space).

По большому счету, векторное пространство — это множество векторов, которые мы можем складывать (vector addition) и умножать на число или скаляр (scalar multiplication).

В частности, сложение и умножение на число двумерных (состоящих из двух компонентов) векторов дает нам двумерный вектор, трехмерных — трехмерный и так далее.

$$ begin{bmatrix} 3 \ 4 end{bmatrix} + 2 cdot begin{bmatrix} 1 \ 2 end{bmatrix} = begin{bmatrix} 5 \ 8 end{bmatrix} $$

При этом сложить, например, двумерный и трехмерный вектор нельзя

$$ begin{bmatrix} 3 \ 4 end{bmatrix} + begin{bmatrix} 4 \ 3 \ 3 end{bmatrix} = ? $$

Также нельзя сформировать векторное пространство из двумерных векторов, лежащих только в первой четверти координатной плоскости. Хотя для таких векторов будет задана операция сложения, при умножении на отрицательный скаляр мы можем выйти за пределы первой четверти.

Поэтому говорят, что векторное пространство должно быть замкнуто относительно операций сложения и умножения на скаляр (closed under vector addition and scalar multiplication).

Двумерное пространтсво вещественных чисел принято обозначать $R^2$, трехмерное $R^3$, n-мерное — $R^n$.

Отметим, что вектор $begin{bmatrix} 1 \ 2 \ 0 end{bmatrix}$ — это вектор в $R^3$ с нулевым третьим компонентом.

Линейная комбинация векторов

Любой вектор внутри одного пространства (например, $R^2$) можно представить как линейную комбинацию конечного числа векторов (linear combination of a finite set of vectors).

$$ 2 cdot begin{bmatrix} 1 \ 2 end{bmatrix} + 3 cdot begin{bmatrix} 2 \ 1 end{bmatrix} = begin{bmatrix} 8 \ 7 end{bmatrix} $$

Под линейной комбинацией, как вы видите, понимается опять же сложение векторов и их умножение на число.

Аксиомы векторных пространств

Операции в векторных пространствах должны отвечать следующим правилам:

$ mathbf u + (mathbf v + mathbf w) = (mathbf u + mathbf v) + mathbf w $
$ mathbf v + mathbf w = mathbf w + mathbf v $
Существует нулевой вектор $ mathbf 0 Rightarrow mathbf 0 + mathbf v = mathbf v, forall mathbf v $
Для каждого $ mathbf v $ существует $ -mathbf v Rightarrow mathbf v + (-mathbf v) $
$ a(b mathbf v) = (ab) mathbf v $
$ 1 mathbf v = mathbf v $
$ a(mathbf v + mathbf w) = a mathbf v + a mathbf w $
$ (a + b) mathbf v = a mathbf v + b mathbf v $

Этим правилам могут отвечать не только векторы действительных чисел в пространстве $R^n$ (Евклидово пространство), но и, в частности, векторы функций. В этом случае речь идет о функциональных пространствах (function spaces).

Видео про абстрактные векторные пространства⧉.

Примечание. Некоторые понятия, упомянутые в видео выше, в частности, линейные преобразования (linear transformations), ядро матрицы (null space) и собственные векторы и значения (eigenvectors and eigenvalues) будут рассмотрены на более поздних занятиях.

Серия видео про алгебраические структуры⧉.

Внутреннее произведение

Скалярное произведение (dot product) является частным случаем внутреннего произведения (inner product) для евклидового пространства.

Приведем простой пример того, почему скалярное произведение может не подойти для векторов, состоящих, например, из комплексных чисел $mathbb C$. Ранее мы сказали, что скалярное произведение вектора самого на себя есть квадрат длины этого вектора, т.е. $mathbf x^T mathbf x = || mathbf x ||^2 $, и нам бы хотелось, чтобы квадрат длины был положителен.

Для действительных векторов это условие выполняется всегда, так как мы возводим в квадрат каждый компонент (вещественное число) такого вектора. Теперь рассмотрим комплексный вектор

$$ mathbf z = begin{bmatrix} 1 \ i end{bmatrix} in mathbb C^2 $$

По правилам скалярного произведения квадрат его длины был бы равен

$$ mathbf z^T mathbf z = begin{bmatrix} 1 & i end{bmatrix} begin{bmatrix} 1 \ i end{bmatrix} = 1 cdot 1 + i cdot i = 1-1 = 0 $$

Для того чтобы квадрат ненулевого вектора не был равен нулю в векторных пространствах комплексных чисел скалярное (а точнее внутреннее) произведение задано как $overline{mathbf z}^T mathbf z$, где $overline{mathbf z}$ является комплексно сопряженным (complex conjugate) к $mathbf z$ вектором. Тогда,

$$ overline{mathbf z}^T mathbf z = begin{bmatrix} 1 & -i end{bmatrix} begin{bmatrix} 1 \ i end{bmatrix} = 1 cdot 1 + (-i) cdot i = 1+1 = 2 $$

Векторное подпространство

Определение

Подпространством (subspace) векторного пространства $K$ называется множество $S$ его элементов, само являющееся векторным пространством относительно введенных в $K$ операций сложения и умножения на число.

Другими словами, чтобы $S$ было подпространством $K$ для каждого $mathbf v, mathbf w in S, K$ и $a in mathbb{R}$ должно выполняться ${ mathbf v + mathbf w, a mathbf v } in S, K$.

Например, выше мы сказали, что векторы $R^2$ первой четверти координатной плоскости не могут образовывать векторное пространство, потому что мы не можем задать для них операцию умножения на число, результатом которой был бы вектор только в этой четверти.

При этом, если мы возьмем на пространстве $R^2$ подпространство всех векторов, лежащих на прямой линии и проходящих через начало координат, то такое подпространство будет отвечать аксиомам векторных пространств.

Примечание. $R^1$ нельзя назвать подпространством $R^2$, потому что у векторов $R^1$ только один компонент, а у векторов $R^2$, даже тех, которые лежат на одной линии, их два.

Пересечение подпространств

Если $S$ и $T$ — подпространства, то $S cap T$ тоже подпространство. Возьмем $mathbf v, mathbf w in S, T$. Тогда $mathbf v + mathbf w in S, T$ и $a mathbf v in S,T$, так как $S$ и $T$ отвечают свойствам подпространств.

Ортогональные подпространства

Подпространство $S$ будет ортогонально подпространству $T$, если каждый вектор в $S$ ортогонален каждому вектору в $T$.

$$ forall mathbf v in S perp forall mathbf w in T $$

Ортогональное дополнение

Если внутри некоторого пространства $K$ существует подпространство $S$, и внутри этого же пространства $K$ можно найти другое ортогональное ему подпространство $S^{perp}$, то такое подпространство называется ортогональным дополнением (orthogonal complement) подпространства $S$.

Более формально, пусть $S$ — подпространство $K$. Тогда ортогональным дополнением $S^{perp}$ будет множество всех векторов $mathbf w in K$, для которых скалярное произведение $mathbf w cdot mathbf v = 0$ для любого $mathbf v in S$.

$$ S^{perp} = { mathbf w in K hspace{5pt} | hspace{5pt} mathbf w cdot mathbf v = 0, hspace{5pt} forall mathbf v in S hspace{2pt} } $$

Покажем, что $S^{perp}$ также является подпространством. Возьмем два вектора $mathbf a, mathbf b in S^{perp} $. Для того чтобы $S^{perp}$ было подпространством, нам нужно продемонстрировать замкнутость относительно сложения и умножения на скаляр.

$$ mathbf a + mathbf b underset{mathord{?}}{in} S^{perp} $$

$$ c cdot mathbf a underset{mathord{?}}{in} S^{perp} $$

Начнем со сложения. По определению ортогонального дополнения

$$ mathbf a cdot mathbf v = 0, hspace{5pt} forall mathbf v in S $$

$$ mathbf b cdot mathbf v = 0, hspace{5pt} forall mathbf v in S $$

Тогда,

$$ (mathbf a + mathbf b) cdot mathbf v = mathbf a cdot mathbf v + mathbf b cdot mathbf v = mathbf 0 + mathbf 0 = mathbf 0 $$

Другими словами, мы показали, что сумма векторов принадлежащих $ S^{perp} $ также ортогонально вектору $mathbf v in S$, а значит принадлежит $ S^{perp} $, $ mathbf a + mathbf b in S^{perp} $. Перейдем к умножению на скаляр.

$$ c cdot mathbf a cdot mathbf v = c cdot ( mathbf a cdot mathbf v) = c cdot mathbf 0 = mathbf 0 $$

Это доказывает, что $ c cdot mathbf a in S^{perp} $.

Таким образом, ортогональное дополнение подпространства само является векторным подпространством.

Отметим, что нулевой вектор всегда принадлежит ортогональному дополнению, поскольку при $c = 0$

$$ c cdot mathbf a = 0 cdot mathbf a = mathbf 0 rightarrow mathbf 0 in S^{perp} $$

Обратите внимание, что нулевой вектор также присутствует в подпространстве $S$, $mathbf 0 in S$.

Более того, $S cap S^{perp} = { mathbf 0 } $. Это легко доказать. Возьмем некоторый вектор $mathbf x$, который одновременно принадлежит $ S $ и $ S^{perp} $, $mathbf x in S, S^{perp}$.

Тогда по определению ортогонального дополнения должно выполняться $mathbf x cdot mathbf x = 0 $. Такому условию отвечает только нулевой вектор.

Линейная независимость векторов

Когда один вектор можно выразить через умножение другого вектора на число говорят, что эти векторы линейно зависимы (linearly dependent). С двумя линейно независимыми (linearly independent) векторами $ mathbf v_1, mathbf v_2 $ такого сделать не получится.

$$ mathbf v_2 neq k mathbf v_1 $$

где k — некоторое число.

Рассмотрим пример трех векторов. Чтобы эти три вектора были линейно независимы, не должно быть возможности выразить третий вектор через линейные комбинации (сложение и умножение на скаляр) первых двух.

$$ mathbf v_3 neq k_1 mathbf v_1 + k_2 mathbf v_2 $$

Если так сделать нельзя, мы попадаем в трехмерное пространство, если можно — останемся на плоскости.

Линейная оболочка

Линейная оболочка (linear span) — это множество всех возможных линейных комбинаций с помощью данного набора векторов.

Если у нас два линейно независимых (двумерных) вектора, то оболочка — $R^2$ (плоскость), если три (трехмерных) вектора, но один из них линейно зависим, то по-прежнему $R^2$.

Оболочка — это ответ на вопрос, какие векторы можно построить с помощью сложения и умножения на скаляр $n$ n-мерных векторов. Линейно зависимый вектор находится внутри оболочки, создаваемой комбинациями других линейно независимых векторов.

Базис пространства

Имея два двумерных линейно независимых вектора (например, $begin{bmatrix} 1 \ 2 end{bmatrix}$ и $begin{bmatrix} 3 \ 1 end{bmatrix}$), мы можем представить любой другой вектор в пространстве $ R^2 $, сложив эти два вектора и умножив их на скаляр. Такие векторы называются базисом пространства (basis of a vector space) $ R^2 $, по сути его координатами.

В целом, базисом называется такое множество линейно независимых векторов внутри векторного пространства, с помощью которых можно выразить любой другой вектор этого пространства.

Базис можно представить как некоторую систему координат, которой пользуются все векторы данного пространства.

Повторим пример с единичными векторами $mathbf i$ и $mathbf j$.

i = np.array([1, 0])

j = np.array([0, 1])

ax = plt.axes()

plt.xlim([—0.07, 3])

plt.ylim([—0.07, 3])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

plt.show()

Приведенный выше базис называется стандартным (standard, natural basis). Это самый «экономный» или удобный способ представить все остальные векторы этого пространства.

При этом выбор такого базиса конечно условен, ничто не мешает мне перейти к другой системе координат, то есть другому базису.

Можно сказать, что координаты вектора имеют смысл только если мы знаем в какой системе координат (каком базисе) они выражены. При этом верно и то, что вектор существует в пространстве вне зависимости от системы координат или базиса.

Смена базиса

Предположим, что у нас есть два вектора исходного стандартного базиса $ mathbf g_1 $ и $ mathbf g_2 $ (на рисунке ниже изображены зеленым цветом). Кроме этого, у нас есть вектор $mathbf r$ (красный). Эти векторы имеют следующие координаты

$$ mathbf g_1 = begin{bmatrix} 1 \ 0 end{bmatrix}, mathbf g_2 = begin{bmatrix} 0 \ 1 end{bmatrix}, mathbf r_g = begin{bmatrix} 3 \ 4 end{bmatrix} $$

Если векторы нового базиса ортогональны (это важно), то мы можем выразить координаты вектора $mathbf r$ в новом базисе. Новым базисом будут следующие векторы $ mathbf b_1 $ и $ mathbf b_2 $ (черные):

$$ mathbf b_1 = begin{bmatrix} 2 \ 1 end{bmatrix}, mathbf b_2 = begin{bmatrix} -2 \ 4 end{bmatrix} $$

Посмотрим на эти векторы на графике.

g1 = np.array([1, 0])

g2 = np.array([0, 1])

r = np.array([3, 4])

b1 = np.array([2, 1])

b2 = np.array([—2, 4])

ax = plt.axes()

plt.xlim([—2.5, 4.5])

plt.ylim([—0.07, 4.5])

plt.grid()

ax.arrow(0, 0, g1[0], g1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, g2[0], g2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, r[0], r[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’)

ax.arrow(0, 0, b1[0], b1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’)

ax.arrow(0, 0, b2[0], b2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’)

plt.show()

Убедимся, что векторы нового базиса $ mathbf b_1 $ и $ mathbf b_2 $ перпендикулярны (ортогональны).

Найдем скалярные и векторные проекции красного вектора $ mathbf r $ на векторы $ mathbf b_1 $ и $ mathbf b_2 $.

scalar_proj_r_on_b1 = np.dot(r, b1) / np.linalg.norm(b1)

vector_proj_r_on_b1 = scalar_proj_r_on_b1 * (b1 / np.linalg.norm(b1))

scalar_proj_r_on_b1.round(1), vector_proj_r_on_b1

scalar_proj_r_on_b2 = np.dot(r, b2) / np.linalg.norm(b2) ** 2

vector_proj_r_on_b2 = scalar_proj_r_on_b2 * b2

scalar_proj_r_on_b2.round(1), vector_proj_r_on_b2

Посмотрим на векторные проекции.

plt.figure(figsize = (6, 6))

ax = plt.axes()

plt.xlim([—2, 4.5])

plt.ylim([—0.07, 4.5])

plt.grid()

ax.arrow(0, 0, r[0], r[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’)

ax.arrow(0, 0, vector_proj_r_on_b1[0], vector_proj_r_on_b1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’)

ax.arrow(0, 0, vector_proj_r_on_b2[0], vector_proj_r_on_b2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’)

plt.show()

В сумме векторные проекции должны дать вектор $ mathbf r_g $ в исходном базисе.

vector_proj_r_on_b1 + vector_proj_r_on_b2

В новом же базисе вектор $ mathbf r_b $ можно выразить, как скалярные проекции вектора $ mathbf r $ на векторы нового базиса $ mathbf b_1 $ и $ mathbf b_2 $.

np.array([scalar_proj_r_on_b1, scalar_proj_r_on_b2]).round(1)

Другими словами,

$$ mathbf r_b approx begin{bmatrix} 4,5 \ 2,2 end{bmatrix} $$

Ортонормированный базис

Если угол между векторами базиса равен 90 градусов, то такой базис называют ортогональным (orthogonal). Если одновременно это единичные (нормализованные) векторы, то такой базис называется ортонормированным (orthonormal).

Ортонормированный базис называют стандартным базисом пространства $R^n$.

$$ forall { mathbf q_1, …, mathbf q_k } in R^n $$

$$ mathbf q_i^T cdot mathbf q_j = begin{cases} 0, i not= j \ 1, i=j end{cases} $$

Хотя векторы базиса не обязательно должны быть ортогональными и иметь единичную норму, во многих случаях это удобно.

Видео про линейную оболочку⧉.

Подведем итог

Мы ввели понятие векторного пространства, подпространства, линейной комбинации векторов, понятия базиса, линейной независимости векторов и линейной оболочки.

Перейдем к изучению матриц и начнем этот путь с рассмотрения линейных преобразований.

Источник

Система векторов называется базисом множества , если:

Все векторы системы принадлежат множеству ;

Система векторов является линейно независимой системой;

Любой вектор из множества представим в виде линейной комбинации векторов этой системы, т. е. .

Если множество Совпадает со всем пространством , то базис является базисом всего линейного пространства.

Числа Называются координатами вектора В базисе , а выражение — разложением вектора По базису .

Теорема (о единственности разложения по данному базису).

Разложение любого вектора по базису является единственным.

Доказательство. Предположим, что для вектора Наряду с разложением имеется другое разложение . Вычитая одно разложение из другого, получим равенство .

Поскольку базисные векторы линейно независимы, то из полученного равенства следуют равенства , что и доказывает теорему.

Следствие. Любые два вектора равны тогда и только тогда, когда равны их координаты в каком – либо базисе.

Таким образом, при фиксированном базисе линейного пространства каждый вектор однозначно определяется своими координатами в этом базисе.

Теорема (о линейных свойствах координат векторов).

При сложении любых двух векторов их координаты в данном базисе складываются, а при умножении любого вектора на любое число координаты умножаются на это число.

Доказательство. Пусть любые два вектора Имеют в базисе разложения , . Из аксиом линейного пространства следует, что сумма векторов И произведение вектора на число представимы в виде , .

Отсюда и теоремы о единственности разложения векторов по данному базису следует истинность доказываемой теоремы.

Теорема о базисном миноре.

Базисные строки (столбцы) линейно независимы и образуют базис в системе всех строк (столбцов) произвольной матрицы размера .

Доказательство.

По определению базиса это означает, что любая строка или столбец матрицы могут быть представлены в виде линейной комбинации базисных строк или базисных столбцов, причем единственным образом. Все рассуждения достаточно провести для строк, так как, транспонировав исходную матрицу, мы получим доказательство для столбцов матрицы .

Линейную независимость базисных строк будем доказывать методом от обратного.

Пусть некоторые базисные строки линейно зависимы. Тогда одна из этих строк является линейной комбинацией остальных строк. Но тогда из свойств определителей следует, что базисный минор равен нулю. Базисный минор по определению не должен быть равен нулю. Таким образом, исходное предположение ложно и базисные строки линейно независимы.

Докажем теперь, что любая строка произвольной матрицы размера является линейной комбинацией базисных строк. Для удобства в обозначениях будем считать, что базисный минор стоит на пересечении первых строк и первых столбцов. Это предположение не ограничивает общности доказательства теоремы, так как всегда можно переставить базисные строки и столбцы таким образом, чтобы базисный минор находился в левом верхнем углу матрицы . При таких перестановках может измениться знак определителя, но он не может стать равным нулю, что изменило бы ранг матрицы.

Пусть – любое число от 1 до , а – любое число от 1 до . Убедимся в том, что любой определитель порядка :

Равен нулю. Если или , то указанный определитель будет равен нулю в силу того, что у него будет два одинаковых столбца или две одинаковые строки. Если оба числа и Строго больше , то любой указанный определитель будет иметь порядок , и равен нулю по определению базисного минора. Таким образом, при любых значениях и наш определитель всегда нулю. Разложим этот определитель по последнему столбцу:

Алгебраические дополнения к элементам последнего столбца с номером ,очевидно, не зависят от элементов с номерами, содержащими . Поэтому в крайней правой части нашего разложения они обозначены буквами , не включающими индекс . Значение всегда не равно нулю, так как оно с точностью до знака совпадает со значением базисного минора. Разделив последнее равенство на число , мы получим, что

Эти равенства справедливы для любых чисел и , и означают, что любая строка с номером Является линейной комбинацией первых базисных строк. Таким образом, теорема полностью доказана.

Из теоремы о базисном миноре вытекают два важных следствия.

1. Для любой матрицы число линейно независимых строк равно числу линейно независимых столбцов и равно рангу матрицы.

2. Определитель любого порядка равен нулю тогда и только тогда, когда его строки или его столбцы линейно зависимы.

Отметим, что по закону контрпозиции равносильное свойству 2 утверждение формулируется следующим образом: определитель отличен от нуля тогда и только тогда, когда его строки или его столбцы линейно независимы.

Доказательство.

Покажем достаточность условия второго следствия. Если строки матрицы линейно зависимы, то по свойству системы зависимых векторов одна из строк является линейной комбинацией остальных строк. Вычитая из этой строки указанную линейную комбинацию, мы, не изменяя величины определителя, получим матрицу, содержащую нулевую строку. Определитель такой матрицы всегда равен нулю, что и требовалось доказать.

Покажем, что условие линейной зависимости столбцов квадратной матрицы является необходимым для равенства нулю определителя матрицы. Если определитель порядка равен нулю, то его базисный минор имеет порядок, заведомо меньший . Но тогда хотя бы одна из строк является не базисной. По теореме о базисном миноре эта строка может быть представлена в виде линейной комбинации базисных строк, что и означает линейную зависимость всех строк исходной матрицы. Следствие полностью доказано.

< Предыдущая		Следующая >

Источник

3. Фундаментальная система решений

Векторное пространство: размерность и базис, разложение вектора по базису

Разложение вектора по базису

Связь между базисами

Алгоритм нахождения базиса системы векторов

Как найти базис системы векторов примеры. Как найти базис данной системы векторов

Понятие размерности векторного пространства и базиса.

Разложение вектора по базису векторного пространства.

Связь между базисами.

Определение линейной зависимости системы векторов

Определение линейной независимости системы векторов

Свойства систем векторов

Базис системы векторов

Алгоритм нахождения базиса системы векторов

Популярное

Свежие записи

Линейное векторное пространство

Размерность и базис векторного пространства

Выбор базиса. Ортонормированность

Норма и скалярное произведение векторов

Приведение произвольного базиса к ортонормированному виду

Подпространства векторных пространств

Заключение

Литература

Определение

Линейная комбинация векторов

Аксиомы векторных пространств

Внутреннее произведение

Векторное подпространство

Определение

Пересечение подпространств

Ортогональные подпространства

Ортогональное дополнение

Линейная независимость векторов

Линейная оболочка

Базис пространства

Смена базиса

Ортонормированный базис

Подведем итог