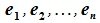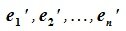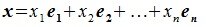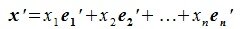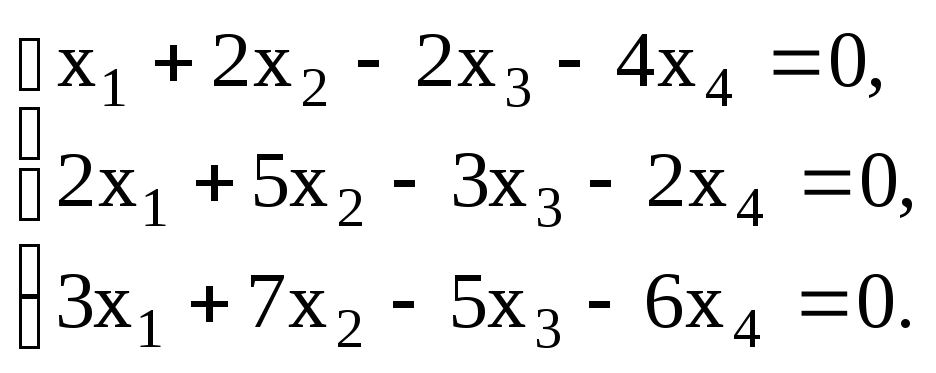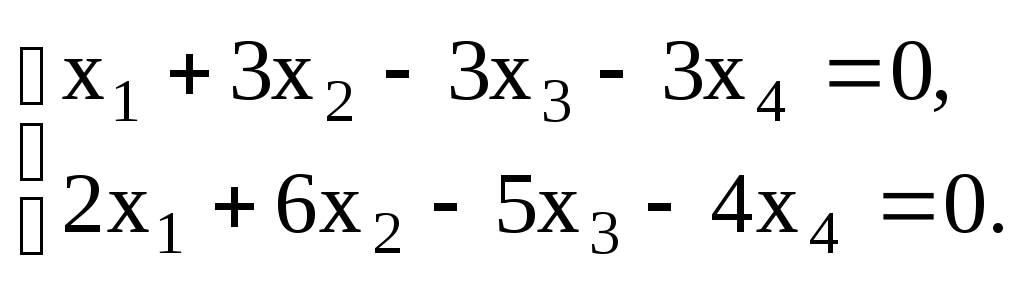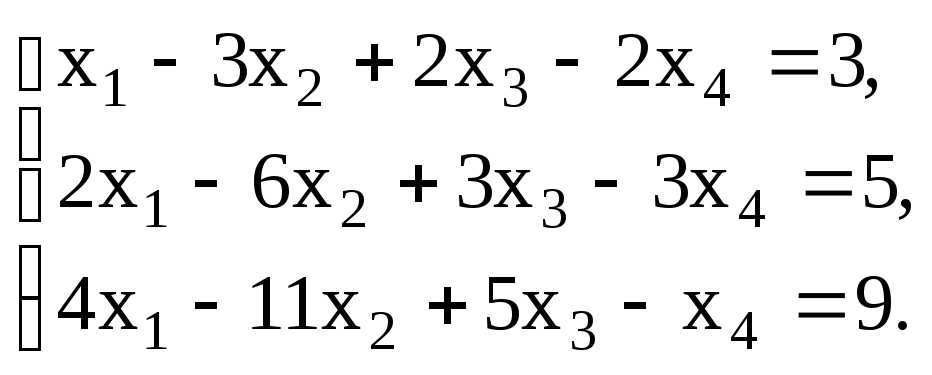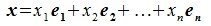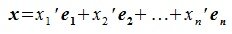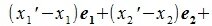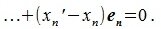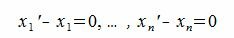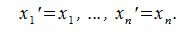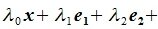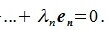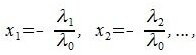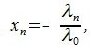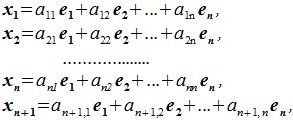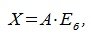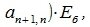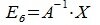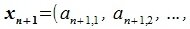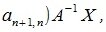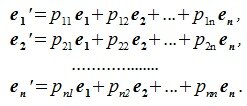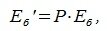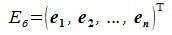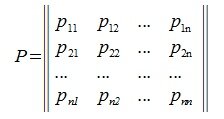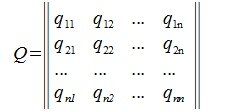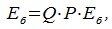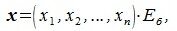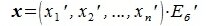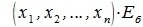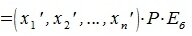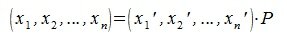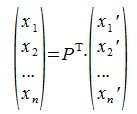Размерность и базис линейного пространства
Определения размерности и базиса
Линейное пространство называется n-мерным, если в нем существует система из
линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число
называется размерностью (числом измерений) линейного пространства
и обозначается
. Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве
найдется система, состоящая из
линейно независимых векторов, то такое пространство называют бесконечномерным (записывают:
). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.
Базисом n-мерного линейного пространства называется упорядоченная совокупность линейно независимых векторов (базисных векторов).
Теорема 8.1 о разложении вектора по базису. Если — базис n-мерного линейного пространства
, то любой вектор
может быть представлен в виде линейной комбинации базисных векторов:
(8.4)
и притом единственным образом, т.е. коэффициенты определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
Действительно, размерность пространства равна
. Система векторов
линейно независима (это базис). После присоединения к базису любого вектора
, получаем линейно зависимую систему
(так как это система состоит из
векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.
Следствие 1. Если — базис пространства
, то
, т.е. линейное пространство является линейной оболочкой базисных векторов.
В самом деле, для доказательства равенства двух множеств достаточно показать, что включения
и
выполняются одновременно. Действительно, с одной стороны, любая линейная комбинация векторов линейного пространства принадлежит самому линейному пространству, т.е.
. С другой стороны, любой вектор пространства по теореме 8.1 можно представить в виде линейной комбинации базисных векторов, т.е.
. Отсюда следует равенство рассматриваемых множеств.
Следствие 2. Если — линейно независимая система векторов линейного пространства
и любой вектор
может быть представлен в виде линейной комбинации (8.4):
, то пространство
имеет размерность
, а система
является его базисом.
В самом деле, в пространстве имеется система
линейно независимых векторов, а любая система
из большего количества векторов
линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы
. Значит,
и
— базис
.
Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему векторов n-мерного линейного пространства
можно дополнить до базиса пространства.
В самом деле, пусть — линейно независимая система векторов n-мерного пространства
. Рассмотрим линейную оболочку этих векторов:
. Любой вектор
образует с векторами
линейно зависимую систему
, так как вектор
линейно выражается через остальные. Поскольку в n-мерном пространстве существует
линейно независимых векторов, то
и существует вектор
, который не принадлежит
. Дополняя этим вектором линейно независимую систему
, получаем систему векторов
, которая также линейно независимая. Действительно, если бы она оказалась линейно зависимой, то из пункта 1 замечаний 8.3 следовало, что
, а это противоречит условию
. Итак, система векторов
линейно независимая. Значит, первоначальную систему векторов удалось дополнить одним вектором без нарушения линейной независимости. Продолжаем аналогично. Рассмотрим линейную оболочку этих векторов:
. Если
, то
— базис и теорема доказана. Если
, то дополняем систему
вектором
и т.д. Процесс дополнения обязательно закончится, так как пространство
конечномерное. В результате получим равенство
, из которого следует, что
— базис пространства
. Теорема доказана.
Замечания 8.4
1. Базис линейного пространства определяется неоднозначно. Например, если — базис пространства
, то система векторов
при любом
также является базисом
. Количество базисных векторов в разных базисах одного и того же конечномерного пространства, разумеется, одно и то же, так как это количество равно размерности пространства.
2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.
3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.
4. Если множество является линейной оболочкой
, то векторы
называют образующими множества
. Следствие 1 теоремы 8.1 в силу равенства
позволяет говорить, что базис — это минимальная система образующих линейного пространства
, так как нельзя уменьшить количество образующих (удалить хотя бы один вектор из набора
) без нарушения равенства
.
5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.
6. Следствие 2 теоремы 8.1 удобно применять для нахождения базиса и размерности линейного пространства. В некоторых учебниках оно берется за определение базиса, а именно: линейно независимая система векторов линейного пространства называется базисом, если любой вектор пространства линейно выражается через векторы
. Количество базисных векторов определяет размерность пространства. Разумеется, что эти определения эквивалентны приведенным выше.
Примеры базисов линейных пространств
Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.
1. Нулевое линейное пространство не содержит линейно независимых векторов. Поэтому размерность этого пространства полагают равной нулю:
. Это пространство не имеет базиса.
2. Пространства имеют размерности 1, 2, 3 соответственно. Действительно, любой ненулевой вектор пространства
, образует линейно независимую систему (см. пункт 1. замечаний 8.2), а любые два ненулевых век тора пространства
коллинеарны, т.е. линейно зависимы (см. пример 8.1). Следовательно,
, а базисом пространства
является любой ненулевой вектор. Аналогично доказывается, что
и
. Базисом пространства
служат любые два неколлинеарных вектора, взятые в определенном порядке (один из них считается первым базисным вектором, другой — вторым). Базисом пространства
являются любые три некомпланарных (не лежащих в одной или параллельных плоскостях) вектора, взятые в определенном порядке. Стандартным базисом в
является единичный вектор
на прямой. Стандартным базисом в
считается базис
, со стоящий из двух взаимно перпендикулярных единичных векторов плоскости. Стандартным базисом в пространстве
считается базис
, составленный из трех единичных попарно перпендикулярных векторов, образующих правую тройку.
3. Пространство содержит не более, чем
, линейно независимых векторов. В самом деле, возьмем
столбцов из
и составим из них матрицу размеров
. Если
, то столбцы линейно зависимы по теореме 3.4 о ранге матрицы. Следовательно,
. В пространстве
не трудно найти п линейно независимых столбцов. Например, столбцы единичной матрицы
линейно независимы. Следовательно, . Пространство
называется n-мерным вещественным арифметическим пространством. Указанный набор векторов считается стандартным базисом пространства
. Аналогично доказывается, что
, поэтому пространство
называют n-мерным комплексным арифметическим пространством.
4. Напомним, что любое решение однородной системы можно представить в виде
, где
, a
— фундаментальная система решений. Следовательно,
, т.е. базисом пространства
решений однородной системы служит ее фундаментальная система решений, а размерность пространства
, где
— количество неизвестных, а
— ранг матрицы системы.
5. В пространстве матриц размеров
можно выбрать 6 матриц:
которые линейно независимы. Действительно, их линейная комбинация
(8.5)
равна нулевой матрице только в тривиальном случае . Прочитав равенство (8.5) справа налево, заключаем, что любая матрица из
линейным образом выражается через выбранные 6 матриц, т.е.
. Следовательно,
, а матрицы
являются базисом (стандартным) этого пространства. Аналогично доказывается, что
.
6. Для любого натурального в пространстве
многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены
линейно независимы, так как их линейная комбинация
равна нулевому многочлену только в тривиальном случае
. Поскольку эта система многочленов линейно независима при любом натуральном л, пространство
бесконечномерное. Аналогично делаем вывод о бесконечной размерности пространства
многочленов с действительными коэффициентами. Пространство
многочленов степени не выше, чем
, конечномерное. Действительно, векторы
образуют базис (стандартный) это го пространства, так как они линейно независимы и любой многочлен из
можно представить в виде линейной комбинации этих векторов:
. Следовательно,
.
7. Пространство непрерывных функций является бесконечно мерным. Действительно, для любого натурального
многочлены
, рассматриваемые как непрерывные функции, образуют линейно независимые системы (см. предыдущий пример).
В пространстве тригонометрических двучленов (частоты
) с действительными коэффициентами базис образуют одночлены
. Они линейно независимы, так как тождественное равенство
возможно только в тривиальном случае
. Любая функция вида
линейно выражается через базисные:
.
8. Пространство действительных функций, определенных на множестве
, в зависимости от области определения
может быть конечномерным или бесконечномерным. Если
— конечное множество, то пространство
конечномерное (например,
). Если
— бесконечное множество, то пространство
бесконечномерное (например, пространство
последовательностей).
9. В пространстве любое положительное число
, не равное единице, может служить базисом. Возьмем, например, число
. Любое положительное число
можно выразить через
, т.е. представить в виде
, где
. Следовательно, размерность этого пространства равна 1, а число
является базисом.
10. Пусть — базис вещественного линейного пространства
. Определим на
линейные скалярные функции
, положив:
При этом, в силу линейности функции , для произвольного вектора
получаем
.
Итак, определены элементов (ковекторов)
сопряженного пространства
. Докажем, что
— базис
.
Во-первых, покажем, что система линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов
и приравняем ее нулевой функции
Подставляя в это равенство , получаем
. Следовательно, система элементов
пространства
линейно независима, так как равенство
возможно только в тривиальном случае.
Во-вторых, докажем, что любую линейную функцию можно представить в виде линейной комбинации ковекторов
. Действительно, для любого вектора
в силу линейности функции
получаем:
т.е. функция представлена в виде линейной комбинации
функций
(числа
— коэффициенты линейной комбинации). Следовательно, система ковекторов
является базисом сопряженного пространства
и
(для конечномерного пространства
).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Линейной
комбинацией векторов
называется вектор
,
где λ1, … , λm– произвольные коэффициенты.
Система
векторов
называется
линейно зависимой, если существует ее
линейная комбинация, равная
,
в которой есть хотя бы один ненулевой
коэффициент.
Система
векторов
называется
линейно независимой, если в любой ее
линейной комбинации, равной
,
все коэффициенты нулевые.
Базисом
системы векторов
называется
ее непустая линейно независимая
подсистема, через которую можно выразить
любой вектор системы.
П р
и м е р 2. Найти базис системы векторов
=
(1, 2, 2, 4),
=
(2, 3, 5, 1),
=
(3, 4, 8, -2),
=
(2, 5, 0, 3) и выразить остальные векторы
через базис.
Р е
ш е н и е. Строим матрицу, в которой
координаты данных векторов располагаем
по столбцам. Приводим ее к ступенчатому
виду.
~
~
~
.
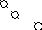
Базис
данной системы образуют векторы
,
,
,
которым соответствуют ведущие элементы
строк, выделенные кружками. Для выражения
вектора
решаем уравнениеx1
+x2
+
x4
=
.
Оно сводится к системе линейных
уравнений, матрица которой получается
из исходной перестановкой столбца,
соответствующего
,
на место столбца свободных членов.
Поэтому для решения системы используем
полученную матрицу в ступенчатом виде,
сделав в ней необходимые перестановки.
Последовательно
находим:
x4
= 0;
x2
= 2;
x1
+ 4 = 3, x1
= -1;
=
—
+2
.
Замечание
1. Если требуется выразить через базис
несколько векторов, то для каждого из
них строится соответствующая система
линейных уравнений. Эти системы будут
отличаться только столбцами свободных
членов. Поэтому для их решения можно
составить одну матрицу, в которой будет
несколько столбцов свободных членов.
При этом каждая система решается
независимо от остальных.
Замечание
2. Для выражения любого вектора достаточно
использовать только базисные векторы
системы, стоящие перед ним. При этом
нет необходимости переформировывать
матрицу, достаточно поставить вертикальную
черту в нужном месте.
У п
р а ж н е н и е 2. Найти базис системы
векторов и выразить остальные векторы
через базис:
а)
=
(1, 3, 2, 0),
=
(3, 4, 2, 1),
=
(1, -2, -2, 1),
=
(3, 5, 1, 2);
б)
=
(2, 1, 2, 3),
=
(1, 2, 2, 3),
=
(3, -1, 2, 2),
=
(4, -2, 2, 2);
в)
=
(1, 2, 3),
=
(2, 4, 3),
=
(3, 6, 6),
=
(4, -2, 1);
=
(2, -6, -2).
-
3. Фундаментальная система решений
Система
линейных уравнений называется однородной,
если все ее свободные члены равны нулю.
Фундаментальной
системой решений однородной системы
линейных уравнений называется базис
множества ее решений.
Пусть
дана неоднородная система линейных
уравнений. Однородной системой,
ассоциированной с данной, называется
система, полученная из данной заменой
всех свободных членов на нули.
Если
неоднородная система совместна и
неопределенна, то ее произвольное
решение имеет вид fн
+ 1fо1+
… + kfоk
,гдеfн– частное
решение неоднородной системы иfо1,
… , fоk–
фундаментальная система решений
ассоциированной однородной системы.
П р
и м е р 3. Найти частное решение
неоднородной системы из примера 1 и
фундаментальную систему решений
ассоциированной однородной системы.
Р е
ш е н и е. Запишем решение, полученное
в примере 1, в векторном виде и разложим
получившийся вектор в сумму по свободным
параметрам, имеющимся в нем, и фиксированным
числовым значениям:
= (x1,
x2,
x3,
x4) =
(–2a + 7b –
2, a, –2b + 1, b) = (–2a,
a, 0, 0) + (7b, 0, –2b, b) + +(–
2, 0, 1, 0) = a(-2, 1, 0, 0) + b(7, 0, -2, 1) + (–
2, 0, 1, 0).
Получаемfн=(–
2, 0, 1, 0), fо1= (-2, 1, 0,
0), fо2= (7, 0, -2, 1).
Замечание.
Аналогично решается задача нахождения
фундаментальной системы решений
однородной системы.
У п
р а ж н е н и е 3.1 Найти фундаментальную
систему решений однородной системы:
а)
б)
в)
2x1 –
x2
+3x3=
0.
У п
р а ж н е н и е 3.2. Найти частное решение
неоднородной системы и фундаментальную
систему решений ассоциированной
однородной системы:
а)
б)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Все курсы > Линейная алгебра > Занятие 2
Продолжим работать в том же ноутбуке⧉
Определение
С понятием вектора тесно связано понятие векторного или линейного пространства (vector space, linear space).
По большому счету, векторное пространство — это множество векторов, которые мы можем складывать (vector addition) и умножать на число или скаляр (scalar multiplication).
В частности, сложение и умножение на число двумерных (состоящих из двух компонентов) векторов дает нам двумерный вектор, трехмерных — трехмерный и так далее.
$$ begin{bmatrix} 3 \ 4 end{bmatrix} + 2 cdot begin{bmatrix} 1 \ 2 end{bmatrix} = begin{bmatrix} 5 \ 8 end{bmatrix} $$
При этом сложить, например, двумерный и трехмерный вектор нельзя
$$ begin{bmatrix} 3 \ 4 end{bmatrix} + begin{bmatrix} 4 \ 3 \ 3 end{bmatrix} = ? $$
Также нельзя сформировать векторное пространство из двумерных векторов, лежащих только в первой четверти координатной плоскости. Хотя для таких векторов будет задана операция сложения, при умножении на отрицательный скаляр мы можем выйти за пределы первой четверти.
Поэтому говорят, что векторное пространство должно быть замкнуто относительно операций сложения и умножения на скаляр (closed under vector addition and scalar multiplication).
Двумерное пространтсво вещественных чисел принято обозначать $R^2$, трехмерное $R^3$, n-мерное — $R^n$.
Отметим, что вектор $begin{bmatrix} 1 \ 2 \ 0 end{bmatrix}$ — это вектор в $R^3$ с нулевым третьим компонентом.
Линейная комбинация векторов
Любой вектор внутри одного пространства (например, $R^2$) можно представить как линейную комбинацию конечного числа векторов (linear combination of a finite set of vectors).
$$ 2 cdot begin{bmatrix} 1 \ 2 end{bmatrix} + 3 cdot begin{bmatrix} 2 \ 1 end{bmatrix} = begin{bmatrix} 8 \ 7 end{bmatrix} $$
Под линейной комбинацией, как вы видите, понимается опять же сложение векторов и их умножение на число.
Аксиомы векторных пространств
Операции в векторных пространствах должны отвечать следующим правилам:
- $ mathbf u + (mathbf v + mathbf w) = (mathbf u + mathbf v) + mathbf w $
- $ mathbf v + mathbf w = mathbf w + mathbf v $
- Существует нулевой вектор $ mathbf 0 Rightarrow mathbf 0 + mathbf v = mathbf v, forall mathbf v $
- Для каждого $ mathbf v $ существует $ -mathbf v Rightarrow mathbf v + (-mathbf v) $
- $ a(b mathbf v) = (ab) mathbf v $
- $ 1 mathbf v = mathbf v $
- $ a(mathbf v + mathbf w) = a mathbf v + a mathbf w $
- $ (a + b) mathbf v = a mathbf v + b mathbf v $
Этим правилам могут отвечать не только векторы действительных чисел в пространстве $R^n$ (Евклидово пространство), но и, в частности, векторы функций. В этом случае речь идет о функциональных пространствах (function spaces).
Видео про абстрактные векторные пространства⧉.
Примечание. Некоторые понятия, упомянутые в видео выше, в частности, линейные преобразования (linear transformations), ядро матрицы (null space) и собственные векторы и значения (eigenvectors and eigenvalues) будут рассмотрены на более поздних занятиях.
Серия видео про алгебраические структуры⧉.
Внутреннее произведение
Скалярное произведение (dot product) является частным случаем внутреннего произведения (inner product) для евклидового пространства.
Приведем простой пример того, почему скалярное произведение может не подойти для векторов, состоящих, например, из комплексных чисел $mathbb C$. Ранее мы сказали, что скалярное произведение вектора самого на себя есть квадрат длины этого вектора, т.е. $mathbf x^T mathbf x = || mathbf x ||^2 $, и нам бы хотелось, чтобы квадрат длины был положителен.
Для действительных векторов это условие выполняется всегда, так как мы возводим в квадрат каждый компонент (вещественное число) такого вектора. Теперь рассмотрим комплексный вектор
$$ mathbf z = begin{bmatrix} 1 \ i end{bmatrix} in mathbb C^2 $$
По правилам скалярного произведения квадрат его длины был бы равен
$$ mathbf z^T mathbf z = begin{bmatrix} 1 & i end{bmatrix} begin{bmatrix} 1 \ i end{bmatrix} = 1 cdot 1 + i cdot i = 1-1 = 0 $$
Для того чтобы квадрат ненулевого вектора не был равен нулю в векторных пространствах комплексных чисел скалярное (а точнее внутреннее) произведение задано как $overline{mathbf z}^T mathbf z$, где $overline{mathbf z}$ является комплексно сопряженным (complex conjugate) к $mathbf z$ вектором. Тогда,
$$ overline{mathbf z}^T mathbf z = begin{bmatrix} 1 & -i end{bmatrix} begin{bmatrix} 1 \ i end{bmatrix} = 1 cdot 1 + (-i) cdot i = 1+1 = 2 $$
Векторное подпространство
Определение
Подпространством (subspace) векторного пространства $K$ называется множество $S$ его элементов, само являющееся векторным пространством относительно введенных в $K$ операций сложения и умножения на число.
Другими словами, чтобы $S$ было подпространством $K$ для каждого $mathbf v, mathbf w in S, K$ и $a in mathbb{R}$ должно выполняться ${ mathbf v + mathbf w, a mathbf v } in S, K$.
Например, выше мы сказали, что векторы $R^2$ первой четверти координатной плоскости не могут образовывать векторное пространство, потому что мы не можем задать для них операцию умножения на число, результатом которой был бы вектор только в этой четверти.
При этом, если мы возьмем на пространстве $R^2$ подпространство всех векторов, лежащих на прямой линии и проходящих через начало координат, то такое подпространство будет отвечать аксиомам векторных пространств.
Примечание. $R^1$ нельзя назвать подпространством $R^2$, потому что у векторов $R^1$ только один компонент, а у векторов $R^2$, даже тех, которые лежат на одной линии, их два.
Пересечение подпространств
Если $S$ и $T$ — подпространства, то $S cap T$ тоже подпространство. Возьмем $mathbf v, mathbf w in S, T$. Тогда $mathbf v + mathbf w in S, T$ и $a mathbf v in S,T$, так как $S$ и $T$ отвечают свойствам подпространств.
Ортогональные подпространства
Подпространство $S$ будет ортогонально подпространству $T$, если каждый вектор в $S$ ортогонален каждому вектору в $T$.
$$ forall mathbf v in S perp forall mathbf w in T $$
Ортогональное дополнение
Если внутри некоторого пространства $K$ существует подпространство $S$, и внутри этого же пространства $K$ можно найти другое ортогональное ему подпространство $S^{perp}$, то такое подпространство называется ортогональным дополнением (orthogonal complement) подпространства $S$.
Более формально, пусть $S$ — подпространство $K$. Тогда ортогональным дополнением $S^{perp}$ будет множество всех векторов $mathbf w in K$, для которых скалярное произведение $mathbf w cdot mathbf v = 0$ для любого $mathbf v in S$.
$$ S^{perp} = { mathbf w in K hspace{5pt} | hspace{5pt} mathbf w cdot mathbf v = 0, hspace{5pt} forall mathbf v in S hspace{2pt} } $$
Покажем, что $S^{perp}$ также является подпространством. Возьмем два вектора $mathbf a, mathbf b in S^{perp} $. Для того чтобы $S^{perp}$ было подпространством, нам нужно продемонстрировать замкнутость относительно сложения и умножения на скаляр.
$$ mathbf a + mathbf b underset{mathord{?}}{in} S^{perp} $$
$$ c cdot mathbf a underset{mathord{?}}{in} S^{perp} $$
Начнем со сложения. По определению ортогонального дополнения
$$ mathbf a cdot mathbf v = 0, hspace{5pt} forall mathbf v in S $$
$$ mathbf b cdot mathbf v = 0, hspace{5pt} forall mathbf v in S $$
Тогда,
$$ (mathbf a + mathbf b) cdot mathbf v = mathbf a cdot mathbf v + mathbf b cdot mathbf v = mathbf 0 + mathbf 0 = mathbf 0 $$
Другими словами, мы показали, что сумма векторов принадлежащих $ S^{perp} $ также ортогонально вектору $mathbf v in S$, а значит принадлежит $ S^{perp} $, $ mathbf a + mathbf b in S^{perp} $. Перейдем к умножению на скаляр.
$$ c cdot mathbf a cdot mathbf v = c cdot ( mathbf a cdot mathbf v) = c cdot mathbf 0 = mathbf 0 $$
Это доказывает, что $ c cdot mathbf a in S^{perp} $.
Таким образом, ортогональное дополнение подпространства само является векторным подпространством.
Отметим, что нулевой вектор всегда принадлежит ортогональному дополнению, поскольку при $c = 0$
$$ c cdot mathbf a = 0 cdot mathbf a = mathbf 0 rightarrow mathbf 0 in S^{perp} $$
Обратите внимание, что нулевой вектор также присутствует в подпространстве $S$, $mathbf 0 in S$.
Более того, $S cap S^{perp} = { mathbf 0 } $. Это легко доказать. Возьмем некоторый вектор $mathbf x$, который одновременно принадлежит $ S $ и $ S^{perp} $, $mathbf x in S, S^{perp}$.
Тогда по определению ортогонального дополнения должно выполняться $mathbf x cdot mathbf x = 0 $. Такому условию отвечает только нулевой вектор.
Линейная независимость векторов
Когда один вектор можно выразить через умножение другого вектора на число говорят, что эти векторы линейно зависимы (linearly dependent). С двумя линейно независимыми (linearly independent) векторами $ mathbf v_1, mathbf v_2 $ такого сделать не получится.
$$ mathbf v_2 neq k mathbf v_1 $$
где k — некоторое число.
Рассмотрим пример трех векторов. Чтобы эти три вектора были линейно независимы, не должно быть возможности выразить третий вектор через линейные комбинации (сложение и умножение на скаляр) первых двух.
$$ mathbf v_3 neq k_1 mathbf v_1 + k_2 mathbf v_2 $$
Если так сделать нельзя, мы попадаем в трехмерное пространство, если можно — останемся на плоскости.
Линейная оболочка
Линейная оболочка (linear span) — это множество всех возможных линейных комбинаций с помощью данного набора векторов.
Если у нас два линейно независимых (двумерных) вектора, то оболочка — $R^2$ (плоскость), если три (трехмерных) вектора, но один из них линейно зависим, то по-прежнему $R^2$.
Оболочка — это ответ на вопрос, какие векторы можно построить с помощью сложения и умножения на скаляр $n$ n-мерных векторов. Линейно зависимый вектор находится внутри оболочки, создаваемой комбинациями других линейно независимых векторов.
Базис пространства
Имея два двумерных линейно независимых вектора (например, $begin{bmatrix} 1 \ 2 end{bmatrix}$ и $begin{bmatrix} 3 \ 1 end{bmatrix}$), мы можем представить любой другой вектор в пространстве $ R^2 $, сложив эти два вектора и умножив их на скаляр. Такие векторы называются базисом пространства (basis of a vector space) $ R^2 $, по сути его координатами.
В целом, базисом называется такое множество линейно независимых векторов внутри векторного пространства, с помощью которых можно выразить любой другой вектор этого пространства.
Базис можно представить как некоторую систему координат, которой пользуются все векторы данного пространства.
Повторим пример с единичными векторами $mathbf i$ и $mathbf j$.
|
i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([—0.07, 3]) plt.ylim([—0.07, 3]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
Приведенный выше базис называется стандартным (standard, natural basis). Это самый «экономный» или удобный способ представить все остальные векторы этого пространства.
При этом выбор такого базиса конечно условен, ничто не мешает мне перейти к другой системе координат, то есть другому базису.
Можно сказать, что координаты вектора имеют смысл только если мы знаем в какой системе координат (каком базисе) они выражены. При этом верно и то, что вектор существует в пространстве вне зависимости от системы координат или базиса.
Смена базиса
Предположим, что у нас есть два вектора исходного стандартного базиса $ mathbf g_1 $ и $ mathbf g_2 $ (на рисунке ниже изображены зеленым цветом). Кроме этого, у нас есть вектор $mathbf r$ (красный). Эти векторы имеют следующие координаты
$$ mathbf g_1 = begin{bmatrix} 1 \ 0 end{bmatrix}, mathbf g_2 = begin{bmatrix} 0 \ 1 end{bmatrix}, mathbf r_g = begin{bmatrix} 3 \ 4 end{bmatrix} $$
Если векторы нового базиса ортогональны (это важно), то мы можем выразить координаты вектора $mathbf r$ в новом базисе. Новым базисом будут следующие векторы $ mathbf b_1 $ и $ mathbf b_2 $ (черные):
$$ mathbf b_1 = begin{bmatrix} 2 \ 1 end{bmatrix}, mathbf b_2 = begin{bmatrix} -2 \ 4 end{bmatrix} $$
Посмотрим на эти векторы на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
g1 = np.array([1, 0]) g2 = np.array([0, 1]) r = np.array([3, 4]) b1 = np.array([2, 1]) b2 = np.array([—2, 4]) ax = plt.axes() plt.xlim([—2.5, 4.5]) plt.ylim([—0.07, 4.5]) plt.grid() ax.arrow(0, 0, g1[0], g1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, g2[0], g2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, r[0], r[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b1[0], b1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, b2[0], b2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) plt.show() |
Убедимся, что векторы нового базиса $ mathbf b_1 $ и $ mathbf b_2 $ перпендикулярны (ортогональны).
Найдем скалярные и векторные проекции красного вектора $ mathbf r $ на векторы $ mathbf b_1 $ и $ mathbf b_2 $.
|
scalar_proj_r_on_b1 = np.dot(r, b1) / np.linalg.norm(b1) vector_proj_r_on_b1 = scalar_proj_r_on_b1 * (b1 / np.linalg.norm(b1)) scalar_proj_r_on_b1.round(1), vector_proj_r_on_b1 |
|
scalar_proj_r_on_b2 = np.dot(r, b2) / np.linalg.norm(b2) ** 2 vector_proj_r_on_b2 = scalar_proj_r_on_b2 * b2 scalar_proj_r_on_b2.round(1), vector_proj_r_on_b2 |
Посмотрим на векторные проекции.
|
plt.figure(figsize = (6, 6)) ax = plt.axes() plt.xlim([—2, 4.5]) plt.ylim([—0.07, 4.5]) plt.grid() ax.arrow(0, 0, r[0], r[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, vector_proj_r_on_b1[0], vector_proj_r_on_b1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, vector_proj_r_on_b2[0], vector_proj_r_on_b2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) plt.show() |
В сумме векторные проекции должны дать вектор $ mathbf r_g $ в исходном базисе.
|
vector_proj_r_on_b1 + vector_proj_r_on_b2 |
В новом же базисе вектор $ mathbf r_b $ можно выразить, как скалярные проекции вектора $ mathbf r $ на векторы нового базиса $ mathbf b_1 $ и $ mathbf b_2 $.
|
np.array([scalar_proj_r_on_b1, scalar_proj_r_on_b2]).round(1) |
Другими словами,
$$ mathbf r_b approx begin{bmatrix} 4,5 \ 2,2 end{bmatrix} $$
Ортонормированный базис
Если угол между векторами базиса равен 90 градусов, то такой базис называют ортогональным (orthogonal). Если одновременно это единичные (нормализованные) векторы, то такой базис называется ортонормированным (orthonormal).
Ортонормированный базис называют стандартным базисом пространства $R^n$.
$$ forall { mathbf q_1, …, mathbf q_k } in R^n $$
$$ mathbf q_i^T cdot mathbf q_j = begin{cases} 0, i not= j \ 1, i=j end{cases} $$
Хотя векторы базиса не обязательно должны быть ортогональными и иметь единичную норму, во многих случаях это удобно.
Видео про линейную оболочку⧉.
Подведем итог
Мы ввели понятие векторного пространства, подпространства, линейной комбинации векторов, понятия базиса, линейной независимости векторов и линейной оболочки.
Перейдем к изучению матриц и начнем этот путь с рассмотрения линейных преобразований.
Базис векторов и линейные действия над векторами аналитическим путём (теория и решение задач)
Базис – это неопределённое количество векторов в векторном пространстве, и абсолютно любой из этих векторов может создавать линейную комбинацию.
Помощь в написании работы
Базис векторов
Система линейно независимых векторов пространства, за которыми можно разложить произвольный вектор – это и есть базис векторов или этого пространства.
Так, согласно доказательству (3), произвольные три некомпланарные векторы 
, 
, 
, образуют в трёхмерном пространстве базис, по которому, согласно формуле (2) можно единственным образом разложить произвольный вектор 
пространства. Векторы , , , которые образуют базис называются базисными.
Будем считать, что базисные векторы , , сведены к точке 
.
Числ 
, про которые упоминалось в разделах “линейно зависимая и линейно независимые системы векторов”, называют координатами вектора в заданном базисе, и пишут:
.
Аналогично, на плоскости базис образуют какие-то два неколлинеарные векторы, а любой некомпланарный с ними может быть разложен по этому базису.
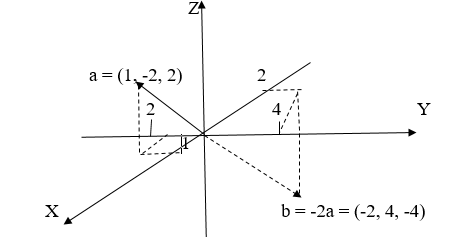
Базисным вектором на прямой линии может быть любой ненулевой вектор.Согласно свойствам линейных операций над векторами, следует, что при сложении и вычитании векторов в данном базисе прибавляются и отнимаются их соответствующие координаты, а при умножении вектора на число умножаются не это число координаты вектора, то есть:
.
.
.
.
.
.Векторы равны, когда у них одинаковые соответствующие координаты.
Линейные действия над векторами аналитическим путём
Если раньше линейные действия над векторами осуществлялись графически, то теперь эти операции можно выполнять аналитически, не пользуясь рисунком. Давайте вспомним и сформулируем линейные действия:
Чтобы прибавлять (отнимать) два вектора, необходимо прибавить (отнять) их соответствующие координаты, то есть: 
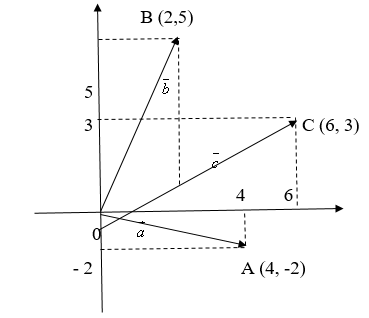
Приведём пример:
Найти сумму векторов 
и 
, заданных на плоскости 
.
Решение:
Согласно правилу 1 у нас получается:
= (6, 3).
Построим эти векторы: 
.
Рис. 3
Мы видим, что четырёхугольник OABC – параллелограмм. Координаты вектора 
мы сначала получили путём вычислений (аналитически), без помощи рисунка. Рисунок только подтверждает правило параллелограмма при прибавлении векторов, поэтому дальше рисунками будем пользоваться для наглядности.
Чтобы умножить вектор на число, необходимо каждую из его координат умножить на это число:
Дан вектор 
Найти 
Решение:
Согласна правилу 2 у нас получается:
Геометрическое изображение смотрите на рис. 4.
Рис. 4
Два вектора равны, если у них равны соответствующие координаты:
.
Теперь вы понимаете, как получить координаты вектора не только графическим путём, но и аналитическим. В дальнейшем у вас не возникнет сложностей по этому поводу.
Как найти базис вектора, пример
В некотором базисе заданы своими координатами векторы 
и 
Разложить вектор 
по базису, который образовался из векторов и 
Решение:
Разложение вектора по базису и 
имеет такой вид:
где числа 
и 
– неизвестные. Чтобы их найти, подставим в последнее равенство координаты векторов 
и , а тогда воспользуемся свойствами 1 и 2:
Согласно свойству 3 про равенство векторов, получим систему уравнений:
Первое равенство умножаем на 1, а второе на (- 2) и в итоге у на получается:
.
Значит, ответ у нас выходит: 
Линейное (векторное) пространство
1. Понятие линейного пространства
Определение 1.1. Множество R элементов x, y, z, … любой природы называется линейным (или векторным) пространством, если выполнены следующие три требования:
- Существует правило, посредством которого любым двум элементам x и y множества R ставится в соответствие третий элемент z этого множества, называемый суммой элементов x и y и обозначаемый z=x+y.
- Существует правило, посредством которого любому элементу x множества R и любому вещественному числу α ставится в соответствие элемент w этого множества, называемый произведением элемента x на число α и обозначаемый w=αx или w=xα.
- Представленные два правила подчинены следующим восьми аксиомам:
- x+y=y+x (переместительное свойство суммы);
- (x+y)+z=x+(y+z) (сочетательное свойство суммы);
- существует нулевой элемент 0 такой, что x+0=x для любого элемента x.
- для любого элемента x существует противоположный элемент элемент x’ такой, что x+x’=0;
- 1·x=x для любого x;
- λ(μx)=(λμ)x (сочетательное свойство относительно числового множителя);
- (λ+μ)x=λx+μx (распределительное свойство относительно числовых множителей);
- λ(x+y)=λx+λy (распределительное свойство относительно суммы элементов).
Элементы линейного (векторного) пространства называются векторами.
2. Базис линейного пространства
Определение 2.1. Совокупность линейно независимых элементов 
пространства R называется базисом этого пространства, если для каждого элемента x пространства R существуют вещественные чиcла 
такие, что выполнено равенство
|
|
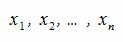
(2.1) |
Равенство (2.1) называется разложением элемента x по базису а числа называются координатами элемента x (относительно базиса ).
Докажем, что любой элемент x линейного пространства R может быть разложен по базису единственным образом.
Пусть существует и другое разложение x:
|
|
(2.2) |
Вычитая (2.1) из (2.2) имеем:
|
|
(2.3) |
Так как базисные элементы линейно независимы из соотношения (2.3) следует, что
или
Следовательно каждый элемент линейного пространства R может быть разложен по базису единственным образом.
Теорема 2.2. При сложении произвольных двух элементов линейного пространства R их координаты (относительно любого базиса пространства R) складываются, а при умножении любого элемента x на любое число α все координаты x умножаются на α.
Доказательство следует из аксиом 1-8 определения 1.1.
3. Размерность линейного пространства
Рассмотрим произвольное вещественное пространство R.
Определение 3.1. Линейное пространство R называется n-мерным, если в нем существует n линейно независимых элементов, а любые (n+1) элементов уже являются линейно зависимыми. При этом число n называется размерностью пространства R.
Размерность пространства обозначают символом dim.
Определение 3.2. Линейное пространство R называется бесконечномерным, если в нем существует любое число линейно независимых элементов.
Теорема 3.3. Пусть R является линейным пространствам размерности n (dim R=n). Тогда любые n линейно независимых элементов этого пространства образуют его базис.
Доказательство. Так как R является n -мерным пространством, то из определения 2.1 следует, что в нем существует совокупность из n линейно независимых элементов . Пусть x — любой элемент из R. Тогда согласно определению 3.1 
линейно зависимы, т.е. существуют числа 
(не все равные нулю) такие, что справедливо равенство
|
|
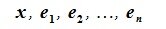
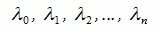
(3.1) |
Заметим, что λ0≠0 т.к. в противном случае из равенства (3.1) следовала, что элементы линейно зависимы. Поделив равенство (3.1) на λ0 и положив
|
|
(3.2) |
получим
|
|
(3.3) |
Из равенства (3.3) следует, что любой вектор из пространства R может быть разложен по элементам и, следовательно, они образуют базис пространства R. ■
Теорема 3.4. Пусть линейное пространство R имеет базис, состоящий из n элементов. Тогда размерность R равна n (dim R=n).
Доказательство. Пусть множество n элементов является базисом пространства R. Достаточно доказать, что любые n+1 элементы 
этого пространства линейно зависимы. Разложив эти элементы по базису, получим:
|
|
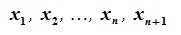
(3.4) |
где a11, a12,…, an+1,n вещественные числа.
Пусть элементы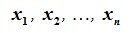 
линейно независимы. Перепишем (3.4) в матричном виде:
|
|
(3.5) |
|
|
(3.6) |
где
,
n×n-матрицы(элементы 
здесь являются вектор-строками),
|
|
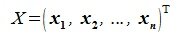
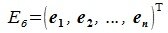
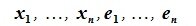
(3.7) |
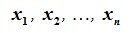
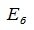
Так как линейно независимы, матрица A имеет обратную матрицу A-1. Решив матричное уравнение (3.5) относительно 
получим :
|
|
(3.8) |
Подставляя (3.8) в (3.6), получим:
|
|
(3.9) |
Как видно из уравнения (3.9)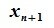 
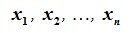
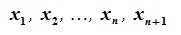
можно представить линейной комбинацией векторов . Следовательно векторы линейно зависимы. ■
4. Замена базиса и преобразование координат
Пусть в пространстве R наряду с исходным базисом имеется другой базис 
. Векторы этого базиса можно выразить через линейную комбинацию векторов исходного базиса следующим образом:
|
|
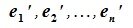
(4.1) |
или
|
|
(4.2) |
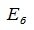
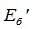
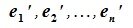
где и 
матрицы составленные из векторов строк и соответственно (
), а матрица P имеет вид:
|
|
(4.3) |
Матрица P называется матрицей замены базиса на .
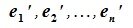
В свою очередь, векторы исходного базиса выражаются через векторы нового следующим соотношением:
|
|
(4.4) |
где
|
|
(4.5) |
Подставляя (4.2) в (4.4) имеем:
|
|
(4.6) |
Из (4.6) следует, что QP=E, где E-единичная матрица, а матрицы Q и P взаимно обратные матрицы.
Рассмотрим как изменяются координаты векторов при замене базиса.
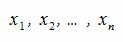
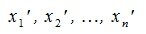
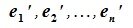
Пусть вектор x имеет координаты в базисе и координаты 
в базисе , тогда
|
|
(4.7) |
или
|
|
(4.8) |
Из (4.8) и из (4.2) имеем:
|
|
(4.9) |
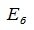
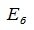
Так как квадратная матрица полного ранга, она имеет обратную матрицу. Умножив левые и правые части уравнения (4.9) на обратную к матрицу получим:
или
|
|
(4.10) |
Матрица PT называется матрицей преобразования координат. Она транспонирована с матрицей замены базиса. Обратная матрица (PT)-1 дает выражения новых координат через старые.
Матрица, обратная к транспонированной для некоторой матрицы, называется контраградиентной с ней.
5. Изоморфизм линейных пространств
Определение 5.1. Два произвольных вещественных линейных пространства R и R’ называются изоморфными, если между элементами этих пространств можно установить взаимно однозначное соответствие так, что если x, y∈R отвечают x’, y’∊R’ соответственно, то элементу x+y∈R отвечает элемент x’+y’∈R’, а для любого вещественного α, элементу αx∈R отвечает элемент αx’∈R’.
Теорема 5.2. Если пространства R и R’ изоморфны, то они имеют одинаковую размерность.
Доказательство. Пусть линейные пространства R и R’ изоморфны, и пусть элементам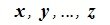 
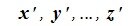
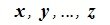
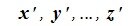
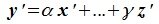
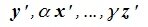
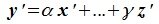
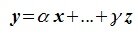
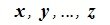
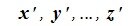
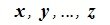
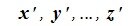
пространства R отвечают элементы 
пространства R’ соответственно. Допустим элементы линейно независимы. Покажем, что элементы 
также линейно независимы. Исходя из обратного предположения допустим, что элементы линейно зависимы. тогда один из них можно представить линейной комбинацией остальных элементов:
. Но элементам 
отвечают элементы 
y в пространстве R, а сумме отвечает сумма 
. Но последнее означает линейную зависимость элементов . Следовательно линейно независимы. Из линейной зависимости элементов следует линейная зависимость элементов . Следовательно максимальное количество линейно независимых векторов для пространств R и R’ одно и то же, т.е. эти пространства имеют одинаковую размерность. ■
Теорема 5.3. Любые два n-мерных вещественных линейных пространства R и R’ изоморфны.
Доказательство. Выберем базисы 
и 
для пространств R и R’ соответственно. Тогда каждый элемент пространства R можно представить линейной комбинацией базисных элементов: 
. Этому элементу в пространстве R’ поставим в соответствие элемент теми же координатами:
. В свою очередь элементу x’ пространства R’ соответствует элемент x пространства R . Отметим, что если элементам x и y пространства R отвечают элементы x’ и y’ пространства R’ соответственно , то исходя из теоремы 2.2 элементу x+y пространства R отвечает элемент x’+y’ пространства R’, а элементу αx отвечает элемент αx’. ■