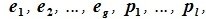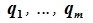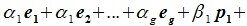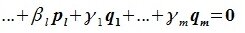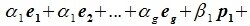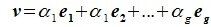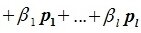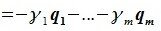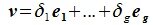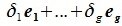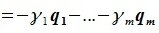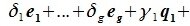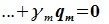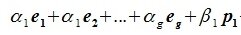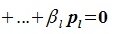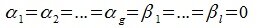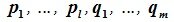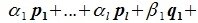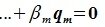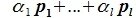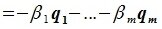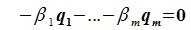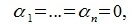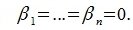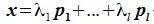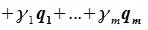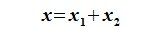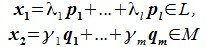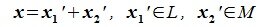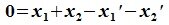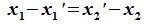Система
векторов
подпространства
называется базисом
этого подпространства, если выполняются
следующие два условия:
1)
система векторов
линейно независима;
2)
каждый вектор подпространства
разлагается по системе векторов
Введенное понятие
базиса подпространства позволяет
сформулировать необходимое и достаточное
условие принадлежности вектора
подпространству.
□ Теорема
1.3. Если
базис подпространства L,
то вектор
принадлежит подпространству L
тогда и только тогда, когда вектор
разлагается по системе векторов
,
т. е.
Необходимость
вытекает из определения базиса
подпространства.
Достаточность
следует из теоремы 1.2. ■
Следствие.
Два
подпространства
и
,
имеющие общий базис
,
совпадают.
Доказательство.
Используя теорему 1.3, имеем следующую
цепочку импликаций:
.
◆
Диагональная
система векторов является базисом
пространства
Действительно, она линейно независима
и каждый n-мерный
вектор разлагается по диагональной
системе. Ниже будет доказано, что
каждое ненулевое подпространство
обладает базисом.
□ Теорема
1.4. Каждую
линейно независимую систему векторов
из подпространства L
можно
дополнить до базиса этого подпространства.
Доказательство.
Если
не является базисом
,
то первое условие из определения базиса
выполняется и, значит, в подпространстве
найдется такой вектор
который не разлагается по векторам
.
Тогда
,
– линейно независимая система векторов
(следствие к теореме 2.10 [1]). Если эта
система все еще не является базисом L,
то в подпространстве
найдется такой вектор
,
что система векторов
линейно независима. В пространстве
каждая система из
вектора линейно зависима (§5, лемма
Штейница [1]). Следовательно, указанный
процесс расширения линейно независимой
системы векторов в подпространстве
остановится и будет сделано не более
шагов,
.
Так как процесс остановился, то каждый
вектор подпространства
разлагается по линейно независимой
системе векторов
и, значит, она является базисом
подпространства. ■
Следствие.
Каждое ненулевое подпространство L
пространства
обладает
базисом.
Доказательство.
Возьмем в подпространстве L
вектор
.
Система, состоящая из одного ненулевого
вектора, линейно независима, и ее можно
дополнить до базиса подпространства
L.
♦
Найдем
теперь базисы подпространств, приведенных
в § 2 [1]. Заметим, что нулевое подпространство
L
= {θ}
не содержит ни одного базиса.
Базисы пространства
□ Теорема
1.5. Линейно
независимая система n-мерных
векторов
является базисом пространства
тогда
и только тогда, когда число векторов в
этой системе равно n,
т. е.
Необходимость.
Дано, что
– базис
.
Рассмотрим систему векторов
(1)
где
–
диагональная система n-мерных
векторов. Так как
и
базисы пространства
,
то они являются базисами системы векторов
(1) и, в силу теоремы 2.15 [1],
.
Достаточность.
Покажем, что линейно независимая система
векторов
–
базис
.
Действительно, если присоединим к этой
системе произвольный n—мерный
вектор
,
то получим линейно зависимую систему
векторов
(§ 5, лемма Штейница [1]). Следовательно,
из теоремы 2.10 [1] вытекает, что вектор
разлагается по векторам
.
■
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подпространство линейного пространства
Определение и размерность подпространства
Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.
Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λ x∈L, где λ— любое вещественное число.
Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.
Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.
Сумма и пересечение подпространств
Пусть L и M — два подпространства пространства R.
Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).
Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).
Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:
dim L+dim M=dim(L+M)+dim(L∩M).
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис 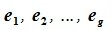
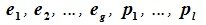
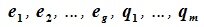
составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).
Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:
Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор
принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:
Из уравнений (6.4) и (6.5) имеем:
Но векторы 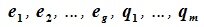
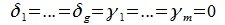
В силу линейной независимости базиса подпространства L имеем:
Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы
линейно независимы. Но любой вектор z из F (по определению суммы подпространств) можно представить суммой x+y, где x∈L, y∈M. В свою очередь x представляется линейной комбинацией векторов 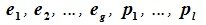
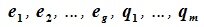
Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:
dim L+dim M−dim(L∩M)=dim(L+M). ■
Прямая сумма подпространств
Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈ L и z∈M.
Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.
Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.
Доказательство. Выберем некоторый базис 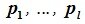
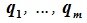
является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:
Так как левая часть (6.13) является вектором подпространства L, а правая часть — вектором подпространства M и L∩M= 0, то
Но векторы 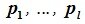
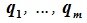
Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.
Пусть x∈R. Разложим его по базису (6.11):
Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x1∈L и x2∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:
Вычитая (6.19) из (6.17), получим
Так как 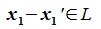
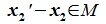
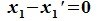
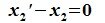
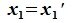
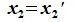
Способы описания подпространств линейного пространства
Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.
Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству . Чтобы установить изоморфизм , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства .
Первый (внутренний) способ. Пусть в пространстве заданы столбцы . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.
Рассматривая линейную оболочку столбцов как линейное подпространство , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства .
Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:
1) составить из данных столбцов матрицу размеров ;
2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;
3) определить размерность и базис подпространства
– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,
– столбцы матрицы , содержащие единичные элементы (в начале каждой «ступеньки»), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.
Таким образом, если подпространство задано своими образующими , то его размерность равна рангу системы столбцов , т.е. , а базисом служит максимальная линейно независимая подсистема образующих.
Второй (внешний) способ. Пусть подпространство задано как множество решений однородной системы уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств , где — множество решений i-го уравнения системы . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства , а базисом служит фундаментальная система решений однородной системы . Способы нахождения фундаментальной системы решений рассмотрены ранее.
Переход от одного способа описания подпространств к другому
Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов . Требуется составить такую однородную систему уравнений, множество решений которой совпадает с , т.е. . Для этого нужно выполнить следующие действия.
1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.
2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .
3. Из последних строк матрицы составить матрицу .
4. Записать искомую систему уравнений .
Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа , чтобы выполнялось равенство . Другими словами, при каких неоднородная система ( уравнений с неизвестными ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.
Пример 8.8. Подпространство задано линейной оболочкой столбцов . Составить систему уравнений, определяющую подпространство .
Решение. 1. Составляем матрицу и блочную матрицу:
2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):
Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу
3. Из последних строк матрицы составляем матрицу искомой системы.
4. Записываем систему уравнений Заданные в условии примера столбцы являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .
Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: . Требуется найти размерность и базис этого подпространства, т.е. представить его в виде линейной оболочки . Для этого нужно выполнить следующие действия.
1. Найти фундаментальную систему решений однородной системы . Искомая размерность .
2. Представить заданное пространство как линейную оболочку .
Первый пункт алгоритма удобно выполнять следующим образом:
– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;
– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу к виду , где — простейший вид матрицы ;
– из последних столбцов матрицы составить фундаментальную матрицу .
Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.
Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.
Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений
Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6
Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .
2. Столбцы являются искомым базисом, так как они линейно независимы и .
http://mathhelpplanet.com/static.php?p=sposoby-opisaniya-podprostranstv
Все курсы > Линейная алгебра > Занятие 2
Продолжим работать в том же ноутбуке⧉
Определение
С понятием вектора тесно связано понятие векторного или линейного пространства (vector space, linear space).
По большому счету, векторное пространство — это множество векторов, которые мы можем складывать (vector addition) и умножать на число или скаляр (scalar multiplication).
В частности, сложение и умножение на число двумерных (состоящих из двух компонентов) векторов дает нам двумерный вектор, трехмерных — трехмерный и так далее.
$$ begin{bmatrix} 3 \ 4 end{bmatrix} + 2 cdot begin{bmatrix} 1 \ 2 end{bmatrix} = begin{bmatrix} 5 \ 8 end{bmatrix} $$
При этом сложить, например, двумерный и трехмерный вектор нельзя
$$ begin{bmatrix} 3 \ 4 end{bmatrix} + begin{bmatrix} 4 \ 3 \ 3 end{bmatrix} = ? $$
Также нельзя сформировать векторное пространство из двумерных векторов, лежащих только в первой четверти координатной плоскости. Хотя для таких векторов будет задана операция сложения, при умножении на отрицательный скаляр мы можем выйти за пределы первой четверти.
Поэтому говорят, что векторное пространство должно быть замкнуто относительно операций сложения и умножения на скаляр (closed under vector addition and scalar multiplication).
Двумерное пространтсво вещественных чисел принято обозначать $R^2$, трехмерное $R^3$, n-мерное — $R^n$.
Отметим, что вектор $begin{bmatrix} 1 \ 2 \ 0 end{bmatrix}$ — это вектор в $R^3$ с нулевым третьим компонентом.
Линейная комбинация векторов
Любой вектор внутри одного пространства (например, $R^2$) можно представить как линейную комбинацию конечного числа векторов (linear combination of a finite set of vectors).
$$ 2 cdot begin{bmatrix} 1 \ 2 end{bmatrix} + 3 cdot begin{bmatrix} 2 \ 1 end{bmatrix} = begin{bmatrix} 8 \ 7 end{bmatrix} $$
Под линейной комбинацией, как вы видите, понимается опять же сложение векторов и их умножение на число.
Аксиомы векторных пространств
Операции в векторных пространствах должны отвечать следующим правилам:
- $ mathbf u + (mathbf v + mathbf w) = (mathbf u + mathbf v) + mathbf w $
- $ mathbf v + mathbf w = mathbf w + mathbf v $
- Существует нулевой вектор $ mathbf 0 Rightarrow mathbf 0 + mathbf v = mathbf v, forall mathbf v $
- Для каждого $ mathbf v $ существует $ -mathbf v Rightarrow mathbf v + (-mathbf v) $
- $ a(b mathbf v) = (ab) mathbf v $
- $ 1 mathbf v = mathbf v $
- $ a(mathbf v + mathbf w) = a mathbf v + a mathbf w $
- $ (a + b) mathbf v = a mathbf v + b mathbf v $
Этим правилам могут отвечать не только векторы действительных чисел в пространстве $R^n$ (Евклидово пространство), но и, в частности, векторы функций. В этом случае речь идет о функциональных пространствах (function spaces).
Видео про абстрактные векторные пространства⧉.
Примечание. Некоторые понятия, упомянутые в видео выше, в частности, линейные преобразования (linear transformations), ядро матрицы (null space) и собственные векторы и значения (eigenvectors and eigenvalues) будут рассмотрены на более поздних занятиях.
Серия видео про алгебраические структуры⧉.
Внутреннее произведение
Скалярное произведение (dot product) является частным случаем внутреннего произведения (inner product) для евклидового пространства.
Приведем простой пример того, почему скалярное произведение может не подойти для векторов, состоящих, например, из комплексных чисел $mathbb C$. Ранее мы сказали, что скалярное произведение вектора самого на себя есть квадрат длины этого вектора, т.е. $mathbf x^T mathbf x = || mathbf x ||^2 $, и нам бы хотелось, чтобы квадрат длины был положителен.
Для действительных векторов это условие выполняется всегда, так как мы возводим в квадрат каждый компонент (вещественное число) такого вектора. Теперь рассмотрим комплексный вектор
$$ mathbf z = begin{bmatrix} 1 \ i end{bmatrix} in mathbb C^2 $$
По правилам скалярного произведения квадрат его длины был бы равен
$$ mathbf z^T mathbf z = begin{bmatrix} 1 & i end{bmatrix} begin{bmatrix} 1 \ i end{bmatrix} = 1 cdot 1 + i cdot i = 1-1 = 0 $$
Для того чтобы квадрат ненулевого вектора не был равен нулю в векторных пространствах комплексных чисел скалярное (а точнее внутреннее) произведение задано как $overline{mathbf z}^T mathbf z$, где $overline{mathbf z}$ является комплексно сопряженным (complex conjugate) к $mathbf z$ вектором. Тогда,
$$ overline{mathbf z}^T mathbf z = begin{bmatrix} 1 & -i end{bmatrix} begin{bmatrix} 1 \ i end{bmatrix} = 1 cdot 1 + (-i) cdot i = 1+1 = 2 $$
Векторное подпространство
Определение
Подпространством (subspace) векторного пространства $K$ называется множество $S$ его элементов, само являющееся векторным пространством относительно введенных в $K$ операций сложения и умножения на число.
Другими словами, чтобы $S$ было подпространством $K$ для каждого $mathbf v, mathbf w in S, K$ и $a in mathbb{R}$ должно выполняться ${ mathbf v + mathbf w, a mathbf v } in S, K$.
Например, выше мы сказали, что векторы $R^2$ первой четверти координатной плоскости не могут образовывать векторное пространство, потому что мы не можем задать для них операцию умножения на число, результатом которой был бы вектор только в этой четверти.
При этом, если мы возьмем на пространстве $R^2$ подпространство всех векторов, лежащих на прямой линии и проходящих через начало координат, то такое подпространство будет отвечать аксиомам векторных пространств.
Примечание. $R^1$ нельзя назвать подпространством $R^2$, потому что у векторов $R^1$ только один компонент, а у векторов $R^2$, даже тех, которые лежат на одной линии, их два.
Пересечение подпространств
Если $S$ и $T$ — подпространства, то $S cap T$ тоже подпространство. Возьмем $mathbf v, mathbf w in S, T$. Тогда $mathbf v + mathbf w in S, T$ и $a mathbf v in S,T$, так как $S$ и $T$ отвечают свойствам подпространств.
Ортогональные подпространства
Подпространство $S$ будет ортогонально подпространству $T$, если каждый вектор в $S$ ортогонален каждому вектору в $T$.
$$ forall mathbf v in S perp forall mathbf w in T $$
Ортогональное дополнение
Если внутри некоторого пространства $K$ существует подпространство $S$, и внутри этого же пространства $K$ можно найти другое ортогональное ему подпространство $S^{perp}$, то такое подпространство называется ортогональным дополнением (orthogonal complement) подпространства $S$.
Более формально, пусть $S$ — подпространство $K$. Тогда ортогональным дополнением $S^{perp}$ будет множество всех векторов $mathbf w in K$, для которых скалярное произведение $mathbf w cdot mathbf v = 0$ для любого $mathbf v in S$.
$$ S^{perp} = { mathbf w in K hspace{5pt} | hspace{5pt} mathbf w cdot mathbf v = 0, hspace{5pt} forall mathbf v in S hspace{2pt} } $$
Покажем, что $S^{perp}$ также является подпространством. Возьмем два вектора $mathbf a, mathbf b in S^{perp} $. Для того чтобы $S^{perp}$ было подпространством, нам нужно продемонстрировать замкнутость относительно сложения и умножения на скаляр.
$$ mathbf a + mathbf b underset{mathord{?}}{in} S^{perp} $$
$$ c cdot mathbf a underset{mathord{?}}{in} S^{perp} $$
Начнем со сложения. По определению ортогонального дополнения
$$ mathbf a cdot mathbf v = 0, hspace{5pt} forall mathbf v in S $$
$$ mathbf b cdot mathbf v = 0, hspace{5pt} forall mathbf v in S $$
Тогда,
$$ (mathbf a + mathbf b) cdot mathbf v = mathbf a cdot mathbf v + mathbf b cdot mathbf v = mathbf 0 + mathbf 0 = mathbf 0 $$
Другими словами, мы показали, что сумма векторов принадлежащих $ S^{perp} $ также ортогонально вектору $mathbf v in S$, а значит принадлежит $ S^{perp} $, $ mathbf a + mathbf b in S^{perp} $. Перейдем к умножению на скаляр.
$$ c cdot mathbf a cdot mathbf v = c cdot ( mathbf a cdot mathbf v) = c cdot mathbf 0 = mathbf 0 $$
Это доказывает, что $ c cdot mathbf a in S^{perp} $.
Таким образом, ортогональное дополнение подпространства само является векторным подпространством.
Отметим, что нулевой вектор всегда принадлежит ортогональному дополнению, поскольку при $c = 0$
$$ c cdot mathbf a = 0 cdot mathbf a = mathbf 0 rightarrow mathbf 0 in S^{perp} $$
Обратите внимание, что нулевой вектор также присутствует в подпространстве $S$, $mathbf 0 in S$.
Более того, $S cap S^{perp} = { mathbf 0 } $. Это легко доказать. Возьмем некоторый вектор $mathbf x$, который одновременно принадлежит $ S $ и $ S^{perp} $, $mathbf x in S, S^{perp}$.
Тогда по определению ортогонального дополнения должно выполняться $mathbf x cdot mathbf x = 0 $. Такому условию отвечает только нулевой вектор.
Линейная независимость векторов
Когда один вектор можно выразить через умножение другого вектора на число говорят, что эти векторы линейно зависимы (linearly dependent). С двумя линейно независимыми (linearly independent) векторами $ mathbf v_1, mathbf v_2 $ такого сделать не получится.
$$ mathbf v_2 neq k mathbf v_1 $$
где k — некоторое число.
Рассмотрим пример трех векторов. Чтобы эти три вектора были линейно независимы, не должно быть возможности выразить третий вектор через линейные комбинации (сложение и умножение на скаляр) первых двух.
$$ mathbf v_3 neq k_1 mathbf v_1 + k_2 mathbf v_2 $$
Если так сделать нельзя, мы попадаем в трехмерное пространство, если можно — останемся на плоскости.
Линейная оболочка
Линейная оболочка (linear span) — это множество всех возможных линейных комбинаций с помощью данного набора векторов.
Если у нас два линейно независимых (двумерных) вектора, то оболочка — $R^2$ (плоскость), если три (трехмерных) вектора, но один из них линейно зависим, то по-прежнему $R^2$.
Оболочка — это ответ на вопрос, какие векторы можно построить с помощью сложения и умножения на скаляр $n$ n-мерных векторов. Линейно зависимый вектор находится внутри оболочки, создаваемой комбинациями других линейно независимых векторов.
Базис пространства
Имея два двумерных линейно независимых вектора (например, $begin{bmatrix} 1 \ 2 end{bmatrix}$ и $begin{bmatrix} 3 \ 1 end{bmatrix}$), мы можем представить любой другой вектор в пространстве $ R^2 $, сложив эти два вектора и умножив их на скаляр. Такие векторы называются базисом пространства (basis of a vector space) $ R^2 $, по сути его координатами.
В целом, базисом называется такое множество линейно независимых векторов внутри векторного пространства, с помощью которых можно выразить любой другой вектор этого пространства.
Базис можно представить как некоторую систему координат, которой пользуются все векторы данного пространства.
Повторим пример с единичными векторами $mathbf i$ и $mathbf j$.
|
i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([—0.07, 3]) plt.ylim([—0.07, 3]) plt.grid() ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
Приведенный выше базис называется стандартным (standard, natural basis). Это самый «экономный» или удобный способ представить все остальные векторы этого пространства.
При этом выбор такого базиса конечно условен, ничто не мешает мне перейти к другой системе координат, то есть другому базису.
Можно сказать, что координаты вектора имеют смысл только если мы знаем в какой системе координат (каком базисе) они выражены. При этом верно и то, что вектор существует в пространстве вне зависимости от системы координат или базиса.
Смена базиса
Предположим, что у нас есть два вектора исходного стандартного базиса $ mathbf g_1 $ и $ mathbf g_2 $ (на рисунке ниже изображены зеленым цветом). Кроме этого, у нас есть вектор $mathbf r$ (красный). Эти векторы имеют следующие координаты
$$ mathbf g_1 = begin{bmatrix} 1 \ 0 end{bmatrix}, mathbf g_2 = begin{bmatrix} 0 \ 1 end{bmatrix}, mathbf r_g = begin{bmatrix} 3 \ 4 end{bmatrix} $$
Если векторы нового базиса ортогональны (это важно), то мы можем выразить координаты вектора $mathbf r$ в новом базисе. Новым базисом будут следующие векторы $ mathbf b_1 $ и $ mathbf b_2 $ (черные):
$$ mathbf b_1 = begin{bmatrix} 2 \ 1 end{bmatrix}, mathbf b_2 = begin{bmatrix} -2 \ 4 end{bmatrix} $$
Посмотрим на эти векторы на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
g1 = np.array([1, 0]) g2 = np.array([0, 1]) r = np.array([3, 4]) b1 = np.array([2, 1]) b2 = np.array([—2, 4]) ax = plt.axes() plt.xlim([—2.5, 4.5]) plt.ylim([—0.07, 4.5]) plt.grid() ax.arrow(0, 0, g1[0], g1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, g2[0], g2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, r[0], r[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b1[0], b1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, b2[0], b2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) plt.show() |
Убедимся, что векторы нового базиса $ mathbf b_1 $ и $ mathbf b_2 $ перпендикулярны (ортогональны).
Найдем скалярные и векторные проекции красного вектора $ mathbf r $ на векторы $ mathbf b_1 $ и $ mathbf b_2 $.
|
scalar_proj_r_on_b1 = np.dot(r, b1) / np.linalg.norm(b1) vector_proj_r_on_b1 = scalar_proj_r_on_b1 * (b1 / np.linalg.norm(b1)) scalar_proj_r_on_b1.round(1), vector_proj_r_on_b1 |
|
scalar_proj_r_on_b2 = np.dot(r, b2) / np.linalg.norm(b2) ** 2 vector_proj_r_on_b2 = scalar_proj_r_on_b2 * b2 scalar_proj_r_on_b2.round(1), vector_proj_r_on_b2 |
Посмотрим на векторные проекции.
|
plt.figure(figsize = (6, 6)) ax = plt.axes() plt.xlim([—2, 4.5]) plt.ylim([—0.07, 4.5]) plt.grid() ax.arrow(0, 0, r[0], r[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, vector_proj_r_on_b1[0], vector_proj_r_on_b1[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, vector_proj_r_on_b2[0], vector_proj_r_on_b2[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) plt.show() |
В сумме векторные проекции должны дать вектор $ mathbf r_g $ в исходном базисе.
|
vector_proj_r_on_b1 + vector_proj_r_on_b2 |
В новом же базисе вектор $ mathbf r_b $ можно выразить, как скалярные проекции вектора $ mathbf r $ на векторы нового базиса $ mathbf b_1 $ и $ mathbf b_2 $.
|
np.array([scalar_proj_r_on_b1, scalar_proj_r_on_b2]).round(1) |
Другими словами,
$$ mathbf r_b approx begin{bmatrix} 4,5 \ 2,2 end{bmatrix} $$
Ортонормированный базис
Если угол между векторами базиса равен 90 градусов, то такой базис называют ортогональным (orthogonal). Если одновременно это единичные (нормализованные) векторы, то такой базис называется ортонормированным (orthonormal).
Ортонормированный базис называют стандартным базисом пространства $R^n$.
$$ forall { mathbf q_1, …, mathbf q_k } in R^n $$
$$ mathbf q_i^T cdot mathbf q_j = begin{cases} 0, i not= j \ 1, i=j end{cases} $$
Хотя векторы базиса не обязательно должны быть ортогональными и иметь единичную норму, во многих случаях это удобно.
Видео про линейную оболочку⧉.
Подведем итог
Мы ввели понятие векторного пространства, подпространства, линейной комбинации векторов, понятия базиса, линейной независимости векторов и линейной оболочки.
Перейдем к изучению матриц и начнем этот путь с рассмотрения линейных преобразований.