Как найти биссектрису угла фото

Была ли эта статья полезной?

Биссектриса угла

2 июня 2018

• Домашняя работа
• Ответы и решения

Сегодня будет очень лёгкий урок. Мы рассмотрим всего один объект — биссектрису угла — и докажем важнейшее её свойство, которое очень пригодится нам в будущем.

Только не надо расслабляться: иногда ученики, желающие получить высокий балл на том же ОГЭ или ЕГЭ, на первом занятии даже не могут точно сформулировать определение биссектрисы.

И вместо того, чтобы заниматься действительно интересными задачами, мы тратим время на такие простые вещи. Поэтому читайте, смотрите — и берите на вооружение.:)

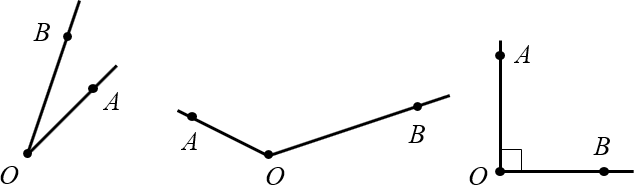
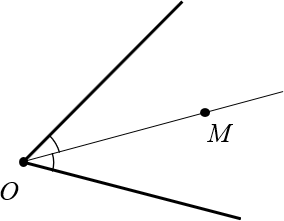
Для начала немного странный вопрос: что такое угол? Правильно: угол — это просто два луча, выходящих из одной точки. Например:

Как видно из картинки, углы могут быть острыми, тупыми, прямыми — это сейчас неважно. Часто для удобства на каждом луче отмечают дополнительную точку и говорят, мол, перед нами угол $AOB$ (записывается как $angle AOB$).

Капитан очевидность как бы намекает, что помимо лучей $OA$ и $OB$ из точки $O$ всегда можно провести ещё кучу лучей. Но среди них будет один особенный — его-то и называют биссектрисой.

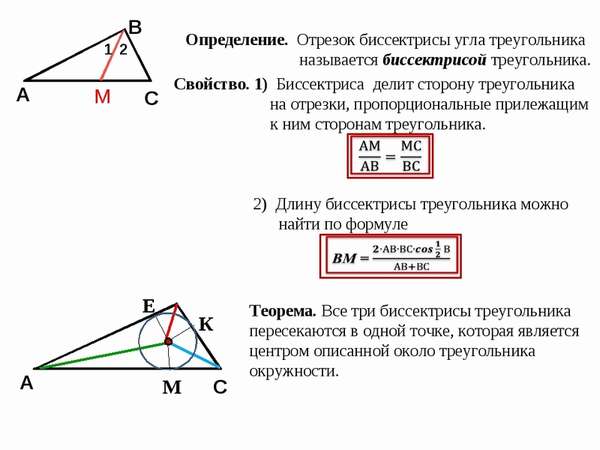
Определение. Биссектриса угла — это луч, который выходит из вершины этого угла и делит угол пополам.

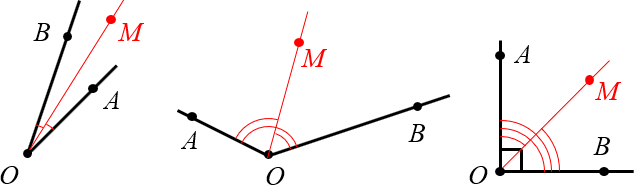
Для приведённых выше углов биссектрисы будут выглядеть так:

Поскольку на реальных чертежах далеко не всегда очевидно, что некий луч (в нашем случае это луч $OM$) разбивает исходный угол на два равных, в геометрии принято помечать равные углы одинаковым количеством дуг (у нас на чертеже это 1 дуга для острого угла, две — для тупого, три — для прямого).

Хорошо, с определением разобрались. Теперь нужно понять, какие свойства есть у биссектрисы.

Основное свойство биссектрисы угла

На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:

Теорема. Биссектриса угла — это геометрическое место точек, равноудалённых от сторон данного угла.

В переводе с математического на русский это означает сразу два факта:

1. Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
2. И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.

Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:

Определение. Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к этой прямой.

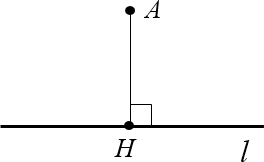
Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $Hin l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.

Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:

Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.

Как и обещал, разобьём доказательство на две части:

1. Расстояния от точки на биссектрисе до сторон угла одинаковы

Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:

Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.

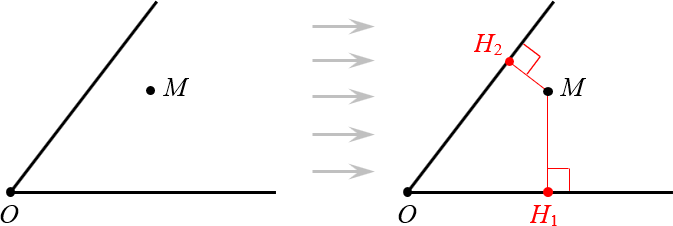
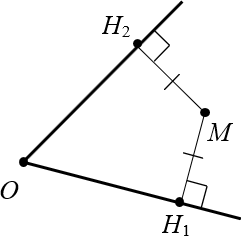
Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M{{H}_{1}}$ и $M{{H}_{2}}$:

Получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. У них общая гипотенуза $OM$ и равные углы:

1. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$ по условию (поскольку $OM$ — биссектриса);
2. $angle M{{H}_{1}}O=angle M{{H}_{2}}O=90{}^circ $ по построению;
3. $angle OM{{H}_{1}}=angle OM{{H}_{2}}=90{}^circ -angle MO{{H}_{1}}$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.

Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M{{H}_{2}}=M{{H}_{1}}$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Что и требовалось доказать.:)

2. Если расстояния равны, то точка лежит на биссектрисе

Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:

Докажем, что луч $OM$ — биссектриса, т.е. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$.

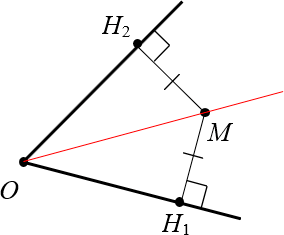
Доказательство. Для начала проведём этот самый луч $OM$, иначе доказывать будет нечего:

Снова получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. Очевидно, что они равны, поскольку:

1. Гипотенуза $OM$ — общая;
2. Катеты $M{{H}_{1}}=M{{H}_{2}}$ по условию (ведь точка $M$ равноудалена от сторон угла);
3. Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_{1}^{2}=OH_{2}^{2}=O{{M}^{2}}-MH_{1}^{2}$.

Следовательно, треугольники $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$ по трём сторонам. В частности, равны их углы: $angle MO{{H}_{1}}=angle MO{{H}_{2}}$. А это как раз и означает, что $OM$ — биссектриса.

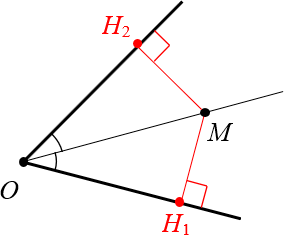
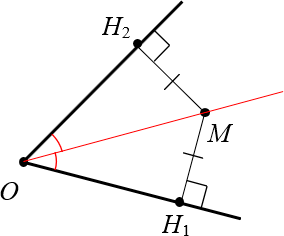
В заключение доказательства отметим красными дугами образовавшиеся равные углы:

Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)

Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.

Смотрите также:

1. Перпендикулярные прямые — определение и свойства
2. Что такое вертикальные углы
3. Следствия из теоремы Виета
4. Работа с формулами в задаче B12
5. Пример решения задачи 15
6. Задача B15: частный случай при работе с квадратичной функцией

Точка (C) называется основанием перпендикуляра.

  

Докажем, что от точки (A), не лежащей на прямой (BC), можно провести перпендикуляр к этой прямой.

Отложим от луча (BC) угол, равный данному, и совместим эти углы накладыванием (представим, что сложим лист бумаги с равными углами по стороне (BC)).

Это противоречие, что означает: через данную точку к прямой можно провести только один перпендикуляр.

У треугольника три стороны, следовательно, можно построить три медианы.

У треугольника три угла и три биссектрисы.

Поэтому для построения высоты необходимо выполнить следующие действия:
1) провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);
2) из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней (перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90°) — это и будет высота.

Так же как медианы и биссектрисы, треугольник имеет три высоты.

Но, как выше упомянуто, для некоторых видов треугольников построение высот и точки их пересечения отличаются. 

Если треугольник с прямым углом, то стороны, образующие прямой угол, можно назвать высотами, так как они перпендикулярны одна к другой. Точкой пересечения высот является общая вершина перпендикулярных сторон.

Если треугольник с тупым углом, то высоты, опущенные с вершин острых углов, выходят вне треугольника к продолжениям сторон. Прямые, на которых расположены высоты, пересекаются вне треугольника.

(AB = BC) — боковые стороны , (AC) — основание.

Первое и второе свойство можно доказать, если докажем равенство двух треугольников, которые образуются, если из угла напротив основания провести биссектрису (BD).

У равных треугольников равны все соответствующие элементы:

2. (AD = DC) — доказано, что биссектриса является медианой.

Можно очень легко самостоятельно доказать и третье, и четвёртое свойства.

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

• CD – внутренняя биссектриса ∠ACB;
• CE – биссектриса угла, смежного с ∠ACB;
• ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Вычисление биссектрисы треугольника с известными свойствами

Математика, как известно, царица наук. Неслучайно это выражение так любят учителя, особенно старой формации. Математика открывается исключительно тем, кто умеет, во-первых, логически мыслить, а во-вторых, тем, кто любит всегда добиваться ответа, оперируя изначальными условиями, не жульничая, а основывая решения на анализе, построение опять-таки логических связей. Эти качества, вынесенные со школьной скамьи, способны модулироваться и к взрослой серьезной жизни как в рабочих, так и в иных сложных моментах.

• Свойства
• Свойства в равнобедренных треугольниках
• Определение биссектрисы треугольника
• Определение длины
• Нахождение величины угла

Сегодня многие сталкиваются с проблемами при решении математических задач еще в начальной школе.

Однако даже те школьники, которые успешно осваивают первичную математическую программу, переходя на новый школьный и жизненный этап, где алгебра отделяется от геометрии, бывает, сталкиваются с серьезными затруднениями. Между тем, один раз выучив и, главное, поняв, как найти биссектрису треугольника, ученик навсегда запомнит эту формулу. Рассмотрим треугольник ABC с тремя проведенными биссектрисами. Как видно из рисунка, все они сходятся в одной точке.

Во-первых, определим, что биссектриса треугольника, и это одно из важнейших ее свойств, делит угол, из которого такой отрезок исходит, пополам. То есть в приведенном примере угол BAD равен углу DAC.

Это интересно: Как найти периметр треугольника.

Свойства

1. Биссектриса треугольника разделяет сторону, к которой она проведена на два отрезка, обладающие свойствами пропорциональности к сторонам, которые прилегают к каждому отрезку, соответственно. Таким образом, BD/CD = AB/AC.
2. Каждый треугольник способен обладать тремя данными отрезками. Другие значимые свойства касаются как частных, так и общих случаев конкретных рассматриваемых треугольников.

Свойства в равнобедренных треугольниках

1. Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
2. Разумеется, что будет верным и обратное свойство. То есть в равнобедренном треугольнике неизменно наблюдается равенство двух его биссектрис.
3. Из сказанного ранее вытекает вывод о том, что биссектриса, исходящая из противоположного основанию, служит также медианой и высотой.
4. Все биссектрисы равностороннего треугольника обладают равенством.

Определение биссектрисы треугольника

Допустим, что в рассматриваемом треугольнике ABC сторона AB = 5 cm, AC = 4 cm. Отрезок CD = 3 cm.

Определение длины

Определить длину можно по следующей формуле. AD = квадратный корень из разности произведения сторон и произведения пропорциональный отрезков.

Найдем длину стороны BC.

• Из свойств известно, что BD/CD = AB/AC.
• Значит, BD/CD = 5/4 = 1,25.
• BD/3 = 5/4.
• Значит, BD = 3,75.
• ABxAC = 54=20.
• CDxBD = 33,75 = 11,25.

Так, для того чтобы рассчитать длину, требуется вычесть из 20 11,25 и извлечь квадратный корень из получившегося 8,75. Результат с учетом тысячных долей получится 2,958.

Данный пример призван также эксплицитно указать на ситуацию, когда значения длины биссектрисы, как и все другие значения в математике, будут выражены не в натуральных числах, однако бояться этого не стоит.

Это интересно: в чем выражается эволюционный характер развития общества?

Нахождение величины угла

Для нахождения углов, образующихся биссектрисой, важно, прежде всего, помнить о сумме углов, неизменно составляющей 180 градусов. Предположим, что угол ABC равен 70 градусам, а угол BCA 50 градусам. Значит, путем простейших вычислений получим, что CAB = 180 (70+50) = 60 градусов.

Если использовать главное свойство, в соответствии с которым угол, из которого она исходит, делится пополам, получим равные значения углов BAD и CAD, каждый из которых будет 60/2 = 30 градусов.

Если требуется дополнительный наглядный пример, рассмотрим ситуацию, когда известен лишь угол BAD равный 28 градусам, а также угол ABC равный 70 градусам. Используя свойство биссектрисы, сразу найдем угол CAB путем умножения значения угла BAD на два. CAB = 282 =56. Значит, BAC = 180 (70+56) или 180 (70+282)= 180 126 = 54 градуса.

Специально не рассматривалась ситуация, когда данный отрезок выступает в качестве медианы или высоты, оставив для этого другие специализированные статьи.

Таким образом, мы рассмотрели такое понятие, как биссектриса треугольника, формула для нахождения длины и углов которой заложена и реализована в приведенных примерах, имеющих целью наглядно показать, каким образом можно использовать для решения тех или иных задач в геометрии. Также к данной теме относятся такие понятия, как медиана и высота. Если данный вопрос прояснился, следует обращаться к дальнейшему изучению различных других свойств треугольника, без которых немыслимо дальнейшее изучение геометрии.

Биссектриса треугольника

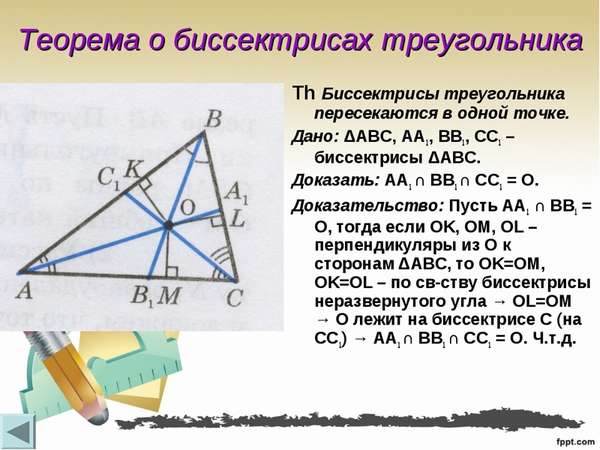
Длина биссектрисы треугольника

Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.

I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.

Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Дано:

СF — биссектриса ∠ABC

Доказательство:

Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.

Рассмотрим треугольники BCF и DCA.

∠BCF=∠DCA (по условию);

Значит, треугольники BFC и DCA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Что и требовалось доказать.

II. Через три стороны треугольника

Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле

По свойству биссектрисы треугольника:

Согласно утверждению 1,

Что и требовалось доказать.

III Через две стороны треугольника и угол между ними.

Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле

Биссектриса угла

Когда-то древние астрономы и математики открыли очень много интересных свойств биссектрисы угла треугольников и других фигур.

Эти знания сильно упростили жизнь людей. Стало легче строить, считать расстояния, даже корректировать стрельбу из пушек… 

Нам же знание этих свойств поможет решить некоторые задания ЕГЭ!

Приступим!

Биссектриса угла — коротко о главном

Биссектриса угла — это линия, делящая угол пополам.

Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.

Теорема 1. Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.

Теорема 2. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.

Теорема 3. Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

Теорема 4. Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

Теорема 5. Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.

Теорема 6. Отношение отрезков, на которые биссектриса делит противоположную сторону, такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.

( displaystyle frac{x}{y}=frac{a}{b})

А теперь подробнее…

Определение биссектрисы угла

Помнишь шутку: «Биссектриса это крыса, которая бегает по углам и делит угол пополам»?

Так вот, настоящее определение биссектрисы угла очень похоже на эту шутку — биссектриса действительно делит пополам угол (а не отрезок, например):

Биссектриса угла – это линия, делящая угол пополам.

Или еще вот такое определение биссектрисы:

Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.

А вот определение биссектрисы треугольника:

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.

Тебе встретилась в задаче биссектриса? Постарайся применить одно (а иногда можешь и несколько) из следующих потрясающих свойств.

Биссектриса равнобедренного треугольника

Биссектриса равнобедренного треугольника, проведенная к основанию, является и медианой, и высотой.

Но представляешь, это ещё не всё. Верна ещё и обратная теорема:

Если в треугольнике биссектриса, проведённая из какого-то угла, совпадает с медианой или с высотой, то этот треугольник равнобедренный.

Мы скоро докажем обе этих теоремы, а пока твердо запомни:

Биссектриса совпадает с высотой и медианой только в равнобедренном треугольнике!

Зачем же это твердо запоминать? Как это может помочь?

А вот представь, что у тебя задача:

Дано: ( AB=5,~angle ~ABD=~angle DBC,~AD=DC. )

Найти: ( displaystyle BC. )

Ты тут же соображаешь, (displaystyle BD ) биссектриса и, о чудо, она разделила сторону ( displaystyle AC ) пополам! (по условию…).

Если ты твердо помнишь, что так бывает только в равнобедренном треугольнике, то делаешь вывод, что AB=BC и значит, пишешь ответ: BC=5.

Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!

Доказательство теорем о совпадении биссектрисы с медианой и высотой в равнобедренном треугольнике

Почему в случае с равнобедренным треугольником биссектриса оказывается одновременно и медианой и высотой?

Как это доказать?

Смотри: у ( triangle ABL ) и ( triangle CBL ) равны стороны ( AB ) и ( BC ), сторона ( BL ) у них вообще общая и ( angle 1=angle 2). (( BL ) – биссектриса!)

И вот, получилось, что два треугольника имеют по две равные стороны и угол между ними.

Вспоминаем первый признак равенства треугольников (не помнишь, загляни в тему «Треугольник») и заключаем, что ( triangle ABL=triangle CBL ), а значит ( AL )= ( CL ) и ( angle 3=angle 4 ).

( AL ) = ( CL ) – это уже хорошо – значит, ( BL ) оказалась медианой.

А вот что такое ( angle 3=angle 4 )?

Готов дальше?

Будет немного сложнее, но пока мы отвлечемся на термины — повторим что такое биссектриса, медиана и высота, чем они похожи и чем они отличаются.

Биссектриса, медиана, высота — определения и отличия

Кстати, а помнишь ли ты все эти термины? Чем они отличаются друг от друга?

Если нет, не страшно. Сейчас разберемся.

• Основание равнобедренного треугольника – это та сторона, которая не равна никакой другой. Посмотри на рисунок, как ты думаешь, какая это сторона? Правильно – это сторона ( AC. );
• Медиана – это линия, проведенная из вершины треугольника и делящая противоположную сторону (это снова ( AC ) пополам. Заметь, мы не говорим: «Медиана равнобедренного треугольника». А знаешь почему? Потому что медиана, проведенная из вершины треугольника, делит противоположную сторону пополам в ЛЮБОМ треугольнике.;
• Высота – это линия, проведенная из вершины и перпендикулярная основанию. Ты заметил? Мы опять говорим о любом треугольнике, а не только о равнобедренном. Высота в ЛЮБОМ треугольнике всегда перпендикулярна основанию.

Чем биссектриса, медиана и высота похожи между собой?

Биссектриса, медиана и высота – все они «выходят» из вершины треугольника и упираются в противоположную сторону и «что-то делают» либо с углом из которого выходят, либо с противоположной стороной.

Чем биссектриса, медиана и высота отличаются между собой?

• Биссектриса делит угол, из которого выходит, пополам.
• Медиана делит противоположную сторону пополам.
• Высота всегда перпендикулярна противоположной стороне.

Вернемся к нашим баранам — к свойствам биссектрисы…

Угол между биссектрисами любого треугольника

B ( triangle ABC )проведем две биссектрисы ( AO )и ( OC ). 

Они пересеклись. Какой же угол получился у точки ( O )?

Давай его посчитаем. Ты помнишь, что сумма углов треугольника равна ( 180{}^circ ) ?

Применим этот потрясающий факт. С одной стороны, из ( triangle ABC ):

( angle A+angle B+angle C=180{}^circ ), то есть ( angle B=180{}^circ text{ }-text{ }left( angle A+angle C right) ).

Теперь посмотрим на ( triangle AOC ):

( angle 2+angle 6+angle 3=180{}^circ )

Но биссектрисы, биссектрисы же!

( angle 2=frac{angle A}{2}; angle 3=frac{angle C}{2} )

Значит ( left( triangle AOC right) )

( frac{angle A}{2}+angle 6+frac{angle C}{2}=180{}^circ ), то есть

( angle 6=180{}^circ -frac{angle A}{2}-frac{angle C}{2} );

(  angle 6=180{}^circ -frac{angle A+angle C}{2} )

Вспомним про ( triangle ABC : angle A+angle C=180{}^circ -angle B )

Значит, ( angle 6=180{}^circ -frac{180{}^circ -angle B}{2}=90+frac{angle B}{2} )

Теперь через буквы

(  angle AOC=90{}^circ +frac{angle B}{2} )

Не удивительно ли?

Получилось, что угол между биссектрисами двух углов зависит только от третьего угла!

Ну вот, две биссектрисы мы посмотрели. А что, если их три?! Пересекутся ли они все в одной точке?

Или будет так:

Биссектриса угла – геометрическое место точек, равноудалённых от сторон угла

Ленивые математики как обычно в двух строчках спрятали четыре.

Итак, что же значит, «Биссектриса – геометрическое место точек»? А это значит, что выполняются сразу два утверждения:

1. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
2. Если у какой-нибудь точки расстояния до сторон угла равны, то эта точка обязательно лежит на биссектрисе.

Видишь разницу между утверждениями 1 и 2? Если не очень, то вспомни Шляпника из «Алисы в стране чудес»: «Так ты еще чего доброго скажешь, будто «Я вижу то, что ем» и «Я ем то, что вижу», — одно и то же!»

Итак, нам нужно доказать утверждения 1 и 2, и тогда утверждение: «биссектриса – это геометрическое место точек, равноудаленных от сторон угла» будет доказано!

Почему же верно 1?

Возьмём любую точку на биссектрисе и назовём её ( displaystyle A. )

Опустим из этой точки перпендикуляры ( displaystyle ) AB и ( displaystyle AC ) на стороны угла.

А теперь… Приготовились вспоминать признаки равенства прямоугольных треугольников! Если ты их подзабыл, то загляни в раздел «Прямоугольный треугольник».

Итак… Два прямоугольных треугольника: ( displaystyle AOC ) и ( displaystyle AOB. ) У них:

Почему же верно 2?

Возьмем какую-то точку ( displaystyle E) внутри угла, для которой расстояние до сторон угла равны.

И соединим точки ( displaystyle E) и ( displaystyle O).

Теперь ( displaystyle triangle EOC=triangle EOB) как прямоугольные по катету и гипотенузе.

Значит, ( displaystyle angle 1=angle 2), то есть ( displaystyle E) лежит на биссектрисе!

Вот и всё!

Как же все это применить при решении задач? Вот например, в задачах часто бывает такая фраза: «Окружность касается сторон угла….». Ну, и найти нужно что-то.

То быстро соображаешь, что:

• Окружность касается сторон угла – значит, ( displaystyle AC=AB). (Правда, для этого нужно ещё знать, что радиус, проведённый в точку касания, перпендикулярен касательной)
• А раз ( displaystyle AC=AB), то ( displaystyle AO) – точно биссектриса!

И можно пользоваться равенством ( displaystyle angle 1=angle 2).

Три биссектрисы в треугольнике пересекаются в одной точке

Из свойства биссектрисы быть геометрическим местом точек, равноудаленных от сторон угла, вытекает следующее утверждение:

Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.

Как именно вытекает? А вот смотри: две-то биссектрисы точно пересекутся, правда?

А третья биссектриса могла бы пройти так:

Но на самом деле-то всё гораздо лучше!

Давай рассмотрим точку пересечения двух биссектрис. Назовём её ( displaystyle O).

Эта точка лежит на биссектрисе ( displaystyle AD). Что из этого следует? 

Правильно! ( displaystyle OK=OM)!

Точка ( displaystyle O) лежит ещё и на биссектрисе ( displaystyle CE), поэтому ( displaystyle OK=ON).

Что мы тут оба раза применяли?

Да пункт 1, конечно же! Если точка лежит на биссектрисе, то она одинаково удалена от сторон угла.

Вот и получилось ( displaystyle OK=OM) и ( displaystyle OK=ON).

Но посмотри внимательно на эти два равенства! Ведь из них следует, что:

Переходим к следующему свойству… Ух и много же свойств у биссектрисы, правда? И это здорово, потому что, чем больше свойств, тем больше инструментов для решения задач про биссектрису.

Биссектриса и параллельность, биссектрисы смежных углов

Тот факт, что биссектриса делит угол пополам, в каких-то случаях приводит к совершенно неожиданным результатам. Вот, например, некоторые из них:

Случай 1

Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

Здорово, правда? Давай поймём, почему так.

С одной стороны, ( displaystyle angle 1=angle 2) — мы же проводим биссектрису!

Но, с другой стороны, ( displaystyle angle 2=angle 3) — как накрест лежащие углы (вспоминаем тему «Параллельные прямые»).

И теперь выходит, что:

Случай 2

Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

Представь треугольник (или посмотри на картинку)

Давай продолжим сторону ( displaystyle AC) за точку ( A). Теперь получилось два угла ( displaystyle A):

• ( displaystyle angle 1) – внутренний угол ( displaystyle triangle ABC)
• ( displaystyle angle 2) – внешний угол ( displaystyle triangle ABC) – он же снаружи, верно?

Так вот, а теперь кому-то захотелось провести не одну, а сразу две биссектрисы: и для ( displaystyle angle 1), и для ( displaystyle angle 2). Что же получится?

А получится прямоугольный ( displaystyle triangle ALK)!

Удивительно, но это именно так.

Разбираемся.

Как ты думаешь, чему равна сумма ( displaystyle angle 1+angle 2+angle 3+angle 4)?

Случай 3

Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.

Видишь, что здесь все так же, как и для внутреннего и внешнего углов?

Или ещё раз подумаем, почему так получается?

Снова, как и для смежных углов,

( angle 1+angle 2+angle 3+angle 4=180{}^circ ) (как соответственные при параллельных основаниях).

И опять, ( angle 2+angle 3 ) составляют ровно половину от суммы ( angle 1+angle 2+angle 3+angle 4=180{}^circ )

Значит, ( angle 2+angle 3=90{}^circ ).

Вывод:

Биссектриса и противоположная сторона

Оказывается, биссектриса угла треугольника делит противоположную сторону не как-нибудь, а специальным и очень интересным образом:

( displaystyle frac{x}{y}=frac{a}{b})

То есть:

Отношение отрезков, на которые биссектриса поделила сторону ( displaystyle AB), такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.

Удивительный факт, не правда ли?

Сейчас мы этот факт докажем, но приготовься: будет немного сложнее, чем раньше.

Снова – выход в «космос» — дополнительное построение!

Проведём прямую ( BKparallel AC).

Зачем? Сейчас увидим.

Продолжим биссектрису ( displaystyle CD) до пересечения с прямой ( displaystyle BK).

Знакомая картинка? Да-да-да, точно так же, как в пункте 4, случай 1 – получается, что ( angle 1=angle 2) (( displaystyle CD) – биссектриса)

( angle 2=angle 3) — как накрест лежащие

( Rightarrow angle 1=angle 3) и ( BC=BL)

Значит, ( BL) – это тоже ( a).

А теперь посмотрим на треугольники ( ACD) и ( BLD).

Что про них можно сказать?

Теперь можешь смело использовать! Разберём ещё одно свойство биссектрис углов треугольника. Самое сложное кончилось – будет проще.

Угол между биссектрисами треугольника

Пусть ( AO) и ( CO) – биссектрисы. 

Найдём ( angle AOC) (помним, что сумма углов треугольника равна ( displaystyle 180{}^circ )).

( angle text{ }!!~!!text{ AOC}=180{}^circ -text{ }!!~!!text{ }frac{angle A}{2}-frac{angle text{C}}{2}=180{}^circ -frac{angle text{A}+angle text{C}}{2}=180{}^circ -frac{180{}^circ -angle text{B}}{2})

Получаем, что 

( angle text{ }!!~!!text{ AOC}=90{}^circ +frac{angle B}{2})

Это знание можно применить в тех задачах, где участвуют две биссектрисы и дан лишь угол ( B), а искомые величины выдерживаются через ( angle AOC) или, наоборот, ( angle AOC) дан, а нужно найти что-то с участием угла ( B).

Основные знания о биссектрисе закончились. Комбинируя эти факты, ты найдёшь ключ к любой задаче о биссектрисе!

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

• тысячи учеников, поступивших в лучшие ВУЗы страны
• автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж — c 2003 года;
• в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
• отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».