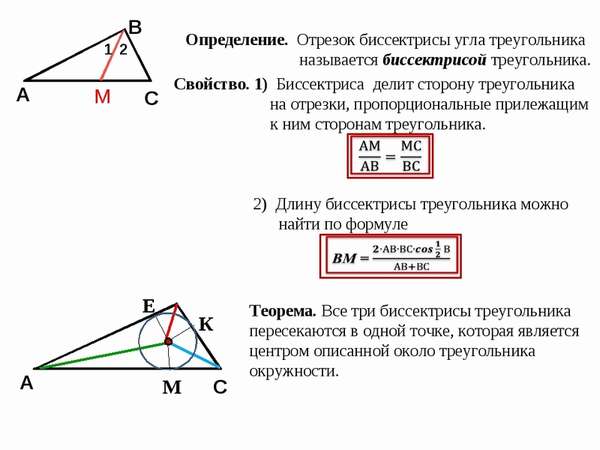
Какими свойствами обладает биссектриса равностороннего треугольника? Как, зная сторону правильного треугольника, найти его биссектрису? Чему равна длина биссектрисы через радиус вписанной и описанной окружностей?
Теорема 1
(свойство биссектрисы равностороннего треугольника)
В равностороннем треугольнике биссектриса, проведённая к любой стороне, является также его медианой и высотой.
Доказательство:

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.
Проведем биссектрису BF.
По свойству равнобедренного треугольника, BF является также его медианой и высотой.
Аналогично, треугольник ABC — равнобедренный с основанием BC, треугольник ABC — равнобедренный с основанием AB, а его биссектрисы AK и CD — еще и медианы и высоты.
Что и требовалось доказать.
Теорема 2
(свойство биссектрис равностороннего треугольника)
Все три биссектрисы равностороннего треугольника равны между собой.
Доказательство:

AK, BF CD — биссектрисы треугольника ABC.
В треугольниках ABF, BCD и CAK:
- AB=BC=CA (по условию)
- ∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника)
- ∠ABF=∠BCD=∠CAK (как как AK, BF CD — биссектрисы равных углов).
Значит, треугольники ABF, BCD и CAK равны (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AK=BF=CD.
Что и требовалось доказать.
Из теорем 1 и 2 следует, что в равностороннем треугольнике все биссектрисы, медианы и высоты равны между собой.
1) Найдём биссектрису равностороннего треугольника через его сторону.

BF — биссектриса, BF=l.
По свойствам равностороннего треугольника, BF — высота ∆ ABC, ∠A=60º.
Из прямоугольного треугольника ABF по определению синуса
Таким образом, формула биссектрисы равностороннего треугольника по его стороне:
2) Найдём биссектрису равностороннего треугольника через радиусы вписанной и описанной окружностей.
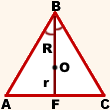
Центр вписанной окружности — точка пересечения биссектрис треугольника. Биссектрисы равностороннего треугольника также являются его медианами. Медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины.
Следовательно, точка O — центр вписанной и описанной окружностей, OF — радиус вписанной окружности, OF=r, BO — радиус описанной окружности, BO=R и BO:OF=2:1.
Отсюда,
Таким образом, длина биссектрисы через радиус вписанной окружности равна
через радиус описанной окружности —
Биссектриса равностороннего треугольника
Какими свойствами обладает биссектриса равностороннего треугольника? Как, зная сторону правильного треугольника, найти его биссектрису? Чему равна длина биссектрисы через радиус вписанной и описанной окружностей?
(свойство биссектрисы равностороннего треугольника)
В равностороннем треугольнике биссектриса, проведённая к любой стороне, является также его медианой и высотой.
Пусть в треугольнике ABC AB=BC=AC.
Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.
Проведем биссектрису BF.
По свойству равнобедренного треугольника, BF является также его медианой и высотой.
Аналогично, треугольник ABC — равнобедренный с основанием BC, треугольник ABC — равнобедренный с основанием AB, а его биссектрисы AK и CD — еще и медианы и высоты.
Что и требовалось доказать .
(свойство биссектрис равностороннего треугольника)
Все три биссектрисы равностороннего треугольника равны между собой.
Пусть в треугольнике ABC AB=BC=AC.
AK, BF CD — биссектрисы треугольника ABC.
В треугольниках ABF, BCD и CAK:
- AB=BC=CA (по условию)
- ∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника)
- ∠ABF=∠BCD=∠CAK (как как AK, BF CD — биссектрисы равных углов).
Значит, треугольники ABF, BCD и CAK равны (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AK=BF=CD.
Что и требовалось доказать .
Из теорем 1 и 2 следует, что в равностороннем треугольнике все биссектрисы, медианы и высоты равны между собой.
1) Найдём биссектрису равностороннего треугольника через его сторону.
В треугольнике ABC AB=BC=AC=a.
BF — биссектриса, BF=l.
По свойствам равностороннего треугольника, BF — высота ∆ ABC, ∠A=60º.
Из прямоугольного треугольника ABF по определению синуса
Таким образом, формула биссектрисы равностороннего треугольника по его стороне:
2) Найдём биссектрису равностороннего треугольника через радиусы вписанной и описанной окружностей.
В правильном треугольнике ABC центры вписанной и описанной окружностей совпадают.
Центр вписанной окружности — точка пересечения биссектрис треугольника. Биссектрисы равностороннего треугольника также являются его медианами. Медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины.
Следовательно, точка O — центр вписанной и описанной окружностей, OF — радиус вписанной окружности, OF=r, BO — радиус описанной окружности, BO=R и BO:OF=2:1.
Таким образом, длина биссектрисы через радиус вписанной окружности равна
Свойства биссектрисы равностороннего треугольника
В данной публикации мы рассмотрим основные свойства биссектрисы равностороннего треугольника, а также разберем пример решения задачи по данной теме.
Примечание: напомним, что равносторонним называется треугольник, в котором равны как все стороны, так и все углы.
Свойства биссектрисы равностороннего треугольника
Свойство 1
Любая биссектриса равностороннего треугольника одновременно является и медианой, и высотой, и серединным перпендикуляром.
BD – биссектриса угла ABC, которая также является:
- высотой, опущенной на сторону AC;
- медианой, делящей сторону AC на два равных отрезка (AD = DC);
Свойство 2
Все три биссектрисы равностороннего треугольника равны между собой.
Свойство 3
Биссектрисы равностороннего треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.
Свойство 4
Точка пересечения биссектрис равностороннего треугольника является центром описанной и вписанной окружностей.
- r – радиус вписанной окружности;
- R – радиус описанной окружности;
- R = 2r.
Свойство 5
Биссектриса равностороннего треугольника делит его на два равновеликих (равных по площади) прямоугольных треугольника.
Примечание: Три биссектрисы равностороннего треугольника делят его на 6 равновеликих прямоугольных треугольников.
Свойство 6
Любая из внешних биссектрис угла равностороннего треугольника параллельна стороне, лежащей напротив данного угла.
- AD и AE – внешние биссектрисы, параллельные BC;
- BK и BL – внешние биссектрисы, параллельные AC;
- CM и CN – внешние биссектрисы, параллельные AB.
Свойство 7
Длину биссектрисы ( la ) равностороннего треугольника можно выразить через его сторону.
где a – сторона треугольника.
Пример задачи
Радиус вписанной в равносторонний треугольник окружности равен 4 см. Найдите длину его стороны.
Решение
Согласно Свойствам 3 и 4, рассмотренным выше, радиус вписанной окружности составляет 1/3 часть от биссектрисы равностороннего треугольника. Следовательно, вся ее длина равняется 12 см (4 см ⋅ 3).
Теперь мы можем найти сторону треугольника с помощью формулы ниже (получена из Свойства 7):
Вычисление биссектрисы треугольника с известными свойствами

- Свойства
- Свойства в равнобедренных треугольниках
- Определение биссектрисы треугольника
- Определение длины
- Нахождение величины угла
Сегодня многие сталкиваются с проблемами при решении математических задач еще в начальной школе.
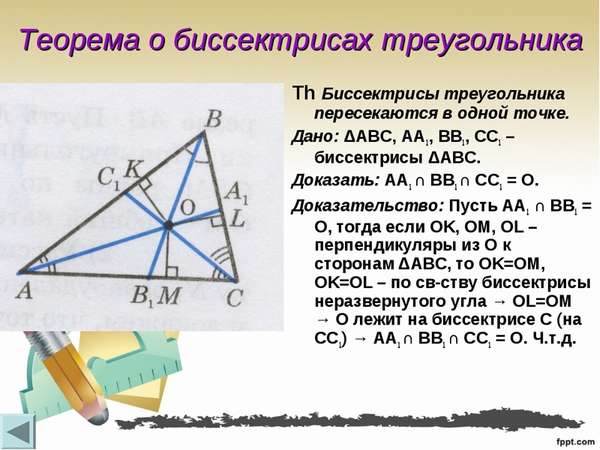
Однако даже те школьники, которые успешно осваивают первичную математическую программу, переходя на новый школьный и жизненный этап, где алгебра отделяется от геометрии, бывает, сталкиваются с серьезными затруднениями. Между тем, один раз выучив и, главное, поняв, как найти биссектрису треугольника, ученик навсегда запомнит эту формулу. Рассмотрим треугольник ABC с тремя проведенными биссектрисами. Как видно из рисунка, все они сходятся в одной точке.
Во-первых, определим, что биссектриса треугольника, и это одно из важнейших ее свойств, делит угол, из которого такой отрезок исходит, пополам. То есть в приведенном примере угол BAD равен углу DAC.
Это интересно: Как найти периметр треугольника.
Свойства
- Биссектриса треугольника разделяет сторону, к которой она проведена на два отрезка, обладающие свойствами пропорциональности к сторонам, которые прилегают к каждому отрезку, соответственно. Таким образом, BD/CD = AB/AC.
- Каждый треугольник способен обладать тремя данными отрезками. Другие значимые свойства касаются как частных, так и общих случаев конкретных рассматриваемых треугольников.
Свойства в равнобедренных треугольниках
Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
- Разумеется, что будет верным и обратное свойство. То есть в равнобедренном треугольнике неизменно наблюдается равенство двух его биссектрис.
- Из сказанного ранее вытекает вывод о том, что биссектриса, исходящая из противоположного основанию, служит также медианой и высотой.
- Все биссектрисы равностороннего треугольника обладают равенством.
Определение биссектрисы треугольника
Допустим, что в рассматриваемом треугольнике ABC сторона AB = 5 cm, AC = 4 cm. Отрезок CD = 3 cm.
Определение длины
Определить длину можно по следующей формуле. AD = квадратный корень из разности произведения сторон и произведения пропорциональный отрезков.

- Из свойств известно, что BD/CD = AB/AC.
- Значит, BD/CD = 5/4 = 1,25.
- BD/3 = 5/4.
- Значит, BD = 3,75.
- ABxAC = 54=20.
- CDxBD = 33,75 = 11,25.
Так, для того чтобы рассчитать длину, требуется вычесть из 20 11,25 и извлечь квадратный корень из получившегося 8,75. Результат с учетом тысячных долей получится 2,958.
Данный пример призван также эксплицитно указать на ситуацию, когда значения длины биссектрисы, как и все другие значения в математике, будут выражены не в натуральных числах, однако бояться этого не стоит.
Это интересно: в чем выражается эволюционный характер развития общества?
Нахождение величины угла
Для нахождения углов, образующихся биссектрисой, важно, прежде всего, помнить о сумме углов, неизменно составляющей 180 градусов. Предположим, что угол ABC равен 70 градусам, а угол BCA 50 градусам. Значит, путем простейших вычислений получим, что CAB = 180 (70+50) = 60 градусов.
Если использовать главное свойство, в соответствии с которым угол, из которого она исходит, делится пополам, получим равные значения углов BAD и CAD, каждый из которых будет 60/2 = 30 градусов.
Если требуется дополнительный наглядный пример, рассмотрим ситуацию, когда известен лишь угол BAD равный 28 градусам, а также угол ABC равный 70 градусам. Используя свойство биссектрисы, сразу найдем угол CAB путем умножения значения угла BAD на два. CAB = 282 =56. Значит, BAC = 180 (70+56) или 180 (70+282)= 180 126 = 54 градуса.
Специально не рассматривалась ситуация, когда данный отрезок выступает в качестве медианы или высоты, оставив для этого другие специализированные статьи.
Таким образом, мы рассмотрели такое понятие, как биссектриса треугольника, формула для нахождения длины и углов которой заложена и реализована в приведенных примерах, имеющих целью наглядно показать, каким образом можно использовать для решения тех или иных задач в геометрии. Также к данной теме относятся такие понятия, как медиана и высота. Если данный вопрос прояснился, следует обращаться к дальнейшему изучению различных других свойств треугольника, без которых немыслимо дальнейшее изучение геометрии.
Биссектриса треугольника 


http://tvercult.ru/nauka/vyichislenie-bissektrisyi-treugolnika-s-izvestnyimi-svoystvami
Найти медиану биссектрису высоту равностороннего треугольника
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Калькулятор — вычислить, найти медиану, биссектрису, высоту
- Подробности
-
Автор: Administrator
-
Опубликовано: 07 октября 2011
-
Обновлено: 13 августа 2021
В данной публикации мы рассмотрим основные свойства биссектрисы равностороннего треугольника, а также разберем пример решения задачи по данной теме.
Примечание: напомним, что равносторонним называется треугольник, в котором равны как все стороны, так и все углы.
-
Свойства биссектрисы равностороннего треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Свойство 7
- Пример задачи
Свойства биссектрисы равностороннего треугольника
Свойство 1
Любая биссектриса равностороннего треугольника одновременно является и медианой, и высотой, и серединным перпендикуляром.
BD – биссектриса угла ABC, которая также является:
- высотой, опущенной на сторону AC;
- медианой, делящей сторону AC на два равных отрезка (AD = DC);
- серединным перпендикуляром, проведенным к AC.
Свойство 2
Все три биссектрисы равностороннего треугольника равны между собой.
AF = BD = CE
Свойство 3
Биссектрисы равностороннего треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.
- AG = 2GF
- BG = 2GD
- CG = 2GE
Свойство 4
Точка пересечения биссектрис равностороннего треугольника является центром описанной и вписанной окружностей.
- r – радиус вписанной окружности;
- R – радиус описанной окружности;
- R = 2r.
Свойство 5
Биссектриса равностороннего треугольника делит его на два равновеликих (равных по площади) прямоугольных треугольника.
S1 = S2
Примечание: Три биссектрисы равностороннего треугольника делят его на 6 равновеликих прямоугольных треугольников.
Свойство 6
Любая из внешних биссектрис угла равностороннего треугольника параллельна стороне, лежащей напротив данного угла.
- AD и AE – внешние биссектрисы, параллельные BC;
- BK и BL – внешние биссектрисы, параллельные AC;
- CM и CN – внешние биссектрисы, параллельные AB.
Свойство 7
Длину биссектрисы (la) равностороннего треугольника можно выразить через его сторону.
где a – сторона треугольника.
Пример задачи
Радиус вписанной в равносторонний треугольник окружности равен 4 см. Найдите длину его стороны.
Решение
Согласно Свойствам 3 и 4, рассмотренным выше, радиус вписанной окружности составляет 1/3 часть от биссектрисы равностороннего треугольника. Следовательно, вся ее длина равняется 12 см (4 см ⋅ 3).
Теперь мы можем найти сторону треугольника с помощью формулы ниже (получена из Свойства 7):
Биссектриса треугольника – это отрезок, делящий любой угол треугольника на два равных угла. Для более
наглядного примера, если угол равняется 120°, то проведенная биссектриса создает уже пару углов по
60 °. В треугольнике можно провести максимум три биссектрисы, по одной из каждого угла. Точка
пересечения всех биссектрис является центром вписанной в треугольник окружности. Биссектриса
обладает особенными свойствами для некоторых видов треугольников, так, например, проведенная из
вершины равнобедренного треугольника будет являться одновременно и высотой, и медианой.
- Длина биссектрисы в треугольнике через две стороны и угол
между ними - Длина биссектрисы в треугольнике через все стороны
- Длина биссектрисы в треугольнике через две стороны и
отрезки - Длина биссектрисы в прямоугольном треугольнике через
катеты - Длина биссектрисы в прямоугольном треугольнике через
гипотенузу и угол - Длина биссектрисы из острого угла в прямоугольном
треугольнике через катет и угол - Длина биссектрисы из острого угла в прямоугольном
треугольнике через катет и гипотенузу - Длина биссектрисы в равнобедренном треугольнике через
боковую сторону и угол при основании - Длина биссектрисы в равнобедренном треугольнике через
основание и угол при основании - Длина биссектрисы в равнобедренном треугольнике через
боковую сторону и угол между боковыми сторонами - Длина биссектрисы в равнобедренном треугольнике через
основание и боковую сторону - Длина биссектрисы в равностороннем треугольнике через
сторону
Через две стороны и угол между ними
Нам дан некий треугольник, известно значение двух сторон и угла между ними. Нам нужно найти
биссектрису. Задача кажется невыполнимой, если не знать формулы:
L = (2bc · cos (α/2)) / b + c
где «L» это непосредственно длина, а «b» и «с» — стороны треугольника, «α» — угол между
ними.
Цифр после
запятой:
Результат в:
В нашем случае биссектриса равняется среднему двух сторон и угла, лежащего между ними.
Пример. Дан треугольник ABC. Известно, что стороны b = 6 см, а сторона c = 9 см.
Угол между двумя сторонами равен 65°. Нам нужно найти биссектрису. Подставив в формулу данные
значения, мы получаем ответ – биссектриса треугольника АВС равна 6 см. Решение легкое, ведь вам
нужно прибегнуть к обычному применению выведенной формулы. 2 × 6 × 9 × cos(65 ÷ 2) / 9 + 6 = 6 см.
Через две стороны и отрезки
Если вам известно 2 стороны треугольника и дано несколько отрезков на стороне, то вам нужно
руководствоваться следующей формулой:
L = √(b * c — a1 * a2)
где b, c — стороны, a1, a2 — длины отрезков, образованных на стороне.
Цифр после
запятой:
Результат в:
Пример. Есть треугольник АВС, у которого известны 2 стороны, 2 и 4 см
соответственно. Также дана пара отрезков на стороне, с показателем 2 см и 2 см. От нас просят найти
биссектрису треугольника АВС. Вместо b и c подставляем наши значения длин сторон, вместо а1 и а2 –
длины отрезков. Проводим вычисление и находим квадратный корень конечного результата. √(2 × 4 — 2 × 2) = 2 см.
Через все стороны
Чтобы отыскать длину биссектрисы треугольника, при известном значении каждой стороны фигуры, нужно
воспользоваться формулой ниже:
L = (√(bc (b + c + a)(b + c — a))) / (b + c)
где a, b, c — стороны.
Цифр после
запятой:
Результат в:
Пример. Нам дан некий треугольник АВС, известна каждая его сторона, допустим а = 10
см, b = 6 см, с = 8 см. Нам нужно отыскать биссектрису треугольника. Для этого подставляем все наши
известные значения в формулу. L = (√(6 * 8 * (6 + 8 + 10)(6 + 8 — 10))) / (6 + 
В прямоугольном треугольнике через гипотенузу и угол
Формула ниже слегка отличается от остальных, ведь тут использует понятие синуса и косинуса.
L = 2c / √2 * ((sin α * cos α) / (sin α + cos α))
где c — гипотенуза, sin α, cos α — угол.
Цифр после
запятой:
Результат в:
Именно данное вычисление поможет вам с поисками длины биссектрисы в прямоугольном треугольнике, если
вам известна одна гипотенуза и угол. «с» — гипотенуза, «а» — угол.
Пример. В прямоугольном треугольнике АВС известно значение гипотенузы и угла «а».
Пользуясь выведенной формулой, вы можете заметить, что от вас требуют синусы и косинусы угла «а».
Для того чтобы правильно посчитать, нужно воспользоваться специальной таблицей синусов и косинусов.
Далее решение не составит особого труда. Пусть гипотенуза c = 10 мм, угол α = 30 градусов,
тогда биссектриса L = 2* 10 / √2 * ((sin 30 * cos 30) / (sin 30 + cos 30)) = 4.48 мм.
В прямоугольном треугольнике через катеты
В прямоугольном треугольнике есть 2 катета и гипотенуза, как найти длину биссектрисы, если нам дано
только значение катетов треугольника. Для этого существует формула:
L = √2 * (ab / (a + b))
где «L» — искомая биссектриса, «а» и «b» — известное значение катетов прямоугольного
треугольника.
Цифр после
запятой:
Результат в:
Пример. Дан некий прямоугольный треугольник АВС, нам известна длина двух катетов,
5.5 см и 6 см. От нас просят найти длину биссектрисы треугольника АВС. √(2) × ((5.5 × 6) ÷ (5.5 + 6)) = 4,06 см.
Из острого угла в прямоугольном треугольнике через катет и угол
Если вам дан только катет и острый угол в прямоугольном треугольнике, используйте формулу:
L = b / cos β/2
где «b» — известный катет, а β — острый угол.
Цифр после
запятой:
Результат в:
Пример. Дан прямоугольный треугольник АВС. Известно, что катет «b» равен 9.7 см.,
угол β равен 45º. Нужно найти биссектрису. Нужно 9.7 поделить на косинус половины 45 град.
Подставляем значения в формулу: L = (9,7)/(cos(45)/(2)) = 10,5 см.
В равнобедренном треугольнике через боковую сторону и угол при основании
Для нахождения длины биссектрисы равнобедренного треугольника с помощью боковой стороны и угла при
основании можно воспользоваться данной формулой:
L = b * sin α
где b — боковая сторона, sin α — угол при основании.
Цифр после
запятой:
Результат в:
Пример. В условии дан равнобедренный треугольник. Известно, что боковая сторона
равна 12 см, а угол основания составляет 60 град. У нас есть все ключевые данные для решения, просто
подставляем их в формулу L = 12 * sin 60 = 10,4 см.
Из острого угла в прямоугольном треугольнике через катет и гипотенузу
Длину биссектрисы в прямоугольном треугольнике можно найти по формуле:
L = b * √(2c / b + c)
где «b» — гипотенуза, а «с» — катет.
Цифр после
запятой:
Результат в:
Пример. АВС –прямоугольный треугольник. Гипотенуза равна 8 см, а катет 3.5 см. L = 8 × √((2 × 3.5) ÷ (8 + 3.5)) = 4 см. Подставив значения в формулу,
мы получим результат, что биссектриса приблизительно равна 4 см.
В равнобедренном треугольнике через основание и угол при основании
Как и в предыдущих случаях, для данной задачи есть специальная формула:
L = a / 2 * tg α
где a — основание, tg α — угол при нижнем основании.
Цифр после
запятой:
Результат в:
Пример. Нам дан равнобедренный треугольник. В условии сказано, что основание «а»
равно 12 см, угол альфа – 60 град. Для решения поставим в формулу значения L = 12 ÷ 2 × tan(60) = 10.4 см
В равнобедренном треугольнике через основание и боковую сторону
Формула, по которой можно найти длину биссектрисы в равнобедренном треугольнике, если по условиям
дано основание и боковая сторона:
L = √(b² — a²/4)
где b и а — основание.
Цифр после
запятой:
Результат в:
Пример. В равнобедренном треугольнике АВС известно, что основание равно 9 см, а
боковая сторона 11 см. Нахождение биссектрисы происходит по формуле выше. L = √(9² — (11² ÷ 4)).
Следовательно, проведя сокращения, вычисления и округления у вас должен получится результат – 10 см.
Это и есть длина биссектрисы.
В равнобедренном треугольнике через боковую сторону и угол между боковыми сторонами
Как и все разы до этого, в данном случае применяется выведенная формула:
L = b * cos β/2
где b является боковой стороной, β – угол, который лежит между боковых сторон.
Цифр после
запятой:
Результат в:
Пример. Дан равнобедренный треугольник, боковая сторона которого равна 6.5 см.
Известно, что угол между боковыми сторонами равен 45 град. Нужно вычислить биссектрису. Используем
прямую формулу: L = 6.5 × cos(45 ÷ 2) = 6.005. После вычислений у нас
получается 6.005. Округляем до десятых и записываем в ответ 6 см.
В равностороннем треугольнике через сторону
Для нахождения длины биссектрисы в равностороннем треугольнике через сторону используйте формулу
ниже:
L = a√3 / 2
где а является стороной треугольника.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим равносторонний треугольник, сторона которого равна 5.8 см. Задача
заключается в нахождение биссектрисы. Для решения у нас есть все нужные данные. Подставим их в
формулу: L = (5.8 × √(3)) ÷ 2. Проведя вычисление, мы получаем ответ 5.02,
это и есть значение длины биссектрисы.
Решение задач по геометрии в школе предусматривает детально рассмотрение понятия биссектрисы и всех
ее свойств включительно. Выходя из некоторых особенностей данного отрезка можно решать задачи
высокого уровня. Главное знать все тонкости и нюансы такого элемента как биссектриса.
В данной публикации приведены примеры наиболее распространенных формул, используемых при вычислении
длины биссектрисы в треугольнике. Каждая формула по-своему уникальна, но не является сложной.
Выучить их все будет трудно, но иметь всегда с собой вполне реально.








 Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.
Первое свойство биссектрис равнобедренного треугольника формулируется в том, что равенство двух биссектрис свидетельствует о равнобедренности этого треугольника. Третья же его биссектриса медиана, а также высота его угла.