Как найти ближайшее число фибоначчи - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Последовательность Фибоначчи – это ряд чисел, в котором каждое последующее число равно сумме двух предыдущих чисел. Числовые последовательности часто встречаются в природе и искусстве в виде спиралей и «золотого сечения». Самый простой способ вычислить последовательность Фибоначчи – это создать таблицу, но такой метод не применим к большим последовательностям. Например, если нужно определить 100-й член последовательности, лучше воспользоваться формулой Бине.

1
Нарисуйте таблицу с двумя столбцами. Количество строк таблицы зависит от количества чисел последовательности Фибоначчи, которые нужно найти.
- Например, если нужно найти пятое число последовательности, нарисуйте таблицу с пятью строками.
- Используя таблицу, нельзя найти некоторое случайное число без вычисления всех предыдущих чисел. Например, если нужно найти 100-е число последовательности, нужно вычислить все числа: от первого до 99-ого. Поэтому таблица применима только для нахождения первых чисел последовательности.
2
В левом столбце напишите порядковые номера членов последовательности. То есть напишите цифры по порядку, начиная с единицы.
- Такие цифры определяют порядковые номера членов (чисел) последовательности Фибоначчи.
- Например, если нужно найти пятое число последовательности, в левой колонке напишите следующие цифры: 1, 2, 3, 4, 5. То есть нужно найти с первого по пятое число последовательности.
3
В первой строке правой колонки напишите 1. Это первое число (член) последовательности Фибоначчи.
- Имейте в виду, что последовательность Фибоначчи всегда начинается с 1. Если последовательность начинается с другого числа, вы неправильно вычислили все числа вплоть до первого.
4
К первому члену (1) прибавьте 0. Получится второе число последовательности.
- Запомните: чтобы найти любое число последовательности Фибоначчи, просто сложите два предыдущих числа.
- Чтобы создать последовательность, не забудьте о 0, который стоит перед 1 (первым членом), поэтому 1 + 0 = 1.
5
Сложите первый (1) и второй (1) члены. Получится третье число последовательности.
- 1 + 1 = 2. Третий член равен 2.
6
Сложите второй (1) и третий (2) члены, чтобы получить четвертое число последовательности.
- 1 + 2 = 3. Четвертый член равен 3.
7
Сложите третий (2) и четвертый (3) члены. Получится пятое число последовательности.
- 2 + 3 = 5. Пятый член равен 5.
8

Сложите два предыдущих числа, чтобы найти любое число последовательности Фибоначчи. Этот метод основан на формуле: $F_{{n}}=F_{{n-1}}+F_{{n-2}}$ .^[1] Эта формула не является замкнутой, поэтому при помощи этой формулы нельзя найти любой член последовательности без вычисления всех предыдущих чисел.

Реклама

1
2

В формулу подставьте порядковый номер числа (вместо ). – это порядковый номер любого искомого члена последовательности.
3

В формулу подставьте золотое сечение. Золотое сечение приблизительно равно 1,618034; подставьте в формулу это число.^[5]
4

Вычислите выражение в скобках. Не забывайте про правильный порядок выполнения математических операций, в котором выражение в скобках вычисляется в первую очередь:.
5

Возведите числа в степени. Возведите в соответствующие степени два числа, которые находятся в числителе.
6

Вычтите два числа. Перед тем как приступить к делению, вычтите числа, которые находятся в числителе.
7
Полученный результат разделите на квадратный корень из 5. Квадратный корень из 5 приблизительно равен 2,236067.
- В нашем примере: ${frac {11,180339}{2,236067}}=5,000002$ .
8
Полученный результат округлите до ближайшего целого числа. Последний результат будет десятичной дробью, которая близка к целому числу. Такое целое число представляет собой число последовательности Фибоначчи.
- Если в вычислениях использовать неокругленные числа, вы получите целое число. Работать с округленными числами намного легче, но в этом случае вы получите десятичную дробь.^[6]
- В нашем примере вы получили десятичную дробь 5,000002. Округлите ее до ближайшего целого числа и получите пятое число последовательности Фибоначчи, которое равно 5.
Реклама

Об этой статье

Эту страницу просматривали 27 790 раз.

Была ли эта статья полезной?

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given a positive integer N, the task is to find the nearest Fibonacci number to the given integer N. If there are two Fibonacci Numbers having same difference from N, then print the smaller value.

Examples:

Input: N = 20
Output: 21
Explanation: Nearest Fibonacci number to 20 is 21.

Input: N = 17
Output: 13

Approach: Follow the steps below to solve the problem:

If N is equal to 0, then print 0 as the result.
Initialize a variable, say ans, to store the Fibonacci Number nearest to N.
Initialize two variables, say First as 0, and Second as 1, to store the first and second terms of the Fibonacci Series.
Store the sum of First and Second in a variable, say Third.
Iterate until the value of Third is at most N and perform the following steps:
- Update the value of First to Second and Second to Third.
- Store the sum of First and Second in the variable Third.
If the absolute difference of Second and N is at most the value of Third and N, then update the value of ans as Second.
Otherwise, update the value of ans as Third.
After completing the above steps, print the value of ans as the result.

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>

using namespace std;

void nearestFibonacci(int num)

{

if (num == 0) {

cout << 0;

return;

}

int first = 0, second = 1;

int third = first + second;

while (third <= num) {

first = second;

second = third;

third = first + second;

}

int ans = (abs(third - num)

>= abs(second - num))

? second

: third;

cout << ans;

}

int main()

{

int N = 17;

nearestFibonacci(N);

return 0;

}

Java

class GFG{

static void nearestFibonacci(int num)

{

if (num == 0)

{

System.out.print(0);

return;

}

int first = 0, second = 1;

int third = first + second;

while (third <= num)

{

first = second;

second = third;

third = first + second;

}

int ans = (Math.abs(third - num) >=

Math.abs(second - num)) ?

second : third;

System.out.print(ans);

}

public static void main (String[] args)

{

int N = 17;

nearestFibonacci(N);

}

Python3

def nearestFibonacci(num):

if (num == 0):

print(0)

return

first = 0

second = 1

third = first + second

while (third <= num):

first = second

second = third

third = first + second

if (abs(third - num) >=

abs(second - num)):

ans = second

else:

ans = third

print(ans)

if __name__ == '__main__':

N = 17

nearestFibonacci(N)

C#

using System;

class GFG{

static void nearestFibonacci(int num)

{

if (num == 0)

{

Console.Write(0);

return;

}

int first = 0, second = 1;

int third = first + second;

while (third <= num)

{

first = second;

second = third;

third = first + second;

}

int ans = (Math.Abs(third - num) >=

Math.Abs(second - num)) ?

second : third;

Console.Write(ans);

}

public static void Main(string[] args)

{

int N = 17;

nearestFibonacci(N);

}

Javascript

<script>

function nearestFibonacci(num)

{

if (num == 0) {

document.write(0);

return;

}

let first = 0, second = 1;

let third = first + second;

while (third <= num) {

first = second;

second = third;

third = first + second;

}

let ans = (Math.abs(third - num)

>= Math.abs(second - num))

? second

: third;

document.write(ans);

}

let N = 17;

nearestFibonacci(N);

</script>

Time Complexity: O(log N)
Auxiliary Space: O(1)

Last Updated :
13 Apr, 2021

Like Article

Save Article

Источник

Нахождение чисел Фибоначчи

Время на прочтение
2 мин

Количество просмотров 22K

Доброго времени суток!
Сегодня я хотел бы рассказать о методе разрешения некоторых рекуррентностей и разобрать классический пример на эту тему.
Начнем с определения рекуррентной формулы:

Рассмотрим задачу, которая формулируется очень просто: нам нужно найти N-ое число Фибоначчи по модулю P, где N <= 10^15, P <= 10^9. Как видно из ограничений, складывать числа тривиальным методом за О(n) не получится, нужно придумывать более быстрый алгоритм, в этой статье речь пойдет об операторном методе с асимптотикой O(log N). Пусть у нас есть вектор столбец , — n-ое число Фибоначчи, постараемся подобрать оператор такой, что будет выполняться равенство . Для чисел Фибоначчи легко найти матрицу этого оператора, если вспомнить рекуррентную формулу , матрица равна , действительно . А учитывая то, что наш оператор подходит не только для первых чисел Фибоначчи, а и для всех, то есть , имеем . Значит мы можем вычислить ответ, возведя матрицу нашего оператора в N-ую степень, для этого воспользуемся алгоритмом логарифмического возведения в степень. Вот код, написанный на java:

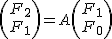
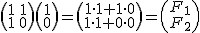
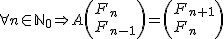
Copy Source | Copy HTML
private static long getFibb(int n) { long a11 = 1, a12 = 1, a21 = 1, a22 = 0; //матрица оператора long r11 = 1, r12 = 0; //вектор-столбец результа long q11 = 0, q12 = 0, q21 = 0, q22 = 0; //вспомогательная матрица при перемножении while (n > 0) { if ((n&1)==1) { q11 = (r11 * a11 + r12 * a21) % MOD; q12 = (r11 * a12 + r12 * a22) % MOD; r11 = q11; r12 = q12; } q11 = (a11 * a11 + a12 * a21) % MOD; q12 = (a11 * a12 + a12 * a22) % MOD; q21 = (a21 * a11 + a22 * a21) % MOD; q22 = (a21 * a12 + a22 * a22) % MOD; a11 = q11; a12 = q12; a21 = q21; a22 = q22; n >>= 1; } return r12; //возвращаем Fn }

Осталось только выдать наш ответ:

Copy Source | Copy HTML
out.println(getFibb(N));

Спасибо за внимание.

Источник

12.1. Простейшие свойства

Напомним, что числа Фибоначчи образуют последовательность, в которой первые два члена равны 0 и 1, а каждый следующий равен сумме двух предыдущих. В соответствии с определением последовательность чисел Фибоначчи

F0 = 0, F1 = 1, F2 = 1, F3	= 2, F4 = 3, F5 = 5, F6 = 8,…
удовлетворяет рекуррентному соотношению
Fn+2	= Fn+1 + Fn.	(1)

Числа Фибоначчи возникают естественным образом во многих задачах. Исторически одной из первых является задача о кроликах, восходящая к Леонардо Пизанскому, которого иногда называют Леонардо Фибоначчи (публикация 1202 г.). В этой задаче требуется определить число пар зрелых кроликов, образовавшихся от одной пары в течение года, если известно, что каждая зрелая пара кроликов ежемесячно рождает новую пару, причем новорожденные кролики достигают зрелости через два месяца.

Обозначим через un, un+1, un+2 число пар зрелых кроликов соответственно через n месяцев, через n + 1 месяц и через n + 2 месяца. Нетрудно убедиться, что un+2 = un+1 + un: к моменту n + 2 зрелости достигают un пар кроликов, родившихся в момент n,

которые добавляются к un+1 паре кроликов, зрелых на момент n + 1.

Рассмотрим еще одну задачу, так называемую задачу о прыгуне. Некоторая величина x увеличивается за единицу времени на 1 или на 2. Требуется определить, сколькими способами может произойти увеличение рассматриваемой величины на n единиц. Обозначим искомое число способов через un. Пусть x(t) – значение величины x в момент времени t. Ясно, что x(1) = x(0) + 1 или x(1) = x(0) + 2 в зависимости от того, на 1 или на 2 изменилась величина x за первый временной промежуток. Имеются два пути достичь значения x(0) + n: вырасти на n – 1 единицу со значения x(0) + 1 или на n – 2 единицы со значения x(0) + 2. Первое может произойти un–1 способами, второе – un–2 способами. Следовательно,

un = un–1 + un–2.

Многие свойства чисел Фибоначчи нетрудно получить по индукции. Например, для любого n ≥ 0 справедливо равенство

1	1 n+1	F	F		(2)
	0		=	n+2	n +1	.
1			F	F
				n +1	n

В самом	деле,	(2) выполняется при n = 0. Следующая
выкладка позволяет сделать индуктивный шаг:
1 1	n+2	F	F	1	1
		=	n+2	n+1		=
1 0			F	F	1	0
			n+1	n

				84
F	+ F	F			F	+3	F
=	n+2		n +1	n+2		= n	n+2	.
	F		+ F	F			F	+2	F
	n+1	n	n +1		n	n +1
Если взять определители матриц, стоящих в правой и левой
частях (2), получится следующее соотношение:
	Fn+2Fn – F 2	= (–1)n+1.
				n+1

Приведем одно из важных свойств чисел Фибоначчи, доказательство которого значительно сложнее и здесь не приводится.

Каждое целое положительное число имеет единственное представление вида

n = Fk1 + Fk2 +K+ Fkr ,

(3)

где k1 ≥ k2 +2; k2 ≥ k3 +2; …, kr–1 ≥ kr +2; kr ≥ 2.

Чтобы получить представление (3) нужно в качестве Fk1

взять наибольшее число Фибоначчи, не превосходящее n, в качестве Fk2 – наибольшее число Фибоначчи, не превосходящее n − Fk1 , и т. д., пока очередной «остаток» не станет равным нулю. Например:

1 = F1; 2 = F2; 3 = F3;4 = F3 + F1; 5 = F4; 8 = F5; 13 = F6; 20 = F6 + F4 + F2.

12.2. Формула Бине и некоторые ее применения

Напомним (см. 11.3, формула (5)), что производящая функция для последовательности чисел Фибоначчи имеет вид

F(z) = F0 + F1z + F2z2 + … =

− z − z2

Корнями характеристического многочлена

k(z) = z2 – z –1

являются числа

б =1+ 5

и в =

1− 5 .

Число Фибоначчи как функция своего номера

представляется в виде:

Fn =

бn −вn

(4)

или

−

1− 5

F =

Формула (4) называется формулой Бине.

Так как α2 = α + 1, то любую степень числа α можно представить в виде целочисленной комбинации aα + b. Оказывается, коэффициентами служат числа Фибоначчи:

αk+2 = Fk+2α + Fk+1.

Формула Бине позволяет убедиться в этом прямой проверкой. Приведем несколько оценок чисел Фибоначчи.

Число Фибоначчи Fn есть ближайшее целое к числу бn . 5

Для доказательства заметим, что |β| < 1, и, значит, |βn| < 1. Следовательно,

F − бn	= бn −вn − бn	= в n	< 1 .	(5)
n	5	5	5	5	2

Из (4) вытекает также следующее свойство.
С ростом n числа Фибоначчи неограниченно сближаются с
членами геометрической прогрессии с начальным членом	1	и
						5

знаменателем α = 52+1 :

					бn
			lim F −			= 0.
			n			5
			n→∞
Отношение соседних чисел Фибоначчи (следующего к
предыдущему) с ростом n стремится к числу	2	≈ 0,618 .
								5 +1
Действительно,
	F		бn −вn				1−(в/ б)n
	n	=				=		.
	Fn+1	бn+1 −вn	+1	б−в(в/ б)n

Так как β/α < 1, то (β/α)n с ростом n стремится к нулю. Следовательно,

lim	Fn	=	1	≈ 0,618 .
	б
n→∞ Fn+1

Из предыдущего равенства следует, что

lim	Fn	=	1	≈ 0,382 .
	б2
n→∞ Fn+2

Установим справедливость формулы, которая дает представление чисел Фибоначчи в виде суммы биномиальных коэффициентов, и как ее следствие получим одно тождество для биномиальных коэффициентов.

При любом n справедливо следующее равенство:

				Fn+1 =		∑Cnk−k .	(6)
						2k ≤n
Заметим сначала, что при четном n равенство (6) имеет вид
	F		= C0 +C1	−1	+… +Cn / 2	,
	n+1		n	n		n / 2
а при нечетном –
	F	= C0	+C1	−1	+… +C(n−1) / 2 .
	n+1		n	n			(n+1) / 2
Например:
F = C0	+C1	+C2	; F = C0	+C1	+C2 .
5	4		3	2			6	5	4	3

Для доказательства (6) воспользуемся производящей

функцией последовательности чисел Фибоначчи:
F(z) = F0	+ F1z + F2z2 +… =	z	.	(7)
	− z − z2
	1

Используя формулу для суммы членов бесконечно убывающей геометрической прогрессии, преобразуем правую часть равенства (7):

Источник

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ …………………………………………………3

1.Леонардо Фибоначчи. Числа Фибоначчи ……………3-4

1.1«Книга об абаке» ……………………………………………….

1.2«Практика геометрии» …………………………………………

1.3«Цветок» …………………………………………………………

1.4«Книга квадратов» ………………………………………………

1.5.Заслуги и достижения Леонардо Фибоначчи ………………….

2. Знакомство с числами Фибоначчи………………….5-6

3. Свойства последовательности Фибоначчи …………..6-7

4. Делимость и числа Фибоначчи………………………8-9

5. Золотое сечение……………………………………….10

6. Спираль Фибоначчи…………………………………11

7.Приложение: Последовательность Фибоначчи и пропорции Золотого сечения в разных сферах жизни :

Животные ………………………………………………12-13
Растения …………………………………………………13-14
Пропорции человеческого тела…………………………14-15
Космос ……………………………………………………15
Скульптура,,живопись, архитектура…………………..16-17
Пирамида Хеопса ……………………………………….17-18.
Поэзия и проза……………………………………………19
Музыка…………………………………………………….20
Числа Фибоначчи в психологии ……………………….20-21

ЗАКЛЮЧЕНИЕ ……………………………………………………………

СПИСОК ЛИТЕРАТУРЫ ………………………………………………..

“Великая книга природы

написана на языке математики”.
Галилео Галилей

Введение.

С давних пор человек стремится окружать себя красивыми вещами. Уже предметы обихода жителей древности, которые, казалось бы, преследовали чисто утилитарную цель – служить хранилищем воды, оружием на охоте и т.д., демонстрируют стремление человека к красоте.

На определенном этапе своего развития человек начал задаваться вопросом: почему тот или иной предмет является красивым и что является основой прекрасного? Уже в Древней Греции изучение сущности красоты, прекрасного, сформировалось в самостоятельную ветвь науки – эстетику, которая у античных философов была

неотделима от космологии. Тогда же родилось представление о том, что основой прекрасного является гармония. Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый – красоту в истине.

Красота скульптуры, красота храма, красота картины, симфонии, поэмы,… что между ними общего? Разве можно сравнить красоту храма с красотой ноктюрна? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты,

объединяющие понятие прекрасного самых различных объектов – от цветка ромашки до красоты обнаженного человеческого тела.

На Земле не всё изучено ,остаётся огромное количество непонятных и необъяснимых явлений.

Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.

Из школьного курса математики хорошо известны такие ученые, как Евклид, Архимед и Герон. Если же мы обратимся к математике средневековья, то не обнаружим такого большого количества выдающихся математических деятелей. Это связано с тем, что математика в эту эпоху развивалась крайне медленно. Однако стоит обратить внимание на сочинение “Liber abacсi” (« Книга об абаке»), написанное знаменитым итальянским математиком Леонардо Фибоначчи в 1202 году, которое дошло до нас в издании от 1228 года. В данной книге содержатся почти все арифметические и алгебраические сведения того времени. Данная работа сыграла большую роль в развитии математики в Западной Европе в течение нескольких следующих столетий.

Данный трактат примечателен тем, что материал поясняется на большом числе интересных математических задач. В своей работе я обратилась к одной из задач, разобранной в этой книге- «Числа Фибоначчи» . О них я услышала на уроке, когда мы изучали способы задания функций натурального аргумента. В данной работе я постараюсь приоткрыть тайны замечательного реккурентного соотношения, открытого около тысячи лет назад, и до сих пор поражающее богатством все новых и новых приложений в математике, искусстве, естественных науках, экономике и многих других науках. Показать связь чисел Фибоначчи с Золотым отношением, кратко познакомить с теорией фракталов. В школьном курсе математики не изучаются числа Фибоначчи, поэтому у меня возник вопрос: какие это числа и какими свойствами они обладают, где применяются. Поэтому я поставила перед собой следующие задачи:

1) Узнать как можно больше об этих числах, о Фибоначчи, его трудах.

2) Проанализировать в чем состоят свойства чисел Фибоначчи

3) Возможности их применения к решению задач.

4) Где встречаются в жизни.

Для того чтобы получить сведения по данным вопросам, я выбрала и изучила первоисточник: книгу Н.Н.Воробьева «Числа Фибоначчи», провела ряд вычислений, по проверке свойств этих чисел. Наиболее интересными были опыты, подтверждающие проявление свойств чисел Фибоначчи в жизни.

1.Леонардо Фибоначчи и его числа

О жизни Фибоначчи известно немного. Неизвестна даже точная дата его рождения. Предполагается, что Фибоначчи родился в 1170 г. в итальянском городе Пиза. Тогда Пиза была одним из крупнейших коммерческих средоточий, активно сотрудничавших с исламским Востоком. Его отец был купцом , по торговым делам часто бывал в Алжире, ему удалось «устроить» своего сына, будущего великого математика Фибоначчи в одну из арабских школ, где он и смог получить превосходное для того времени математическое образование. Леонардо изучал там математику у арабских учителей. Позже посетил Египет, Сирию, Византию, Сицилию. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки.

1.1.«Книга об абаке»

Фибоначчи написал несколько математических трудов: . Наиболее известным из них является «Liber abaci»(книга об абаке – счетной доске). Этот труд вышел при жизни Фибоначчи в двух изданиях в 1202 г. и 1228 г. Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной. Первые пять глав книги посвящены арифметике целых чисел на основе десятичной нумерации. В VI и VII главе Леонардо излагает действия над обыкновенными дробями. В VIII–X книгах изложены приёмы решения задач коммерческой арифметики, основанные на пропорциях. В XI главе рассмотрены задачи на смешение. В XII главе приводятся задачи на суммирование рядов — арифметической и геометрической прогрессий, ряда квадратов и, впервые в истории математики, возвратного ряда. В XIII главе излагается правило двух ложных положений и ряд других задач, приводимых к линейным уравнениям. В XIV главе Леонардо на числовых примерах разъясняет способы приближённого извлечения квадратного и кубического корней. Наконец, в XV главе собран ряд задач на применение теоремы Пифагора и большое число примеров на квадратные уравнения. «Книга абака» резко возвышается над европейской арифметико-алгебраической литературой XII–XIV вв. разнообразием и силой методов, богатством задач, доказательностью изложения. Последующие математики широко черпали из неё как задачи, так и приёмы их решения.

1.2 «Практика геометрии»

«Практика геометрии» (Practica geometriae, 1220) содержит разнообразные теоремы, относящиеся к измерительным методам. Наряду с классическими результатами Фибоначчи приводит свои собственные — например, первое доказательство того, что три медианы треугольника пересекаются в одной точке (Архимеду этот факт был известен, но если его доказательство и существовало, до нас оно не дошло).

1.3. «Цветок»

В трактате «Цветок» (Flos, 1225) Фибоначчи исследовал кубическое уравнение x3 + 2×2 + 10x = 20, предложенное ему Иоанном Палермским на математическом состязании при дворе императора Фридриха II. Сам Иоанн Палермский почти наверняка заимствовал это уравнение из трактата Омара Хайяма «О доказательствах задач алгебры», где оно приводится как пример одного из видов в классификации кубических уравнений. Леонардо Пизанский исследовал это уравнение, показав, что его корень не может быть рациональным или же иметь вид одной из квадратичных иррациональностей, встречающихся в X книге Начал Евклида, а затем нашёл приближённое значение корня в шестидесятеричных дробях, равное 1;22,07,42,33,04,40, не указывая, однако, способа своего решения.

1.4. «Книга квадратов»

«Книга квадратов» (Liber quadratorum, 1225), содержит ряд задач на решение неопределённых квадратных уравнений. В одной из задач, также предложенной Иоанном Палермским, требовалось найти рациональное квадратное число, которое, будучи увеличено или уменьшено на 5, вновь даёт рациональные квадратные числа.

С представлением «средневековье» в нашем сознании ассоциируется разгул инквизиции, костры, на каковых сжигали ведьм и еретиков, крестовые походы за «телом господним». Наука в те поры явно не была приоритетом. В этих условиях появление книги по математике «Liber abaci» («Книга об абаке»), написанной в 1202 году итальянским математиком Леонардо Пизано Фибоначчи, стало важным событием в научной жизни общества.

1.5. Заслуги и достижения Леонардо Фибоначчи

Каково же было содержание написанной Фибоначчи книги-энциклопедии, в которой насчитывалось целых пятнадцать глав? Оказывается, в ней рассматривался весьма обширный круг вопросов:

индусская система нумерации;
правила действий над целыми числами;
дроби и смешанные числа;
разложение чисел на простые множители;
признаки делимости; учение об иррациональных величинах;
способы приближенного вычисления квадратных и кубических корней;
свойства пропорции;
арифметическая и геометрическая прогрессии;
линейные уравнения и их системы.

Подробнее остановлюсь на одной из самых интересных работ Фибоначчи — Числа Фибоначчи

2. Знакомство с числами Фибоначчи

Исходная формулировка задачи – «Сколько пар кроликов в один год от одной пары рождается?» Рассмотрим предлагаемое автором решение. Представим, что некто поместил пару кроликов в огороженном со всех сторон месте и хочет узнать, сколько пар кроликов родится при этом в течение года. По условию задачи природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения. Проведем мысленный эксперимент и узнаем, сколько пар кроликов будет в каждом последующем месяце. Так как первая пара в первом месяце даст потомство, то всего будет 2 пары, причем первая пара рождает и в следующем месяце. То есть во втором месяце окажется три пары и две из них в следующем месяце дадут потомство. Получится, что в третьем месяце будет пять пар кроликов и три пары дадут потомство в следующем месяце. То есть в четвертом месяце будет 8 пар кроликов, и пять из них будут давать потомство. Это значит, что в пятом месяце будет 13 пар, из которых 8 дадут потомство в следующем месяце. Проведя аналогичные рассуждения, получим, что в шестом месяце будет 21 пара, в седьмом 34 пары, в восьмом 55 пар, в девятом 89 пар, в десятом 144 пары, в одиннадцатом 233 пары, в двенадцатом 377 пар – столько пар произвела первая пара в данном месте к концу одного года. Можно заметить, что число пар кроликов в текущем месяце равняется сумме пар кроликов за два предшествующих месяца. Математически решение этой задачи приводит к появлению последовательности чисел u1 , u2 , … un ,в которой каждый член равен сумме двух предыдущих, то есть для любого n>2

3. Свойства чисел Фибоначчи

Числа Фибоначчи или Последовательность Фибоначчи — числовая последовательность, обладающая рядом замечательных свойств. Зная особенности суммарной последовательности Фибоначчи ученые смогли выяснить, что им подчиняются многие особенности жизни, времени, деятельности человека. В законах природы, как и в законах математики имеется важнейший элемент – ритмичность. Свойства чисел последовательности используются не только в математике и физике, но и в природе, архитектуре, биологии, астрономии, изобразительном искусстве. При помощи этих чисел описываются разнообразные процессы во вселенной. Свойства чисел последовательности Фибоначчи, сделал их основой технического анализа. Я изучила простейшие свойства чисел Фибоначчи и проверила их верность на примерах. Рассмотрим некоторые из них:

1,1,2,3,5,8,13,21,34,55,89,144,…

1. Отношение каждого числа к последующему более и более стремится к 0.618 по увеличению порядкового номера. Отношение же каждого числа к предыдущему стремится к 1.618 (обратному к 0.618). 13:21=0,619… 21:34=0,618…

2. При делении каждого числа на следующее за ним, через одно получается число 0.382; наоборот – соответственно 2.618. 55:144=0,382… 144:55=2,618…

3. Сумма первых n чисел Фибоначчи равна: u1 + u2 +… + un = un+2 – u2, где u2 = 1

4. Сумма чисел Фибоначчи с нечетными номерами равна: u1 + u3 + u5 … + u2 n -1 = u2 n

5. Сумма чисел Фибоначчи с четными номерами равна: u2 + u4 + … + u2 n = u2 n +1 – 1

6. Формула суммы квадратов первых n чисел Фибоначчи выглядит так:

u1 2 + u2 2 +… + un 2 = un un +1

Соотношения между числами Фибоначчи удобно доказывать при помощи метода полной индукции. Сущность метода заключается в том, что для доказательства, что некоторого утверждения справедливого для всякого натурального числа достаточно двух условий : А) Утверждение имеет место для числа 1.Б) Из справедливости доказываемого утверждения для произвольного числа n, следует его справедливость для числа n+1.

Простейшей реализацией идеи индукции в применении к числам Фибоначчи является само определение чисел Фибоначчи. Оно состоит в указании двух первых чисел Фибоначчи: u1 = 1 и u2 = 1 и в индуктивном переходе от un и un +1 к un +2 , даваемым рекуррентным соотношением un + un +1 = un +2 .Отсюда автоматически следует, что если некоторая последовательность чисел начинается с двух единиц, а каждое из следующих получается сложением двух предыдущих, то эта последовательность является последовательностью чисел Фибоначчи.

Аналогично только что доказанным свойствам чисел Фибоначчи можно установить еще и такие свойства этих чисел:

7. u1 u2 + u2 u3 + u3 u4 + …+ u2n — 1 u2n = u2 2n

8. u1 u2 + u2 u3 + u3 u4 + …+ u2n+1 u2n = u2 2n+1 – 1

9. nu1 + (n-1)u2 +(n-2) u3 + …+2un – 1 + un = un+4 — (n-3)

10. u1 + 2 u2 + 3u3 + …+ nun = nun+2 – un+3 +2.

11. Любое число Фибоначчи можно определить и непосредственно, как некоторую функцию его номера. для этого исследуют различные последовательности u1 , u2 , …, un , …, удовлетворяющие соотношению un = un-2 + un-1

12. Числа Фибоначчи могут составить основу своеобразно «фибоначчисвой» системы счисления, т. е., представления любого натурального числа а в виде некоторой последовательности «цифр» ф1 ф2 .. .фг .

Рассмотренные мною свойства являются не всеми свойствами занимательных чисел, они требуют более глубокого знания математики.

4.Делимость чисел и свойства последовательности Фибоначчи

Вторая глава рассматривает свойства чисел Фибоначчи, касающиеся их делимости.

Легко заметить, что:

Каждое третье число Фибоначчи- делится на 2
Каждое четвертое число Фибоначчи- делится на 3
Каждое шестое число Фибоначчи-делится на 4
Каждое пятнадцатое число Фибоначчи- оканчивается нулем

Если существует хотя бы одно число Фибоначчи un делящееся на m, то таких делящихся на m чисел Фибоначчи можно найти сколь угодно много. Ими будут, кроме un , например, числа u2 n , u3 n ., u4 n …

Оказывается, что по заданному числу m можно найти хотя бы одно делящееся на него число Фибоначчи. Это доказывает следующая теорема:

Каково бы ни было целое число m, среди первых m2 —1 чисел Фибоначчи найдется хотя бы одно, делящееся на m.

Эта теорема не утверждает ничего о том, какое именно число Фибоначчи разделится на m. Она говорит только, что первое число Фибоначчи, делящееся на m, не должно быть особенно большим. Рассмотрим справедливость этой теоремы на конкретном примере. Пусть m = 5, тогда m2 —1 = 24, то есть n = 24

№ п-п	1	2	3	4	5	6	7	8	9	10	11	12
Числа	1	1	2	3	5	8	13	21	34	55	89	144

№ п-п	13	14	15	16	17	18	19	20	21	22	23	24
Числа	233	377	610	987	1597	2584	4181	6765	10946	17711	28657	46368

Вывод: Приняв за m число 5. Из 24 чисел последовательности Фибоначчи на m делится 4 числа. Теорема верна.

Теорема. Соседние числа Фибоначчи взаимно просты.

О делимости чисел Фибоначчи можно судить, рассматривая делимость их номеров. Рассмотрим, несколько «признаков делимости» чисел Фибоначчи. Под признаком делимости мы понимаем здесь признак, по которому можно определить, делится или нет то или иное число Фибоначчи на некоторое данное число.

Число Фибоначчи четно тогда и только тогда, когда его номер делится на 3.
Число Фибоначчи делится на 3 тогда и только тогда, когда его номер делится на 4.
Число Фибоначчи делится на 4 тогда и только тогда, когда его номер делится на 6.
Число Фибоначчи делится на 5 тогда и только тогда, когда его номер делится на 5.
Число Фибоначчи делится на 7 тогда и только тогда, когда его номер делится на 8.
Число Фибоначчи делится на 16 тогда и только тогда, когда его номер делится на

Доказательства всех этих признаков делимости и всех других, подобных им, легко проводится .

Рассмотрим следующее свойство: Если число Фибоначчи имеет нечетный номер, то все его нечетные делители имеют вид 4 t+1.

Вернемся к нечетным номерам рассматриваемой последовательности чисел Фибоначчи.

№ п-п	5	7	11	13	17	19	23
Числа	5	13	89	233	1597	4181	28657
4t+1	5:4= 1+1	13:4=3+1	89:4=22+1	233:4=58+1	1597:4=399+1	4181:4=1045+1	28657:4=7164+1

5.ЧИСЛА ФИБОНАЧЧИ И ЗОЛОТОЕ СЕЧЕНИЕ

Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием красивого изображения предмета.

Последовательность Фибоначчи стремится к постоянному соотношению. Это отношение иррационально, представляет собой число с бесконечной последовательность десятичных чисел в дробной части. Члены последовательности связаны между собой соотношениями. Если член последовательности разделить на предшествующий ему, то величина будет колебаться примерно Ф = 1,618. Число Фи ( число Фидия). Греческая буква Ф (число PHI), которой обозначают величину золотого сечения, является первой буквой в имени знаменитого греческого скульптора Фидия, который широко использовал золотое сечение в своих скульптурных произведениях.

Соотношения 1,618 и 0,618. называются фибоначчиевыми коэффициентами.

Уже давно в своих творения люди предпочитают правильные геометрические формы – квадрат, круг, равнобедренный треугольник, пирамиду и т. д. в пропорциях сооружений отдаются предпочтения целочисленным соотношениям.

Из многих пропорций, которыми издавна пользовался человек при создании гармонических произведений, существует одна, единственная и неповторимая, обладающая уникальными свойствами. Эту пропорцию называли по разному – «золотой», «божественной», «золотым

сечением», «золотым числом», «золотой серединой». Загадка притягательной силы золотого сечения давно волнует человечество. «Эта наша пропорция, высокочтимый герцог, достойна

такой привилегии и такого превосходства, какие только можно высказать по поводу ее безграничных возможностей» – этими словами начиналась одна из главных книг монаха ордена францисканцев Луки Пачоли « О божественной пропорции». «Золотое сечение» назвал эту пропорцию друг Пачоли великий итальянский живописец, скульптор, архитектор, ученый инженер Леонардо до Винчи.

Золотое сечение с древности рассматривалось, как эстетически самое благоприятное отношение. Через Золотое сечение числа Фибоначчи проявляют свои свойства. Поскольку целое всегда состоит из частей, то части находятся в определенном отношении к друг другу и к целому. Принцип Золотого сечения – это принцип гармоничной пропорции.

Разделим отрезок АВ единичной длины на две части точкой C так, чтобы большая из его частей являлась средним пропорциональным между меньшей его частью и всем отрезком. Обозначим искомую длину большей части отрезка через х. Тогда условие нашей задачи дает пропорцию: . Положительным корнем является . Получаем, что отношения в пропорции равны (). Это деление и есть Золотое сечение или деление отрезка в крайнем и среднем отношении. Отрезки Золотой пропорции выражаются бесконечными и рациональными дробями b = 0,618; a = 0,382. Числа 0,618: 0,382 – коэффициенты последовательности Фибоначчи. На этой последовательности базируются все геометрические фигуры.

Ряд Фибоначчи тесно связан с золотым сечением. Так как число 0.618 представляет собой постоянный коэффициент золотого сечения, т.е. любой отрезок делится таким образом, что отношение между его меньшей и большей частью равно соотношению между большей частью и всем отрезком и равно 0.618. Таким образом, число ϕ = 0.618, известно еще как золотой коэффициент или золотая середина.

Золотым треугольником назовем равнобедренный треугольник, у которого отношение основания к боковой стороне равно φ, где φ=0,618033989…

Его свойства:

Биссектрисы при основании равны и отсекают от боковых сторон отрезки, равные φ, считая от вершины.
Медиана золотого треугольника, проведенная к боковой стороне равна( √3+Ф)/2.
Высота, проведенная к основанию, равна ( Ф√2+Ф)/2
Высота ,проведенная к боковой стороне, равна (√2+Ф)/2
Площадь золотого треугольника( Ф√2+Ф)/4
Радиус описанной окружности R =Ф/√2+Ф
Радиус вписанной окружности r =√2+Ф/ 2Ф

Пирамида называется золотой, если каждая ее грань-золотой треугольник.

Некоторые ее свойства:

Высота золотой пирамиды равна √2Ф/(2+Ф)
Объем золотой пирамиды равен Ф√Ф/6√2
Двугранные углы
Радиус описанной сферы R=√3+2Ф/2√2
Радиус вписанной сферы r= Ф√Ф/2√8Ф+6
Площадь поверхности S= Ф√2+Ф

Природа не пользуется золотым сечением сразу. Она его получает путем последовательных итераций и для порождения золотого сечения пользуется другим рядом, — рядом Фибоначчи.

Знаменитый ряд чисел Фибоначчи образует изначальный принцип золотого соотношения.

В чем разница между спиралями золотого сечения и спиралью Фибоначчи? Спираль золотого сечения идеальна. Она соответствует Первоисточнику гармонии. Эта спираль не имеет ни начала, ни конца. Она бесконечна. Спираль Фибоначчи имеет начало, от которого она начинает “раскрутку”. Это очень важное свойство. Оно позволяет Природе после очередного замкнутого цикла осуществлять строительство новой спирали с “нуля”.

6.Спираль Фибоначчи

Если построить прямоугольник со сторонами 21см и 34см (золотой прямоугольник), равными двум соседним числам последовательности , а затем отрезов от него квадрат, сторона которого равна меньшей стороне (стороне = 21см) прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Мы будем отрезать квадраты до тех пор, пока не получим квадраты со сторонами 1см. Золотой прямоугольник можно разбить на более мелкие, с размерами, соответствующими соседним числам Фибоначчи.

Соединив диагонали квадратов, система начнет приобретать некую форму — мы увидим так называемую «Спираль Фибоначчи».

Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали.

Гете называл спираль «кривой жизни». Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д.

Фибоначчи напомнил миру о таком явлении, как Золотое сечение.

Приложение:

7.Последовательность Фибоначчи и пропорции золотого сечения в разных сферах жизни

Пьер Kюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

Важно отметить, что Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи. Пpиведенные ниже примеры показывают присутствие этой математической последовательности в разных сферах жизни и еще раз доказывают связь с Золотым сечением и последовательностью Фибоначчи.

7.1.Последовательность Фибоначчи в строении животных

Числа Фибоначчи проявляются в морфологии различных организмов.Многие насекомые в горизонтальном разрезе имеют простые асимметричные формы, основанные на золотом сечении. . Например, морские звезды. Число лучей у них отвечает ряду чисел Фибоначчи и равно 5, 8, 13, 21, 34, 55. У хорошо знакомого комара — три пары ног, брюшко делится на восемь сегментов, на голове пять усиков — антенн. Личинка комара членится на 12 сегментов. Число позвонков у многих домашних животных равно 55.

У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья,ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2, 3, 5, 8.

Очень совершенна форма стрекозы, которая создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста . как 62 к 38.

У живородящей ящерицы четко прослеживается золотая пропорция. Расстояние от головы до задних конечностей так относится к расстоянию от задних конечностей до кончика хвоста как расстояние от задних конечностей до кончика хвоста ко всей длине ящерицы.

Строение форм представителей более высокого уровня животного мира тоже подчиняется закону Фибоначчи. Например: у черепахи в панцире имеется 13 сросшихся пластин, из них 5 пластин в центре, а 8 по краям, на лапках 5 пальцев, а позвоночник содержит 34 позвонка; панцирь современных крабов состоит из 13 пластин, а древних содержал 8 пластин.

Раковина наутилуса. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Форма спирально завитой раковины привлекла внимание Архимеда. Дело в том, что отношение измерений завитков раковины постоянно и равно 1.618, т.е. числу Фи. Архимед изучал спираль раковин и вывел уравнение спирали.

Причем во многих изданиях сказано, что это спираль золотого сечения, но это неверно – это спираль Фибоначчи. Спираль Фибоначчи имеет начало, от которого она начинает “раскрутку”. Это очень важное свойство. Оно позволяет Природе после очередного замкнутого цикла осуществлять строительство новой спирали с “нуля”.

Можно увидеть совершенство рукавов спирали, но если посмотреть на начало, то он не выглядит таким совершенным. Два самых внутренних ее изгиба фактически равны. Второй и третий изгибы чуть ближе приближаются к «фи». Потом, наконец, получается эта изящная плавная спираль. Вспомните отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее. Будет понятно, что моллюск в точности следует математике ряда Фибоначчи.

7.2. Последовательность Фибоначчи в растениях.

Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Cпираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Cовместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения.

Понаблюдаем за ростом и развитием стеблей и цветов. Каждая его новая ветвь, прорастая, дает начало другим ветвям. Рассматривая старые и новые ветви совместно, мы обнаружим число Фибоначчи в каждой из горизонтальных плоскостей.

Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д.

Так спирали подсолнухов всегда соотносятся с рядом Фибоначчи. Даже в обычной сосновой шишке можно увидеть эту двойную спираль Фибоначчи. Первая спираль идет в одну сторону, вторая — в другую. Если посчитать число чешуек в спирали, вращающейся в одном направлении, и число чешуек в другой спирали, можно увидеть, что это всегда два последовательных числа ряда Фибоначчи. Может быть восемь в одном направлении и 13 в другом, или 13 в одном и 21 в другом 3.

7.3. Последовательность Фибоначчи в строении человеческого тела

В 1855г. немецкий исследователь золотого сечения профессор Цейзиг опубликовал свой труд «Эстетические исследования». Он измерил около 2 тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618. Расстояние от уровня плеча до макушки головы и размера головы равно 0.618. Расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 0.618. Расстояние точки пупа и от коленей до ступней равно 0.618. Расстояние от кончика подбородка до кончика верхней губы до ноздрей равно 0.618. Расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 0.618. собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора. Если внимательно посмотреть на

указательный палец, то вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг. Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца). Кроме того, соотношения между средним пальцем и мизинцем также равно числу золотого сечения. У человека 2 руки, пальцы на каждой руке состоят из трех фаланг (за исключением большого пальца). На каждой руке имеется пять пальцев, т. е. всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Все эти цифры 2,3, 5 и 8 есть числа последовательности Фибоначчи. Друнвало Мелхиседек в книге «Древняя тайна Цветка Жизни» пишет: «Да Винчи вычислил, что, если нарисовать квадрат вокруг тела, потом провести диагональ от ступней до кончиков вытянутых пальцев, а затем провести параллельную горизонтальную линию (вторую из этих параллельных линий) от пупка к стороне квадрата, то эта горизонтальная линия пересечет диагональ точь-в-точь в пропорции «фи», как и вертикальную линию от головы до ступней. Если считать, что пупок находится в той совершенной точке, а не слегка выше для женщин или чуть ниже для мужчин, то это означает, что тело человека поделено в пропорции «фи» от макушки до ступней.

Если бы эти линии были единственными, где в человеческом теле имеется пропорция фи, это, вероятно, было бы только интересным фактом. На самом деле пропорция фи обнаруживается в тысячах мест по всему телу, а это не просто совпадение. Вот некоторые явственные места в теле человека, где обнаруживается пропорция фи. Длина каждой фаланги пальца находится в пропорции «фи» к следующей фаланге. Та же пропорция отмечается для всех пальцев рук и ног. Если соотнести длину предплечья с длиной ладони, то получится пропорция «фи», так же длина плеча относится к длине предплечья. Или отнесите длину голени к длине стопы и длину бедра к длине голени. Пропорция фи обнаруживается во всей скелетной системе. Она обычно отмечается в тех местах, где что-то сгибается или меняет направление. Она также обнаруживается в отношениях размеров одних частей тела к другим.

Чтобы исследовать сколько, учащихся моего класса имеют гармоничность в строении (телосложении), мною были произведены некоторые измерения (рост и расстояние от стопы до пупочной линии, расстояние от ключицы до локтя и от локтя до кончиков пальцев, длина указательного пальца и длина первых двух фалангов. Для эксперимента были взяты все учащиеся моего класса (9- го класса). Таким образом, 40% обследуемых учащихся подтвердили гармонию своего тела.

7.4. Последовательность Фибоначчи в космосе

Из истории астрономии известно, что И. Тициус, немецкий астроном XVIII в., с помощью этого ряда (Фибоначчи) нашел закономерность и порядок в расстояниях между планетами солнечной системы.Однако один случай, который, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Наблюдение за этим участком неба привело к открытию пояса астероидов. Произошло это уже после смерти Тициуса в начале XIX в.

7.5 .Последовательность Фибоначчи в скульптуре

Наука и искусство – два высших начала культуры. Их высшая цель – быть дополняющими друг другу. Из многих искусств, допускающих математическое описание, мы рассмотрим только пять : скульптура, живопись, музыка, литература и архитектура.

Известно, что древние скульпторы знали и использовали золотую пропорцию как критерий гармонии, канон красоты, корни которой лежат в пропорциях человеческого тела. Эталонами красоты человеческого тела, образцами гармонического телосложения издавна и по праву считаются великие творения греческих скульпторов. В создании своих творений мастера использовали принцип золотой пропорции. Например греческий скульптор Леохард (4 до н. э.) создал статую Аполлона Бельведерского, воплотившего представления древних греков о мужской красоте.

Линии, проведенные на снимке, определяют основные пропорции тела. Эти пропорции связаны с золотым сечением и числами Фибоначчи.

7.6. Последовательность Фибоначчи в живописи

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”. Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в. Портрет Моны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Зрачок левого глаза, через который проходит вертикальная ось полотна, находится на пересечении двух биссектрис верхнего золотого треугольника, которые с одной стороны, делят пополам углы при основании золотого треугольника, а с другой стороны, в точках пересечения с бедрами треугольника делят их в пропорции золотого сечения. Таким образом, Леонардо да Винчи использовал в своей картине не только принцип симметрии, но и золотое сечение.

7.7 .Последовательность Фибоначчи в архитектуре

Уже давно в своих творения люди предпочитают правильные геометрические формы – квадрат, круг, равнобедренный треугольник, пирамиду и т. д. в пропорциях сооружений

отдаются предпочтения целочисленным соотношениям. Из многих пропорций, которыми издавна пользовался человек при создании гармонических произведений, существует одна, единственная и неповторимая, обладающая уникальными свойствами. Эту пропорцию называли по разному – «золотой», «божественной», «золотым сечением», «золотым числом», «золотой серединой». Загадка притягательной силы золотого сечения давно волнует человечество. «Эта наша пропорция, высокочтимый герцог, достойна

Одним из красивейших произведений древнегреческой архитектуры является Парфенон рис3.– храм богини Афины, возведенный в 5 веке до н.э. в ознаменование победы над персами. Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618.

7.8. Последовательность Фибоначчи в пирамиде Хеопса

Великая Пирамида Хеопса — чудо света древнего и современного. От подножия до вершины она достигает 137, 3 м, а до того, как утратила верхушку, высота ее была 146,7 Немногим более 100 лет назад она была самым высоким сооружением в мире. Стороны ее основания равны 230, 4 м, а до потери облицовки — 232, 4 м. Площадь ее основания составляет 5, 4 га.

Измерения показали, что длина периметра у основания Пирамиды, деленная на ее удвоенную величину практически составила 3, 14159… то есть число . Открытие этого числа в размерах Пирамиды Хеопса произвел сенсацию. Из «папируса Ринда», хранящегося в настоящее время в британском музее и найденного А.Х.Риндоу в 1858 г., стало известно, что египтяне занимались числом .ногие пытались разгадать секреты пирамиды в Гизе. В отличие от других египетских пирамид это не гробница, а скоpее неразрешимая головоломка из числовых комбинаций. Замечательные изобpетательность, мастерство, время и труд аpхитектоpов пирамиды, использованные ими пpи возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Их эпоха была дописьменной, доиероглифической и символы были единственным средством записи открытий. Kлюч к геометро-математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.

Площадь тpеугольника: 356 x 440 / 2 = 78320

Площадь квадpата: 280 x 280 = 78400

Длина грани пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды -484.4 фута (147.6 м). Длина гpани, деленная на высоту, приводит к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13) — это числа из последовательности Фибоначчи. Эти интересные наблюдения подсказывают, что конструкция пирамиды основана на пропорции Ф=1,618.

Это удивило ученых, поскольку первые исторические сведения о Золотом сечении появились только спустя 2000 лет после сооружения Пирамиды. Позднее была обнаружена еще одна закономерность: площадь боковой поверхности Пирамиды относится к площади основания, как площадь полной поверхности Пирамиды к площади боковой поверхности.

Некоторые современные ученые склоняются к интерпретации, что древние египтяне построили ее с единственной целью — передать знания, которые они хотели сохранить для грядущих поколений. Интенсивные исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет центральную роль.

7.9. Последовательность Фибоначчи в поэзии и прозе

Золотое сечение в поэзии в первую очередь проявляется как наличие определенного момента стихотворения (кульминации, смыслового перелома, главной мысли произведения) в строке, приходящейся в точку деления общего числа строк стихотворения в золотой пропорции.

Произведения А.С. Пушкина – образец наиболее выдающихся творений русской культуры, образец высочайшего уровня гармонии. Законы стихосложения неразрывно связаны с математическими законами. Так, например, можно установить закономерную связь между многими стихотворениями А.С.Пушкина и числами Фибоначчи, с Золотым сечением. Стихотворный текст настолько совершенен, что в нём обязательно действуют математические законы. Примером могут служить такие стихотворения Пушкина, как «Сапожник», «Не дорого ценю я громкие слова…», «Вакхическая песня», роман «Евгений Онегин» Рассмотрим его знаменитую «Вакхическую песню». В стихотворении всего 16 строк. Ставшая крылатой десятая строка стихотворения «Да здравствуют музы, да здравствует разум!» концентрирует в себе мысль стихотворения. Где расположена эта строка? Точно на линии золотого сечения (16 : 10 = 1.6). В рассказе «Станционный смотритель» 377 строк. Кульминационный момент рассказа – это известие о том, что дочь смотрителя уехала с гусаром. Этот момент отражен во фразе, которая является 214 строкой. Здесь почти точное соответствие золотой пропорции ( 377 : 214 = 1.76) .

В маленьком рассказе «Гробовщик» всего 229 строк. Со 139 строки начинается описание страшного сна гробовщика. И здесь переломный момент рассказа приходится почти точно на золотую пропорцию (226 : 139 = 1.6) .Совпадение кульминационных моментов в произведениях А.С. Пушкина с золотой пропорцией удивительно близкое. Чувство гармонии у него было развито необыкновенно, что объективно подтверждает гениальность великого поэта и писателя.

Рассмотрим роман «Евгений Онегин» и проведем анализ, в котором прослеживаются математические законы. Начнем с величины стихотворения, то есть с количества строк в нем. Казалось бы, этот параметр стихотворения может меняться произвольно. Однако оказалось, что это не так. Например, проведенный Н. Васютинским анализ стихотворений А. С. Пушкина с этой точки зрения показал, что размеры стихов распределены весьма неравномерно; оказалось, что Пушкин явно предпочитает размеры в 5, 8, 13, 21 и 34 строк (числа Фибоначчи). Этот роман состоит из 8 глав, в каждой из них в среднем около 50 стихов. Наиболее отточенной и эмоционально насыщенной является восьмая глава. В ней 51 стих. Вместе с письмом Евгения Онегина к Татьяне (60 строк) это точно соответствует числу Фибоначчи 55! Ритм онегинской строфы несет глубокую смысловую нагрузку. Четыре формообразующих элемента строфы — это, как правило, и четыре содержательных элемента: тема развитие кульминация афористическая концовка. Онегинская строфа была настолько оригинальным и индивидуальным изобретением Пушкина, что после Пушкина почти никто из поэтов не рисковал прикасаться к его детищу. Кульминацией главы является объяснение Евгения в любви к Татьяне -строка «Бледнеть и гаснуть … вот блаженство!» Эта строка делит восьмую главу на две части — в первой 477 строк, а во второй — 295 строк. Их отношение равно 1, 617! Тончайшее соответствие величине золотой пропорции!

7.10. Последовательность Фибоначчи в музыке

В композиции многих музыкальных произведений отмечается наличие некоторого «кульминационного взлета», высшей точки, причем такое построение характерно не только для произведения в целом, но и для его отдельных частей. Такая высшая точка крайне редко расположена в центре произведения или его композиционной части, обычно она смещена, ассиметрична. Изучая восьмитактные мелодии Бетховена, Шопена, Скрябина, советский музыковед Л. Мазель установил, что во многих из них вершина, или высшая точка, приходится на сильную долю шестого такта или на мелкую последнюю долю пятого такта, т.е. находится в точке золотого сечения.

Наиболее обширное исследование проявлений золотого сечения в музыке было предпринято Л. Сабанеевым. Им было изучено две тысячи произведений различных композиторов. По наблюдениям Л. Сабанеева, в музыкальных произведениях различных композиторов обычно констатирует не одно золотое сечение, а целая серия подобных сечений. В изученных 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений.

7.11.Числа Фибоначчи в психологии.

Числа Фибоначчи и Золотое сечение также используется и в психологии. Например, чтобы выяснить, как развивается механизм творчества, В.В. Клименко воспользовался математикой, а именно законами чисел Фибоначчи и пропорцией «золотого сечения» — законами природы и жизни человека.

Если развернуть в ряд числа Фибоначчи, то получим: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т.д. Отношение между числами Фибоначчи составляет 0,618. Развитие человека также происходит соответственно данной пропорции и подчиняется закону ее чисел, разделяя нашу жизнь на этапы с теми или иными доминантами механизма творчества.

Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет:

0 — начало отсчета — ребенок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;
1 — ребенок овладел ходьбой и осваивает ближайшее окружение;
2 — понимает речь и действует, пользуясь словесными указаниями;
3 — действует посредством слова, задает вопросы;
5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребенку охватить мир во всей его целостности;
8 — на передний план выходят чувства. Им служит воображение, а мышление силами своей критичности направлено на поддержку внутренней и внешней гармонии жизни;
13 — начинает работать механизм таланта, направленный на превращение приобретенного в процессе наследования материала, развивая свой собственный талант;
21 — механизм творчества приблизился к состоянию гармонии и делаются попытки выполнять талантливую работу;
34 — гармония мышления, чувств, воображения и психомоторики: рождается способность к гениальной работе;
55 — в этом возрасте, при условии сохраненной гармонии души и тела, человек готов стать творцом. И так далее…

ЗАКЛЮЧЕНИЕ

Изучив и проанализировав первоисточник Н.Н.Воробьева «Числа Фибоначчи», а так же дополнительную литературу я пришла к следующим выводам:

Все в природе подчиняется цикличности и закономерности, которую можно объяснить при помощи последовательности Фибоначчи и Золотого сечения.
Изучение свойств последовательности Фибоначчи позволяет применять ее для решения многих практических и теоретических задач в различных сферах деятельности человека
Многие свойства чисел Фибоначчи до конца не изучены.

Я убедилась, что природа творит красоту по законам математики. Эти законы действуют в независимости от нашего знания, от чьего-то желания принимать или не принимать их.
В своей работе, конечно же, невозможно до мельчайших подробностей изложить суть этого вопроса, но я постаралась отразить наиболее интересные и весомые аспекты. Я рассказала о Леонардо Пизанском и дала понятное определение и свойства чисел последовательности Фибоначчи; затем, на ярких примерах показала присутствие чисел Фибоначчи и Золотого сечения в разных сферах нашей жизни. Я еще раз убедилась в недосягаемой красоте математики, что Математика- не только «царица всех наук», но и и является одним из связующих звеньев науки, природы и искусства.

Я убеждена, что данная тема будет актуальна еще долгое время, и будут открываться все новые и новые факты, подтверждающие присутствие и влияние последовательности Фибоначчи на нашу жизнь.

Список литературы:

Н Висютинский Н.А. « Золотая пропорция». – М. : Молодая гвардия, 1990 г.

2. Я. Виленкин, Л. П. Шибасов, З. Ф. Шибасова «За страницами учебника математики»

3. Воробьев Н.Н. «Числа Фибоначчи», М: Наука 1978.

4. Интернет-ресурсы: Фибоначчи. [Электронный ресурс]. Числа Фибоначчи.

5. Кардемский Б.А., Математическая смекалка, М., Наука, 1984

6. Энциклопедический словарь юного математика, М., Педагогика, 1989

7. 3.http://www.stock.narod.ru/fibo.htm Гринбаум О.Н. Онегинская строфа.

Источник