Для двух наборов векторов, как найти ближайший вектор во втором наборе для каждого вектора в первом наборе?
Дано: Два множества векторов размерности D S1 представлен матрицей N*D и, соответственно, S2 представлен матрицей M*D
Я ищу элегантный способ получить для каждого вектора s1 в S1 ближайший сосед s2 в S2 и соответствующее расстояние.
Разумеется, простой подход состоял бы в том, чтобы иметь два цикла и получить
Тем не менее, должен быть более элегантный и эффективный способ сделать это.
Ага. С могущественной силой bsxfun и permute , с sum и тире reshape . Это будет первая часть, где вы вычисляете парные расстояния между точкой в S1 и другой точкой в S2 :
Последнее, что вам нужно сейчас, это определить ближайший вектор в S2 для каждого из S1 . Это можно сделать, используя min :
dist будет содержать наименьшее расстояние между точкой в S1 с точкой в S2 , а ind скажет вам, какая точка была.
Этот код выглядит очень пугающим, но пусть он разбивается на куски.
permute(S2, [3 2 1]) : Это берет матрицу S2 , которая является матрицей M x D и перемешивает размеры так, чтобы она становилась матрицей 1 x D x M . теперь почему мы хотели бы сделать что? Пусть переместится на следующую часть, и это будет иметь больше смысла.
bsxfun(@minus, S1. ) : bsxfun обозначает B Инара S Ingleton Е X Pansion FUN их. То, bsxfun делает bsxfun , состоит в том, что если у вас есть два входа, в которых один или оба входа имеют одноэлементный размер, или если любой из обоих входов имеет только одно измерение, которое имеет значение 1, каждый вход реплицируется в их размерах синглтона в соответствии с размером другой вход, а затем к этим входам прилагается элементарная операция для создания вашего вывода. В этом случае я хочу вычесть эти два вновь сформированных входа вместе.
Таким образом, учитывая, что S1 является N x D . или технически, это N x D x 1 , и учитывая, что S2 является M x D , который я переставлял так, чтобы он становился 1 x D x M , мы создадим новая матрица, длина которой равна N x D x M Первый вход будет дублировать себя как трехмерную матрицу, где каждый срез равен S1 и это N x D S2 теперь представляет собой трехмерную матрицу, но она представлена таким образом, что каждая строка в исходной матрице представляет собой срез в трехмерной матрице, где каждый срез состоит всего из одной строки. Это дублируется для N строк.
Теперь мы применим операцию @minus , и эффект этого заключается в том, что для каждого выходного среза i в этой новой матрице это дает вам разницу в компоненте между точкой i в S2 со всеми остальными точками в S1 . Например, для фрагмента №1 строка # 1 дает вам разницу между точками № 1 в S2 и точке №1 в S1 . Строка № 2 дает вам существенные различия между точкой № 1 в S2 и точке № 2 S1 и т.д.
sum((. ).^2, 2) : Мы хотим найти евклидово расстояние между одной точкой и другой точкой, поэтому мы суммируем эти расстояния по квадрату по каждому столбцу независимо друг от друга. В результате получается новая трехмерная матрица, в которой каждый срез содержит N значений, где имеется N расстояний для каждой из M точек. Например, первый срез даст вам расстояния от точки № 1 в S2 со всеми остальными точками в S1 .
out = reshape(. size(S1,1), size(S2,1)); : Теперь мы изменим это так, чтобы он стал матрицей M x N так что каждая пара строк и столбцов (i,j) дает вам расстояния между точками i в S1 и j в S2 , тем самым завершая вычисления.
Выполнение [dist,ind] = min(out, [], 2); определяет наименьшее расстояние между точкой в S1 с другими точками в S2 . dist даст вам наименьшие расстояния, в то время как ind скажет вам, какой именно вектор. Поэтому для каждого элемента в dist он дает наименьшее расстояние между точкой i в S1 и одной из S2 , а ind указывает вам, какой вектор был принадлежащим S2 .
Мы можем проверить, что это дает нам правильные результаты, используя ваш предложенный подход циклы через каждую пару точек и вычисление нормы. Позвольте создать S1 и S2 :
Более аккуратно отображается:
Используя подход цикла, у нас есть этот код:
Получим эту матрицу:
Аналогично, если мы запустили код, который я написал, мы также получаем:
Чтобы завершить процесс, найдем наименьшие расстояния и соответствующие векторы:
Поэтому для первого вектора в S1 ближайший вектор к этому в S2 был первым, с расстоянием 5.3852. Аналогично, второй вектор S1 , ближайший вектор в S2 был вторым, с расстоянием 6. Вы можете повторить это для других значений и увидеть, что это правильно.
Найти ближайший Вектор из списка векторов / Python
Если вам дан список из 10 векторов, называемых A, которые представляют разные группы. Тогда у вас есть временной ряд векторов v1, v2. vn, каждый из которых также является вектором. Мне было интересно,есть ли способ найти «ближайший» вектор в A для каждого v1, v2. vn если вы определяете некоторую метрику расстояния?
есть ли быстрый способ сделать это, кроме зацикливания и просто сравнения всех записей?
Edit: Нет, я не спрашиваю, Как сделать k-means или что-то вроде что.
3 ответов
можно использовать пространственное KDtree в scipy. Он использует быстрый алгоритм для определения следующих точек для векторов произвольной размерности.
редактировать: извините, если вы ищете произвольные метрики, дерево, подобное структуре, все еще может быть вариантом.
это устанавливает KDTree со всеми точками в A, что позволяет выполнять быстрый пространственный поиск внутри него. Такие запрос принимает вектор и возвращает ближайшего соседа в A для него:
первое возвращаемое значение-это расстояние до ближайшего соседа, а второе его положение в A, такое, что вы можете получить его, например, следующим образом:
Если вы определяете метрику, вы можете использовать ее в мин:
таким образом, некоторый пример кода:
Это возвращает переменные d и i. d сохраняет ближайшее расстояние I возвращает индекс, при котором это происходит
Как найти самый близкий Вектор от Положения по умолчанию?
В моем проекте C# у меня есть Множество Vector3. Теперь я хочу найти самый близкий Vector3 от положения камеры. Положение камеры — также объект Vector3. Как я могу сделать это?
Спасибо за вашу помощь!
Я думаю, что можно просто вычесть векторы друг от друга, чтобы получить длину Векторов (Величина)
Тогда можно вычислить, расстояние со взятием sqrt от полномочий координат как вышеупомянутый код делает.
extensionmethod, если вы хотели бы
Я не уверен, работает ли это, потому что я написал его в блокноте ++:)
Вы могли использовать Vector3. Расстояние (камера, otherObject) в петле, держат самый низкий объект расстояния во временной переменной т.е.
http://askdev.ru/q/nayti-blizhayshiy-vektor-iz-spiska-vektorov-python-438405/
http://answer-id.com/ru/55541969
Let’s say I have several points / vectors (in 2D to keep it simple, but could be of any dimension)
[x1, y1]
[x2, y2]
[x3, y3]
....
[xn, yn]
If I pick some point [x', y'], how do I find the closest point to it?
For a more concrete / practical example, imagine these are coordinates of houses. If I have thousands of houses in the database, I’d love to find the closest house to my house. Or more generally, I’d like to find the K closest houses to my house.
One brute-force way to do this is to cycle through each point and find its distance to your point/house and just pick the smallest one. But with thousands or even millions of data points it’s not efficient at all.
Is there a faster algorithm at all? Or am I stuck trying to check each point one at a time?
Методы приближенного поиска ближайших соседей
Время на прочтение
11 мин
Количество просмотров 43K
Довольно часто программисты и специалисты из области data science сталкиваются с задачей поиска похожих профилей пользователей или подбора схожей музыки. Решения могут сводиться к преобразованию объектов в векторную форму и поиску ближайших.
Мы тоже столкнулись с необходимостью поиска ближайших соседей в задаче распознавания лиц. Там мы формируем векторные представления лиц при помощи нейросети и ищем ближайшие векторы уже известных людей. Изначально для поиска мы выбрали Annoy, как хорошо известный и проверенный алгоритм, используемый в том числе в Spotify. Но быстро поняли, что с его аппетитами по памяти мы либо не вмещаемся в RAM, либо сильно теряем в точности. Это привело к небольшому исследованию. О результатах которого пойдет речь ниже.
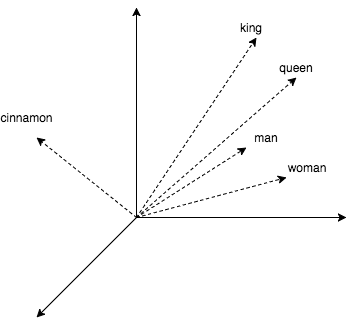
Чтобы разбавить теорию практикой, в статье будет немного кода, где мы ищем ближайших соседей для слов. Получим их векторные представления, используя популярный word2vec. Этот алгоритм выдает близкие векторы для семантически похожих слов. В word2vec CBOW векторные представления получаются как побочный продукт обучения небольшой нейросети, которая предсказывает слово по его окружению. Любопытно, что с векторами можно проворачивать арифметические операции наподобие king + (woman – man) = queen.
Посмотрим, как с этим работать в коде.
model = gensim.models.KeyedVectors.load_word2vec_format('./GoogleNews-vectors-negative300.bin', binary=True)
start = time.time()
pprint.pprint(model.wv.most_similar(positive=['king']))
print('time:', time.time() - start)
print('king + (woman - man) = ', model.wv.most_similar(positive=['woman', 'king'], negative=['man'])[0])
print('Japan + (Moscow - Russia) = ', model.wv.most_similar(positive=['Moscow', 'Japan'], negative=['Russia'])[0])Получаем:
[(u'kings', 0.7138045430183411),
(u'queen', 0.6510956883430481),
(u'monarch', 0.6413194537162781),
(u'crown_prince', 0.6204219460487366),
(u'prince', 0.6159993410110474),
(u'sultan', 0.5864823460578918),
(u'ruler', 0.5797567367553711),
(u'princes', 0.5646552443504333),
(u'Prince_Paras', 0.5432944297790527),
(u'throne', 0.5422105193138123)]
time: 0.236690998077
king + (woman - man) = (u'queen', 0.7118192911148071)
Japan + (Moscow - Russia) = (u'Tokyo', 0.8696038722991943)В примере выше использовалась библиотека для работы с текстом gensim и word2vec модель (1,5 Гбайт) от Google, которая насчитывает 3 миллиона слов и коротких фраз. В выводе кода видно, что к королю близки королевы, монархи и принцы. Также мы убедились, что арифметика с векторами работает. Однако четверть секунды на один запрос — не очень привлекательно, а ведь в gensim сравнительно хорошая реализация bruteforce-поиска (с подсчетом расстояний до всех известных объектов). Далее мы рассмотрим методы, позволяющие сократить это время в сотни раз лишь с небольшими потерями в точности.
Но начнем с простой идеи: попробуем сузить пространство поиска, разделив его плоскостью на две половины. А во время поиска будем считать расстояния только до тех соседей, которые оказались по ту же сторону от плоскости, что и запрос.
nbrs = NearestNeighbors(algorithm='brute', metric='cosine')
nbrs.fit(model.wv.syn0norm)
king_vec = model.wv['king'][np.newaxis, :]
# замерим скорость поиска сосдей к королю без разделения пространства и заодно выведем результат
start = time.time()
idxs = nbrs.kneighbors(king_vec, return_distance=False, n_neighbors=10)[0]
print('full search time:', time.time() - start)
print([model.wv.index2word[idx] for idx in idxs])
# выберем 2 случайных вектора и получем коэффициенты задающие плоскость между ними
vec1_idx = random.randint(0, model.wv.syn0norm.shape[0])
vec2_idx = random.randint(0, model.wv.syn0norm.shape[0])
plane = model.wv.syn0norm[vec1_idx] - model.wv.syn0norm[vec2_idx]
# в результате следующего умножения матрица-вектор, мы получим вектор.
# Знаки элементов этого вектора указывают с какой стороны разделяющей плоскости оказалось слово
scalar = model.wv.syn0norm.dot(np.transpose(plane))
# определим с какой стороны плоскости запрос и подготовим бинарную маску для выборки векторов по ту же сторону плоскости
if king_vec.dot(plane) > 0:
mask = scalar > 0
else:
mask = scalar < 0
print('elements in mask:', mask.sum())
half_nbrs = NearestNeighbors(algorithm='brute', metric='cosine')
half_nbrs.fit(model.wv.syn0norm[mask])
half_index2word = list(compress(model.wv.index2word, mask))
start = time.time()
idxs = half_nbrs.kneighbors(king_vec, return_distance=False, n_neighbors=10)[0]
print('half search time:', time.time() - start)
print([half_index2word[idx] for idx in idxs])Получаем:
full search time: 20.3163180351
[u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']
elements in mask: 1961204
half search time: 9.15824007988
[u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']Так мы сократили вычисления вдвое, потеряв в точности только рядом с плоскостью. В кое-каких алгоритмах, которые мы рассмотрим дальше, используются похожие трюки.
1. HNSW
В 2011 году был опубликован один из лучших алгоритмов поиска ближайших соседей Navigable Small World (NSW). В 2016-м появился его наследник Hierarchical Navigable Small World (HNSW).
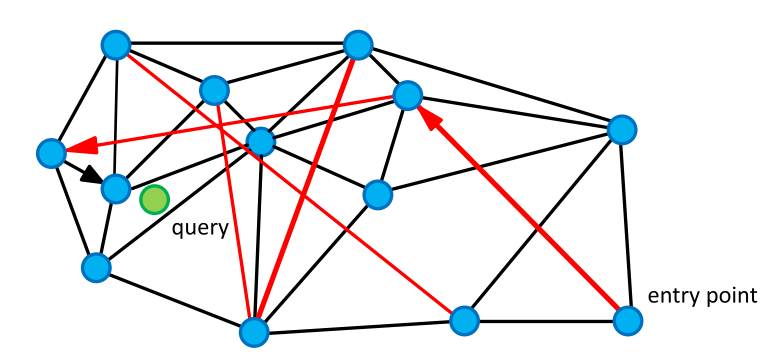
Начнем с родительского алгоритма NSW. Он основан на графе «мир тесен». Эти графы имеют любопытную и полезную нам особенность: пара вершин с большой вероятностью не смежна, но они достижимы за сравнительно небольшое число шагов ( в среднем). Такие графы встречаются довольно часто. К примеру, нейронные сети мозга, группы в социальных сетях и семантическая сеть WordNet — это графы SW. В нашем случае вершинами являются векторы, а ребра соединяют их с ближайшими. В графе также представлены ребра, соединяющие вершины на большом расстоянии.
Для поиска соседей мы обходим граф в поисках вершин с минимальным расстоянием до запроса. Начинаем со случайной вершины, считаем расстояние от непосещенных вершин «друзей» (вершин, соединенных с текущей ребром) до запроса и переходим в вершину с наименьшим расстоянием. Длинные ребра придают графу свойства тесного мира и позволяют быстро перемещаться в область близких к запросу объектов, а короткие — жадно искать ближайших соседей.
По мере обхода графа обновляем небольшой список ближайших соседей и останавливаемся, если на очередной итерации список не обновился.
Псевдокод
K-NNSearch(object q, integer: m, k)
1 TreeSet [object] tempRes, candidates, visitedSet, result
2 for (i←0; i < m; i++) do:
3 put random entry point in candidates
4 tempRes←null
5 repeat:
6 get element c closest from candidates to q
7 remove c from candidates
8 //check stop condition:
9 if c is further than k-th element from result
10 than break repeat
11 //update list of candidates:
12 for every element e from friends of c do:
13 if e is not in visitedSet than
14 add e to visitedSet, candidates, tempRes
15
16 end repeat
17 //aggregate the results:
18 add objects from tempRes to result
19 end for
20 return best k elements from resultindex = nmslib.init(space='cosinesimil', method='sw-graph')
nmslib.addDataPointBatch(index, np.arange(model.wv.syn0.shape[0], dtype=np.int32), model.wv.syn0)
index.createIndex({}, print_progress=True)
start = time.time()
items = nmslib.knnQuery(index, 10, king_vec.tolist())
print(time.time() - start)
print([model.wv.index2word[idx] for idx in items])Получаем:
0.000545024871826
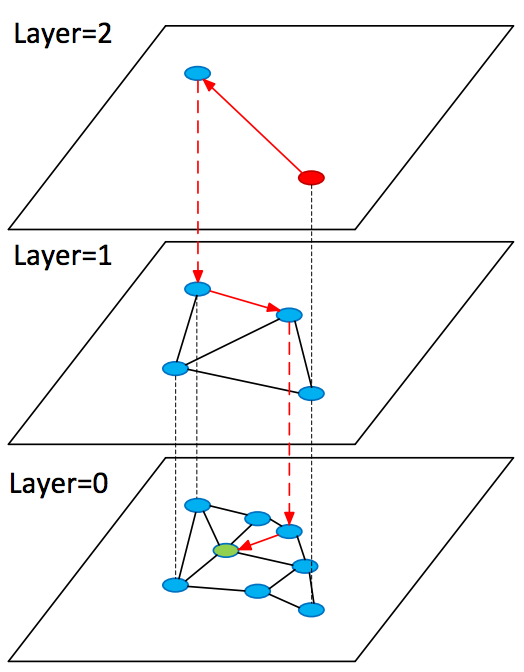
[u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'royal']Рассмотрим развитие описанной выше идеи в алгоритме Hierarchical Navigable Small World (HNSW). Он во многом схож с NSW, однако теперь мы имеем дело с иерархией графов: на нулевом слое представлены все объекты, а по мере увеличения слоя — все меньшая и меньшая их подвыборка. При этом все объекты на слое есть и на слое
.
При поиске старт происходит со случайной вершины в графе верхнего слоя, там мы быстро находим близкие к запросу вершины (кандидаты) и возобновляем поиск с них на предыдущем слое.
Псевдокод
SearchAtLayer (object q, Set[object] enterPoints, integer: M, ef, layer)
1 Set [object] visitedSet
2 priority_queue [object] candidates (closer - first), result (further - first)
3 candidates, visitedSet, result ← enterPoints
7
4 repeat:
5 object c =candidates.top()
6 candidates.pop()
7 //check stop condition:
8 if d(c,q)>d(result.top(),q) do:
9 break
10 //update list of candidates:
11 for_each object e from c.friends(layer) do:
12 if e is not in visitedSet do:
13 add e to visitedSet
14 if d(e, q)< d(result.top(),q) or result.size()<ef do:
15 add e to candidates, result
16 if result.size()>ef do:
17 result.pop()
18 return best k elements from result
K-NNSearch (object query, integer: ef)
1 Set [object] tempRes, enterPoints=[enterpoint]
2 for i=maxLayer downto 1 do:
3 tempRes=SearchAtLayer (query, enterPoints, M, 1, i)
4 enterPoints =closest elements from tempRes
5 tempRes=SearchAtLayer (query, enterPoints, M, ef, 0)
6 return best K of tempRes1.1. Pros & Cons
+ Алгоритм просто понять
+ Он показывает state-of-the-art результаты
+ Существует эффективная реализация в библиотеке nmslib
+ Небольшие дополнительные расходы памяти на хранение ребер графа
– Алгоритм не поддерживает сжатие векторных представлений, которое мы рассмотрим далее
index = nmslib.init(space='cosinesimil', method='hnsw')
nmslib.addDataPointBatch(index, np.arange(model.wv.syn0.shape[0], dtype=np.int32), model.wv.syn0)
index.createIndex({}, print_progress=True)
start = time.time()
items = nmslib.knnQuery(index, 10, king_vec.tolist())
print(time.time() - start)
print([model.wv.index2word[idx] for idx in items])Получаем:
0.000469923019409
[u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']2. FAISS
В марте 2017 года Facebook представила свое решение для ANN — библиотеку FAISS. Она объединяет множество методов и алгоритмов. В алгоритме, который мы рассмотрим ниже, расстояния до групп векторов будут приближаться расстоянием до опорной точки рядом с ними. Так мы можем выяснить расстояния от запроса до небольшого количества опорных точек, а затем полным перебором посчитать расстояния до векторов, принадлежащих опорной точке, которая ближе остальных к запросу. Разберем этот алгоритм по частям.
2.1. ADC — asymmetric distance computation
Рассмотрим подробнее следующую идею: расстояния до групп векторов можно приблизить расстояниями до опорных точек рядом с ними. Опорные точки делят пространство на области. Для поиска опорных точек в FAISS используется широко известный алгоритм кластеризации k-means, векторам сопоставляются полученные центроиды.
(0.1, 0.2) → 1 (0.5, -0.2) → 2 (0.1, 0.1) → 1 (0.6, -0.1) → 2
Векторы коллекции аппроксимируются своими центроидами , где
и
— множество центроидов. Тогда расстояние от запроса
до
может быть приближено
. Такой способ вычисления дистанции называют асимметричным. Простыми словами: мы разбили пространство на области и сказали, что расстояние от запроса до группы векторов, попавших в одну область, приблизительно равно расстоянию до центроида, образующего эту область.
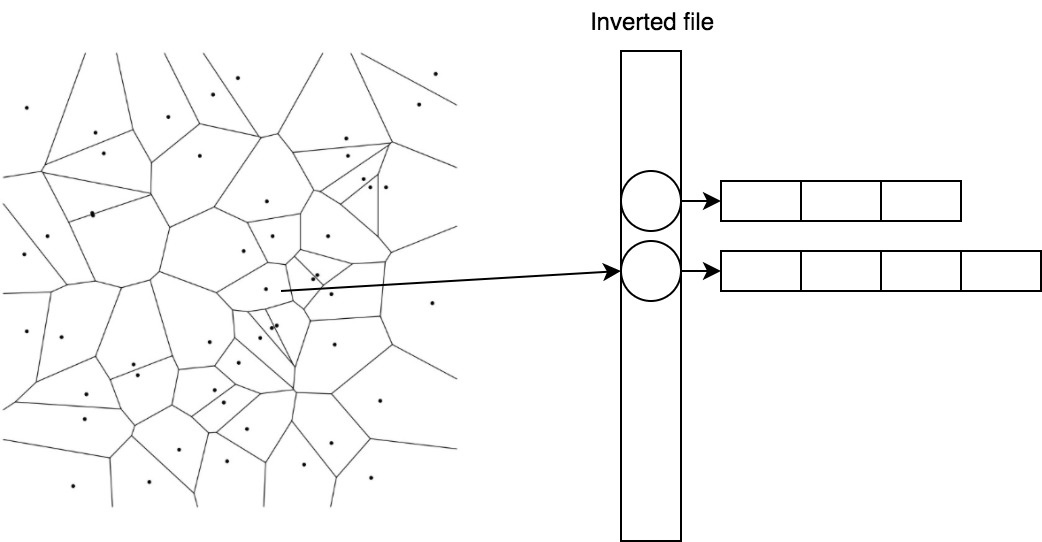
Эффективно хранить и быстро получать векторы, принадлежащие центроиду, помогает простой трюк под названием inverted file.
2.2. IVF — inverted file
В IVF мы инвертируем присвоение. Теперь центроидам сопоставляются списки векторов.
1 → [(0.1, 0.2), (0.1, 0.1)] 2 → [(0.5, -0.2), (0.6, -0.1)]
Так мы можем быстро находить кандидатов, посчитав расстояния до центроидов, а затем брать уже готовый список для ближайшего.
2.3. PQ — product quantizer
Последняя составляющая, которой мы коснемся в статье, называется product quantizer. Она обеспечивает сжатие векторов с потерями и применяется, когда векторные представления не влезают в память. Предположим, что наши векторы имеют размерность 128 и мы хотим кодировать их 64 битами (всего 0,5 бита на компоненту), тогда нам придется заниматься квантованием с количеством центроидов, равным . Это нетривиальная задача
, которая также требует огромной обучающей выборки.
Упростим задачу, разбив вектор на частей
, и по традиции найдем 256 центроидов для каждой из частей. То есть вектор можно переписать как набор индексов центроидов — например
, а занимает это хозяйство
байт.
Такой вид кодирования будем применять к остаточным векторам ,
, и тогда
2.4. Поиск
А теперь соберем все это в одной схеме.
Для запроса находим
ближайших центроидов, собираем списки векторов, соответствующих этим центроидам, и считаем до них расстояния, используя остаточные векторы, а затем выбираем
ближайших.
import faiss
index = faiss.index_factory(model.wv.syn0norm.shape[1], 'IVF16384,Flat')
index.verbose = True
train = model.wv.syn0norm[np.random.binomial(1, 1./3, size=model.wv.syn0norm.shape[0]).astype(bool)]
index.train(train)
index.add(model.wv.syn0norm)
index.nprobe = 100
start = time.time()
distances, items = index.search(king_vec, 10)
print(time.time() - start)
print([model.wv.index2word[idx] for idx in items[0]])Получаем:
0.0048999786377
[u'king', u'kings', u'queen', u'monarch', u'crown_prince', u'prince', u'sultan', u'ruler', u'princes', u'Prince_Paras']2.5. Pros & Cons
+ Поддержка сжатия
+ Малые накладные расходы на хранение центроидов
+ Возможность вычислений на GPU*
– В пять раз медленнее HNSW на CPU
* Мы не смогли быстро завести GPU-реализацию из коробки и решили не тратить время на это.
3. ANNOY
Идея деления пространства плоскостями хорошо реализована в Annoy. Алгоритм прекрасно описан автором в блоге, рекомендую прочесть, если хотите разобраться в деталях. Я попробую коротко изложить суть. В алгоритме мы рекурсивно делим пространство плоскостями, образуя бинарное дерево. В каждом узле дерева хранится вектор, задающий текущую плоскость. При поиске мы начинаем с корня и выбираем дочернюю ноду на основе положения запроса относительно плоскости. Так мы спускаемся к листовым элементам дерева, в которых хранятся векторы, оказавшиеся по одну сторону группы плоскостей (это небольшой кусочек пространства), они с высокой вероятностью окажутся искомыми ближайшими соседями. Посмотрим на достоинства и недостатки Annoy по сравнению с другими алгоритмами.
3.1. Pros & Cons
+ Алгоритм просто понять
– Он требует много памяти
– Проигрывает в скорости работы
4. Сравнение алгоритмов
У каждого из алгоритмов есть набор параметров, будь то максимальное количество друзей для вершины (в NSW, HNSW) или количество центроидов (в FAISS). Эти параметры влияют на объем потребляемой памяти, качество и скорость поиска. Автор Annoy реализовал тесты для группы ANN алгоритмов в репозитории ann-benchmarks на разных параметрах. В них оценивается точность поиска десяти ближайших соседей в датасетах, полученных при помощи алгоритмов GloVe и SIFT.
GloVe — это еще один способ получить векторные представления слов, он превосходит word2vec по всем показателям при обучении на корпусе одного размера. Датасет составлен из 1,2 миллиона векторных представлений слов, обученных на 2 миллиардах твитов. SIFT — старый алгоритм получения ключевых точек изображения и их векторных представлений, устойчивых к трансформациям. Он использовался для распознавания объектов, и важной частью этого распознавания был поиск похожих векторных представлений. Есть несколько вариаций датасетов, нас интересует SIFT 1M, содержащий миллион векторов.
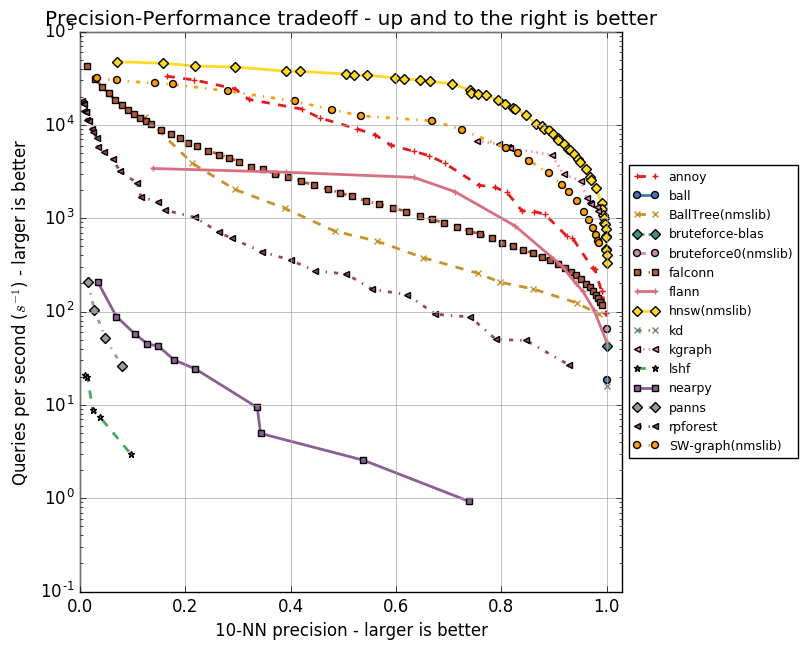
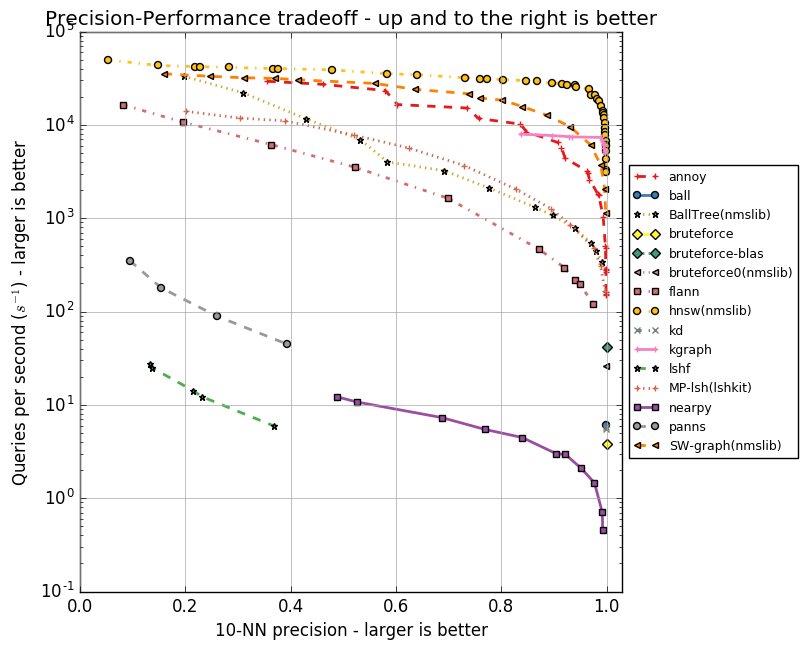
Ниже приведу графики, отражающие взаимосвязь скорости работы алгоритмов и точности поиска десяти ближайших соседей. Алгоритмы представлены группами точек, каждая из точек — это запуск теста на наборе параметров.
Видно, что HNSW уверенно лидирует. Однако на графиках нет FAISS. Facebook самостоятельно сравнил HNSW и FAISS в разных конфигурациях, результаты приведены в таблице.
| Method | search time | 1-R@1 | index size | index build time |
|---|---|---|---|---|
| Flat-CPU | 9.100 s | 1.0000 | 512 MB | 0 s |
| nmslib (hnsw) | 0.081 s | 0.8195 | 512 + 796 MB | 173 s |
| IVF16384,Flat | 0.538 s | 0.8980 | 512 + 8 MB | 240 s |
| IVF16384,Flat (Titan X) | 0.059 s | 0.8145 | 512 + 8 MB | 5 s |
| Flat-GPU (Titan X) | 0.753 s | 0.9935 | 512 MB | 0 s |
В таблице методы FAISS без сжатия, в частности IVF16384,Flat. Значит, используется IVFADC c 16 384 центроидами. Расходы памяти указаны для случая с миллионом векторов размерности 128 в float32. HNSW в пять раз быстрее при вычислениях на CPU, но на хранение ребер графа () требуется больше памяти, чем на центроиды (
).
5. Заключение
Мы рассмотрели ряд алгоритмов, применяемых для быстрого поиска ближайших соседей. Annoy проиграл и по памяти, и по скорости работы, но идея хороша и может помочь в решении смежных задач. Например, удобный для чистки датасета алгоритм поиска аномалий isolation forest очень похож по своей задумке. FAISS — отличное решение при ограничениях по памяти, с ним вполне можно уложить миллиард векторных представлений в 60 Гбайт RAM, используя IVF16384, PQ64. Однако если память не узкое место, то стоит выбрать HNSW.
P. S. Самыми интересными оказались публикации об алгоритмах в FAISS. Там, к примеру, можно прочесть об оптимизации под GPU, об улучшенном методе квантования (Optimized Product Quantization) и о более хитром способе построении индекса (inverted multi-index).
P. P. S. Для себя мы выбрали HNSW.
6. Литература
- Approximate Nearest Neighbor Search Small World Approach
- Approximate nearest neighbor algorithm based on navigable small world graphs
- Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs
- Product quantization for nearest neighbor search
- SEARCHING IN ONE BILLION VECTORS: RE-RANK WITH SOURCE CODING
- GloVe: Global Vectors for Word Representation
- Object Recognition from Local Scale-Invariant Features
- Isolation Forest
- Billion-scale similarity search with GPUs
- Optimized Product Quantization
- The inverted multi-index
Найти ближайший Вектор из списка векторов / Python
Если вам дан список из 10 векторов, называемых A, которые представляют разные группы. Тогда у вас есть временной ряд векторов v1, v2,…, vn, каждый из которых также является вектором. Мне было интересно,есть ли способ найти «ближайший» вектор в A для каждого v1, v2,…, vn если вы определяете некоторую метрику расстояния?
есть ли быстрый способ сделать это, кроме зацикливания и просто сравнения всех записей?
Edit: Нет, я не спрашиваю, Как сделать k-means или что-то вроде что.
3 ответов
можно использовать пространственное KDtree в scipy. Он использует быстрый алгоритм для определения следующих точек для векторов произвольной размерности.
редактировать: извините, если вы ищете произвольные метрики, дерево, подобное структуре, все еще может быть вариантом.
вот пример:
>>> from scipy import spatial
>>> A = [[0,1,2,3,4], [4,3,2,1,0], [2,5,3,7,1], [1,0,1,0,1]]
>>> tree = spatial.KDTree(A)
это устанавливает KDTree со всеми точками в A, что позволяет выполнять быстрый пространственный поиск внутри него.
Такие запрос принимает вектор и возвращает ближайшего соседа в A для него:
>>> tree.query([0.5,0.5,0.5,0.5,0.5])
(1.1180339887498949, 3)
первое возвращаемое значение-это расстояние до ближайшего соседа, а второе его положение в A, такое, что вы можете получить его, например, следующим образом:
>>> A[ tree.query([0.5,0.5,0.5,0.5,0.5])[1] ]
[1, 0, 1, 0, 1]
Если вы определяете метрику, вы можете использовать ее в мин:
closest = min(A, key=distance)
таким образом, некоторый пример кода:
# build a KD-tree to compare to some array of vectors 'centall'
tree = scipy.spatial.KDTree(centall)
print 'shape of tree is ', tree.data.shape
# loop through different regions and identify any clusters that belong to a different region
[d1, i1] = tree.query(group1)
[d2, i2] = tree.query(group2)
Это возвращает переменные d и i.
d сохраняет ближайшее расстояние
I возвращает индекс, при котором это происходит
надеюсь, что это помогает.
Вы можете использовать пространственный KDtree в scipy. Он использует быстрый алгоритм дерева для определения близких точек для векторов произвольной размерности.
Изменить: извините, если вы ищете произвольные показатели расстояния, структура, подобная дереву, все еще может быть вариантом.
Вот пример:
>>> from scipy import spatial
>>> A = [[0,1,2,3,4], [4,3,2,1,0], [2,5,3,7,1], [1,0,1,0,1]]
>>> tree = spatial.KDTree(A)
Это устанавливает KDTree со всеми точками в A, что позволяет выполнять быстрые пространственные поиски в нем.
Такой запрос принимает вектор и возвращает ближайшего соседа в A:
>>> tree.query([0.5,0.5,0.5,0.5,0.5])
(1.1180339887498949, 3)
Первое возвращаемое значение — это расстояние ближайшего соседа, а второе — его положение в A, так что вы можете получить его, например, следующим образом:
>>> A[ tree.query([0.5,0.5,0.5,0.5,0.5])[1] ]
[1, 0, 1, 0, 1]